Scaling Theory of a Polymer Ejecting from a Cavity into a Semi-Space
Abstract
:1. Introduction
2. Scaling Theory of Ejection Dynamics
3. Simulation Model and Setup
4. Results
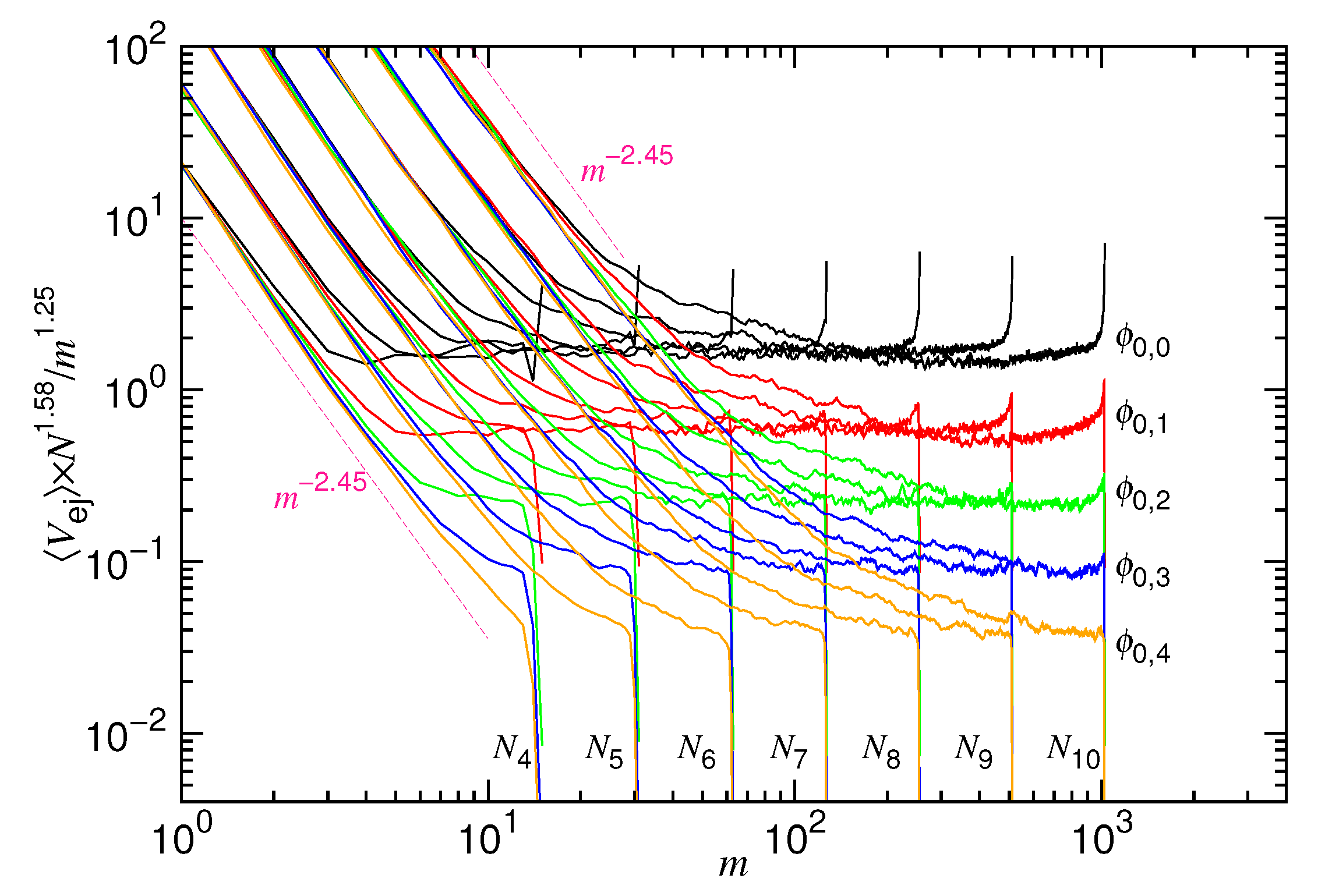
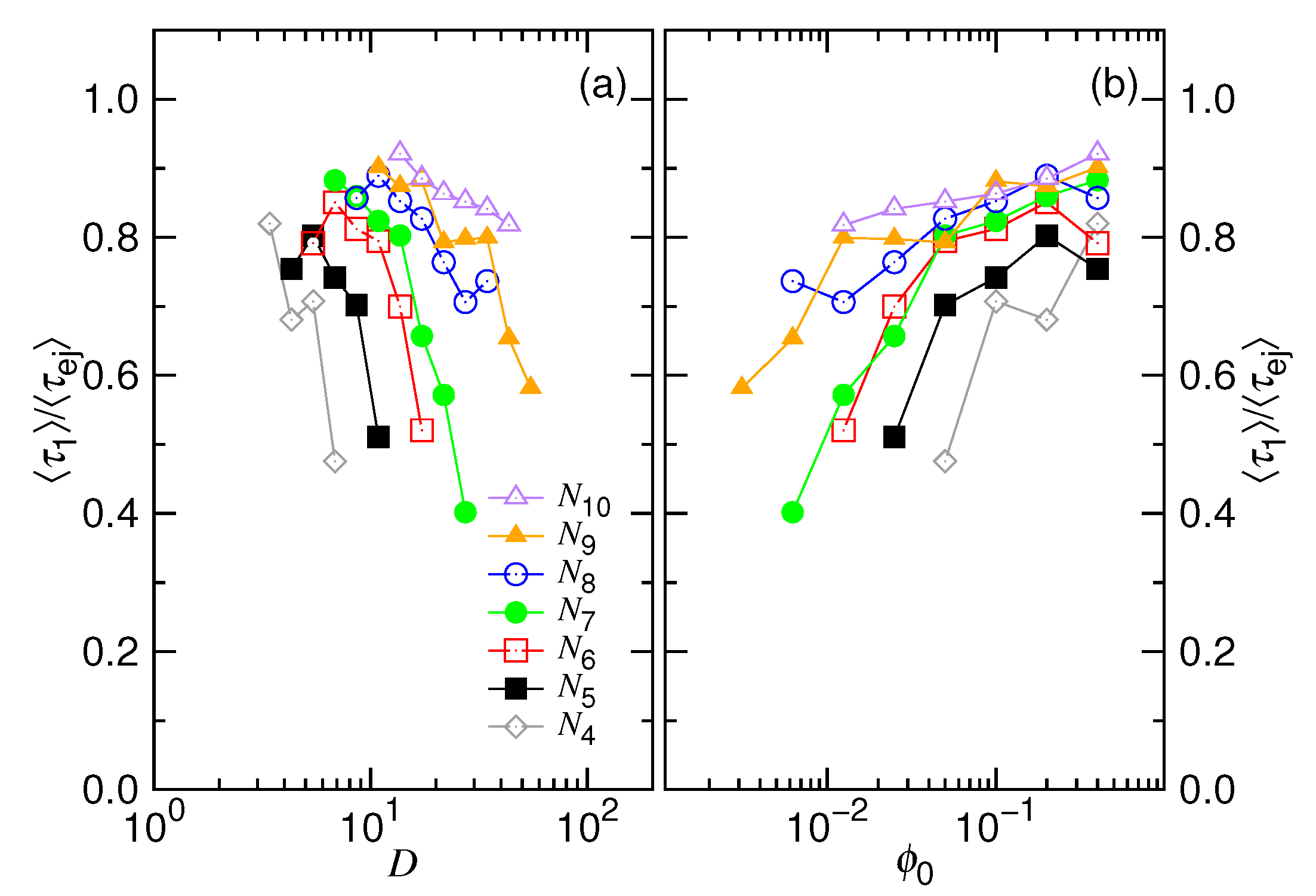
4.1. Ejection Velocity
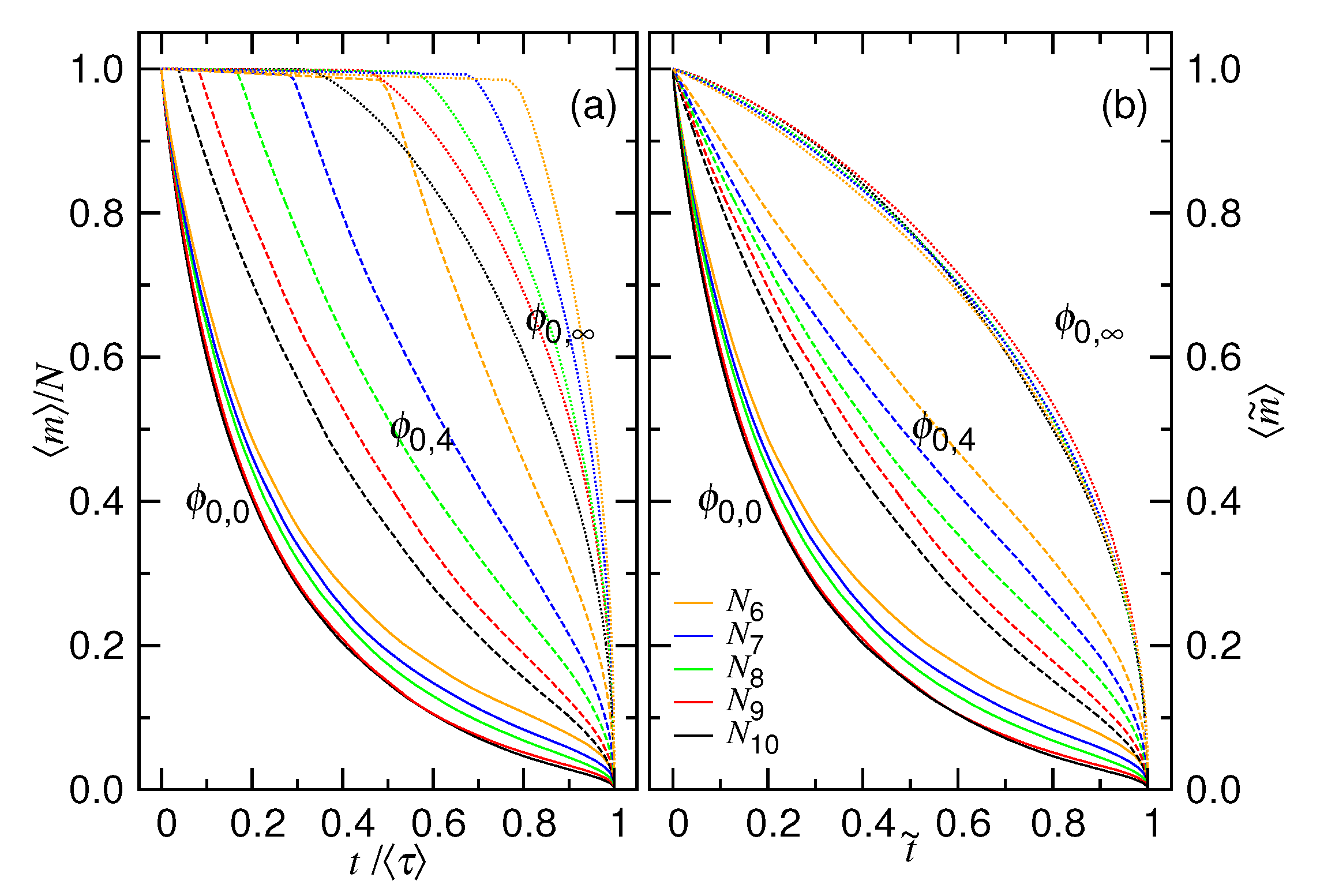
4.2. Time Variation of the Number of Monomers in the Cavity
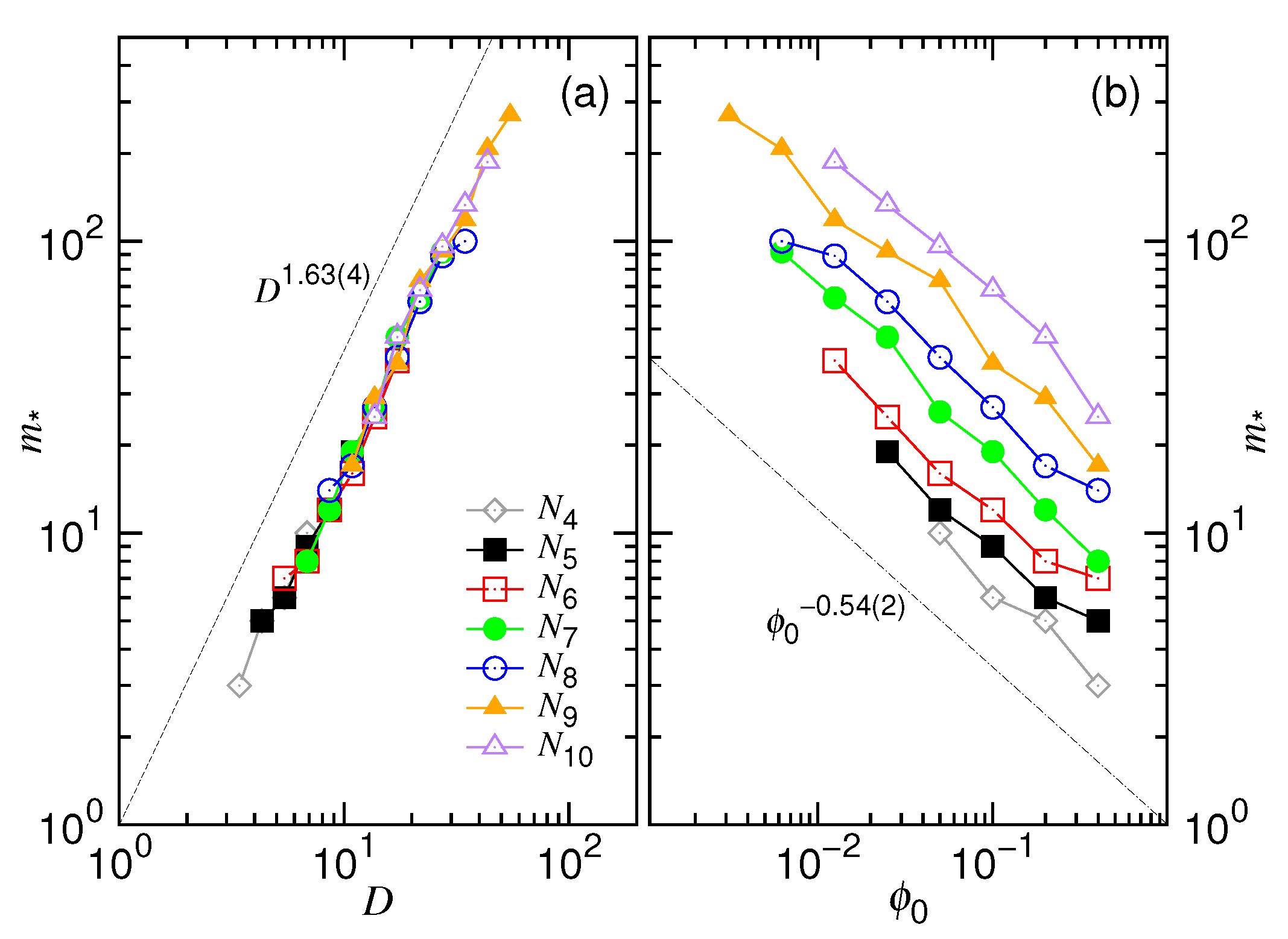
4.3. Ejection Time and Nucleation Time
5. Discussions and Conclusions
Supplementary Materials
Funding
Conflicts of Interest
References
- Molineux, I.J.; Panja, D. Popping the cork: Mechanisms of phage genome ejection. Nat. Rev. Microbiol. 2013, 11, 194–204. [Google Scholar] [CrossRef]
- Purohit, P.K.; Inamdar, M.M.; Grayson, P.D.; Squires, T.M.; Kondev, J.; Phillips, R. Forces during Bacteriophage DNA Packaging and Ejection. Biophys. J. 2005, 88, 851–866. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Skanata, M.M.; Stein, D. Entropic cages for trapping DNA near a nanopore. Nat. Commun. 2015, 6, 6222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, X.; Zimny, P.; Zhang, Y.; Rana, A.; Nagel, R.; Reisner, W.; Dunbar, W.B. Flossing DNA in a Dual Nanopore Device. Small 2019, 16, 1905379. [Google Scholar] [CrossRef] [PubMed]
- Cadinu, P.; Campolo, G.; Pud, S.; Yang, W.; Edel, J.B.; Dekker, C.; Ivanov, A.P. Double Barrel Nanopores as a New Tool for Controlling Single-Molecule Transport. Nano Lett. 2018, 18, 2738–2745. [Google Scholar] [CrossRef] [PubMed]
- Bhaskar, S.; Lim, S. Engineering protein nanocages as carriers for biomedical applications. NPG Asia Mater. 2017, 9, e371. [Google Scholar] [CrossRef]
- Zárybnický, V. Mechanism of T-even DNA ejection. J. Theor. Biol. 1969, 22, 33–42. [Google Scholar] [CrossRef]
- Gabashvili, I.S.; Grosberg, A.Y. Dynamics of Double Stranded DNA Reptation From Bacteriophage. J. Biomol. Struct. Dyn. 1992, 9, 911–920. [Google Scholar] [CrossRef]
- Tzlil, S.; Kindt, J.T.; Gelbart, W.M.; Ben-Shaul, A. Forces and Pressures in DNA Packaging and Release from Viral Capsids. Biophys. J. 2003, 84, 1616–1627. [Google Scholar] [CrossRef] [Green Version]
- Inamdar, M.M.; Gelbart, W.M.; Phillips, R. Dynamics of DNA Ejection from Bacteriophage. Biophys. J. 2006, 91, 411–420. [Google Scholar] [CrossRef] [Green Version]
- Grayson, P.; Evilevitch, A.; Inamdar, M.M.; Purohit, P.K.; Gelbart, W.M.; Knobler, C.M.; Phillips, R. The effect of genome length on ejection forces in bacteriophage lambda. Virology 2006, 348, 430–436. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Löf, D.; Schillén, K.; Jönsson, B.; Evilevitch, A. Forces Controlling the Rate of DNA Ejection from Phage λ. J. Mol. Biol. 2007, 368, 55–65. [Google Scholar] [CrossRef] [PubMed]
- São-José, C.; de Frutos, M.; Raspaud, E.; Santos, M.A.; Tavares, P. Pressure Built by DNA Packing Inside Virions: Enough to Drive DNA Ejection in Vitro, Largely Insufficient for Delivery into the Bacterial Cytoplasm. J. Mol. Biol. 2007, 374, 346–355. [Google Scholar] [CrossRef] [PubMed]
- Evilevitch, A.; Lavelle, L.; Knobler, C.M.; Raspaud, E.; Gelbart, W.M. Osmotic pressure inhibition of DNA ejection from phage. Proc. Natl. Acad. Sci. USA 2003, 100, 9292–9295. [Google Scholar] [CrossRef] [Green Version]
- Molineux, I.J. Fifty-three years since Hershey and Chase; much ado about pressure but which pressure is it? Virology 2006, 344, 221–229. [Google Scholar] [CrossRef] [Green Version]
- Grayson, P.; Molineux, I.J. Is phage DNA ‘injected’ into cells—biologists and physicists can agree. Curr. Opin. Microbiol. 2007, 10, 401–409. [Google Scholar] [CrossRef] [Green Version]
- Panja, D.; Molineux, I.J. Dynamics of bacteriophage genome ejectionin vitroandin vivo. Phys. Biol. 2010, 7, 045006. [Google Scholar] [CrossRef] [Green Version]
- Lemay, S.G.; Panja, D.; Molineux, I.J. Role of osmotic and hydrostatic pressures in bacteriophage genome ejection. Phys. Rev. E 2013, 87, 022714. [Google Scholar] [CrossRef] [Green Version]
- Muthukumar, M. Polymer translocation through a hole. J. Chem. Phys. 1999, 111, 10371. [Google Scholar] [CrossRef]
- Muthukumar, M. Translocation of a Confined Polymer through a Hole. Phys. Rev. Lett. 2001, 86, 3188–3191. [Google Scholar] [CrossRef]
- Muthukumar, M. Polymer escape through a nanopore. J. Chem. Phys. 2003, 118, 5174–5184. [Google Scholar] [CrossRef]
- Muthukumar, M. Polymer Translocation; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar] [CrossRef]
- Kantor, Y.; Kardar, M. Anomalous dynamics of forced translocation. Phys. Rev. E 2004, 69, 021806. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cacciuto, A.; Luijten, E. Self-Avoiding Flexible Polymers under Spherical Confinement. Nano Lett. 2006, 6, 901–905. [Google Scholar] [CrossRef] [PubMed]
- Cacciuto, A.; Luijten, E. Confinement-driven translocation of a flexible polymer. Phys. Rev. Lett. 2006, 96, 238104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sakaue, T.; Yoshinaga, N. Dynamics of Polymer Decompression: Expansion, Unfolding, and Ejection. Phys. Rev. Lett. 2009, 102, 148302. [Google Scholar] [CrossRef] [Green Version]
- Milchev, A. Single-polymer dynamics under constraints: Scaling theory and computer experiment. J. Phys. Condens. Matter 2011, 23, 103101. [Google Scholar] [CrossRef]
- Palyulin, V.V.; Ala-Nissila, T.; Metzler, R. Polymer translocation: The first two decades and the recent diversification. Soft Matter 2014, 10, 9016. [Google Scholar] [CrossRef] [Green Version]
- Buyukdagli, S.; Sarabadani, J.; Ala-Nissila, T. Theoretical Modeling of Polymer Translocation: From the Electrohydrodynamics of Short Polymers to the Fluctuating Long Polymers. Polymers 2019, 11, 118. [Google Scholar] [CrossRef] [Green Version]
- Marenduzzo, D.; Micheletti, C.; Orlandini, E.; Sumners, D.W. Topological friction strongly affects viral DNA ejection. Proc. Natl. Acad. Sci. USA 2013, 110, 20081–20086. [Google Scholar] [CrossRef] [Green Version]
- Park, C.B.; Kwon, S.; Sung, B.J. The effects of a knot and its conformational relaxation on the ejection of a single polymer chain from confinement. J. Chem. Phys. 2019, 151, 054901. [Google Scholar] [CrossRef]
- Ali, I.; Marenduzzo, D.; Yeomans, J.M. Polymer Packaging and Ejection in Viral Capsids: Shape Matters. Phys. Rev. Lett. 2006, 96, 208102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Polson, J.M. Polymer translocation into and out of an ellipsoidal cavity. J. Chem. Phys. 2015, 142, 174903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Polson, J.M.; Heckbert, D.R. Polymer translocation into cavities: Effects of confinement geometry, crowding, and bending rigidity on the free energy. Phys. Rev. E 2019, 100, 012504. [Google Scholar] [CrossRef] [PubMed]
- Sean, D.; Slater, G.W. Highly driven polymer translocation from a cylindrical cavity with a finite length. J. Chem. Phys. 2017, 146, 054903. [Google Scholar] [CrossRef] [PubMed]
- Lawati, A.A.; Ali, I.; Barwani, M.A. Effect of Temperature and Capsid Tail on the Packing and Ejection of Viral DNA. PLoS ONE 2013, 8, e52958. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matsuyama, A.; Yano, M. Ejection Dynamics of a Semiflexible DNA Polymer from a Capsid. J. Phys. Soc. Jpn. 2012, 81, 034802. [Google Scholar] [CrossRef]
- Zhang, K.; Luo, K. Polymer translocation into a confined space: Influence of the chain stiffness and the shape of the confinement. J. Chem. Phys. 2014, 140, 094902. [Google Scholar] [CrossRef]
- Linna, R.P.; Suhonen, P.M.; Piili, J. Rigidity-induced scale invariance in polymer ejection from capsid. Phys. Rev. E 2017, 96, 052402. [Google Scholar] [CrossRef] [Green Version]
- Ali, I.; Marenduzzo, D.; Yeomans, J. Ejection Dynamics of Polymeric Chains from Viral Capsids: Effect of Solvent Quality. Biophys. J. 2008, 94, 4159–4164. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.; Luo, K. Effects of the internal friction and the solvent quality on the dynamics of a polymer chain closure. J. Chem. Phys. 2015, 142, 124901. [Google Scholar] [CrossRef]
- Piili, J.; Suhonen, P.M.; Linna, R.P. Uniform description of polymer ejection dynamics from capsid with and without hydrodynamics. Phys. Rev. E 2017, 95, 052418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ali, I.; Marenduzzo, D. Influence of ions on genome packaging and ejection: A molecular dynamics study. J. Chem. Phys. 2011, 135, 095101. [Google Scholar] [CrossRef] [PubMed]
- de Haan, H.W.; Slater, G.W. Mapping the variation of the translocation α scaling exponent with nanopore width. Phys. Rev. E 2010, 81, 051802. [Google Scholar] [CrossRef] [PubMed]
- Linna, R.P.; Moisio, J.E.; Suhonen, P.M.; Kaski, K. Dynamics of polymer ejection from capsid. Phys. Rev. E 2014, 89, 052702. [Google Scholar] [CrossRef] [Green Version]
- Hamidabad, M.N.; Abdolvahab, R.H. Translocation through a narrow pore under a pulling force. Sci. Rep. 2019, 9, 17885. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.C.; Hsiao, P.Y. Scaling Behaviors of a Polymer Ejected from a Cavity through a Small Pore. Phys. Rev. Lett. 2019, 123, 267801. [Google Scholar] [CrossRef] [Green Version]
- Yeh, J.W.; Taloni, A.; Chen, Y.L.; Chou, C.F. Entropy-Driven Single Molecule Tug-of-War of DNA at Micro-Nanofluidic Interfaces. Nano Lett. 2012, 12, 1597–1602. [Google Scholar] [CrossRef]
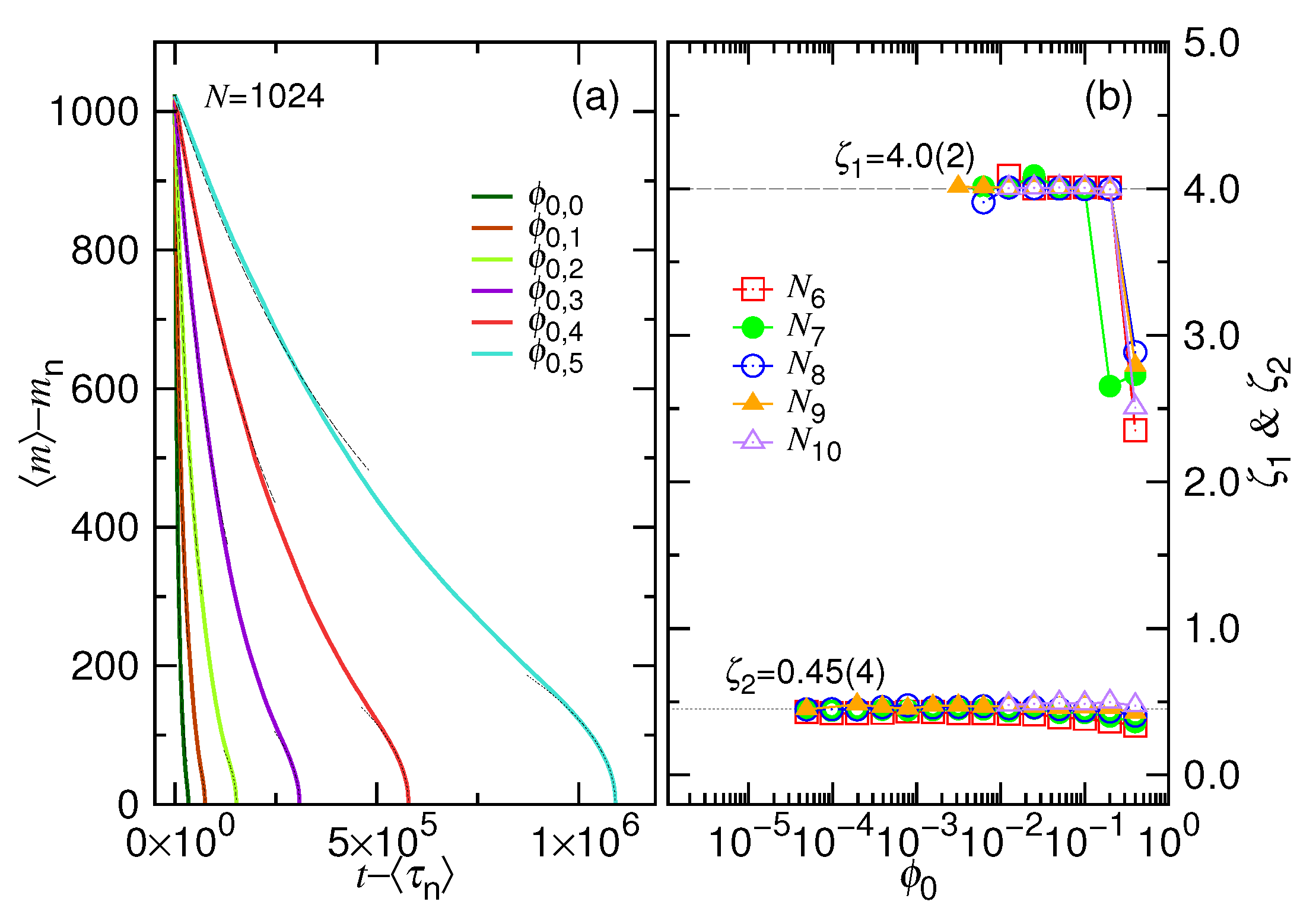
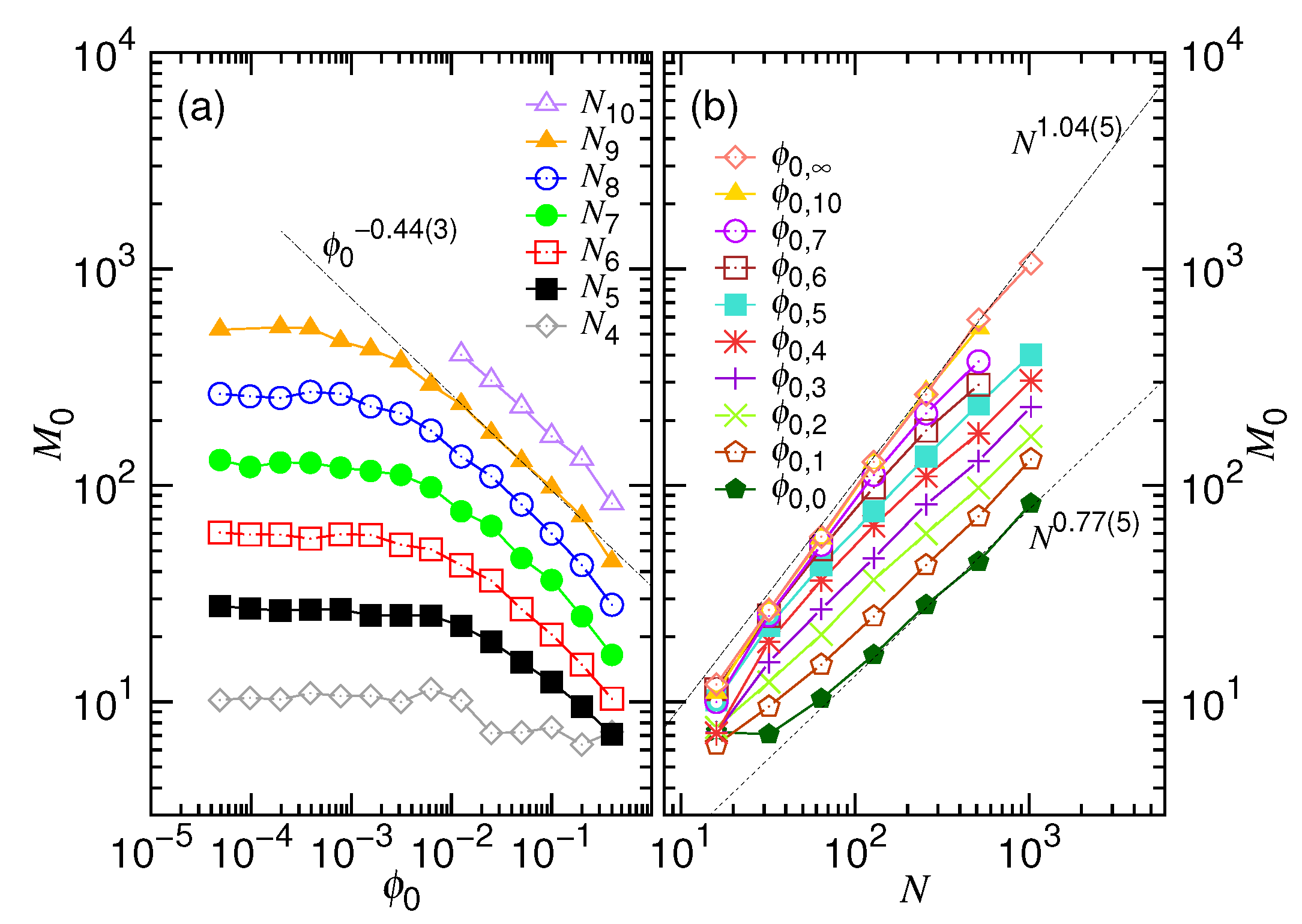
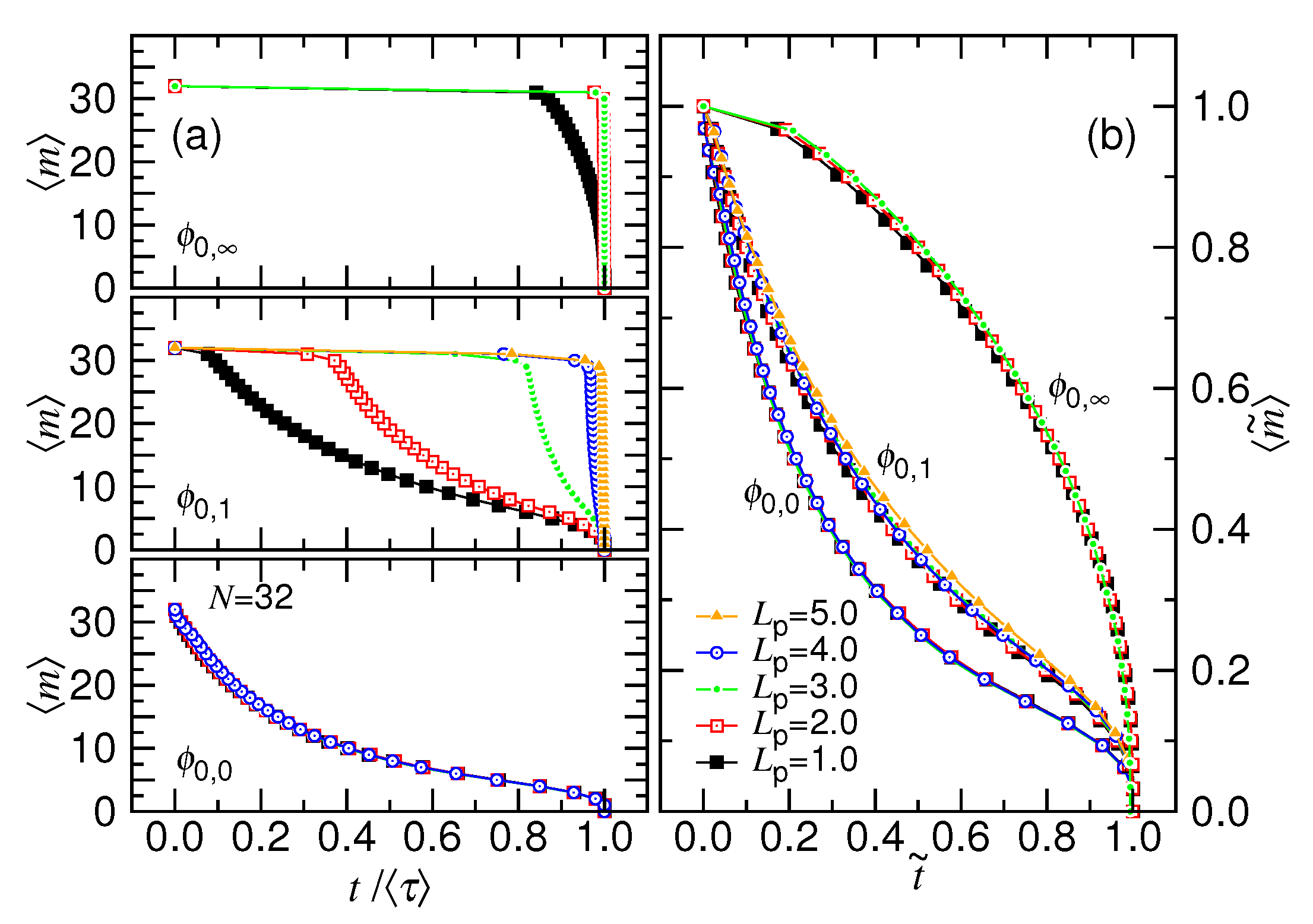
- In this study, N*, D*, ϕ* are used to denote the critical values for the chain length, the cavity diameter, and the initial volume fraction, respectively (refer to Table 1 too). Beyond N* (or similarly, beyond ϕ* or below D*), the process is proceeded via the confined and then the non-confined stage. Below N* (or below ϕ* or beyond D*), the system experiences only the latter stage. N* takes a scaling form of (D/σ)1/ν and is, in fact, identical to m*. However, a subtle difference exists in the meaning. The m* is the demarcation number in a process which separates the confined and the non-confined stage. To have the two stages occurred, N must be greater than N*. The system is at the confined stage when N ≥ m > m*, and evolves to be at the non-confined stage as m becomes smaller than m*. In brief, the notation of m* is used to denote the number m which demarcates the two stages in a process, while N* is the critical chain length to judge whether a process is proceeded via the two stages or not.
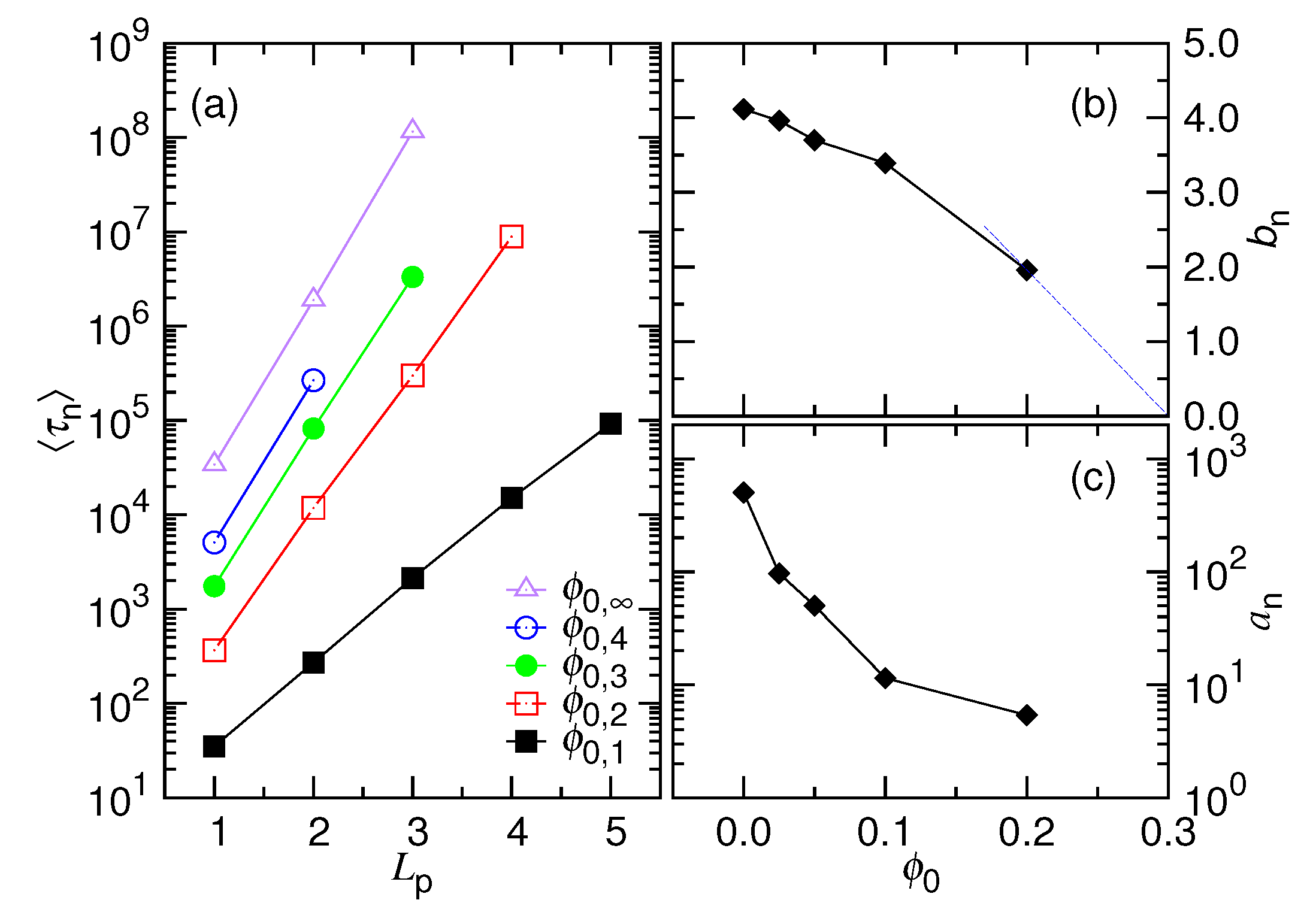
- In a scaling analysis, people pay attention to the dominated term of scaling and do not take much care about the prefactor. However, when the two scaling times, τ1 and τ2, are added together to be the ejection time τej in Table 1, we have to place back the ignored prefactors A1 and A2, because the two prefactors give the necessary weightings for the two terms. Eq. 8 is also a sum of the two velocity scalings. With the same consideration, we put back the prefactors, which are 1/A1 and 1/A2, respectively. The relative size of A1 and A2 can be estimated from the simulations. The choice, A1 = 0.04 and A2 = 1.0, produces the prediction curves in Figure 2 similar to the simulation ones in Figure 4.
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1. [Google Scholar] [CrossRef] [Green Version]
- Suppose that a polymer takes the conformation of a yarn ball of radius Rm and consider the following two cases: (1) the polymer diffuses across a wall through a pore of length Lp and (2) the polymer diffuses in a bulk solution over the same distance. The required time is longer for the previous case due to the restriction of the space. The factor for the increase of time can be estimated by calculating the ratio of the number of monomers transported in the two cases, which is equal to the cap volume over the pore volume . For a short pore length, the factor is about and scales as m1/df. This effect of space restriction is taken into account by involving the factor in the friction coefficient. At the confined stage, the fractal dimension of chain is 3, which gives x1 = 1/3. At the non-confined stage, df = 1/ν. It contributes a scaling mν to the friction coefficient for the nucleation time.
- Ford, I.J. Statistical mechanics of nucleation: A review. Proc. Inst. Mech. Eng. C 2004, 218, 883–899. [Google Scholar] [CrossRef]
- Kalikmanov, V. Nucleation Theory; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Kramers, H. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica 1940, 7, 284–304. [Google Scholar] [CrossRef]
- Hänggi, P.; Talkner, P.; Borkovec, M. Reaction-rate theory: Fifty years after Kramers. Rev. Mod. Phys. 1990, 62, 251–341. [Google Scholar] [CrossRef]
- Dion, M.B.; Oechslin, F.; Moineau, S. Phage diversity, genomics and phylogeny. Nat. Rev. Microbiol. 2020, 18, 125–138. [Google Scholar] [CrossRef] [PubMed]
- Doi, M. Onsager’s variational principle in soft matter. J. Phys. Condens. Matter 2011, 23, 284118. [Google Scholar] [CrossRef]
- Doi, M. Soft Matter Physics; Oxford University Press: Oxford, UK, 2013. [Google Scholar] [CrossRef]
- Rossmann, M.G. Structure of viruses: A short history. Q. Rev. Biophys. 2013, 46, 133–180. [Google Scholar] [CrossRef]
- Twarock, R.; Luque, A. Structural puzzles in virology solved with an overarching icosahedral design principle. Nat. Commun. 2019, 10, 4414. [Google Scholar] [CrossRef] [Green Version]
- Luque, A.; Reguera, D. The Structure of Elongated Viral Capsids. Biophys. J. 2010, 98, 2993–3003. [Google Scholar] [CrossRef] [Green Version]
- Rossmann, M.G.; Rao, V.B. (Eds.) Viral Molecular Machines; Springer: Boston, MA, USA, 2012. [Google Scholar] [CrossRef]
- Wan, W.; Kolesnikova, L.; Clarke, M.; Koehler, A.; Noda, T.; Becker, S.; Briggs, J.A.G. Structure and assembly of the Ebola virus nucleocapsid. Nature 2017, 551, 394–397. [Google Scholar] [CrossRef] [Green Version]
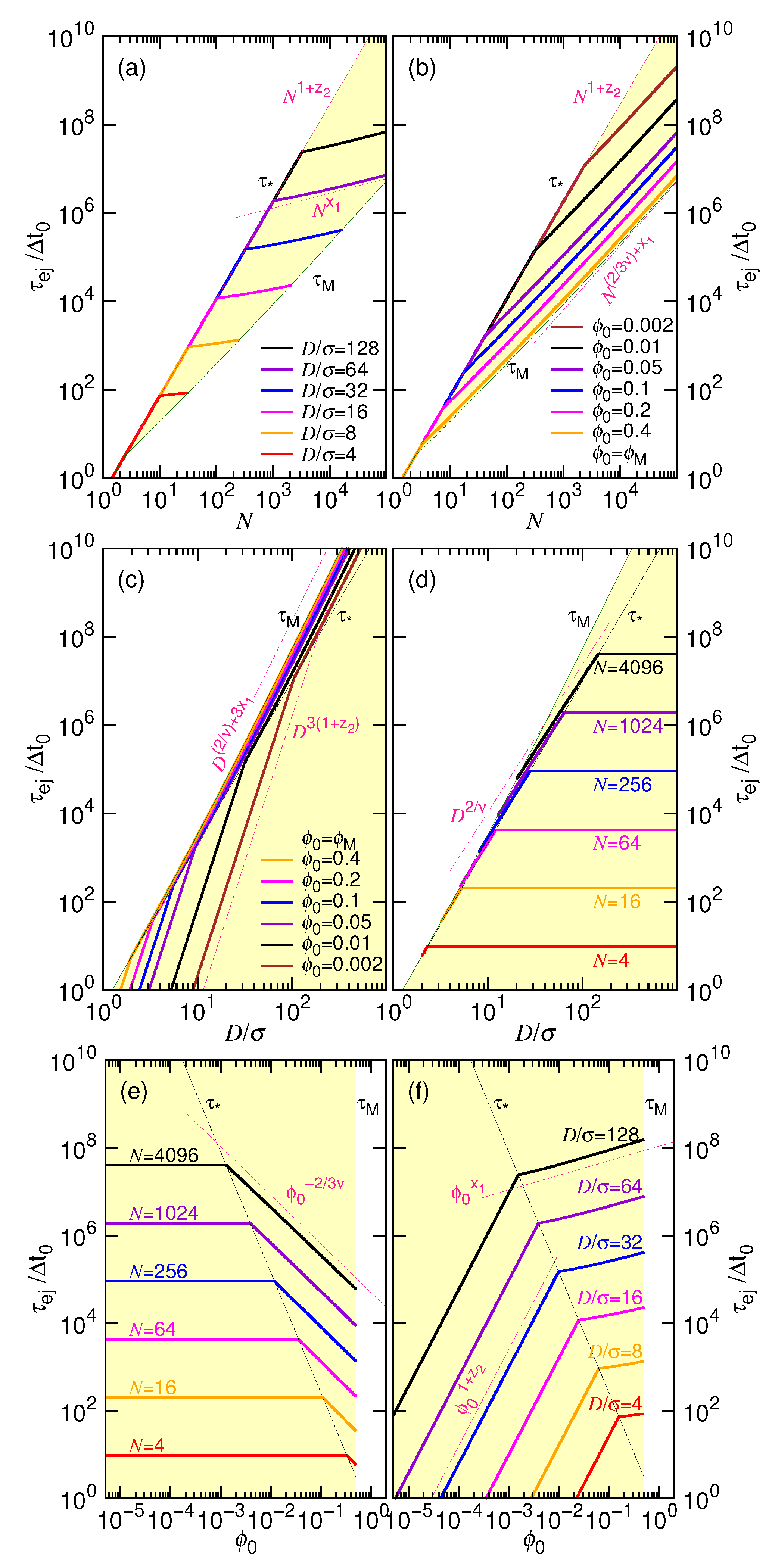




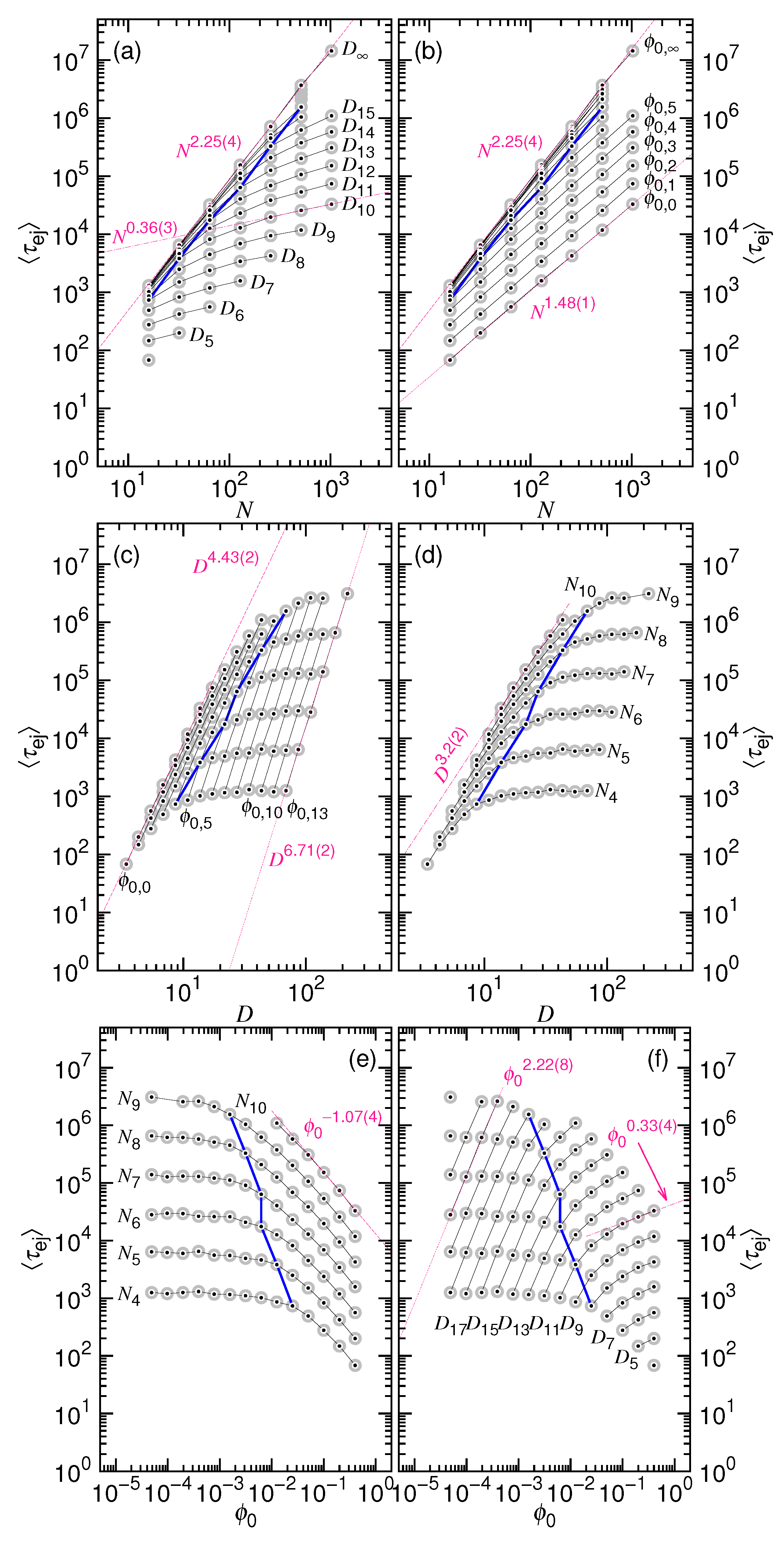


| Ejection time as a function of N and D | if D is fixed | if N is fixed | |
| (a) | |||
| Ejection time as a function of and N | if N is fixed | if is fixed | |
| (b) | |||
| Ejection time as a function of D and | if is fixed | if D is fixed | |
| (c) | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsiao, P.-Y. Scaling Theory of a Polymer Ejecting from a Cavity into a Semi-Space. Polymers 2020, 12, 3014. https://doi.org/10.3390/polym12123014
Hsiao P-Y. Scaling Theory of a Polymer Ejecting from a Cavity into a Semi-Space. Polymers. 2020; 12(12):3014. https://doi.org/10.3390/polym12123014
Chicago/Turabian StyleHsiao, Pai-Yi. 2020. "Scaling Theory of a Polymer Ejecting from a Cavity into a Semi-Space" Polymers 12, no. 12: 3014. https://doi.org/10.3390/polym12123014
APA StyleHsiao, P.-Y. (2020). Scaling Theory of a Polymer Ejecting from a Cavity into a Semi-Space. Polymers, 12(12), 3014. https://doi.org/10.3390/polym12123014






