Robustness of Empirical Vibration Correlation Techniques for Predicting the Instability of Unstiffened Cylindrical Composite Shells in Axial Compression
Abstract
:1. Introduction
- -
- presenting results of one of the largest test programs to-date concerning the application of VCT for evaluating the axial buckling load of unstiffened cylindrical CFRP shells;
- -
- proposing an empirical modification of the existing VCT analysis that increases the accuracy of estimates of the buckling load;
- -
- evaluating the robustness of VCT with respect to variations in shell geometry, mounting and loading methods, and the preload.
2. Empirical VCT Techniques
3. Materials and Methods
3.1. Material
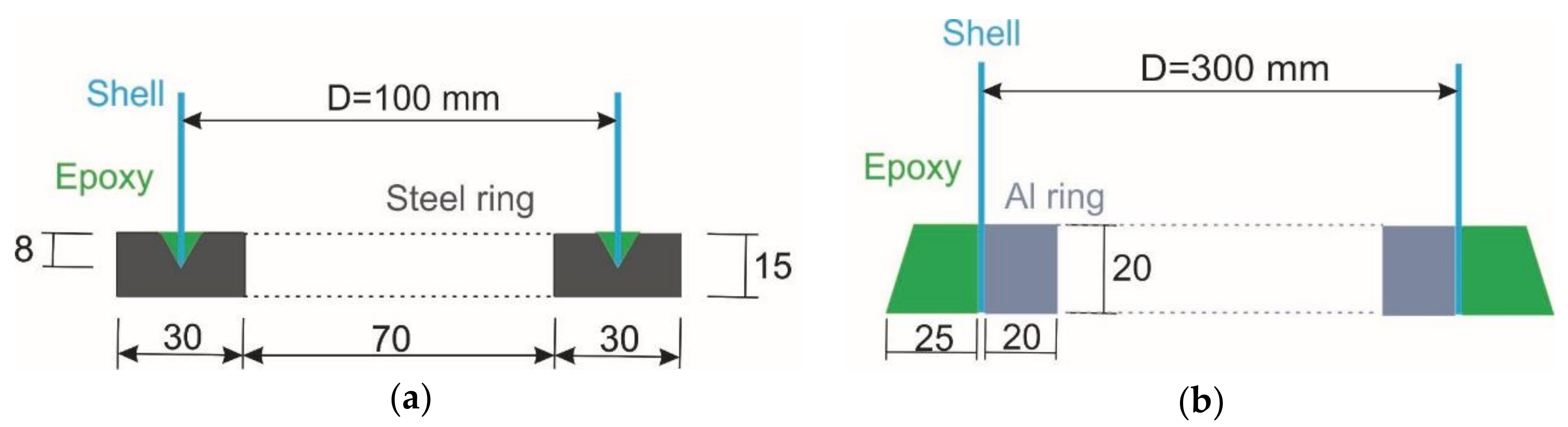
3.2. Manufacture of Shells
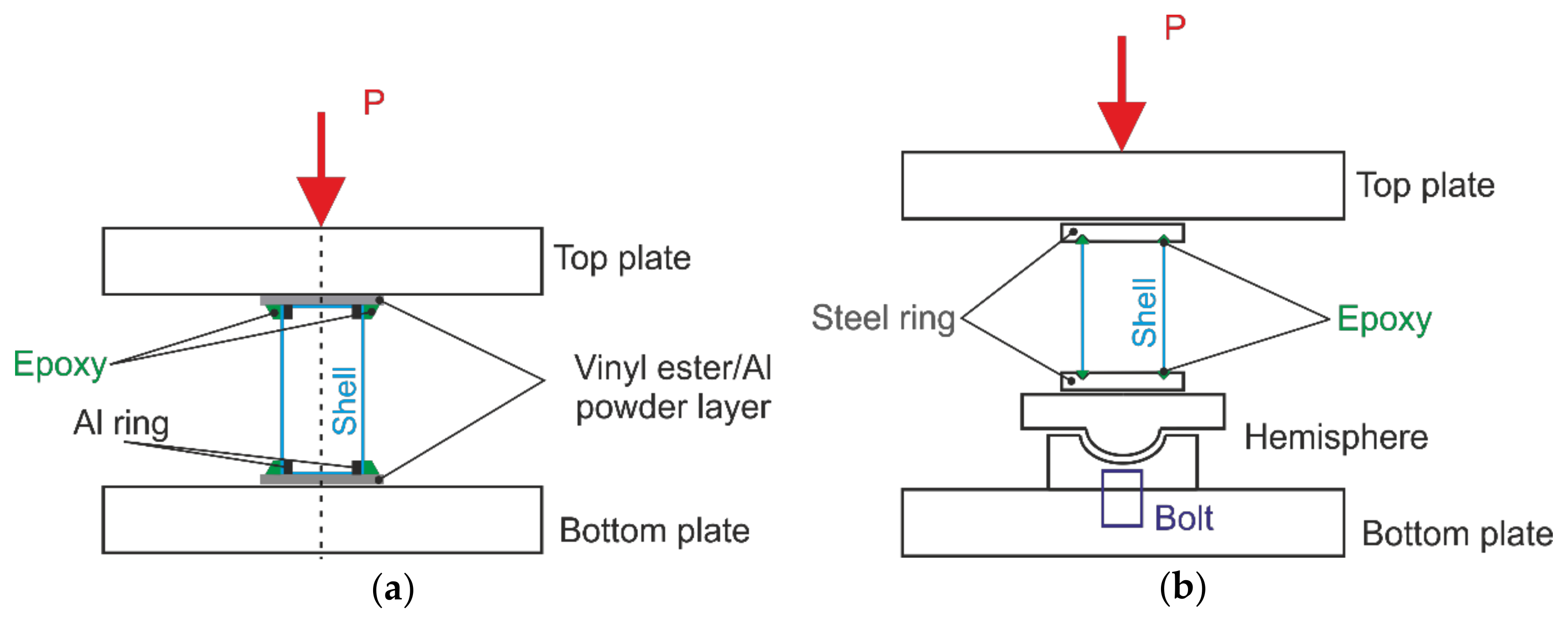
3.3. Tests
3.3.1. Characterization of Shell Thickness
3.3.2. Shell Buckling Tests
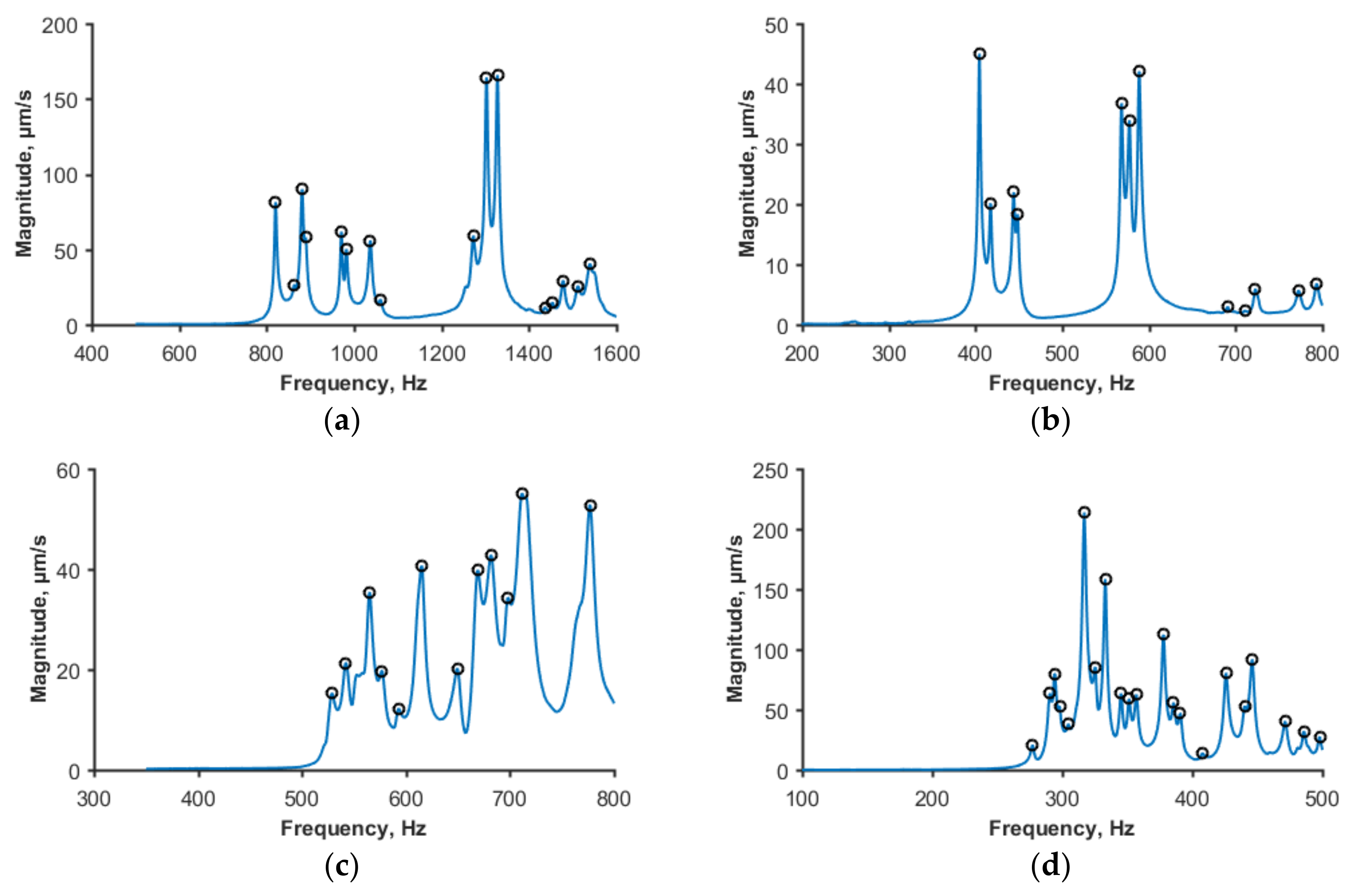
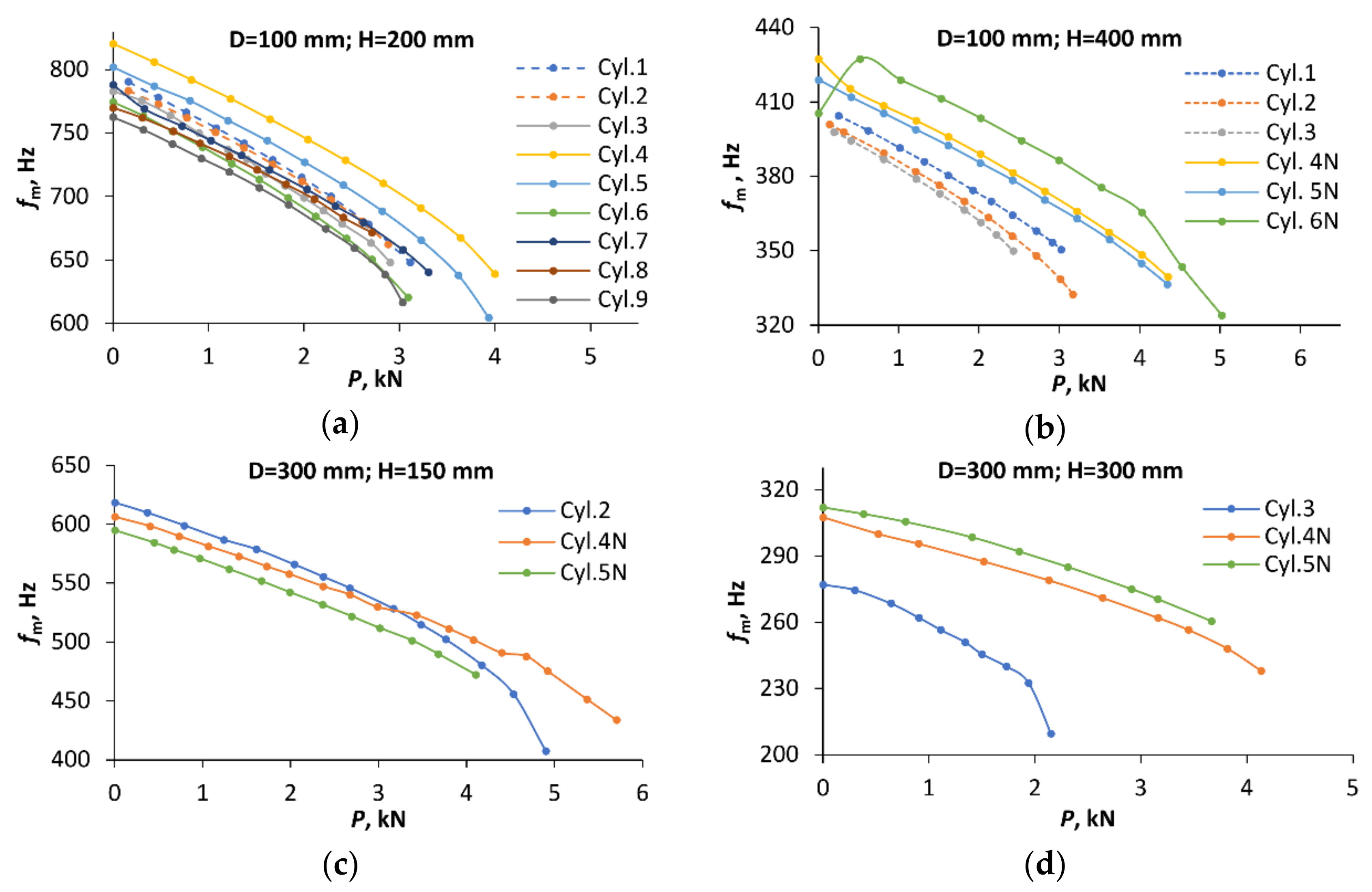
3.3.3. Characterization of Vibration Response
4. Results and Discussion
4.1. Buckling Loads and Modes
4.2. Vibration Spectra and Modes
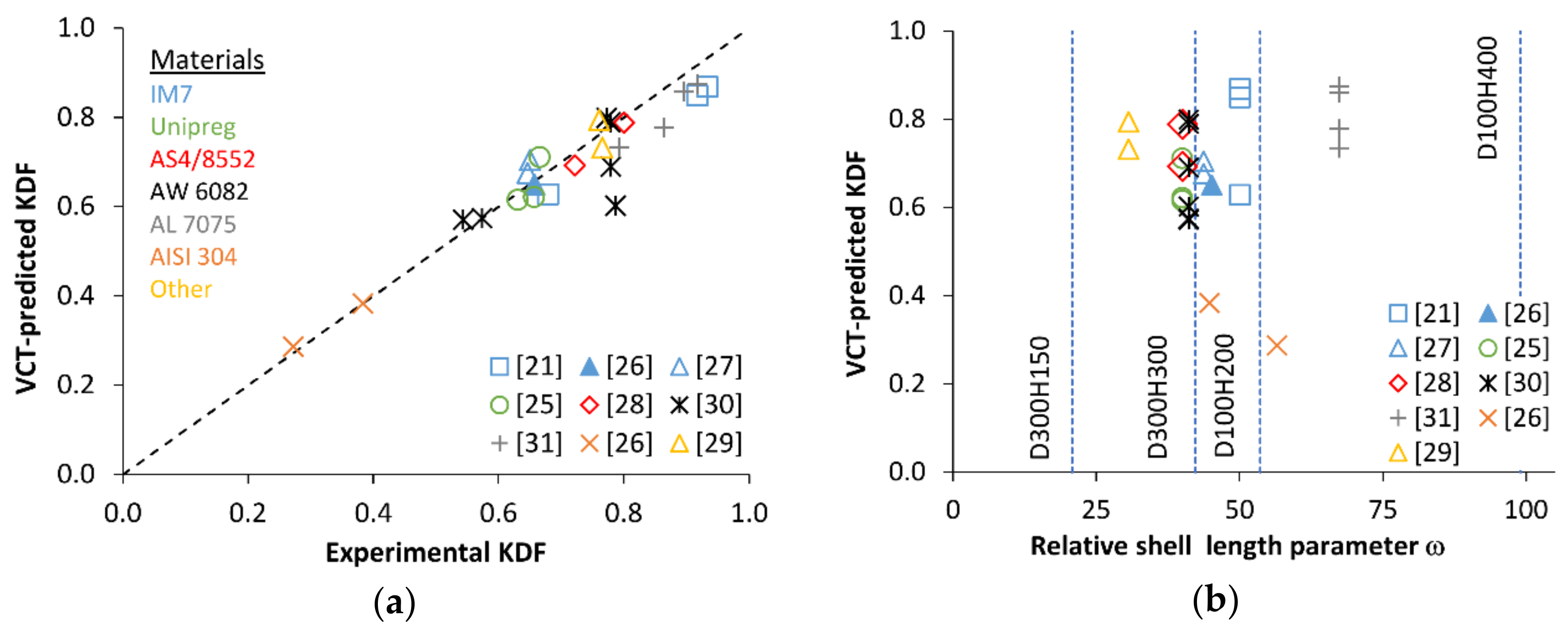
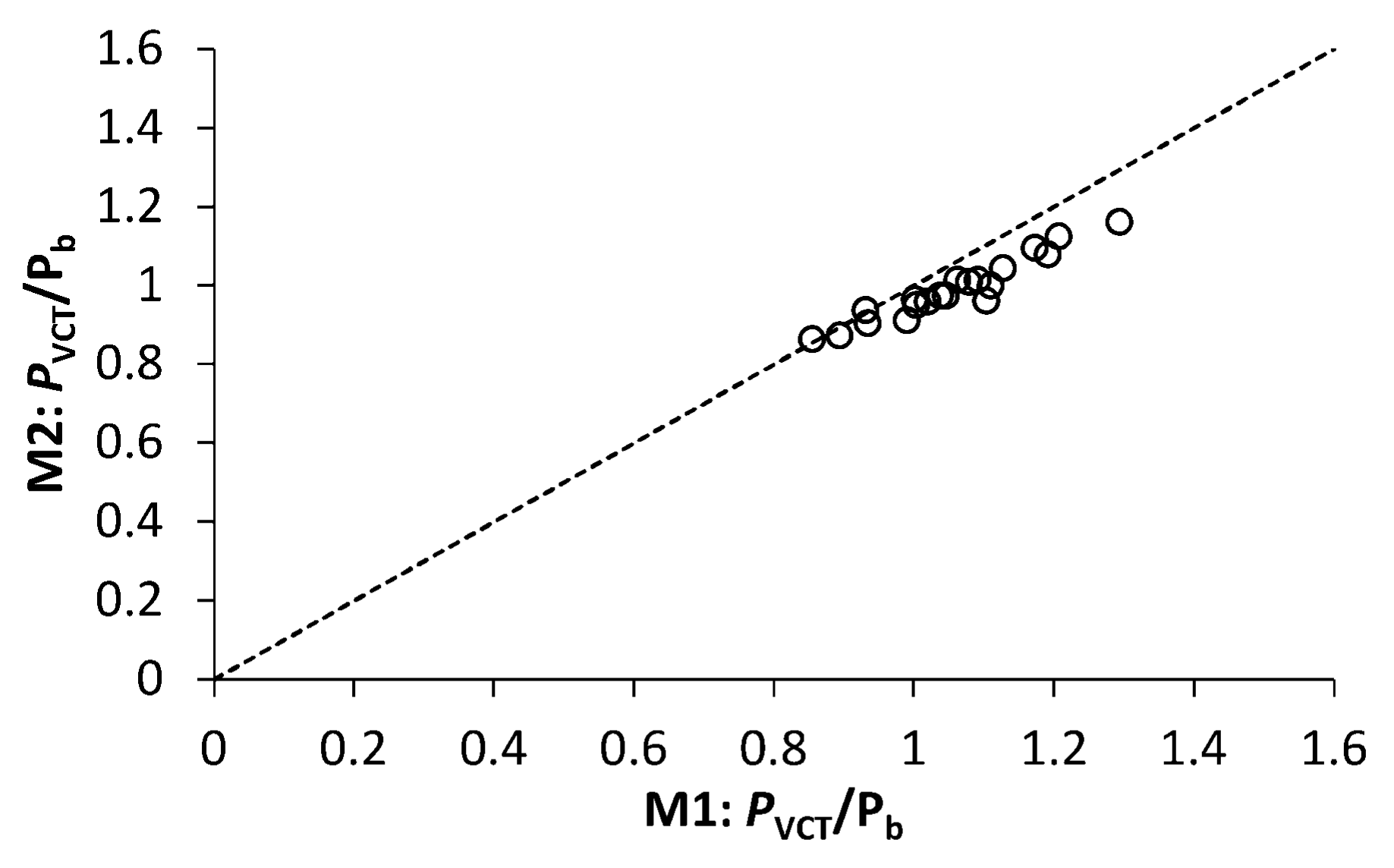
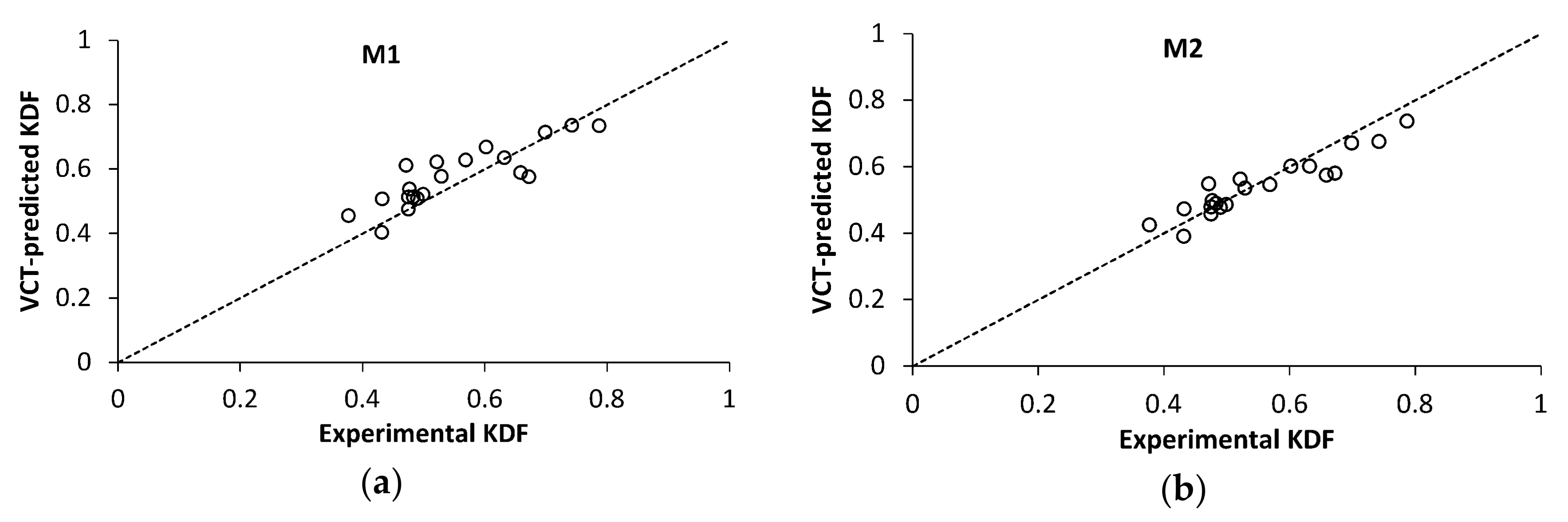
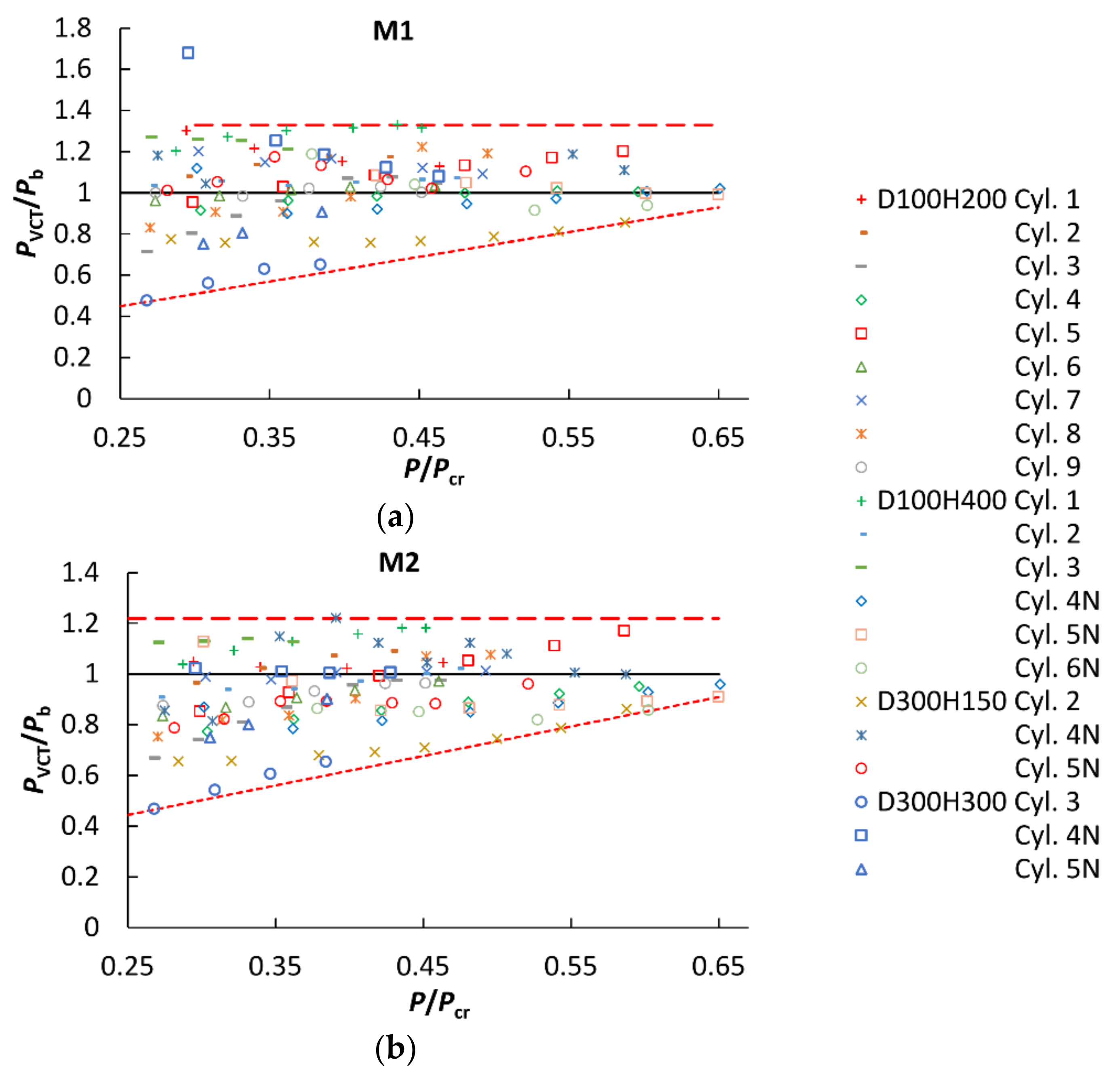
4.3. VCT-Based Prediction of the Critical Load
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mouritz, A. Fibre–polymer composites for aerospace structures and engines. In Introduction to Aerospace Materials, 1st ed.; Woodhead Publishing Ltd.: Cambridge, UK, 2012; Chapter 15; pp. 338–393. [Google Scholar]
- McCarville, D.A.; Guzman, J.C.; Dillon, A.K.; Jackson, J.R.; Birkland, J.O. Design, manufacture and test of cryotank components. In Comprehensive Composite Materials II; Beaumont, P.W.R., Zweben, C.H., Eds.; Elsevier Ltd.: Amsterdam, The Netherlands, 2018; Volume 3, pp. 153–179. [Google Scholar]
- Peterson, J.P.; Seide, P.; Weingarten, V.I. Buckling of Thin-Walled Circular Cylinders; NASA SP–8007; NASA: Washington, DC, USA, 1965; revised 1968. [Google Scholar]
- Takano, A. Statistical knockdown factors of buckling anisotropic cylinders under axial compression. J. Appl. Mech. 2012, 79, 051004. [Google Scholar] [CrossRef]
- Castro, S.G.P.; Zimmermann, R.; Arbelo, M.A.; Khakimova, R.; Hilburger, M.W.; Degenhardt, R. Geometric imperfections and lower-bound methods used to calculate knock-down factors for axially compressed composite cylindrical shells. Thin Walled Struct. 2014, 74, 118–132. [Google Scholar] [CrossRef]
- Wagner, H.N.R.; Hühne, C.; Niemann, S.; Khakimova, R. Robust design criterion for axially loaded cylindrical shells—Simulation and validation. Thin Walled Struct. 2017, 115, 154–162. [Google Scholar] [CrossRef]
- Wagner, H.N.R.; Hühne, C.; Niemann, S. Robust knockdown factors for the design of axially loaded cylindrical and conical composite shells—Development and validation. Compos. Struct. 2017, 173, 281–303. [Google Scholar] [CrossRef]
- Wagner, H.N.R.; Hühne, C.; Niemann, S.; Tian, K.; Wang, B.; Hao, P. Robust knockdown factors for the design of cylindrical shells under axial compression: Analysis and modeling of stiffened and unstiffened cylinders. Thin Walled Struct. 2018, 127, 629–645. [Google Scholar] [CrossRef]
- Wagner, H.N.R.; Hühne, C.; Elishakoff, I. Probabilistic and deterministic lower-bound design benchmarks for cylindrical shells under axial compression. Thin Walled Struct. 2020, 146, 106451. [Google Scholar] [CrossRef]
- Bolotin, V.V. Statistical aspects in the theory of structural stability. In Dynamic Stability of Structures; Herrmann, G., Ed.; Pergamon Press: Oxford, UK, 1967; pp. 67–81. [Google Scholar]
- Schillo, C.; Kriegesmann, B.; Krause, D. Reliability based calibration of safety factors for unstiffened cylindrical composite shells. Compos. Struct. 2017, 168, 798–812. [Google Scholar] [CrossRef]
- Starnes, J.H., Jr.; Hilburger, M.W.; Nemeth, M.P. The effects of initial imperfections on the buckling of composite cylindrical shells. In Composite Structures: Theory and Practice; Grant, P., Rousseau, Q.C., Eds.; ASTM STP 1383; American Society for Testing and Materials: West Conshohocken, PA, USA, 2000; pp. 529–550. [Google Scholar]
- Hilburger, M.W.; Starnes, J.H., Jr. Effects of imperfections on the buckling response of compression-loaded composite shells. Int. J. Non Linear Mech. 2002, 37, 623–643. [Google Scholar] [CrossRef] [Green Version]
- Hilburger, M.W.; Starnes, J.H., Jr. Effects of imperfections of the buckling response of composite shells. Thin Walled Struct. 2004, 42, 369–397. [Google Scholar] [CrossRef]
- Schillo, C.; Röstermundt, D.; Krause, D. Experimental and numerical study on the influence of imperfections on the buckling load of unstiffened CFRP shells. Compos. Struct. 2015, 131, 128–138. [Google Scholar] [CrossRef]
- Hühne, C.; Zimmermann, R.; Rolfes, R.; Geier, B. Sensitivities to geometrical and loading imperfections on buckling of composite cylindrical shells. In Proceedings of the European Conference on Spacecraft Structures, Materials and Mechanical Testing, Toulouse, France, 11–13 December 2002; pp. 1–12. [Google Scholar]
- Kepple, J.; Prusty, B.G.; Pearce, G.; Kelly, D.; Thomson, R.; Degenhardt, R. Influence of imperfections on axial buckling load of composite cylindrical shells. In Proceedings of the 19th International Conference on Composite Materials, Montreal, QC, Canada, 28 July–2 August 2013; pp. 1–10. [Google Scholar]
- Singer, J.; Arbocz, J.; Weller, T. Vibration correlation techniques (VCT). In Buckling Experiments, Experimental Methods in Buckling of Thin-Walled Structures; John Wiley & Sons, Inc.: New York, NY, USA, 2002; Volume 2, Chapter 15.2; pp. 1244–1284. [Google Scholar]
- Virgin, L.N. Vibration of Axially-Loaded Structures; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Abramovich, H.; Govich, D.; Grunwald, A. Buckling prediction of panels using the vibration correlation technique. Prog. Aerosp. Sci. 2015, 78, 62–73. [Google Scholar] [CrossRef]
- Franzoni, F.; Odermann, F.; Labans, E.; Bisagni, C.; Arbelo, M.A.; Degenhardt, R. Experimental validation of the vibration correlation technique robustness to predict buckling of unstiffened composite cylindrical shells. Compos. Struct. 2019, 224, 111107. [Google Scholar] [CrossRef]
- Shahgholian-Ghahfarokhi, D.; Rahimi, G.; Liaghat, G.; Degenhardt, R.; Franzoni, F. Buckling prediction of composite lattice sandwich cylinders (CLSC) through the vibration correlation technique (VCT): Numerical assessment with experimental and analytical verification. Compos. B 2020, 199, 108252. [Google Scholar] [CrossRef]
- Arbelo, M.A.; de Almeida, S.F.M.; Donadon, M.V.; Rett, S.R.; Degenhardt, R.; Castro, S.G.P.; Kalnins, K.; Ozoliņš, O. Vibration correlation technique for the estimation of real boundary conditions and buckling load of unstiffened plates and cylindrical shells. Thin Walled Struct. 2014, 79, 119–128. [Google Scholar] [CrossRef]
- Franzoni, F.; Degenhardt, R.; Albus, J.; Arbelo, M.A. Vibration correlation technique for predicting the buckling load of imperfection-sensitive isotropic cylindrical shells: An analytical and numerical verification. Thin Walled Struct. 2019, 140, 236–247. [Google Scholar] [CrossRef]
- Arbelo, M.A.; Kalnins, K.; Ozolins, O.; Skukis, E.; Castro, S.G.P.; Degenhardt, R. Experimental and numerical estimation of buckling load on unstiffened cylindrical shells using a vibration correlation technique. Thin Walled Struct. 2015, 94, 273–279. [Google Scholar] [CrossRef]
- Kalnins, K.; Arbelo, M.A.; Ozolins, O.; Skukis, E.; Castro, S.G.P.; Degenhardt, R. Experimental nondestructive test for estimation of buckling load on unstiffened cylindrical shells using vibration correlation technique. Shock Vib. 2015. [Google Scholar] [CrossRef] [Green Version]
- Skukis, E.; Ozolins, O.; Kalnins, K.; Arbelo, M.A. Experimental test for estimation of buckling load on unstiffened cylindrical shells by vibration correlation technique. Procedia Eng. 2017, 172, 1023–1030. [Google Scholar] [CrossRef]
- Labans, E.; Abramovich, H.; Bisagni, C. An experimental vibration-buckling investigation on classical and variable angle tow composite shells under axial compression. J. Sound Vib. 2019, 449, 315–329. [Google Scholar] [CrossRef]
- Shahgholian-Ghahfarokhi, D.; Rahimi, G. Buckling load prediction of grid-stiffened composite cylindrical shells using the vibration correlation technique. Compos. Sci. Technol. 2018, 167, 470–481. [Google Scholar] [CrossRef]
- Skukis, E.; Ozolins, O.; Andersons, J.; Kalnins, K.; Arbelo, M.A. Applicability of the vibration correlation technique for estimation of the buckling load in axial compression of cylindrical isotropic shells with and without circular cutouts. Shock Vib. 2017. [Google Scholar] [CrossRef] [Green Version]
- Franzoni, F.; Odermann, F.; Wilckens, D.; Skukis, E.; Kalnins, K.; Arbelo, M.A.; Degenhardt, R. Assessing the axial buckling load of a pressurized orthotropic cylindrical shell through vibration correlation technique. Thin Walled Struct. 2019, 137, 353–366. [Google Scholar] [CrossRef]
- Tian, K.; Huang, L.; Sun, Y.; Du, K.; Hao, P.; Wang, B. Fast buckling load numerical prediction method for imperfect shells under axial compression based on POD and vibration correlation technique. Compos. Struct. 2020, 252, 112721. [Google Scholar] [CrossRef]
- European Standard. Eurocode: EN 1993-1-6 Eurocode 3—Design of Steel Structures—Part 1–6: Strength and Stability of Shell Structures; European Committee for Standardization: Brussels, Belgium, 2007. [Google Scholar]
- Jansen, E. The influence of initial geometric imperfections on composite shell stability and vibrations. In Stability and Vibrations of Thin Walled Composite Structures; Abramovich, H., Ed.; Woodhead Publishing Inc.: Cambridge, UK; Volume 2, Chapter 10; pp. 509–548.




| Longitudinal Young’s Modulus E11, GPa | Transverse Young’s Modulus E22, GPa | In-Plane Shear Modulus G12, GPa | Poisson’s Ratio ν12 | ||
|---|---|---|---|---|---|
| Tension | Compression | Tension | Compression | ||
| 116.4 | 91.7 | 6.7 | 6.4 | 3.6 | 0.34 |
| Shell Geometry | Load Introduction | Critical Load Pb, kN | ||
|---|---|---|---|---|
| Diameter D, mm | Height H, mm | Wall Thickness t, mm | ||
| 100 | 200 | 0.294 (0.001) 1 | Hemispherical joint | 3.05 (0.21) 1 |
| 0.273 (0.010) | Parallel plates | 3.65 (0.49) | ||
| 400 | 0.298 (0.005) | Hemispherical joint | 2.97 (0.39) | |
| 0.355 (0.019) | Parallel plates | 4.96 (0.29) | ||
| 300 | 150 | 0.359 (0.014) | Parallel plates | 5.63 (0.21) |
| 300 | 0.336 (0.046) | 3.88 (0.51) | ||
| Cylinder Diameter and Height, mm | Loading | Cylinder Number | Buckling Load Pb, kN | Load Range in Vibration Tests | VCT-Predicted Buckling Load | ||||
|---|---|---|---|---|---|---|---|---|---|
| M1 | M2 | ||||||||
| Min. P/Pb | Max. P/Pb | PVCT, kN | Relat. Error δ, % | PVCT, kN | Relat. Error δ, % | ||||
| D = 100 H = 200 | Hemi- spherical joint | 01 | 3.20 | 0.05 | 0.97 | 3.61 | 12.9 | 3.34 | 4.5 |
| 02 | 2.90 | 0.05 | 0.99 | 3.40 | 17.4 | 3.17 | 9.3 | ||
| Parallel plates | 03 | 3.35 | 0 | 0.93 | 3.50 | 4.7 | 3.26 | 2.5 | |
| 04 | 4.24 | 0 | 0.94 | 4.26 | 0.4 | 4.03 | 5.0 | ||
| 05 | 4.42 | 0 | 0.89 | 3.95 | 10.5 | 3.85 | 12.8 | ||
| 06 | 3.29 | 0 | 0.94 | 3.41 | 3.7 | 3.2 | 2.6 | ||
| 07 | 3.55 | 0.09 | 0.93 | 3.87 | 9.1 | 3.59 | 1.2 | ||
| 08 | 3.50 | 0 | 0.95 | 4.17 | 19.3 | 3.77 | 7.7 | ||
| 09 | 3.19 | 0 | 0.95 | 3.19 | 0.2 | 3.07 | 3.5 | ||
| D = 100 H = 400 | Hemi- spherical joint | 01 | 3.15 | 0.08 | 0.97 | 4.08 | 29.4 | 3.66 | 16.2 |
| 02 | 3.23 | 0.04 | 0.99 | 3.43 | 6.3 | 3.27 | 1.2 | ||
| 03 | 2.52 | 0.08 | 0.96 | 3.04 | 20.8 | 2.83 | 12.4 | ||
| Parallel plates | 04N | 4.67 | 0.08 | 0.93 | 4.77 | 1.9 | 4.48 | 4.2 | |
| 05N | 4.96 | 0 | 0.88 | 4.91 | 0.9 | 4.51 | 9.0 | ||
| 06N | 5.26 | 0.10 | 0.95 | 4.9 | 6.8 | 4.92 | 6.4 | ||
| D = 300 H = 150 | Parallel plates | 02 | 5.61 | 0 | 0.87 | 4.8 | 14.4 | 4.84 | 13.8 |
| 04N | 5.85 | 0 | 0.98 | 6.49 | 11.0 | 5.84 | 0.1 | ||
| 05N | 5.44 | 0 | 0.92 | 6.0 | 10.4 | 5.22 | 4.0 | ||
| D = 300 H = 300 | Parallel plates | 03 | 3.29 | 0 | 0.65 | 2.14 | 34.9 | 2.15 | 34.6 |
| 04N | 4.24 | 0 | 0.97 | 4.57 | 8.0 | 4.27 | 0.7 | ||
| 05N | 4.11 | 0 | 0.89 | 3.84 | 6.5 | 3.71 | 9.8 | ||
| Relative Length Parameter of Shell | Mean Relative Error of Prediction δ, % | |
|---|---|---|
| M1 | M2 | |
| 21 | 11.9 | 6.0 |
| 42 | 7.3 | 5.3 |
| 54 | 8.7 | 5.5 |
| 99 | 11.0 | 8.2 |
| Loading and Boundary Conditions | Mean Relative Error of Prediction δ, % | |
|---|---|---|
| M1 | M2 | |
| Steel ring, hemispherical joint | 17.4 | 8.7 |
| Steel ring, parallel plates | 5.8 | 5.5 |
| Potted, parallel plates | 10.1 | 5.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skukis, E.; Jekabsons, G.; Andersons, J.; Ozolins, O.; Labans, E.; Kalnins, K. Robustness of Empirical Vibration Correlation Techniques for Predicting the Instability of Unstiffened Cylindrical Composite Shells in Axial Compression. Polymers 2020, 12, 3069. https://doi.org/10.3390/polym12123069
Skukis E, Jekabsons G, Andersons J, Ozolins O, Labans E, Kalnins K. Robustness of Empirical Vibration Correlation Techniques for Predicting the Instability of Unstiffened Cylindrical Composite Shells in Axial Compression. Polymers. 2020; 12(12):3069. https://doi.org/10.3390/polym12123069
Chicago/Turabian StyleSkukis, Eduards, Gints Jekabsons, Jānis Andersons, Olgerts Ozolins, Edgars Labans, and Kaspars Kalnins. 2020. "Robustness of Empirical Vibration Correlation Techniques for Predicting the Instability of Unstiffened Cylindrical Composite Shells in Axial Compression" Polymers 12, no. 12: 3069. https://doi.org/10.3390/polym12123069




