A Numerical Investigation on the Collision Behavior of Polymer Droplets
Abstract
:1. Introduction
2. Numerical Framework
2.1. Governing Equations
2.2. Power-Law Viscosity Model
3. Verification
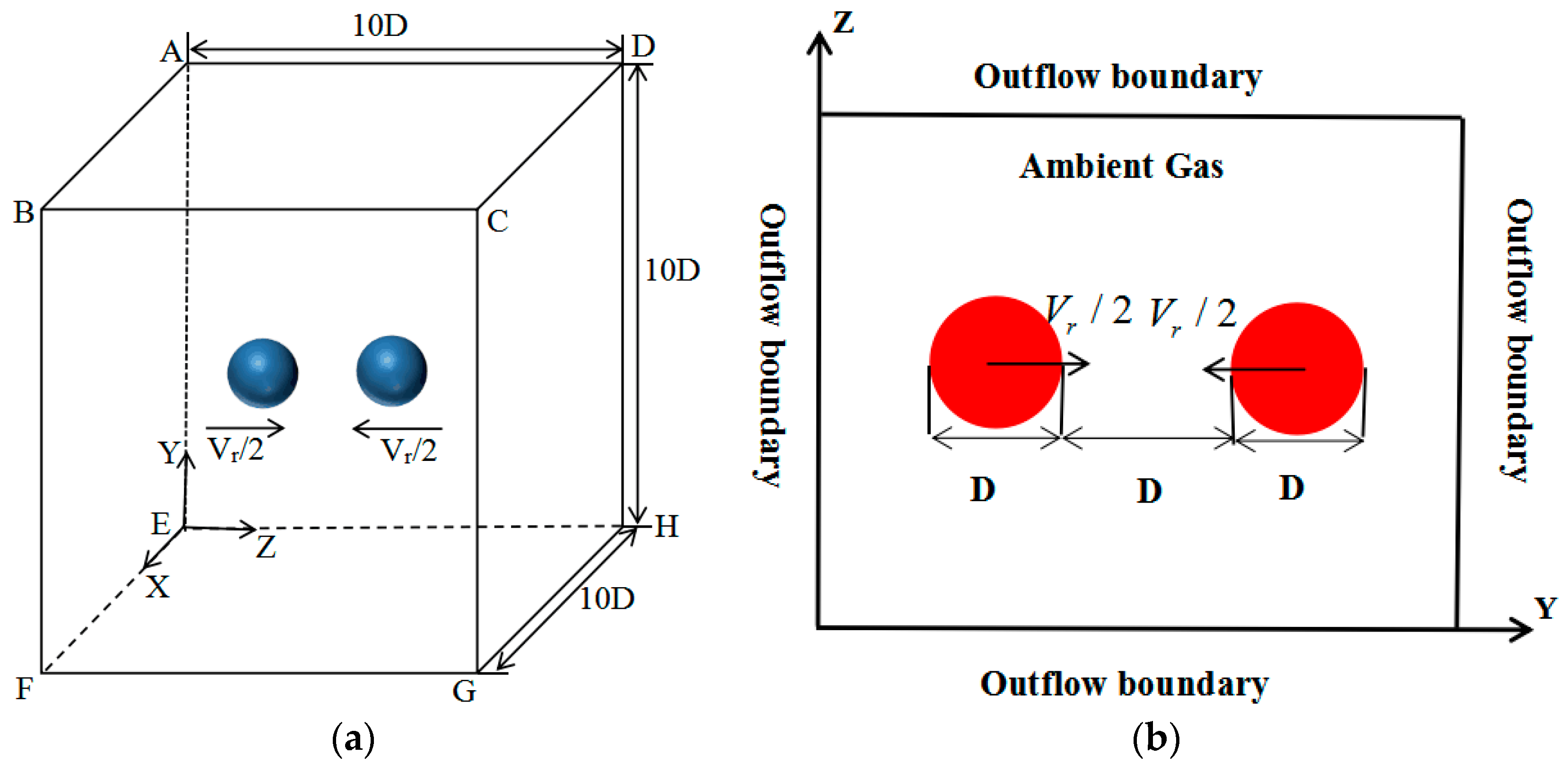
3.1. Computational Setup
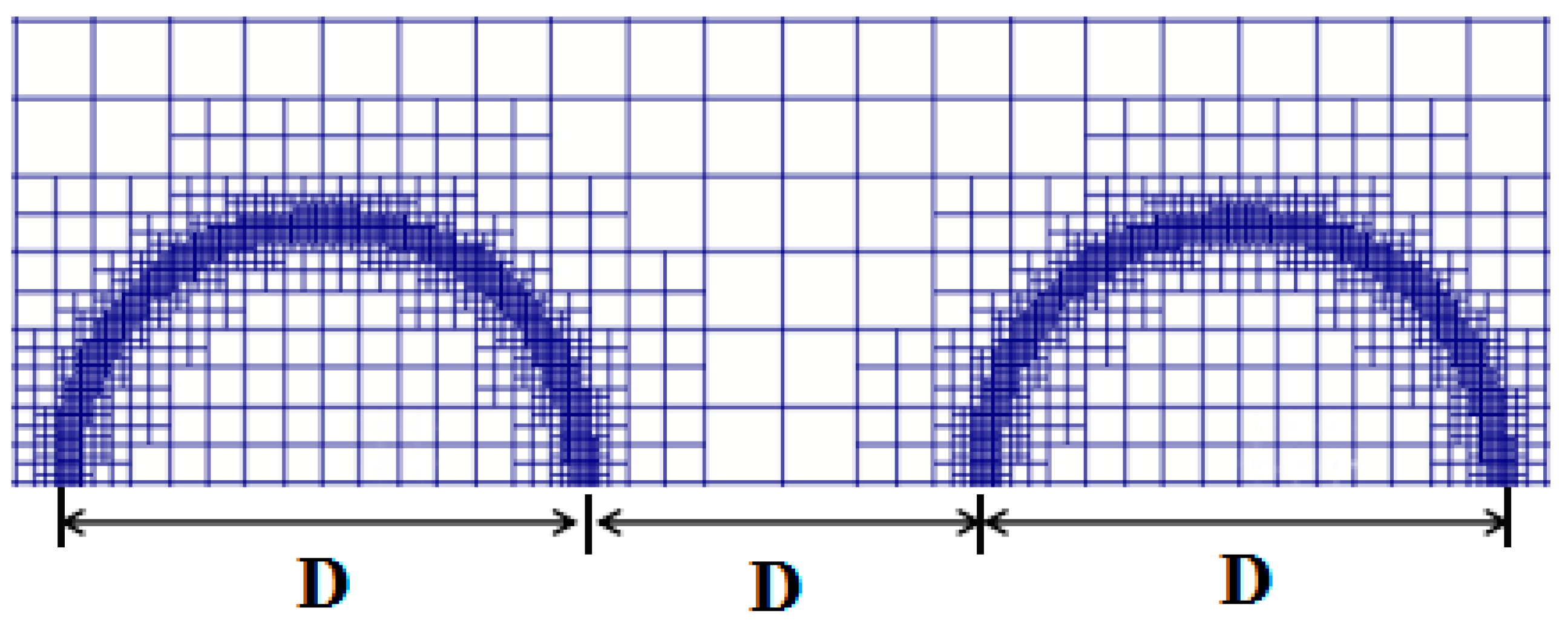
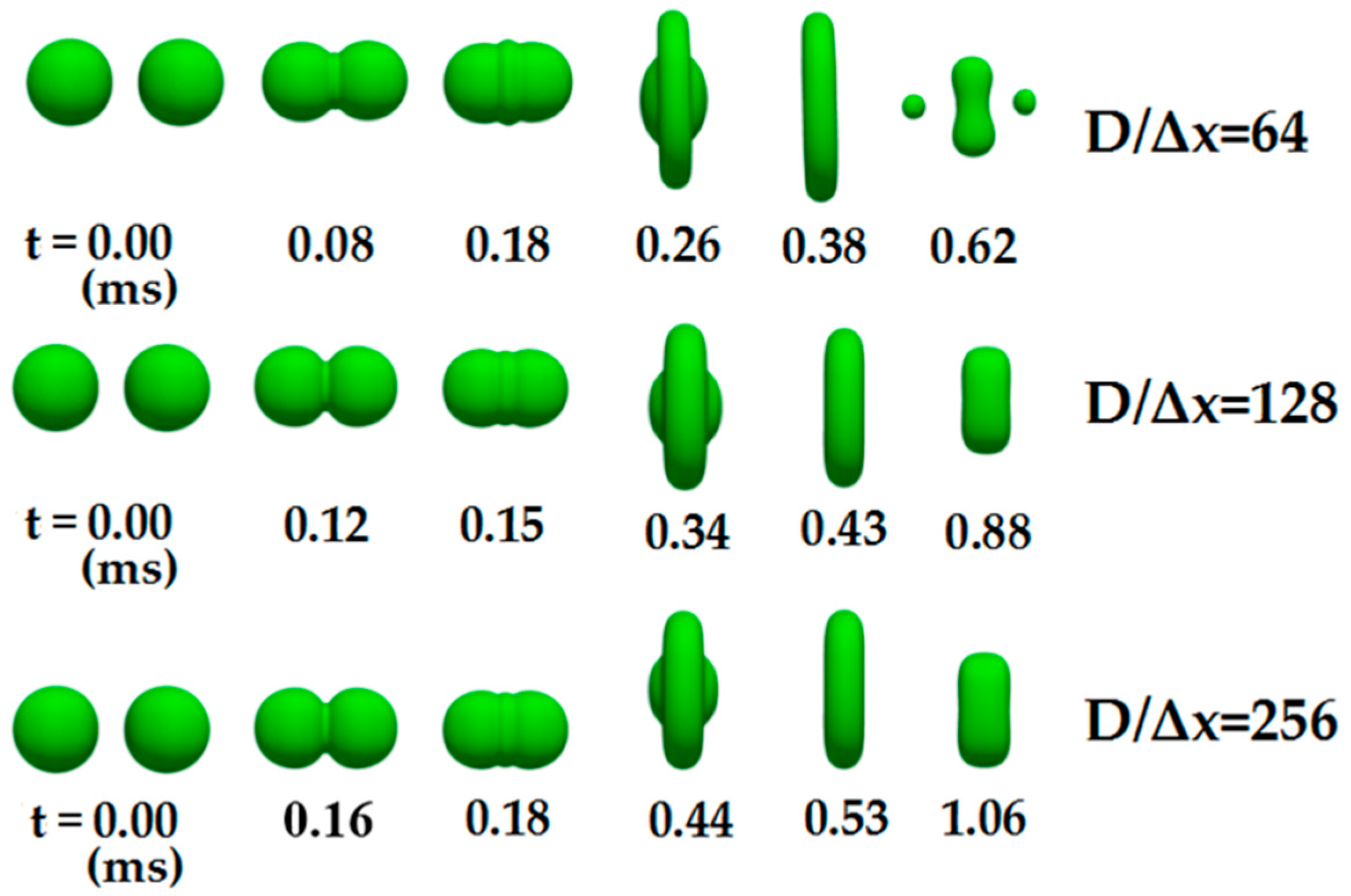
3.2. Verification of Grid Independence
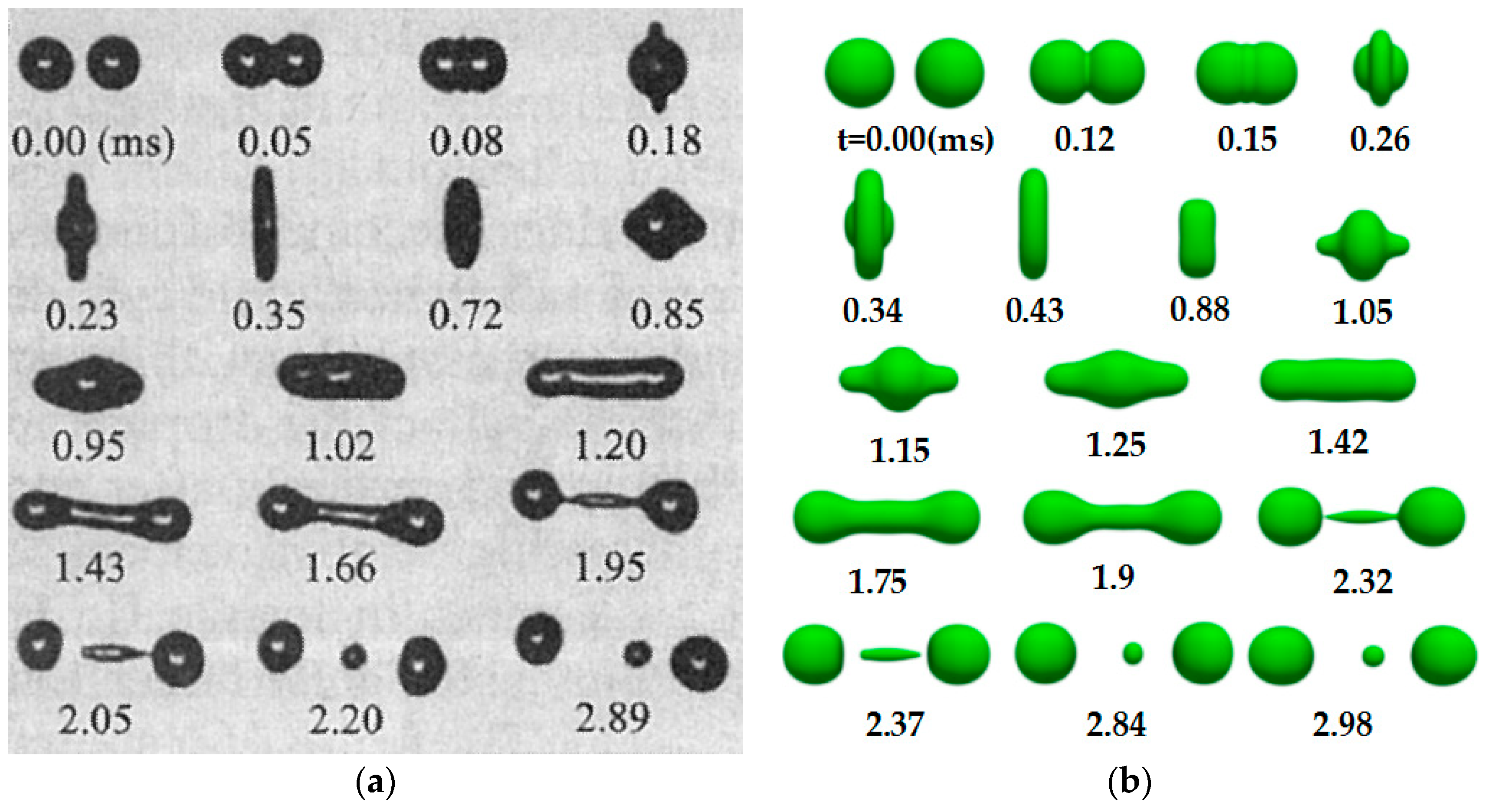
3.3. Experimental Verification
4. Results and Discussion
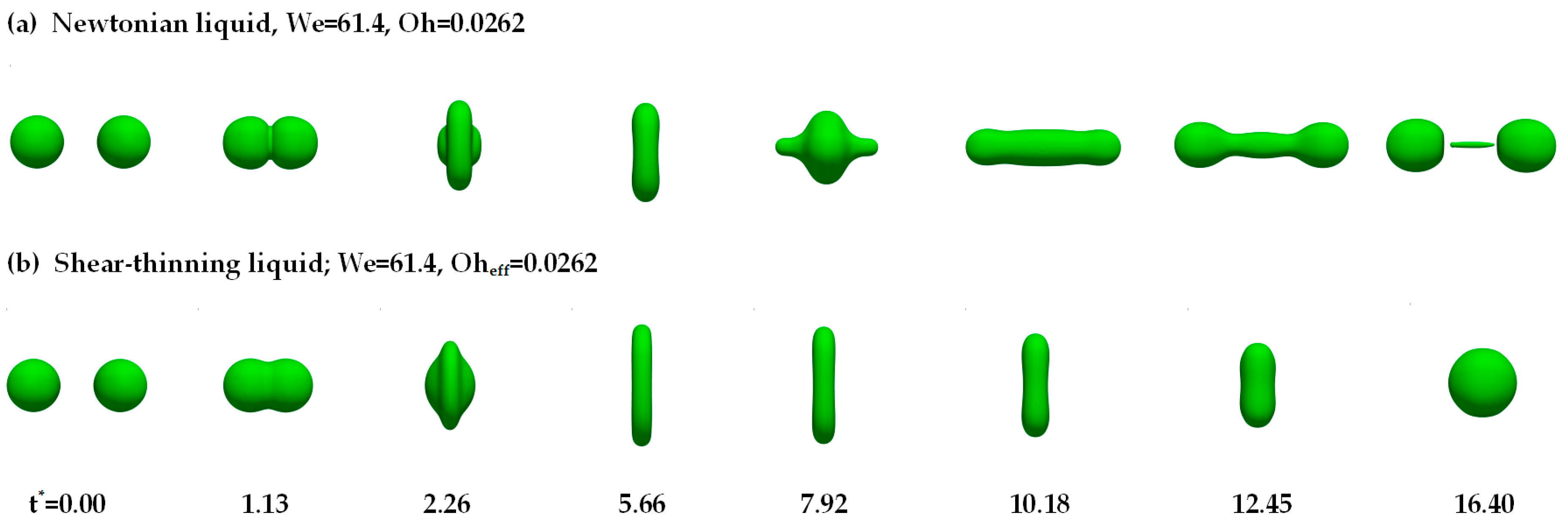
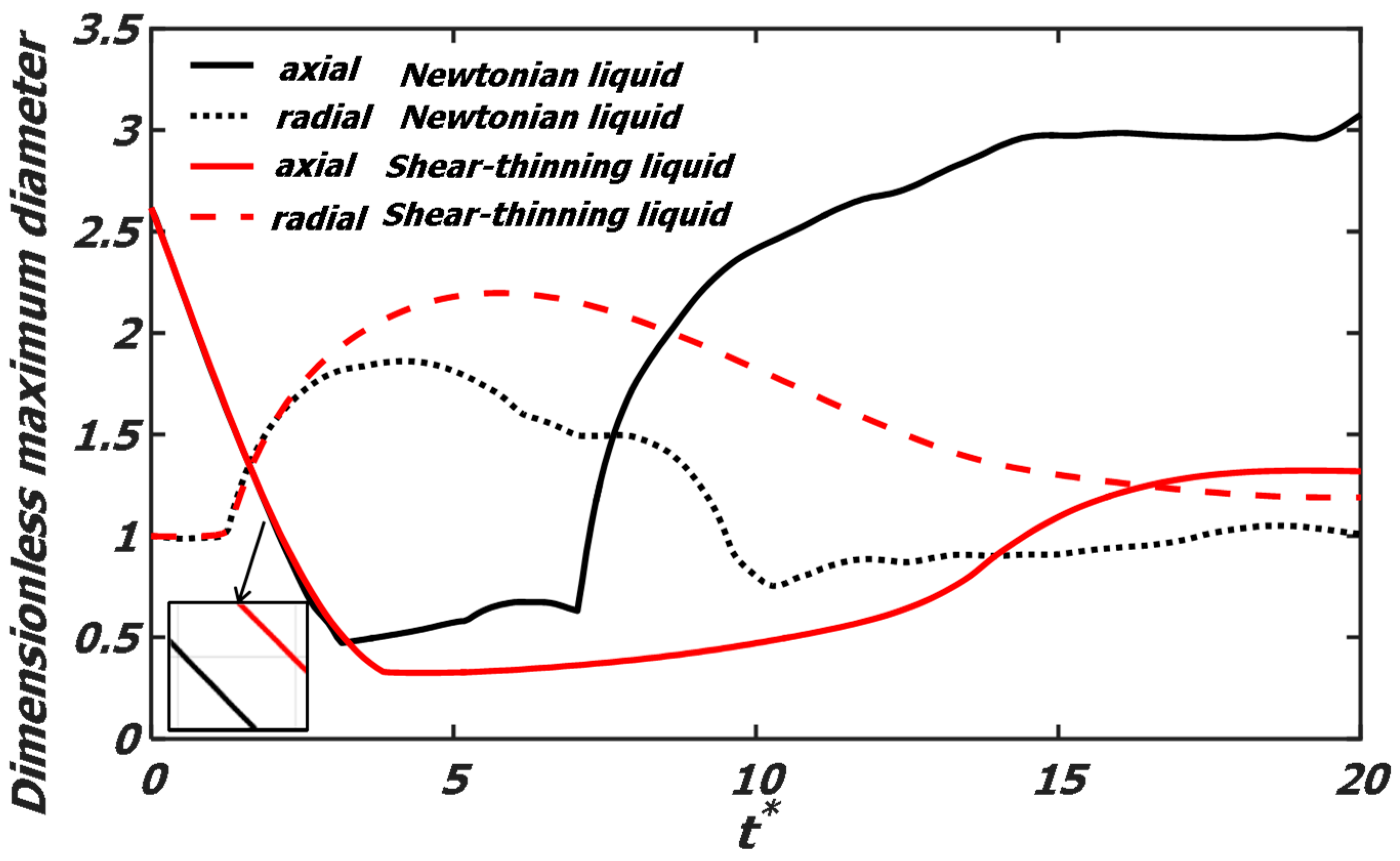
4.1. A Comparison of the Collision Behavior of the Droplets of the Newtonian and Shear-Thinning Liquid
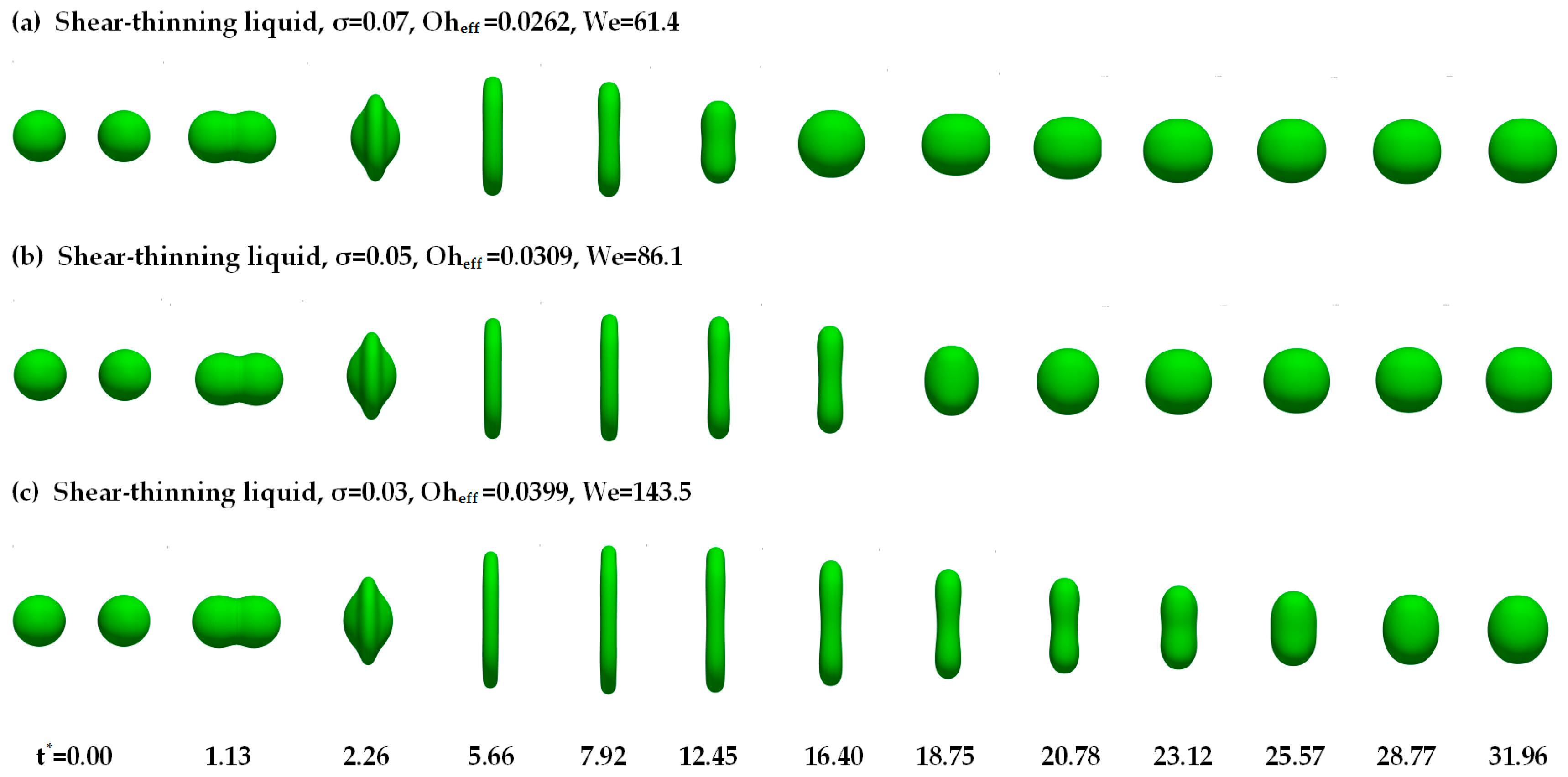
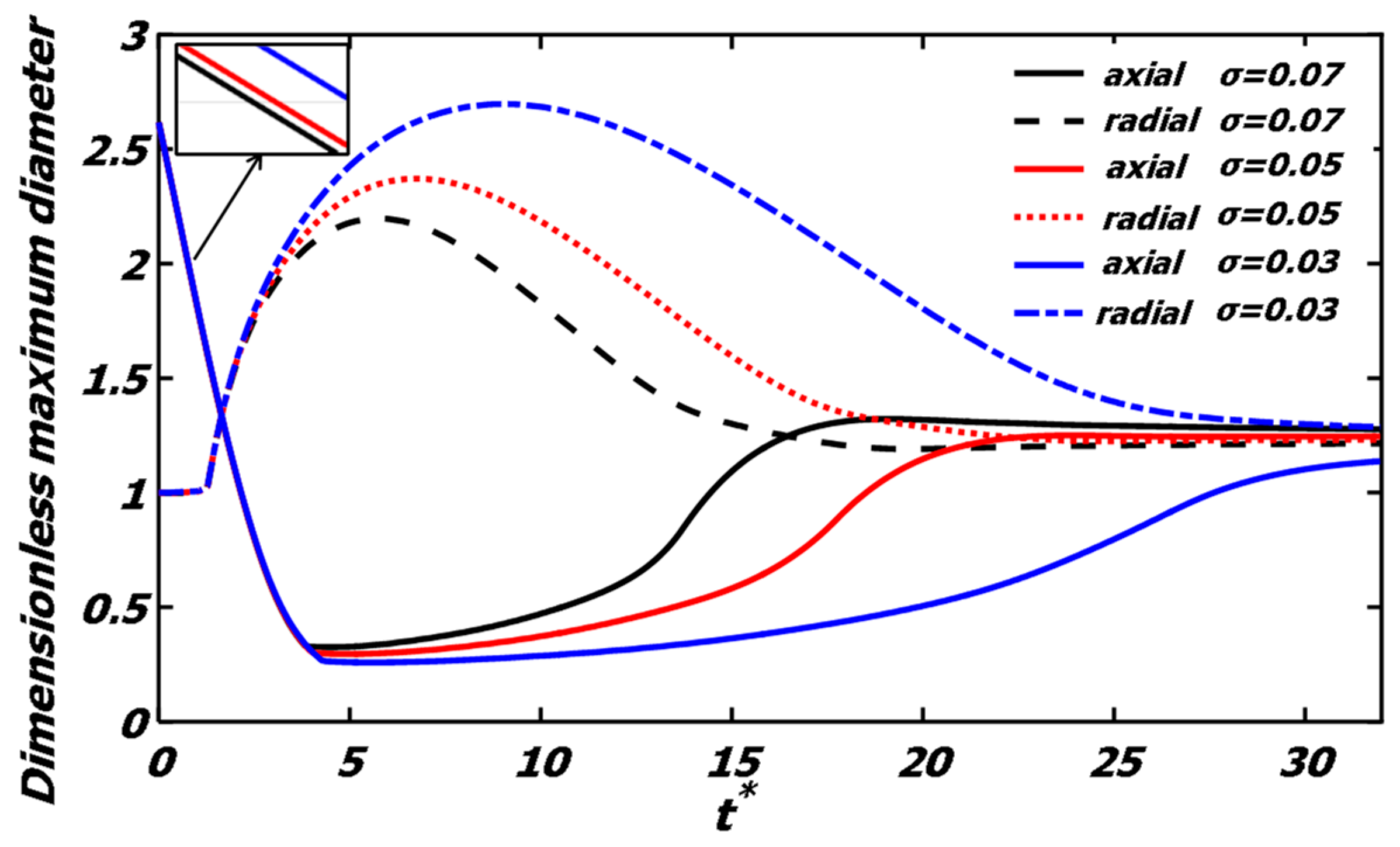
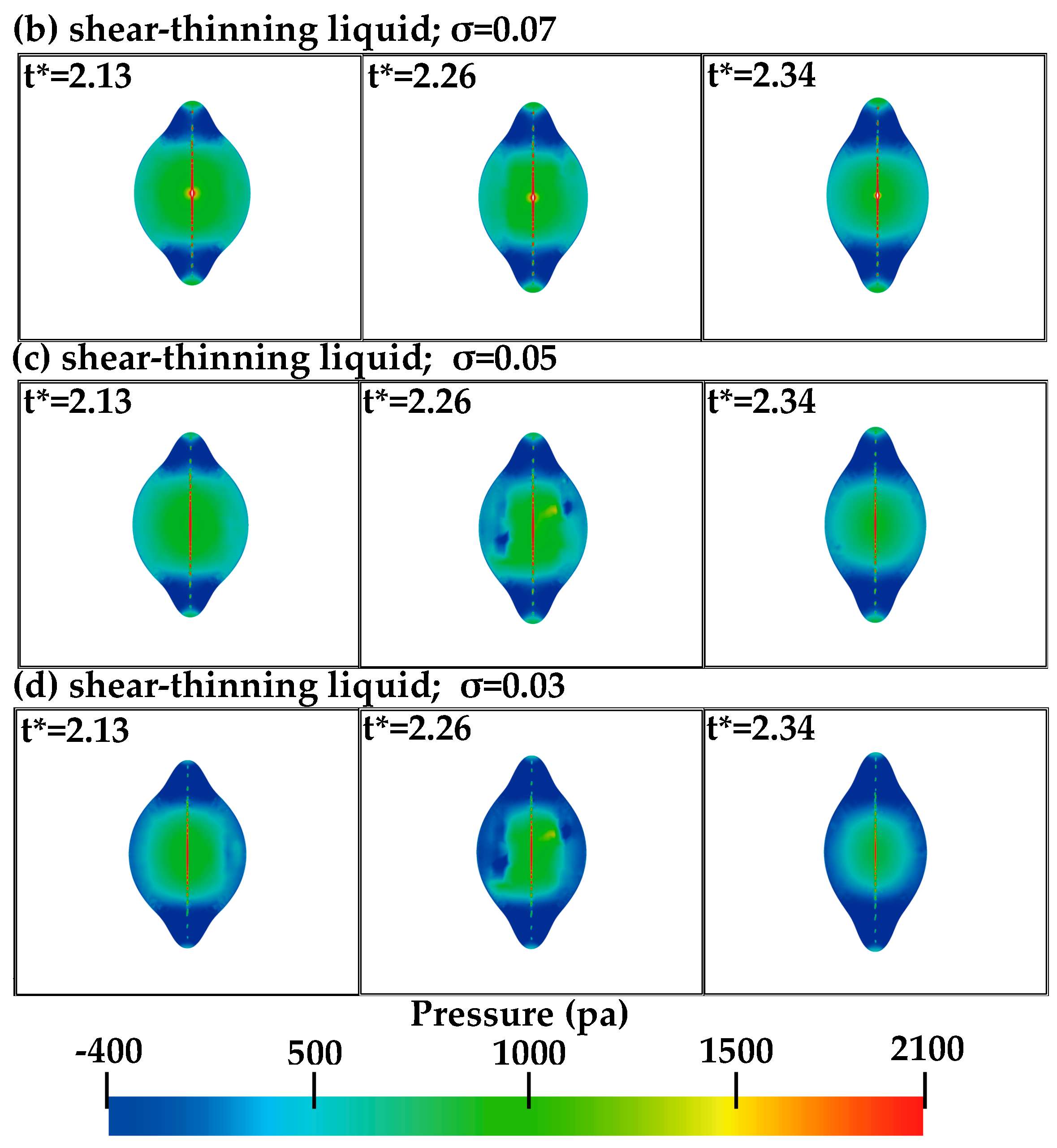
4.2. The Surface Tension Effect
4.3. The Internal Flow Fields
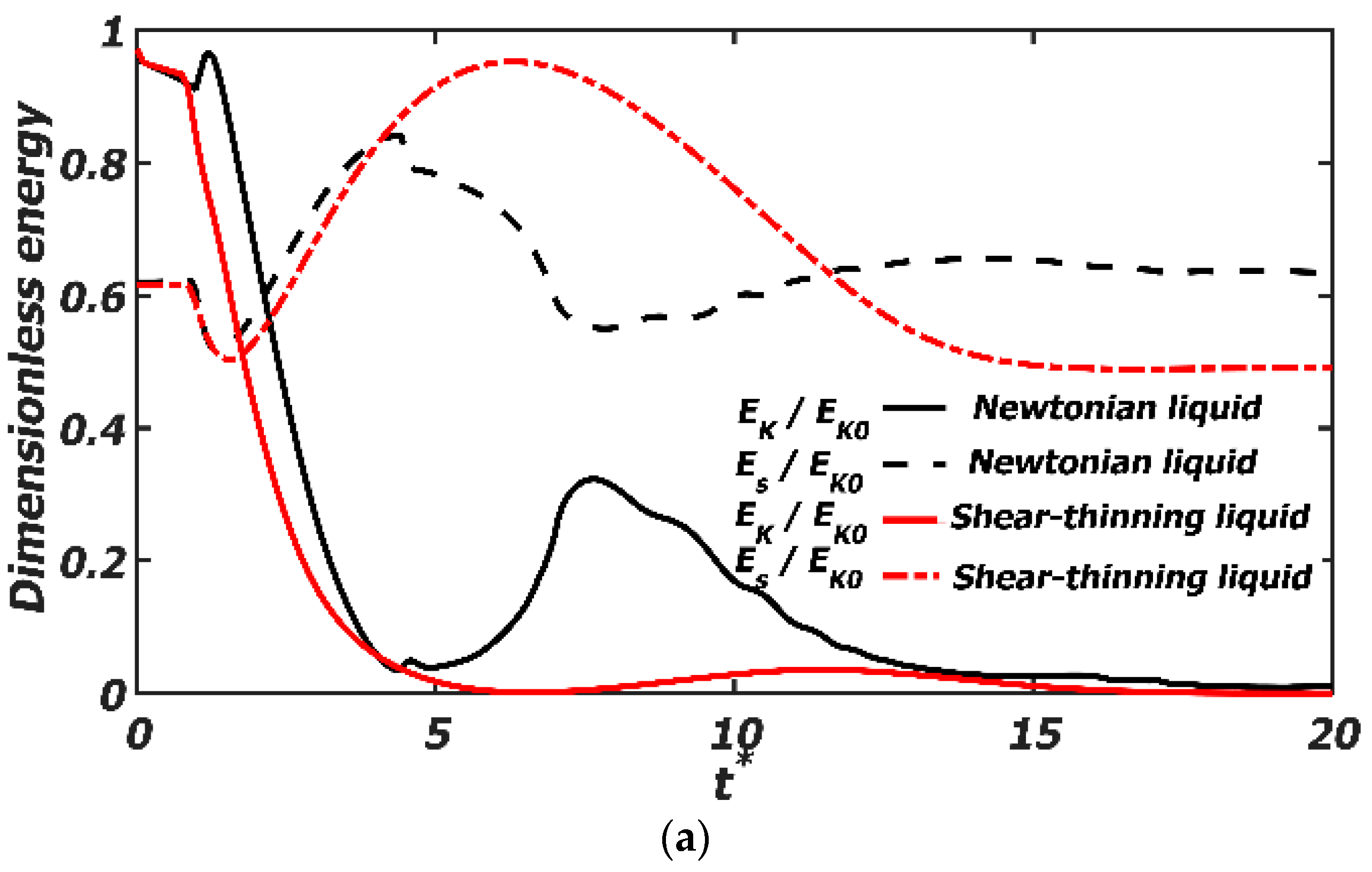
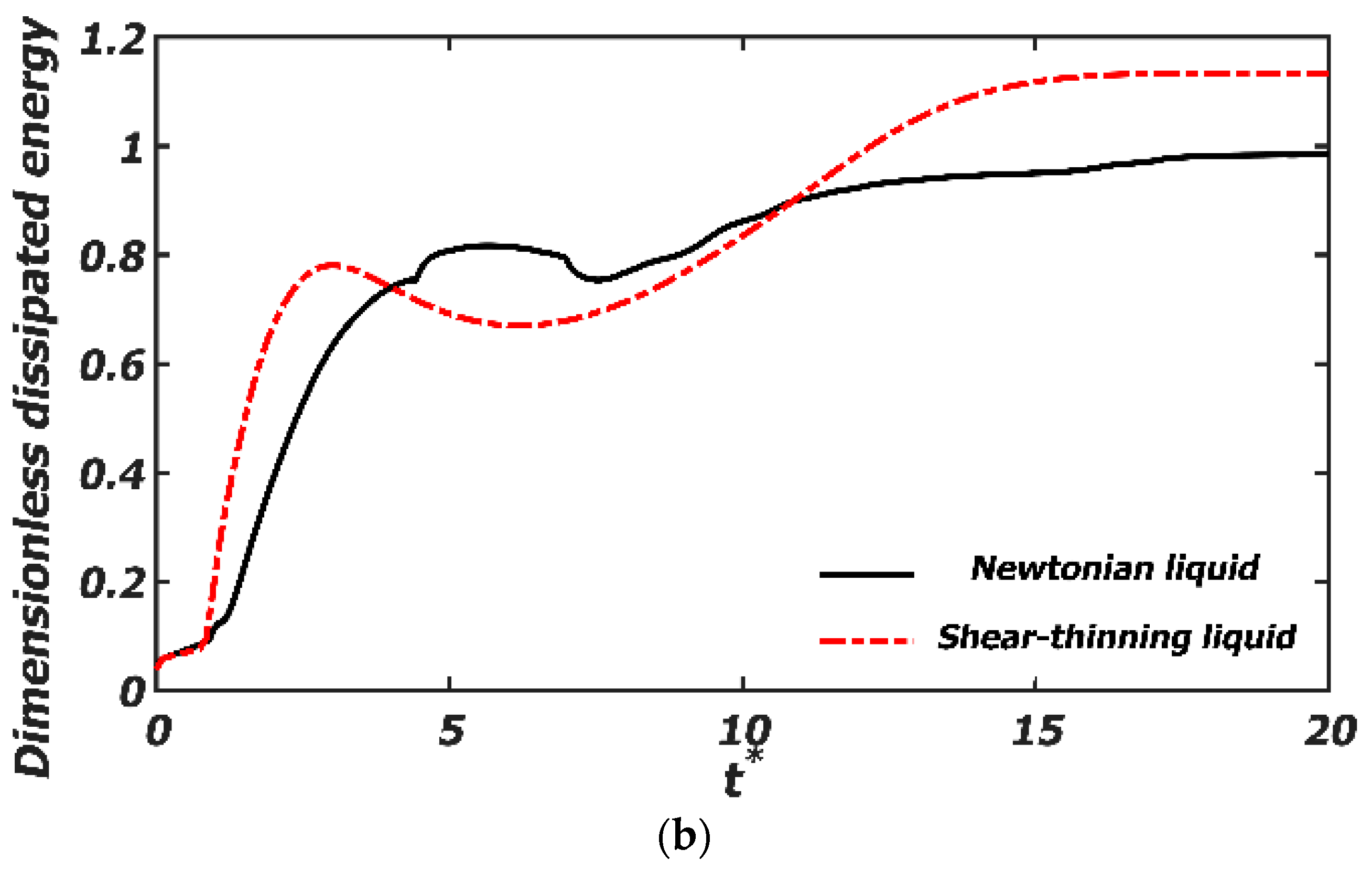
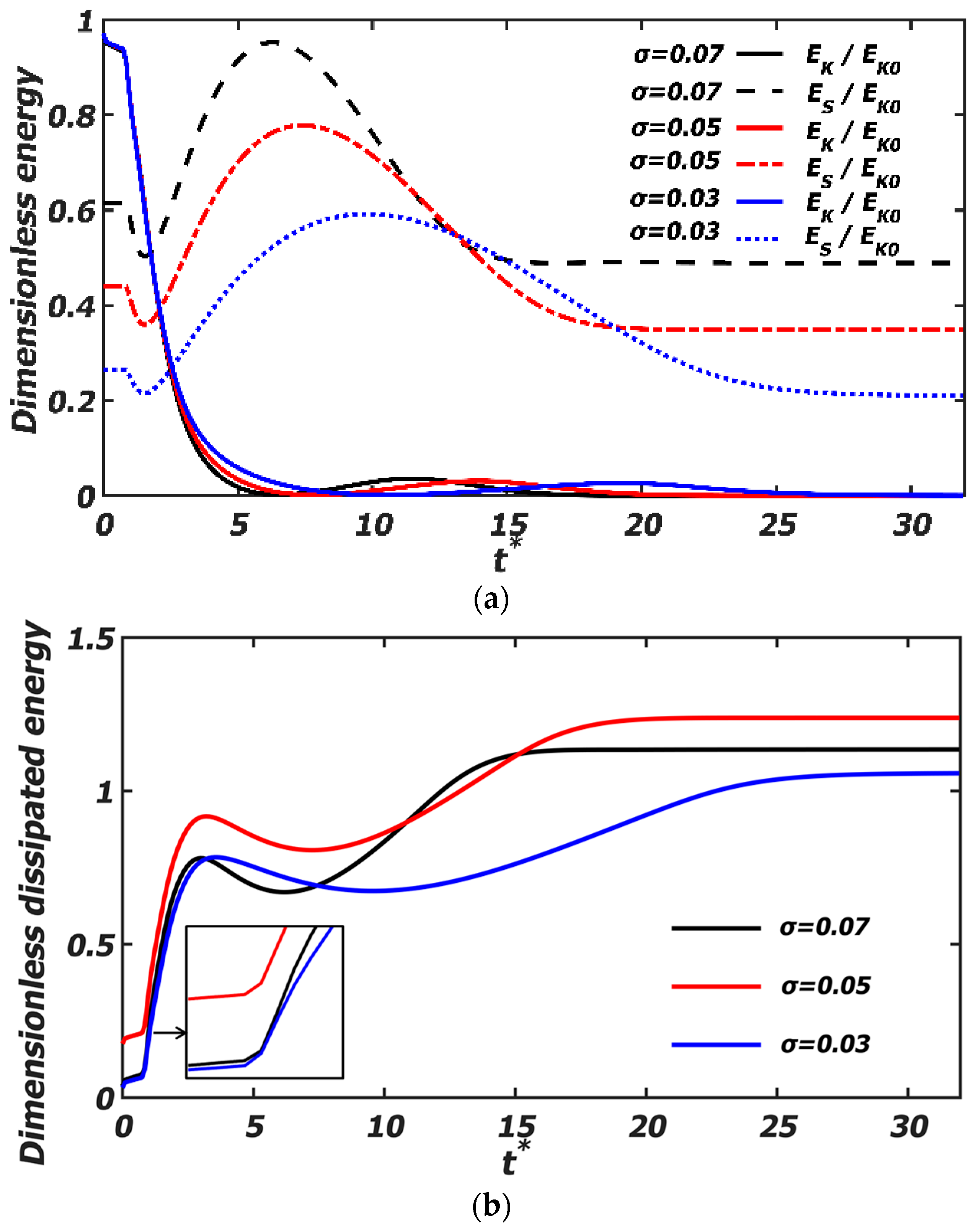
4.4. Energy Evolution
5. Conclusions
- (1)
- For binary polymer droplets collision, permanent coalescence occurs. Compared with the Newtonian liquid, the maximum deformation of the polymer droplets is promoted, and the colliding droplets coalesce more slowly. By decreasing the surface tension, the maximum deformation is promoted, and the coalescence time for the droplets is delayed.
- (2)
- Compared with the Newtonian liquid, at the initial stage, the larger high-pressure and stagnant flow region appears near the center of the polymer droplets. During the collision process, the flow re-direction phenomenon is suppressed, which makes that the separation is hardly possible. By decreasing the surface tension of the polymer droplets, the stagnant flow region at the center of the droplets decreases. At a low surface tension, due to the non-synchronization in the movement of the interface front, the pressure is not smooth and distributes asymmetrically near the center of droplets.
- (3)
- The energy evolution shows that the dissipated energy of the shear-thinning liquid increases faster than that of the Newtonian liquid. By decreasing the surface tension of the polymer droplets, the surface energy decreases, and the dissipated energy increases. At a low surface tension, due to the decreased surface energy being far greater than the increased kinetic energy, the dissipated energy decreases.
Author Contributions
Funding
Conflicts of Interest
References
- Cho, K.Y.; Pourpoint, T.L.; Son, S.F. Microexplosion investigation of monomethylhydrazine gelled droplet with OH planar laser-induced fluorescence. J. Propuls. Power 2013, 29, 1303–1310. [Google Scholar] [CrossRef]
- Yang, H.; Fang, K.; Liu, X.; Cai, Y.; An, F. Effect of cotton cationization using copolymer nanospheres on ink-jet printing of different fabrics. Polymers 2018, 10, 1219. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, Y.W.; Fang, K.J.; Ren, Y.F.; Tang, Z.Y.; Wang, R.Q.; Chen, W.C.; Xie, R.Y.; Shi, Z.; Hao, L.Y. Inkjet Printable and Self-Curable Disperse Dyes/P(St-BA-MAA) Nanosphere Inks for Both Hydrophilic and Hydrophobic Fabrics. Polymers 2018, 10, 1402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Acosta-Vélez, G.; Linsley, C.; Zhu, T.; Wu, W.; Wu, B. Photocurable Bioinks for the 3D Pharming of Combination Therapies. Polymers 2018, 10, 1372. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, Z.Y.; Fang, K.J.; Song, Y.W.; Sun, F.Y. Jetting Performance of Polyethylene Glycol and Reactive Dye Solutions. Polymers 2019, 11, 739. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, D.; Zhang, Y.; Bai, Y.; Tai, X.; Wang, W.; Wang, G. Preparation and Property of Perflfluoropolyether Emulsions. Polymers 2019, 11, 932. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, B.; Li, X.H.; Zhang, W.; Fu, C.; Wang, Y.; Fu, S.Q. Study on Demulsifification-Flocculation Mechanism of Oil-Water Emulsion in Produced Water from Alkali/Surfactant/Polymer Flooding. Polymers 2019, 11, 395. [Google Scholar] [CrossRef] [Green Version]
- Fortelný, I.; Jůza, J. Description of the droplet size evolution in flowing immiscible polymer blends. Polymers 2019, 11, 761. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.J.; Umemura, A.; Law, C.K. An experimental investigation on the collision behavior of hydrocarbon droplets. J. Fluid Mech. 1992, 234, 171–190. [Google Scholar] [CrossRef]
- Willis, K.D.; Orme, M. Binary droplet collisions in a vacuum environment: An experimental investigation of the role of viscosity. Exp. Fluids 2003, 34, 28–41. [Google Scholar] [CrossRef]
- Gotaas, C.; Havelka, P.; Jakobsen, H.A.; Svendsen, H.F.; Hase, M. Effect of viscosity on droplet-droplet collision outcome: Experimental study and numerical comparison. Phys. Fluids 2007, 19, 102106. [Google Scholar] [CrossRef]
- Dai, M.; Schmidt, D.P. Numerical simulation of head-on droplet collision: Effect of viscosity on maximum deformation. Phys. Fluids 2005, 17, 041701. [Google Scholar] [CrossRef]
- Kuschel, M.; Sommerfeld, M. Investigation of droplet collisions for solutions with different solids content. Exp. Fluids 2013, 54, 1440. [Google Scholar] [CrossRef]
- Sommerfeld, M.; Kuschel, M. Modelling droplet collision outcomes for different substances and viscosities. Exp. Fluids 2016, 57, 187. [Google Scholar] [CrossRef]
- Chen, R.H.; Chen, C.T. Collision between immiscible drops with large surface tension difference: Diesel oil and water. Exp. Fluids 2006, 41, 453–461. [Google Scholar] [CrossRef]
- Planchette, C.; Lorenceau, E.; Brenn, G. The onset of fragmentation in binary liquid drop collisions. J. Fluid Mech. 2012, 702, 5–25. [Google Scholar] [CrossRef] [Green Version]
- Pan, K.L.; Tseng, Y.H.; Chen, J.C.; Huang, K.L.; Wang, C.H.; Lai, M.C. Controlling droplet bouncing and coalescence with surfactant. J. Fluid Mech. 2016, 799, 603–636. [Google Scholar] [CrossRef]
- Qian, J.; Law, C.K. Regimes of coalescence and separation in droplet collision. J. Fluid Mech. 1997, 331, 59–80. [Google Scholar] [CrossRef]
- Amani, A.; Balcazar, N.; Gutiérrez, E.; Oliva, A. Numerical study of binary droplets collision in the main collision regimes. Chem. Eng. J. 2019, 370, 477–498. [Google Scholar] [CrossRef]
- Li, X.G.; Fritsching, U. Numerical investigation of binary droplet collisions in all relevant collision regimes. J. Comput. Multiph. Flows 2011, 3, 207–224. [Google Scholar] [CrossRef]
- Saroka, M.D.; Ashgriz, N.; Movassat, M. Numerical Investigation of Head-on Binary Drop Collisions in a Dynamically Inert Environment. J. Appl. Fluid Mech. 2012, 5, 23–37. [Google Scholar]
- Masato, Y.; Jumpei, S.; Kosuke, S. Numerical simulation of head-on collision dynamics of binary droplets with various diameter ratios by the two-phase lattice kinetic scheme. Comput. Fluids 2018, 168, 304–317. [Google Scholar]
- Finotello, G.; Padding, J.T.; Deen, N.G.; Jongsma, A.; Innings, F.; Kuipers, J.A.M. Effect of viscosity on droplet-droplet collisional interaction. Phys. Fluids 2017, 29, 067102. [Google Scholar] [CrossRef] [Green Version]
- Finotello, G.; Kooiman, R.F.; Padding, J.T.; Buist, K.A.; Innings, A.J.F.; Kuipers, J.A.M. The dynamics of milk droplet–droplet collisions. Exp. Fluids 2018, 59, 17. [Google Scholar] [CrossRef] [Green Version]
- Finotello, G.; De, S.; Vrouwenvelder, J.C.R.; Padding, J.T.; Buist, K.A.; Jongsma, A.; Innings, F.; Kuipers, J.A.M. Experimental investigation of non-Newtonian droplet collisions: The role of extensional viscosity. Exp. Fluids 2018, 59, 113. [Google Scholar] [CrossRef] [Green Version]
- Jiang, T.; Lu, L.G.; Lu, W.G. Numerical study of collision process between two equal diameter liquid micro-droplets using a modified smoothed particle hydrodynamics method. Acta Phys. Sin. 2013, 62, 224701. [Google Scholar]
- Motzigemba, M.; Roth, N.; Bothe, D.; Warnecke, H.J.; Prüss, J.; Wielage, K.; Weigand, B. The effect of non-Newtonian flow behavior on binary droplet collisions: VOF-simulation and experimental analysis. Zaragoza 2002, 9, 11. [Google Scholar]
- Focke, C.; Bothe, D. Computational analysis of binary collisions of shear-thinning droplets. J. Non Newton. Fluid 2011, 166, 799–810. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, J.; Zhen, H.; Hu, X. Numerical Simulation on Head-On Binary Collision of Gel Propellant Droplets. Energies 2013, 6, 204–219. [Google Scholar] [CrossRef]
- Sun, K.; Zhang, P.; Law, C.K.; Wang, T. Collision dynamics and internal mixing of droplets of non-Newtonian liquids. Phys. Rev. Appl. 2015, 4, 054013. [Google Scholar] [CrossRef]
- Mark, S.; Elbridge, G.P. A coupled Level Set and Volume-of-Fluid method for computing 3D and axisymmetric incompressible two-phase flows. J. Comput. Phys. 2000, 162, 301–337. [Google Scholar]
- Kwakkel, M.; Breugem, W.P.; Boersma, B.J. Extension of a CLSVOF method for droplet-laden flows with a coalescence/breakup mode. J. Comput. Phys. 2013, 253, 166–188. [Google Scholar] [CrossRef]
- Dianat, M.; Skarysz, M.; Garmory, A. A Coupled Level Set and Volume of Fluid method for automotive exterior water management applications. Int. J. Multiph. Flow 2017, 91, 19–38. [Google Scholar] [CrossRef] [Green Version]
- Weller, H.G. The Development of a New Flame Area Combustion Model Using Conditional Averaging; Thermo-Fluids Section Report TF 9307; Imperial College of Science, Technology and Medicine: London, UK, 1993. [Google Scholar]

| Case | Liquid | σ (kg/s2) | Vr (m/s) | Oheff | We | Re | Ca |
|---|---|---|---|---|---|---|---|
| A | Newtonian liquid | 0.0265 | 2.52 | 0.0262 | 61.4 | 301.60 | 0.202 |
| B | Shear-thinning liquid | 0.07 | 3.58 | 0.0262 | 61.4 | 491.56 | 0.1251 |
| C | Shear-thinning liquid | 0.05 | 3.58 | 0.0309 | 86.1 | 491.56 | 0.1752 |
| D | Shear-thinning liquid | 0.03 | 3.58 | 0.0399 | 143.5 | 491.56 | 0.2920 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, L.; Cong, H.; Zhu, C. A Numerical Investigation on the Collision Behavior of Polymer Droplets. Polymers 2020, 12, 263. https://doi.org/10.3390/polym12020263
Qian L, Cong H, Zhu C. A Numerical Investigation on the Collision Behavior of Polymer Droplets. Polymers. 2020; 12(2):263. https://doi.org/10.3390/polym12020263
Chicago/Turabian StyleQian, Lijuan, Hongchuan Cong, and Chenlin Zhu. 2020. "A Numerical Investigation on the Collision Behavior of Polymer Droplets" Polymers 12, no. 2: 263. https://doi.org/10.3390/polym12020263




