Pyrolytic Kinetics of Polystyrene Particle in Nitrogen Atmosphere: Particle Size Effects and Application of Distributed Activation Energy Method
Abstract
:1. Introduction
2. Literature Review
3. Traditional Kinetic Methods
4. Distributed Activation Energy Method
5. Experimental
6. Results and Discussion
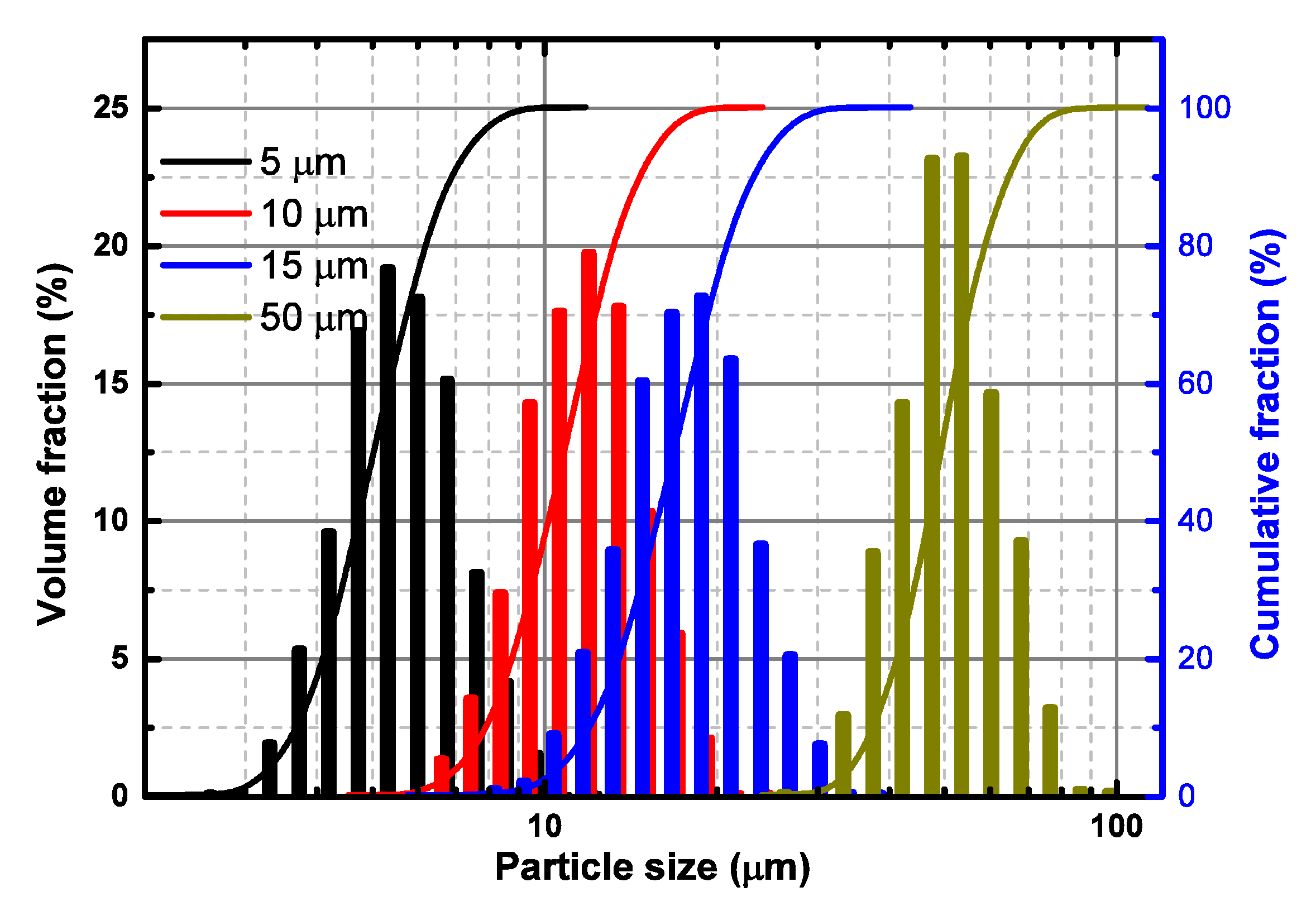
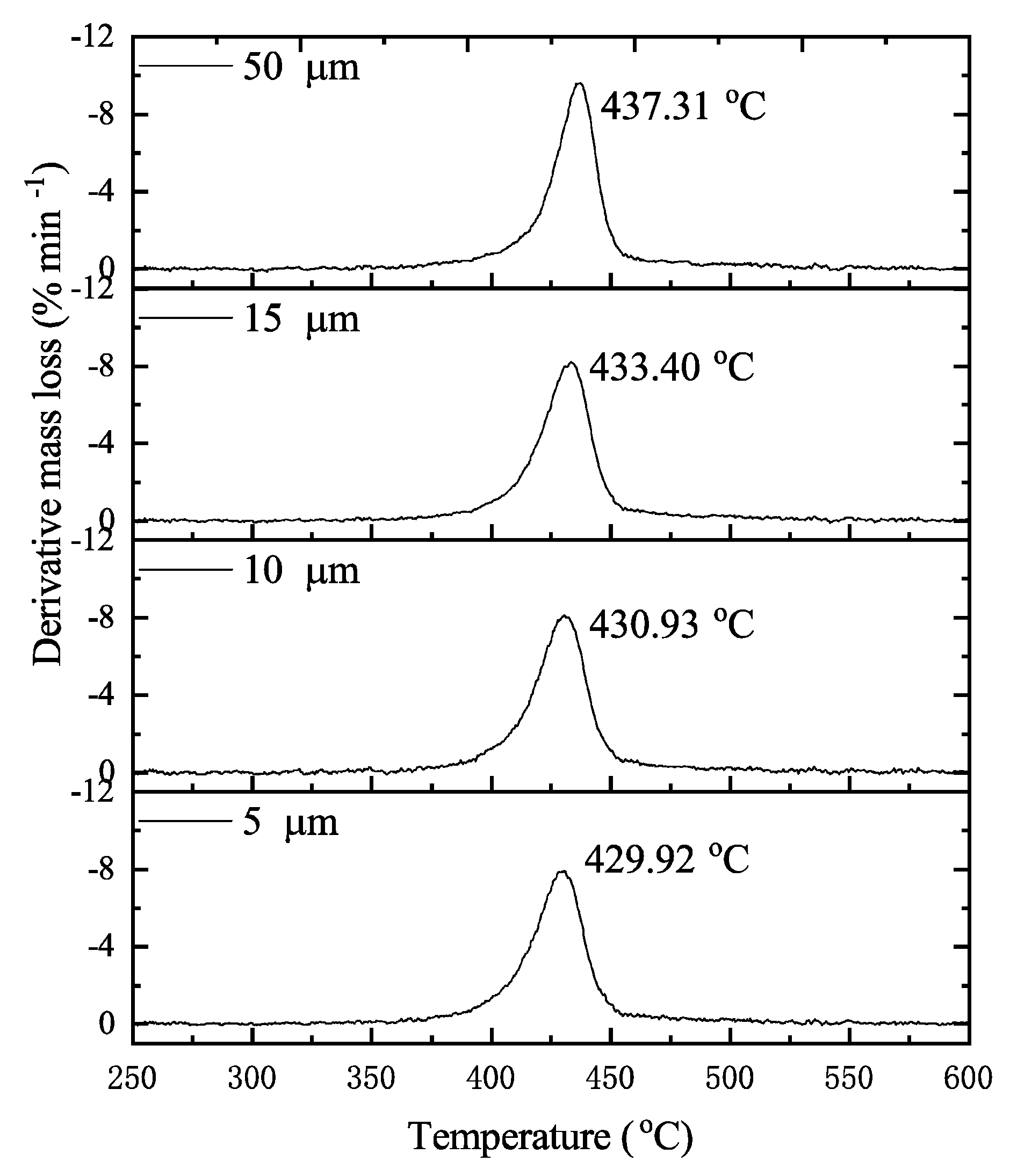
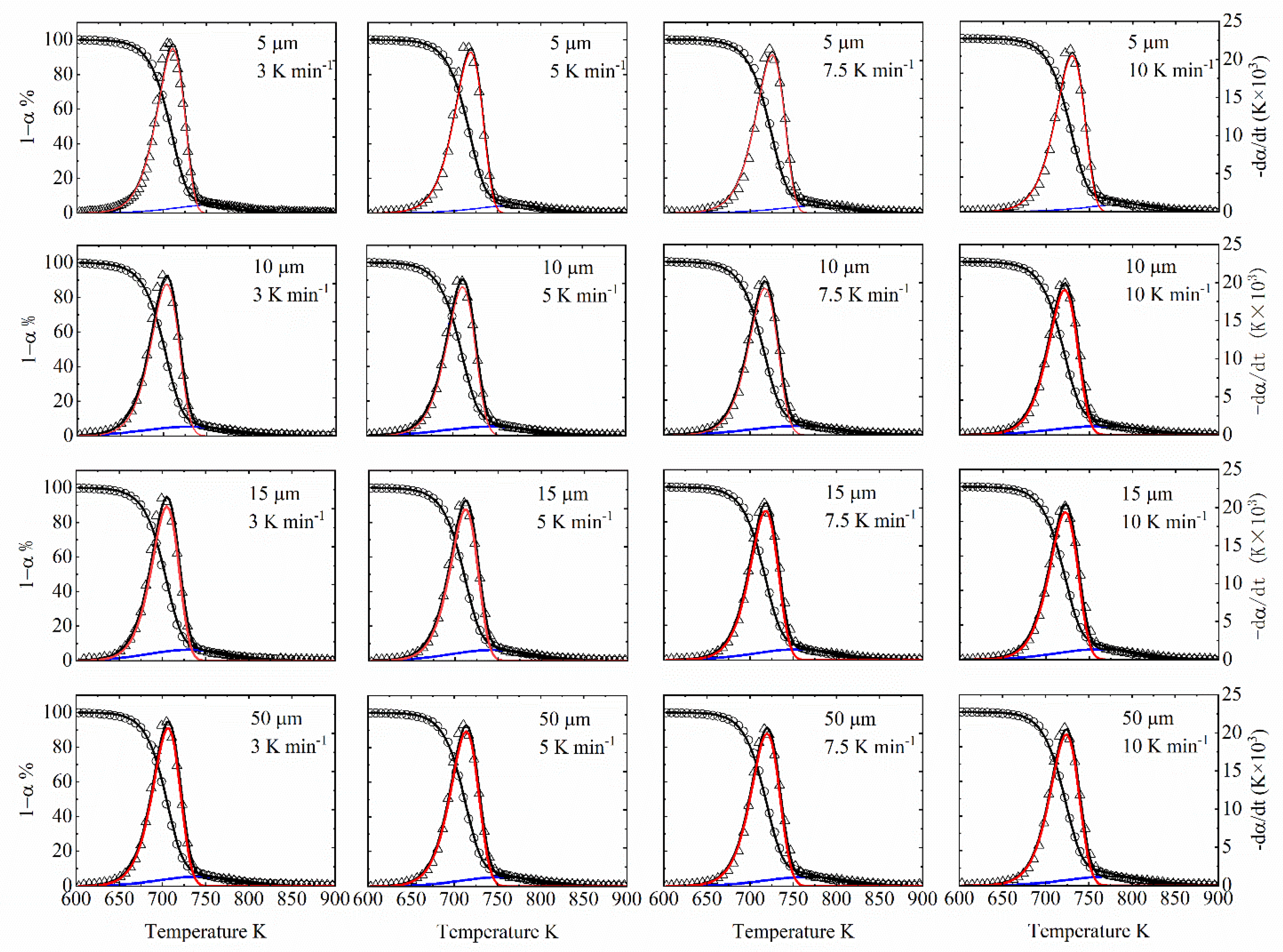
6.1. Pyrolytic Characteristics Observations
6.2. Kinetics Parameters
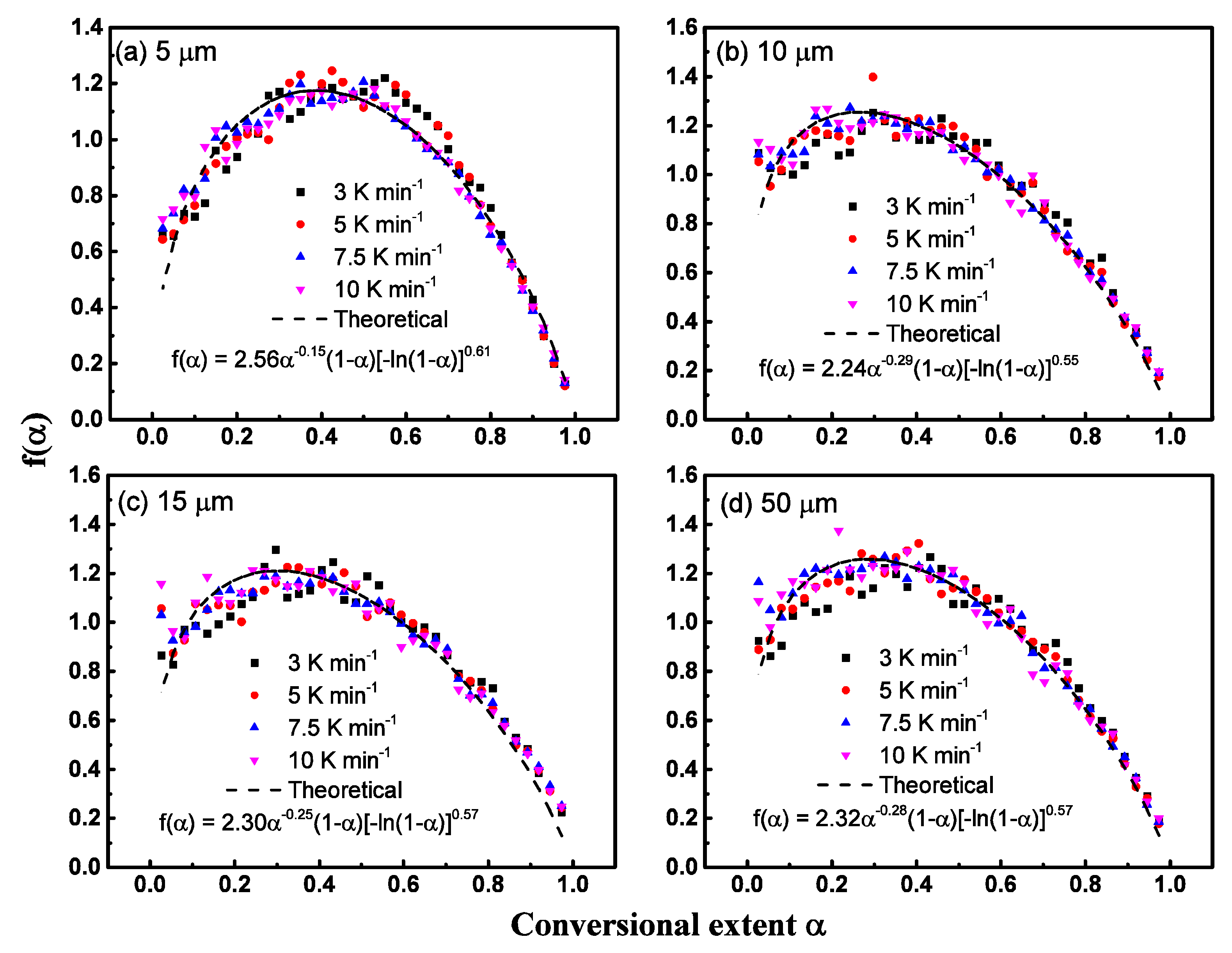
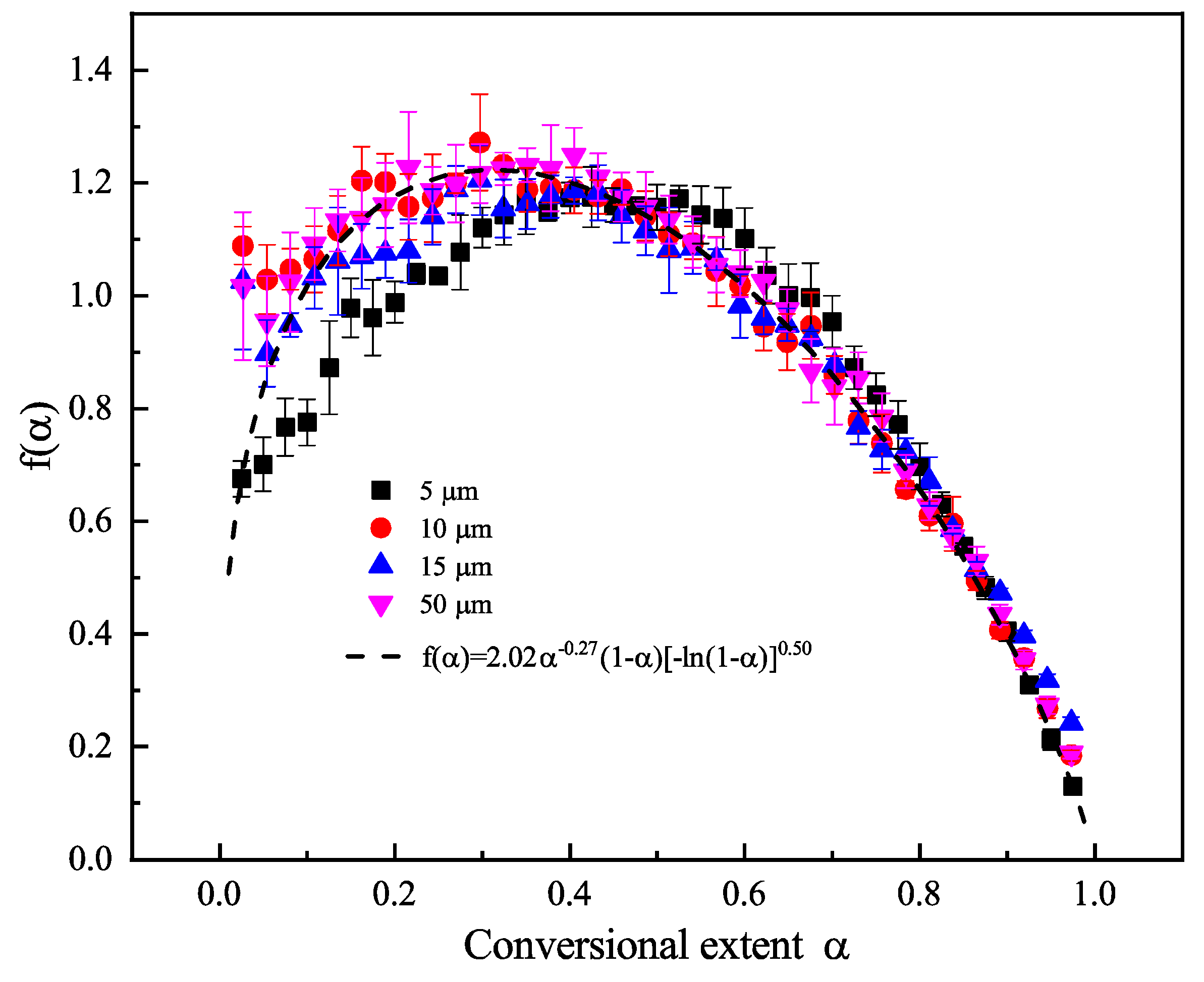
6.3. Model Fitting Method and Compensation Effects
6.4. Numerical Reconstruction
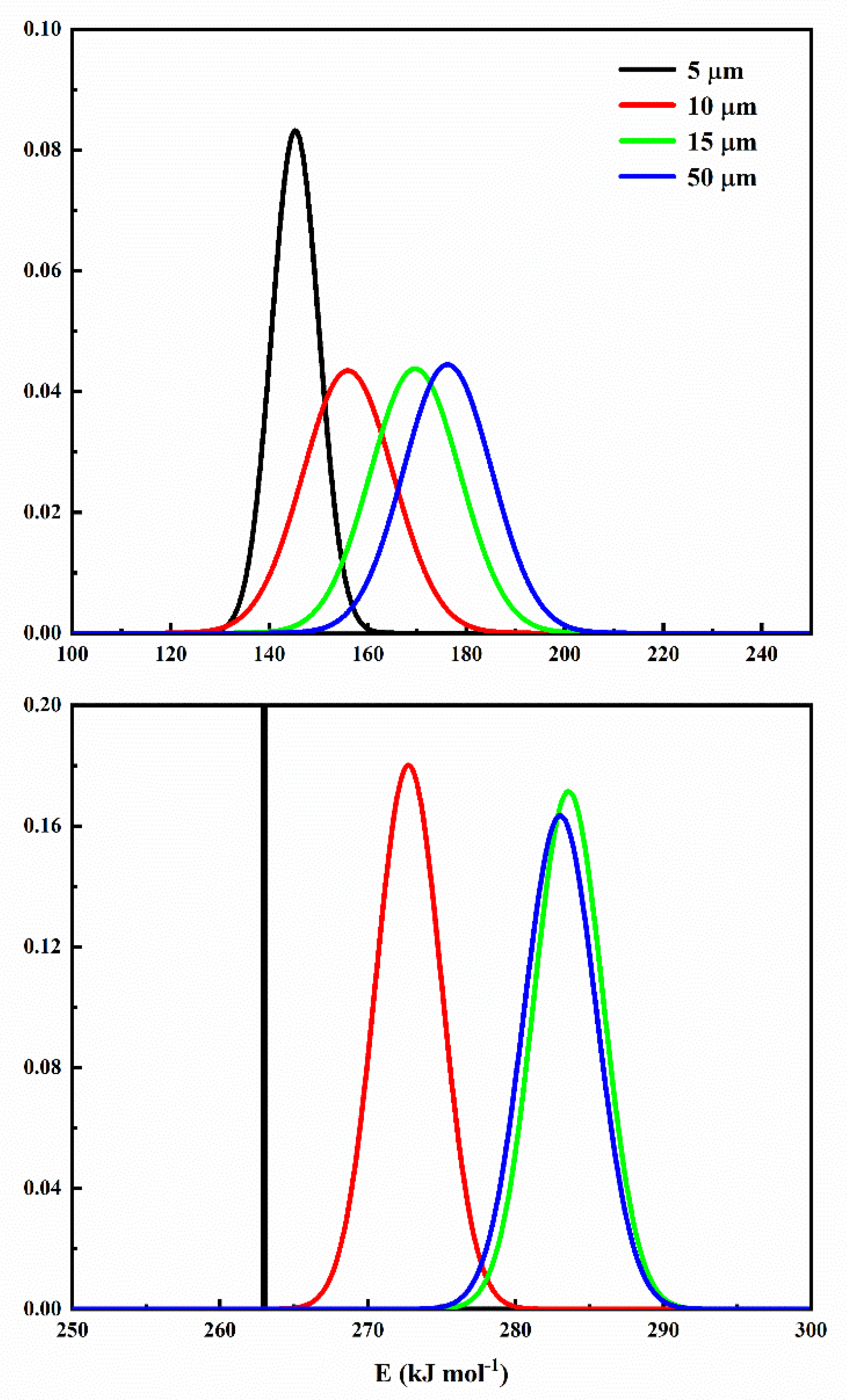
6.5. Step-Reaction Separation by Distributed Activation Energy Method
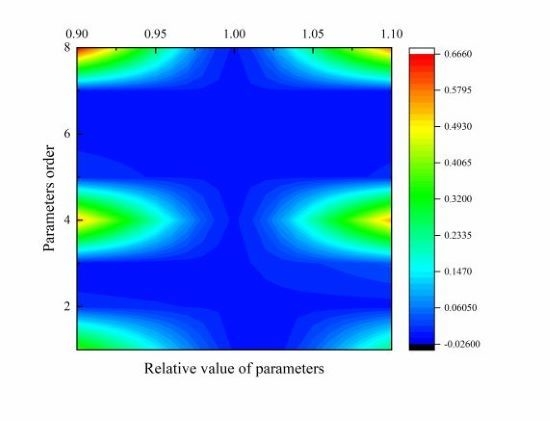
6.6. Sensitivity Analysis of DAEM Parameters
7. Conclusion
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, D.; Jiang, L.; Lu, S.; Cao, C.; Zhang, H.-P. Particle size effects on thermal kinetics and pyrolysis mechanisms of energetic 5-amino-1h-tetrazole. Fuel 2018, 217, 553–560. [Google Scholar] [CrossRef]
- Ding, Y.; Fukumoto, K.; Ezekoye, O.A.; Lu, S.; Wang, C.; Li, C. Experimental and numerical simulation of multi-component combustion of typical charring material. Combustion Flame 2020, 211, 417–429. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, W.; Yu, L.; Lu, K. The accuracy and efficiency of GA and PSO optimization schemes on estimating reaction kinetic parameters of biomass pyrolysis. Energy 2019, 176, 582–588. [Google Scholar] [CrossRef]
- Jiao, L.; Xu, G.; Wang, Q.; Xu, Q.; Sun, J. Kinetics and volatile products of thermal degradation of building insulation materials. Thermochim. Acta 2012, 547, 120–125. [Google Scholar] [CrossRef]
- Jiao, L.; Sun, J. A thermal degradation study of insulation materials extruded polystyrene. Procedia Eng. 2014, 71, 622–628. [Google Scholar] [CrossRef] [Green Version]
- Cheng, J.; Pan, Y.; Yao, J.; Wang, X.; Pan, F.; Jiang, J. Mechanisms and kinetics studies on the thermal decomposition of micron Poly (methyl methacrylate) and polystyrene. J. Loss Prev. Process Ind. 2016, 40, 139–146. [Google Scholar] [CrossRef]
- Shen, J.; Wang, X.S.; Garcia-Perez, M.; Mourant, D.; Rhodes, M.J.; Li, C.Z. Effects of particle size on the fast pyrolysis of oil mallee woody biomass. Fuel 2009, 88, 1810–1817. [Google Scholar] [CrossRef]
- Marcilla, A.; García, A.N.; Pastor, M.V.; León, M.; Sánchez, A.; Gómez, D. Thermal decomposition of the different particles size fractions of almond shells and olive stones. Thermal behaviour changes due to the milling processes. Thermochim. Acta 2013, 564, 24–33. [Google Scholar] [CrossRef]
- Di Blasi, C. Kinetic and heat transfer control in the slow and flash pyrolysis of solids. Ind. Eng. Chem. Res. 1996, 35, 37–46. [Google Scholar] [CrossRef]
- Hanson, S.; Patrick, J.W.; Walker, A. The effect of coal particle size on pyrolysis and steam gasification. Fuel 2002, 81, 531–537. [Google Scholar] [CrossRef]
- Yu, D.; Xu, M.; Sui, J.; Liu, X.; Yu, Y.; Cao, Q. Effect of coal particle size on the proximate composition and combustion properties. Thermochim. Acta 2005, 439, 103–109. [Google Scholar] [CrossRef]
- Kissinger, H.E. Reaction kinetics in differential thermal analysis. Anal. Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Akahira, T.; Sunose, T. Method of determining activation deterioration constant of electrical insulating materials. Res. Rep. Chiba. Inst. Technol. 1971, 16, 22–31. [Google Scholar]
- Flynn, J.H.; Wall, L.A. A quick, direct method for the determination of activation energy from thermogravimetric data. J. Polym. Sci. Pol. Lett. 1966, 4, 323–328. [Google Scholar] [CrossRef]
- Ozawa, T. A new method of analyzing thermogravimetric data. Bull. Chem. Soc. Jap. 1965, 38, 1881–1886. [Google Scholar] [CrossRef] [Green Version]
- Tang, W.; Liu, Y.; Zhang, H.; Wang, C. New approximate formula for Arrhenius temperature integral. Thermochim. Acta 2003, 408, 39–43. [Google Scholar] [CrossRef]
- Tang, W.; Chen, D.; Wang, C. Kinetic study on the thermal dehydration of CaCO3·H2O by the master plots method. Aiche J. 2006, 52, 2211–2216. [Google Scholar]
- Vyazovkin, S.; Dollimore, D. Linear and nonlinear procedures in isoconversional computations of the activation energy of nonisothermal reactions in solids. J. Chem. Inf. Comput. Sci. 1996, 36, 42–45. [Google Scholar] [CrossRef]
- Vyazovkin, S. Advanced isoconversional method. J. Anal. Calorim. 1997, 49, 1493–1499. [Google Scholar] [CrossRef]
- Vyazovkin, S. Evaluation of activation energy of thermally stimulated solid-state reactions under arbitrary variation of temperature. J. Comput. Chem. 1997, 18, 393–402. [Google Scholar] [CrossRef]
- Farjas, J.; Roura, P. Isoconversional analysis of solid state transformations. J. Anal. Calorim. 2011, 105, 757–766. [Google Scholar] [CrossRef]
- Li, K.Y.; Huang, X.; Fleischmann, C.; Rein, G.; Ji, J. Pyrolysis of medium-density fiberboard: Optimized search for kinetics scheme and parameters via a genetic algorithm driven by Kissinger’s method. Energy Fuels 2014, 28, 6130–6139. [Google Scholar] [CrossRef] [Green Version]
- Li, K.; Pau, D.S.W.; Wang, J.; Ji, J. Modelling pyrolysis of charring materials: Determining flame heat flux using bench-scale experiments of medium density fibreboard (MDF). Chem. Eng. Sci. 2015, 123, 39–48. [Google Scholar] [CrossRef]
- Li, K.Y.; Pau, D.S.W.; Hou, Y.N.; Ji, J. Modeling pyrolysis of charring materials: Determining kinetic properties and heat of pyrolysis of medium density fiberboard. Ind. Eng. Chem. Res. 2013, 53, 141–149. [Google Scholar] [CrossRef]
- Gao, X.; Jiang, L.; Xu, Q.; Wu, W.-Q.; Mensah, R.A. Thermal kinetics and reactive mechanism of cellulose nitrate decomposition by traditional multi kinetics and modeling calculation under isothermal and non-isothermal conditions. Ind. Crop. Prod. 2020, 145, 112085. [Google Scholar] [CrossRef]
- Li, K.; Pau, D.S.; Zhang, H. Pyrolysis of polyurethane foam: Optimized search for kinetic properties via simultaneous K–K method, genetic algorithm and elemental analysis. Fire Mater. 2016, 40, 800–817. [Google Scholar] [CrossRef]
- Chen, R.; Xu, X.; Lu, S.; Zhang, Y.; Lo, S. Pyrolysis study of waste phenolic fibre-reinforced plastic by thermogravimetry/Fourier transform infrared/mass spectrometry analysis. Energy Convers. Manag. 2018, 165, 555–566. [Google Scholar] [CrossRef]
- Chen, R.; Li, Q.; Zhang, Y.; Xu, X.; Zhang, D. Pyrolysis kinetics and mechanism of typical industrial non-tyre rubber wastes by peak-differentiating analysis and multi kinetics methods. Fuel 2019, 235, 1224–1237. [Google Scholar] [CrossRef]
- Kong, S.; Huang, X.; Li, K.; Song, X. Adsorption/desorption isotherms of CH4 and C2H6 on typical shale samples. Fuel 2019, 255, 115632. [Google Scholar] [CrossRef]
- Gao, Z.; Wan, H.; Ji, J.; Bi, Y. Experimental prediction on the performance and propagation of ceiling jets under the influence of wall confinement. Energy 2019, 178, 378–385. [Google Scholar] [CrossRef]
- Vand, V. A theory of the irreversible electrical resistance changes of metallic films evaporated in vacuum. Proc. Phys. Soc. 1943, 55, 222. [Google Scholar] [CrossRef]
- Pitt, G.J. The kinetic of the evolution of volatile products from coal. Fuel 1962, 41, 267–274. [Google Scholar]
- Cao, H.Q.; Duan, Q.L.; Chai, H.; Li, X.-X.; Sun, J.-H. Experimental study of the effect of typical halides on pyrolysis of ammonium nitrate using model reconstruction. J. Hazard. Mater. 2020, 384, 121297. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Jiang, L.; He, J.J.; Sun, J.-H. Kinetic triplet determination and modified mechanism function construction for thermo-oxidative degradation of waste polyurethane foam using conventional methods and distributed activation energy model method. Energy 2019, 175, 1–13. [Google Scholar] [CrossRef]
- Chai, H.; Duan, Q.; Jiang, L.; Gong, L.; Chen, H.; Sun, J. Theoretical and experimental study on the effect of nitrogen content on the thermal characteristics of nitrocellulose under low heating rates. Cellulose 2019, 26, 763–776. [Google Scholar] [CrossRef]
- Koga, N.; Malek, J. Accommodation of the actual solid-state process in the kinetic model function. Part 2. Applicability of the empirical kinetic model function to diffusion-controlled reactions. Thermochim. Acta 1996, 282, 69–80. [Google Scholar] [CrossRef]

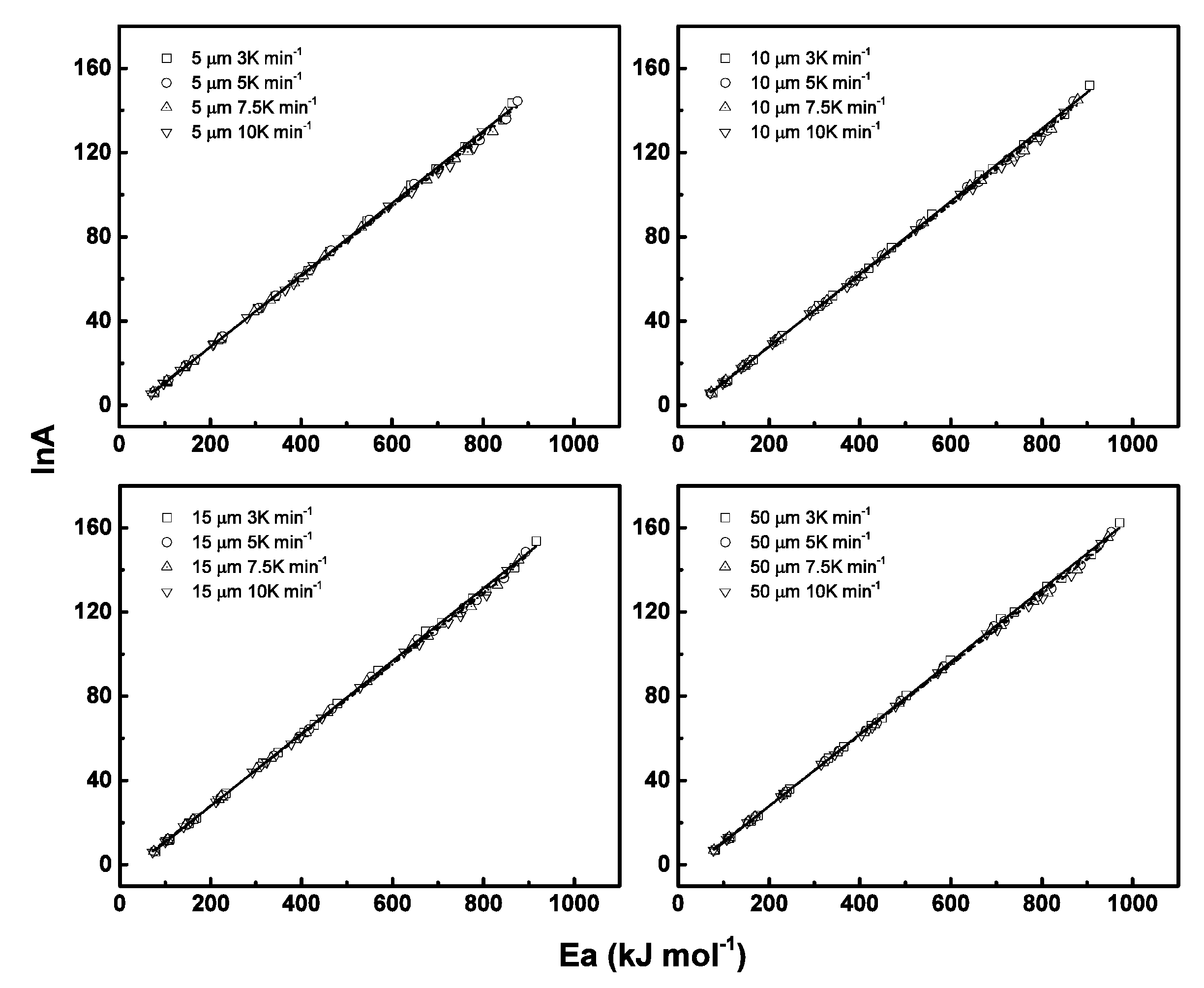

| Methods | Expression | Description |
|---|---|---|
| Flynn–Wall–Ozawa method | logβ = log (AEa/Rg(α)) − 2.315 − 0.4567Ea/RT | Modified general isoconversional equation by Doyle approximation. |
| Kissinger–Akahira–Sunose | ln(β/T2) = ln(AR/Eag(a)) − Ea/RT | Modified general isoconversional equation by Coats-Redfern approximation. |
| Tang et al. | ln(β/T1.894661) = ln[AEa/Rg(α)] + 3.635041 − 1.894661lnEa − 1.001450Ea/RT | Tang et al. proposed an improved approximation for temperature integral. |
| β (oC·min−1) | T0 (oC) | Tp (oC) | Tf (oC) | αmax |
|---|---|---|---|---|
| 5 µm | ||||
| 3 | 367 | 430 | 535 | 91 |
| 5 | 351 | 438 | 545 | 92 |
| 7.5 | 369 | 443 | 528 | 91 |
| 10 | 349 | 447 | 530 | 92 |
| 10 µm | ||||
| 3 | 378 | 431 | 572 | 92 |
| 5 | 378 | 437 | 531 | 91 |
| 7.5 | 381 | 458 | 528 | 90 |
| 10 | 379 | 460 | 534 | 91 |
| 15 µm | ||||
| 3 | 368 | 433 | 524 | 90 |
| 5 | 369 | 440 | 534 | 91 |
| 7.5 | 386 | 446 | 529 | 90 |
| 10 | 382 | 449 | 529 | 91 |
| 50 µm | ||||
| 3 | 375 | 437.31 | 537.50 | 90 |
| 5 | 381 | 444.23 | 534.04 | 90 |
| 7.5 | 385 | 451.87 | 530.90 | 89 |
| 10 | 359 | 455.82 | 535.81 | 90 |
| 3 °C min−1 | 5 °C min−1 | 7.5 °C min−1 | 10 °C min−1 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | lnA | Ea | r2 | Model | lnA | Ea | r2 | Model | lnA | Ea | r2 | Model | lnA | Ea | r2 | |
| 5 µm | 8 | 73.17 | 462.33 | 0.998 | 8 | 73.54 | 466.64 | 0.999 | 8 | 70.47 | 451.10 | 0.999 | 8 | 66.29 | 426.76 | 0.998 |
| 12 | 45.99 | 304.33 | 0.998 | 12 | 46.41 | 307.16 | 0.999 | 12 | 44.47 | 296.76 | 0.998 | 12 | 41.76 | 280.52 | 0.998 | |
| 13 | 32.32 | 225.33 | 0.998 | 13 | 32.75 | 227.42 | 0.999 | 13 | 31.39 | 219.59 | 0.998 | 13 | 29.41 | 207.40 | 0.998 | |
| 10 µm | 8 | 75.06 | 469.28 | 0.990 | 8 | 71.09 | 448.69 | 0.988 | 8 | 71.57 | 453.59 | 0.987 | 8 | 68.97 | 439.20 | 0.988 |
| 12 | 47.26 | 308.99 | 0.990 | 12 | 44.76 | 295.22 | 0.987 | 12 | 45.22 | 298.44 | 0.986 | 12 | 43.56 | 288.83 | 0.988 | |
| 13 | 33.28 | 228.84 | 0.989 | 13 | 31.52 | 218.48 | 0.987 | 13 | 31.95 | 220.87 | 0.986 | 13 | 30.77 | 213.65 | 0.987 | |
| 15 µm | 8 | 76.54 | 478.30 | 0.993 | 8 | 74.02 | 466.03 | 0.993 | 8 | 72.31 | 458.14 | 0.992 | 8 | 69.84 | 444.63 | 0.992 |
| 12 | 48.26 | 315.00 | 0.993 | 12 | 46.73 | 306.77 | 0.992 | 12 | 45.71 | 301.48 | 0.992 | 12 | 44.15 | 292.45 | 0.992 | |
| 13 | 34.03 | 233.35 | 0.992 | 13 | 33.00 | 227.15 | 0.992 | 13 | 32.32 | 223.15 | 0.992 | 13 | 31.22 | 216.36 | 0.992 | |
| 50 µm | 8 | 80.36 | 502.22 | 0.989 | 8 | 77.78 | 489.67 | 0.984 | 8 | 76.64 | 485.47 | 0.983 | 8 | 75.33 | 478.41 | 0.983 |
| 12 | 50.81 | 330.93 | 0.987 | 12 | 49.24 | 322.52 | 0.984 | 12 | 48.61 | 319.68 | 0.982 | 12 | 47.82 | 314.95 | 0.982 | |
| 13 | 35.96 | 245.28 | 0.988 | 13 | 34.89 | 238.94 | 0.983 | 13 | 34.51 | 236.78 | 0.982 | 13 | 33.99 | 233.22 | 0.981 | |
| 3 K min−1 | 5 K min−1 | 7.5 K min−1 | 10 K min−1 | |||||
|---|---|---|---|---|---|---|---|---|
| Particle Size | kiso | Tiso | kiso | Tiso | kiso | Tiso | kiso | Tiso |
| 5 µm | 0.001446 | 704.10 | 0.002360 | 711.74 | 0.003338 | 719.24 | 0.004233 | 722.76 |
| 10 µm | 0.001407 | 697.77 | 0.002181 | 705.57 | 0.003241 | 712.49 | 0.004162 | 716.62 |
| 15 µm | 0.001447 | 698.59 | 0.002301 | 706.27 | 0.003332 | 713.09 | 0.004265 | 717.20 |
| 50 µm | 0.001482 | 701.24 | 0.00233 | 708.72 | 0.003393 | 715.68 | 0.004423 | 719.17 |
| Component | Parameter | 5 µm | 10 µm | 15 µm | 50 µm |
|---|---|---|---|---|---|
| Component 1 | lnA1 | 38.7179 | 40.8492 | 42.6370 | 42.4292 |
| 0.0063 | 2.2146 | 2.3269 | 2.4410 | ||
| E0,1 | 262.9934 | 272.7594 | 283.5884 | 283.0256 | |
| n1 | 0.9004 | 0.8426 | 0.8339 | 0.8613 | |
| Component 2 | lnA2 | 16.3841 | 18.9673 | 21.2544 | 21.8706 |
| 4.7951 | 9.1801 | 9.1128 | 8.9726 | ||
| E0,2 | 145.3102 | 155.9962 | 169.6331 | 176.2200 | |
| n2 | 0.1153 | 0.1614 | 0.1744 | 0.1430 |
| Fitness | ||||
|---|---|---|---|---|
| Particle Size | 3 K min−1 | 5 K min−1 | 7.5 K min−1 | 10 K min−1 |
| 5 µm | 98.06 | 98.01 | 98.20 | 98.29 |
| 10 µm | 98.39 | 98.77 | 98.77 | 98.78 |
| 15 µm | 98.13 | 98.74 | 98.75 | 98.71 |
| 50 µm | 98.52 | 98.72 | 98.70 | 98.79 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Yang, X.-R.; Gao, X.; Xu, Q.; Das, O.; Sun, J.-H.; Kuzman, M.K. Pyrolytic Kinetics of Polystyrene Particle in Nitrogen Atmosphere: Particle Size Effects and Application of Distributed Activation Energy Method. Polymers 2020, 12, 421. https://doi.org/10.3390/polym12020421
Jiang L, Yang X-R, Gao X, Xu Q, Das O, Sun J-H, Kuzman MK. Pyrolytic Kinetics of Polystyrene Particle in Nitrogen Atmosphere: Particle Size Effects and Application of Distributed Activation Energy Method. Polymers. 2020; 12(2):421. https://doi.org/10.3390/polym12020421
Chicago/Turabian StyleJiang, Lin, Xin-Rui Yang, Xu Gao, Qiang Xu, Oisik Das, Jin-Hua Sun, and Manja Kitek Kuzman. 2020. "Pyrolytic Kinetics of Polystyrene Particle in Nitrogen Atmosphere: Particle Size Effects and Application of Distributed Activation Energy Method" Polymers 12, no. 2: 421. https://doi.org/10.3390/polym12020421
APA StyleJiang, L., Yang, X.-R., Gao, X., Xu, Q., Das, O., Sun, J.-H., & Kuzman, M. K. (2020). Pyrolytic Kinetics of Polystyrene Particle in Nitrogen Atmosphere: Particle Size Effects and Application of Distributed Activation Energy Method. Polymers, 12(2), 421. https://doi.org/10.3390/polym12020421