Investigation of the Thermal Conductivity of Resin-Based Lightweight Composites Filled with Hollow Glass Microspheres
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of HGM/EP LWTI Composites
2.3. Characterization and Measurements
3. Results
3.1. The Morphology and Density of HGM/EP LWTI Composites
3.2. The Flexural Properties of HGM/EP LWTI Composites
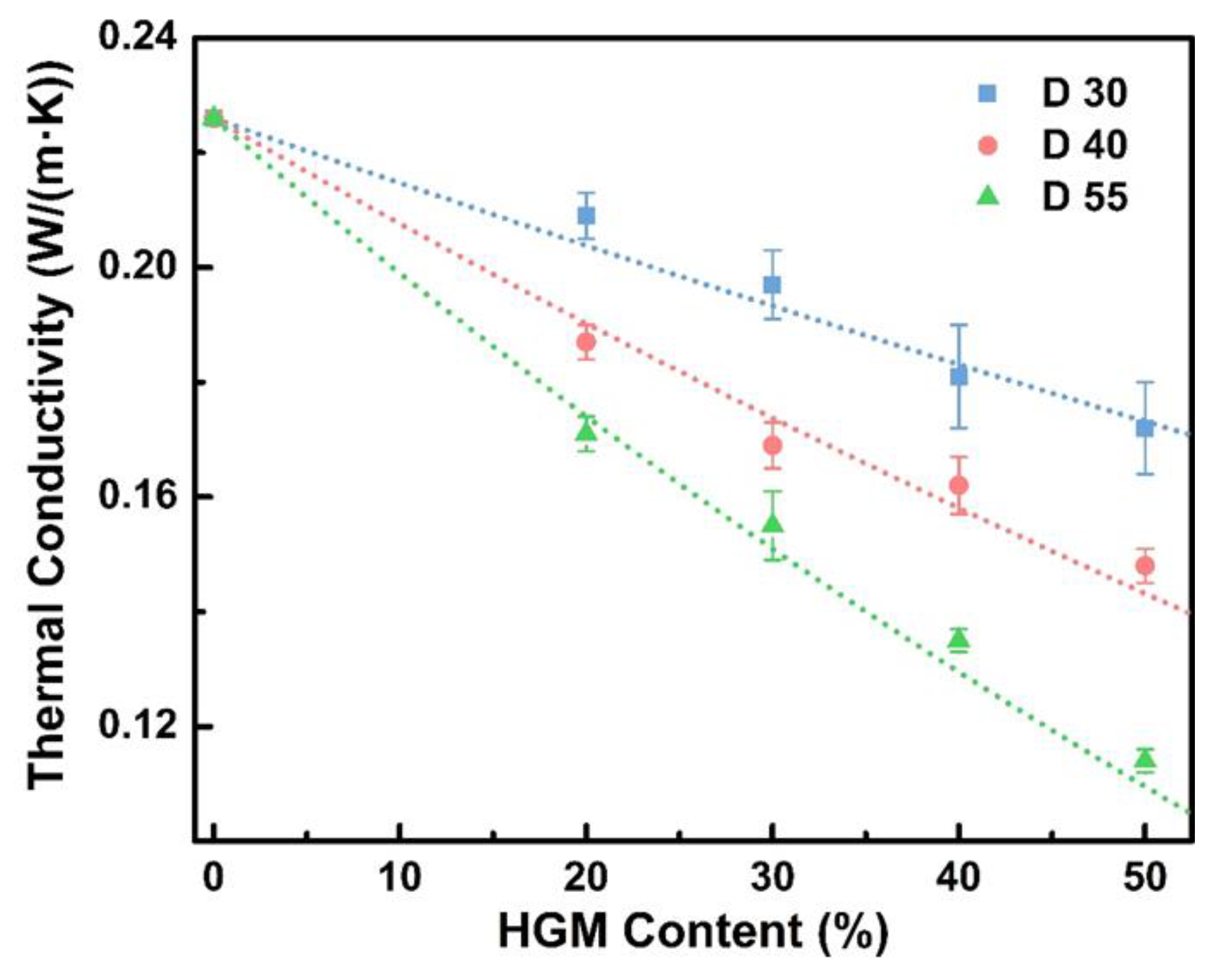
3.3. The Thermal Conductivity of HGM/EP LWTI Composites
3.3.1. Thermal Conductivity Model for HGM/EP LWTI Composites
- (1)
- The HGMs, epoxy resin, and the LWTI composites formed using them are all isotropic.
- (2)
- The HGMs are evenly dispersed throughout the resin matrix, and the matrix resin evenly surrounds the surface of the HGMs.
- (3)
- The effect of bubbles on the composite properties is ignored (excluding the hollow interior of the HGMs).
3.3.2. The Experimental Thermal Conductivity Results
3.4. Insulation Mechanism of HGM/EP LWTI Composites
3.4.1. The Gaseous Convection within the HGMs
3.4.2. The Thermal Radiation on the Surface of the HGMs
3.4.3. The Solid and Gaseous Conduction
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Van de Kamp, J.; Hook, S.E.; Williams, A.; Tanner, J.E.; Bodrossy, L. Baseline characterization of aerobic hydrocarbon degrading microbial communities in deep-sea sediments of the Great Australian Bight, Australia. Env. Microbiol. 2019, 21, 1782–1797. [Google Scholar] [CrossRef] [PubMed]
- Qiao, Y.; Wang, X.; Zhang, X.; Xing, Z. Investigation of flexural properties of hollow glass microsphere filled resin-matrix composites. Pigment Resin Technol. 2016, 45, 426–430. [Google Scholar] [CrossRef]
- Kark, S.; Brokovich, E.; Mazor, T.; Levin, N. Emerging conservation challenges and prospects in an era of offshore hydrocarbon exploration and exploitation. Conserv. Biol. 2015, 29, 1573–1585. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shahrokhabadi, S.; Cao, T.D.; Vahedifard, F. Thermal Effects on Hydromechanical Response of Seabed-Supporting Hydrocarbon Pipelines. Int. J. Geomech. 2020, 20, 1–16. [Google Scholar] [CrossRef]
- Otomi, O.K.; Onochie, U.P.; Obanor, A.I. Steady state analysis of heat transfer in a fully buried crude oil pipeline. Int. J. Heat Mass Transf. 2020, 146, 118893. [Google Scholar] [CrossRef]
- Guo, L.; Tong, W.; Xu, Y.; Ye, H. Composites with excellent insulation and high adaptability for lightweight envelopes. Energies 2019, 12, 53. [Google Scholar] [CrossRef] [Green Version]
- Herrera-Ramírez, L.C.; Cano, M.; Guzman de Villoria, R. Low thermal and high electrical conductivity in hollow glass microspheres covered with carbon nanofiber–polymer composites. Compos. Sci. Technol. 2017, 151, 211–218. [Google Scholar] [CrossRef]
- Gupta, N.; Ye, R.; Porfiri, M. Comparison of tensile and compressive characteristics of vinyl ester/glass microballoon syntactic foams. Compos. Part B Eng. 2010, 41, 236–245. [Google Scholar] [CrossRef]
- Cavasin, M.; Giannis, S.; Salvo, M.; Casalegno, V.; Sangermano, M. Mechanical and thermal characterization of an epoxy foam as thermal layer insulation for a glass fiber reinforced polymer. J. Appl. Polym. Sci. 2018, 135, 1–7. [Google Scholar] [CrossRef]
- Swetha, C.; Kumar, R. Quasi-static uni-axial compression behaviour of hollow glass microspheres/epoxy based syntactic foams. Mater. Des. 2011, 32, 4152–4163. [Google Scholar] [CrossRef]
- Xu, S.; Chen, L.; Gong, M.; Hu, X.; Zhang, X.; Zhou, Z. Characterization and engineering application of a novel ceramic composite insulation material. Compos. Part B Eng. 2017, 111, 143–147. [Google Scholar] [CrossRef]
- Wang, M.; Xu, Y.; Liu, Y.; Wu, W.; Xu, S. Synthesis of Sb-doped SnO2 (ATO) hollow microspheres and its application in photo-thermal shielding coating. Prog. Org. Coatings 2019, 136, 105229. [Google Scholar] [CrossRef]
- Wang, S.; Luo, R.; Ni, Y. Preparation and characterization of resin-derived carbon foams reinforced by hollow ceramic microspheres. Mater. Sci. Eng. A 2010, 527, 3392–3395. [Google Scholar] [CrossRef]
- Liao, Y.; Wu, X.; Liu, H.; Chen, Y. Thermal conductivity of powder silica hollow spheres. Thermochim. Acta 2011, 526, 178–184. [Google Scholar] [CrossRef]
- Patankar, S.N.; Kranov, Y.A. Hollow glass microsphere HDPE composites for low energy sustainability. Mater. Sci. Eng. A 2010, 527, 1361–1366. [Google Scholar] [CrossRef]
- Ruckdeschel, P.; Kemnitzer, T.W.; Nutz, F.A.; Senker, J.; Retsch, M. Hollow silica sphere colloidal crystals: Insights into calcination dependent thermal transport. Nanoscale 2015, 7, 10059–10070. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shunmugasamy, V.C.; Pinisetty, D.; Gupta, N. Viscoelastic properties of hollow glass particle filled vinyl ester matrix syntactic foams: Effect of temperature and loading frequency. J. Mater. Sci. 2013, 48, 1685–1701. [Google Scholar] [CrossRef]
- Jia, Z.; Wang, Z.; Hwang, D.; Wang, L. Prediction of the Effective Thermal Conductivity of Hollow Sphere Foams. ACS Appl. Energy Mater. 2018, 1, 1146–1157. [Google Scholar] [CrossRef]
- Zhang, X.C.; Xia, X.L.; Li, D.H.; Sun, C. Theoretical modeling and inverse analysis of thermal conductivity of skeletons in SiO2 nano-insulation materials. Nanomaterials 2019, 9, 934. [Google Scholar] [CrossRef] [Green Version]
- Liao, Y.; Wu, X.; Wang, Z.; Yue, R.; Liu, G.; Chen, Y. Composite thin film of silica hollow spheres and waterborne polyurethane: Excellent thermal insulation and light transmission performances. Mater. Chem. Phys. 2012, 133, 642–648. [Google Scholar] [CrossRef]
- Pietrak, K.; Wiśniewski, T. A review of models for effective thermal conductivity of composite materials. J. Power Technol. 2015, 95, 14–24. [Google Scholar]
- Gedler, G.; Antunes, M.; Borca-Tasciuc, T.; Velasco, J.I.; Ozisik, R. Effects of graphene concentration, relative density and cellular morphology on the thermal conductivity of polycarbonate-graphene nanocomposite foams. Eur. Polym. J. 2016, 75, 190–199. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Chen, A.N.; Lin, X.; Wu, J.M.; Chen, S.; Cheng, L.J.; Chen, Y.; Wen, S.F.; Li, C.H.; Shi, Y.S. Lightweight mullite ceramics with controlled porosity and enhanced properties prepared by SLS using mechanical mixed FAHSs/polyamide12 composites. Ceram. Int. 2019, 45, 20803–20809. [Google Scholar] [CrossRef]
- Gu, J.; Zhang, Q.; Dang, J.; Xie, C. Thermal conductivity epoxy resin composites filled with boron nitride. Polym. Adv. Technol. 2012, 23, 1025–1028. [Google Scholar] [CrossRef]
- Qiao, Y.; Wang, X.; Zhang, X.; Xing, Z. Thermal conductivity and compressive properties of hollow glass microsphere filled epoxy-matrix composites. J. Reinf. Plast. Compos. 2015, 34, 1413–1421. [Google Scholar] [CrossRef]
- Chau, M.; Kopera, B.A.F.; Machado, V.R.; Tehrani, S.M.; Winnik, M.A.; Kumacheva, E.; Retsch, M. Reversible transition between isotropic and anisotropic thermal transport in elastic polyurethane foams. Mater. Horizons 2017, 4, 236–241. [Google Scholar] [CrossRef] [Green Version]
- Kulesa, A.T.; Robinson, M.J. Analytical study of structural thermal insulating syntactic foams. Compos. Struct. 2015, 119, 551–558. [Google Scholar] [CrossRef]
- Liang, J.Z. Thermal conductivity of PP/Al(OH)3/Mg(OH)2 composites. Compos. Part. B Eng. 2013, 44, 248–252. [Google Scholar] [CrossRef]
- Liang, J.Z. Estimation of thermal conductivity for polypropylene/hollow glass bead composites. Compos. Part. B Eng. 2014, 56, 431–434. [Google Scholar] [CrossRef]
- Ganapathy, D.; Singh, K.; Phelan, P.E.; Prasher, R. An effective unit cell approach to compute the thermal conductivity of composites with cylindrical particles. J. Heat Transf. 2005, 127, 553–559. [Google Scholar] [CrossRef]
- Geisler, M.; Vidi, S.; Ebert, H.P. Study on the Principle Mechanisms of Heat Transfer for Cryogenic Insulations: Especially Accounting for the Temperature-Dependent Deposition–Evacuation of the Filling Gas (Self-Evacuating Systems). Int. J. Thermophys. 2016, 37, 1–13. [Google Scholar] [CrossRef]
- Ruckdeschel, P.; Philipp, A.; Retsch, M. Understanding Thermal Insulation in Porous, Particulate Materials. Adv. Funct. Mater. 2017, 27, 1–11. [Google Scholar] [CrossRef]
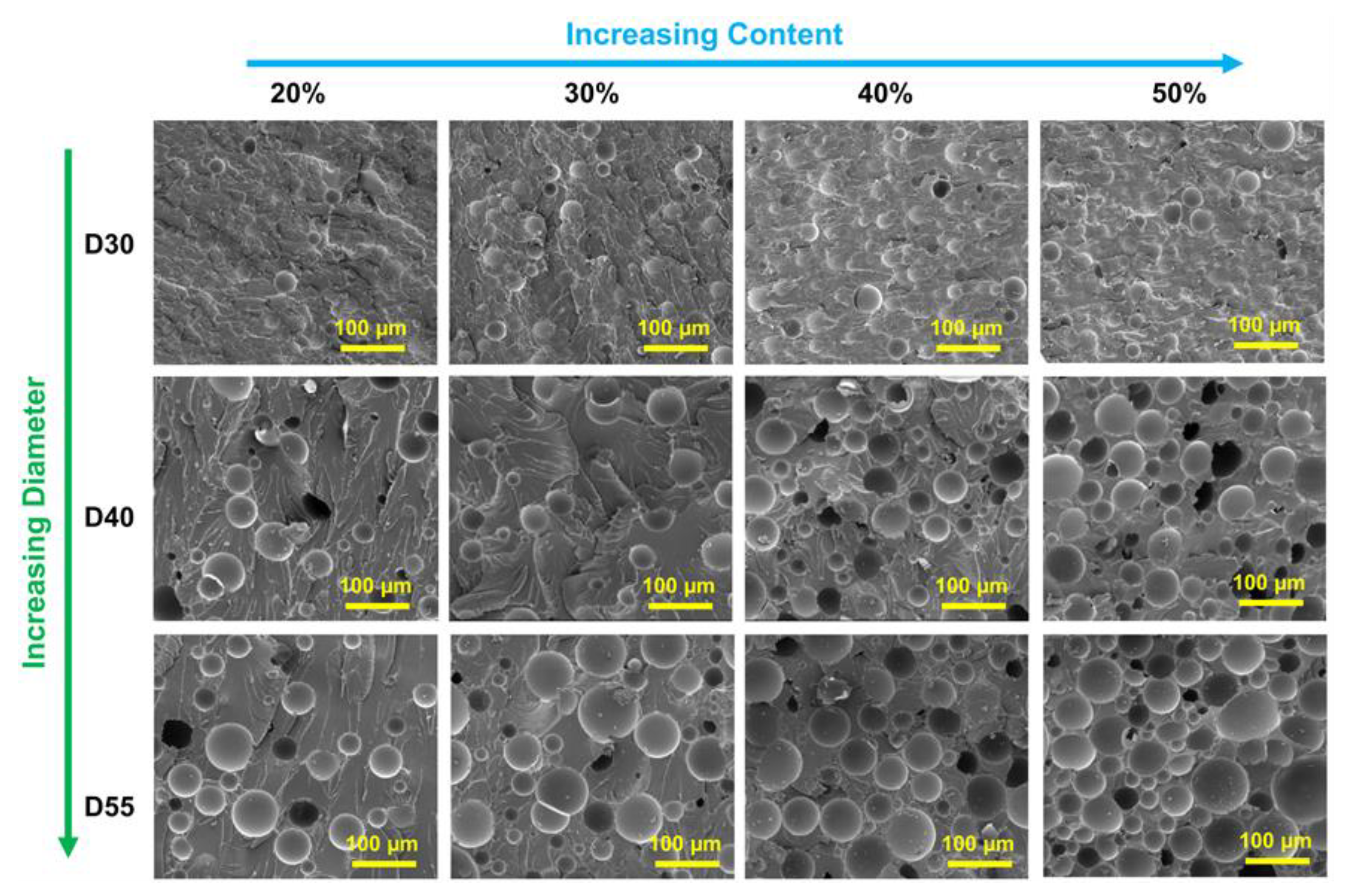



| Diameter (μm) | Content of HGMs (vol.%) | ρth (g/cm3) | ρexp (g/cm3) | φv (%) |
|---|---|---|---|---|
| 30 | 20 | 1.071 | 1.045 | 2.41 |
| 30 | 1.012 | 0.979 | 3.28 | |
| 40 | 0.953 | 0.912 | 4.33 | |
| 50 | 0.895 | 0.845 | 5.50 | |
| 40 | 20 | 1.005 | 1.027 | 2.17 |
| 30 | 0.946 | 0.915 | 3.33 | |
| 40 | 0.865 | 0.831 | 4.03 | |
| 50 | 0.785 | 0.743 | 5.34 | |
| 55 | 20 | 0.981 | 0.930 | 5.18 |
| 30 | 0.877 | 0.826 | 5.86 | |
| 40 | 0.773 | 0.709 | 8.39 | |
| 50 | 0.670 | 0.591 | 11.71 |
| Thermal Conductivity (W/(m·K)) | Volume Fraction | |||
|---|---|---|---|---|
| 20% | 30% | 40% | 50% | |
| D30 | 0.204 | 0.193 | 0.183 | 0.173 |
| D40 | 0.190 | 0.174 | 0.158 | 0.143 |
| D55 | 0.174 | 0.151 | 0.129 | 0.110 |
| HGMs Content (vol.%) | Type | Thermal Conductivity Theoretical Value (W/(m·K)) | Thermal Conductivity of Actual Value (W/(m·K)) | Error (%) |
|---|---|---|---|---|
| 20 | D30 | 0.204 | 0.209 | 2.532 |
| D40 | 0.190 | 0.187 | 1.710 | |
| D55 | 0.174 | 0.171 | 1.755 | |
| 30 | D30 | 0.193 | 0.197 | 1.918 |
| D40 | 0.174 | 0.169 | 2.738 | |
| D55 | 0.151 | 0.155 | 2.679 | |
| 40 | D30 | 0.183 | 0.181 | 1.137 |
| D40 | 0.158 | 0.162 | 2.474 | |
| D55 | 0.129 | 0.135 | 4.246 | |
| 50 | D30 | 0.173 | 0.172 | 0.685 |
| D40 | 0.143 | 0.148 | 3.363 | |
| D55 | 0.110 | 0.114 | 4.090 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Z.; Ke, H.; Wang, X.; Zheng, T.; Qiao, Y.; Chen, K.; Zhang, X.; Zhang, L.; Bai, C.; Li, Z. Investigation of the Thermal Conductivity of Resin-Based Lightweight Composites Filled with Hollow Glass Microspheres. Polymers 2020, 12, 518. https://doi.org/10.3390/polym12030518
Xing Z, Ke H, Wang X, Zheng T, Qiao Y, Chen K, Zhang X, Zhang L, Bai C, Li Z. Investigation of the Thermal Conductivity of Resin-Based Lightweight Composites Filled with Hollow Glass Microspheres. Polymers. 2020; 12(3):518. https://doi.org/10.3390/polym12030518
Chicago/Turabian StyleXing, Zhipeng, Hongjun Ke, Xiaodong Wang, Ting Zheng, Yingjie Qiao, Kaixuan Chen, Xiaohong Zhang, Lili Zhang, Chengying Bai, and Zhuoran Li. 2020. "Investigation of the Thermal Conductivity of Resin-Based Lightweight Composites Filled with Hollow Glass Microspheres" Polymers 12, no. 3: 518. https://doi.org/10.3390/polym12030518
APA StyleXing, Z., Ke, H., Wang, X., Zheng, T., Qiao, Y., Chen, K., Zhang, X., Zhang, L., Bai, C., & Li, Z. (2020). Investigation of the Thermal Conductivity of Resin-Based Lightweight Composites Filled with Hollow Glass Microspheres. Polymers, 12(3), 518. https://doi.org/10.3390/polym12030518






