Influence of Polymer Concentration and Nozzle Material on Centrifugal Fiber Spinning
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Rheological Characterization
2.3. Fiber Characterization
2.4. Contact Angle
2.5. Force to Push Polymer Solution from Different Nozzle Materials
3. Results
3.1. Fiber Spinning Setup
3.2. Characterization of Polymer Solutions
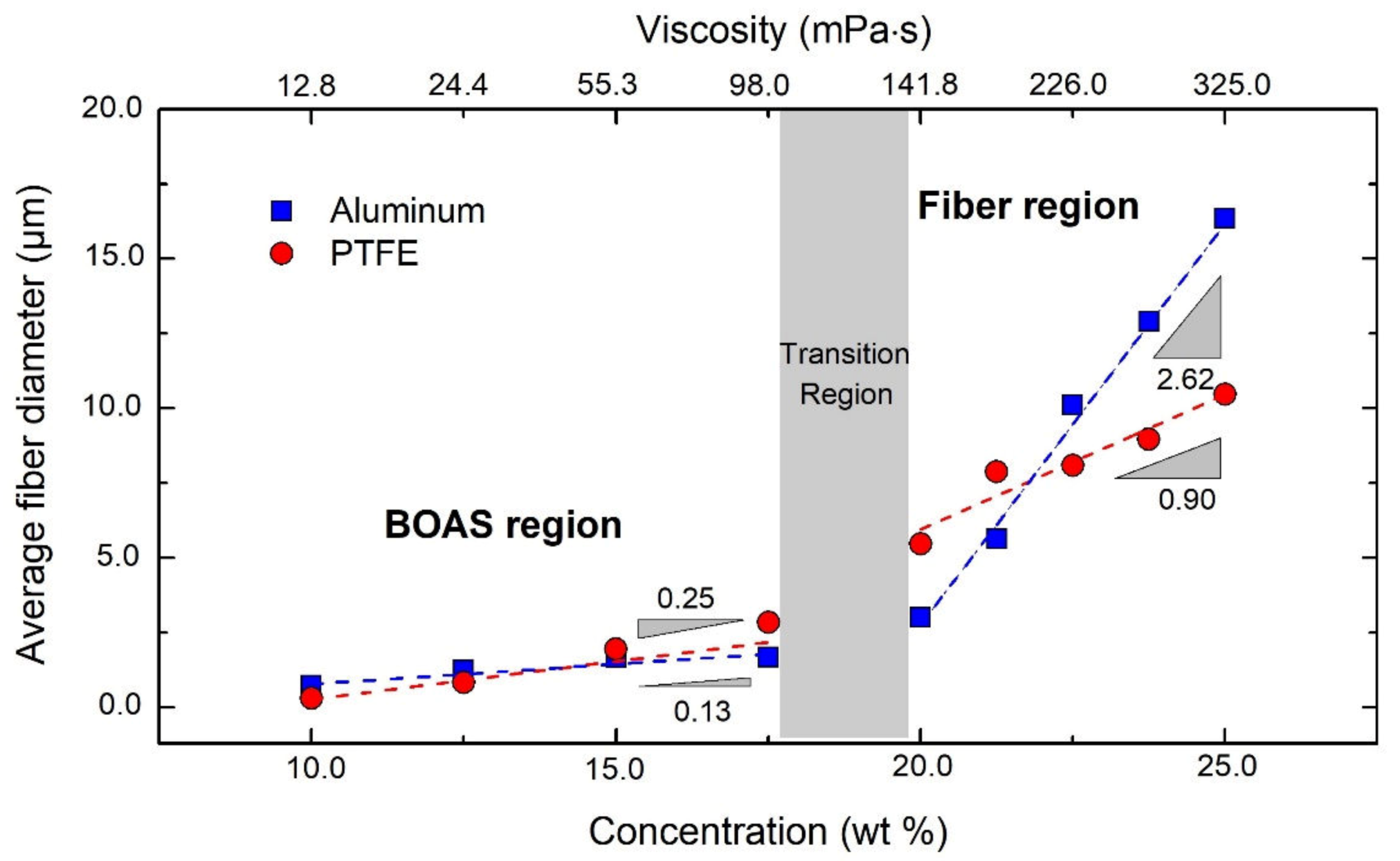
3.3. Changes to Fiber Morphology with Polymer Concentration
4. Discussion
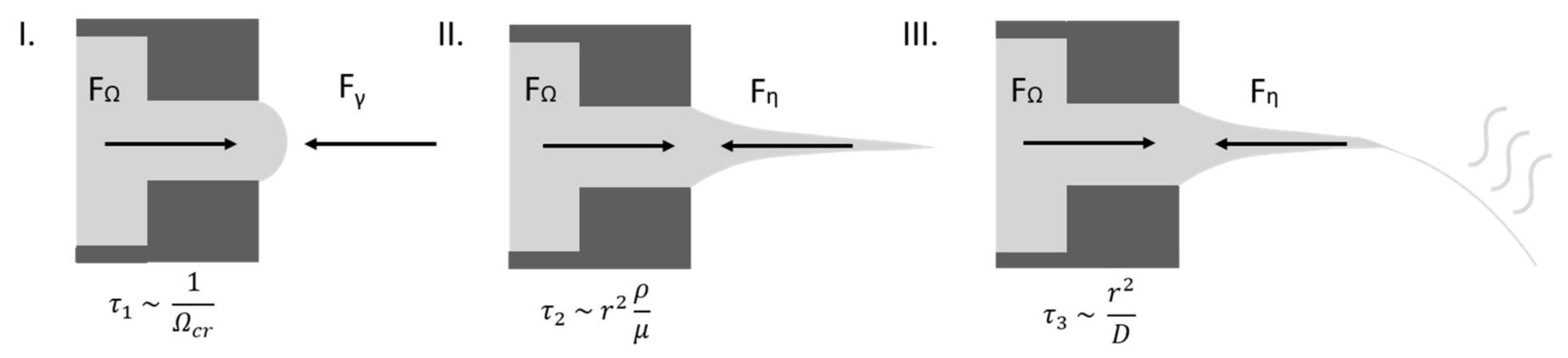
4.1. Fiber Morphology
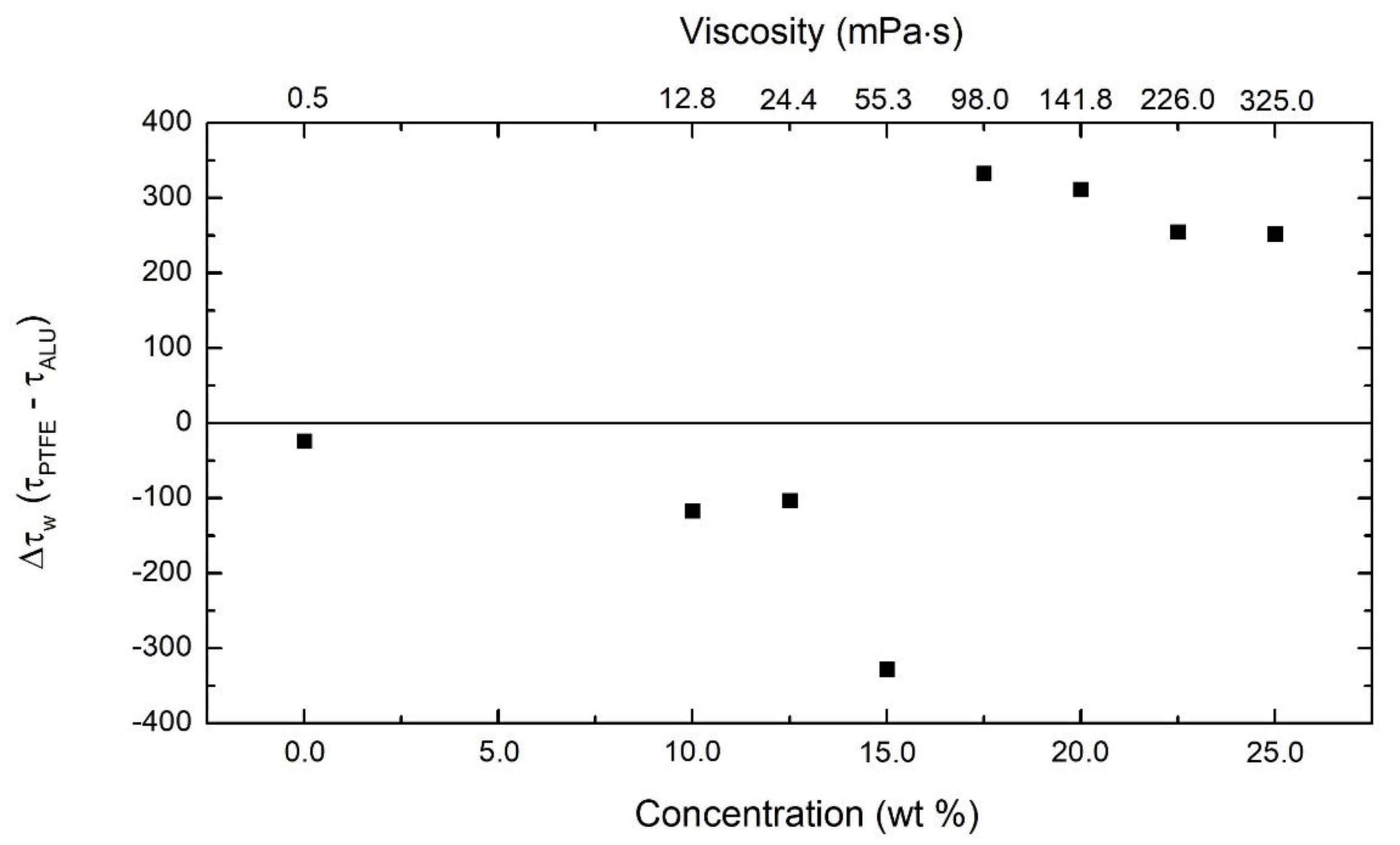
4.2. Polymer Solution‒Wall Interactions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barhoum, A.; Rasouli, R.; Yousefzadeh, M.; Rahier, H.; Bechelany, M. Nanofiber Technology: History and Developments. In Handbook of Nanofibers; Barhoum, A., Bechelany, M., Makhlouf, A., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 1–42. [Google Scholar] [CrossRef]
- Huang, Z.-M.; Zhang, Y.Z.; Kotaki, M.; Ramakrishna, S. A review on polymer nanofibers by electrospinning and their applications in nanocomposites. Compos. Sci. Technol. 2003, 63, 2223–2253. [Google Scholar] [CrossRef]
- Maity, S.; Gon, D.P.; Paul, P. A review of flax nonwovens: Manufacturing, properties, and applications. J. Nat. Fibers 2014, 11, 365–390. [Google Scholar] [CrossRef]
- Yoon, K.; Hsiao, B.S.; Chu, B. Functional nanofibers for environmental applications. J. Mater. Chem. 2008, 18, 5326–5334. [Google Scholar] [CrossRef]
- Malwal, D.; Gopinath, P. Fabrication and applications of ceramic nanofibers in water remediation: A review. Crit. Rev. Environ. Sci. Technol. 2016, 46, 500–534. [Google Scholar] [CrossRef]
- Filatov, Y.; Budyka, A.; Kirichenko, V. Electrospinning of micro-and nanofibers: Fundamentals in separation and filtration processes. J. Eng. Fibers Fabr. 2007, 3, 488. [Google Scholar]
- Calderón, M.Á.R.; Zhao, W. Applications of polymer nanofibers in bio-materials, biotechnology and biomedicine: A review. In Proceedings of the TMS 2014: 143rd Annual Meeting & Exhibition, San Diego, CA, USA, 16–20 February 2014; pp. 401–414. [Google Scholar]
- Pham, Q.P.; Sharma, U.; Mikos, A.G. Electrospinning of polymeric nanofibers for tissue engineering applications: A review. Tissue Eng. 2006, 12, 1197–1211. [Google Scholar] [CrossRef] [Green Version]
- Venugopal, J.; Ramakrishna, S. Applications of polymer nanofibers in biomedicine and biotechnology. Appl. Biochem. Biotechnol. 2005, 125, 147–157. [Google Scholar] [CrossRef]
- Ding, B.; Yu, J. Electrospun Nanofibers for Energy and Environmental Applications; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Thavasi, V.; Singh, G.; Ramakrishna, S. Electrospun nanofibers in energy and environmental applications. Energy Environ. Sci. 2008, 1, 205–221. [Google Scholar] [CrossRef]
- Ramakrishna, S.; Fujihara, K.; Teo, W.-E.; Yong, T.; Ma, Z.; Ramaseshan, R. Electrospun nanofibers: Solving global issues. Mater. Today 2006, 9, 40–50. [Google Scholar] [CrossRef]
- Wei, Q. Functional Nanofibers and Their Applications; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Min, X.; Sun, B.; Chen, S.; Fang, M.; Wu, X.; Liu, Y.G.; Abdelkader, A.; Huang, Z.; Liu, T.; Xi, K.; et al. A textile-based SnO2 ultra-flexible electrode for lithium-ion batteries. Energy Storage Mater. 2019, 16, 597–606. [Google Scholar] [CrossRef] [Green Version]
- Doshi, J.; Reneker, D.H. Electrospinning process and applications of electrospun fibers. J. Electrost. 1995, 35, 151–160. [Google Scholar] [CrossRef]
- Reneker, D.H.; Chun, I. Nanometre diameter fibres of polymer, produced by electrospinning. Nanotechnology 1996, 7, 216. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, G.; Reneker, D.H. Structure and morphology of small diameter electrospun aramid fibers. Polym. Int. 1995, 36, 195–201. [Google Scholar] [CrossRef]
- Zargham, S.; Bazgir, S.; Tavakoli, A.; Rashidi, A.S.; Damerchely, R. The effect of flow rate on morphology and deposition area of electrospun nylon 6 nanofiber. J. Eng. Fibers Fabr. 2012, 7, 155892501200700414. [Google Scholar] [CrossRef] [Green Version]
- Bakar, S.; Fong, K.; Eleyas, A.; Nazeri, M. Effect of voltage and flow rate electrospinning parameters on polyacrylonitrile electrospun fibers. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Penang, Malaysia, 6–7 December 2017; p. 012076. [Google Scholar]
- Hutten, I.M. Chapter 5—Processes for Nonwoven Filter Media. In Handbook of Nonwoven Filter Media, 2nd ed.; Hutten, I.M., Ed.; Butterworth-Heinemann: Oxford, UK, 2016; pp. 276–342. [Google Scholar] [CrossRef]
- Badrossamay, M.R.; McIlwee, H.A.; Goss, J.A.; Parker, K.K. Nanofiber Assembly by Rotary Jet-Spinning. Nano Lett. 2010, 10, 2257–2261. [Google Scholar] [CrossRef] [Green Version]
- Mellado, P.; McIlwee, H.A.; Badrossamay, M.R.; Goss, J.A.; Mahadevan, L.; Kit Parker, K. A simple model for nanofiber formation by rotary jet-spinning. Appl. Phys. Lett. 2011, 99, 203107. [Google Scholar] [CrossRef] [Green Version]
- Golecki, H.M.; Yuan, H.; Glavin, C.; Potter, B.; Badrossamay, M.R.; Goss, J.A.; Phillips, M.D.; Parker, K.K. Effect of solvent evaporation on fiber morphology in rotary jet spinning. Langmuir 2014, 30, 13369–13374. [Google Scholar] [CrossRef] [Green Version]
- Ren, L.; Ozisik, R.; Kotha, S.P.; Underhill, P.T. Highly Efficient Fabrication of Polymer Nanofiber Assembly by Centrifugal Jet Spinning: Process and Characterization. Macromolecules 2015, 48, 2593–2602. [Google Scholar] [CrossRef]
- McEachin, Z.; Lozano, K. Production and characterization of polycaprolactone nanofibers via forcespinning™ technology. J. Appl. Polym. Sci. 2012, 126, 473–479. [Google Scholar] [CrossRef]
- Lu, Y.; Li, Y.; Zhang, S.; Xu, G.; Fu, K.; Lee, H.; Zhang, X. Parameter study and characterization for polyacrylonitrile nanofibers fabricated via centrifugal spinning process. Eur. Polym. J. 2013, 49, 3834–3845. [Google Scholar] [CrossRef]
- Ren, L.; Pandit, V.; Elkin, J.; Denman, T.; Cooper, J.A.; Kotha, S.P. Large-scale and highly efficient synthesis of micro-and nano-fibers with controlled fiber morphology by centrifugal jet spinning for tissue regeneration. Nanoscale 2013, 5, 2337–2345. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Zhang, Z.; Lu, B.; Mei, S.; Xu, Q.; Liu, F. Research on parametric model for polycaprolactone nanofiber produced by centrifugal spinning. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 186. [Google Scholar] [CrossRef]
- Ravishankar, P.; Khang, A.; Laredo, M.; Balachandran, K. Using Dimensionless Numbers to Predict Centrifugal Jet-Spun Nanofiber Morphology. J. Nanomater. 2019, 2019. [Google Scholar] [CrossRef]
- Tepekiran, B.N.; Calisir, M.D.; Polat, Y.; Akgul, Y.; Kilic, A. Centrifugally spun silica (SiO2) nanofibers for high-temperature air filtration. Aerosol Sci. Technol. 2019, 53, 921–932. [Google Scholar] [CrossRef]
- Yang, S.B.; Yeum, J.H. Morphological Comparison of Aligned Poly(vinyl alcohol) Nanofibers Fabricated by Modified Electrospinning and Centrifugal Jet Spinning Techniques. J. Nanosci. Nanotechnol. 2017, 17, 9056–9062. [Google Scholar] [CrossRef]
- Fauzi, A.; Edikresnha, D.; Munir, M.M. Synthesis of Styrofoam Fibers Using Rotary Forcespinning Technique. In Materials Science Forum; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2015; pp. 279–284. [Google Scholar]
- Weng, B.C.; Xu, F.H.; Garza, G.; Alcoutlabi, M.; Salinas, A.; Lozano, K. The Production of Carbon Nanotube Reinforced Poly(vinyl) Butyral Nanofibers by the Forcespinning (R) Method. Polym. Eng. Sci. 2015, 55, 81–87. [Google Scholar] [CrossRef]
- Zander, N.E. Formation of melt and solution spun polycaprolactone fibers by centrifugal spinning. J. Appl. Polym. Sci. 2015, 132. [Google Scholar] [CrossRef]
- Zhmayev, Y.; Divvela, M.J.; Ruo, A.C.; Huang, T.; Joo, Y.L. The jetting behavior of viscoelastic Boger fluids during centrifugal spinning. Phys. Fluids 2015, 27, 123101. [Google Scholar] [CrossRef]
- Du, J.; Liu, D.B.; Chen, S.Q.; Wan, D.C.; Pu, H.T. A novel method for fabricating continuous polymer nanofibers. Polymer 2016, 102, 209–213. [Google Scholar] [CrossRef]
- Li, X.L.; Chen, H.H.; Yang, B. Centrifugally spun starch-based fibers from amylopectin rich starches. Carbohydr. Polym. 2016, 137, 459–465. [Google Scholar] [CrossRef]
- Andrade, P.O.; Santo, A.M.E.; Costa, M.M.; Lobo, A.O. Production of rotary jet spun ultrathin fibers of poly-butylene adipate-co- terephthalate (PBAT) filled with nanocomposites. In Advances in Microscopic Imaging; Beaurepaire, E., Pavone, F.S., So, P.T.C., Eds.; OSA Publishing: Washington, DC, USA, 2017; Volume 10414. [Google Scholar]
- Vo, P.; Doan, H.; Kinashi, K.; Sakai, W.; Tsutsumi, N.; Huynh, D. Centrifugally Spun Recycled PET: Processing and Characterization. Polymers 2018, 10, 680. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiong, C.D.; Li, X.L.; Hou, T.; Yang, B. Stability and spinnability of modified melamine-formaldehyde resin solution for centrifugal spinning. J. Appl. Polym. Sci. 2018, 135, 46072. [Google Scholar] [CrossRef]
- Padilla-Gainza, V.; Morales, G.; Rodriguez-Tobias, H.; Lozano, K. Forcespinning technique for the production of poly(d,l-lactic acid) submicrometer fibers: Process-morphology-properties relationship. J. Appl. Polym. Sci. 2019, 136, 47643. [Google Scholar] [CrossRef]
- Noroozi, S.; Alamdari, H.; Arne, W.; Larson, R.G.; Taghavi, S.M. Regularized string model for nanofibre formation in centrifugal spinning methods. J. Fluid Mech. 2017, 822, 202–234. [Google Scholar] [CrossRef] [Green Version]
- Taghavi, S.M.; Larson, R.G. Regularized thin-fiber model for nanofiber formation by centrifugal spinning. Phys. Rev. E 2014, 89, 023011. [Google Scholar] [CrossRef]
- Zhiming, Z.; Jun, S.; Yaoshuai, D.; Binbin, L. Research on modeling, simulation and experiment based on centrifugal spinning method. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 488. [Google Scholar] [CrossRef]
- Ren, L.; Kotha, S.P. Centrifugal jet spinning for highly efficient and large-scale fabrication of barium titanate nanofibers. Mater. Lett. 2014, 117, 153–157. [Google Scholar] [CrossRef] [Green Version]
- Ewoldt, R.H.; Johnston, M.T.; Caretta, L.M. Experimental challenges of shear rheology: How to avoid bad data. In Complex Fluids in Biological Systems; Springer: Berlin/Heidelberg, Germany, 2015; pp. 207–241. [Google Scholar]
- Barnes, H.A.; Hutton, J.F.; Walters, K. An Introduction to Rheology; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Macosko, C.W.; Larson, R.G. Rheology: Principles, Measurements, and Applications; Wiley-VCH: New York, NY, USA, 1994. [Google Scholar]
- Graessley, W.W. Polymer chain dimensions and the dependence of viscoelastic properties on concentration, molecular weight and solvent power. Polymer 1980, 21, 258–262. [Google Scholar] [CrossRef]
- Clasen, C.; Plog, J.P.; Kulicke, W.-M.; Owens, M.; Macosko, C.; Scriven, L.E.; Verani, M.; McKinley, G.H. How dilute are dilute solutions in extensional flows? J. Rheol. 2006, 50, 849–881. [Google Scholar] [CrossRef] [Green Version]
- Fetters, L.J.; Hadjichristidis, N.; Lindner, J.S.; Mays, J.W. Molecular Weight Dependence of Hydrodynamic and Thermodynamic Properties for Well-Defined Linear Polymers in Solution. J. Phys. Chem. Ref. Data 1994, 23, 619–640. [Google Scholar] [CrossRef]
- Palangetic, L.; Reddy, N.K.; Srinivasan, S.; Cohen, R.E.; McKinley, G.H.; Clasen, C. Dispersity and spinnability: Why highly polydisperse polymer solutions are desirable for electrospinning. Polymer 2014, 55, 4920–4931. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, S.; Chhatre, S.S.; Mabry, J.M.; Cohen, R.E.; McKinley, G.H. Solution spraying of poly (methyl methacrylate) blends to fabricate microtextured, superoleophobic surfaces. Polymer 2011, 52, 3209–3218. [Google Scholar] [CrossRef] [Green Version]
- Shenoy, S.L.; Bates, W.D.; Frisch, H.L.; Wnek, G.E. Role of chain entanglements on fiber formation during electrospinning of polymer solutions: Good solvent, non-specific polymer–polymer interaction limit. Polymer 2005, 46, 3372–3384. [Google Scholar] [CrossRef]
- McKee, M.G.; Wilkes, G.L.; Colby, R.H.; Long, T.E. Correlations of solution rheology with electrospun fiber formation of linear and branched polyesters. Macromolecules 2004, 37, 1760–1767. [Google Scholar] [CrossRef]
- Haward, S.J.; Sharma, V.; Butts, C.P.; McKinley, G.H.; Rahatekar, S.S. Shear and Extensional Rheology of Cellulose/Ionic Liquid Solutions. Biomacromolecules 2012, 13, 1688–1699. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: New York, NY, USA, 2003; Volume 23. [Google Scholar]
- Colby, R.H. Structure and linear viscoelasticity of flexible polymer solutions: Comparison of polyelectrolyte and neutral polymer solutions. Rheol. Acta 2010, 49, 425–442. [Google Scholar] [CrossRef]
- Doan, H.N.; Nguyen, D.K.; Vo, P.P.; Hayashi, K.; Kinashi, K.; Sakai, W.; Tsutsumi, N.; Huynh, D.P. Facile and Scalable Fabrication of Porous Polystyrene Fibers for Oil Removal by Centrifugal Spinning. ACS Omega 2019, 4, 15992–16000. [Google Scholar] [CrossRef]
- Li, Y.; Zou, C.; Shao, J.; Zhang, X. Preparation of SiO2/PS superhydrophobic fibers with bionic controllable micro–nano structure via centrifugal spinning. RSC Adv. 2017, 7, 11041–11048. [Google Scholar] [CrossRef] [Green Version]
- Leng, G.; Zhang, X.; Shi, T.; Chen, G.; Wu, X.; Liu, Y.; Fang, M.; Min, X.; Huang, Z. Preparation and properties of polystyrene/silica fibres flexible thermal insulation materials by centrifugal spinning. Polymer 2019, 185, 121964. [Google Scholar] [CrossRef]
- Eggers, J. Nonlinear dynamics and breakup of free-surface flows. Rev. Mod. Phys. 1997, 69, 865. [Google Scholar] [CrossRef] [Green Version]
- Clasen, C.; Bico, J.; Entov, V.; McKinley, G. ‘Gobbling drops’: The jetting–dripping transition in flows of polymer solutions. J. Fluid Mech. 2009, 636, 5–40. [Google Scholar] [CrossRef] [Green Version]
- Dinic, J.; Zhang, Y.; Jimenez, L.N.; Sharma, V. Extensional Relaxation Times of Dilute, Aqueous Polymer Solutions. ACS Macro Lett. 2015, 4, 804–808. [Google Scholar] [CrossRef]
- Oliveira, M.S.; Yeh, R.; McKinley, G.H. Iterated stretching, extensional rheology and formation of beads-on-a-string structures in polymer solutions. J. Non-Newton. Fluid Mech. 2006, 137, 137–148. [Google Scholar] [CrossRef] [Green Version]
- Bhat, P.P.; Appathurai, S.; Harris, M.T.; Pasquali, M.; McKinley, G.H.; Basaran, O.A. Formation of beads-on-a-string structures during break-up of viscoelastic filaments. Nat. Phys. 2010, 6, 625–631. [Google Scholar] [CrossRef] [Green Version]
- Mhetar, V.; Archer, L.A. Slip in Entangled Polymer Solutions. Macromolecules 1998, 31, 6639–6649. [Google Scholar] [CrossRef]
- Joshi, Y.M.; Lele, A.K.; Mashelkar, R. A unified wall slip model. J. Non-Newton. Fluid Mech. 2000, 94, 135–149. [Google Scholar] [CrossRef]
- Archer, L.; Chen, Y.L.; Larson, R. Delayed slip after step strains in highly entangled polystyrene solutions. J. Rheol. 1995, 39, 519–525. [Google Scholar] [CrossRef]
- Denn, M.M. Extrusion instabilities and wall slip. Annu. Rev. Fluid Mech. 2001, 33, 265–287. [Google Scholar] [CrossRef] [Green Version]
- Migler, K.; Liu, C.H.; Pine, D.J. Structure evolution of a polymer solution at high shear rates. Macromolecules 1996, 29, 1422–1432. [Google Scholar] [CrossRef]
- Rezvantalab, H.; Zhu, G.R.; Larson, R.G. The effect of wall depletion and hydrodynamic interactions on stress-gradient-induced polymer migration. Soft Matter 2016, 12, 5883–5897. [Google Scholar] [CrossRef]
- Neto, C.; Evans, D.R.; Bonaccurso, E.; Butt, H.-J.; Craig, V.S. Boundary slip in Newtonian liquids: A review of experimental studies. Rep. Prog. Phys. 2005, 68, 2859. [Google Scholar] [CrossRef]
- Hatzikiriakos, S.G. Slip mechanisms in complex fluid flows. Soft Matter 2015, 11, 7851–7856. [Google Scholar] [CrossRef] [PubMed]
- Malkin, A.Y.; Patlazhan, S.A. Wall slip for complex liquids—Phenomenon and its causes. Adv. Colloid Interface Sci. 2018, 257, 42–57. [Google Scholar] [CrossRef] [PubMed]
- Hemminger, O.; Boukany, P.E. Microscopic origin of wall slip during flow of an entangled DNA solution in microfluidics: Flow induced chain stretching versus chain desorption. Biomicrofluidics 2017, 11, 044118. [Google Scholar] [CrossRef]
- Wang, S.Q. From Wall Slip to Bulk Shear Banding in Entangled Polymer Solutions. Macromol. Chem. Phys. 2019, 220, 1800327. [Google Scholar] [CrossRef]

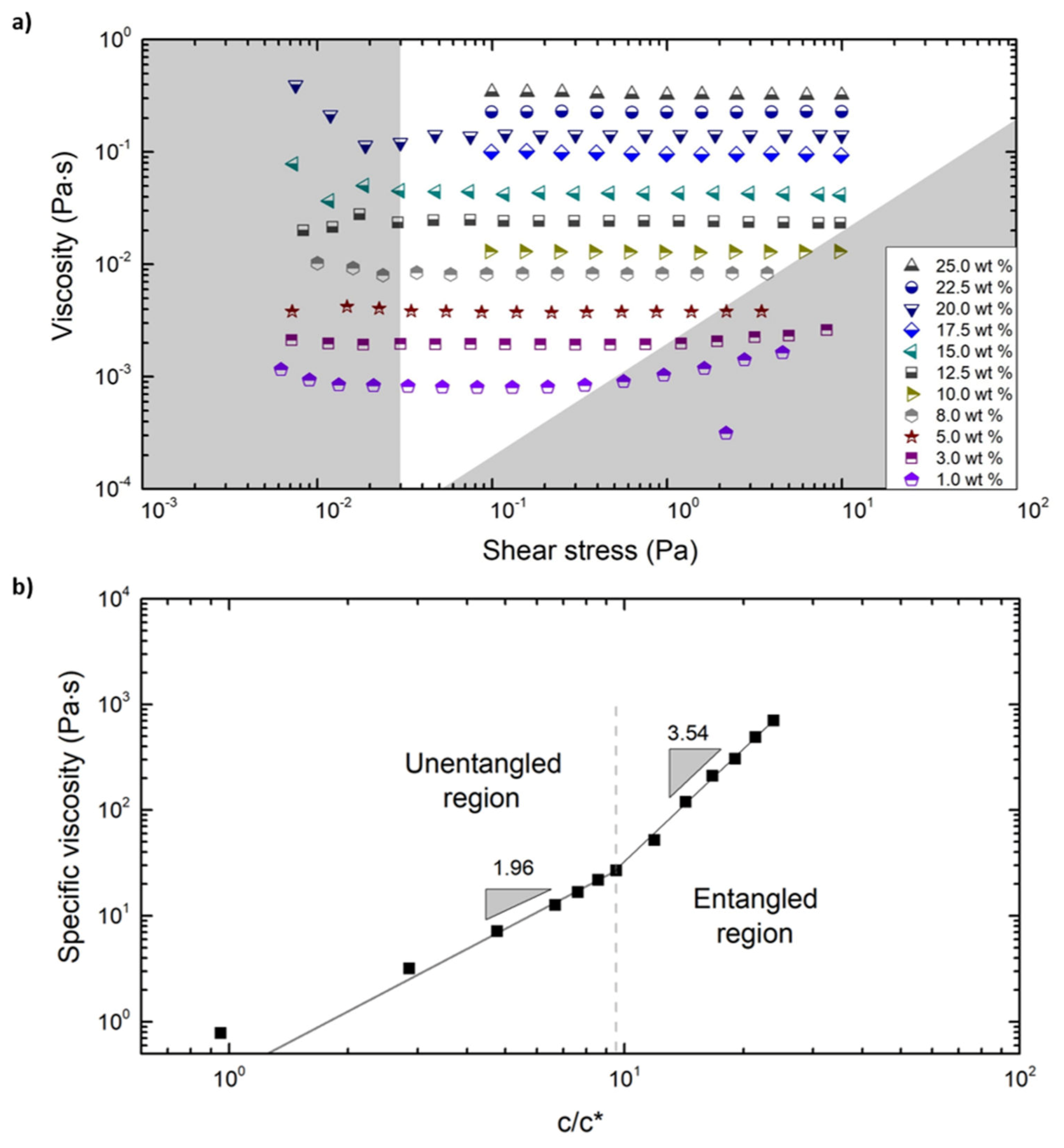
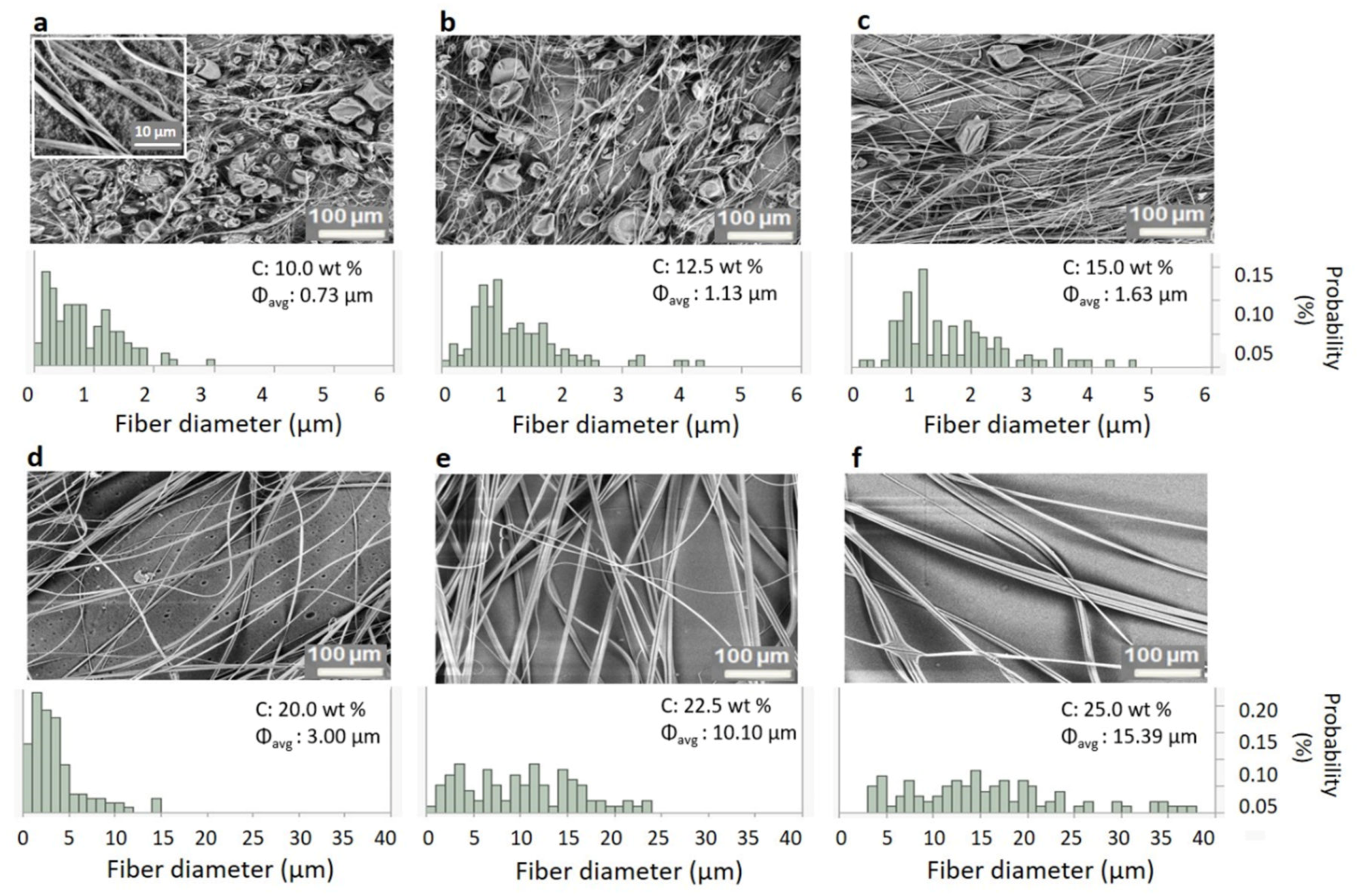

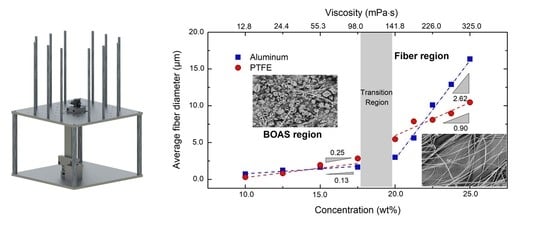
| c (wt %) | η0 (Pa∙s) | ηsp (-) | Φ (ALU) (µm) | SD (µm) | Φ (PTFE) (µm) | SD (µm) |
|---|---|---|---|---|---|---|
| 10.0 | 0.013 | 26.8 | 0.73 | 0.58 | 0.28 | 0.19 |
| 12.5 | 0.024 | 52.0 | 1.13 | 0.77 | 0.76 | 0.63 |
| 15.0 | 0.055 | 119.2 | 1.63 | 0.88 | 1.69 | 1.29 |
| 17.5 | 0.098 | 212.0 | 1.68 | 1.19 | 2.46 | 2.30 |
| 20.0 | 0.142 | 307.3 | 3.00 | 2.94 | 5.42 | 4.70 |
| 22.5 | 0.226 | 490.3 | 10.10 | 5.79 | 8.08 | 5.44 |
| 25.0 | 0.325 | 705.5 | 15.39 | 10.05 | 10.46 | 5.16 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Merchiers, J.; Meurs, W.; Deferme, W.; Peeters, R.; Buntinx, M.; Reddy, N.K. Influence of Polymer Concentration and Nozzle Material on Centrifugal Fiber Spinning. Polymers 2020, 12, 575. https://doi.org/10.3390/polym12030575
Merchiers J, Meurs W, Deferme W, Peeters R, Buntinx M, Reddy NK. Influence of Polymer Concentration and Nozzle Material on Centrifugal Fiber Spinning. Polymers. 2020; 12(3):575. https://doi.org/10.3390/polym12030575
Chicago/Turabian StyleMerchiers, Jorgo, Willem Meurs, Wim Deferme, Roos Peeters, Mieke Buntinx, and Naveen K. Reddy. 2020. "Influence of Polymer Concentration and Nozzle Material on Centrifugal Fiber Spinning" Polymers 12, no. 3: 575. https://doi.org/10.3390/polym12030575