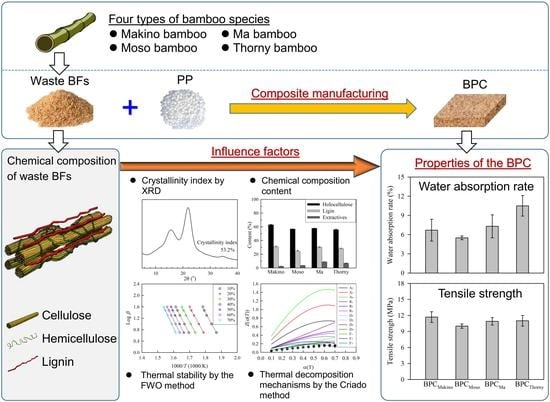
Utilization of Waste Bamboo Fibers in Thermoplastic Composites: Influence of the Chemical Composition and Thermal Decomposition Behavior
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Manufacturing Process of the Bamboo–Polypropylene Composites (BPCs)
2.3. Chemical Composition Analysis
2.4. X-ray Diffraction (XRD)
2.5. Thermal Decomposition Kinetics Analysis
2.6. Determination of BPC Properties
2.7. Analysis of Variance
3. Results and Discussion
3.1. Chemical Composition and Thermal Stability of Various BFs
3.2. Thermal Decomposition Kinetics of Various BFs
3.3. Characteristic Properties of the BPCs
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chung, M.J.; Wang, S.Y. Physical and mechanical properties of composites made from bamboo and woody wastes in Taiwan. J. Wood Sci. 2019, 65, 57. [Google Scholar] [CrossRef]
- Obata, Y.; Takeuchi, K.; Soma, N.; Kanayama, K. Recycling of wood waste as sustainable industrial resources—Design of energy saving wood-based board for floor heating systems. Energy 2006, 31, 2341–2349. [Google Scholar] [CrossRef]
- Li, Y.; Yin, L.; Huang, C.; Meng, Y.; Fu, F.; Wang, S.; Wu, Q. Quasi-static and dynamic nanoindentation to determine the influence of thermal treatment on the mechanical properties of bamboo cell walls. Holzforschung 2015, 69, 909–914. [Google Scholar] [CrossRef]
- Liu, H.; Jiang, Z.; Fei, B.; Hse, C.; Sun, Z. Tensile behaviour and fracture mechanism of moso bamboo (Phyllostachys pubescens). Holzforschung 2015, 69, 47–52. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.; Zhang, X.; Sun, Z.; Jiang, Z. In situ detection of the fracture behaviour of moso bamboo (Phyllostachys pubescens) by scanning electron microscopy. Holzforschung 2016, 70, 1183–1190. [Google Scholar] [CrossRef]
- Chung, M.J.; Wang, S.Y. Effects of peeling and steam-heating treatment on basic properties of two types of bamboo culms (Phyllostachys makinoi and Phyllostachys pubescens). J. Wood Sci. 2017, 63, 473–482. [Google Scholar] [CrossRef]
- Obataya, E.; Kitin, P.; Yamauchi, H. Bending characteristics of bamboo (Phyllostachys pubescens) with respect to its fiber–foam composite structure. Wood Sci. Technol. 2007, 41, 385–400. [Google Scholar] [CrossRef]
- Yang, T.-C.; Lee, T.-Y. Effects of density and heat treatment on the physico-mechanical properties of unidirectional round bamboo stick boards (UBSBs) made of Makino bamboo (Phyllostachys makinoi). Constr. Build. Mater. 2018, 187, 406–413. [Google Scholar] [CrossRef]
- Alsaeed, T.; Yousif, B.F.; Ku, H. The potential of using date palm fibres as reinforcement for polymeric composites. Mater. Des. 2013, 43, 177–184. [Google Scholar] [CrossRef]
- Bledzki, A.K.; Reihmane, S.; Gassan, J. Thermoplastics reinforced with wood fillers: A literature review. Polym. Plast. Technol. Eng. 1998, 37, 451–468. [Google Scholar] [CrossRef]
- Dittenber, D.B.; Ganga Rao, H.V.S. Critical review of recent publications on use of natural composites in infrastructure. Compos. Part A 2012, 43, 1419–1429. [Google Scholar] [CrossRef]
- Kumar, V.; Tyagi, L.; Sinha, S. Wood flour—reinforced plastic composites: A review. Rev. Chem. Eng. 2011, 27, 253–264. [Google Scholar] [CrossRef]
- Saba, N.; Paridah, M.T.; Jawaid, M. Mechanical properties of kenaf fibre reinforced polymer composite: A review. Constr. Build. Mater. 2015, 76, 87–96. [Google Scholar] [CrossRef]
- Hsu, C.-Y.; Yang, T.-C.; Wu, T.-L.; Hung, K.-C.; Wu, J.-H. Effects of a layered structure on the physicomechanical properties and extended creep behavior of bamboo-polypropylene composites (BPCs) determined by the stepped isostress method. Holzforschung 2018, 72, 589–597. [Google Scholar] [CrossRef]
- Yang, G.; Zhang, Y.; Shao, H.; Hu, X. A comparative study of bamboo Lyocell fiber and other regenerated cellulose fibers. Holzforschung 2009, 63, 18–22. [Google Scholar] [CrossRef]
- Yang, T.-C.; Wu, T.-L.; Hung, K.-C.; Chen, Y.-L.; Wu, J.-H. Mechanical properties and extended creep behavior of bamboo fiber reinforced recycled poly(lactic acid) composites using the time–temperature superposition principle. Constr. Build. Mater. 2015, 93, 558–563. [Google Scholar] [CrossRef]
- Yu, Y.; Tian, G.; Wang, H.; Fei, B.; Wang, G. Mechanical characterization of single bamboo fibers with nanoindentation and microtensile technique. Holzforschung 2011, 65, 113–119. [Google Scholar] [CrossRef]
- Ashori, A.; Nourbakhsh, A. Reinforced polypropylene composites: Effects of chemical compositions and particle size. Bioresour. Technol. 2010, 101, 2515–2519. [Google Scholar] [CrossRef]
- Bouafif, H.; Koubaa, A.; Perré, P.; Cloutier, A. Effects of fiber characteristics on the physical and mechanical properties of wood plastic composites. Compos. Part A 2009, 40, 1975–1981. [Google Scholar] [CrossRef]
- Ou, R.; Xie, Y.; Wolcott, M.P.; Sui, S.; Wang, Q. Morphology, mechanical properties, and dimensional stability of wood particle/high density polyethylene composites: Effect of removal of wood cell wall composition. Mater. Des. 2014, 58, 339–345. [Google Scholar] [CrossRef]
- Bledzki, A.K.; Sperber, V.E.; Faruk, O. Natural and Wood Fiber Reinforcement in Polymers; Rapra Technology LTD.: Birmingham, UK, 2002. [Google Scholar]
- Nabi Saheb, D.; Jog, J.P. Natural fiber polymer composites: A review. Adv. Polym. Technol. 1999, 18, 351–363. [Google Scholar] [CrossRef]
- Vyazovkin, S. Advanced isoconversional method. J. Therm. Anal. 1997, 49, 1493–1499. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Dollimore, D. Linear and nonlinear procedures in iso-conversional computations of the activation energy of nonisothermal reactions in solids. J. Chem. Inf. Comput. Sci. 1996, 36, 42–45. [Google Scholar] [CrossRef]
- Di Blasi, C. Modeling chemical and physical process and biomass pyrolysis. Prog. Energy Combust. Sci. 2008, 34, 47–90. [Google Scholar] [CrossRef]
- Órfão, J.J.M.; Antunes, F.J.A.; Figueiredo, J.L. Pyrolysis kinetics of lignocellulosic materials–three independent reactions model. Fuel 1999, 78, 349–358. [Google Scholar] [CrossRef]
- Popescu, M.C.; Popescu, C.M.; Lisa, G.; Sakata, Y. Evaluation of morphological and chemical aspects of different wood species by spectroscopy and thermal methods. J. Mol. Struct. 2011, 988, 65–72. [Google Scholar] [CrossRef]
- Criado, J.M.; Málek, J.; Ortega, A. Applicability of the master plots in kinetic analysis of non-isothermal data. Themochim. Acta 1989, 147, 377–385. [Google Scholar] [CrossRef]
- Hung, K.-C.; Wu, J.-H. Mechanical and interfacial properties of plastic composite panels made from esterified bamboo particles. J. Wood Sci. 2010, 56, 216–221. [Google Scholar] [CrossRef]
- Pérez-Maqueda, L.A.; Criado, J.M. The accuracy of Senum and Yang’s approximation to the Arrhenius integral. J. Therm. Anal. Calorim. 2000, 60, 909–915. [Google Scholar] [CrossRef]
- Flynn, J.H.; Wall, L.A. General treatment for the thermogravimetry of polymers. J. Res. Nat. Bureau Stand. 1966, 70A, 487–523. [Google Scholar] [CrossRef]
- Ozawa, T. A new method of analyzing thermogravimetric data. Bull. Chem. Soc. Jap. 1965, 38, 1881–1886. [Google Scholar] [CrossRef]
- Hung, K.-C.; Wu, J.-H. Characteristics and thermal decomposition kinetics of wood-SiO2 composites derived by the sol-gel process. Holzforschung 2017, 71, 233–240. [Google Scholar] [CrossRef]
- Hung, K.-C.; Wu, J.-H. Comparison of physical and thermal properties of various wood-inorganic composites (WICs) derived by the sol-gel process. Holzforschung 2018, 72, 379–386. [Google Scholar] [CrossRef]
- Hung, K.-C.; Yeh, H.; Yang, T.-C.; Wu, T.-L.; Xu, J.-W.; Wu, J.-H. Characterization of wood-plastic composites made with different lignocellulosic materials that vary in their morphology, chemical composition and thermal stability. Polymers 2017, 9, 726. [Google Scholar] [CrossRef] [PubMed]
- Núñez, L.; Fraga, F.; Núñez, M.R.; Villanueva, M. Thermogravimetric study of the decomposition process of the system BADGE (n = 0)/1,2 DCH. Polymer 2000, 41, 4635–4641. [Google Scholar] [CrossRef]
- Bianchi, O.; Martins, J. DeN.; Fiorio, R.; Oliveira, R.V.B.; Canto, L.B. Changes in activation energy and kinetic mechanism during EVA crosslinking. Polym. Test. 2011, 30, 616–624. [Google Scholar] [CrossRef]
- Poletto, M.; Zattera, A.J.; Santana, R.M.C. Thermal decomposition of wood: Kinetics and degradation mechanisms. Bioresour. Technol. 2012, 126, 7–12. [Google Scholar] [CrossRef]
- Yang, H.; Yan, R.; Chen, H.; Lee, D.H.; Zheng, C. Characteristics of hemicellulose, cellulose and lignin pyrolysis. Fuel 2007, 86, 1781–1788. [Google Scholar] [CrossRef]
- Grønli, M.G.; Várhegyi, G.; Di Blasi, C. Thermogravimetric analysis and devolatilization kinetics of wood. Ind. Eng. Chem. Res. 2002, 41, 4201–4208. [Google Scholar] [CrossRef]
- Poletto, M.; Zattera, A.J.; Forte, M.M.C.; Santana, R.M.C. Thermal decomposition of wood: Influence of wood components and cellulose crystallite size. Bioresour. Technol. 2012, 109, 148–153. [Google Scholar] [CrossRef]
- Shebani, A.N.; van Reenen, A.J.; Meincken, M. The effect of wood extractives on the thermal stability of different wood species. Thermochim. Acta 2008, 471, 43–50. [Google Scholar] [CrossRef]
- John, M.J.; Thomas, S. Biofibres and biocomposites. Carbohydr. Polym. 2008, 71, 343–364. [Google Scholar] [CrossRef]
- Doddapaneni, T.R.K.C.; Konttinen, J.; Hukka, T.I.; Moilanen, A. Influence of torrefaction pretreatment on the pyrolysis of Eucalyptus clone: A study on kinetics, reaction mechanism and heat flow. Ind. Crop. Prod. 2016, 92, 244–254. [Google Scholar] [CrossRef]
- Mishra, G.; Kumar, J.; Bhaskar, T. Kinetic studies on the pyrolysis of pinewood. Bioresour. Technol. 2015, 182, 282–288. [Google Scholar] [CrossRef]
- Singh, S.; Chakraborty, J.P.; Mondal, M.K. Intrinsic kinetics, thermodynamic parameters and reaction mechanism of non-isothermal degradation of torrefied Acacia nilotica using isoconversional methods. Fuel 2020, 259, 116263. [Google Scholar] [CrossRef]
- Jarvis, M. Chemistry: Cellulose stacks up. Nature 2003, 426, 611–612. [Google Scholar] [CrossRef]
- Ali, A.; Shaker, K.; Nawab, Y.; Jabbar, M.; Hussain, T.; Militky, J.; Baheti, V. Hydrophobic treatment of natural fibers and their composites-A review. J. Ind. Text. 2018, 47, 2153–2183. [Google Scholar] [CrossRef]





| Kinetic Mechanism | Kinetic Model | Algebraic Expression | |
|---|---|---|---|
| f(α) | g(α) | ||
| Nucleation and growth | |||
| Avrami equation | A2 | 2(1 − α)[ − ln(1 − α)]1/2 | [ − ln(1 − α)]1/2 |
| Avrami equation | A3 | 3(1 − α)[ − ln(1 − α)]2/3 | [ − ln(1 − α)]1/3 |
| Avrami equation | A4 | 4(1 − α)[ − ln(1 − α)]3/4 | [ − ln(1 − α)]1/4 |
| Geometrical: Phase boundary-controlled reaction | |||
| Linear contraction | R1 | 1 | α |
| Contracting area | R2 | 2(1 − α)1/2 | 1 − (1 − α)1/2 |
| Contracting volume | R3 | 3(1 − α)2/3 | 1 − (1 − α)1/3 |
| Diffusion | |||
| One-dimensional | D1 | (1/2)α | α2 |
| Two-dimensional (Valensi equation) | D2 | [ − ln(1 − α)]−1 | (1 − α)ln(1 − α)+α |
| Three-dimensional (Jander equation) | D3 | (3/2)(1 − α)2/3 [1 − (1 − α)1/3]−1 | [1 − (1 − α)1/3]2 |
| Three-dimensional (Ginstling-Brounshtein equation) | D4 | (3/2)[(1 − α) − 1/3 − 1]−1 | [1 − (2/3)α] − (1 − α)2/3 |
| Reaction-order: Random nucleation on the individual particle | |||
| 1st order (One nucleus) | F1 | (1 − α) | − ln(1 − α) |
| 2nd order (Two nuclei) | F2 | (1 − α)2 | [(1 − α)−1] − 1 |
| 3rd order (Three nuclei) | F3 | (1 − α)3 | (1/2)[(1 − α)−2] − 1 |
| Bamboo Species | Chemical Composition | ||
|---|---|---|---|
| Holocellulose (%) | Lignin (%) | Extractives (%) | |
| Makino | 62.5 ± 0.8 a | 30.7 ± 1.0 a | 2.9 ± 0.5 d |
| Moso | 57.1 ± 0.6 b,c | 24.5 ± 1.2 b | 3.8 ± 0.4 c |
| Ma | 58.0 ± 0.7 b | 30.3 ± 0.5 a | 8.5 ± 0.5 a |
| Thorny | 56.0 ± 0.6 c | 28.1 ± 0.9 a | 6.9 ± 0.3 b |
| Bamboo Species | Items | Conversion Rate (α) | ||||||
|---|---|---|---|---|---|---|---|---|
| 10% | 20% | 30% | 40% | 50% | 60% | 70% | ||
| Makino | Ea (kJ/mol) | 188 | 186 | 193 | 198 | 202 | 206 | 217 |
| R2 | 0.9960 | 0.9992 | 0.9992 | 0.9995 | 0.9994 | 0.9999 | 0.9997 | |
| Moso | Ea (kJ/mol) | 171 | 172 | 180 | 188 | 196 | 201 | 214 |
| R2 | 0.9979 | 0.9998 | 0.9990 | 0.9988 | 0.9988 | 0.9990 | 0.9986 | |
| Ma | Ea (kJ/mol) | 173 | 170 | 176 | 181 | 181 | 183 | 191 |
| R2 | 0.9941 | 0.9966 | 0.9939 | 0.9969 | 0.9971 | 0.9969 | 0.9969 | |
| Thorny | Ea (kJ/mol) | 179 | 173 | 177 | 178 | 178 | 182 | 198 |
| R2 | 0.9954 | 0.9948 | 0.9934 | 0.9927 | 0.9937 | 0.9928 | 0.9918 | |
| Code | Density (g/cm3) | MC (%) | WAR After 24 Soaking (%) |
|---|---|---|---|
| BPCMakino | 0.78 ± 0.02 a | 2.81 ± 0.27 b | 6.7 ± 1.7 b |
| BPCMoso | 0.80 ± 0.02 a | 2.87 ± 0.16 b | 5.5 ± 0.3 b |
| BPCMa | 0.77 ± 0.05 a | 3.09 ± 0.17 a,b | 7.3 ± 1.8 b |
| BPCThorny | 0.78 ± 0.02 a | 3.25 ± 0.10 a | 10.5 ± 1.6 a |
| Code | Tensile properties | Flexural properties | ||
|---|---|---|---|---|
| TS (MPa) | TM (MPa) | MOR (MPa) | MOE (MPa) | |
| BPCMakino | 11.7 ± 1.0 a | 1130 ± 106 a | 25.0 ± 2.3 a | 1741 ± 156 a,b |
| BPCMoso | 10.0 ± 0.4 b | 987 ± 68 b | 25.1 ± 1.3 a | 1482 ± 210 b |
| BPCMa | 10.9 ± 0.7 a,b | 1110 ± 85 a,b | 27.7 ± 4.5 a | 1958 ± 291 a |
| BPCThorny | 11.0 ± 1.0 a,b | 1097 ± 65 a,b | 26.0 ± 2.1 a | 1808 ± 198 a |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeh, C.-H.; Yang, T.-C. Utilization of Waste Bamboo Fibers in Thermoplastic Composites: Influence of the Chemical Composition and Thermal Decomposition Behavior. Polymers 2020, 12, 636. https://doi.org/10.3390/polym12030636
Yeh C-H, Yang T-C. Utilization of Waste Bamboo Fibers in Thermoplastic Composites: Influence of the Chemical Composition and Thermal Decomposition Behavior. Polymers. 2020; 12(3):636. https://doi.org/10.3390/polym12030636
Chicago/Turabian StyleYeh, Chin-Hao, and Teng-Chun Yang. 2020. "Utilization of Waste Bamboo Fibers in Thermoplastic Composites: Influence of the Chemical Composition and Thermal Decomposition Behavior" Polymers 12, no. 3: 636. https://doi.org/10.3390/polym12030636
APA StyleYeh, C.-H., & Yang, T.-C. (2020). Utilization of Waste Bamboo Fibers in Thermoplastic Composites: Influence of the Chemical Composition and Thermal Decomposition Behavior. Polymers, 12(3), 636. https://doi.org/10.3390/polym12030636