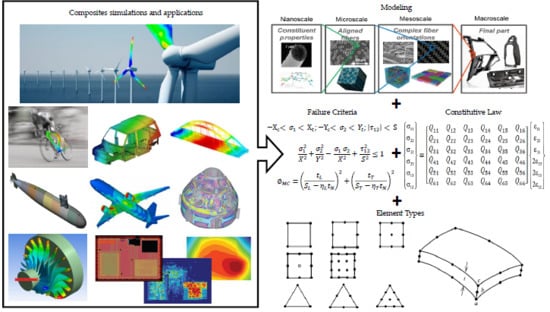
Application of the Finite Element Method in the Analysis of Composite Materials: A Review
Abstract
:1. Introduction
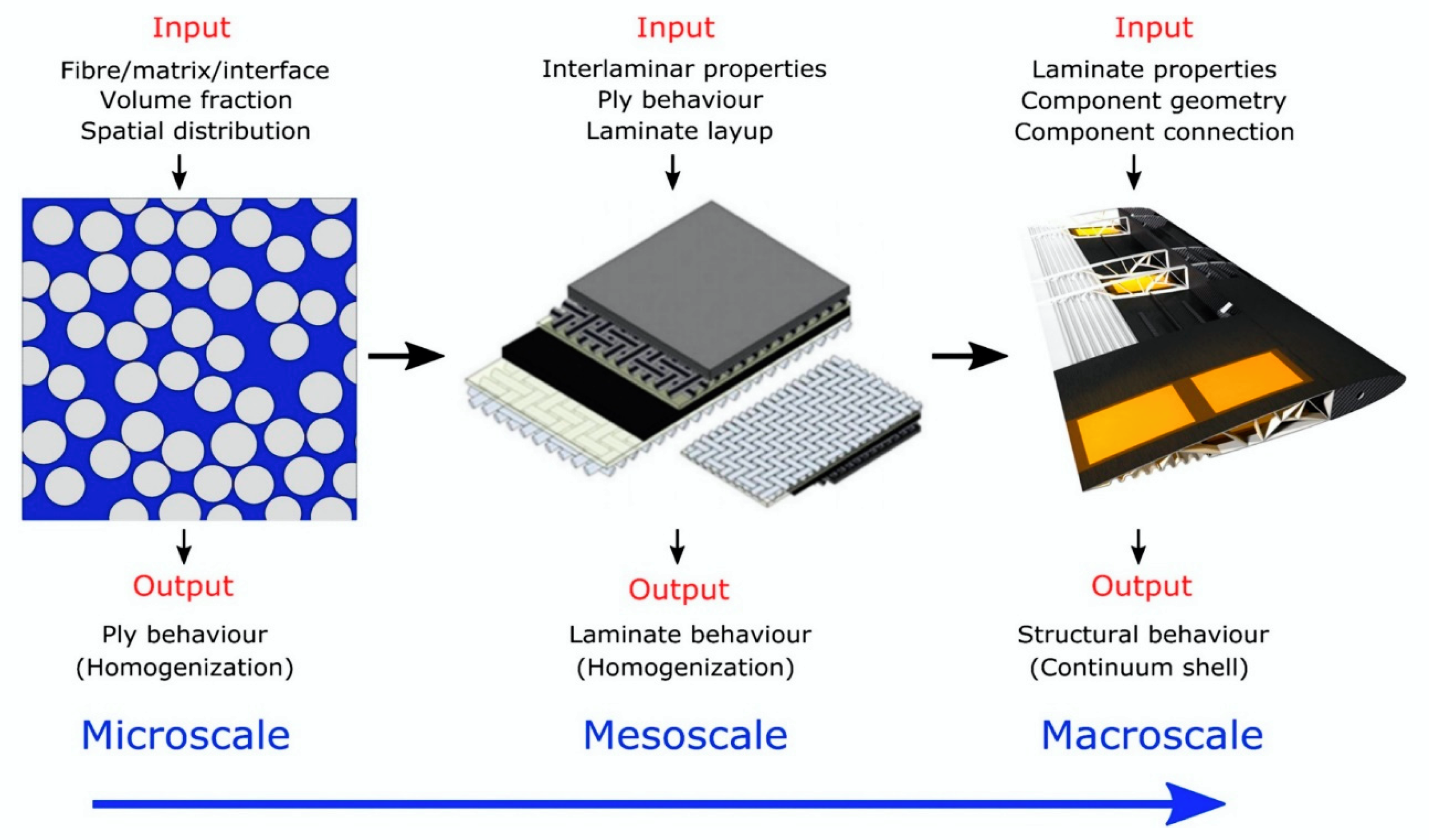
2. Modelling
- ➢
- Microscale—study the composite material’s behavior, for which interactions from constituent materials are examined in detail as defined by heterogeneous material behavior.
- ➢
- Macroscale—study the composite material behavior considered to be homogeneous, and the effects of all constituent materials are detected only by the composite material’s mean apparent properties.
Cohesive Zone Model
3. Constitutive Laws of a Composite Material
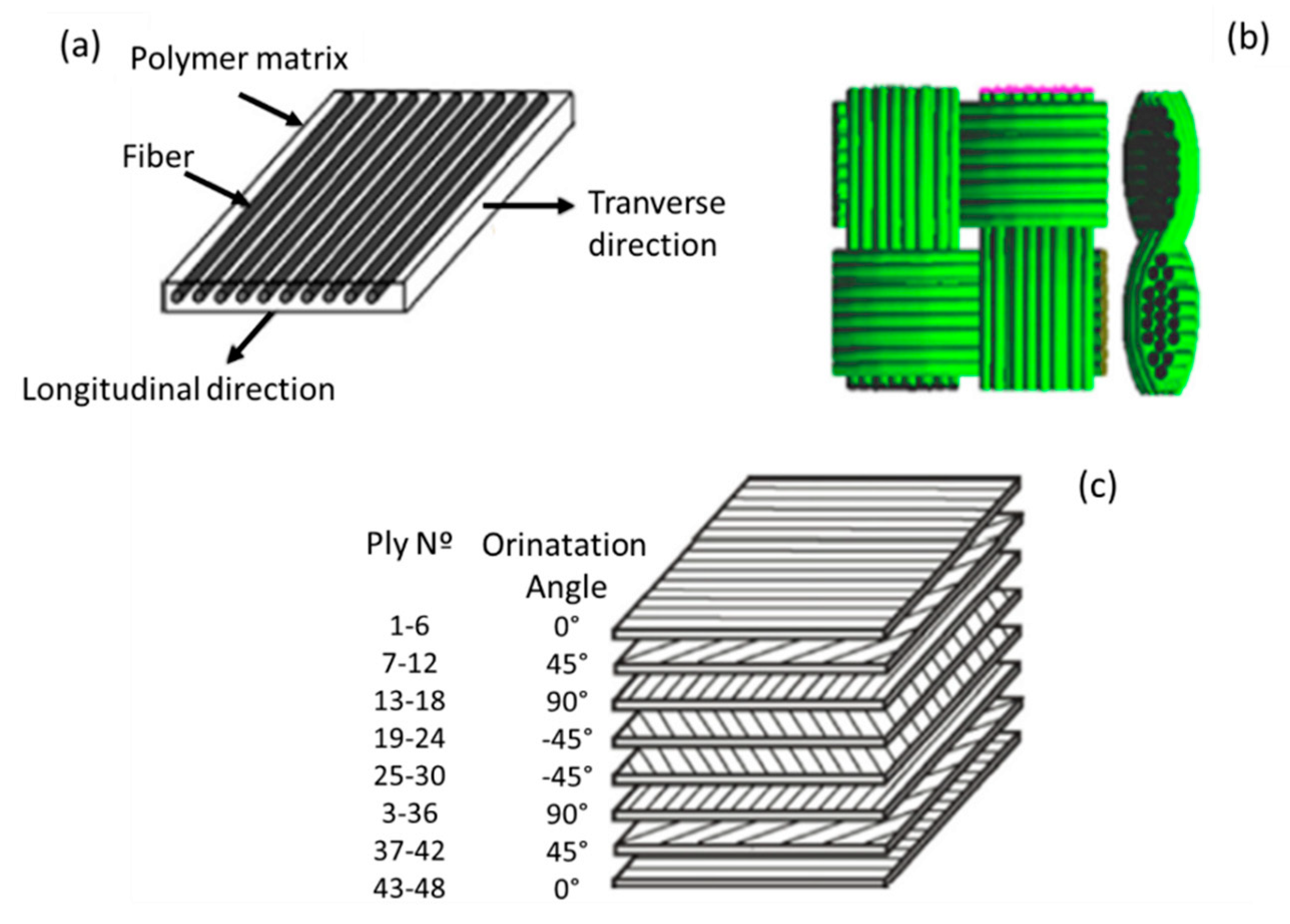
3.1. Anisotropic Material
3.2. Orthotropic Material
- ➢
- The angular deformations are independent of normal stress;
- ➢
- Linear deformations are independent of tangential stresses;
- ➢
- Each tangential tension causes only angular deformation in the plane in which it acts.
3.3. Transverse Isotropic Material
- ➢
- The linear deformations in the plane x2 x3 caused by the normal stress σ11 are equal;
- ➢
- The linear deformations ε22 and ε33 caused by the normal stress σ22 are equal to the deformations ε33 and ε 22, respectively, caused by a tension σ22 = σ33;
- ➢
- Each tangential tension only causes angular deformation in the plane in which it acts;
- ➢
- The angular strain γ23 caused by a stress σ 23 is equal to an angular strain γ13 caused by stress σ13 = σ23.
4. Failure Criteria
- ➢
- It does not intrinsically consider differences in tensile and compressive strength;
- ➢
- It does not present good results in the state of loading by compression in the three main axes;
- ➢
- It supposes that a hydrostatic state of stresses cannot cause failure—in the case of anisotropic materials, a hydrostatic state of stress causes shear deformation and failure.
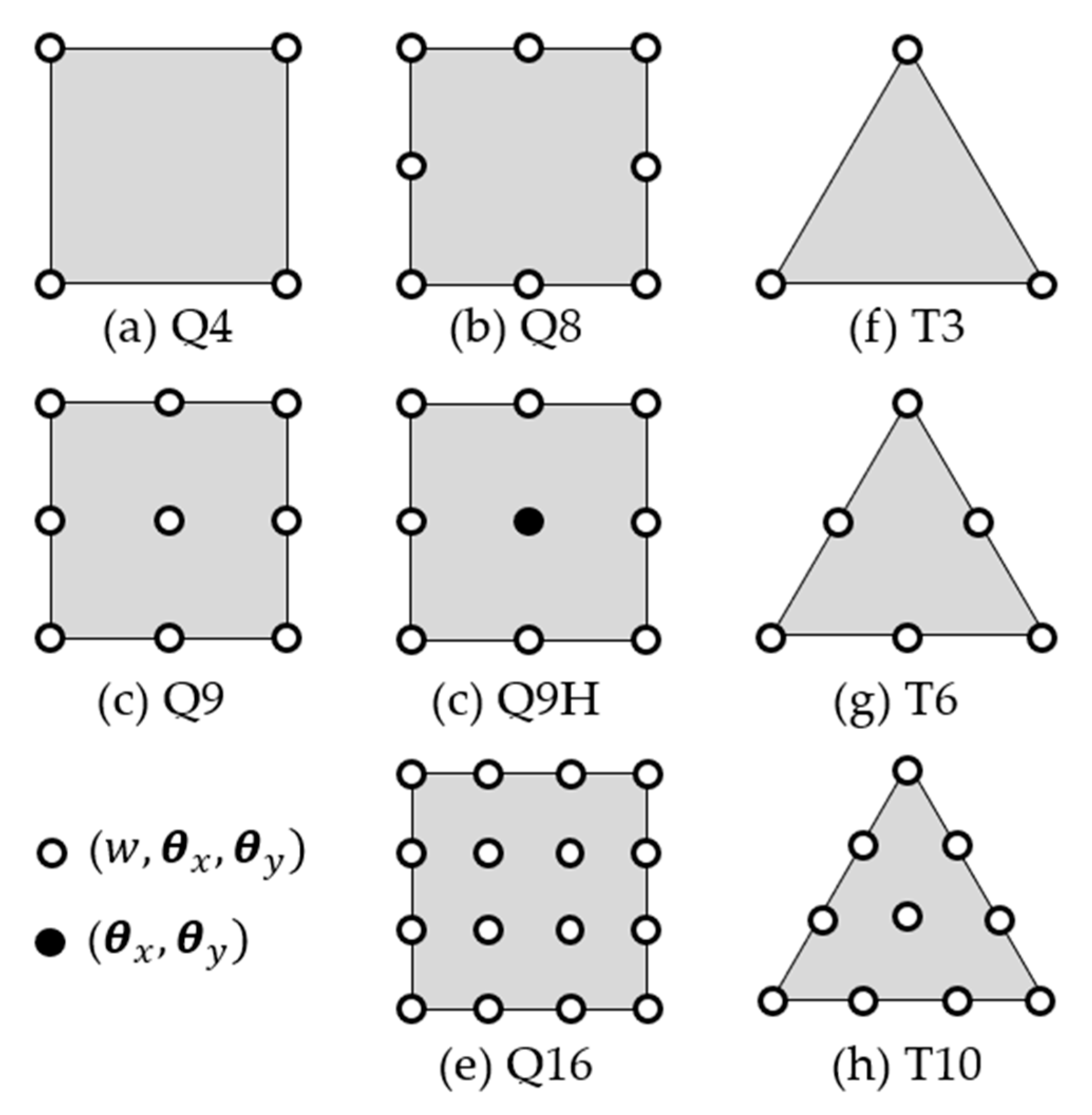
5. Types of Elements Applied in Composite Modelling
- ➢
- The constitutive equations of each layer are orthotropic;
- ➢
- The constitutive equations of the element depend on the kinematic considerations of the plate/shell theory employed and its implementation on the element;
- ➢
- The symmetry of the material is as important as the geometry and symmetry of the loading when trying to use conditions of symmetry in the models.
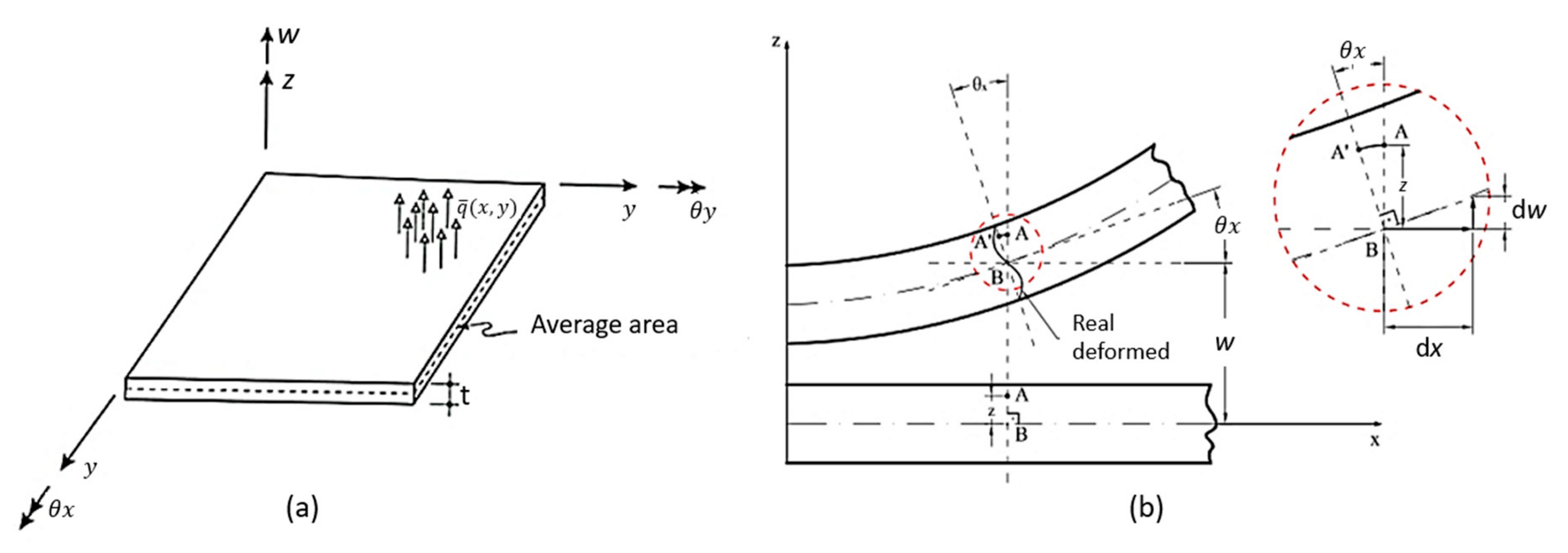
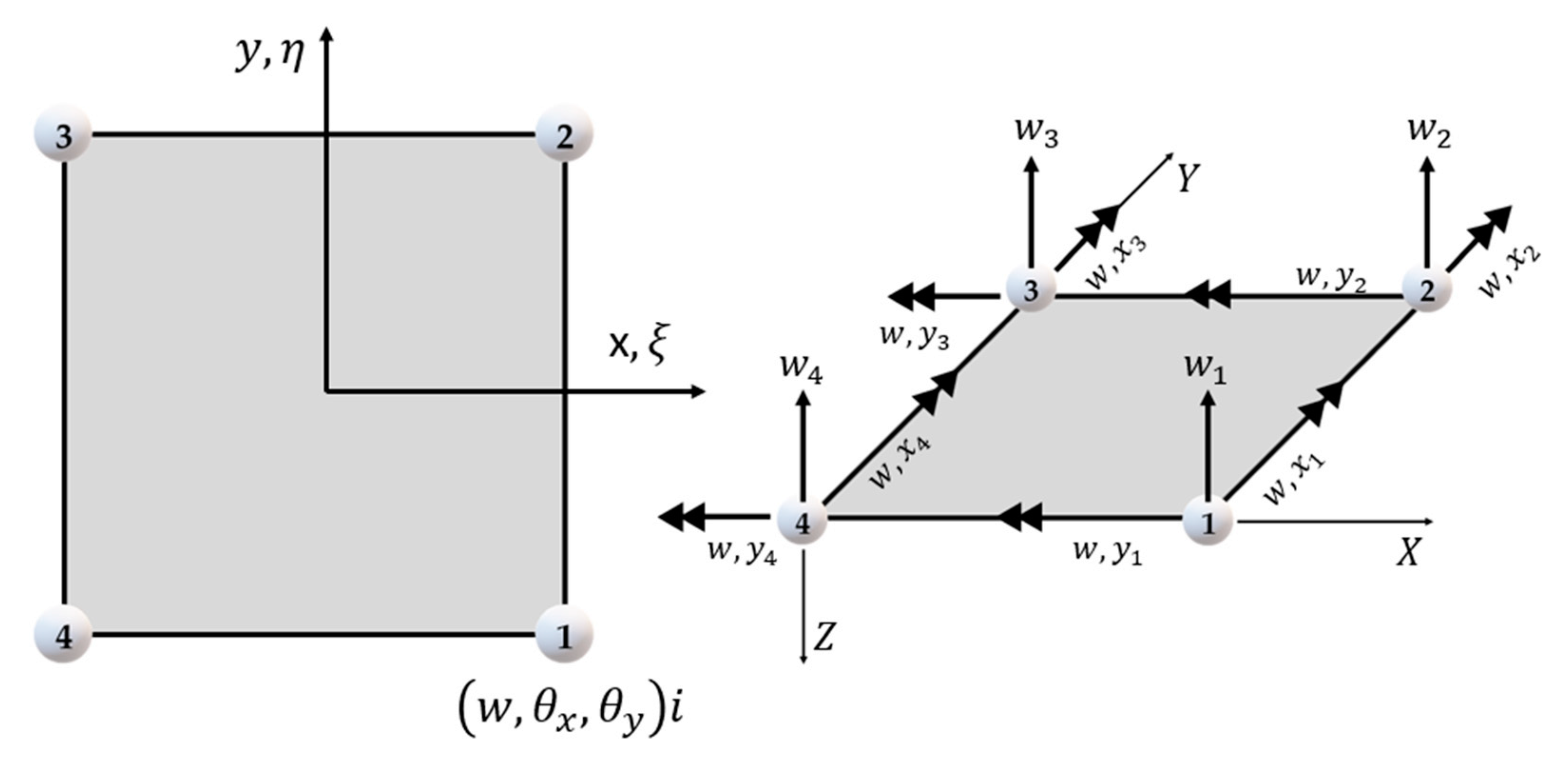
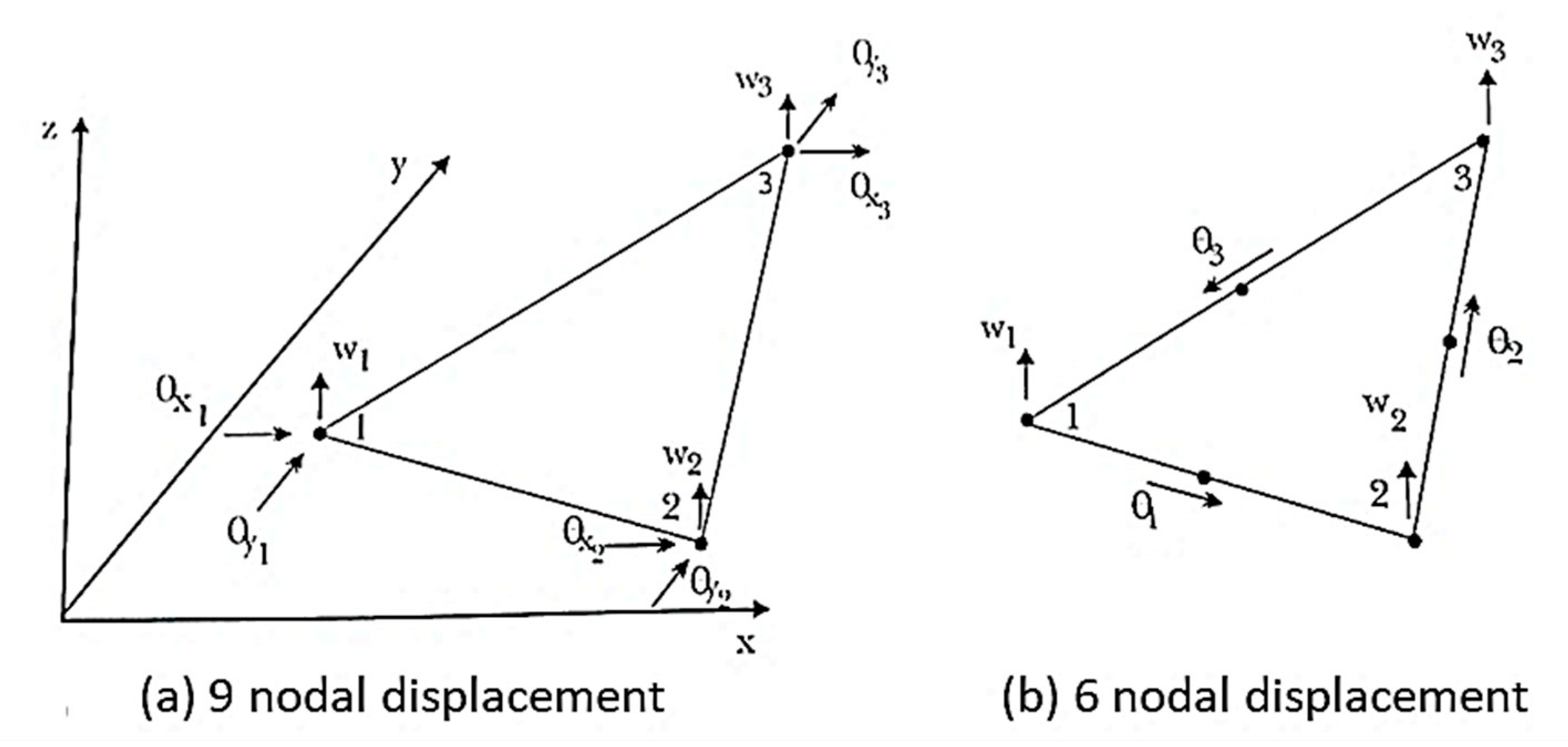
5.1. Plate Element
5.1.1. Elements of Kirchhoff Theory
- ➢
- Any point P (x, y) on the average surface of the plate moves only in the z direction—that is, it has only vertical displacement w (x, y);
- ➢
- The normal stress in the z-direction (σz) is negligible;
- ➢
- The longitudinal strain is zero at any point on the plate, i.e., = 0;
- ➢
- A straight and normal line to the average surface before loading and cutting the median plane of the plate at point P (x, y) remains straight and normal to the plane tangent to the average surface at that point after loading, and therefore, the shear deformations e are zero.
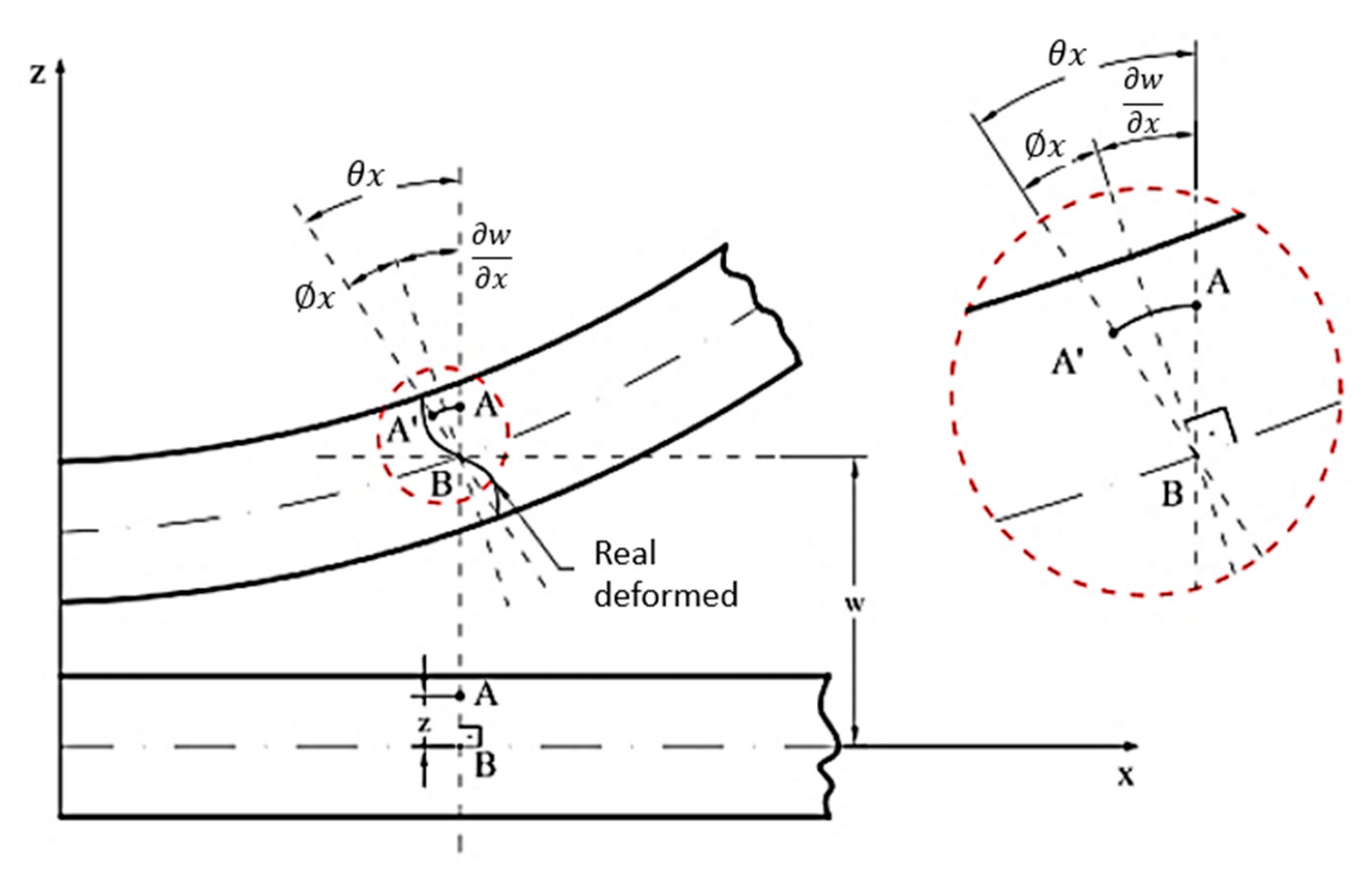
5.1.2. Elements of Mindlin Theory
- ➢
- Any point P (x, y) on the average surface of the plate moves only in the z direction—that is, it has only vertical displacement w (x, y);
- ➢
- The normal stress in the z direction (σz) is negligible;
- ➢
- The vertical longitudinal strain is zero at any point on the plate—i.e., εz = 0;
- ➢
- A straight and normal line to the average surface before loading and cutting the median plane of the plate at point P (x, y), remains straight after loading, and straight but not necessarily normal to this plane, after deformation.
5.1.3. Theory of Kirchhoff versus Theory of Mindlin
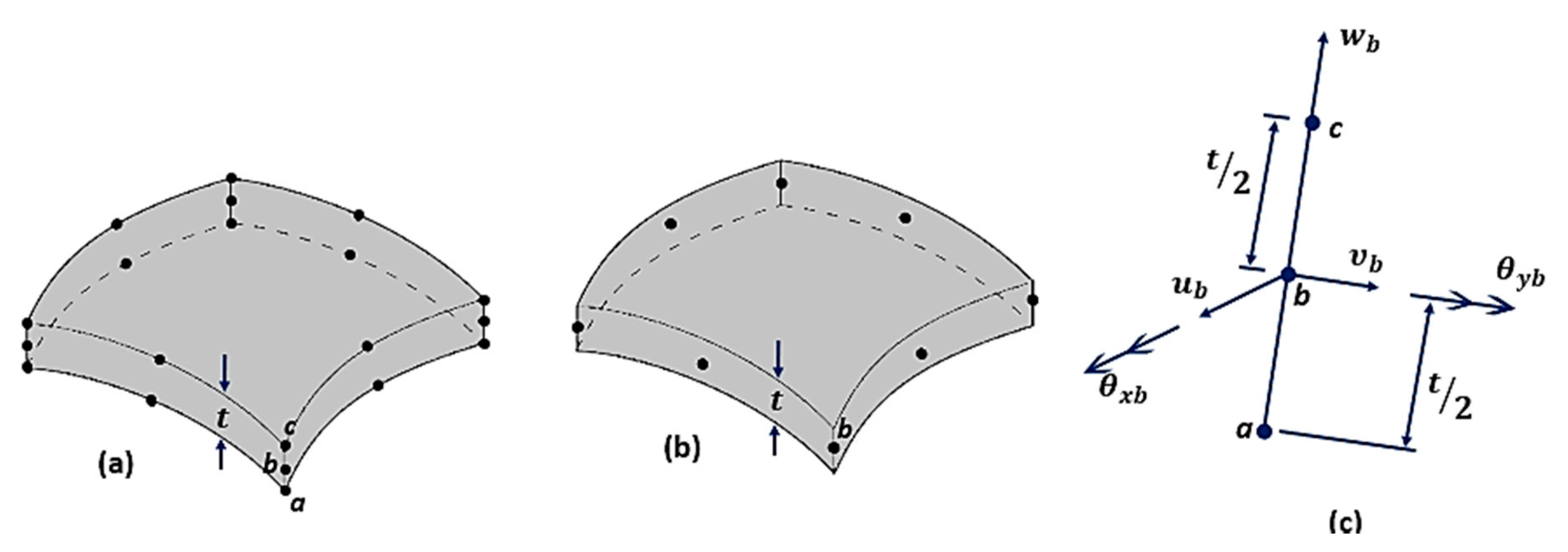
5.2. Shell Element
5.2.1. Shell Theories
The Theory of Flat Plate
Three-Dimensional Elements
Degenerate Shell Element of the Three-Dimensional Element
5.2.2. Shell Element Types
Flat Elements
Curved elements (with Reissner–Mindlin Hypotheses)
- ➢
- Working with the shell hypothesis from the beginning, obtaining, in a simple way, a wide range of elements;
- ➢
- Developing curved elements that only need C0 continuity;
- ➢
- Using only linear displacements and rotations as degrees of freedom, making it possible the use shell elements to discretize beam and plate elements;
- ➢
- Considering the effect of shear strain on a wide variety of thicknesses.
- ➢
- For plates, initially, shear rotations were separated from the plate and worked on the tension-deformation relationships with the resultant stress, excluding, consequently, integration along with thickness in the rigidity matrix and nodal forces equivalence expressions;
- ➢
- For shells, working with total rotation and stress components results in expressions of rigidity matrix and equivalent nodal forces that require integration along with thickness. Note that plate elements could also be formulated the same way.
Asymmetric Shell with Asymmetric Loading
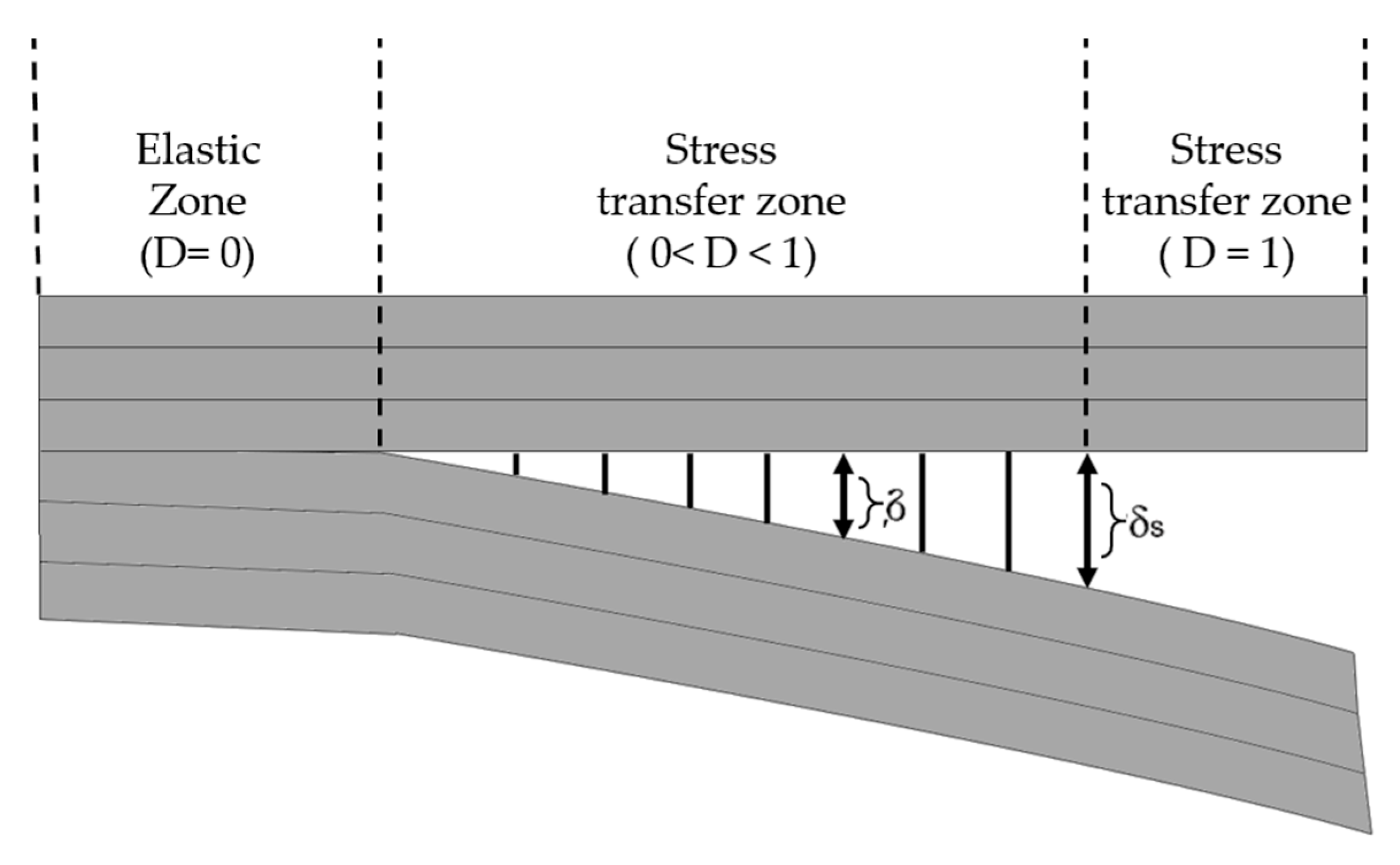
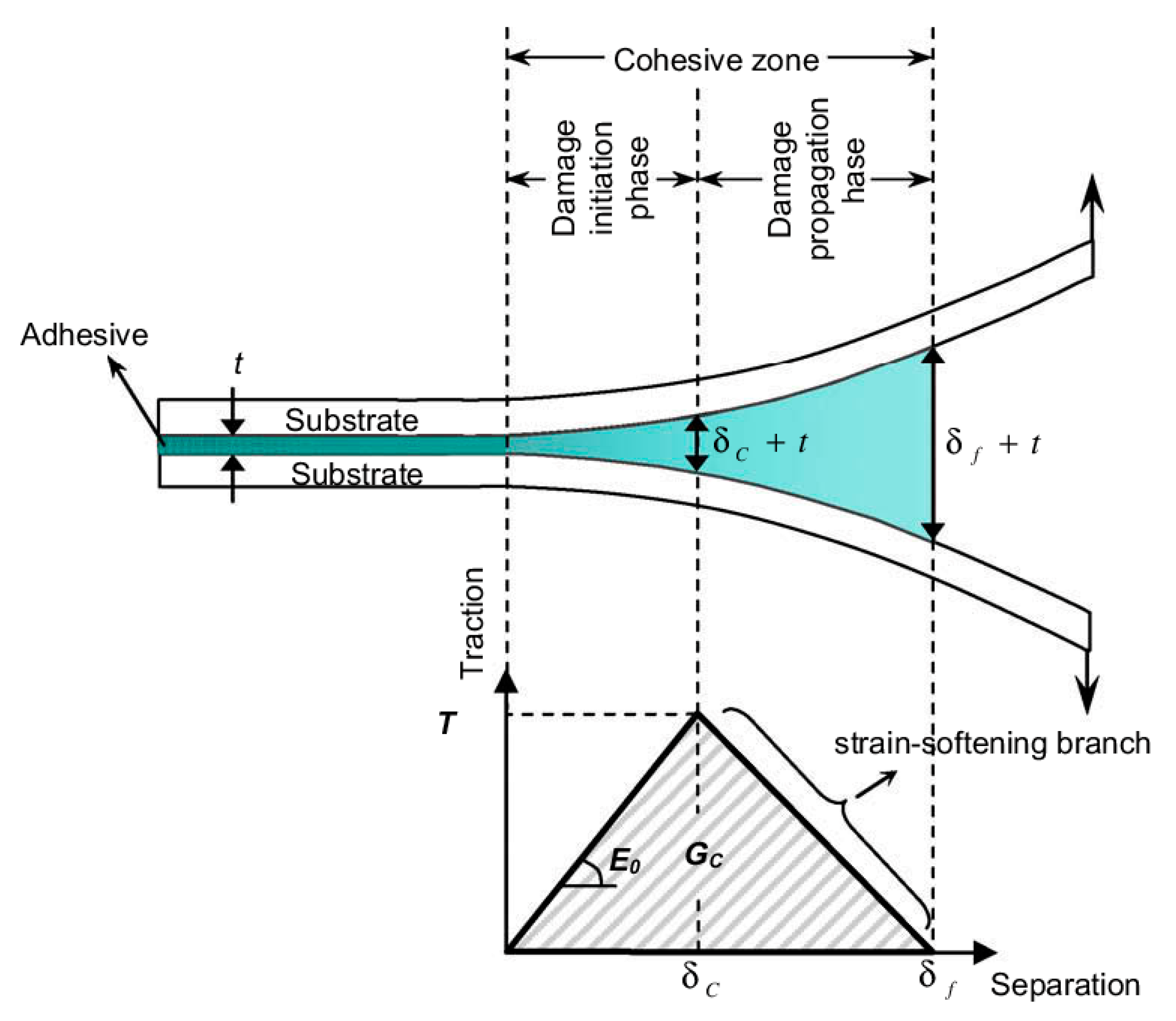
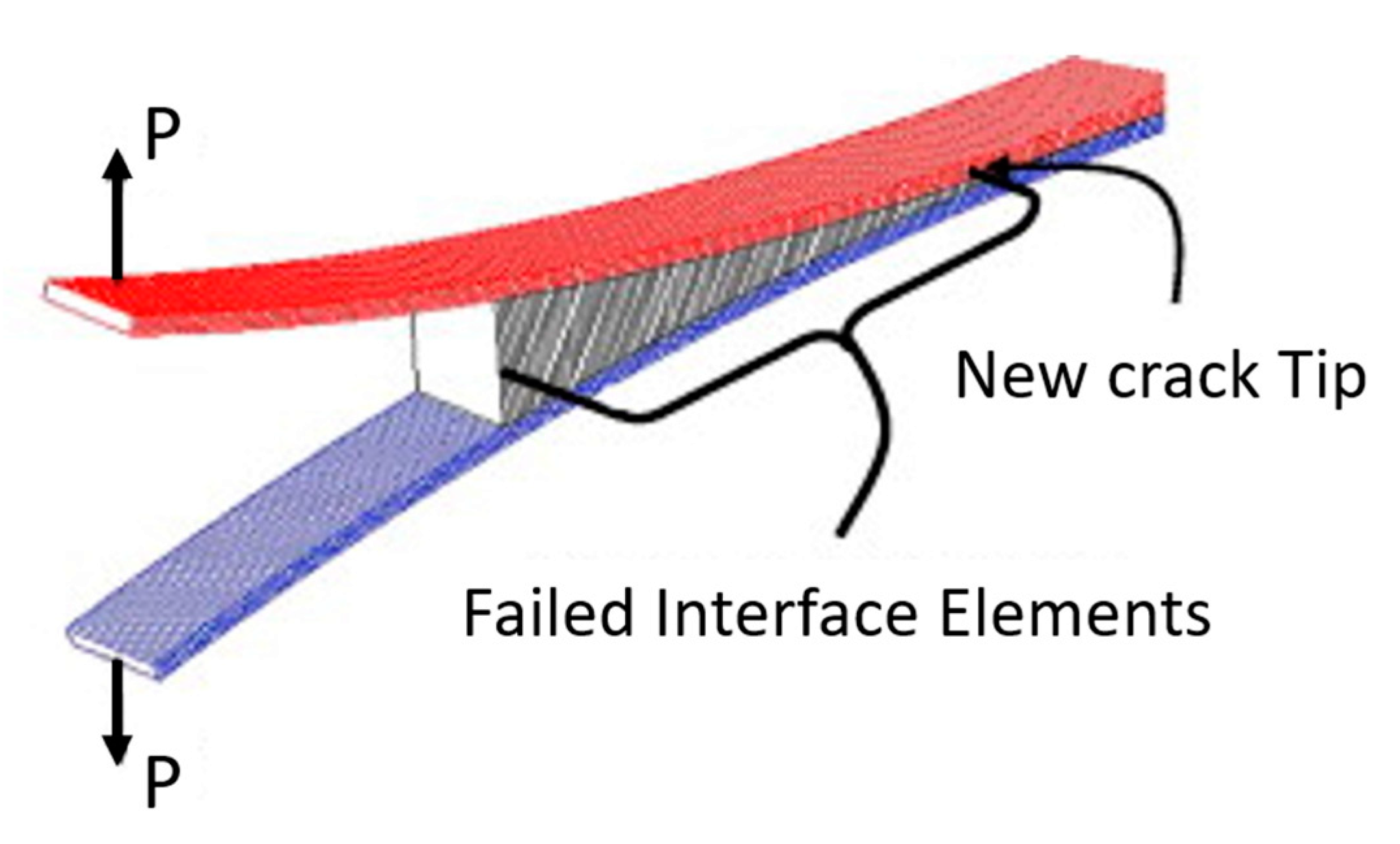
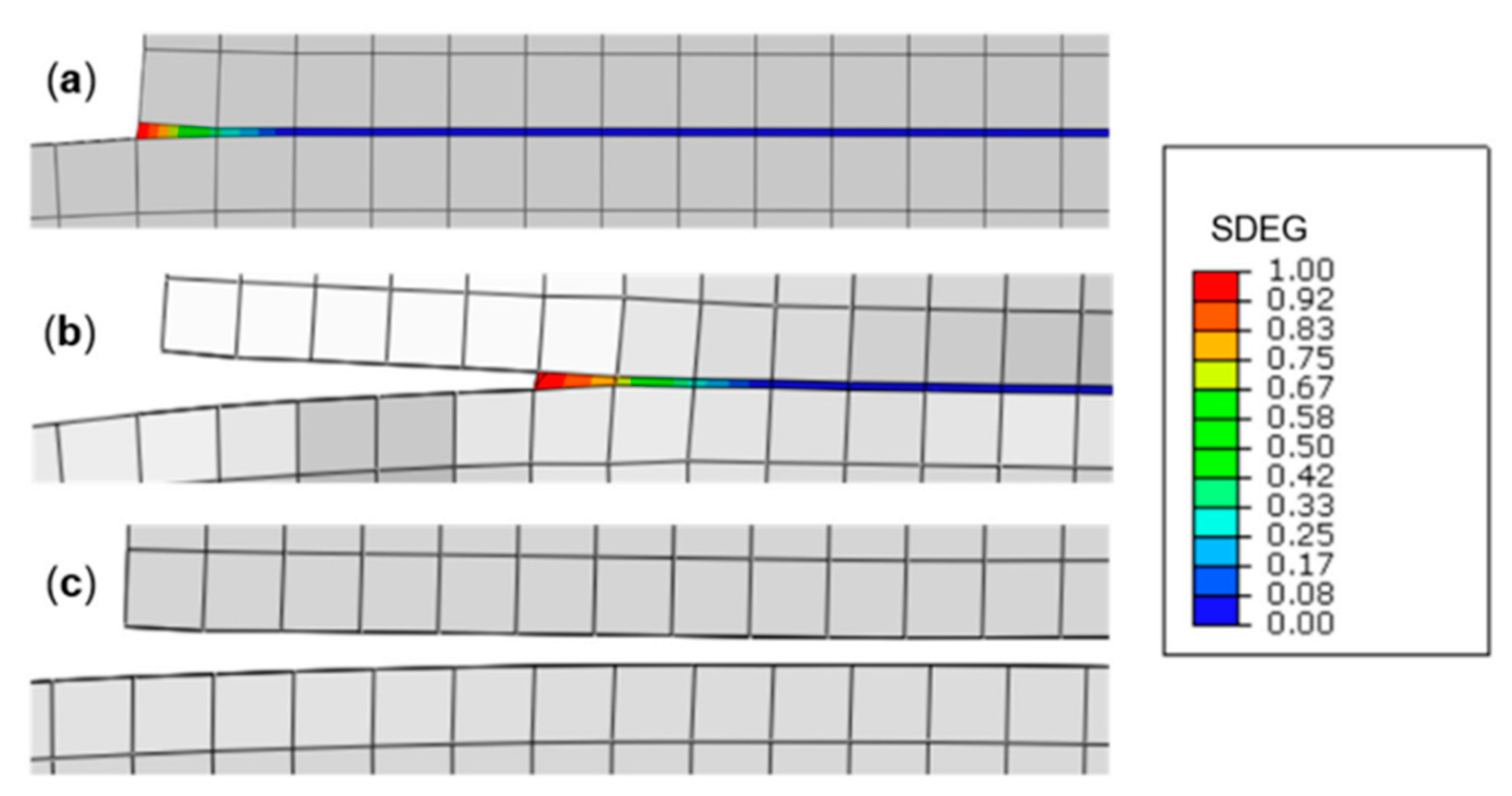
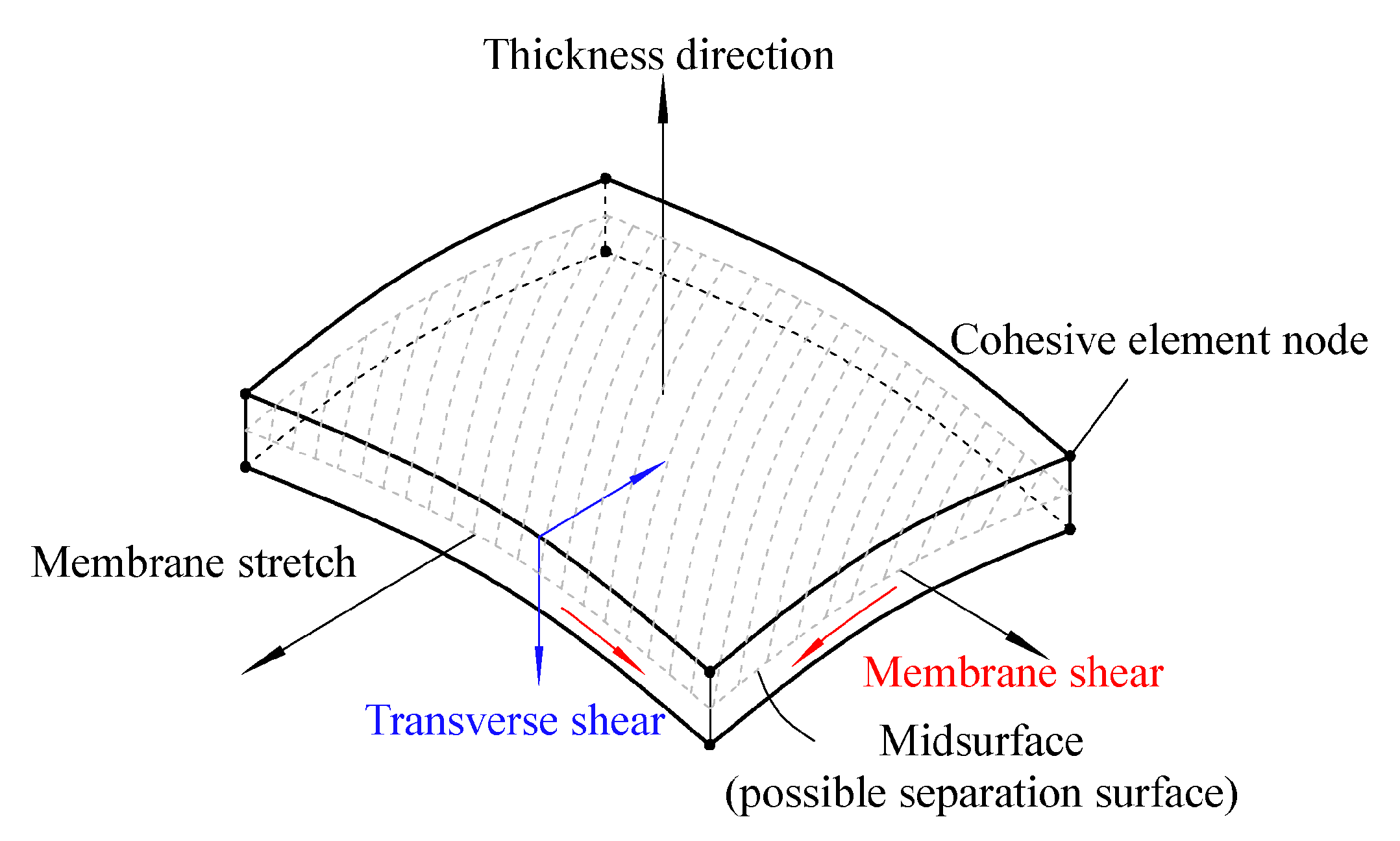
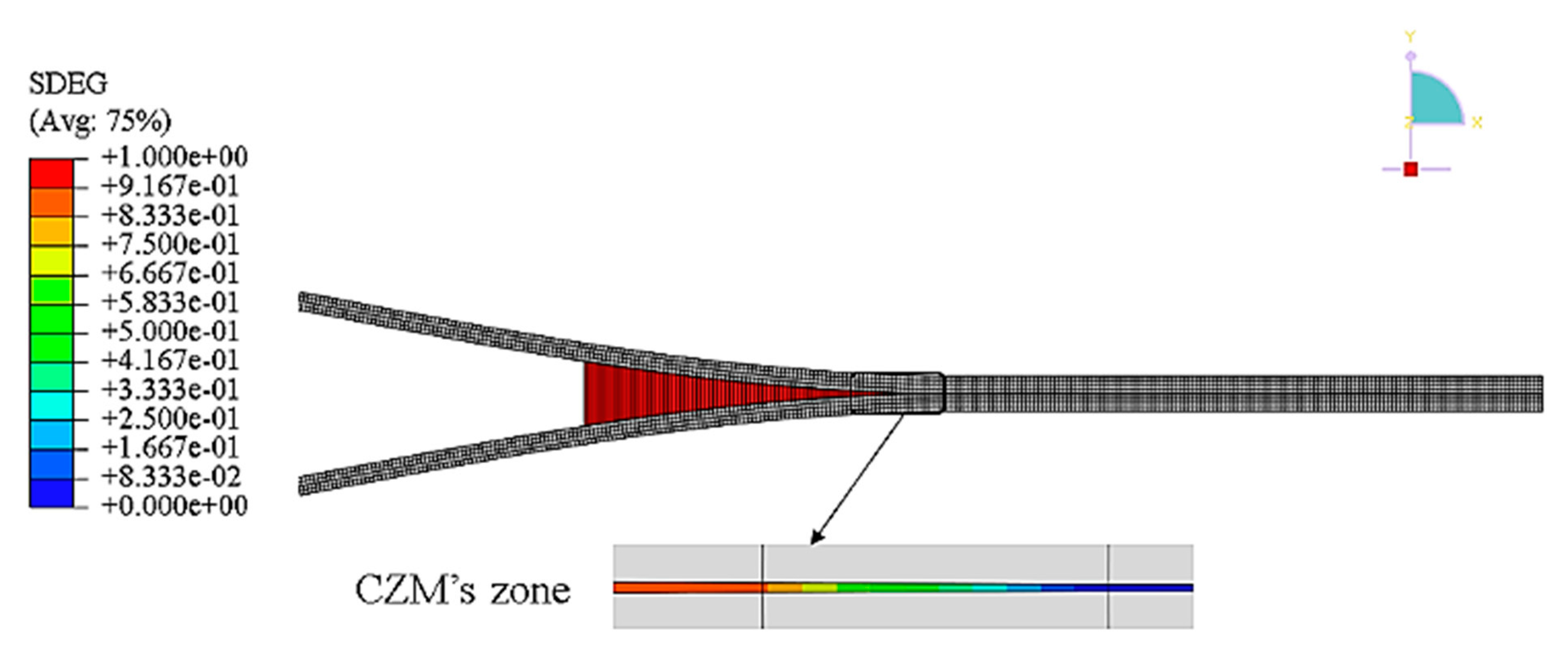
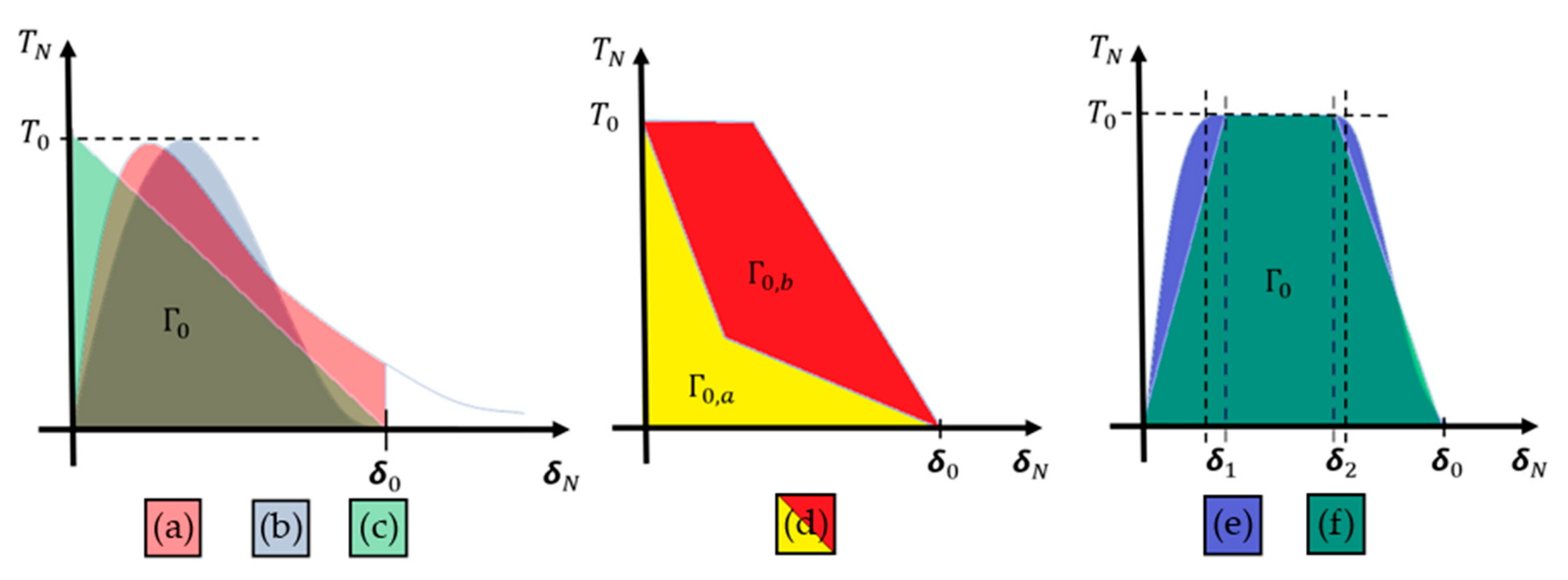
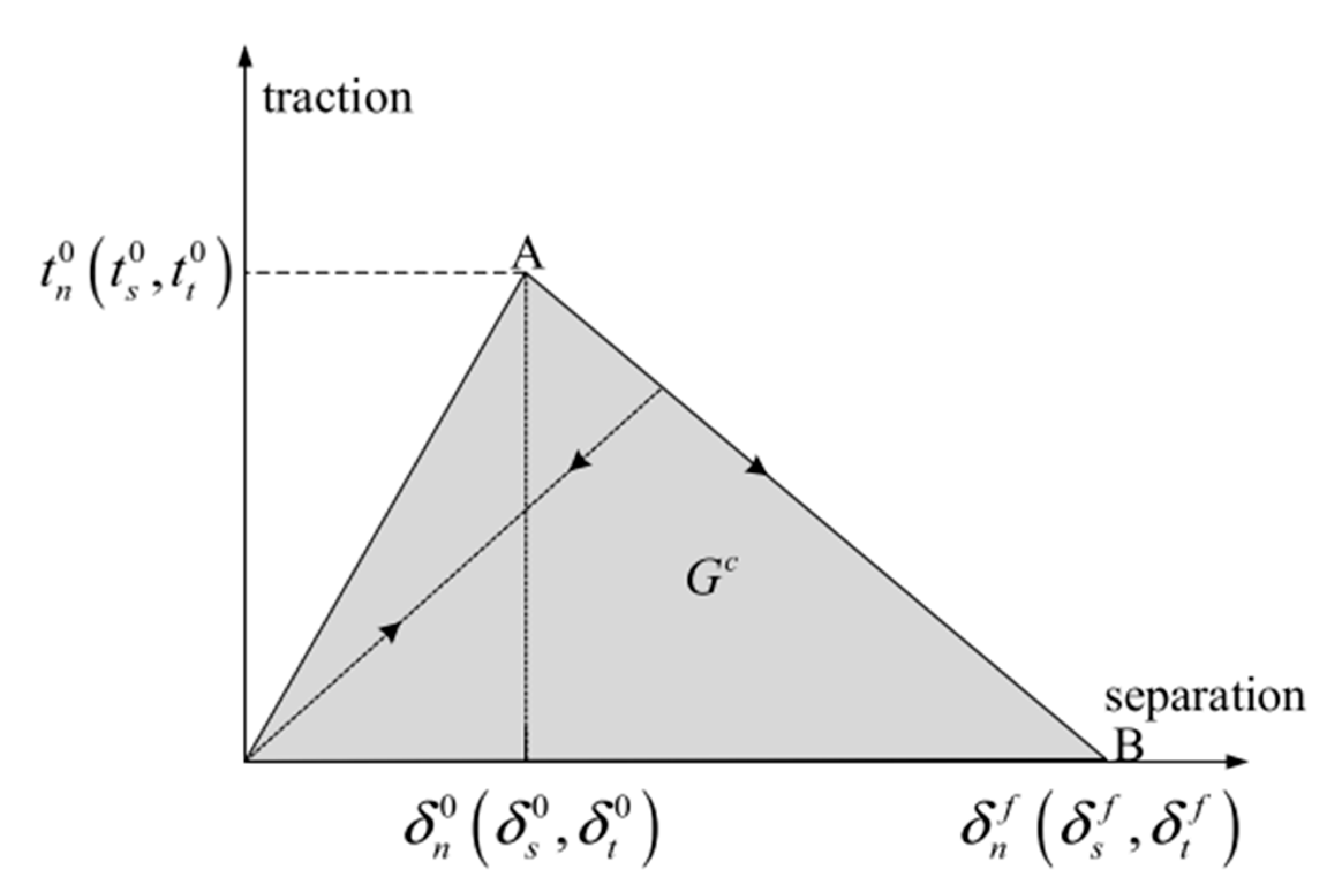
5.3. Cohesive Elements
- ➢
- Continuum-based modeling;
- ➢
- Laterally unconstrained adhesive patche;
- ➢
- Traction-separation based modeling.
5.3.1. Continuum-Based Modeling
5.3.2. Laterally Unconstrained Adhesive Patche
5.3.3. Traction-Separation-Based Modeling
5.3.4. Cohesive Element Types
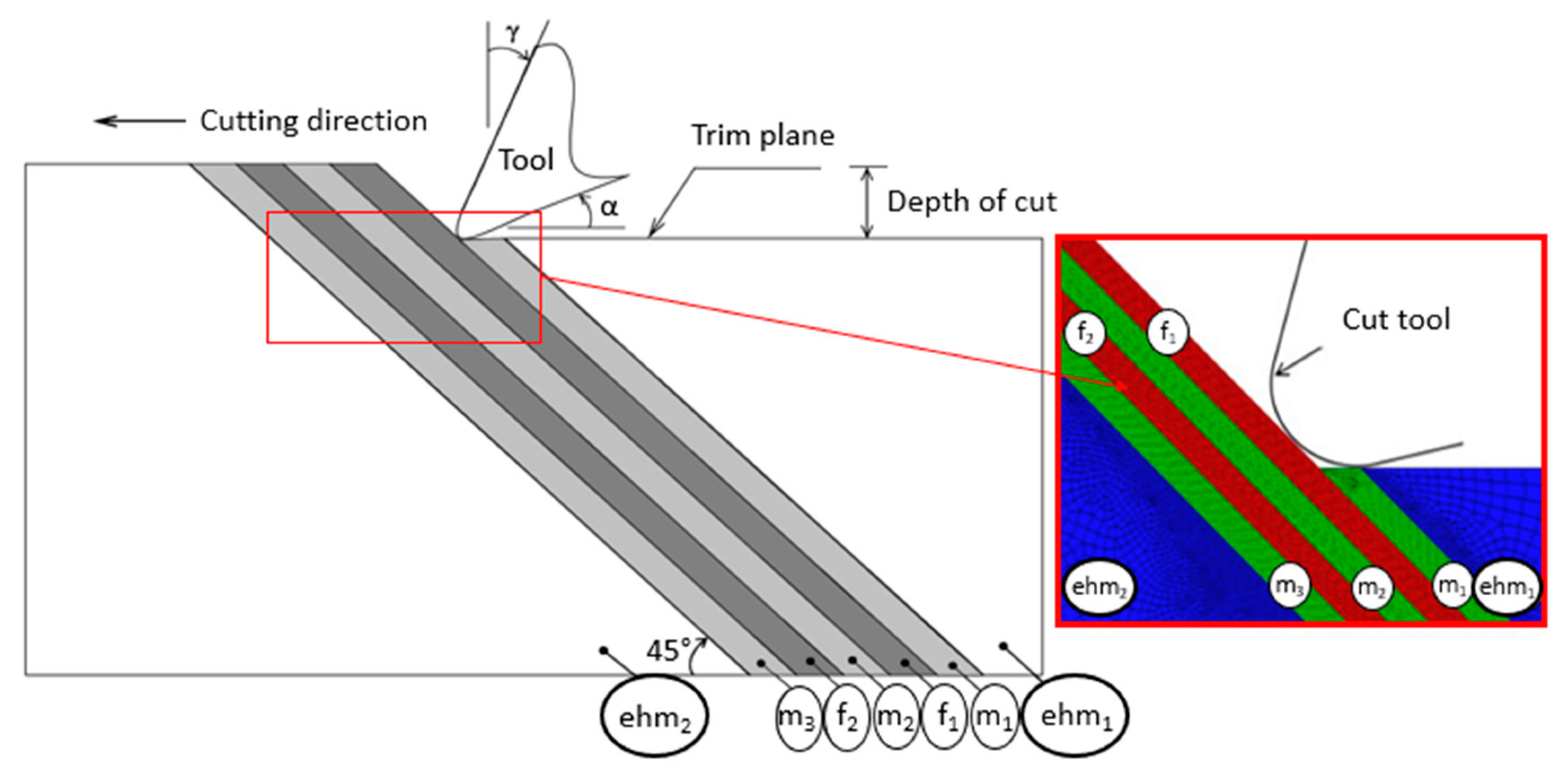
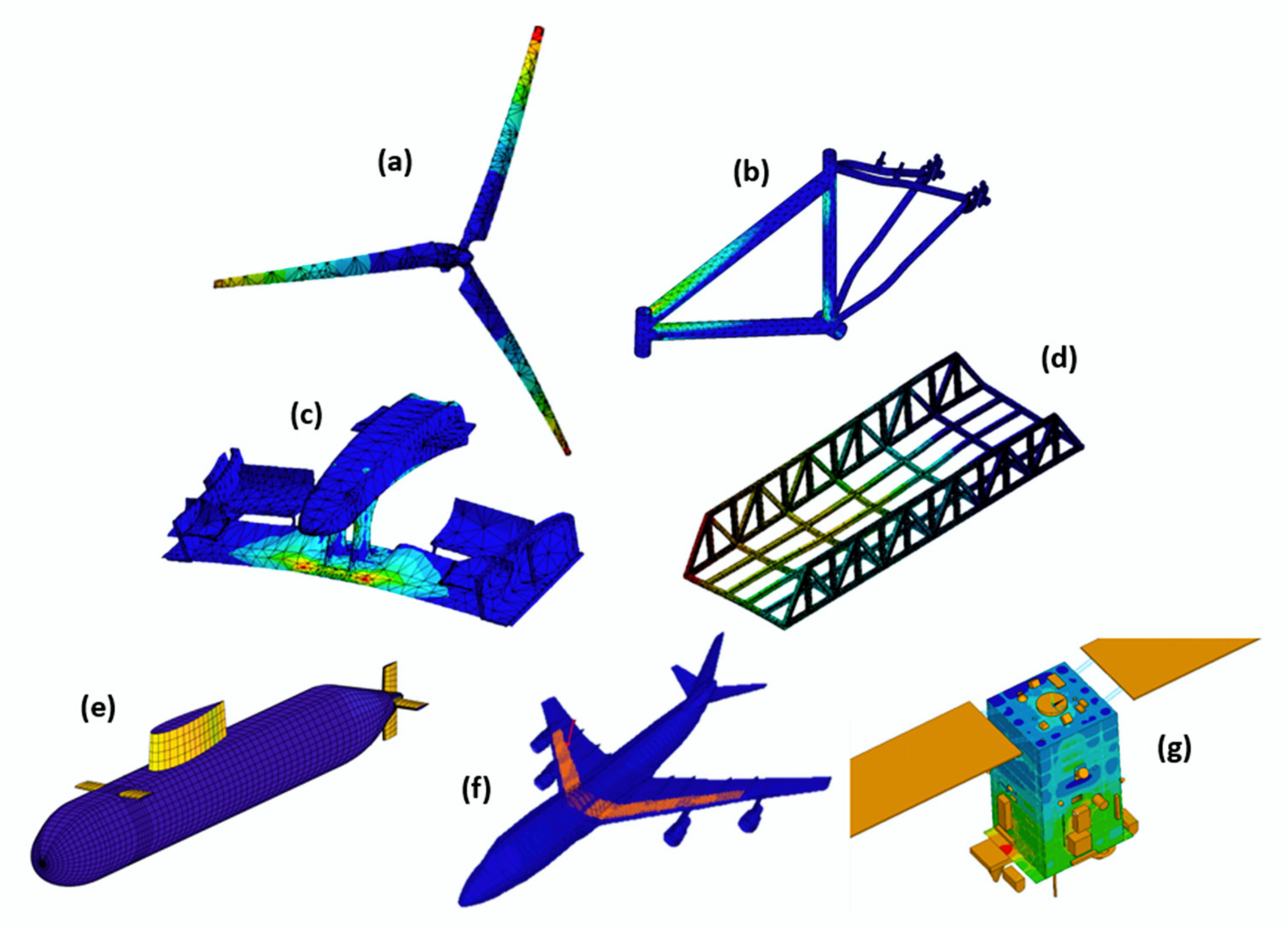
6. Main Applications of Finite Elements in the Study of Composite Materials
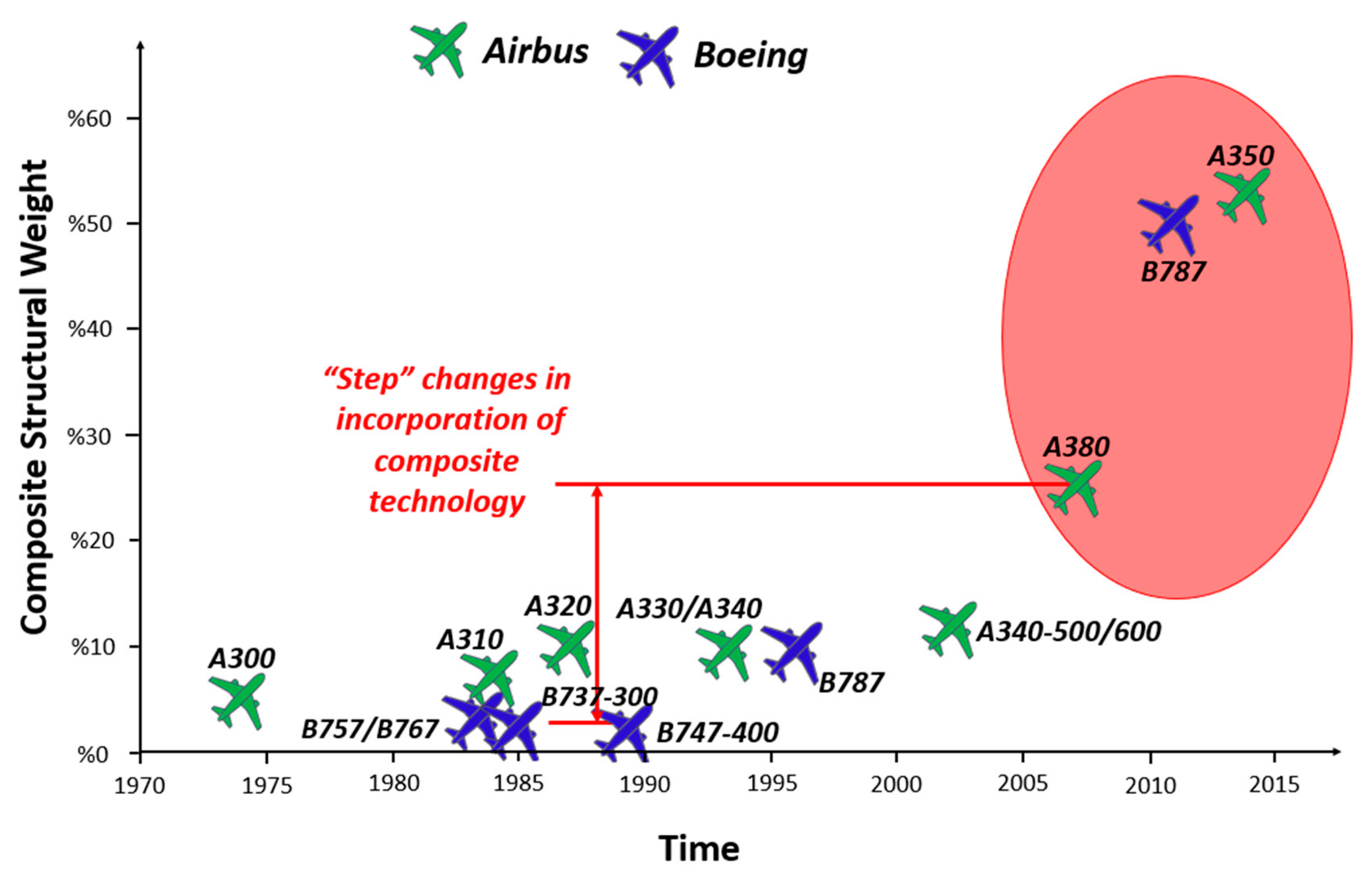
6.1. Aronautical
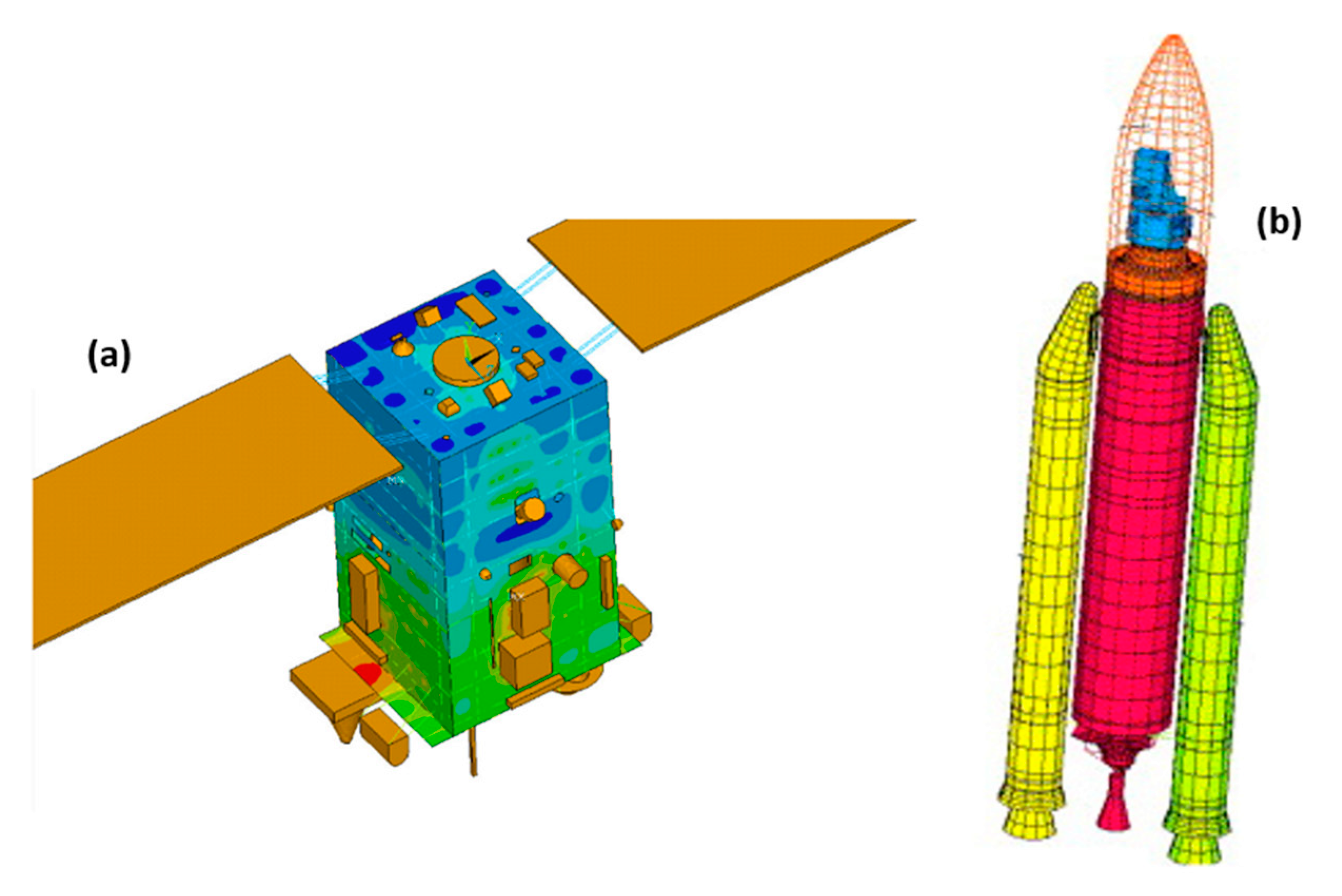
6.2. Space
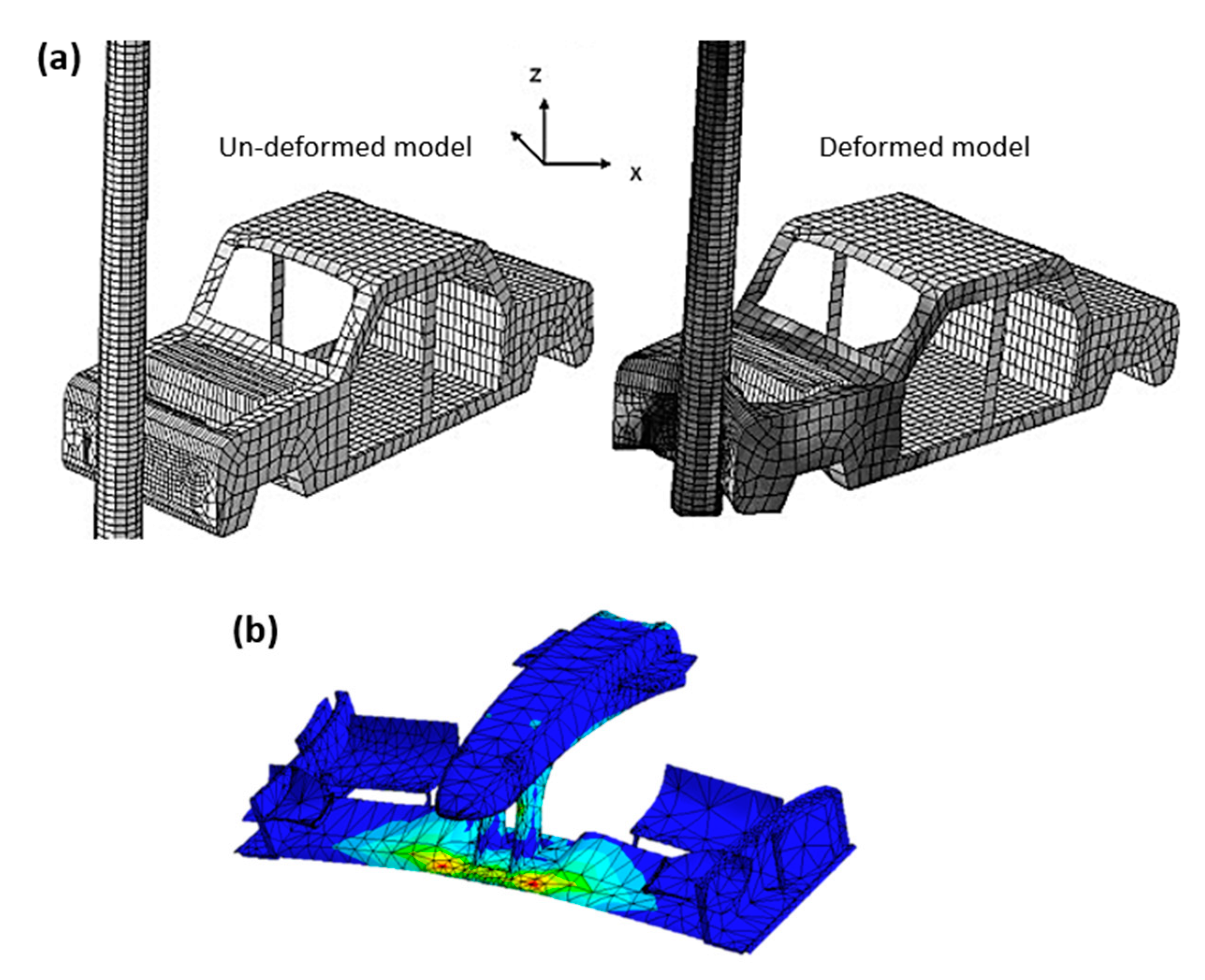
6.3. Automotive
6.4. Naval
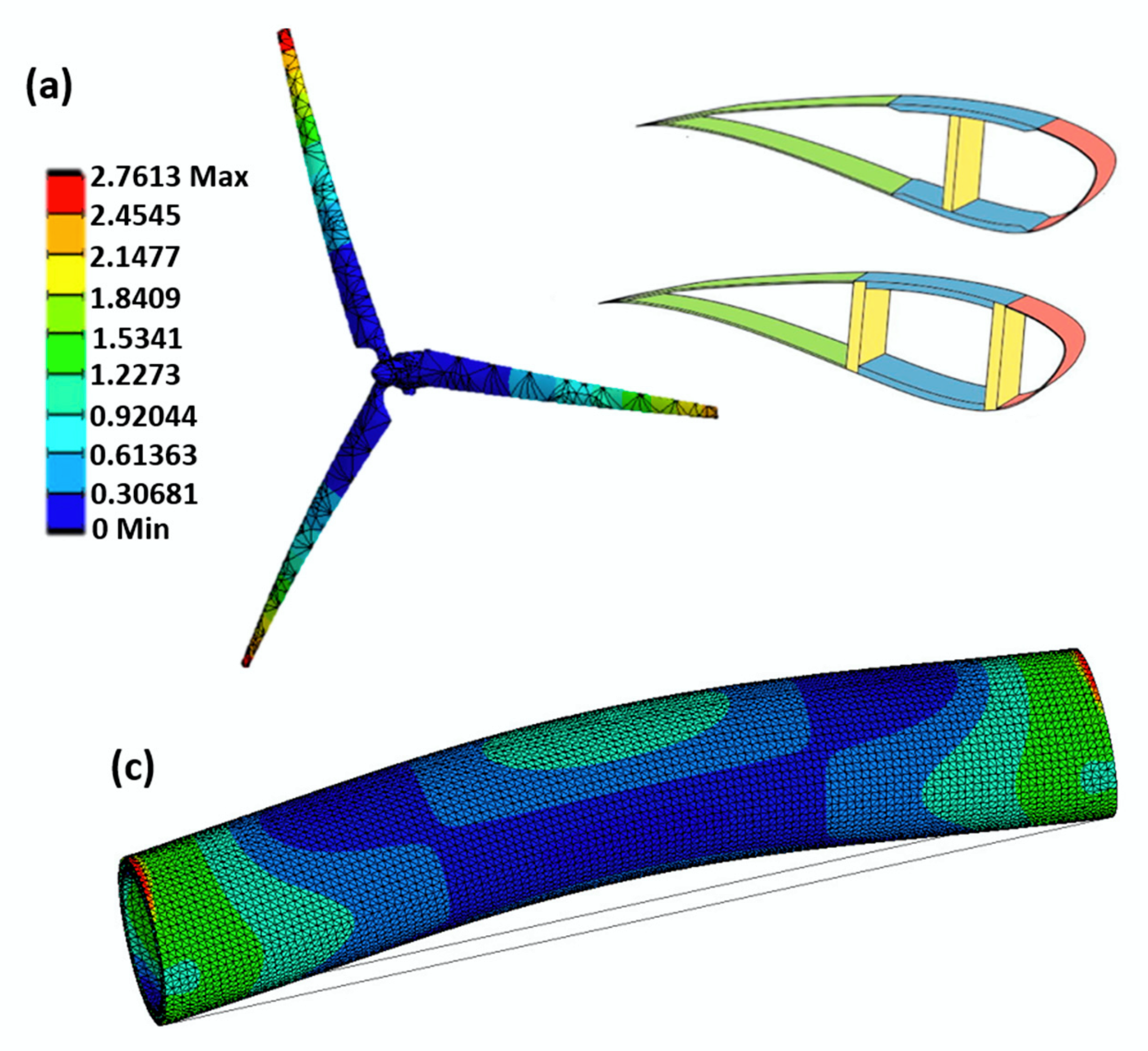
6.5. Energy
6.6. Civil Construction
6.7. Sports
6.8. Manufacturing
6.9. High-Performance Electronics
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rezende, M.C.; Costa, M.L.; Botelho, E.C. Compósitos Estruturais: Tecnologia e Prática, 1st ed.; Artliber: São Paulo, Brazil, 2011. [Google Scholar]
- Callister Junior, W.D.; Rethwisch, D.G. Materials Science and Engineering: An. Introduction, 8th ed.; LTC: São Paulo, Brazil, 2013. [Google Scholar]
- Kaw, A.K. Mechanics of Composite Materials, 2nd ed.; Taylor & Francis: Boca Raton, FL, USA, 2006. [Google Scholar]
- Composite Materials Research Progress, 1st ed.; Durand, L.P. (Ed.) Nova Science Publishers, Inc.: New York, NY, USA, 2008. [Google Scholar]
- Chung, D.D.L. Composite Materials. In Engineering Materials and Processes, 2nd ed.; Springer: London, UK, 2010. [Google Scholar]
- Levy Neto, F.; Pardini, L.C. Compósitos Estruturais: Ciência e Tecnologia, 2nd ed.; Edgar Blücher: São Paulo, Brazil, 2016. [Google Scholar]
- Berthelot, J.-M. Composite Materials: Mechanical Behavior and Structural Analysis, 1st ed.; Springer Science & Business Media: New York, NY, USA, 1999. [Google Scholar]
- Gay, D. Composite Materials: Design and Applications, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Teti, R. Machining of Composite Materials. CIRP Ann. 2002, 51, 611–634. [Google Scholar] [CrossRef]
- Gay, D.; Hoa, S.V.; Tsai, S.W. Composite Materials: Design and Applications, 4th ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Li, Y.; Li, W.; Lin, X.; Yang, M.; Zhao, Z.; Zhang, X.; Dong, P.; Xu, N.; Sun, Q.; Dai, Y.; et al. Theoretical modeling of the temperature dependent tensile strength for particulate-polymer composites. Compos. Sci. Technol. 2019, 184, 107881. [Google Scholar] [CrossRef]
- Liu, D.; Tang, Y.; Cong, W.L. A review of mechanical drilling for composite laminates. Compos. Struct. 2012, 94, 1265–1279. [Google Scholar] [CrossRef]
- Xu, J.; Mkaddem, A.; El Mansori, M. Recent advances in drilling hybrid FRP/Ti composite: A state-of-the-art review. Compos. Struct. 2016, 135, 316–338. [Google Scholar] [CrossRef] [Green Version]
- Katsoulis, C.; Kandola, B.K.; Myler, P.; Kandare, E. Post-fire flexural performance of epoxy-nanocomposite matrix glass fibre composites containing conventional flame retardants. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1389–1399. [Google Scholar] [CrossRef]
- Matadi Boumbimba, R.; Froustey, C.; Viot, P.; Olive, J.M.; Léonardi, F.; Gerard, P.; Inoubli, R. Preparation and mechanical characterisation of laminate composites made of glass fibre/epoxy resin filled with tri bloc copolymers. Compos. Struct. 2014, 116, 414–422. [Google Scholar] [CrossRef] [Green Version]
- Xing, J.; Du, C.; He, X.; Zhao, Z.; Zhang, C.; Li, Y. Finite Element Study on the Impact Resistance of Laminated and Textile Composites. Polymers 2019, 11, 1798. [Google Scholar] [CrossRef] [Green Version]
- Jia, Z.; Bai, Y.; Wang, F.; Ma, J.; Cheng, D.; Zhang, Z. Effect of drill flute direction on delamination at the exit in drilling Carbon Fiber Reinforced Plastic. Polym. Compos. 2019, 40, E1434–E1440. [Google Scholar] [CrossRef]
- Moura, M.F.S.F.; Morais, A.B.; Magalhães, A.G. Materiais Compósitos: Materiais, Fabrico e Comportamento Mecânico, 1st ed.; Publindústria: Porto, Portugal, 2005. [Google Scholar]
- Ghafoori, E.; Prinz, G.; Mayor, E.; Nussbaumer, A.; Motavalli, M.; Herwig, A.; Fontana, M. Finite Element Analysis for Fatigue Damage Reduction in Metallic Riveted Bridges Using Pre-Stressed CFRP Plates. Polymers 2014, 6, 1096–1118. [Google Scholar] [CrossRef] [Green Version]
- Martinelli, E.; Napoli, A.; Nunziata, B.; Realfonzo, R. RC Beams Strengthened with Mechanically Fastened Composites: Experimental Results and Numerical Modeling. Polymers 2014, 6, 613–633. [Google Scholar] [CrossRef] [Green Version]
- Cook, R.D. Finite Element Modeling for Stress Analysis, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1995. [Google Scholar]
- Tenek, L.T.; Argyris, J. Finite Element Analysis for Composite Structures. In Solid Mechanics and Its Applications; Gladwell, G.M., Ed.; Springer: Dordrecht, The Netherlands, 1998; Volume 59. [Google Scholar]
- Dandekar, C.R.; Shin, Y.C. Modeling of machining of composite materials: A review. Int. J. Mach. Tools Manuf. 2012, 57, 102–121. [Google Scholar] [CrossRef]
- Lasri, L.; Nouari, M.; El Mansori, M. Modelling of chip separation in machining unidirectional FRP composites by stiffness degradation concept. Compos. Sci. Technol. 2009, 69, 684–692. [Google Scholar] [CrossRef]
- Zhao, L.G.; Warrior, N.A.; Long, A.C. Finite element modelling of damage progression in non-crimp fabric reinforced composites. Compos. Sci. Technol. 2006, 66, 36–50. [Google Scholar] [CrossRef]
- Arola, D.; Ramulu, M. Orthogonal cutting of fiber-reinforced composites: A finite element analysis. Int. J. Mech. Sci. 1997, 39, 597–613. [Google Scholar] [CrossRef]
- Barbero, E.J. Finite Element Analysis of Composite Materials Using Ansys, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Mkaddem, A.; Demirci, I.; Mansori, M. El A micro–macro combined approach using FEM for modelling of machining of FRP composites: Cutting forces analysis. Compos. Sci. Technol. 2008, 68, 3123–3127. [Google Scholar] [CrossRef]
- Yang, L.; Yan, Y.; Liu, Y.; Ran, Z. Microscopic failure mechanisms of fiber-reinforced polymer composites under transverse tension and compression. Compos. Sci. Technol. 2012, 72, 1818–1825. [Google Scholar] [CrossRef]
- Venu Gopala Rao, G.; Mahajan, P.; Bhatnagar, N. Machining of UD-GFRP composites chip formation mechanism. Compos. Sci. Technol. 2007, 67, 2271–2281. [Google Scholar] [CrossRef]
- Jones, R.M. Mechanics of Composite Materials, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Hinton, M.J.; Kaddour, A.S.; Soden, P.D. Failure Criteria in Fibre-Reinforced-Polymer Composites; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Tan, W.; Naya, F.; Yang, L.; Chang, T.; Falzon, B.G.; Zhan, L.; Molina-Aldareguía, J.M.; González, C.; Llorca, J. The role of interfacial properties on the intralaminar and interlaminar damage behaviour of unidirectional composite laminates: Experimental characterization and multiscale modelling. Compos. Part B Eng. 2018, 138, 206–221. [Google Scholar] [CrossRef] [Green Version]
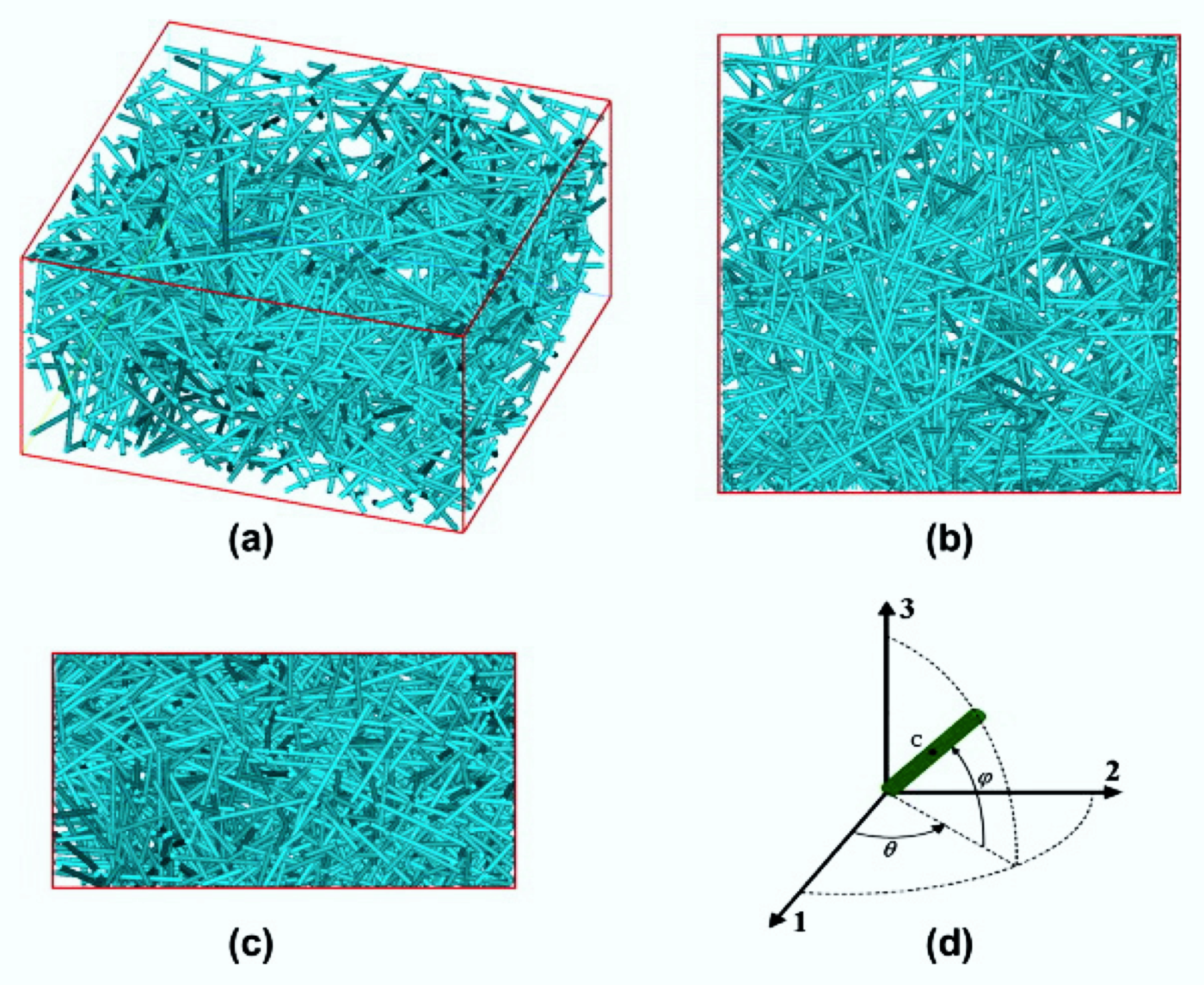
- Aboudi, J.; Arnold, S.M.; Bednarcyk, B.A. Micromechanics of Composite Materials; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Ma, J.; Du, W.; Gao, W.; Wriggers, P.; Xue, X. Multiscale finite element analysis of uncertain-but-bounded heterogeneous materials at finite deformation. Finite Elem. Anal. Des. 2018, 149, 15–31. [Google Scholar] [CrossRef]
- Li, D.; Wang, Z.; Zhang, C. A multi-level and multi-site mesh refinement method for the 2D problems with microstructures. Mech. Adv. Mater. Struct. 2019. [Google Scholar] [CrossRef]
- Elliott, J.A. Novel approaches to multiscale modelling in materials science. Int. Mater. Rev. 2011, 56, 207–225. [Google Scholar] [CrossRef]
- Koloor, S.S.R.; Rahimian-Koloor, S.M.; Karimzadeh, A.; Hamdi, M.; Petrů, M.; Tamin, M.N. Nano-Level Damage Characterization of Graphene/Polymer Cohesive Interface under Tensile Separation. Polymers 2019, 11, 1435. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.-X.; Shen, H.-S. Nonlinear vibration and bending of sandwich plates with nanotube-reinforced composite face sheets. Compos. Part B Eng. 2012, 43, 411–421. [Google Scholar] [CrossRef]
- Wang, Z.-X.; Shen, H.-S. Nonlinear vibration of nanotube-reinforced composite plates in thermal environments. Comput. Mater. Sci. 2011, 50, 2319–2330. [Google Scholar] [CrossRef]
- Bostanabad, R.; Liang, B.; Gao, J.; Liu, W.K.; Cao, J.; Zeng, D.; Su, X.; Xu, H.; Li, Y.; Chen, W. Uncertainty quantification in multiscale simulation of woven fiber composites. Comput. Methods Appl. Mech. Eng. 2018, 338, 506–532. [Google Scholar] [CrossRef]
- Stier, B.; Simon, J.-W.; Reese, S. Numerical and experimental investigation of the structural behavior of a carbon fiber reinforced ankle-foot orthosis. Med. Eng. Phys. 2015, 37, 505–511. [Google Scholar] [CrossRef]
- Mao, J.Z.; Sun, X.S.; Ridha, M.; Tan, V.B.C.; Tay, T.E. A Modeling Approach Across Length Scales for Progressive Failure Analysis of Woven Composites. Appl. Compos. Mater. 2013, 20, 213–231. [Google Scholar] [CrossRef]
- Yin, H.; Zhao, Y. Introduction to the Micromechanics of Composite Materials, 1st ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Shaik, A.; Salvi, A. A Multi Scale Approach for Analysis of Fiber Reinforced Composites. Mater. Today Proc. 2017, 4, 3197–3206. [Google Scholar] [CrossRef]
- Mustafa, G.; Suleman, A.; Crawford, C. Probabilistic micromechanical analysis of composite material stiffness properties for a wind turbine blade. Compos. Struct. 2015, 131, 905–916. [Google Scholar] [CrossRef]
- Multiscale Modeling and Simulation of Composite Materials and Structures, 1st ed.; Kwon, Y.W.; Allen, D.H.; Talreja, R. (Eds.) Springer: Boston, MA, USA, 2008. [Google Scholar]
- Linde, P.; Pleitner, J.; De Boer, H.; Carmone, C. Modelling and Simulation of Fibre Metal Laminates. In Proceedings of the ABAQUS Users’ Conference, Boston, MA, USA, 24–27 May 2004; pp. 421–439. [Google Scholar]
- Tian, W.; Qi, L.; Zhou, J.; Liang, J.; Ma, Y. Representative volume element for composites reinforced by spatially randomly distributed discontinuous fibers and its applications. Compos. Struct. 2015, 131, 366–373. [Google Scholar] [CrossRef]
- Lu, Z.; Yuan, Z.; Liu, Q. 3D numerical simulation for the elastic properties of random fiber composites with a wide range of fiber aspect ratios. Comput. Mater. Sci. 2014, 90, 123–129. [Google Scholar] [CrossRef]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- Li, S.; Sitnikova, E. Representative Volume Elements and Unit Cells, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Feito, N.; Díaz-Álvarez, J.; López-Puente, J.; Miguelez, M.H. Experimental and numerical analysis of step drill bit performance when drilling woven CFRPs. Compos. Struct. 2018, 184, 1147–1155. [Google Scholar] [CrossRef]
- Mechcomp3 3rd International Conference of Mechanics of Composite; Ferreira, A.J.M.; Viola, E.; Tornabene, F.; Fantuzzi, N. (Eds.) Structural and Computational Mechanics Book Series; Società Editrice Esculapio: Bologna, Italy, 2017. [Google Scholar]
- Chandra, N.; Li, H.; Shet, C.; Ghonem, H. Some issues in the application of cohesive zone models for metal–ceramic interfaces. Int. J. Solids Struct. 2002, 39, 2827–2855. [Google Scholar] [CrossRef]
- Porous Rock Fracture Mechanics: With Application to Hydraulic Fracturing, Drilling and Structural Engineering, 1st ed.; Shojaei, A.K.; Shao, J. (Eds.) Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Comprehensive Satructural Integrety, 1st ed.; Milne, I.; Ritchie, R.O.; Karihaloo, B. (Eds.) Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Structural Integrity and Durability of Advanced Composites: Innovative Modelling Methods and Intelligent Design, 1st ed.; Beaumont, P.W.R.; Soutis, C.; Hodzic, A. (Eds.) Woodhead: Lincolnshire, IL, USA, 2015. [Google Scholar]
- De Morais, A.B. Mode I cohesive zone model for delamination in composite beams. Eng. Fract. Mech. 2013, 109, 236–245. [Google Scholar] [CrossRef]
- Abena, A.; Soo, S.L.; Essa, K. Modelling the orthogonal cutting of UD-CFRP composites: Development of a novel cohesive zone model. Compos. Struct. 2017, 168, 65–83. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.; Cox, B. Cohesive models for damage evolution in laminated composites. Int. J. Fract. 2005, 133, 107–137. [Google Scholar] [CrossRef]
- Xie, J.; Waas, A.M.; Rassaian, M. Closed-form solutions for cohesive zone modeling of delamination toughness tests. Int. J. Solids Struct. 2016, 88, 379–400. [Google Scholar] [CrossRef]
- Dávila, C.G.; Camanho, P.P.; Turon, A. Cohesive Elements for Shells; NASA/TP-2007-214869, L-19341; NASA: Hampton, UK, 2007. [Google Scholar]
- Harper, P.W.; Hallett, S.R. Cohesive zone length in numerical simulations of composite delamination. Eng. Fract. Mech. 2008, 75, 4774–4792. [Google Scholar] [CrossRef] [Green Version]
- Fatigue and Fracture of Adhesively-Bonded Composite Joints, 1st ed.; Vassilopoulos, A.P. (Ed.) Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Katnam, K.B.; Sargent, J.P.; Crocombe, A.D.; Khoramishad, H.; Ashcroft, I.A. Characterisation of moisture-dependent cohesive zone properties for adhesively bonded joints. Eng. Fract. Mech. 2010, 77, 3105–3119. [Google Scholar] [CrossRef]
- Khoramishad, H.; Crocombe, A.D.; Katnam, K.B.; Ashcroft, I.A. Predicting fatigue damage in adhesively bonded joints using a cohesive zone model. Int. J. Fatigue 2010, 32, 1146–1158. [Google Scholar] [CrossRef]
- Liu, P.F.; Zheng, J.Y. Recent developments on damage modeling and finite element analysis for composite laminates: A review. Mater. Des. 2010, 31, 3825–3834. [Google Scholar] [CrossRef]
- Marine Applications of Advanced Fibre-Reinforced Composites; Graham-Jones, J.; Summerscales, J. (Eds.) Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Tillmann, V.B. Análise Estrutural de Elementos Compósitos Com a Utilização do Método de Elementos Finitos; Universidade Federal de Santa Catarina: Florianópolis, Brazil, 2015. [Google Scholar]
- Azevedo, C.A.C. de Formulação Alternativa para Análise de Domínios Não-Homogêneos e Inclusões Anisotrópicas via Mec; Universidade de São Paulo: São Paulo, Brazil, 2007. [Google Scholar]
- Daniel, I. Engineering Mechanics of Composites Material, 2nd ed.; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Bednarcyk, B.A.; Aboudi, J.; Arnold, S.M. Micromechanics of composite materials governed by vector constitutive laws. Int. J. Solids Struct. 2017, 110, 137–151. [Google Scholar] [CrossRef]
- Structural Analysis. In Solid Mechanics and Its Applications, 1st ed.; Bauchau, O.A.; Craig, J.I. (Eds.) Springer: Dordrecht, The Netherlands, 2009; Volume 163. [Google Scholar]
- Soriano, H.L. Método de Elementos Finitos em Análise de Estruturas; EdUSP: São Paulo, Brazil, 2003. [Google Scholar]
- Vanalli, L. O MEC e o MEF Aplicados a Análise de Problemas Viscoplasticos em Meios Anisotrópicos e Compostos; Universidade de São Paulo: São Paulo, Brazil, 2004. [Google Scholar]
- Barbero, E.J. Finite Element Analysis of Composite Materials, 1st ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Gladwell, G.M.L. Finite Element Analysis of Composite Laminates. In Solid Mechanics and Its Applications; Gladwell, G.M.L. Springer: Dordrecht, The Netherlands, 1992; Volume 7. [Google Scholar]
- Ojo, S.O.; Ismail, S.O.; Paggi, M.; Dhakal, H.N. A new analytical critical thrust force model for delamination analysis of laminated composites during drilling operation. Compos. Part. B Eng. 2017, 124, 207–217. [Google Scholar] [CrossRef] [Green Version]
- Feng, W.W. A Failure Criterion for Composite Materials. J. Compos. Mater. 1991, 25, 88–100. [Google Scholar] [CrossRef]
- Mendonça, P.D.T.R. Materiais Compostos & Estruturas-Sanduíche: Projetos e Análises, 1st ed.; Manole Ltd.a.: Tamboré, Brazil, 2005. [Google Scholar]
- Zhao, S.Y.; Xue, P. New Two-Dimensional Polynomial Failure Criteria for Composite Materials. Adv. Mater. Sci. Eng. 2014, 2014, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Daniel, I.M.; Werner, B.T.; Fenner, J.S. Strain-rate-dependent failure criteria for composites. Compos. Sci. Technol. 2011, 71, 357–364. [Google Scholar] [CrossRef]
- Ashouri Vajari, D. A micromechanical study of porous composites under longitudinal shear and transverse normal loading. Compos. Struct. 2015, 125, 266–276. [Google Scholar] [CrossRef]
- Paris, F. A Study of Failure Criteria of Fibrous Composite Materials; NASA/CR-2001-210661; NASA: Hampton, UK, 2001. [Google Scholar]
- Qing, H.; Mishnaevsky, L. 3D constitutive model of anisotropic damage for unidirectional ply based on physical failure mechanisms. Comput. Mater. Sci. 2010, 50, 479–486. [Google Scholar] [CrossRef]
- Yeh, H.-Y.; Murphy, H.C.; Yeh, H.-L. An Investigation of Failure Criterion for New Orthotropic Ceramic Matrix Composite Materials. J. Reinf. Plast. Compos. 2009, 28, 441–459. [Google Scholar] [CrossRef]
- Camanho, P.P.; Dávila, C.G. Mixed-Mode Decohesion Finite Elements for the Simulation of Delamination in Composite Materials; NASA/ TM-2002-211737; NASA: Hampton, UK, 2002. [Google Scholar]
- Shokrieh, M.M. Residual Stresses in Composite Materials, 1st ed.; Woodhead: Cambridge, UK, 2014. [Google Scholar]
- Vasiliev, V.V.; Morozov, E.V. Advanced Mechanics of Composite Materials, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Martiny, P.; Lani, F.; Kinloch, A.J.; Pardoen, T. A maximum stress at a distance criterion for the prediction of crack propagation in adhesively-bonded joints. Eng. Fract. Mech. 2013, 97, 105–135. [Google Scholar] [CrossRef] [Green Version]
- Bobrov, A.V.; Sarbaev, B.S.; Shirshov, Y.Y. Deformation and strength properties of a carbon–carbide composite with 2D reinforcement under plane stress state. J. Mach. Manuf. Reliab. 2016, 45, 145–151. [Google Scholar] [CrossRef]
- Jiang, H.; Ren, Y.; Liu, Z.; Zhang, S.; Wang, X. Evaluations of failure initiation criteria for predicting damages of composite structures under crushing loading. J. Reinf. Plast. Compos. 2018, 37, 1279–1303. [Google Scholar] [CrossRef]
- Promis, G.; Bach, T.Q.; Gabor, A.; Hamelin, P. Failure behavior of E-glass fiber- and fabric-reinforced IPC composites under tension and compression loading. Mater. Struct. 2014, 47, 631–645. [Google Scholar] [CrossRef]
- Pyttel, T.; Liebertz, H.; Cai, J. Failure criterion for laminated glass under impact loading and its application in finite element simulation. Int. J. Impact Eng. 2011, 38, 252–263. [Google Scholar] [CrossRef]
- Chang, K.J. Further studies of the maximum stress criterion on the angled crack problem. Eng. Fract. Mech. 1981, 14, 125–142. [Google Scholar] [CrossRef]
- Luo, C.; Xiong, J. Static Pull and Push Bending Properties of RTM-made TWF Composite Tee-joints. Chin. J. Aeronaut. 2012, 25, 198–207. [Google Scholar] [CrossRef] [Green Version]
- Hart-Smith, L. Predictions of a generalized maximum-shear-stress failure criterion for certain fibrous composite laminates. Compos. Sci. Technol. 1998, 58, 1179–1208. [Google Scholar] [CrossRef]
- Hiroshima, N.; Hatta, H.; Koyama, M.; Goto, K.; Kogo, Y. Optimization of flywheel rotor made of three-dimensional composites. Compos. Struct. 2015, 131, 304–311. [Google Scholar] [CrossRef]
- Raftery, G.M.; Harte, A.M. Nonlinear numerical modelling of FRP reinforced glued laminated timber. Compos. Part B Eng. 2013, 52, 40–50. [Google Scholar] [CrossRef]
- Zhao, L.; Qin, T.; Zhang, J.; Shenoi, R.A. Modified maximum stress failure criterion for composite π joints. J. Compos. Mater. 2013, 47, 2995–3008. [Google Scholar] [CrossRef]
- Feng, P.; Meng, X.; Chen, J.-F.; Ye, L. Mechanical properties of structures 3D printed with cementitious powders. Constr. Build. Mater. 2015, 93, 486–497. [Google Scholar] [CrossRef] [Green Version]
- Koerber, H.; Xavier, J.; Camanho, P.P.; Essa, Y.E.; Martín de la Escalera, F. High strain rate behaviour of 5-harness-satin weave fabric carbon–epoxy composite under compression and combined compression–shear loading. Int. J. Solids Struct. 2015, 54, 172–182. [Google Scholar] [CrossRef]
- Echaabi, J.; Trochu, F.; Gauvin, R. Review of Failure Criteria of Fibrous Composite Materials. Polym. Compos. 1996, 17, 786–798. [Google Scholar] [CrossRef]
- Ferreira, L.B.M.; Júniora, R.C.S.F.; Forda, E.T.L.C. Analysis of failure criteria in laminas reinforced with unidirectional Curaua fiber fabric. Mater. Res. 2019, 22, 1–7. [Google Scholar] [CrossRef]
- De Luca, A.; Caputo, F. A review on analytical failure criteria for composite materials. AIMS Mater. Sci. 2017, 4, 1165–1185. [Google Scholar] [CrossRef]
- Ataş, A. Open hole compressive strength and damage mechanisms: Maximum stress versus Hashin criteria. Plast. Rubber Compos. 2015, 44, 280–290. [Google Scholar] [CrossRef]
- Vasiliev, V.V.; Morozov, E.V. Advanced Mechanics of Composite Materials and Structures, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Barbero, E.J. Introduction to Composite Materials Design, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Mkaddem, A.; El Mansori, M. Finite element analysis when machining UGF-reinforced PMCs plates: Chip formation, crack propagation and induced-damage. Mater. Des. 2009, 30, 3295–3302. [Google Scholar] [CrossRef]
- Yang, C.; Jiao, G.; Guo, H. Failure criteria for C/SiC composites under plane stress state. Theor. Appl. Mech. Lett. 2014, 4, 021007. [Google Scholar] [CrossRef] [Green Version]
- Mohamadi, M.; Heshmati, M. Failure analysis of glass-reinforced polyester mortar pipes with different cores subjected to combined loading. J. Sandw. Struct. Mater. 2019, 21, 2616–2653. [Google Scholar] [CrossRef]
- Fragoudakis, R. A numerical approach to determine fiber orientations around geometric discontinuities in designing against failure of GFRP laminates. Int. J. Struct. Integr. 2019, 10, 371–379. [Google Scholar] [CrossRef]
- Rao, P.M.; Walter, T.R.; Sankar, B.; Subhash, G.; Yen, C.F. Analysis of failure modes in three-dimensional woven composites subjected to quasi-static indentation. J. Compos. Mater. 2014, 48, 2473–2491. [Google Scholar] [CrossRef]
- Heidari-Rarani, M.; Khalkhali-Sharifi, S.S.; Shokrieh, M.M. Effect of ply stacking sequence on buckling behavior of E-glass/epoxy laminated composites. Comput. Mater. Sci. 2014, 89, 89–96. [Google Scholar] [CrossRef]
- Garmsiri, K.; Jalal, M. Multiobjective optimization of composite cylindrical shells for strength and frequency using genetic algorithm and neural networks. Sci. Eng. Compos. Mater. 2014, 21, 529–536. [Google Scholar] [CrossRef]
- Liu, C. Reliability Analysis of Composite Laminates Based on Generating Function Approach. J. Mech. Eng. 2019, 55, 67. [Google Scholar] [CrossRef]
- Morgado, T.; Silvestre, N.; Correia, J.R. Simulation of fire resistance behaviour of pultruded GFRP columns. Thin Walled Struct. 2019, 135, 521–536. [Google Scholar] [CrossRef]
- Naik, N.K.; Sekher, Y.C. Damage in Laminated Composites Due to Low Velocity Impact. J. Reinf. Plast. Compos. 1998, 17, 1232–1263. [Google Scholar] [CrossRef]
- Singh, S.; Kumar, A. Postbuckling response and failure of symmetric laminates under in-plane shear. Compos. Sci. Technol. 1998, 58, 1949–1960. [Google Scholar] [CrossRef]
- Jen, M. Strength and life in thermoplastic composite laminates under static and fatigue loads. Part I: Experimental. Int. J. Fatigue 1998, 20, 605–615. [Google Scholar] [CrossRef]
- Daniel, I.M. Yield and failure criteria for composite materials under static and dynamic loading. Prog. Aerosp. Sci. 2016, 81, 18–25. [Google Scholar] [CrossRef] [Green Version]
- Rohwer, K. Predicting fiber composite damage and failure. J. Compos. Mater. 2015, 49, 2673–2683. [Google Scholar] [CrossRef] [Green Version]
- Rao, G.V.G.; Mahajan, P.; Bhatnagar, N. Three-dimensional macro-mechanical finite element model for machining of unidirectional-fiber reinforced polymer composites. Mater. Sci. Eng. A 2008, 498, 142–149. [Google Scholar] [CrossRef]
- Tsai, S.W.; Hahn, H.T. Introduction to Composite Materials, 1st ed.; Technomic Publishing: Chicago, IL, USA, 1980. [Google Scholar]
- Guidi, E.S.; de Azevedo Silva, F. Study of Stress Concentration in Polymeric Composites Using Finite Element Method. In Proceedings of the SAE Technical Papers, São Paulo, Brazil, 12 April 2010; pp. 1–10. [Google Scholar]
- Guidi, E.S.; de Azevedo Silva, F. Analysis of mechanical behavior in bending of polymer composites using the finite elements method. In Proceedings of the SAE Technical Papers, São Paulo, Brazil, 12 April 2009; p. 7. [Google Scholar]
- Takkar, S.; Gupta, K.; Tiwari, V.; Singh, S.P. Dynamics of Rotating Composite Disc. J. Vib. Eng. Technol. 2019, 7, 629–637. [Google Scholar] [CrossRef]
- Al-Saadi, A.; Aravinthan, T.; Lokuge, W. Numerical Investigation on Hollow Pultruded Fibre Reinforced Polymer Tube Columns. In ACMSM25: Lecture Notes in Civil Engineering; Wang, C., Ho, J., Kitipornchai, S., Eds.; Springer: Berlin, Germany, 2020; pp. 455–465. [Google Scholar]
- Turan, K. Joint angle effect on the failure behavior of pinned joint composite plates. J. Compos. Mater. 2013, 47, 3027–3039. [Google Scholar] [CrossRef]
- Muthusamy, P.; Sivakumar, S.M. A constituent-behavior-motivated model for damage in fiber reinforced composites. Comput. Mater. Sci. 2014, 94, 163–172. [Google Scholar] [CrossRef]
- Rajpal, D.; Kassapoglou, C.; De Breuker, R. Aeroelastic optimization of composite wings including fatigue loading requirements. Compos. Struct. 2019, 227, 111248. [Google Scholar] [CrossRef]
- Imran, M.; Shi, D.; Tong, L.; Waqas, H.M. Design optimization of composite submerged cylindrical pressure hull using genetic algorithm and finite element analysis. Ocean Eng. 2019, 190, 106443. [Google Scholar] [CrossRef]
- Fathallah, E.; Qi, H.; Tong, L.; Helal, M. Design optimization of lay-up and composite material system to achieve minimum buoyancy factor for composite elliptical submersible pressure hull. Compos. Struct. 2015, 121, 16–26. [Google Scholar] [CrossRef]
- Cousigné, O.; Moncayo, D.; Coutellier, D.; Camanho, P.; Naceur, H.; Hampel, S. Development of a new nonlinear numerical material model for woven composite materials accounting for permanent deformation and damage. Compos. Struct. 2013, 106, 601–614. [Google Scholar] [CrossRef]
- Hu, H.-T.; Lin, W.-P.; Tu, F.-T. Failure analysis of fiber-reinforced composite laminates subjected to biaxial loads. Compos. Part B Eng. 2015, 83, 153–165. [Google Scholar] [CrossRef]
- Sulaiman, S.; Borazjani, S.; Tang, S.H. Finite element analysis of filament-wound composite pressure vessel under internal pressure. IOP Conf. Ser. Mater. Sci. Eng. 2013, 50, 012061. [Google Scholar] [CrossRef] [Green Version]
- Osei-Antwi, M.; de Castro, J.; Vassilopoulos, A.P.; Keller, T. Fracture in complex balsa cores of fiber-reinforced polymer sandwich structures. Constr. Build. Mater. 2014, 71, 194–201. [Google Scholar] [CrossRef]
- Liu, X.; Gasco, F.; Goodsell, J.; Yu, W. Initial failure strength prediction of woven composites using a new yarn failure criterion constructed by deep learning. Compos. Struct. 2019, 230, 111505. [Google Scholar] [CrossRef]
- Li, W.; Cai, H.; Li, C.; Wang, K.; Fang, L. Micro-mechanics of failure for fatigue strength prediction of bolted joint structures of carbon fiber reinforced polymer composite. Compos. Struct. 2015, 124, 345–356. [Google Scholar] [CrossRef]
- Helal, M.; Huang, H.; Wang, D.; Fathallah, E. Numerical Analysis of Sandwich Composite Deep Submarine Pressure Hull Considering Failure Criteria. J. Mar. Sci. Eng. 2019, 7, 377. [Google Scholar] [CrossRef] [Green Version]
- Debski, H.; Teter, A. Numerical and experimental studies on the limit state of fibre-reinforced composite columns with a lipped channel section under quasi-static compression. Compos. Struct. 2015, 133, 1–7. [Google Scholar] [CrossRef]
- Sun, E.; Ghoshal, P.K.; Fair, R.J.; Lassiter, S.R.; Brindza, P. Quench-Back Management for Fast Decaying Currents in SHMS Superconducting Magnets at Jefferson Lab. IEEE Trans. Appl. Supercond. 2020, 30, 1–13. [Google Scholar] [CrossRef]
- Vignoli, L.L.; de Castro, J.T.P.; Meggiolaro, M.A. Stress concentration issues in unidirectional laminates. J. Brazilian Soc. Mech. Sci. Eng. 2019, 41, 462. [Google Scholar] [CrossRef]
- Tsai, S.W.; Wu, E.M. A General Theory of Strength for Anisotropic Materials. J. Compos. Mater. 1971, 5, 58–80. [Google Scholar] [CrossRef]
- Siqueira, E.J.; Silva, F.A.; Botelho, E.C. Estudo dos Critérios de Falhas em Compósitos PPS/Fibras de Carbono Utilizando Elementos Finitos. Epistem. Transversalis 2017, 6, 1–11. [Google Scholar]
- Kawai, M.; Morishita, M.; Tomura, S.; Takumida, K. Inelastic behavior and strength of fiber-metal hybrid composite: Glare. Int. J. Mech. Sci. 1998, 40, 183–198. [Google Scholar] [CrossRef]
- Mechanics of Composite Materials, 1st ed.; Hashin, Z.; Herakovich, C.T. (Eds.) Elsevier: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Hashin, Z. Fatigue Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1981, 48, 846–852. [Google Scholar] [CrossRef]
- Hashin, Z. Failure Criteria for Unidirectional Fiber Compsites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Isbilir, O.; Ghassemieh, E. Three-dimensional numerical modelling of drilling of carbon fiber-reinforced plastic composites. J. Compos. Mater. 2014, 48, 1209–1219. [Google Scholar] [CrossRef]
- Isbilir, O.; Ghassemieh, E. Numerical investigation of the effects of drill geometry on drilling induced delamination of carbon fiber reinforced composites. Compos. Struct. 2013, 105, 126–133. [Google Scholar] [CrossRef]
- Fan, X.L.; Wang, T.J.; Sun, Q. Damage evolution of sandwich composite structure using a progressive failure analysis methodology. Procedia Eng. 2011, 10, 530–535. [Google Scholar] [CrossRef] [Green Version]
- Guillaumat, L.; Hamdoun, Z. Reliability model of drilled composite materials. Compos. Struct. 2006, 74, 467–474. [Google Scholar] [CrossRef]
- Cepero-Mejias, F.; Phadnis, V.A.; Curiel-Sosa, J.L. Machining induced damage in orthogonal cutting of UD composites: FEA based assessment of Hashin and Puck criteria. Procedia CIRP 2019, 82, 332–337. [Google Scholar] [CrossRef]
- Larbi Chaht, F.; Mokhtari, M.; Benzaama, H. Using a Hashin Criteria to predict the Damage of composite notched plate under traction and torsion behavior. Frattura Integrità Strutt. 2019, 13, 331–341. [Google Scholar] [CrossRef] [Green Version]
- Santiuste, C.; Sánchez-Sáez, S.; Barbero, E. A comparison of progressive-failure criteria in the prediction of the dynamic bending failure of composite laminated beams. Compos. Struct. 2010, 92, 2406–2414. [Google Scholar] [CrossRef] [Green Version]
- Ghannadpour, S.A.M.; Kurkaani Barvaj, A.; Tornabene, F. A semi-analytical investigation on geometric nonlinear and progressive damage behavior of relatively thick laminated plates under lateral pressure and end-shortening. Compos. Struct. 2018, 194, 598–610. [Google Scholar] [CrossRef]
- Hamza, K.; Shash, A.Y.; Abdrabou, M. Design criteria of multilayer fibers reinforced composite in bulky 3D loaded applications. Compos. Part B Eng. 2018, 137, 92–101. [Google Scholar] [CrossRef]
- Kim, D.-H.; Kim, S.-W. Evaluation of bird strike-induced damages of helicopter composite fuel tank assembly based on fluid-structure interaction analysis. Compos. Struct. 2019, 210, 676–686. [Google Scholar] [CrossRef]
- Kress, G. Examination of Hashin’s failure criteria for Part B of the second world-wide failure exercise: Comparison with test data. J. Compos. Mater. 2013, 47, 867–891. [Google Scholar] [CrossRef]
- Kress, G. Examination of Hashin’s failure criteria for the second world-wide failure exercise. J. Compos. Mater. 2012, 46, 2539–2561. [Google Scholar] [CrossRef]
- Gu, J.; Chen, P. Some modifications of Hashin’s failure criteria for unidirectional composite materials. Compos. Struct. 2017, 182, 143–152. [Google Scholar] [CrossRef]
- Thomson, D.M.; Cui, H.; Erice, B.; Hoffmann, J.; Wiegand, J.; Petrinic, N. Experimental and numerical study of strain-rate effects on the IFF fracture angle using a new efficient implementation of Puck’s criterion. Compos. Struct. 2017, 181, 325–335. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, J. Low velocity impact response of GLARE laminates based on a new efficient implementation of Puck’s criterion. Thin Walled Struct. 2019, 144, 106321. [Google Scholar] [CrossRef]
- Modeling Damage, Fatigue and Failure of Composite Materials; Talreja, R.; Varna, J. (Eds.) Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Puck, A.; Schürmann, H. Failure analysis of FRP laminates by means of physically based phenomenological models. Compos. Sci. Technol. 2002, 62, 1633–1662. [Google Scholar] [CrossRef]
- De Macedo, R.Q.; Ferreira, R.T.L.; Guedes, J.M.; Donadon, M.V. Intraply failure criterion for unidirectional fiber reinforced composites by means of asymptotic homogenization. Compos. Struct. 2017, 159, 335–349. [Google Scholar] [CrossRef]
- De Macedo, R.Q.; Guedes, J.M.; Luiz Ferreira, R.T.; Donadon, M.V. A failure criteria for unidirectional fiber reinforced composites based on micromechanics by asymptotic homogenization. In Proceedings of the VII European Congress on Computational Methods in Applied Sciences and Engineering, Athens, Greece, 5–10 June 2016; pp. 6664–6674. [Google Scholar]
- Deuschle, H.M.; Puck, A. Application of the Puck failure theory for fibre-reinforced composites under three-dimensional stress: Comparison with experimental results. J. Compos. Mater. 2013, 47, 827–846. [Google Scholar] [CrossRef]
- Puck, A.; Deuschle, H.M. Progress in the puck failure theory for fibre reinforced composites: Analytical solutions for 3D-stress. Compos. Sci. Technol. 2002, 62, 371–378. [Google Scholar] [CrossRef]
- Kim, S.-Y.; Shim, C.S.; Sturtevant, C.; Kim, D.; Song, H.C. Mechanical properties and production quality of hand-layup and vacuum infusion processed hybrid composite materials for GFRP marine structures. Int. J. Nav. Archit. Ocean Eng. 2014, 6, 723–736. [Google Scholar] [CrossRef] [Green Version]
- Soden, P. A comparison of the predictive capabilities of current failure theories for composite laminates. Compos. Sci. Technol. 1998, 58, 1225–1254. [Google Scholar] [CrossRef]
- Schirmaier, F.J.; Weiland, J.; Kärger, L.; Henning, F. A new efficient and reliable algorithm to determine the fracture angle for Puck’s 3D matrix failure criterion for UD composites. Compos. Sci. Technol. 2014, 100, 19–25. [Google Scholar] [CrossRef]
- Gadade, A.M.; Lal, A.; Singh, B.N. Accurate stochastic initial and final failure of laminated plates subjected to hygro-thermo-mechanical loadings using Puck’s failure criteria. Int. J. Mech. Sci. 2016, 114, 177–206. [Google Scholar] [CrossRef]
- Puck, A.; Schürmann, H. Failure analysis of FRP laminates by means of physically based phenomenological models. In Failure Criteria in Fibre-Reinforced-Polymer Composites; Hinton, M.J., Kaddour, A.S., Soden, P.D., Eds.; Elsevier: Amsterdam, The Netherlands, 2004; pp. 832–876. [Google Scholar]
- Puck, A.; Schürmann, H. Failure analysis of FRP laminates by means of physically based phenomenological models. Compos. Sci. Technol. 1998, 58, 1045–1067. [Google Scholar] [CrossRef]
- Cepero-Mejías, F.; Curiel-Sosa, J.L.; Zhang, C.; Phadnis, V.A. Effect of cutter geometry on machining induced damage in orthogonal cutting of UD polymer composites: FE study. Compos. Struct. 2019, 214, 439–450. [Google Scholar] [CrossRef]
- Arouche, M.M. Estudo Numérico-Experimental de Materiais Compósitos Utilizados no Reparo de Estruturas Navais; Centro Federal de Educação Tecnológica Celso Suckow Da Fonseca: Rio de Janeiro, Brazil, 2015. [Google Scholar]
- Daniel, I.M.; Ishai, O. Engineering mechanics of composite materials, 2nd ed.; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Tita, V.; Carvalho, J.; Santos, N.C. Estudo do comportamento mecânico de materiais compósitos utilizando o método dos elementos finitos. In Proceedings of the II Congresso Nacional de Engenharia Mecânica–Conem, João Pessoa, Brazil, 12–16 August 2002; p. 11. [Google Scholar]
- Diniz, C.A. Otimização Estrutural de Elementos em Compósitos Usando Redes Neurais Artificiais; Universidade Federal de Itajubá: Itajubá, Brazil, 2017. [Google Scholar]
- Carvalho, G.P. de Avaliação de Critérios de Falhas de Compósitos Poliméricos Reforçados Aplicados a Vigas sob Carregamento de Flexão; Univerisdade de São Paulo: São Paulo, Brazil, 2003. [Google Scholar]
- Gagliardo, D.P. Análise de Estruturas Sanduíche: Parâmetros de Projeto; Universidade Estadual de Campinas: Campinas, Brazil, 2008. [Google Scholar]
- Campos, V.B.O. Análise de Critérios de Falha em Lâmina Reforçada com Tecido Híbrido de Fibra de Vidro e Carbono; Universidade Federal do Rio Grande do Norte: Natal, Brazil, 2017. [Google Scholar]
- Laurin, F.; Carrere, N.; Maire, J.-F. Strength prediction methods for composite structures. In Numerical Modelling of Failure in Advanced Composite Materials; Camanho, P.P., Hallett, S.R., Eds.; Elsevier: Cambridge, UK, 2015. [Google Scholar]
- Failure and Damage Analysis of Advanced Materials; Altenbach, H.; Sadowski, T. (Eds.) Springer: Berlin, Germany, 2015. [Google Scholar]
- Khan, A.; Johnson, E.; Kapania, R.; Batra, R.; Guimard, J.-M. Progressive Failure Analysis of Laminated Composite Structures Based on Puck’s Failure Criteria. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012. [Google Scholar]
- Dávila, C.G.; Camanho, P.P.; Rose, C.A. Failure criteria for FRP laminates. J. Compos. Mater. 2005, 39, 323–345. [Google Scholar] [CrossRef]
- Deuschle, H.M. 3D Failure Analysis of UD Fibre Reinforced Composites: Puck’s Theory within FEA; University of Stuttgart: Stuttgart, Germany, 2010. [Google Scholar]
- Daniel, I.M.; Luo, J.J.; Schubel, P.M.; Werner, B.T. Interfiber/interlaminar failure of composites under multi-axial states of stress. Compos. Sci. Technol. 2009, 69, 764–771. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; De, J.P.; Kelly, D.W. The hierarchical concept in finite element analysis. Comput. Struct. 1983, 16, 53–65. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Emeritus, F. The Finite Element Method: The Basis, 5th ed.; Butterworth-Heinemann: Oxford, UK, 2000; Volume 1. [Google Scholar]
- Cheng, Z.-Q.; Batra, R.C. Deflection relationships between the homogeneous Kirchhoff plate theory and different functionally graded plate theories. Arch. Mech. 2000, 52, 143–158. [Google Scholar]
- Azevedo, F.M. Método dos Elementos Finitos, 1st ed.; Faculdade de Engenharia da Universidade do Porto: Porto, Brazil, 2003. [Google Scholar]
- Matthews, F.L.; Davies, G.A.O.; Hitchings, D.; Soutis, C. Finite Element Modelling of Composite Materials and Structures, 2nd ed.; Woodhead: Cambridge, UK, 2003. [Google Scholar]
- Zienkiewicz, O.C.; Emeritus, F. The Finite Element Method: Solid Mechanics, 5th ed.; Butterworth-Heinemann: Oxford, UK, 2000; Volume 2. [Google Scholar]
- Adams, V.; Askenazi, A. Building Better Products with Finit Elements Analysis, 1st ed.; Onword Press: New York, NY, USA, 1999. [Google Scholar]
- Ugural, A.C. Stresses in Plates and Shells; McGraw Hill: New York, NY, USA, 1981. [Google Scholar]
- Timoshenko, S.; Woinowsky-Krieger, S. Thoery of Plates and Shells, 2nd ed.; Mc Graw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Vaz, L.E. Método dos Elementos Finitos em Análise de Estruturas; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Valsiliev, V.V.; Morozov, E.V. Mechanics and Analysis of Composite Materials; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Shell-Like Structures; Altenbach, H.; Eremeyev, V. (Eds.) Springer International Publishing: Cham, Switzerland, 2017; Volume 572. [Google Scholar]
- Tsiatas, G.C. A new Kirchhoff plate model based on a modified couple stress theory. Int. J. Solids Struct. 2009, 46, 2757–2764. [Google Scholar] [CrossRef] [Green Version]
- Phadnis, V.A.; Roy, A.; Silberschmidt, V.V. Finite element analysis of drilling in carbon fiber reinforced polymer composites. J. Phys. Conf. Ser. 2012, 382, 012014. [Google Scholar] [CrossRef] [Green Version]
- Nguyen-Xuan, H.; Rabczuk, T.; Bordas, S.; Debongnie, J.F. A smoothed finite element method for plate analysis. Comput. Methods Appl. Mech. Eng. 2008, 197, 1184–1203. [Google Scholar] [CrossRef] [Green Version]
- Chai, Y.B.; Li, W.; Gong, Z.X. An edge-based smoothed three-node Mindlin plate element (ES-MIN3) for static. In Proceedings of the 5th International Conference on Computational Methods, Cambridge, UK, 25–27 May 2015; pp. 1–15. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Too, J.M. Reduced integration technique in general analysis of plates and shells. Int. J. Numer. Methods Eng. 1971, 3, 275–290. [Google Scholar] [CrossRef]
- Altenbach, J.; Altenbach, H.; Eremeyev, V.A. On generalized Cosserat-type theories of plates and shells: A short review and bibliography. Arch. Appl. Mech. 2010, 80, 73–92. [Google Scholar] [CrossRef] [Green Version]
- Lu, P.; He, L.H.; Lee, H.P.; Lu, C. Thin plate theory including surface effects. Int. J. Solids Struct. 2006, 43, 4631–4647. [Google Scholar] [CrossRef] [Green Version]
- Norrie, D.H.; Vries, G. de The Finite Element Method: Fundamentals and Applications, 1st ed.; Academic Press: Cambridge, MA, USA, 1973. [Google Scholar]
- Saliba, S.S.; Penna, S.S.; Pitangueira, R.L. Abordagem Orientada a Objetos Para Implementação Computacional de Elementos Finitos de PLacas. Cad. Eng. Estrut. 2011, 13, 37–54. [Google Scholar]
- Schneider, P.; Kienzler, R.; Böhm, M. Modeling of consistent second-order plate theories for anisotropic materials. ZAMM Z. Angew. Math. Mech. 2014, 94, 21–42. [Google Scholar] [CrossRef]
- Saliba, S.S. Implementação Computacional e Análise Crítica de Elementos Finitos de Placas; Universidade Federal de Minas Gerais: Belo Horizonte, Brazil, 2007. [Google Scholar]
- Ota, N.S.N. O Elemento Finito T6-3I na Análise de Placas e Dinâmica de Cascas; Universidade de São Paulo: São Paulo, Brazil, 2016. [Google Scholar]
- Chróścielewski, J.; Gilewski, W.; Kreja, I. Fifty years of Finite Element Analysis pf plate and shells (1960-2010). In Proceedings of the 19th International Conference on Computer Methods in Mechanics, Warsaw, Poland, 9–12 May 2011; pp. 1–2. [Google Scholar]
- Gileva, L.; Shaydurov, V.; Dobronets, B. The Triangular Hermite Finite Element Complementing the Bogner-Fox-Schmit Rectangle. Appl. Math. 2013, 4, 50–56. [Google Scholar] [CrossRef] [Green Version]
- Barik, M.; Mukhopadhyay, M. A new stiffened plate element for the analysis of arbitrary plates. Thin Walled Struct. 2002, 40, 625–639. [Google Scholar] [CrossRef]
- Greimann, L.F.; Lynn, P.P. Finite Element Analysis of plate Pending with Transversal Sahear Deformation. Nucl. Eng. Des. 1970, 14, 223–230. [Google Scholar] [CrossRef]
- Ke, L.-L.; Wang, Y.-S.; Yang, J.; Kitipornchai, S. Free vibration of size-dependent Mindlin microplates based on the modified couple stress theory. J. Sound Vib. 2012, 331, 94–106. [Google Scholar] [CrossRef]
- Huang, H.-C. Static and Dynamic Analyses of Plates and Shells: Theory, Software and Applications, 1st ed.; Springer: London, UK, 1989. [Google Scholar]
- Shell Structures: Theory and Applications, 1st ed.; Pietraszkiewicz, W.; Witkowski, W. (Eds.) CRC Press: Gdansk, Poland, 2017; Volume 4. [Google Scholar]
- Shell Structures: Theory and Applications, 1st ed.; Kreja, I.; Pietraszkiewicz, W. (Eds.) CRC Press: Gdańsk-Jurata, Poland, 2010; Volume 2. [Google Scholar]
- Alves, A.D.R.S.; Leggerini, M.R.C. Análise estrutural de cascas via elementos finitos em concreto armado. Rev. Grad. 2011, 4, 1–20. [Google Scholar]
- Jawad, M.H. Various Applications of the Membrane Theory. In Theory and Design of Plate and Shell Structures; Springer: Boston, MA, USA, 1994; pp. 193–220. [Google Scholar]
- Ferreira, A.J.M. Análise por Elementos Finitos de Estruturas Tipo Casca em Materiais Compósitos; Universidade do Porto: Porto, Portugal, 1990. [Google Scholar]
- Buckling of Shell Structures, on Land, in the Sea and in the Air, 1st ed.; Jullien, J.F. (Ed.) CRC Press: Lyon, France, 1991. [Google Scholar]
- Monneau, R. Justification of the Nonlinear Kirchhoff-Love Theory of Plates as the Application of a New Singular Inverse Method. Arch. Ration. Mech. Anal. 2003, 169, 1–34. [Google Scholar] [CrossRef] [Green Version]
- Ajeje, F.H. Abordagem orientada a objetos para implementação computacional de elementos finitos de cascas planos; Universidade Federal de Minas Gerais: Belo Horizonte, Brazil, 2009. [Google Scholar]
- Shell Structures: Theory and Applications, 1st ed.; Pietraszkiewicz, W.; Górki, J. (Eds.) CRC Press: Gdansk, Poland, 2013; Volume 3. [Google Scholar]
- Rankin, C.C.; Regelbrugge, M.; Hurlbut, B. Advanced Decohesion Elements for the Simulation of Composite Delamination. In Proceedings of the 2010 SIMULIA Customer Conference, Providence, Rhode Island, 25–27 May 2010; pp. 1–12. [Google Scholar]
- Simulia Abaqus Analysis User’s Guide: Cohesive Elements. Available online: https://abaqus-docs.mit.edu/2017/English/SIMACAEELMRefMap/simaelm-c-cohesiveoverview.htm (accessed on 10 March 2020).
- Flores-Johnson, E.A.; Shen, L.; Guiamatsia, I.; Nguyen, G.D. Numerical investigation of the impact behaviour of bioinspired nacre-like aluminium composite plates. Compos. Sci. Technol. 2014, 96, 13–22. [Google Scholar] [CrossRef]
- Cabello, M.; Turon, A.; Zurbitu, J.; Renart, J.; Sarrado, C.; Martínez, F. Progressive failure analysis of DCB bonded joints using a new elastic foundation coupled with a cohesive damage model. Eur. J. Mech. A/Solids 2017, 63, 22–35. [Google Scholar] [CrossRef]
- Wang, G.-D.; Melly, S.K. Three-dimensional finite element modeling of drilling CFRP composites using Abaqus/CAE: A review. Int. J. Adv. Manuf. Technol. 2018, 94, 599–614. [Google Scholar] [CrossRef]
- Xu, X.-P.; Needleman, A. Numerical simulations of fast crack growth in brittle solids. J. Mech. Phys. Solids 1994, 42, 1397–1434. [Google Scholar] [CrossRef]
- Simulations for Design and Manufacturing; Dixit, U.S.; Kant, R. (Eds.) Lecture Notes on Multidisciplinary Industrial Engineering; Springer: Singapore city, Singapore, 2018. [Google Scholar]
- Espinha, R.S.L. Suporte Topológico em Paralelo para Malhas de Elementos Finitos em Análises Dinâmicas de Fratura e Fragmentação; Pontifícia Universidade Católica: Rio de Janeiro, Brazil, 2011. [Google Scholar]
- Guilpin, A.; Franciere, G.; Barton, L.; Blacklock, M.; Birkett, M. A Numerical and experimental study of adhesively- bonded polyethylene pipelines. Polymers (Basel) 2019, 11, 1531. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiong, X.; Xiao, Q. Meso-Scale Simulation of Concrete Based on Fracture and Interaction Behavior. Appl. Sci. 2019, 9, 2986. [Google Scholar] [CrossRef] [Green Version]
- Murali Krishna, M.; Shunmugam, M.S.; Siva Prasad, N. A study on the sealing performance of bolted flange joints with gaskets using finite element analysis. Int. J. Press. Vessel. Pip. 2007, 84, 349–357. [Google Scholar] [CrossRef]
- Nelson, N.R.; Prasad, N.S. Sealing behavior of twin gasketed flange joints. Int. J. Press. Vessel. Pip. 2016, 138, 45–50. [Google Scholar] [CrossRef]
- Scheider, I. Micromechanical based derivation of traction-separation laws for cohesive model simulations. Procedia Eng. 2009, 1, 17–21. [Google Scholar] [CrossRef] [Green Version]
- Park, K.; Paulino, G.H. Cohesive Zone Models: A Critical Review of Traction-Separation Relationships Across Fracture Surfaces. Appl. Mech. Rev. 2011, 64, 060802. [Google Scholar] [CrossRef]
- Ridha, M.; Tan, V.B.C.; Tay, T.E. Traction–separation laws for progressive failure of bonded scarf repair of composite panel. Compos. Struct. 2011, 93, 1239–1245. [Google Scholar] [CrossRef]
- Heidari-Rarani, M.; Sayedain, M. Finite element modeling strategies for 2D and 3D delamination propagation in composite DCB specimens using VCCT, CZM and XFEM approaches. Theor. Appl. Fract. Mech. 2019, 103, 102246. [Google Scholar] [CrossRef]
- Hu, P.; Shi, Z.W.; Wang, X.X.; Li, W.D.; Zhou, S.G.; Han, X. Strength Degradation of Adhesively Bonded Single-Lap Joints in a Cyclic-Temperature Environment Using a Cohesive Zone Model. J. Adhes. 2015, 91, 587–603. [Google Scholar] [CrossRef]
- Arafah, D.Z.R. Fracture Assessment of Cracked Components under Biaxial Loading; Politecnico Di Milano: Milano, Italy, 2014. [Google Scholar]
- Sun, M.; Chang, M.; Wang, Z.; Li, H.; Sun, X. Experimental and Simulation Study of Low-Velocity Impact on Glass Fiber Composite Laminates with Reinforcing Shape Memory Alloys at Different Layer Positions. Appl. Sci. 2018, 8, 2405. [Google Scholar] [CrossRef] [Green Version]
- Camanho, P.P.; Davila, C.G.; de Moura, M.F. Numerical Simulation of Mixed-Mode Progressive Delamination in Composite Materials. J. Compos. Mater. 2003, 37, 1415–1438. [Google Scholar] [CrossRef]
- Schwalbe, K.-H.; Scheider, I.; Cornec, A. Guidelines for Applying Cohesive Models to the Damage Behaviour of Engineering Materials and Structures. In Springer Briefs in Applied Sciences and Technology, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Budiman, B.A.; Takahashi, K.; Inaba, K.; Kishimoto, K. Evaluation of interfacial strength between fiber and matrix based on cohesive zone modeling. Compos. Part A Appl. Sci. Manuf. 2016, 90, 211–217. [Google Scholar] [CrossRef] [Green Version]
- Best of Automotive. ANSYS Advant. Mag. 2016, Special Issue, 55.
- Wong, K. Many Composite Layers to Address. Available online: https://www.digitalengineering247.com/article/many-composite-layers-to-address/ansys-f1-front-wing-failure-plot/ (accessed on 15 January 2020).
- Anaglyph Laminate Tools. Available online: https://www.anaglyph.co.uk/laminate_tools.htm (accessed on 15 January 2020).
- Structural Design & Analysis, I. FIBERSIM: Design, Analyze, and Manufacture Composites. Available online: https://structures.aero/software/fibersim/ (accessed on 14 January 2020).
- Siemens Industry Software Inc. The End-to-End Design and Manufacturing Solution for Composite Parts: FIBERSIM. Available online: https://www.plm.automation.siemens.com/global/pt/products/nx/fibersim.html (accessed on 14 January 2020).
- Altair Engineering Inc. Products. Available online: https://altairhyperworks.com/ (accessed on 15 January 2020).
- Autodesk Inc. Helius Composite: Composite Material Design Simulation Tools. Available online: https://www.autodesk.com/products/helius-composite/overview (accessed on 14 January 2020).
- Collier Research Corporation Hyper Sizer. Available online: https://hypersizer.com/ (accessed on 15 January 2020).
- NISA NISA—Composite. Available online: https://www.nisasoftware.com/composite (accessed on 14 January 2020).
- Donaldson, B.; Sloan, J. Next-Gen Aerospace: Advanced Materials and Processes. GBM Suppl. Next Gen. Aerosp. 2019, 76. [Google Scholar]
- TenCate Advanced Composites North America TenCate Composite Materials Replace Titanium for Orion Space Capsule Heatshield and Backshell Structure. Available online: https://www.toraytac.com/company/news/2014/12/5/TenCate-composite-materials-replace-titanium-for-Orion-space-capsule-heatshield-and-backshell-structure (accessed on 20 September 2018).
- Laflamme Ingénierie Engineering of Advanced Composite Materials. Available online: http://www.laflamme-ing.com/en/engineering-services/engineering-of-composite-materials/%0A (accessed on 4 May 2018).
- Dlubal Software GmbH Software de Cálculo Estrutural e Dimensionamento: Software para Análise Estrutural e Dimensionamento de Pontes. Available online: https://www.dlubal.com/pt/solucoes/areas/pontes (accessed on 20 January 2020).
- Abdel-Nasser, Y.A. Frontal crash simulation of vehicles against lighting columns using FEM. Alexandria Eng. J. 2013, 52, 295–299. [Google Scholar] [CrossRef] [Green Version]
- Venås, J.V.; Kvamsdal, T. Isogeometric boundary element method for acoustic scattering by a submarine. Comput. Methods Appl. Mech. Eng. 2020, 359, 112670. [Google Scholar] [CrossRef]
- Lee, K.; Han, S.E.; Hong, J.W. Analysis of impact of large commercial aircraft on a prestressed containment building. Nucl. Eng. Des. 2013, 265, 431–449. [Google Scholar] [CrossRef]
- Skvortsov, Y.V.; Glushkov, S.V.; Chernyakin, S.A. Space Factors Influence on the Size Stability of Small Spacecraft Structure Elements. Procedia Eng. 2017, 185, 105–109. [Google Scholar] [CrossRef]
- Gondaliya, R.; Sypeck, D.; Zhu, F. Improving Damage Tolerance of Composite Sandwich Structure Subjected to Low Velocity Impact Loading: Experimental Analy: UAsis. In Proceedings of the 31st American Society for Composites, Williamsburg, VA, USA, 19–22 September 2016. [Google Scholar]
- Rayavarapu, V. To the Test. ANSYS Advant. Mag. 2016, 2, 42–44. [Google Scholar]
- Zhou, Y.; Sun, Y.; Huang, T. SPH-FEM Design of Laminated Plies under Bird-Strike Impact. Aerospace 2019, 6, 112. [Google Scholar] [CrossRef] [Green Version]
- Bouvet, C.; Rivallant, S.; Barrau, J.J. Low velocity impact modeling in composite laminates capturing permanent indentation. Compos. Sci. Technol. 2012, 72, 1977–1988. [Google Scholar] [CrossRef] [Green Version]
- Abrate, S. Impact on Composite Structures, 1st ed.; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Hongkarnjanakul, N.; Bouvet, C.; Rivallant, S. Validation of low velocity impact modelling on different stacking sequences of CFRP laminates and influence of fibre failure. Compos. Struct. 2013, 106, 549–559. [Google Scholar] [CrossRef] [Green Version]
- Carbon Freight Ligten Up. ANSYS Advant. Mag. 2017, 2, 44–45.
- Huang, Y.; Yang, Z.; Liu, A.; Fu, J. Nonlinear Buckling Analysis of Functionally Graded Graphene Reinforced Composite Shallow Arches with Elastic Rotational Constraints under Uniform Radial Load. Materials 2018, 11, 910. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Z.; Huang, Y.; Liu, A.; Fu, J.; Wu, D. Nonlinear in-plane buckling of fixed shallow functionally graded graphene reinforced composite arches subjected to mechanical and thermal loading. Appl. Math. Model. 2019, 70, 315–327. [Google Scholar] [CrossRef]
- Díez-Pascual, A.M.; Naffakh, M.; Marco, C.; Ellis, G.; Gómez-Fatou, M.A. High-performance nanocomposites based on polyetherketones. Prog. Mater. Sci. 2012, 57, 1106–1190. [Google Scholar] [CrossRef]
- Moniruzzaman, M.; Winey, K.I. Polymer Nanocomposites Containing Carbon Nanotubes. Macromolecules 2006, 39, 5194–5205. [Google Scholar] [CrossRef]
- Rahman, A.; Ali, I.; Al Zahrani, S.M.; Eleithy, R.H. A review of the applications of nanocarbon polymer composites. Nano 2011, 6, 185–203. [Google Scholar] [CrossRef]
- Sahoo, N.G.; Rana, S.; Cho, J.W.; Li, L.; Chan, S.H. Polymer nanocomposites based on functionalized carbon nanotubes. Prog. Polym. Sci. 2010, 35, 837–867. [Google Scholar] [CrossRef]
- Carballeira, P. Mechanical and Electrical Properties of Carbon Nanofiber–Ceramic Nanoparticle–Polymer Composites; Technische Universität Kaiserslautern: Kaiserslautern, Germany, 2010. [Google Scholar]
- Scarponi, C. Hemp fiber composites for the design of a Naca cowling for ultra-light aviation. Compos. Part B Eng. 2015, 81, 53–63. [Google Scholar] [CrossRef]
- Meng, Y.; Yan, L.; Huang, W.; Zhang, T.; Du, Z. Structural design and analysis of a composite wing with high aspect ratio. J. Zhejiang Univ. A 2019, 20, 781–793. [Google Scholar] [CrossRef]
- Tam, M.; Yang, Z.; Zhao, S.; Yang, J. Vibration and Buckling Characteristics of Functionally Graded Graphene Nanoplatelets Reinforced Composite Beams with Open Edge Cracks. Materials 2019, 12, 1412. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Safe and Sound with Simulation. ANSYS Advant. Mag. 2019, 4, 60.
- Yue, K.; Liu, W.; Li, G.; Ji, J.; Yu, D. Numerical simulation of RCS for carrier electronic warfare airplanes. Chin. J. Aeronaut. 2015, 28, 545–555. [Google Scholar] [CrossRef] [Green Version]
- James, K.A.; Kennedy, G.J.; Martins, J.R.R.A. Concurrent aerostructural topology optimization of a wing box. Comput. Struct. 2014, 134, 1–17. [Google Scholar] [CrossRef]
- Gad-el-Hak, I. Fluid–Structure Interaction for Biomimetic Design of an Innovative Lightweight Turboexpander. Biomimetics 2019, 4, 27. [Google Scholar] [CrossRef] [Green Version]
- Space Structures Spacecraft Structures. Available online: https://spacestructures.de/references_sc-struct.php (accessed on 4 February 2020).
- Vasiliev, V.V.; Razin, A.F. Anisogrid composite lattice structures for spacecraft and aircraft applications. Compos. Struct. 2006, 76, 182–189. [Google Scholar] [CrossRef]
- Pindado, S.; Roibas-Millan, E.; Cubas, J.; Garcia, A.; Sanz, A.; Franchini, S.; Perez-Grande, I.; Alonso, G.; Perez-Alvarez, J.; Sorribes-Palmer, F.; et al. The UPMSat-2 Satellite: An Academic Project within Aerospace Engineering Education. In Proceedings of the 2nd Annual International Conference, Athens, Greece, 19–22 June 2017. [Google Scholar]
- Engineering the Internet of Things. ANSYS Advant. Mag. 2016, 2, 60.
- Capiez-Lernout, E.; Pellissetti, M.; Pradlwarter, H.; Schueller, G.I.; Soize, C. Data and model uncertainties in complex aerospace engineering systems. J. Sound Vib. 2006, 295, 923–938. [Google Scholar] [CrossRef] [Green Version]
- Jung, K.-H.; Kim, D.-H.; Kim, H.-J.; Park, S.-H.; Jhang, K.-Y.; Kim, H.-S. Finite element analysis of a low-velocity impact test for glass fiber-reinforced polypropylene composites considering mixed-mode interlaminar fracture toughness. Compos. Struct. 2017, 160, 446–456. [Google Scholar] [CrossRef]
- Richardson, M.O.W.; Wisheart, M.J. Review of low-velocity impact properties of composite materials. Compos. Part A Appl. Sci. Manuf. 1996, 27, 1123–1131. [Google Scholar] [CrossRef]
- Evci, C.; Gülgeç, M. An experimental investigation on the impact response of composite materials. Int. J. Impact Eng. 2012, 43, 40–51. [Google Scholar] [CrossRef]
- Chiacchiarelli, L.M.; Cerrutti, P.; Flores-Johnson, E.A. Compressive behavior of rigid polyurethane foams nanostructured with bacterial nanocellulose at low and intermediate strain rates. J. Appl. Polym. Sci. 2020, 137, 48701. [Google Scholar] [CrossRef]
- Simon, U.; Segelflugzeugbau, A.S. Gliding Farther and Faster. ANSYS Advant. Mag. 2019, 4, 34–37. [Google Scholar]
- Waterman, P. Composite Simulation Tips for New Users. Digit. Eng. 2015. Available online: https://www.digitalengineering247.com/article/simulating-composites-6-tips-for-new-users/ (accessed on 1 February 2020).
- Heimbs, S.; Strobl, F. Crash Simulation of an F1 Racing Car Front Impact Structure. In Proceedings of the 7th European LS-DYNA Conference, Salzburg, Austria, 14–15 May 2009; pp. 1–8. [Google Scholar]
- He, X.D.; Hong, Y.; Wang, R.G. Hydroelastic optimisation of a composite marine propeller in a non-uniform wake. Ocean Eng. 2012, 39, 14–23. [Google Scholar] [CrossRef]
- Ma, S.; Mahfuz, H. Finite element simulation of composite ship structures with fluid structure interaction. Ocean Eng. 2012, 52, 52–59. [Google Scholar] [CrossRef]
- Pemberton, R.; Summerscales, J.; Graham-Jones, J. (Eds.) Marine Composites; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Chen, F.; Liu, L.; Lan, X.; Li, Q.; Leng, J.; Liu, Y. The study on the morphing composite propeller for marine vehicle. Part I: Design and numerical analysis. Compos. Struct. 2017, 168, 746–757. [Google Scholar] [CrossRef]
- MESH Engineering & Software Co Resolving Vibration Induced Engineering Problems. Available online: http://www.mesh.com.tr/vibration-analyses.html. (accessed on 9 February 2020).
- Forrister, T. Analyzing Wind Turbine Blades with the Composite Materials Module. Available online: https://www.comsol.com/blogs/analyzing-wind-turbine-blades-with-the-composite-materials-module/ (accessed on 1 February 2020).
- Weifei, H. Reliability-Based Design Optimization of Composite Wind Turbine Blades for Fatigue Life under Wind Load Uncertainty; University of Iowa: Iowa City, IA, USA, 2015. [Google Scholar]
- Barnes, R.H.; Morozov, E.V. Structural optimisation of composite wind turbine blade structures with variations of internal geometry configuration. Compos. Struct. 2016, 152, 158–167. [Google Scholar] [CrossRef]
- Oliveira, M.N. De Powering Up for the Future. ANSYS Advant. Mag. 2019, 1, 32–37. [Google Scholar]
- Oil and Gas. ANSYS Advant. Mag. 2013, Special Issue, 28.
- Oil and Gas. ANSYS Advant. Mag. 2015, Special Issue, 32.
- Jha, V.; Latto, J.; Dodds, N.; Anderson, T.A.; Finch, D.; Vermilyea, M. Qualification of Flexible Fiber-Reinforced Pipe for 10,000-Foot Water Depths. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 9 May 2013. [Google Scholar]
- Duncan, M.; Niu, H.; Conley, J.R.; Edmondson, S.J.; Holub, J.; Andrenacci, A.; Gujare, N. Flexible Reinforced Pipe and Reinforcement Tape. U.S. Patent No. 9,726,306, 8 August 2017. [Google Scholar]
- Chi, P.D.; Narayanaswamy, S.; Edmans, B. Multiscale Analysis of Multilayer Composite Pipes. In Proceedings of the 7th International Conference on Multiscale Materials Modeling, Berkeley, CA, USA, 6–10 October 2014. [Google Scholar]
- Guz, I.A.; Menshykova, M.; Paik, J.K. Thick-walled composite tubes for offshore applications: An example of stress and failure analysis for filament-wound multi-layered pipes. Ships Offshore Struct. 2017, 12, 304–322. [Google Scholar] [CrossRef] [Green Version]
- Seker, B.S.; Cakir, F.; Dogangun, A.; Uysal, H. Investigation of the structural performance of a masonry domed mosque by experimental tests and numerical analysis. Earthq. Struct. 2014, 6, 335–350. [Google Scholar] [CrossRef]
- Altunışık, A.C.; Genç, A.F. Earthquake response of heavily damaged historical masonry mosques after restoration. Nat. Hazards Earth Syst. Sci. 2017, 17, 1811–1821. [Google Scholar] [CrossRef] [Green Version]
- Varkonyi, B.; Belnoue, J.P.-H.; Kratz, J.; Hallett, S.R. Predicting consolidation-induced wrinkles and their effects on composites structural performance. Int. J. Mater. Form. 2019, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Najafgholipour, M.A.; Dehghan, S.M.; Dooshabi, A.; Niroomandi, A. Finite Element Analysis of Reinforced Concrete Beam-Column Connections with Governing Joint Shear Failure Mode. Lat. Am. J. Solids Struct. 2017, 14, 1200–1225. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Liu, A.; Yang, J.; Fu, J.; Yang, B. Dynamic buckling of functionally graded graphene nanoplatelets reinforced composite shallow arches under a step central point load. J. Sound Vib. 2020, 465, 115019. [Google Scholar] [CrossRef]
- Khelifa, M.; Auchet, S.; Méausoone, P.J.; Celzard, A. Finite element analysis of flexural strengthening of timber beams with Carbon Fibre-Reinforced Polymers. Eng. Struct. 2015, 101, 364–375. [Google Scholar] [CrossRef]
- Scholz, M.-S.; Blanchfield, J.P.; Bloom, L.D.; Coburn, B.H.; Elkington, M.; Fuller, J.D.; Gilbert, M.E.; Muflahi, S.A.; Pernice, M.F.; Rae, S.I.; et al. The use of composite materials in modern orthopaedic medicine and prosthetic devices: A review. Compos. Sci. Technol. 2011, 71, 1791–1803. [Google Scholar] [CrossRef]
- Zou, D.; He, T.; Dailey, M.; Smith, K.E.; Silva, M.J.; Sinacore, D.R.; Mueller, M.J.; Hastings, M.K. Experimental and computational analysis of composite ankle-foot orthosis. J. Rehabil. Res. Dev. 2014, 51, 1525–1536. [Google Scholar] [CrossRef]
- Upender, V.; Srikanth, E.; Karthik, G.; Kumar, N. Design Modeling and Optimization of a “Prosthetic Runner Blade. Natl. Tech. Res. Organ. India 2018, 5, 64–70. [Google Scholar]
- Hamzah, M.; Gatta, A. Design of a Novel Carbon-Fiber Ankle-Foot Prosthetic using Finite Element Modeling. IOP Conf. Ser. Mater. Sci. Eng. 2018, 433, 012056. [Google Scholar] [CrossRef]
- Jia, Y.; Wei, X.; Pu, J.; Xie, P.; Wen, T.; Wang, C.; Lian, P.; Xue, S.; Shi, Y. A Numerical Feasibility Study of Kinetic Energy Harvesting from Lower Limb Prosthetics. Energies 2019, 12, 3824. [Google Scholar] [CrossRef] [Green Version]
- Cahyono, S.I.; Anwar, M.; Diharjo, K.; Triyono, T.; Hapid, A.; Kaleg, S. Finite element analysis of electric bicycle frame geometries. AIP Conf. Proc. 2017. [Google Scholar] [CrossRef] [Green Version]
- Chidambaram, P.K.; Ramakrishanan, R. Manufacturing, Testing of Polymer Nanocomposite and Analysis of Tennis Racket Frame. Int. J. Eng. Technol. Innov. 2014, 4, 59–67. [Google Scholar]
- Tryggvason, H.; Starker, F.; Lecomte, C.; Jonsdottir, F. Use of dynamic FEA for design modification and energy analysis of a variable stiffness prosthetic foot. Appl. Sci. 2020, 10, 650. [Google Scholar] [CrossRef] [Green Version]
- Tsao, C.C. Drilling processes for composites. In Machining Technology for Composite Materials; Hocheng, H., Ed.; Elsevier: Amsterdam, The Netherlands, 2012; pp. 17–64. [Google Scholar]
- Usui, S.; Wadell, J.; Marusich, T. Finite Element Modeling of Carbon Fiber Composite Orthogonal Cutting and Drilling. Procedia CIRP 2014, 14, 211–216. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.; Reiner, J.; Bacca, M.; Altintas, Y.; Vaziri, R. A study of energy dissipating mechanisms in orthogonal cutting of UD-CFRP composites. Compos. Struct. 2019, 220, 460–472. [Google Scholar] [CrossRef]
- Patel, D.A.; Buch, V.R. Drilling of glass fiber reinforced polymer composite (GFRP): A review. Int. J. Recent Sci. Res. 2018, 9, 25059–25062. [Google Scholar]
- Fernández-Pérez, J.; Cantero, J.L.; Díaz-Álvarez, J.; Miguélez, M.H. Influence of cutting parameters on tool wear and hole quality in composite aerospace components drilling. Compos. Struct. 2017, 178, 157–161. [Google Scholar] [CrossRef]
- Rahme, P.; Landon, Y.; Lachaud, F.; Piquet, R.; Lagarrigue, P. Delamination-free drilling of thick composite materials. Compos. Part A Appl. Sci. Manuf. 2015, 72, 148–159. [Google Scholar] [CrossRef]
- Nikishkov, Y.; Makeev, A.; Seon, G. Progressive fatigue damage simulation method for composites. Int. J. Fatigue 2013, 48, 266–279. [Google Scholar] [CrossRef]
- ANSYS Inc Composite Materials for Aerospace. Available online: https://www.ansys.com/solutions/solutions-by-industry/high-tech/composite-materials-for-high-performance-electronics (accessed on 10 January 2020).
- Operating Systems for Supercomputers and High Performance Computing, 1st ed.; Gerofi, B.; Ishikawa, Y.; Riesen, R.; Wisniewski, R.W. (Eds.) High-Performance Computing Series; Springer: Singapore city, Singapore, 2019. [Google Scholar]
- Zhai, S.; Zhang, P.; Xian, Y.; Zeng, J.; Shi, B. Effective thermal conductivity of polymer composites: Theoretical models and simulation models. Int. J. Heat Mass Transf. 2018, 117, 358–374. [Google Scholar] [CrossRef]
- Ngo, I.-L.; Byon, C. A generalized correlation for predicting the thermal conductivity of composites with heterogeneous nanofillers. Int. J. Heat Mass Transf. 2015, 90, 894–899. [Google Scholar] [CrossRef]
- Ngo, I.L.; Byon, C.; Lee, B.J. Analytical study on thermal conductivity enhancement of hybrid-filler polymer composites under high thermal contact resistance. Int. J. Heat Mass Transf. 2018, 126, 474–484. [Google Scholar] [CrossRef]


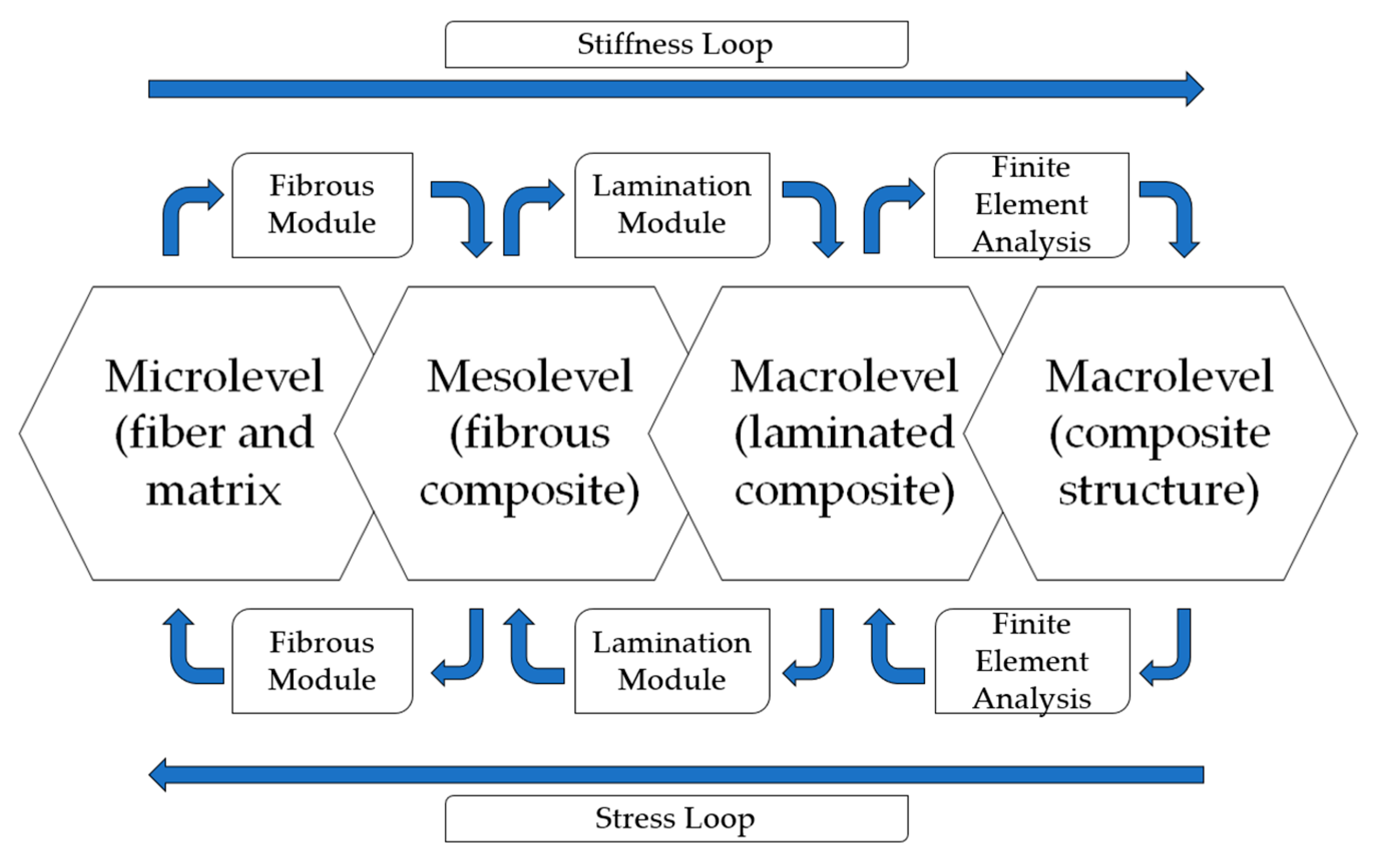
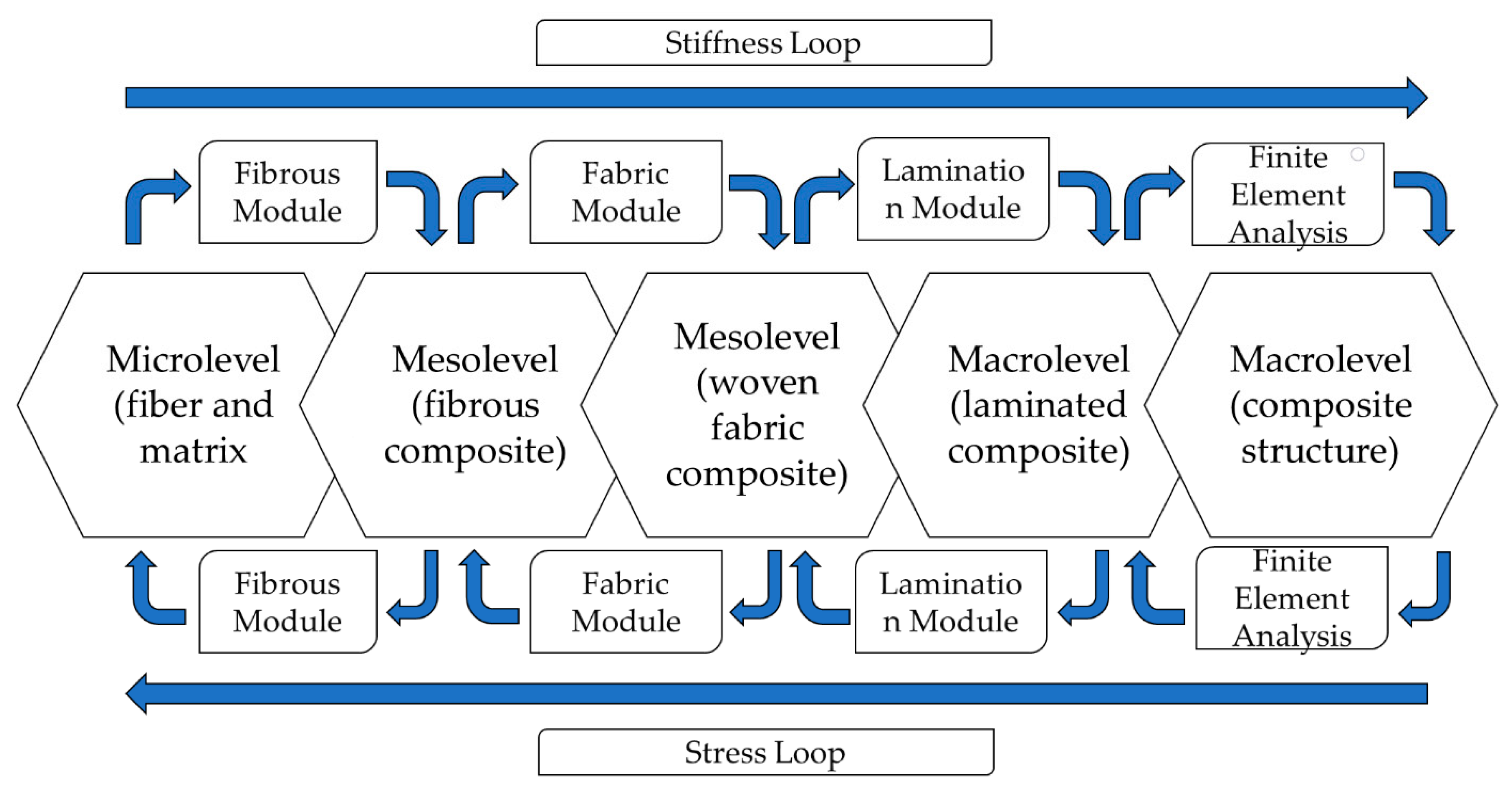
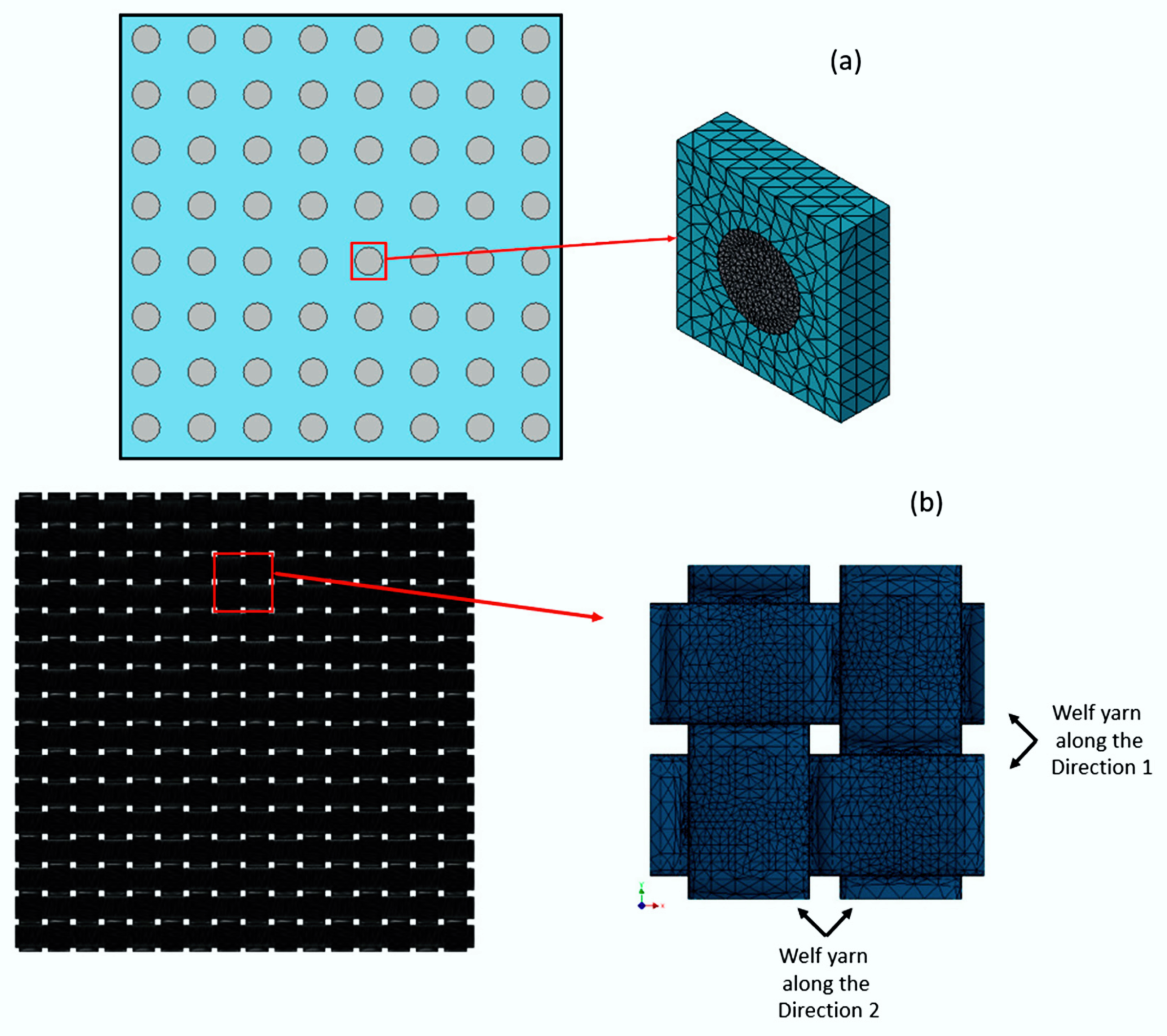
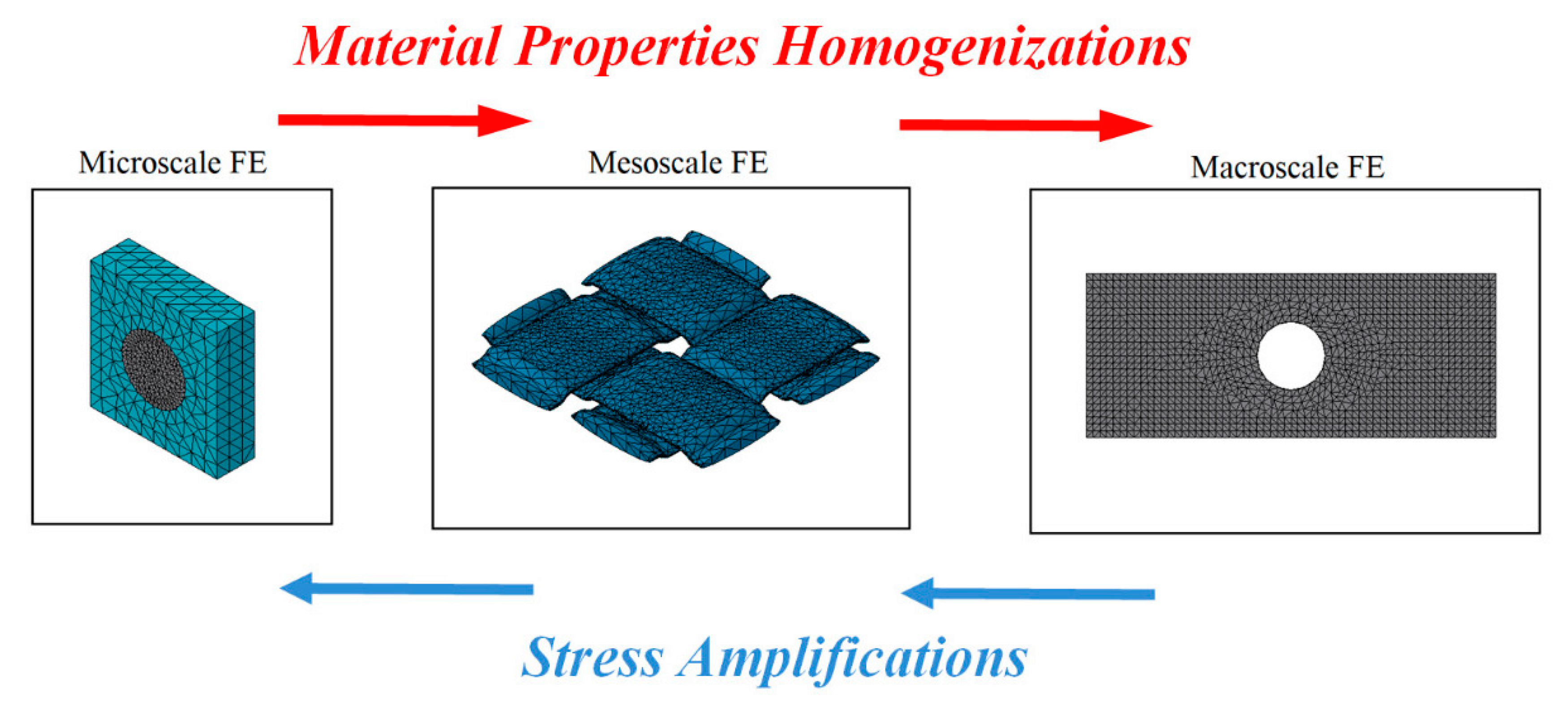

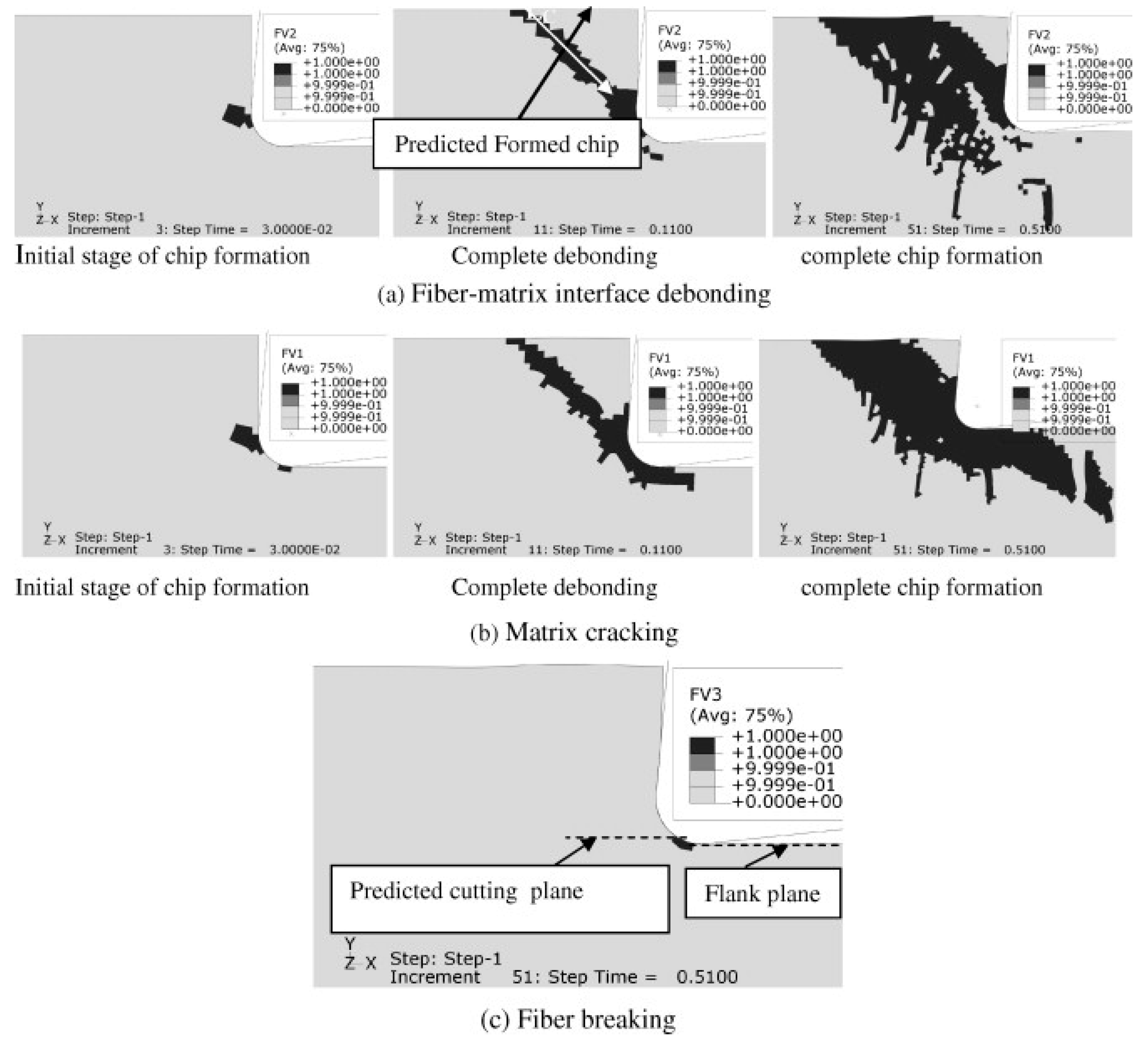
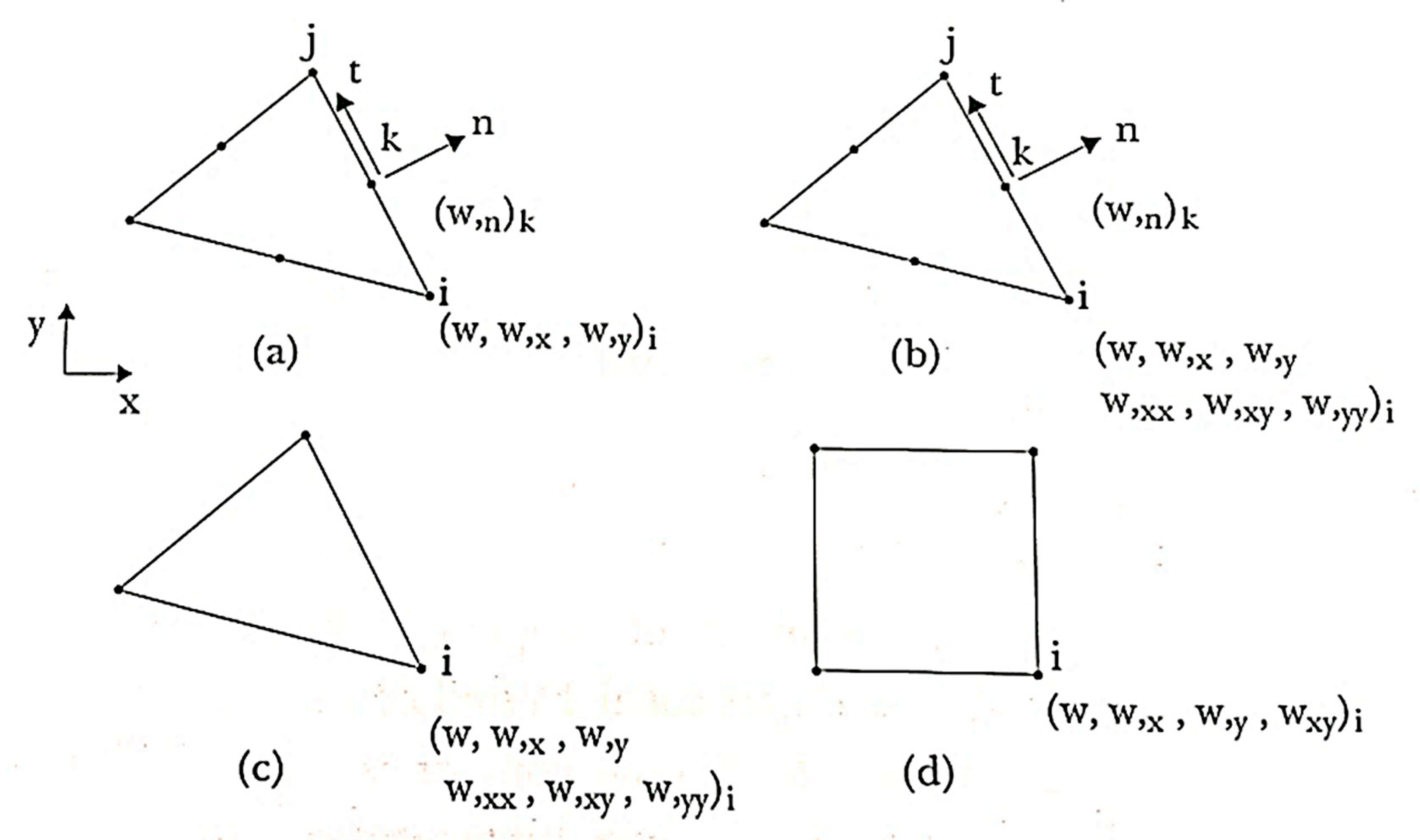
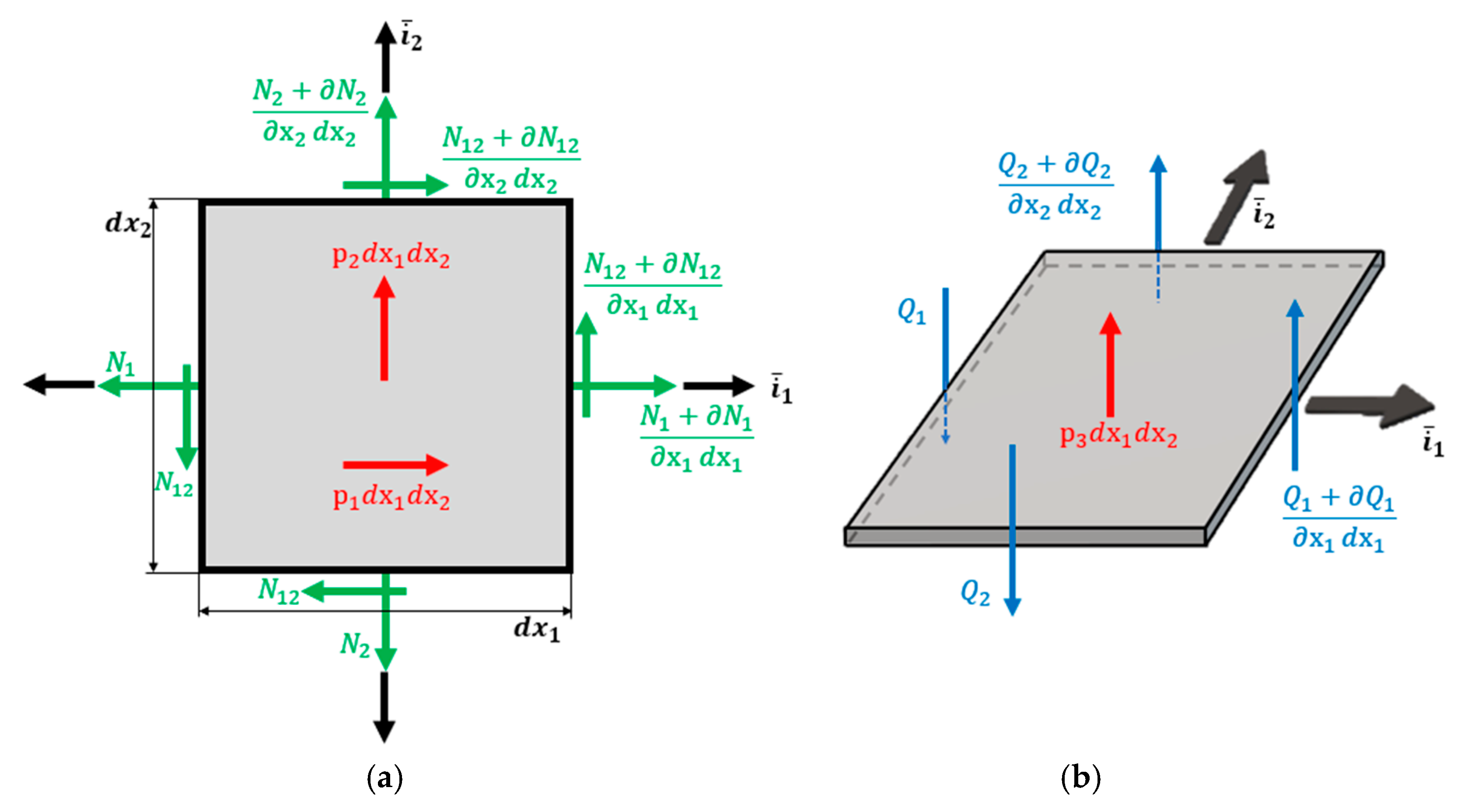
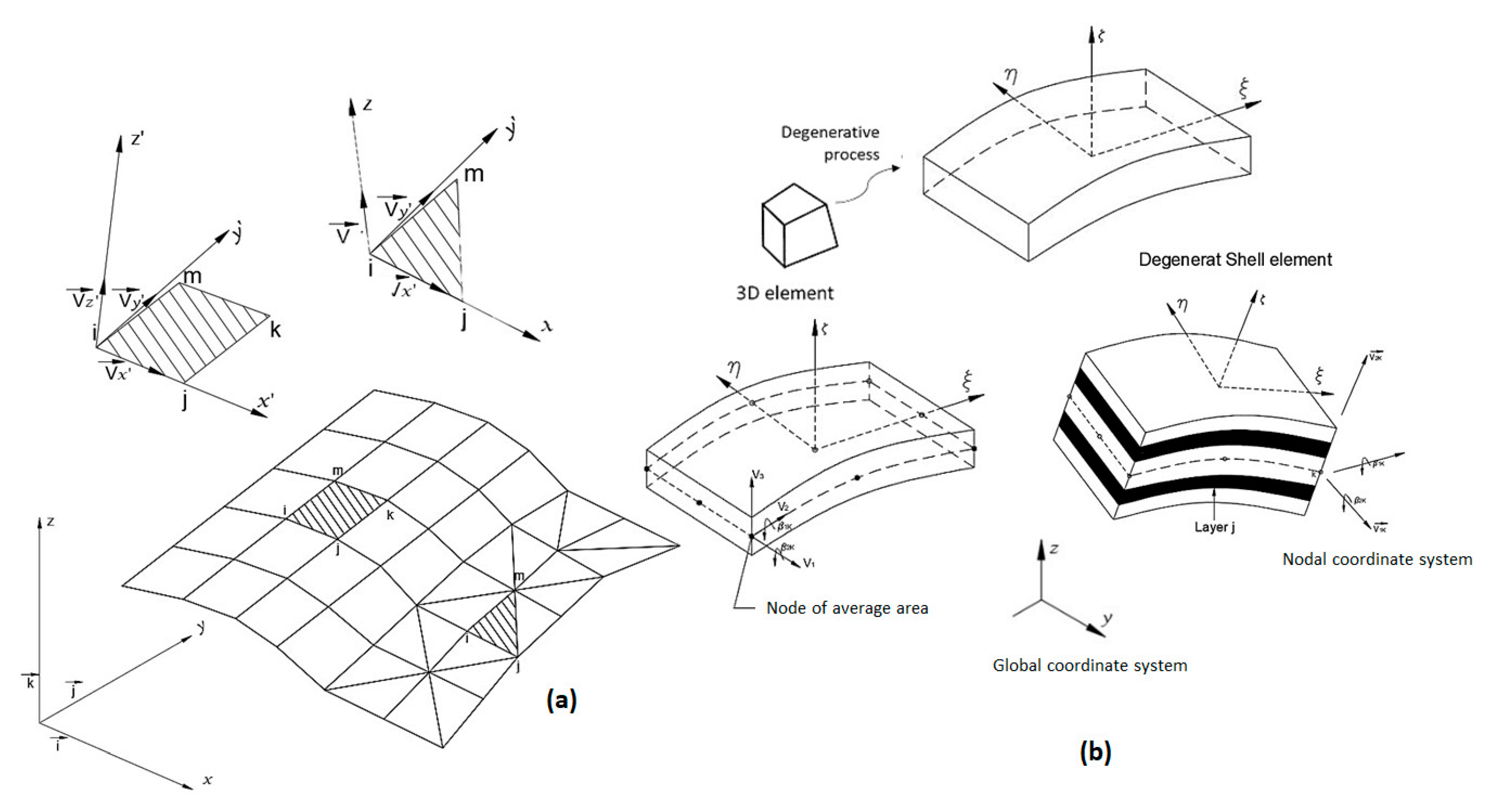

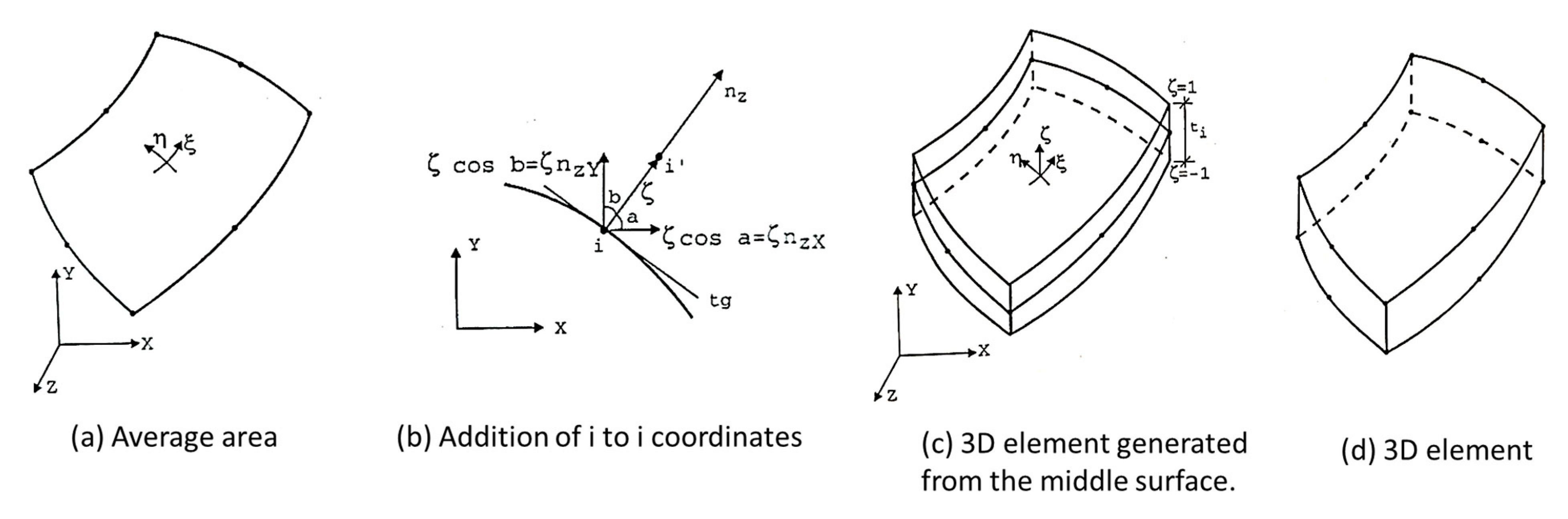
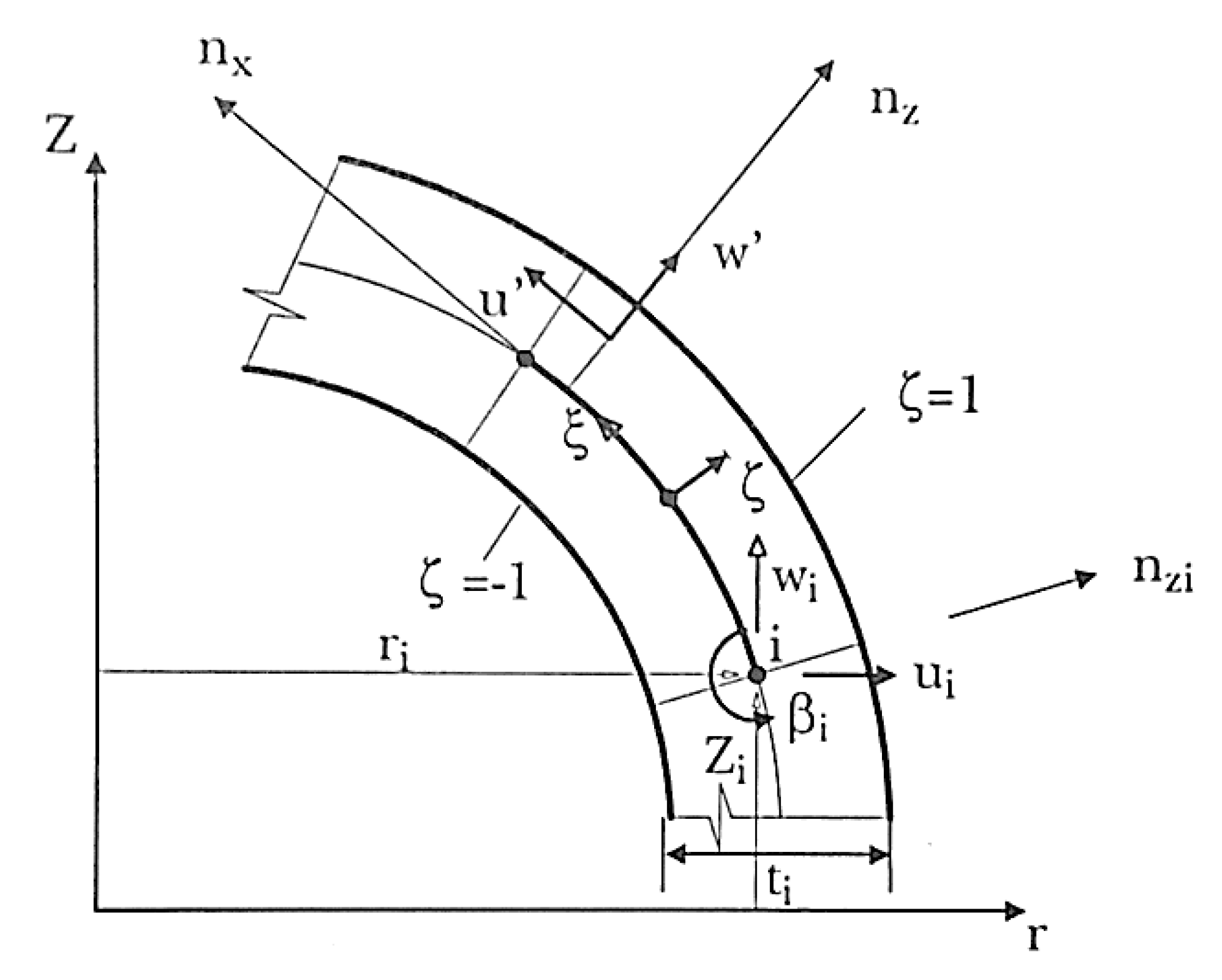







| Failure Criteria | Formula | References |
|---|---|---|
| Maximum Stress | ; ; | [32,65,72,83,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109] |
| Tsai–Hill | [26,28,82,85,87,105,106,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124] | |
| Tsai–Wu | [82,83,85,87,106,111,122,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147] | |
| Hashin | ;; ; | [24,83,85,87,93,104,105,107,122,127,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163] |
| Puck–Schürmann | [84,106,155,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
David Müzel, S.; Bonhin, E.P.; Guimarães, N.M.; Guidi, E.S. Application of the Finite Element Method in the Analysis of Composite Materials: A Review. Polymers 2020, 12, 818. https://doi.org/10.3390/polym12040818
David Müzel S, Bonhin EP, Guimarães NM, Guidi ES. Application of the Finite Element Method in the Analysis of Composite Materials: A Review. Polymers. 2020; 12(4):818. https://doi.org/10.3390/polym12040818
Chicago/Turabian StyleDavid Müzel, Sarah, Eduardo Pires Bonhin, Nara Miranda Guimarães, and Erick Siqueira Guidi. 2020. "Application of the Finite Element Method in the Analysis of Composite Materials: A Review" Polymers 12, no. 4: 818. https://doi.org/10.3390/polym12040818
APA StyleDavid Müzel, S., Bonhin, E. P., Guimarães, N. M., & Guidi, E. S. (2020). Application of the Finite Element Method in the Analysis of Composite Materials: A Review. Polymers, 12(4), 818. https://doi.org/10.3390/polym12040818