A Novel Approach to Atomistic Molecular Dynamics Simulation of Phenolic Resins Using Symthons
Abstract
:1. Introduction
2. Materials and Methods
2.1. Software and Hardware
2.2. Initial Unit Cell Construction
2.3. Script Iterations
2.3.1. Geometry Optimisation
2.3.2. Molecular Dynamics
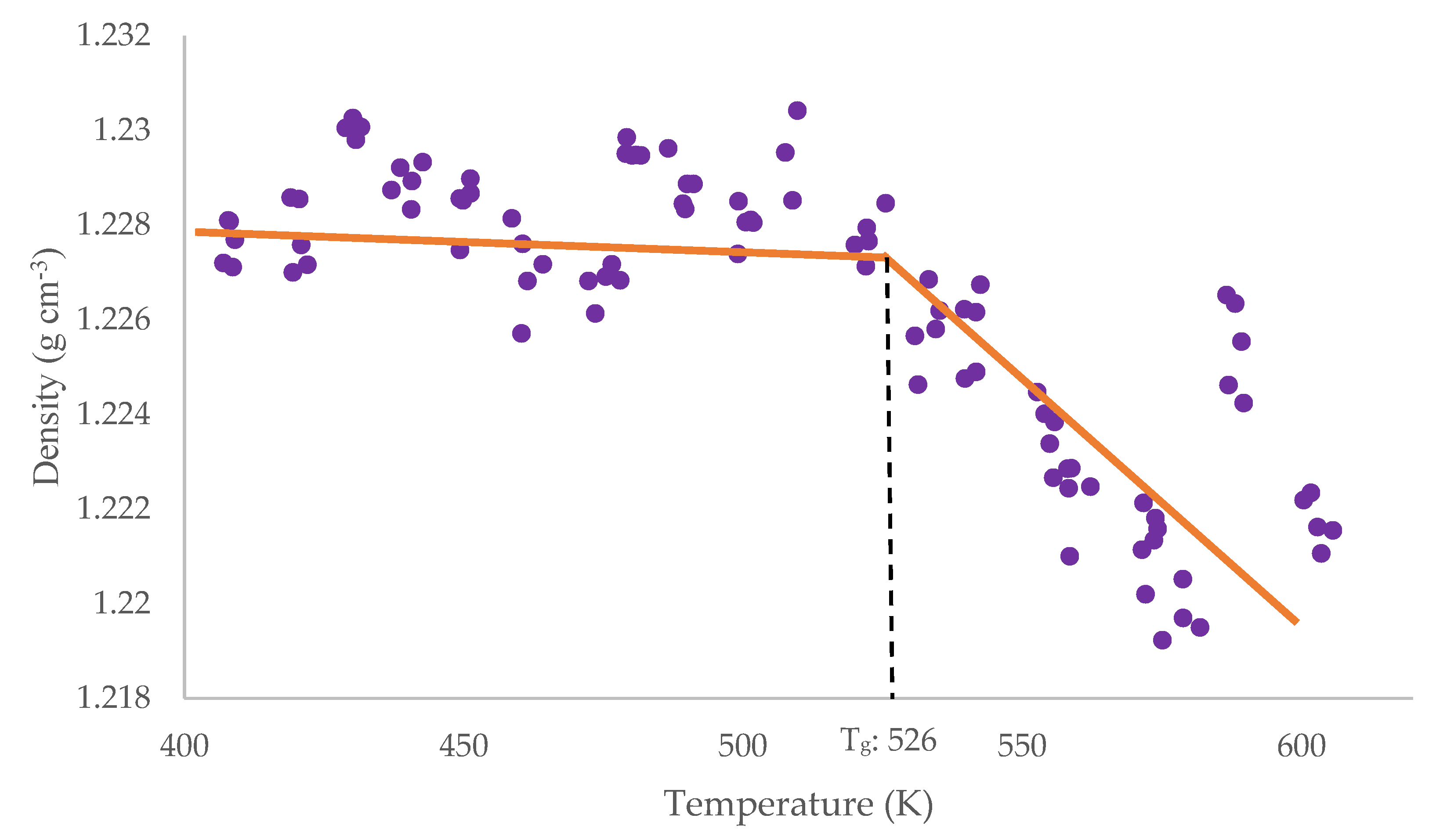
2.4. Tg Simulation
3. Results and Discussion
3.1. Simulation Outcomes
3.2. Evaluation of Novel Modelling Concepts
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hall, S.A.; Howlin, B.J.; Hamerton, I.; Baidak, A.; Billaud, C.; Ward, S. Solving the problem of building models of crosslinked polymers: An example focussing on validation of the properties of crosslinked epoxy resins. PLoS ONE 2012, 7, 1–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Demir, B.; Walsh, T. A robust and reproducible procedure for cross-linking thermoset polymers using molecular simulation. Soft Matter 2016, 12, 2453–2464. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, L.; Cui, L.; Zhang, Y.; Du, X. Molecular dynamics simulation of cross-linked epoxy resin and its interaction energy with graphene under two typical force fields. Comput. Mater. Sci. 2018, 143, 240–247. [Google Scholar] [CrossRef]
- KomarovChiu, P.V.; Yu-Tsung, C.; Shih-Ming, C.; Khalatur, P.G.; Reineker, P. Highly cross-linked epoxy resins: An atomistic molecular dynamics simulation combined with a mapping/reverse mapping procedure. Macromolecules 2007, 40, 8104–8113. [Google Scholar] [CrossRef]
- Ni, B.; Sinnott, S.B.; Mikulski, P.T.; Harrison, J.A. Compression of carbon nanotubes filled with C60, CH4, or Ne: Predictions from molecular dynamics simulations. Phys. Rev. Lett. 2002, 88, 1–4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, J.; Jiang, D.; Scarpa, F.; Peng, H. Enhancement of pullout energy in a single-walled carbon nanotube-polyethylene composite system via auxetic effect. Compos. Part A 2013, 55, 188–194. [Google Scholar] [CrossRef]
- Maruyama, S. A molecular dynamics simulation of heat conduction of a finite length single-walled carbon nanotube. Microscale Thermophys. Eng. 2003, 7, 41–50. [Google Scholar] [CrossRef]
- Hattemer, G.D.; Arya, G. Viscoelastic properties of polymer-grafted nanoparticle composites from molecular dynamics simulations. Macromolecules 2015, 48, 1240–1255. [Google Scholar] [CrossRef]
- Han, Y.; Elliott, J. Molecular dynamics simulations of the elastic properties of polymer/carbon nanotube composites. Comput. Mater. Sci. 2007, 39, 315–323. [Google Scholar] [CrossRef]
- Zhu, R.; Pan, E.; Roy, A.K. Molecular dynamics study of the stress–strain behavior of carbon-nanotube reinforced Epon 862 composites. Mater. Sci. Eng. A 2007, 447, 51–57. [Google Scholar] [CrossRef]
- Mortazavi, B.; Bardon, J.; Ahzi, S. Interphase effect on the elastic and thermal conductivity response of polymer nanocomposite materials: 3D finite element study. Comp. Mat. Sci. 2013, 69, 100–106. [Google Scholar] [CrossRef]
- Mortia, H.; Tanaka, K.; Kajiyama, T.; Nishi, T.; Doi, M. Study of the glass transition temperature of polymer surface by coarse-grained molecular dynamics simulation. Macromolecules 2006, 39, 6233–6237. [Google Scholar] [CrossRef]
- Gardziella, A.; Pilato, L.A.; Knop, A. Phenolic Resins Chemistry, Applications, Standardization, Safety and Ecology, 2nd ed.; Gardziella, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 109–115. ISBN 978-3-642-08484-3. [Google Scholar]
- Cornick, M. Foam. In Phenolic Resins: A Century of Progress; Pilato, L., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 189–208. ISBN 978-3-642-04713-8. [Google Scholar]
- Hou, T.H.; Bai, J.M.; Baughman, J.M. Processing and properties of a phenolic composite system. J. Reinf. Plast. Compos. 2006, 25, 495–502. [Google Scholar] [CrossRef] [Green Version]
- Mottram, J.; Geary, B.; Taylor, R. Thermal expansion of phenolic resin and phenolic-fibre composites. J. Mater. Sci. 1992, 27, 5015–5026. [Google Scholar] [CrossRef]
- Haupt, R.A.; Sellers, T. Characterizations of phenol-formaldehyde resol resins. Ind. Eng. Chem. Res. 1994, 33, 693–697. [Google Scholar] [CrossRef]
- Guo, Z.; Li, H.; Han, W.; Zhao, T. Thermal stability of novolac cured with polyborosilazane. J. Appl. Polym. Sci. 2013, 128, 3356–3364. [Google Scholar] [CrossRef]
- Lee, Y.-K.; Kim, D.-J.; Kim, H.-J.; Hwang, T.-S.; Rafailovich, M.; Sokolov, J. Activation energy and curing behavior of resol- and novolac-type phenolic resins by differential scanning calorimetry and thermogravimetric analysis. J. Appl. Polym. Sci. 2003, 89, 2589–2596. [Google Scholar] [CrossRef]
- Bai, D.; Zhang, X.; Chen, G.; Wang, W. Replacement mechanism of methane hydrate with carbon dioxide from microsecond molecular dynamics simulations. Energy Environ. Sci. 2012, 5, 7033–7041. [Google Scholar] [CrossRef]
- Tildesley, D.J.; Allen, M.P. Computational Simulation of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017; ISBN 9780198803195. [Google Scholar]
- Schneider, R.; Sharma, A.R.; Rai, A. Introduction to Molecular Dynamics. Lect. Notes Phys. 2008, 739, 3–40. [Google Scholar] [CrossRef]
- Monk, J.D.; Haskins, J.B.; Bauschlicher, C.W., Jr.; Lawson, J.W. Molecular dynamics simulations of phenolic resin: Construction of atomistic models. Polymer 2015, 62, 39–49. [Google Scholar] [CrossRef]
- Li, T.; Cao, M.; Liang, J.; Xie, X.; Du, G. Theoretical confirmation of the quinone methide hypothesis for the condensation reactions in phenol-formaldehyde resin synthesis. Polymers 2017, 9, 45. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Škalamera, D.; Antol, I.; Mlinaric-Majerski, K.; Vancik, H.; Phillips, D.L.; Ma, J.; Basaric, N. Ultrafast adiabatic photodehydration of 2-hydroxymethylphenol and the formation of quinone methide. Chem. Eur. J. 2018, 24, 9426–9435. [Google Scholar] [CrossRef] [PubMed]
- Patel, M.; Patel, J. Synthesis and characterization of phenolic resins with ethylene bridges. Die Angew. Makromol. Chem. 1981, 91, 71–77. [Google Scholar] [CrossRef]
- Izumi, A.; Nakao, T.; Shibayama, M. Atomistic molecular dynamics study of cross-linked phenolic resins. Soft Matter 2012, 8, 5283–5292. [Google Scholar] [CrossRef]
- Shudo, Y.; Izumi, A.; Hagita, K.; Nakao, T.; Shibayama, M. Structure-mechanical property relationships in crosslinked phenolic resin investigated by molecular dynamics simulation. Polymer 2017, 116, 506–514. [Google Scholar] [CrossRef]
- Izumi, A.; Shudo, Y.; Hagita, K.; Shibayama, M. Molecular dynamics simulations of cross-linked phenolic resins using a united-atom model. Macromol. Theory Simul. 2018, 27, 1700103–1700111. [Google Scholar] [CrossRef]
- Li, J.; Jumpei, S.; Waizumi, H.; Oya, Y.; Huang, Y.; Kishimoto, N.; Okabe, T. A multiscale model for the synthesis of thermosetting resins: From the addition reaction to cross-linked network formation. Chem. Phys. Lett. 2019, 720, 64–69. [Google Scholar] [CrossRef]
- Manfredi, L.B.; Osa, O.; Fernandez, N.G.; Vazquez, A. Structure-properties relationship for resols with different formaldehyde/phenol molar ratio. Polymer 1999, 40, 3867–3875. [Google Scholar] [CrossRef]
- Grenier-Loustalot, M.F.; Larroque, S.; Grenier, P.; Leca, J.P.; Bedel, D. Phenolic resins: 1. mechanisms and kinetics of phenol and of the first polycondensates towards formaldehyde in solution. Polymer 1994, 35, 3046–3054. [Google Scholar] [CrossRef]
- Monni, J.; Alvila, L.; Pakkanen, T.T. Structural and physical changes in phenol-formaldehyde resol resin, as a function of the degree of condensation of the resol solution. Ind. Eng. Chem. Res. 2007, 46, 6916–6924. [Google Scholar] [CrossRef]
- Lenghaus, K.; Qiao, G.G.; Solomon, D.H. Model studies of the curing of resole phenol-formaldehyde resins Part 1. The behaviour of ortho quinone methide in a curing resin. Polymer 2000, 41, 1973–1979. [Google Scholar] [CrossRef]
- Sun, H. COMPASS: An ab Initio force-field optimized for condensed-phase applications overview with details on alkane and benzene compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Debye, P. Näherungsformeln für die Zylinderfunktionen für große Werte des Arguments und unbeschränkt veränderliche Werte des Index. Math. Ann. 1909, 67, 535–558. [Google Scholar] [CrossRef] [Green Version]
- Hestenes, M.R.; Stiefel, E. Methods of Conjugate Gradients for Solving Linear Systems. J. Res. Natl. Bur. Stand. 1952, 49, 409–436. [Google Scholar] [CrossRef]
- Shewchuk, J.R. An Introduction to the Conjugate Gradient Method Without the Agonizing Pain; Technical Report; Carnegie Mellon University: Pittsburgh, PA, USA, 1994. [Google Scholar]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Martys, N.S.; Mountain, R.D. Velocity Verlet algorithm for dissipative-particle-dynamics-based models of suspensions. Phys. Rev. E 1999, 59, 3733–3736. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Zhang, Z.; Xu, L.; Li, P. Study of the glass transition temperature and the mechanical properties of PET/modified silica nanocomposite by molecular dynamics simulation. Eur. Polym. J. 2016, 75, 36–45. [Google Scholar] [CrossRef]
- Nair, C.P.R. Advances in addition-cure phenolic resins. Prog. Polym. Sci. 2004, 29, 401–498. [Google Scholar] [CrossRef]
- Roe, R.J. MD simulation study of glass transition and short time dynamics in polymer liquids. In Atomistic Modeling of Physical Properties; Monnerie, L., Suter, U.W., Eds.; Springer: Berlin, Germany, 1994; Volume 116, pp. 111–144. ISBN 978-3-540-57827-7. [Google Scholar]
- Martyna, G.J.; Tobias, D.J.; Klein, M.L. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 1994, 101, 4177–4189. [Google Scholar] [CrossRef]
- Andersen, H.C. Molecular dynamics simulations at constant pressure and/or temperature. J. Chem. Phys. 1980, 72, 2384–2393. [Google Scholar] [CrossRef] [Green Version]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Tuckerman, M.E.; Liu, Y.; Ciccotti, G.; Martyna, G.J. Non-Hamiltonian molecular dynamics: Generalizing Hamiltonian phase space principles to non-Hamiltonian systems. J. Chem. Phys. 2001, 115, 1678–1702. [Google Scholar] [CrossRef]
- Keffer, D.J.; Baig, C.; Adhangale, P.; Edwards, B.J. A generalized Hamiltonian-based algorithm for rigorous equilibrium molecular dynamics simulation in the isobaric–isothermal ensemble. Mol. Sim. 2006, 32, 345–356. [Google Scholar] [CrossRef]
- Uline, M.J.; Corti, D.S. Molecular dynamics at constant pressure: Allowing the system to control volume fluctuations via a “shell” particle. Entropy 2013, 15, 3941–3969. [Google Scholar] [CrossRef] [Green Version]





| F:P Ratio 1 | Density/g cm−3 | Degree of Cure/% | Maximum Theoretical Degree of Cure/% | Initial Atom Count | Final Atom Count | Final Potential Energy/kcal mol−1 |
|---|---|---|---|---|---|---|
| 1.0 | 1.223 | 66.1 | 66.7 | 10,013 | 8261 | −13,367 |
| 1.2 | 1.222 | 79.1 | 80.0 | 10,057 | 8039 | −11,051 |
| 1.4 | 1.205 | 91.6 | 93.3 | 10,044 | 7790 | −5107 |
| 1.5 | 1.182 | 96.8 | 100.0 | 10,032 | 7659 | −2975 |
| 1.6 | 1.141 | 97.3 | 100.0 | 10,012 | 7489 | 2491 |
| 1.8 | 1.142 | 99.5 | 100.0 | 10,020 | 7220 | 43,785 |
| 2.0 | 1.207 | 99.2 | 100.0 | 10,017 | 6947 | 41,185 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bone, M.A.; Macquart, T.; Hamerton, I.; Howlin, B.J. A Novel Approach to Atomistic Molecular Dynamics Simulation of Phenolic Resins Using Symthons. Polymers 2020, 12, 926. https://doi.org/10.3390/polym12040926
Bone MA, Macquart T, Hamerton I, Howlin BJ. A Novel Approach to Atomistic Molecular Dynamics Simulation of Phenolic Resins Using Symthons. Polymers. 2020; 12(4):926. https://doi.org/10.3390/polym12040926
Chicago/Turabian StyleBone, Matthew A., Terence Macquart, Ian Hamerton, and Brendan J. Howlin. 2020. "A Novel Approach to Atomistic Molecular Dynamics Simulation of Phenolic Resins Using Symthons" Polymers 12, no. 4: 926. https://doi.org/10.3390/polym12040926
APA StyleBone, M. A., Macquart, T., Hamerton, I., & Howlin, B. J. (2020). A Novel Approach to Atomistic Molecular Dynamics Simulation of Phenolic Resins Using Symthons. Polymers, 12(4), 926. https://doi.org/10.3390/polym12040926







