Development of an Analytical Model to Describe the Disperse Melting in Wave-Dispersion Screws
Abstract
:1. Introduction
2. Melting Models
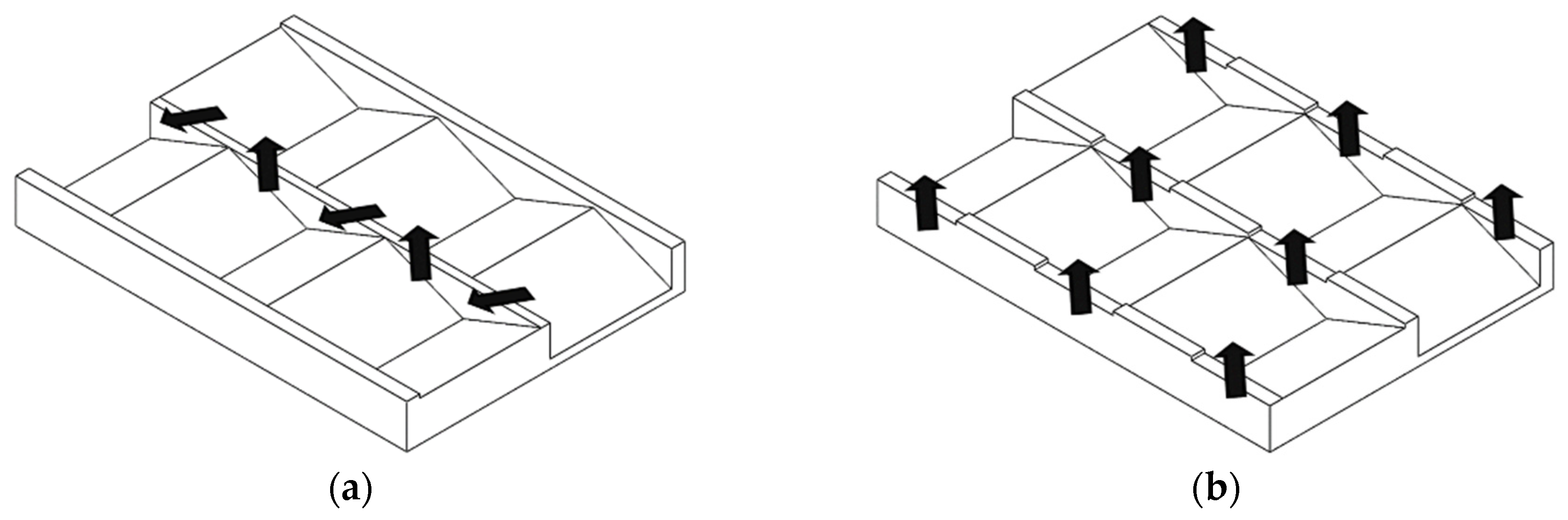
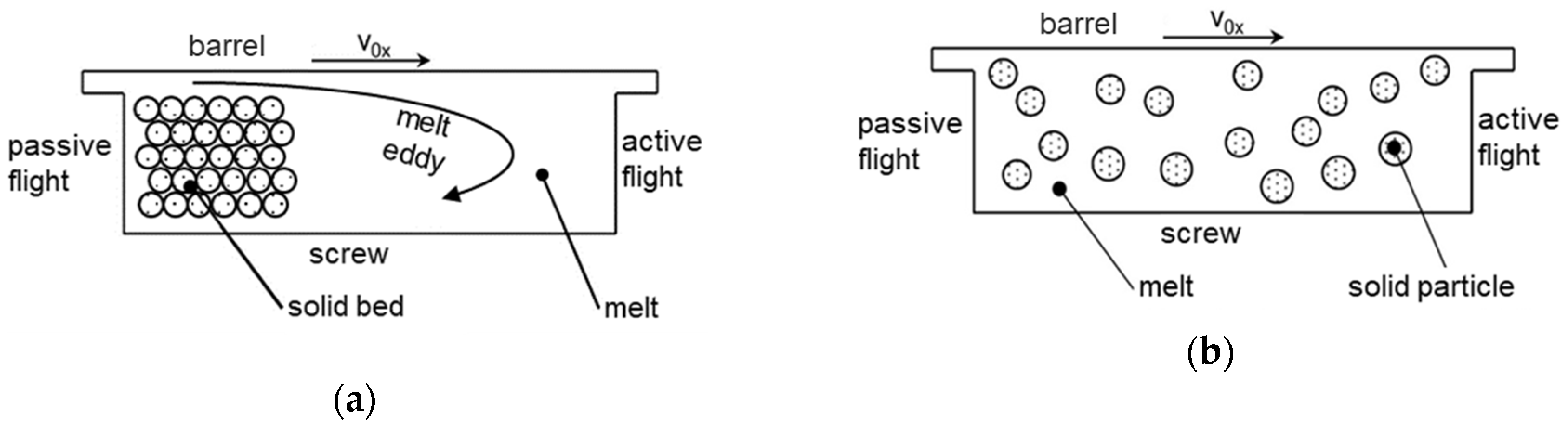
2.1. Conventional Melting Model
2.2. Disperse Melting Model
3. Mathematical Treatment of Existing Melting Models
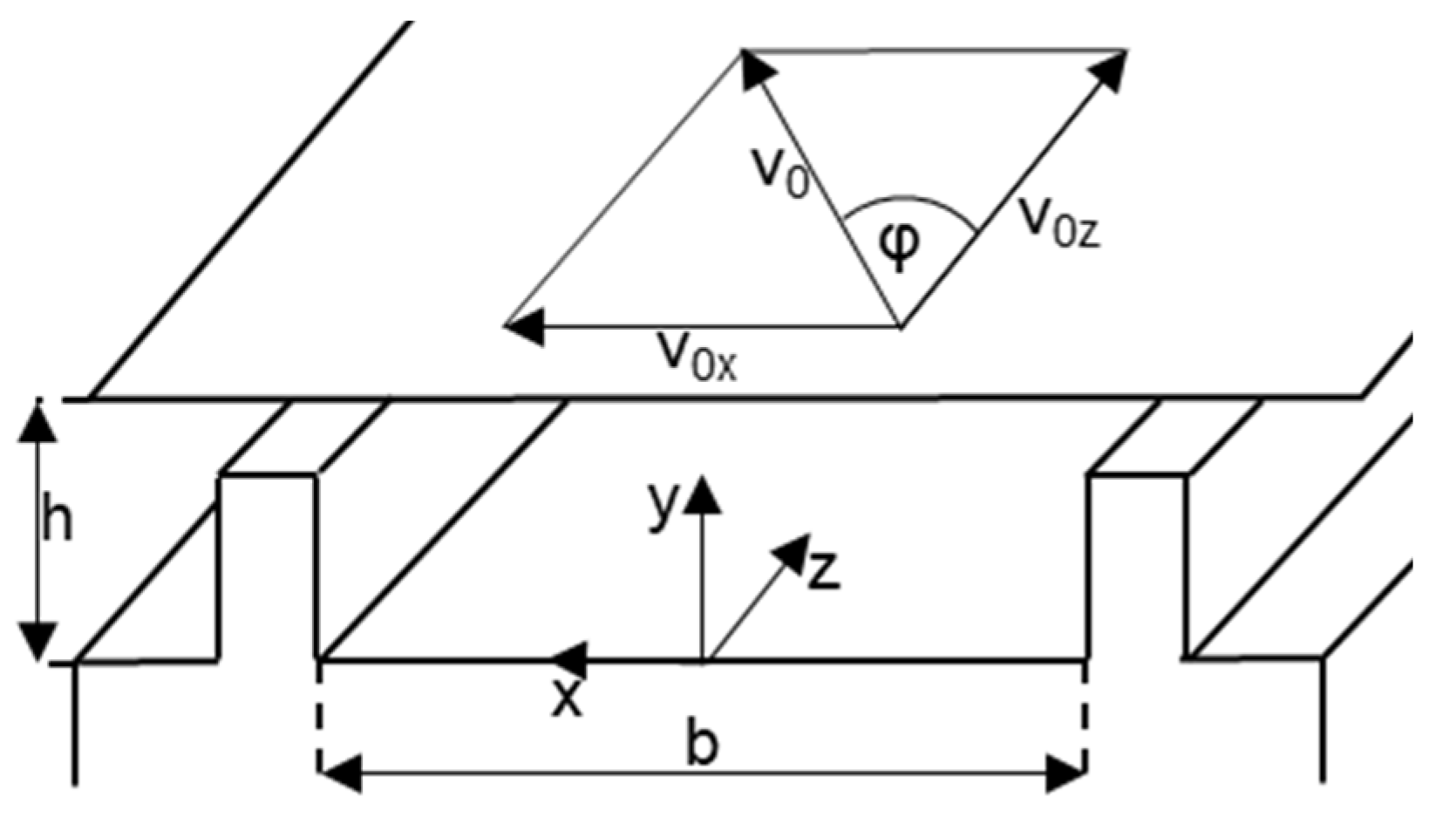
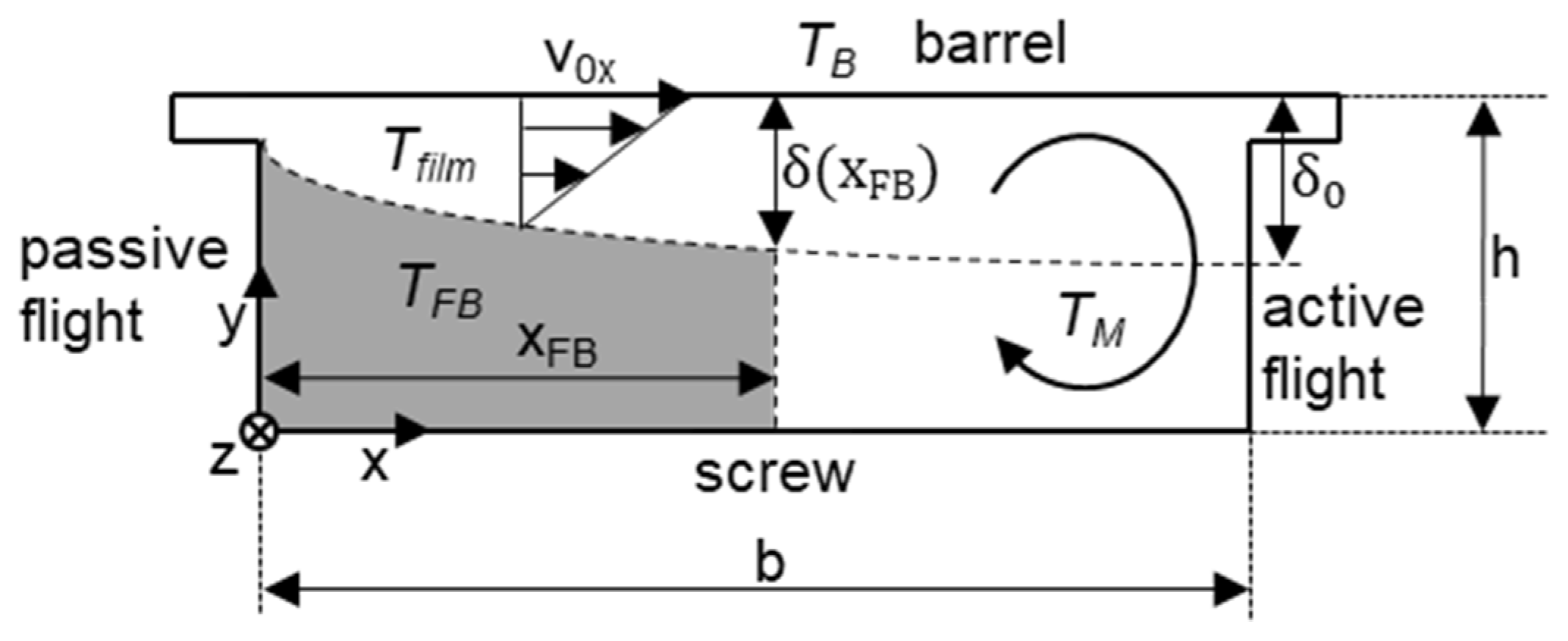
3.1. Conventional Melting Model
- Constant material parameters in the considered calculation section.
- Applying kinematic reversal.
- Incompressible melt → .
- Stationary flow, therefore no time-dependent changes → .
- Melt channel completely filled with wall-adhering melt.
- Velocity components only in channel length direction z → .
- Neglecting the heat flow in the channel length and channel width direction, temperature gradient is formed only in channel height direction → .
- Channel height significantly smaller than channel width, so influence of flight negligible. Due to purely viscous material, normal stresses negligible → .
- Consideration of Fourier law of heat conduction → .
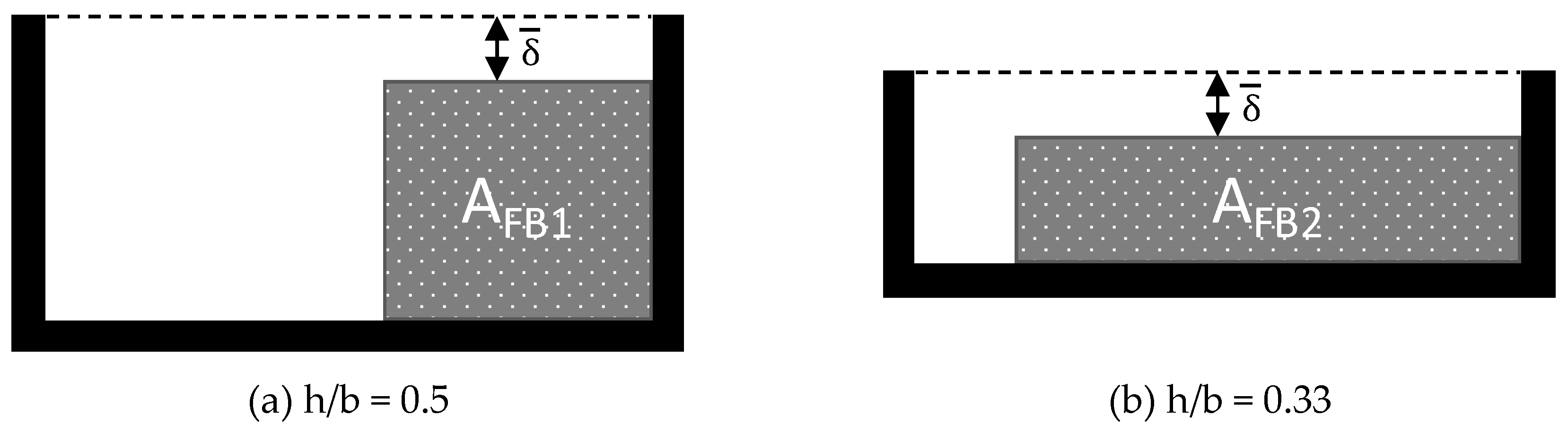
3.2. Disperse Melting Model
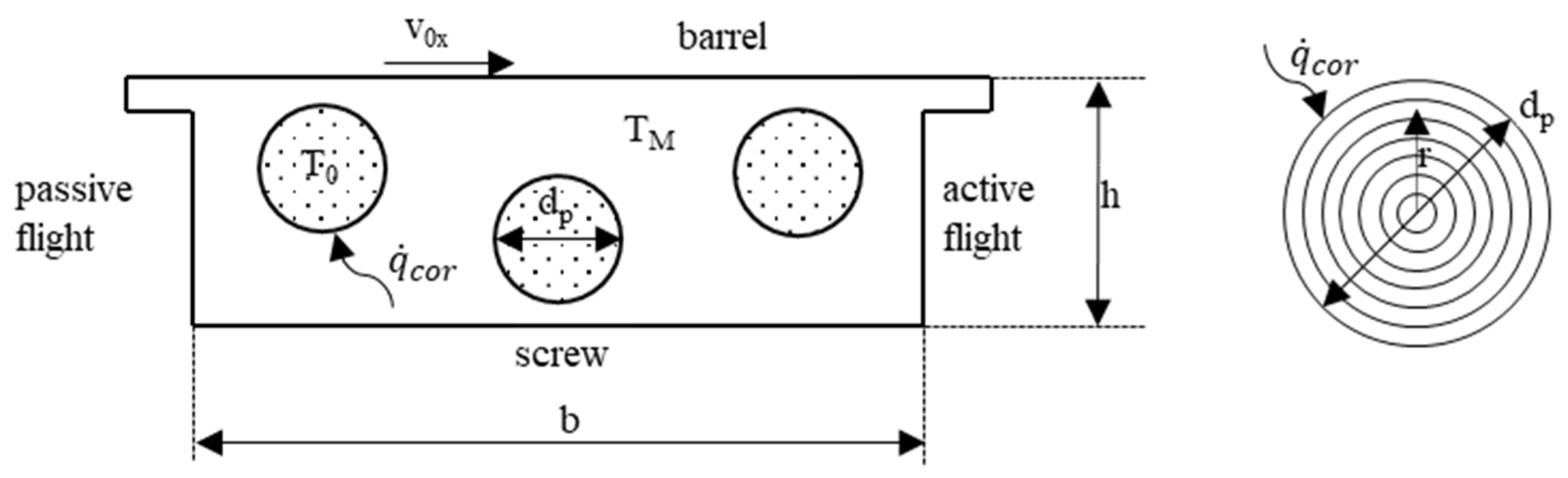
4. Novel Disperse Melting Model
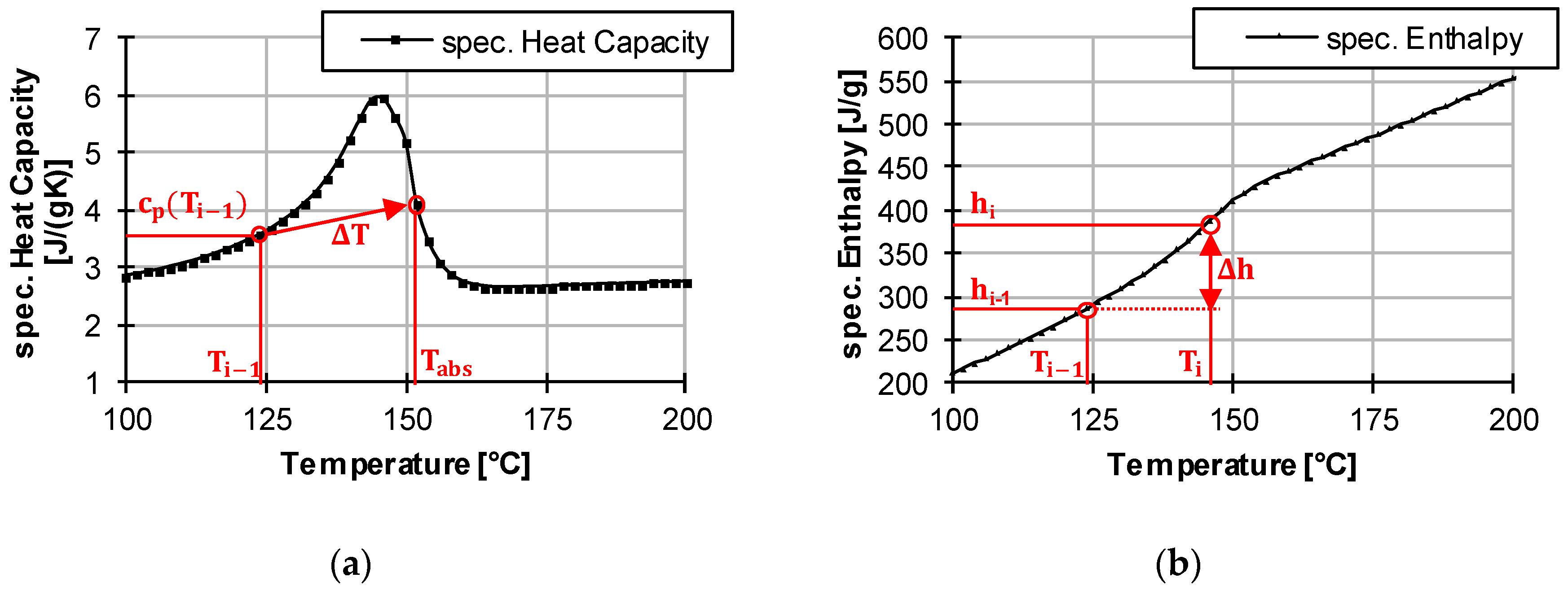
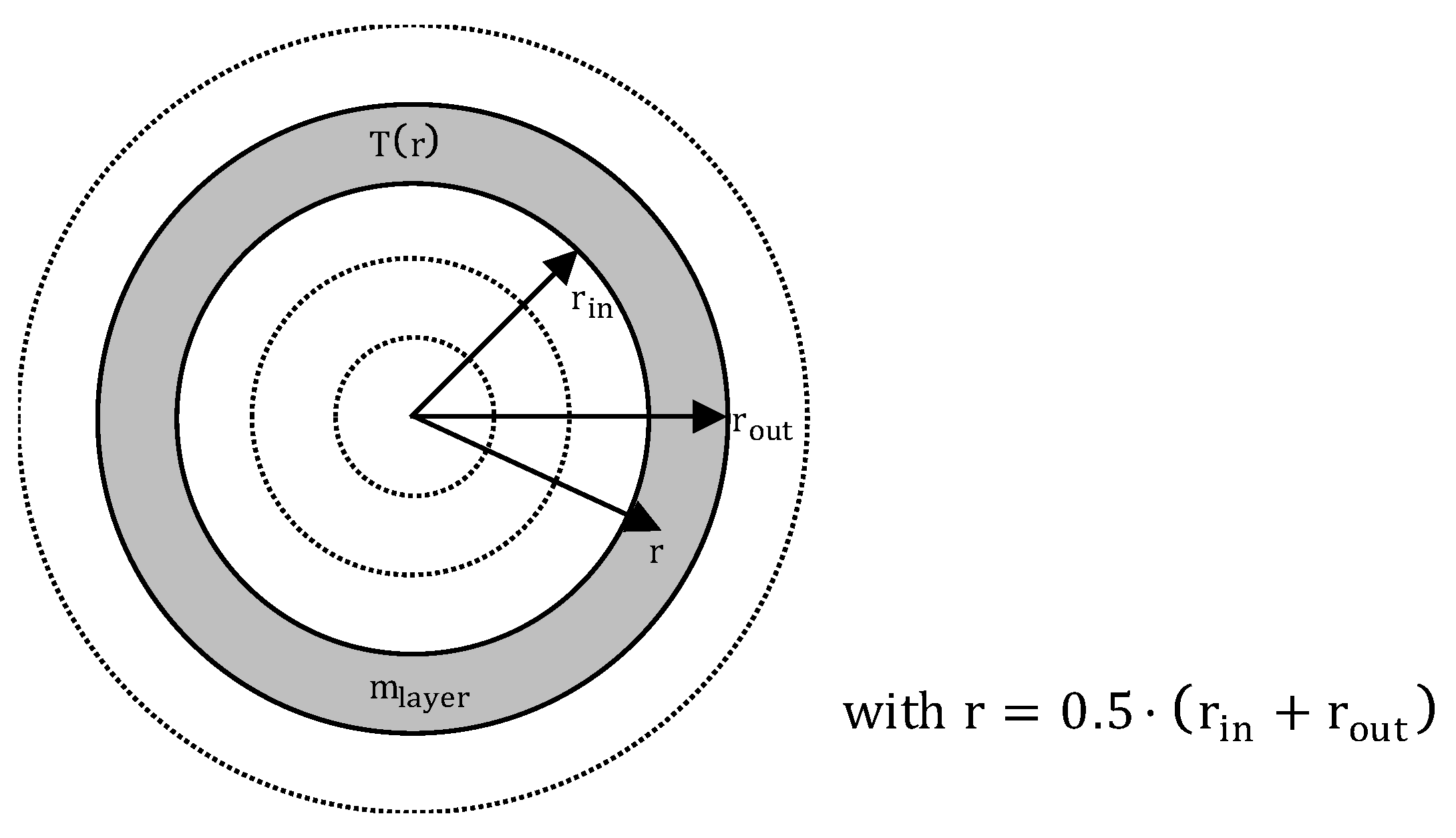
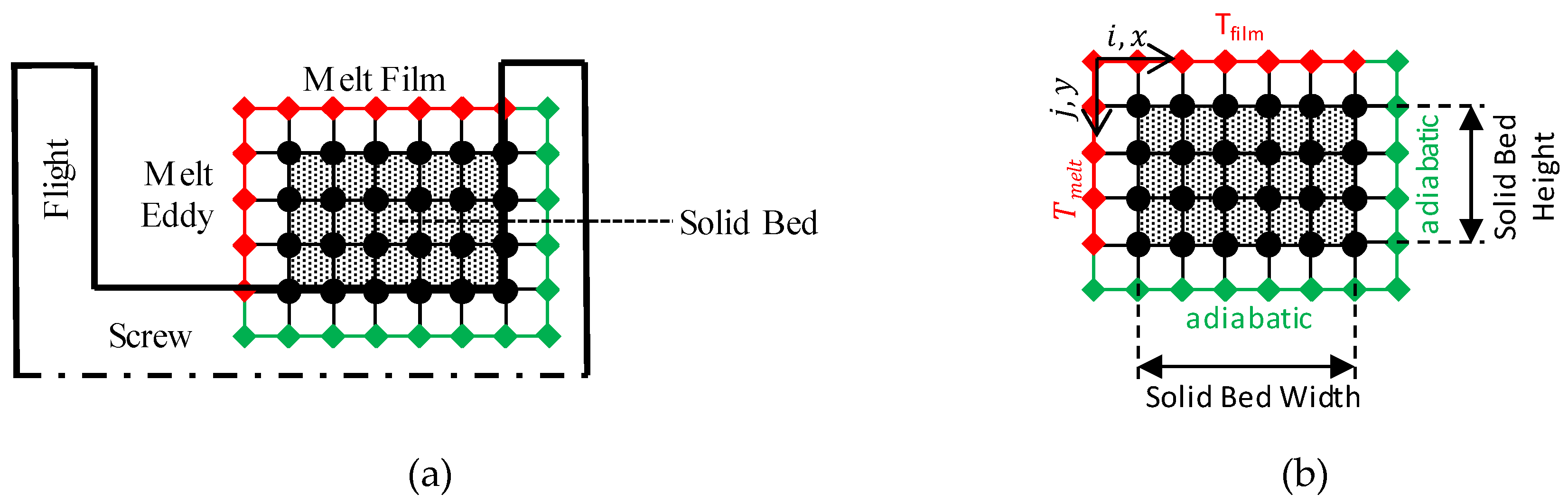
4.1. Temperature Profile in Particle and Melting of Particle
4.2. Temperature Development of the Melt
4.3. Determination of the Particle Temperature at the Beginning of Disperse Melting
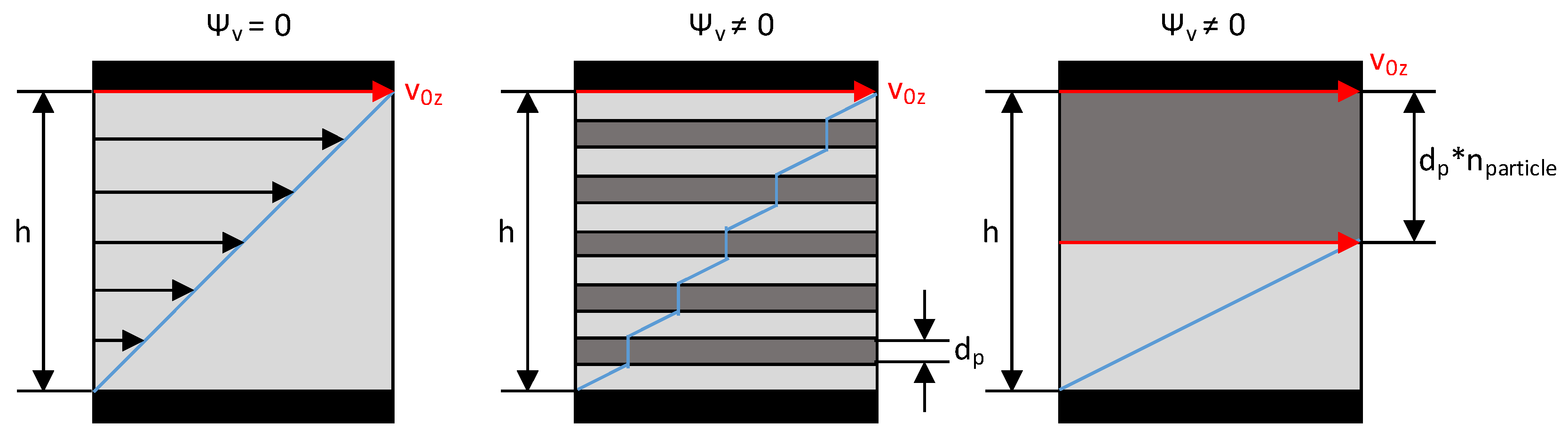
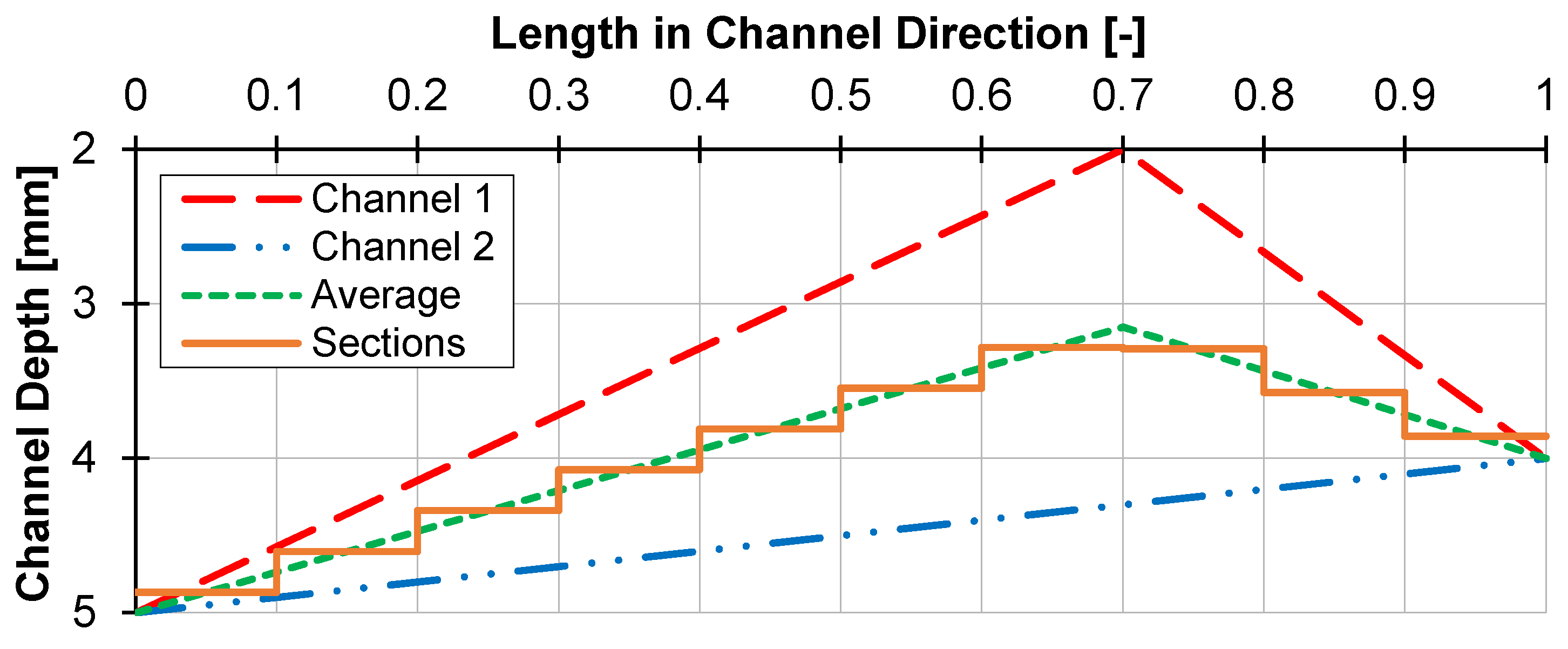
4.4. Application on Wave-Dispersion Screws
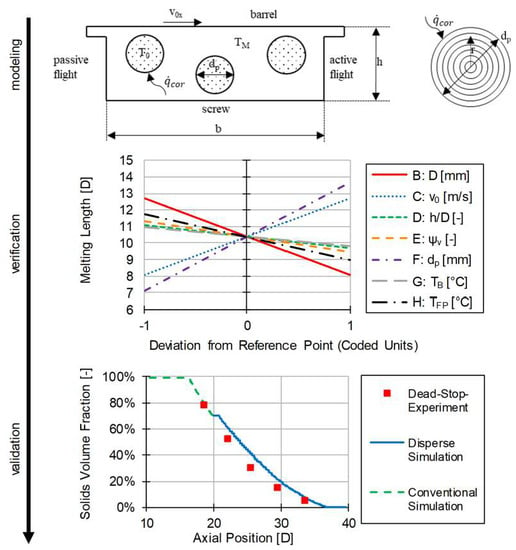
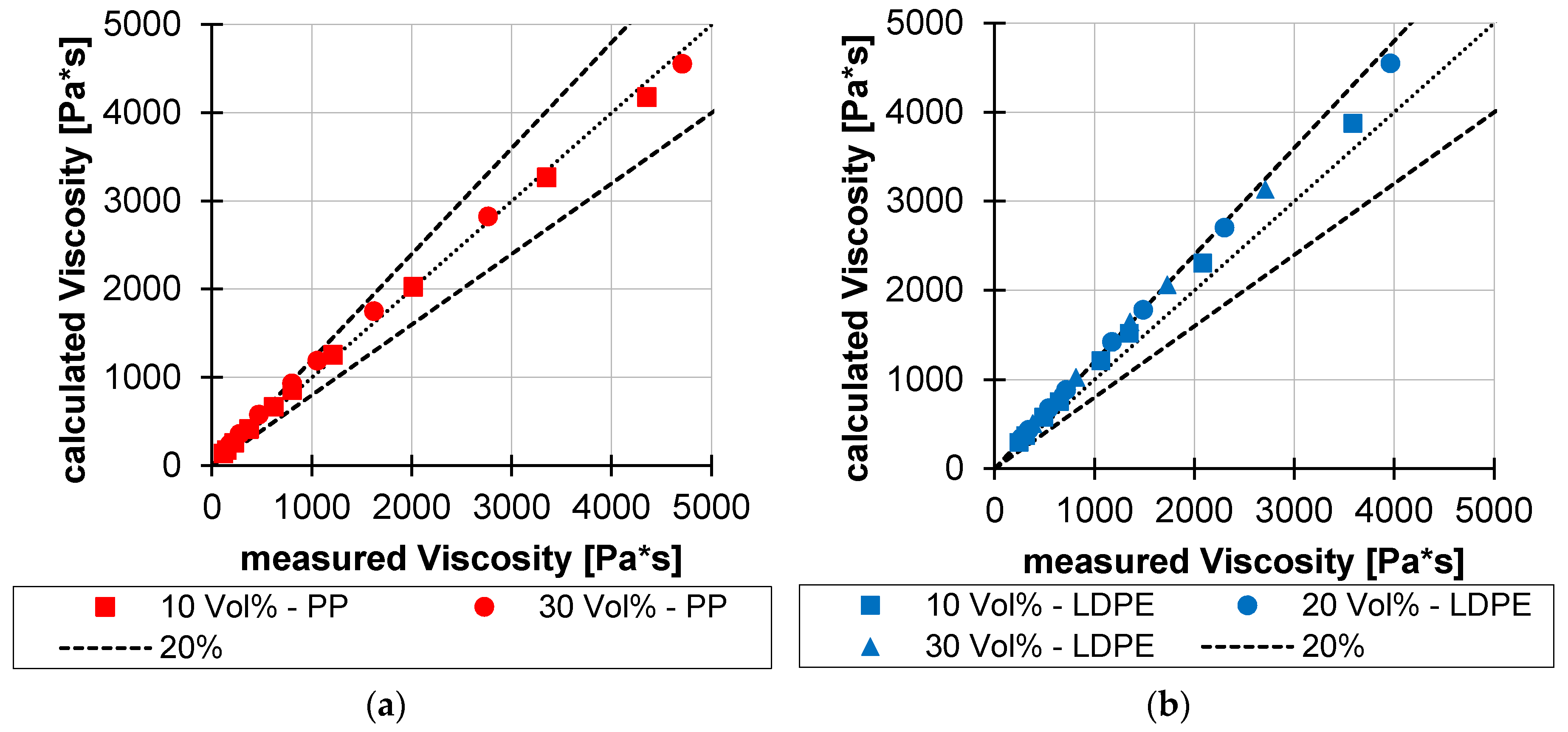
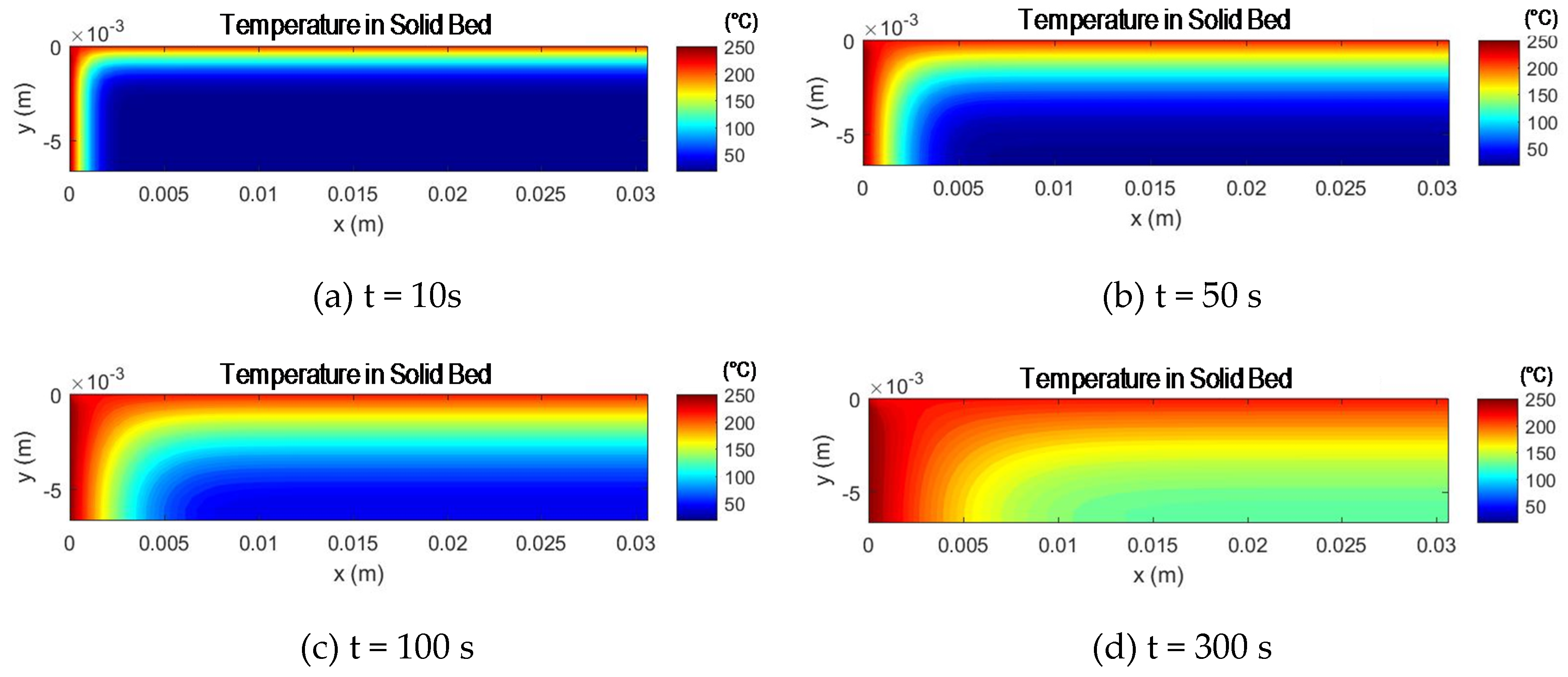
5. Verification
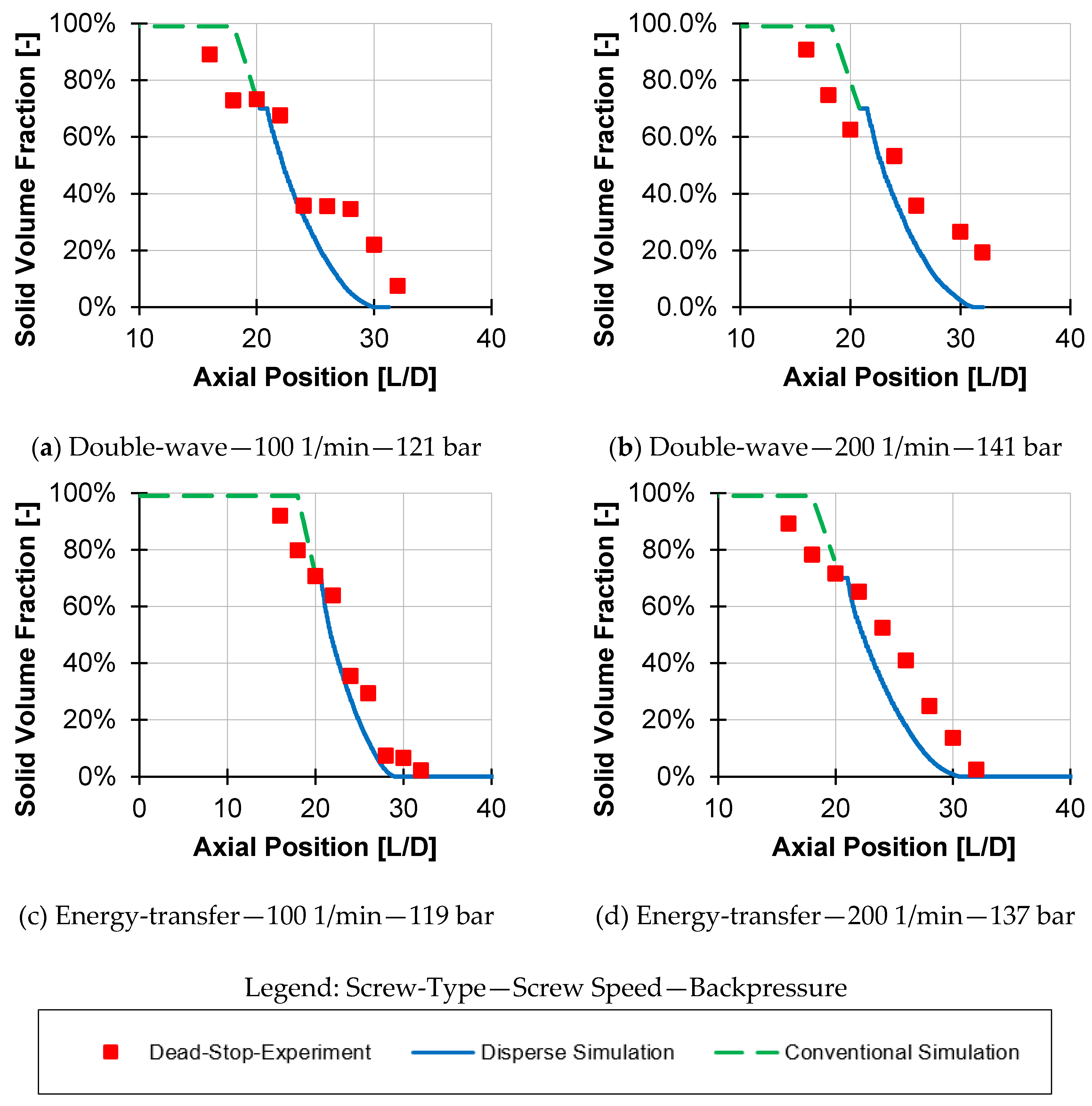
6. Validation
7. Discussion and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| Roman Characters | |
| temperature conductivity | |
| temperature conductivity of solid | |
| cross-sectional area of the channel | |
| cross-sectional area of the melt eddy | |
| cross-sectional area of the melt film | |
| surface area of particle | |
| cross-sectional area of the solid bed | |
| channel width | |
| Brinkmann number | |
| contour exponent | |
| constants of linearization | |
| specific heat capacity | |
| specific heat capacity of the solid | |
| specific heat capacity of the melt | |
| specific heat capacity at TM | |
| particle diameter | |
| screw diameter | |
| energy of cooling | |
| correction factor of convection | |
| correction factor of channel depth | |
| Fourier number | |
| Graetz number | |
| channel depth | |
| specific enthalpy | |
| specific melting enthalpy | |
| specific solid enthalpy | |
| i, j | variable for fdm-nodes in solid bed width and height direction |
| correction factors according to [16] | |
| consistency factor of power law | |
| corrected consistency factor of power law | |
| consistency factor of power law at temperature TFL | |
| mass | |
| mass of melt | |
| mass flow | |
| melting mass flow | |
| flow exponent of power law | |
| number of particles | |
| screw speed | |
| pressure | |
| specific heat flow | |
| corrected specific heat flow | |
| heat flow | |
| corrected heat flow | |
| complete corrected heat flow of all particles | |
| radius of particle as control variable | |
| absolute radius of the particle | |
| time | |
| maximum time step for stability | |
| temperature | |
| temperature difference because of dissipation | |
| temperature difference because of cooling | |
| temperature of solid bed | |
| temperature of solid bed | |
| melting temperature | |
| temperature of melt | |
| initial temperature of particle | |
| temperature of barrel | |
| constants for temperature polynomial | |
| velocity | |
| velocity in x-direction, y-direction, z-direction | |
| circumferential speed of screw | |
| resulting speed in axial-direction x or channel-direction z | |
| relative speed according to [16] | |
| melting velocity of polymer according to [31] | |
| volume of channel | |
| volume of particle | |
| volume of melt | |
| volume flow rate | |
| solid bed width | |
| distance in equidistant FDM calculation grid | |
| z | length in channel direction |
| Greek Characters | |
| parameter for the temperature dependence of viscosity | |
| shear rate | |
| melt film thickness at position x | |
| average melt film thickness | |
| starting melt film thickness at x = b | |
| dimensionless length | |
| relative viscosity | |
| viscosity of pure polymer | |
| viscosity of polymer with solids | |
| dimensionless tempature | |
| therm conductivity | |
| thermal conductivity of solid | |
| thermal conductivity of melt at TM | |
| Eigenvalue | |
| dimensionless height | |
| density | |
| density at melt temperature | |
| solid density | |
| shear sess | |
| pitch angle | |
| solids vume fraction | |
Appendix A: Final Equation to Describe the Melt Temperature in the Screw Channel According to [25]
Appendix B: Simulation Points of the Design of Experiment
| No. | Throughput [kg/h] | Screw Diameter [mm] | Screw Speed [m/s] | Ch. Depth Ratio [h/D] | Initial Solid Fraction of Disperse Melting [-] |
|---|---|---|---|---|---|
| 1 | 50 | 30 | 0.785 | 0.167 | 0.7 |
| 2 | 50 | 30 | 0.785 | 0.167 | 0.3 |
| 3 | 50 | 30 | 0.785 | 0.083 | 0.7 |
| 4 | 50 | 30 | 0.785 | 0.083 | 0.3 |
| 5 | 150 | 30 | 2.356 | 0.167 | 0.7 |
| 6 | 150 | 30 | 2.356 | 0.167 | 0.3 |
| 7 | 150 | 30 | 2.356 | 0.083 | 0.7 |
| 8 | 150 | 30 | 2.356 | 0.083 | 0.3 |
| 9 | 140 | 60 | 0.660 | 0.140 | 0.7 |
| 10 | 140 | 60 | 0.660 | 0.140 | 0.3 |
| 11 | 140 | 60 | 0.660 | 0.070 | 0.7 |
| 12 | 140 | 60 | 0.660 | 0.070 | 0.3 |
| 13 | 420 | 60 | 1.979 | 0.140 | 0.7 |
| 14 | 420 | 60 | 1.979 | 0.140 | 0.3 |
| 15 | 420 | 60 | 1.979 | 0.070 | 0.7 |
| 16 | 420 | 60 | 1.979 | 0.070 | 0.3 |
| 17 | 200 | 75 | 0.628 | 0.132 | 0.7 |
| 18 | 200 | 75 | 0.628 | 0.132 | 0.3 |
| 19 | 200 | 75 | 0.628 | 0.067 | 0.7 |
| 20 | 200 | 75 | 0.628 | 0.067 | 0.3 |
| 21 | 600 | 75 | 1.885 | 0.132 | 0.7 |
| 22 | 600 | 75 | 1.885 | 0.132 | 0.3 |
| 23 | 600 | 75 | 1.885 | 0.067 | 0.7 |
| 24 | 600 | 75 | 1.885 | 0.067 | 0.3 |
| 25 | 260 | 90 | 0.613 | 0.127 | 0.7 |
| 26 | 260 | 90 | 0.613 | 0.127 | 0.3 |
| 27 | 260 | 90 | 0.613 | 0.063 | 0.7 |
| 28 | 260 | 90 | 0.613 | 0.063 | 0.3 |
| 29 | 780 | 90 | 1.791 | 0.127 | 0.7 |
| 30 | 780 | 90 | 1.791 | 0.127 | 0.3 |
| 31 | 780 | 90 | 1.791 | 0.063 | 0.7 |
| 32 | 780 | 90 | 1.791 | 0.063 | 0.3 |
| 33 | 400 | 120 | 0.565 | 0.118 | 0.7 |
| 34 | 400 | 120 | 0.565 | 0.118 | 0.3 |
| 35 | 400 | 120 | 0.565 | 0.059 | 0.7 |
| 36 | 400 | 120 | 0.565 | 0.059 | 0.3 |
| 37 | 1200 | 120 | 1.696 | 0.118 | 0.7 |
| 38 | 1200 | 120 | 1.696 | 0.118 | 0.3 |
| 39 | 1200 | 120 | 1.696 | 0.059 | 0.7 |
| 40 | 1200 | 120 | 1.696 | 0.059 | 0.3 |
| 41 | 1200 | 250 | 0.524 | 0.098 | 0.7 |
| 42 | 1200 | 250 | 0.524 | 0.098 | 0.3 |
| 43 | 1200 | 250 | 0.524 | 0.049 | 0.7 |
| 44 | 1200 | 250 | 0.524 | 0.049 | 0.3 |
| 45 | 3600 | 250 | 1.440 | 0.098 | 0.7 |
| 46 | 3600 | 250 | 1.440 | 0.098 | 0.3 |
| 47 | 3600 | 250 | 1.440 | 0.049 | 0.7 |
| 48 | 3600 | 250 | 1.440 | 0.049 | 0.3 |
| Level | Particle Diameter [mm] | Barrel Temperature [°C] | Particle Inlet Temperature [°C] |
|---|---|---|---|
| Low | 1 | 180 | 20 |
| Middle | 3 | 200 | 50 |
| High | 5 | 220 | 80 |
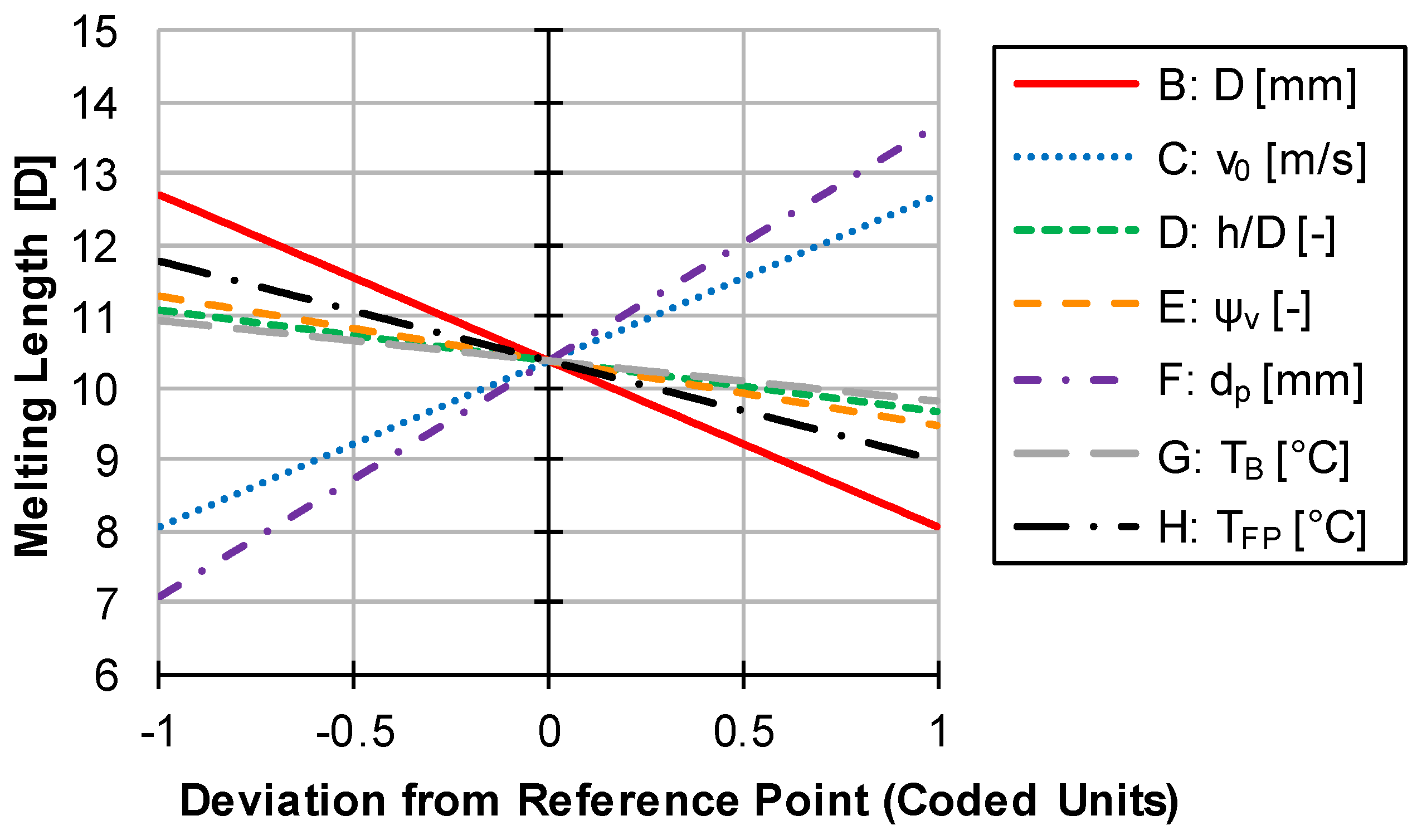
Appendix C: Regression from DoE for the Required Melting Length
Regression in Coded Units
| Unit/Level | B-D [mm] | C-v0 [m/s] | D-h/D [-] | E-ψv [-] | F-dp [mm] | G-TB [°C] | H-TFP [°C] |
|---|---|---|---|---|---|---|---|
| −1 | 30 | 0.524 | 0.049 | 0.3 | 1 | 180 | 20 |
| 0 | 140 | 1.44 | 0.108 | 0.5 | 3 | 200 | 50 |
| 1 | 250 | 2.356 | 0.167 | 0.7 | 5 | 220 | 80 |
Anova
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 4,310.983 | 15.000 | 287.399 | 120.491 | 7.20 × 10−141 |
| B-D | 774.333 | 1.000 | 774.333 | 324.636 | 4.61 × 10−54 |
| C-v0 | 1,090.859 | 1.000 | 1,090.859 | 457.339 | 5.46 × 10−69 |
| D-h/D | 68.091 | 1.000 | 68.091 | 28.547 | 1.51× 10−7 |
| E-ψv | 212.918 | 1.000 | 212.918 | 89.265 | 2.53 × 10−19 |
| F-dp | 895.785 | 1.000 | 895.785 | 375.555 | 4.37 × 10−60 |
| G-TB | 30.432 | 1.000 | 30.432 | 12.759 | 3.96 × 10−4 |
| H-TFP | 126.656 | 1.000 | 126.656 | 53.100 | 1.61 × 10−12 |
| BE | 45.594 | 1.000 | 45.594 | 19.115 | 1.56 × 10−5 |
| BH | 24.903 | 1.000 | 24.903 | 10.441 | 1.33 × 10−3 |
| CE | 60.160 | 1.000 | 60.160 | 25.222 | 7.60 × 10−7 |
| CF | 60.995 | 1.000 | 60.995 | 25.572 | 6.40 × 10−7 |
| CH | 7.609 | 1.000 | 7.609 | 3.190 | 7.48 × 10−2 |
| DE | 48.806 | 1.000 | 48.806 | 20.462 | 7.95 × 10−6 |
| DF | 14.876 | 1.000 | 14.876 | 6.237 | 1.29 × 10−2 |
| EF | 13.973 | 1.000 | 13.973 | 5.858 | 1.59 × 10−2 |
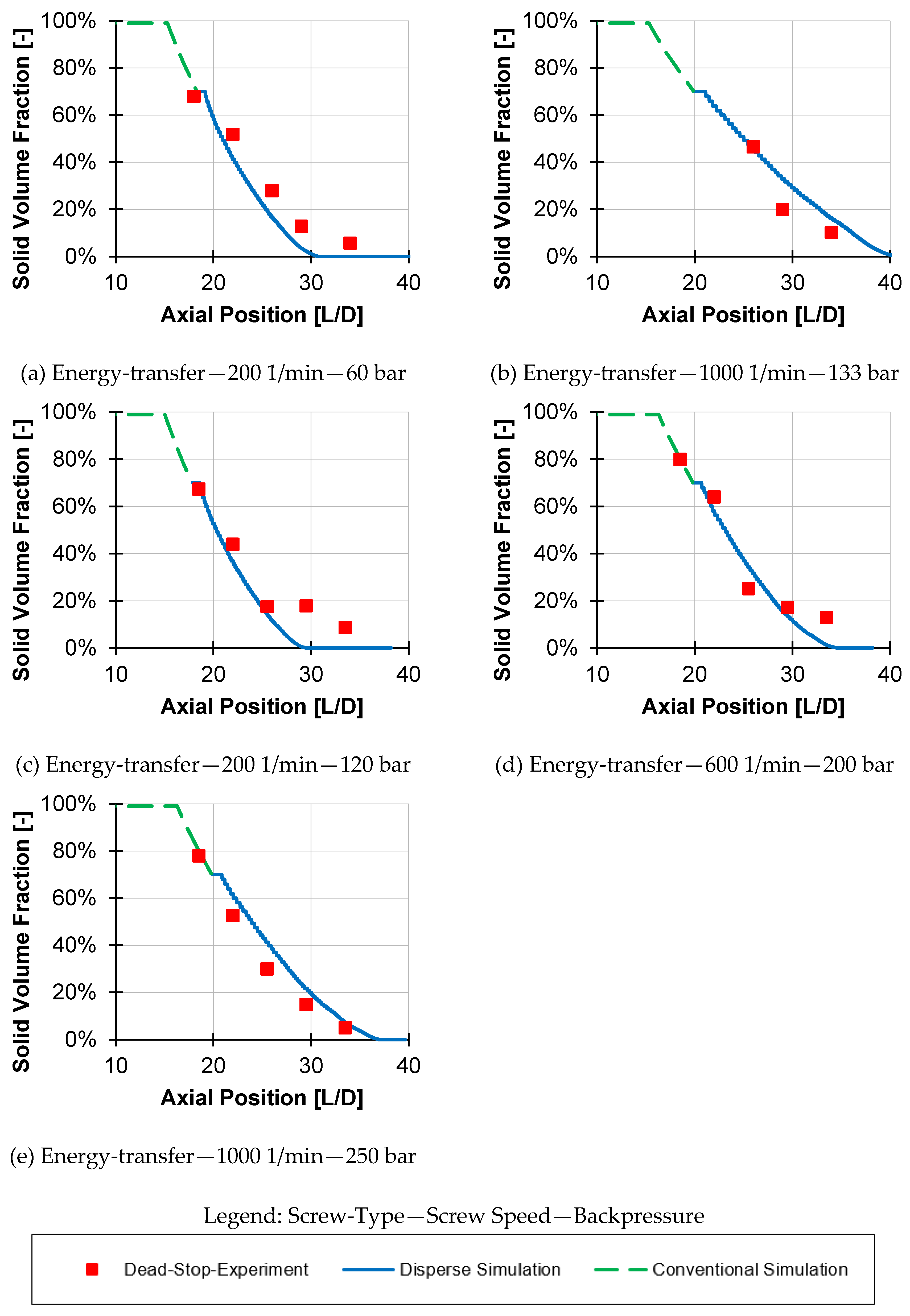
Appendix D: Results of Cooling/Pulling-Out Experiment
References
- Kruder, G.A. Extruder Screws. U.S. Patent 3,870,284, 11 March 1975. [Google Scholar]
- Hörmann, H. Theoretische und Experimentelle Betrachtung Schnelllaufender Einschneckenextruder. Ph.D. Thesis, Paderborn University, Paderborn, Germany, 2014. [Google Scholar]
- Pape, J. Grundlagen der Prozesssimulation von Einschneckenkonzepten zur Hochleistungsplastifizierung. Ph.D. Thesis, Paderborn University, Paderborn, Germany, 2006. [Google Scholar]
- Kruder, G.A. Extrusion Apparatus and Method. U.S. Patent 4,173,417, 06 November 1979. [Google Scholar]
- Chung, C. Extrusion of Polymers: Theory and Practice, 2nd ed.; Carl Hanser Verlag: Munich/Vienna, Germany, 2011. [Google Scholar]
- Heathe, W.R. Double Wave Screw. U.S. Patent 6,227,692, 08 May 2001. [Google Scholar]
- Hensen, F.; Knappe, W.; Potente, H. Handbuch der Kunststoff-Extrusionstechnik I–Grundlagen; Carl Hanser Verlag: Munich/Vienna, Germany, 1989. [Google Scholar]
- Chung, C.I.; Barr, R.A. Energy Efficient Extruder Screw. U.S. Patent 4,405,239A, 20 September 1983. [Google Scholar]
- Somers, S.A.; Spalding, M.A.; Dooley, J.; Hyun, K.S. An experimental study of the flows in an Energy Transfer Screw. In SPE ANTEC Technical Papers; Society of Plastics Engineers: San Francisco, CA, USA, 2002. [Google Scholar]
- Myers, J.A.; Ruberg, M.; Waterfield, R.; Elsass, M.; Kelsay, S. Experimental study of the energy efficiency of different screw designs for injection molding. In SPE ANTEC Technical Papers; Society of Plastics Engineers: Milwaukee, WI, USA, 2008. [Google Scholar]
- Anger, K.; Pape, J. Auf die Geometrie kommt es an–Extruder steigert Mischgüte. Plastverarbeiter 2006, 10, 126–128. [Google Scholar]
- Schneider, F.J.; Pape, J. Einschneckenextruder Mit Einem Genuteten Einzugssystem. EU-Patent EP 2838704 B1, 17 February 2016. [Google Scholar]
- Dörner, M.; Schöppner, V. Analysis of the advantageous Process and Mixing Behaviour of Wave-Dispersion Screws in Single Screw Extrusion. In Presented at the Society of Plastics Engineers’ ANTEC® 2020: The Virtual Edition; Society of Plastics Engineers: Brookfield, CT, USA, 2020. [Google Scholar]
- Marschik, C.; Dörner, M.; Roland, W.; Miethlinger, J.; Steinbichler, G.; Schöppner, V. Application of Network Analysis to Flow Systems with Alternating Wave Channels: Part A (Pressure Flows). Polymers 2019, 11, 1488. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marschik, C.; Dörner, M.; Roland, W.; Miethlinger, J.; Schöppner, V.; Steinbichler, G. Application of Network Analysis to Flow Systems with Alternating Wave Channels: Part B. Drag -Pressure Flows. Polymers 2020. planned/not yet released. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Potente, H. An Analytical Model of Partial and Thorough Melting in Single-screw Extruders. Int. Polym. Process. 1991, 4, 297–303. [Google Scholar] [CrossRef]
- Tadmor, Z. Fundamentals of Plasticating Extrusion. Polym. Eng. Sci. 1966, 7, 185–190. [Google Scholar] [CrossRef]
- Huang, H. A Study on the Dispersive Melting Mechanism of Polymers in an Extruder. Unpublished Master’s Thesis, South China University of Technology, Guangzhou, China, 1989. [Google Scholar]
- Peng, Y.; Huang, H. A Study of the Dispersive Melting Mechanism of Polymers in an Extruder. In Proceedings of the Annual Meeting of Polym. Process. Soc. 6, Paper 04-19, Nice, France, 17–20 April 1990. [Google Scholar]
- Huang, H.; Peng, Y. Theoretical Modeling of Dispersive Melting Mechanism of Polymers in an Extruder. Adv. Polym. Technol. 1993, 12, 343–352. [Google Scholar] [CrossRef]
- Rauwendaal, C. Comparison of two melting models. Adv. Polym. Technol. 1996, 2, 135–144. [Google Scholar] [CrossRef]
- Thümen, A. Disperses Aufschmelzen in Doppelschneckenextrudern. Ph.D. Thesis, Paderborn University, Paderborn, Germany, 2008. [Google Scholar]
- Chung, C.I.; Barr, R.A. A Novel Energy Efficient Screw Design. In SPE ANTEC Technical Papers; Society of Plastics Engineers: Chicago, IL, USA, 1983. [Google Scholar]
- Tadmor, Z.; Gogos, G. Principles of Polymer Processing; John Wiley & Sons: New York, NY, USA; Brisbane, Australia; Chichester, UK; Toronto, ON, Canada, 1979. [Google Scholar]
- Lakemeyer, C. Temperaturberechnung Intern Innentemperierter Einschnecken. Ph.D. Thesis, Paderborn University, Paderborn, Germany, 2015. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Oxford University Press: Oxford, UK, 1973. [Google Scholar]
- Raasch, J. Beanspruchung und Verhalten Suspendierter Feststoffteilchen in Scherströmungen hoher Zähigkeit. Ph.D. Thesis, Technische Hochschule Karlsruhe, Karlsruhe, Germany, 1961. [Google Scholar]
- Potente, H.; Melisch, U. Theoretical and Experimental Investigations of the Melt Pellets in Co-Rotating Twin-Screw Extruders. Int. Polym. Process. 1996, 2, 101–108. [Google Scholar] [CrossRef]
- Maron, S.H.; Pierce, P.E. Application of ree-eyring generalized flow-theory to suspensions of spherical particles. J. Colloid Interface Sci. 1956, 1, 80–95. [Google Scholar] [CrossRef]
- Mooney, M. The viscosity of a concentrated suspension of spherical particles. J. Colloid Interface Sci. 1951, 2, 162–170. [Google Scholar] [CrossRef]
- Rauwendaal, C. Polymer Extrusion, 5th ed.; Carl Hanser Verlag: Munich/Vienna, Germany, 2014. [Google Scholar]
- VDI-Wärmeatlas, 11th ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2013.
- Erdmann, R.G. Finite-Difference Solution to the 2-D Heat Equation, Lecture, University of Arizona, USA, 2009. Available online: http://www.u.arizona.edu/~erdmann/mse350/_downloads/2D_heat_equation.pdf (accessed on 7 April 2020).
- Potente, H.; Lutterbeck, J.; Menges, G. Scale-Up of Single Screw Extruders. In SPE ANTEC Technical Papers; Society of Plastics Engineers: Boston, MA, USA, 1981. [Google Scholar]
- Schall, C. Simulative und experimentelle Untersuchung des Prozessverhaltens von Wave-Schnecken Gegenüber einer 3-Zonen- und Barriereschnecke. Unpublished Master‘s Thesis, Paderborn University, Paderborn, Germany, 2019. [Google Scholar]
- Altinkaynak, A.; Gupta, M.; Spalding, M.A. Melting in a Single Screw Extruder – Experiments and 3D Finite Element Simulations. Int. Polym. Process. 2011, 2, 182–197. [Google Scholar] [CrossRef]
- Michaeli, W.; Hopmann, C.; Grammel, S. A Fully Three Dimensional Numerical Approach Simulating the Melting Zone in a Single-Screw-Extruder. In SPE ANTEC Technical Papers; Society of Plastics Engineers: Orlando, FL, USA, 2012. [Google Scholar]
- Karrenberg, G. Einsatz innovativer Simulationstechniken zur Entwicklung eines High-Speed-Extrusionskonzeptes auf Basis von Feststoff-Schmelze-Trennung. Ph.D. Thesis, University of Duisburg-Essen, Duisburg, Germany, 2016. [Google Scholar]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dörner, M.; Marschik, C.; Schöppner, V.; Steinbichler, G. Development of an Analytical Model to Describe the Disperse Melting in Wave-Dispersion Screws. Polymers 2020, 12, 946. https://doi.org/10.3390/polym12040946
Dörner M, Marschik C, Schöppner V, Steinbichler G. Development of an Analytical Model to Describe the Disperse Melting in Wave-Dispersion Screws. Polymers. 2020; 12(4):946. https://doi.org/10.3390/polym12040946
Chicago/Turabian StyleDörner, Marius, Christian Marschik, Volker Schöppner, and Georg Steinbichler. 2020. "Development of an Analytical Model to Describe the Disperse Melting in Wave-Dispersion Screws" Polymers 12, no. 4: 946. https://doi.org/10.3390/polym12040946
APA StyleDörner, M., Marschik, C., Schöppner, V., & Steinbichler, G. (2020). Development of an Analytical Model to Describe the Disperse Melting in Wave-Dispersion Screws. Polymers, 12(4), 946. https://doi.org/10.3390/polym12040946