Motion of an Elastic Capsule in a Trapezoidal Microchannel under Stokes Flow Conditions
Abstract
1. Introduction
2. Problem Description
2.1. Fluid Dynamics
2.2. Membrane Dynamics
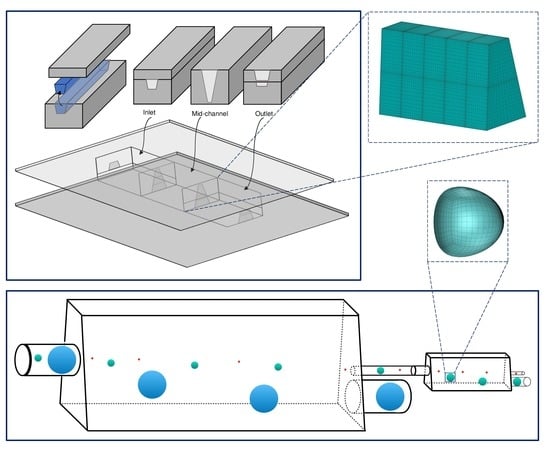
2.3. Computational Methodology
3. Results
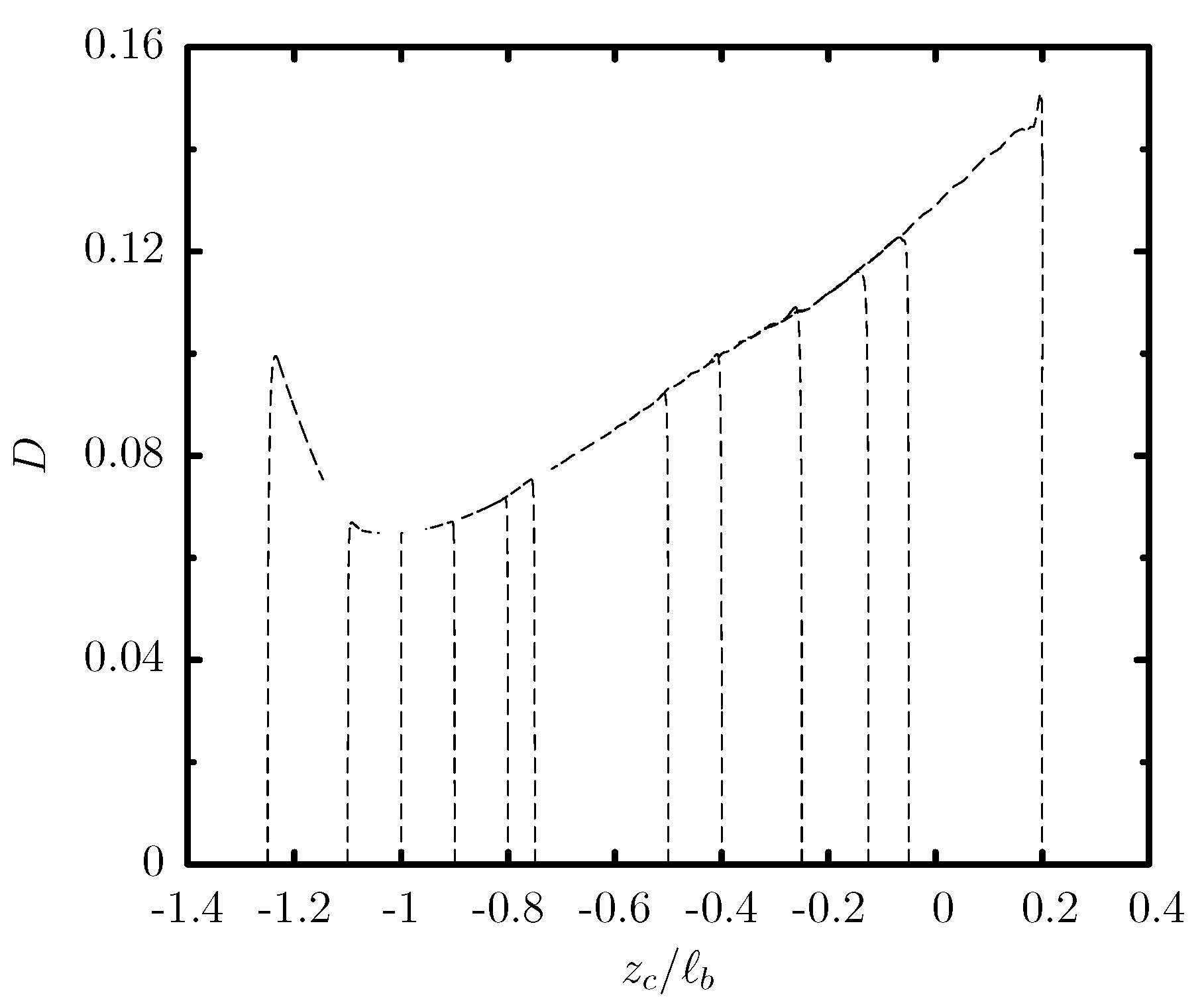
3.1. Capsule Migration from Different Initial Positions
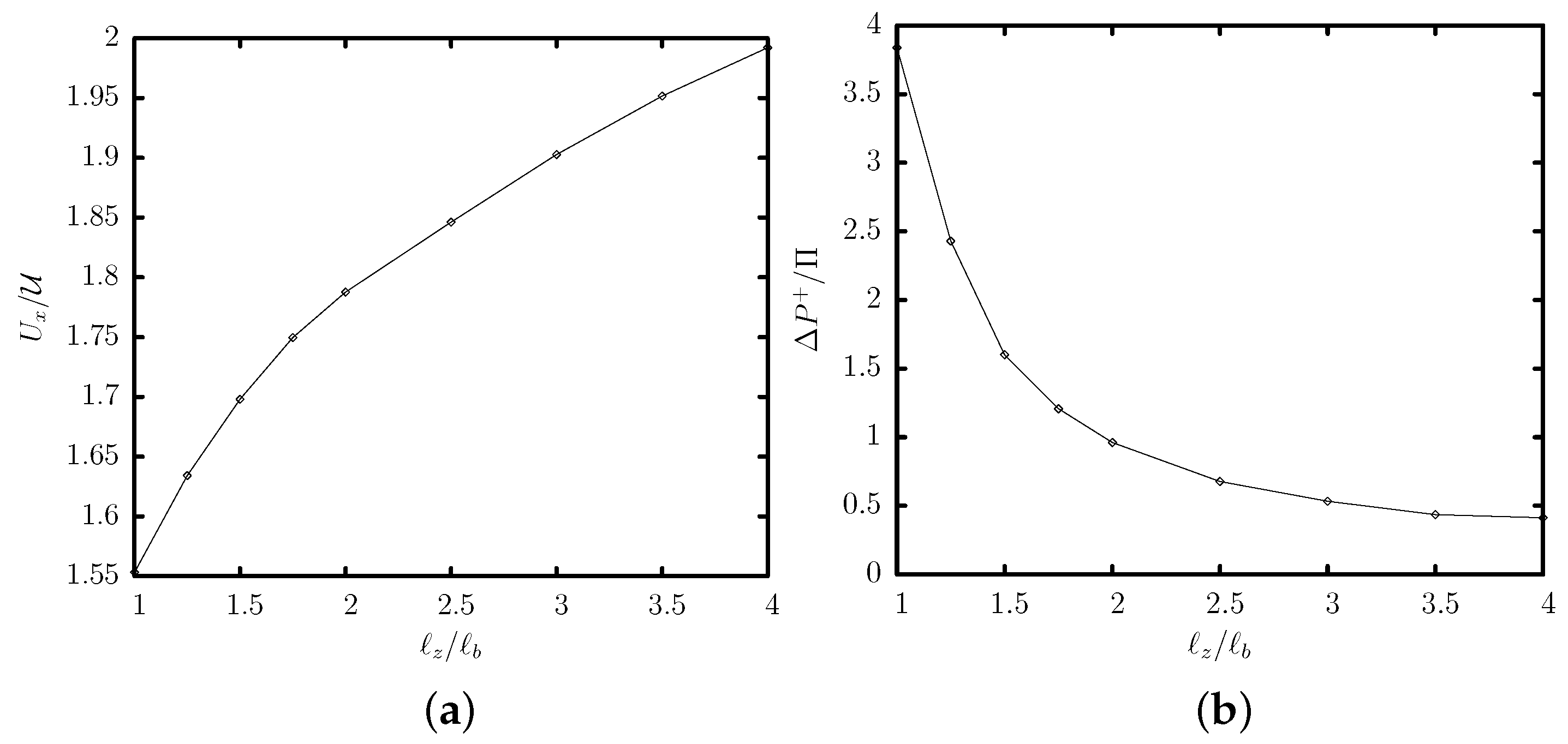
3.2. Effects of the Channel Geometry and Capsule Size
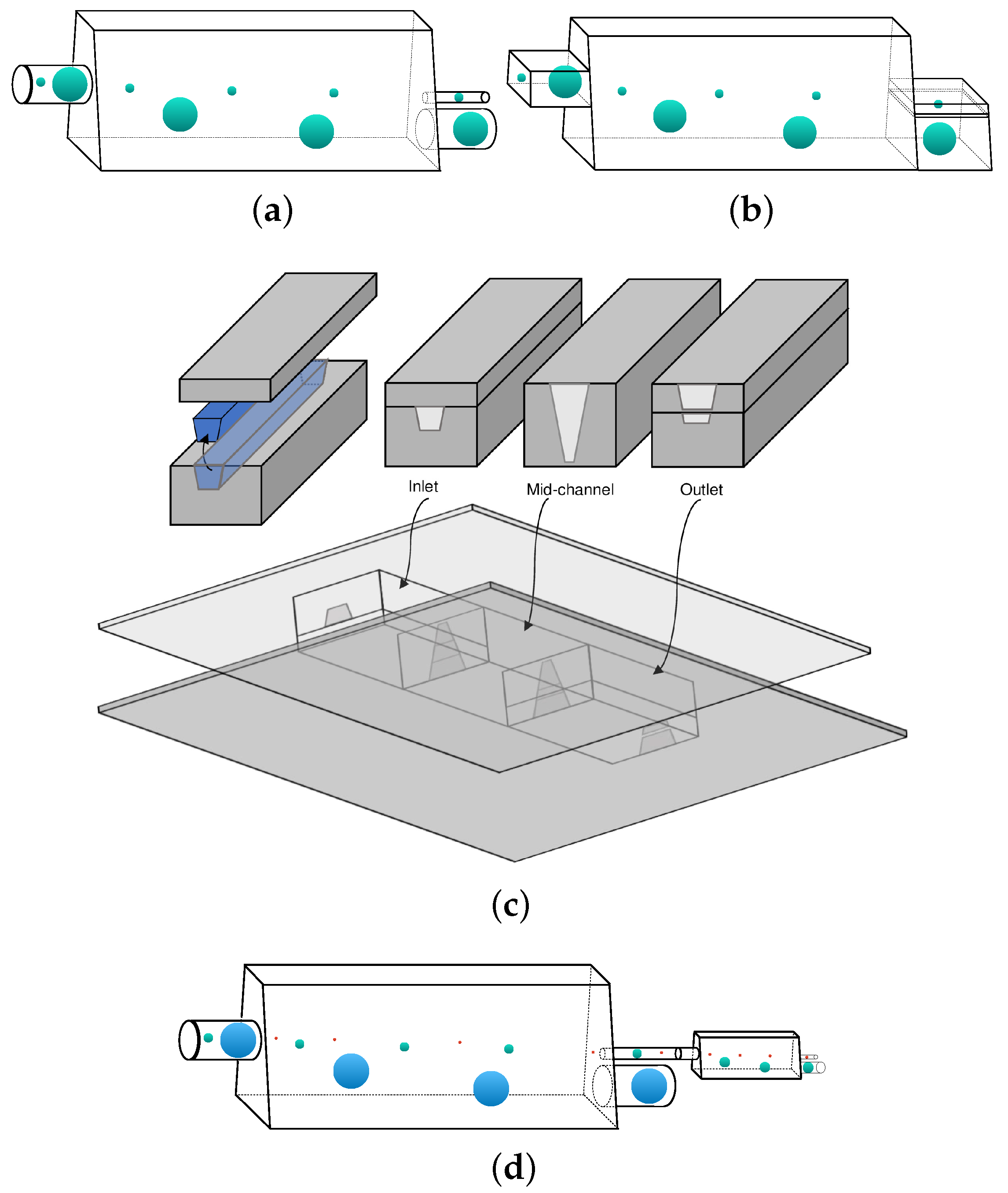
3.3. Design of A Capsule Sorting Microdevice
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Coupier, G.; Farutin, A.; Minetti, C.; Podgorski, T.; Misbah, C. Shape diagram of vesicles in Poiseuille flow. Phys. Rev. Lett. 2012, 108, 178106. [Google Scholar] [CrossRef] [PubMed]
- Yow, H.N.; Routh, A.F. Formation of liquid core–polymer shell microcapsules. Soft Matter 2006, 2, 940–949. [Google Scholar] [CrossRef]
- Chen, P.W.; Erb, R.M.; Studart, A.R. Designer polymer-based microcapsules made using microfluidics. Langmuir 2012, 28, 144–152. [Google Scholar] [CrossRef] [PubMed]
- Jeoffroy, E.; Demirors, A.F.; Schwendimann, P.; Dos Santos, S.; Danzi, S.; Hauser, A.; Partl, M.N.; Studart, A.R. One-Step Bulk Fabrication of Polymer-Based Microcapsules with Hard–Soft Bilayer Thick Shells. ACS Appl. Mater. Interfaces 2017, 9, 37364–37373. [Google Scholar] [CrossRef]
- Abkarian, M.; Faivre, M.; Horton, R.; Smistrup, K.; Best-Popescu, C.A.; Stone, H.A. Cellular-scale hydrodynamics. Biomed. Mater. 2008, 3, 034011. [Google Scholar] [CrossRef]
- Alexeev, A.; Balazs, A.C. Designing smart systems to selectively entrap and burst microcapsules. Soft Matter 2007, 3, 1500–1505. [Google Scholar] [CrossRef]
- Popel, A.S.; Johnson, P.C. Microcirculation and hemorheology. Annu. Rev. Fluid Mech. 2005, 37, 43–69. [Google Scholar] [CrossRef]
- Antia, M.; Herricks, T.; Rathod, P.K. Microfluidic Modeling of Cell-Cell Interactions in Malaria Pathogenesis. PLoS Pathog. 2007, 3, e99. [Google Scholar] [CrossRef]
- Shelby, J.P.; White, J.; Ganesan, K.; Rathod, P.K.; Chiu, D.T. A microfluidic model for single-cell capillary obstruction by Plasmodium falciparum-infected erythrocytes. Proc. Natl. Acad. Sci. USA 2003, 100, 14618–14622. [Google Scholar] [CrossRef]
- Fedosov, D.A.; Lei, H.; Caswell, B.; Suresh, S.; Karniadakis, G.E. Multiscale modeling of red blood cell mechanics and blood flow in malaria. PLoS Comput. Biol. 2011, 7, e1002270. [Google Scholar] [CrossRef]
- Braunmüller, S.; Schmid, L.; Franke, T. Dynamics of red blood cells and vesicles in microchannels of oscillating width. J. Phys. Condens. Matter 2011, 23, 184116. [Google Scholar] [CrossRef] [PubMed]
- Kuriakose, S.; Dimitrakopoulos, P. Deformation of an elastic capsule in a rectangular microfluidic channel. Soft Matter 2013, 9, 4284–4296. [Google Scholar] [CrossRef] [PubMed]
- McWhirter, J.L.; Noguchi, H.; Gompper, G. Flow-induced clustering and alignment of vesicles and red blood cells in microcapillaries. Proc. Natl. Acad. Sci. USA 2009, 106, 6039–6043. [Google Scholar] [CrossRef] [PubMed]
- Lefebvre, Y.; Barthes-Biesel, D. Motion of a capsule in a cylindrical tube: Effect of membrane pre-stress. J. Fluid Mech. 2007, 589, 157–181. [Google Scholar] [CrossRef]
- Kuriakose, S.; Dimitrakopoulos, P. Motion of an elastic capsule in a square microfluidic channel. Phys. Rev. E 2011, 84, 011906. [Google Scholar] [CrossRef]
- Hu, X.Q.; Sévénié, B.; Salsac, A.V.; Leclerc, E.; Barthès-Biesel, D. Characterizing the membrane properties of capsules flowing in a square-section microfluidic channel: Effects of the membrane constitutive law. Phys. Rev. E 2013, 87, 063008. [Google Scholar] [CrossRef]
- Koolivand, A.; Dimitrakopoulos, P. Deformation of an elastic capsule in a microfluidic T-junction: Settling shape and moduli determination. Microfluid. Nanofluidics 2017, 21, 89. [Google Scholar] [CrossRef]
- Hou, H.W.; Bhagat, A.A.S.; Chong, A.G.L.; Mao, P.; Tan, K.S.W.; Han, J.; Lim, C.T. Deformability based cell margination—a simple microfluidic design for malaria-infected erythrocyte separation. Lab Chip 2010, 10, 2605–2613. [Google Scholar] [CrossRef]
- Bhagat, A.A.S.; Bow, H.; Hou, H.W.; Tan, S.J.; Han, J.; Lim, C.T. Microfluidics for cell separation. Med. Biol. Eng. Comput. 2010, 48, 999–1014. [Google Scholar] [CrossRef]
- Lee, M.G.; Shin, J.H.; Bae, C.Y.; Choi, S.; Park, J.K. Label-free cancer cell separation from human whole blood using inertial microfluidics at low shear stress. Anal. Chem. 2013, 85, 6213–6218. [Google Scholar] [CrossRef]
- Doddi, S.K.; Bagchi, P. Lateral migration of a capsule in a plane Poiseuille flow in a channel. Int. J. Multiph. Flow 2008, 34, 966–986. [Google Scholar] [CrossRef]
- Li, H.; Ma, G. Modeling performance of a two-dimensional capsule in a microchannel flow: Long-term lateral migration. Phys. Rev. E 2010, 82, 026304. [Google Scholar] [CrossRef] [PubMed]
- Kilimnik, A.; Mao, W.; Alexeev, A. Inertial migration of deformable capsules in channel flow. Phys. Fluids 2011, 23, 123302. [Google Scholar] [CrossRef]
- Singh, R.K.; Li, X.; Sarkar, K. Lateral migration of a capsule in plane shear near a wall. J. Fluid Mech. 2014, 739, 421–443. [Google Scholar] [CrossRef]
- Qi, Q.M.; Shaqfeh, E.S. Theory to predict particle migration and margination in the pressure-driven channel flow of blood. Phys. Rev. Fluids 2017, 2, 093102. [Google Scholar] [CrossRef]
- Raffiee, A.H.; Dabiri, S.; Ardekani, A.M. Elasto-inertial migration of deformable capsules in a microchannel. Biomicrofluidics 2017, 11, 064113. [Google Scholar] [CrossRef]
- Hao, P.F.; He, F.; Zhu, K.Q. Flow characteristics in a trapezoidal silicon microchannel. J. Micromech. Microeng. 2005, 15, 1362. [Google Scholar] [CrossRef]
- Guan, G.; Wu, L.; Bhagat, A.A.; Li, Z.; Chen, P.C.; Chao, S.; Ong, C.J.; Han, J. Spiral microchannel with rectangular and trapezoidal cross-sections for size based particle separation. Sci. Rep. 2013, 3, 1475. [Google Scholar] [CrossRef]
- Wu, L.; Guan, G.; Hou, H.W.; Bhagat, A.A.S.; Han, J. Separation of leukocytes from blood using spiral channel with trapezoid cross-section. Anal. Chem. 2012, 84, 9324–9331. [Google Scholar] [CrossRef]
- Kim, J.A.; Lee, J.; Wu, C.; Nam, S.; Di Carlo, D.; Lee, W. Inertial focusing in non-rectangular cross-section microchannels and manipulation of accessible focusing positions. Lab Chip 2016, 16, 992–1001. [Google Scholar] [CrossRef]
- Moloudi, R.; Oh, S.; Yang, C.; Warkiani, M.E.; Naing, M.W. Inertial particle focusing dynamics in a trapezoidal straight microchannel: Application to particle filtration. Microfluid. Nanofluidics 2018, 22, 33. [Google Scholar] [CrossRef]
- Koolivand, A.; Shahrokhi, M.; Farahzadi, H. Optimal control of molecular weight and particle size distributions in a batch suspension polymerization reactor. Iran. Polym. J. 2019, 28, 735–745. [Google Scholar] [CrossRef]
- Tian, G.; Koolivand, A.; Arden, N.S.; Lee, S.; O’Connor, T.F. Quality risk assessment and mitigation of pharmaceutical continuous manufacturing using flowsheet modeling approach. Comput. Chem. Eng. 2019, 129, 106508. [Google Scholar] [CrossRef]
- Dimitrakopoulos, P.; Higdon, J. On the displacement of three-dimensional fluid droplets from solid surfaces in low-Reynolds-number shear flows. J. Fluid Mech. 1998, 377, 189–222. [Google Scholar] [CrossRef]
- Wang, Y.; Dimitrakopoulos, P. A three-dimensional spectral boundary element algorithm for interfacial dynamics in Stokes flow. Phys. Fluids 2006, 18, 082106. [Google Scholar] [CrossRef]
- Tsai, T.; Miksis, M.J. Dynamics of a drop in a constricted capillary tube. J. Fluid Mech. 1994, 274, 197–217. [Google Scholar] [CrossRef]
- Borhan, A.; Pallinti, J. Buoyancy-driven motion of viscous drops through cylindrical capillaries at small Reynolds numbers. Ind. Eng. Chem. Res. 1995, 34, 2750–2761. [Google Scholar] [CrossRef]
- Coulliette, C.; Pozrikidis, C. Motion of an array of drops through a cylindrical tube. J. Fluid Mech. 1998, 358, 1–28. [Google Scholar] [CrossRef]
- Skalak, R.; Tozeren, A.; Zarda, R.; Chien, S. Strain energy function of red blood cell membranes. Biophys. J. 1973, 13, 245. [Google Scholar] [CrossRef]
- Barthes-Biesel, D.; Diaz, A.; Dhenin, E. Effect of constitutive laws for two-dimensional membranes on flow-induced capsule deformation. J. Fluid Mech. 2002, 460, 211–222. [Google Scholar] [CrossRef]
- Park, S.Y.; Dimitrakopoulos, P. Transient dynamics of an elastic capsule in a microfluidic constriction. Soft Matter 2013, 9, 8844–8855. [Google Scholar] [CrossRef] [PubMed]
- Pozrikidis, C. Modeling and Simulation of Capsules and Biological Cells; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Lac, E.; Barthes-Biesel, D.; Pelekasis, N.; Tsamopoulos, J. Spherical capsules in three-dimensional unbounded Stokes flows: Effect of the membrane constitutive law and onset of buckling. J. Fluid Mech. 2004, 516, 303–334. [Google Scholar] [CrossRef]
- Dodson, W.R.; Dimitrakopoulos, P. Dynamics of strain-hardening and strain-softening capsules in strong planar extensional flows via an interfacial spectral boundary element algorithm for elastic membranes. J. Fluid Mech. 2009, 641, 263–296. [Google Scholar] [CrossRef][Green Version]
- Dimitrakopoulos, P. Analysis of the variation in the determination of the shear modulus of the erythrocyte membrane: Effects of the constitutive law and membrane modeling. Phys. Rev. E 2012, 85, 041917. [Google Scholar] [CrossRef] [PubMed]
- Timoshenko, S.P.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Dodson, W.R., III; Dimitrakopoulos, P. Spindles, cusps, and bifurcation for capsules in Stokes flow. Phys. Rev. Lett. 2008, 101, 208102. [Google Scholar] [CrossRef] [PubMed]
- Dimitrakopoulos, P.; Kuriakose, S. Determining a membrane’s shear modulus, independent of its area-dilatation modulus, via capsule flow in a converging micro-capillary. Soft Matter 2015, 11, 2782–2793. [Google Scholar] [CrossRef]
- Leclerc, E.; Kinoshita, H.; Fujii, T.; Barthès-Biesel, D. Transient flow of microcapsules through convergent–divergent microchannels. Microfluid. Nanofluidics 2012, 12, 761–770. [Google Scholar] [CrossRef]
- de Loubens, C.; Deschamps, J.; Boedec, G.; Leonetti, M. Stretching of capsules in an elongation flow, a route to constitutive law. J. Fluid Mech. 2015, 767, R3. [Google Scholar] [CrossRef]
- Farutin, A.; Misbah, C. Analytical and numerical study of three main migration laws for vesicles under flow. Phys. Rev. Lett. 2013, 110, 108104. [Google Scholar] [CrossRef]
- Magnaudet, J.; Takagi, S.; Legendre, D. Drag, deformation and lateral migration of a buoyant drop moving near a wall. J. Fluid Mech. 2003, 476, 115–157. [Google Scholar] [CrossRef]
- Utada, A.; Lorenceau, E.; Link, D.; Kaplan, P.; Stone, H.; Weitz, D. Monodisperse double emulsions generated from a microcapillary device. Science 2005, 308, 537–541. [Google Scholar] [CrossRef] [PubMed]
- Duncanson, W.J.; Lin, T.; Abate, A.R.; Seiffert, S.; Shah, R.K.; Weitz, D.A. Microfluidic synthesis of advanced microparticles for encapsulation and controlled release. Lab Chip 2012, 12, 2135–2145. [Google Scholar] [CrossRef] [PubMed]
- Wyss, H.M.; Franke, T.; Mele, E.; Weitz, D.A. Capillary micromechanics: Measuring the elasticity of microscopic soft objects. Soft Matter 2010, 6, 4550–4555. [Google Scholar] [CrossRef]
- Guckenberger, D.J.; de Groot, T.E.; Wan, A.M.; Beebe, D.J.; Young, E.W. Micromilling: A method for ultra-rapid prototyping of plastic microfluidic devices. Lab Chip 2015, 15, 2364–2378. [Google Scholar] [CrossRef] [PubMed]
- Lefebvre, Y.; Leclerc, E.; Barthès-Biesel, D.; Walter, J.; Edwards-Lévy, F. Flow of artificial microcapsules in microfluidic channels: A method for determining the elastic properties of the membrane. Phys. Fluids 2008, 20, 123102. [Google Scholar] [CrossRef]
- Bai, B.F.; Luo, Z.Y.; Wang, S.Q.; He, L.; Lu, T.J.; Xu, F. Inertia effect on deformation of viscoelastic capsules in microscale flows. Microfluid. Nanofluidics 2013, 14, 817–829. [Google Scholar] [CrossRef]
- Carroll, R.M.; Gupta, N.R. Inertial effects on the flow of capsules in cylindrical channels. Int. J. Multiph. Flow 2016, 87, 114–123. [Google Scholar] [CrossRef]
- Chen, Y.; Li, P.; Huang, P.H.; Xie, Y.; Mai, J.D.; Wang, L.; Nguyen, N.T.; Huang, T.J. Rare cell isolation and analysis in microfluidics. Lab Chip 2014, 14, 626–645. [Google Scholar] [CrossRef]
- Shields IV, C.W.; Reyes, C.D.; López, G.P. Microfluidic cell sorting: A review of the advances in the separation of cells from debulking to rare cell isolation. Lab Chip 2015, 15, 1230–1249. [Google Scholar] [CrossRef]
- Chasis, J.; Agre, P.; Mohandas, N. Decreased membrane mechanical stability and in vivo loss of surface area reflect spectrin deficiencies in hereditary spherocytosis. J. Clin. Investig. 1988, 82, 617–623. [Google Scholar] [CrossRef]
- Suresh, S. Mechanical response of human red blood cells in health and disease: Some structure-property-function relationships. J. Mater. Res. 2006, 21, 1871–1877. [Google Scholar] [CrossRef]
- Da Costa, L.; Mohandas, N.; Sorette, M.; Grange, M.J.; Tchernia, G.; Cynober, T. Temporal differences in membrane loss lead to distinct reticulocyte features in hereditary spherocytosis and in immune hemolytic anemia. Blood 2001, 98, 2894–2899. [Google Scholar] [CrossRef] [PubMed]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koolivand, A.; Dimitrakopoulos, P. Motion of an Elastic Capsule in a Trapezoidal Microchannel under Stokes Flow Conditions. Polymers 2020, 12, 1144. https://doi.org/10.3390/polym12051144
Koolivand A, Dimitrakopoulos P. Motion of an Elastic Capsule in a Trapezoidal Microchannel under Stokes Flow Conditions. Polymers. 2020; 12(5):1144. https://doi.org/10.3390/polym12051144
Chicago/Turabian StyleKoolivand, Abdollah, and Panagiotis Dimitrakopoulos. 2020. "Motion of an Elastic Capsule in a Trapezoidal Microchannel under Stokes Flow Conditions" Polymers 12, no. 5: 1144. https://doi.org/10.3390/polym12051144
APA StyleKoolivand, A., & Dimitrakopoulos, P. (2020). Motion of an Elastic Capsule in a Trapezoidal Microchannel under Stokes Flow Conditions. Polymers, 12(5), 1144. https://doi.org/10.3390/polym12051144