Study on Cellulose Acetate Butyrate/Plasticizer Systems by Molecular Dynamics Simulation and Experimental Characterization
Abstract
1. Introduction
2. MD Simulation
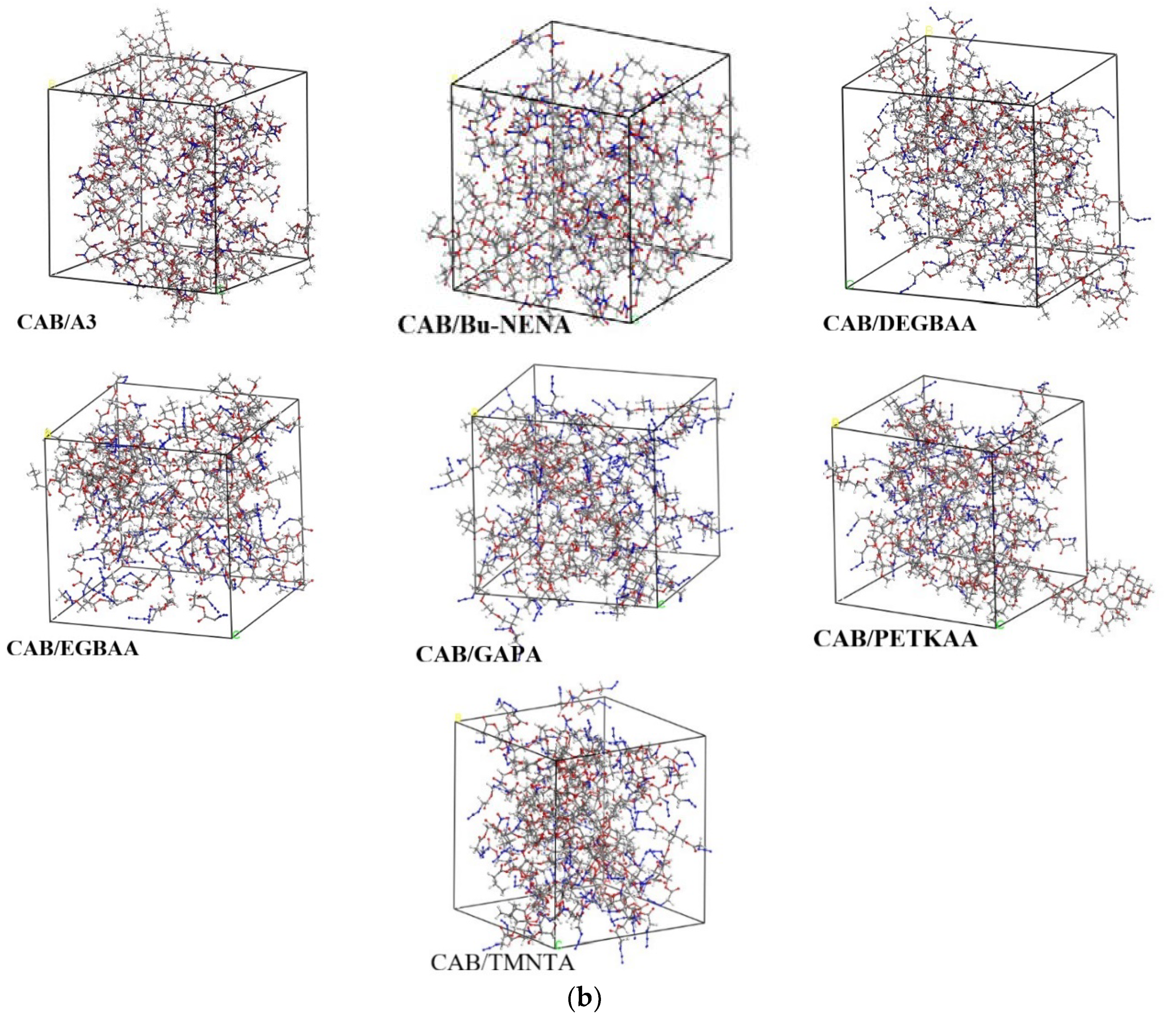
2.1. Construction of Models
2.2. Calculations
3. Experiments and Characterization
3.1. Materials
3.2. Preparation of CAB/Plasticizer Mixed Systems
3.3. Characterizations
4. Results and Discussion
4.1. MD Simulation
4.1.1. Solubility Parameter
4.1.2. Binding Energy
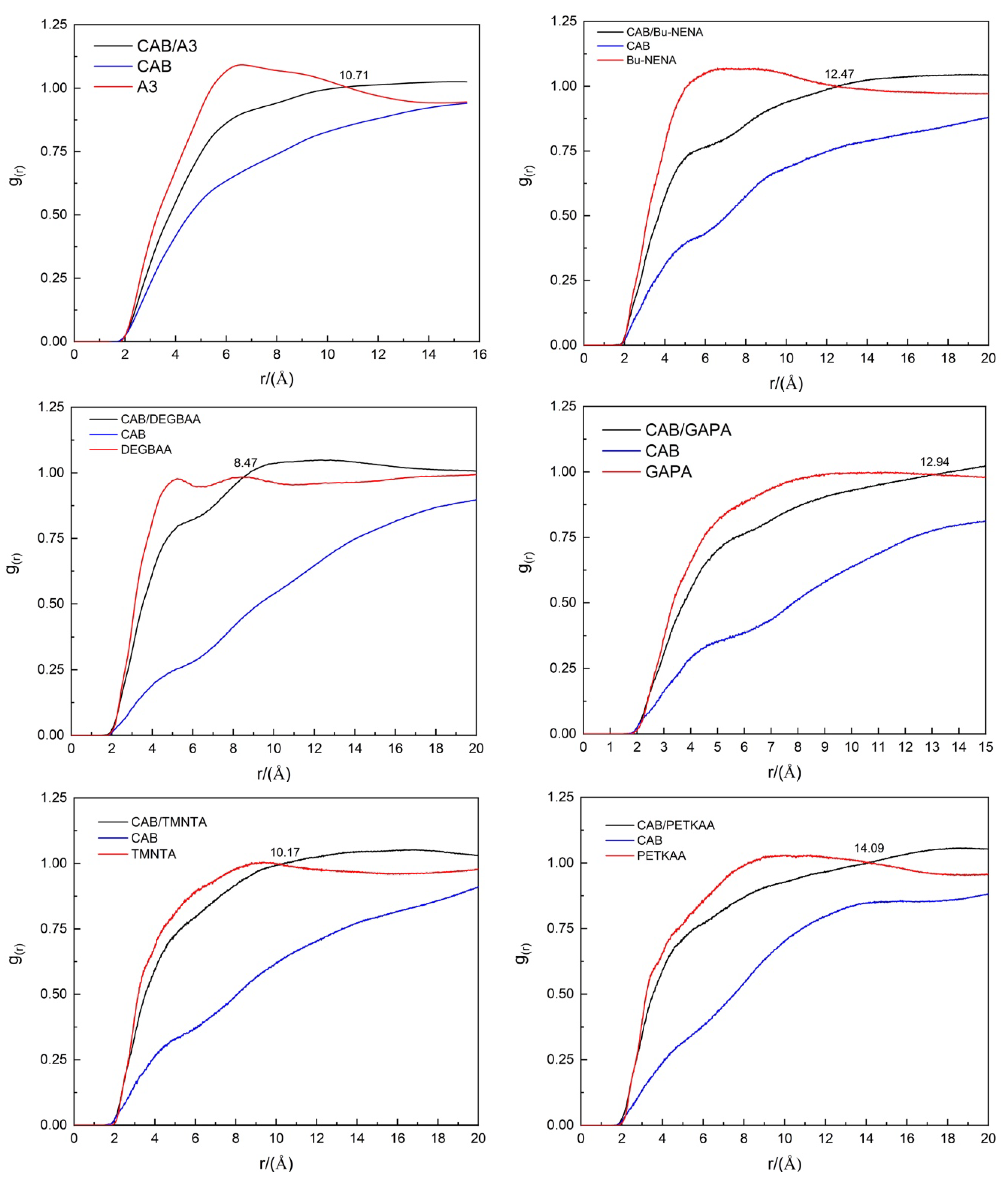
4.1.3. Radial Distribution Function (RDF)
4.1.4. Simulation of Mechanical Properties
4.2. Experimental Characterization
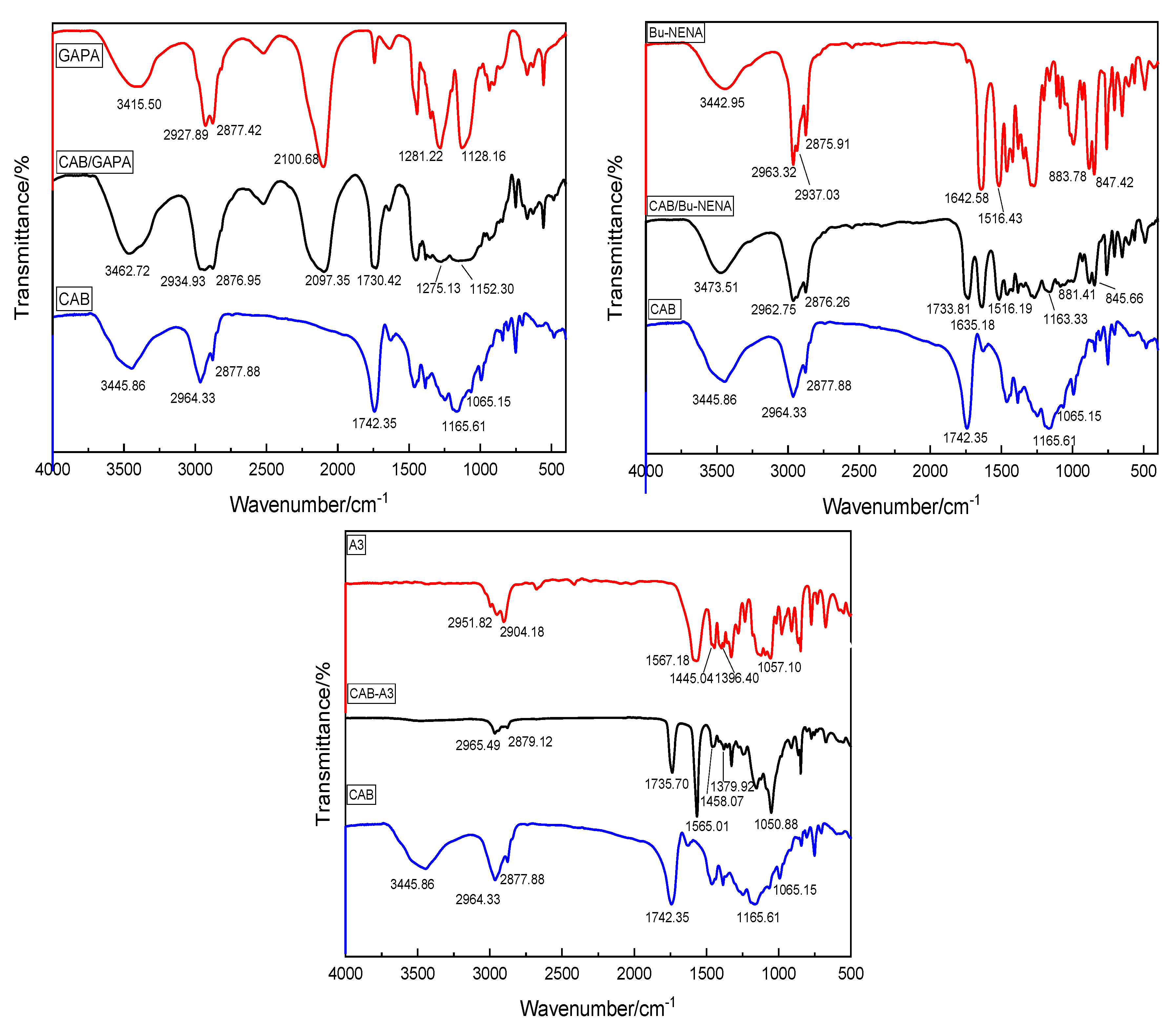
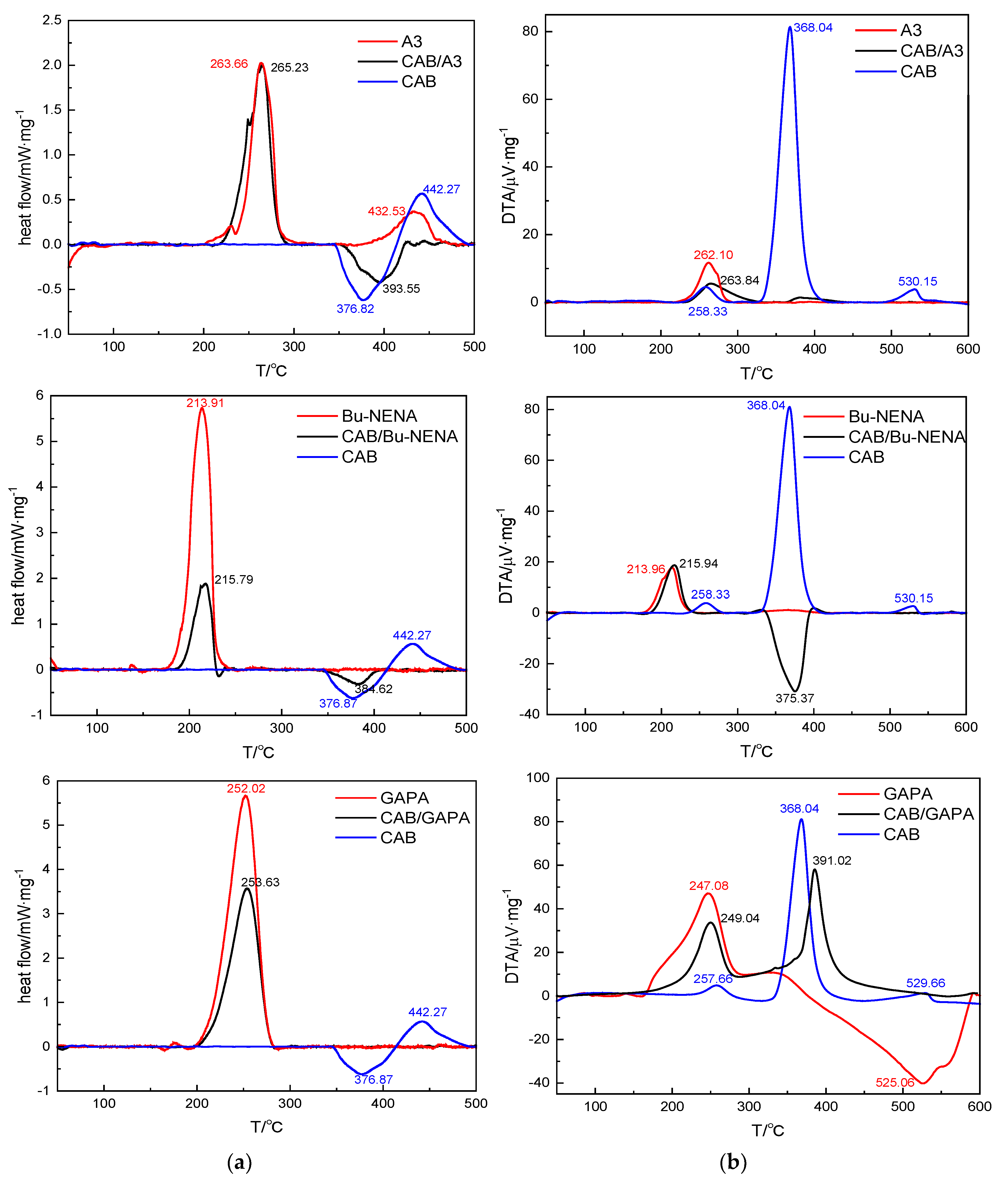
4.2.1. Chemical Stability
4.2.2. Compatibility
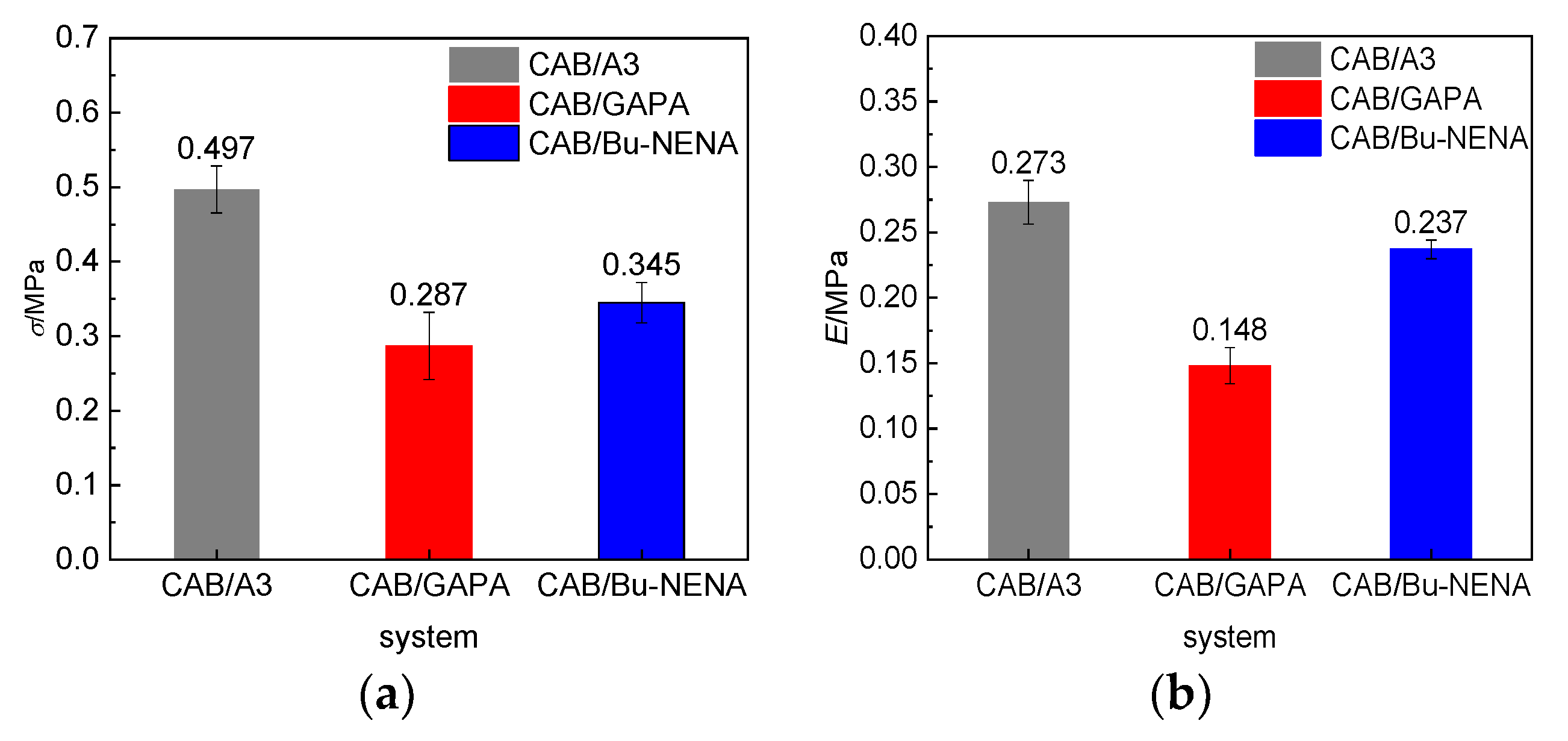
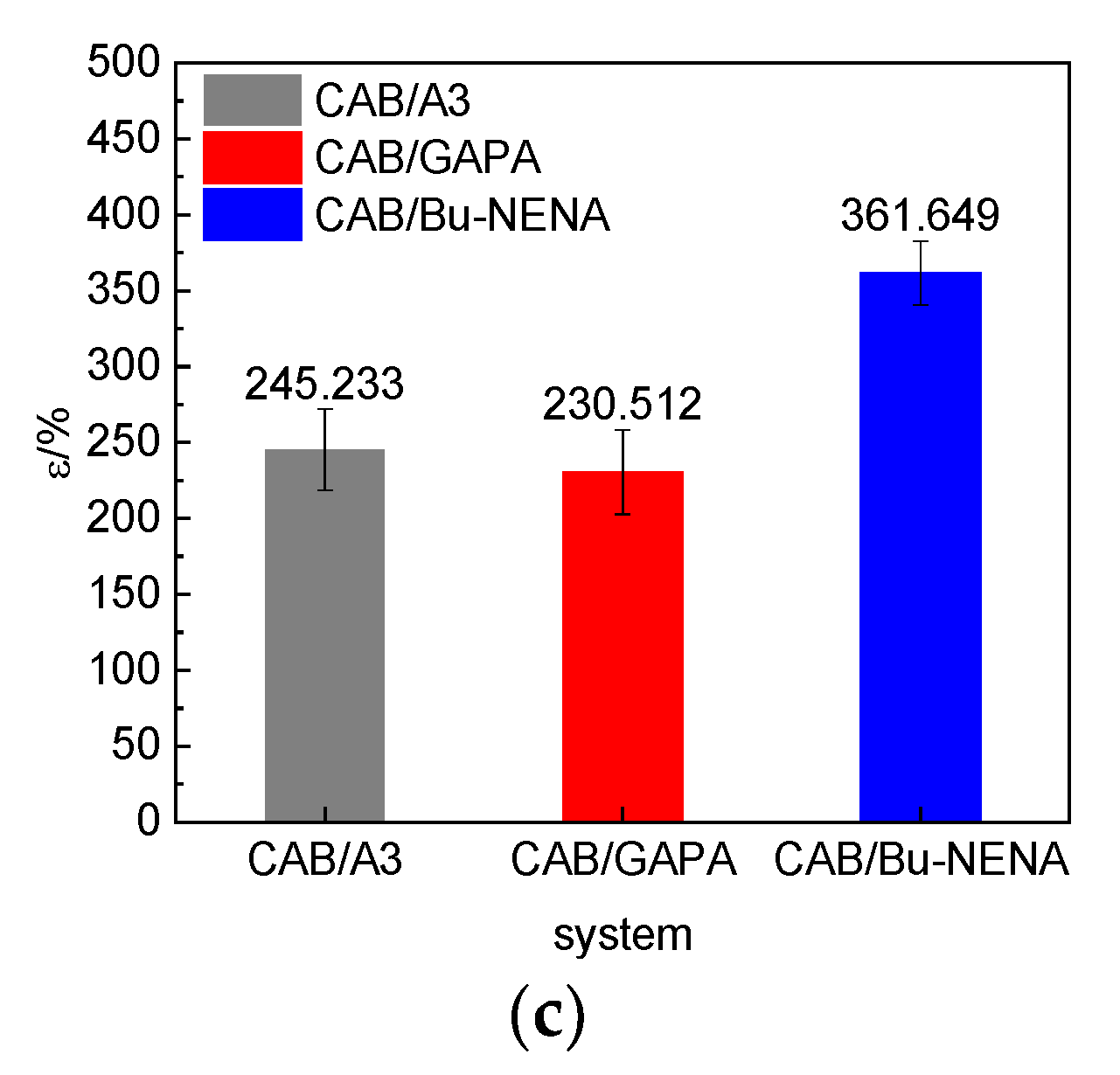
4.2.3. Mechanical Properties
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Podshivalov, A.; Besson, F.; Budtova, T.; Bronnikov, S. Morphology and improved impact strength of cellulose acetate butyrate blended with polyethylene copolymer. eXPRESS Polym. Lett. 2018, 12, 856–866. [Google Scholar] [CrossRef]
- Li, X.; Chen, S.; Wang, X.; Shang, F.; Dong, W.; Yu, Z.; Yu, Y.; Zou, H.; Jin, S.; Chen, Y. Effect of polymer binders on safety and detonation properties of ε-CL-20-based pressed-polymer-bonded explosives. Mater. Express 2017, 7, 209–215. [Google Scholar] [CrossRef]
- Lan, G.; Jin, S.; Jing, B.; Chen, Y.; Wang, D.; Li, J.; Wang, N.; Chen, M. Investigation into the Temperature Adaptability of HNIW-based PBXs. Propellants Explos. Pyrotech. 2019, 44, 327–336. [Google Scholar] [CrossRef]
- Dandekar, A.; Roberts, Z.A.; Paulson, S.; Chen, W.; Son, S.F.; Koslowski, M. The effect of the particle surface and binder properties on the response of polymer bonded explosives at low impact velocities. Comput. Mater. Sci. 2019, 166, 170–178. [Google Scholar] [CrossRef]
- Badgujar, D.; Talawar, M.; Zarko, V.; Mahulikar, P. New directions in the area of modern energetic polymers: An overview. Cpmbust. Explo. Shock+ 2017, 53, 371–387. [Google Scholar] [CrossRef]
- Singh, A.; Radhakrishnan, S.; Vijayalakshmi, R.; Talawar, M.; Kumar, A.; Kumar, D. Screening of polymer-plasticizer systems for propellant binder applications: An experimental and simulation approach. J. Energy Mater. 2019, 37, 365–377. [Google Scholar] [CrossRef]
- Bergh, M.; Caleman, C. A validation study of the general amber force field applied to energetic molecular crystals. J. Energy Mater. 2016, 34, 62–75. [Google Scholar] [CrossRef]
- Jangid, S.K.; Radhakrishnan, S.; Solanki, V.J.; Singh, M.K.; Pandit, G.; Vijayalakshmi, R.; Sinha, R.K. Evaluation studies on partial replacement of RDX by spherical NTO in HTPB-based insensitive sheet explosive formulation. J. Energy Mater. 2019, 37, 320–330. [Google Scholar] [CrossRef]
- Cruz, J.N.; Moraes, E.S.; Pantoja, R.P.; Pereira, T.S.; Mota, G.V.; Neto, A.M.J.C. Sensors Using the Molecular Dynamics of Explosives in Carbon Nanotubes Under External Uniform Electric Fields. J. Nanosci. Nanotechnol. 2019, 19, 5687–5691. [Google Scholar] [CrossRef]
- Yılmaz, G.A.; Şen, D.; Kaya, Z.T.; Tinçer, T. Effect of inert plasticizers on mechanical, thermal, and sensitivity properties of polyurethane-based plastic bonded explosives. J. Appl. Polym. Sci. 2014, 131. [Google Scholar] [CrossRef]
- Sun, H. COMPASS: An ab initio force-field optimized for condensed-phase applications overview with details on alkane and benzene compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- El-Sakhawy, M.; Kamel, S.; Salama, A.; Sarhan, H.A. Carboxymethyl cellulose acetate butyrate: A review of the preparations, properties, and applications. J. Drug Deliv. 2014, 2014, 575969. [Google Scholar] [CrossRef]
- Wingborg, N.; Eldsater, C. 2,2-Dinitro-1,3-Bis-Nitrooxy-Propane (NPN): A New Energetic Plasticizer. Propellants Explos. Pyrotech. 2002, 27, 314–319. [Google Scholar] [CrossRef]
- Drees, D.; Loffel, D.; Messmer, A.; Schmid, K. Synthesis and Characterization of Azido Plasticizer. Propellants Explos. Pyrotech. 1999, 24, 159–162. [Google Scholar] [CrossRef]
- Kumari, D.; Singh, H.; Patil, M.; Thiel, W.; Pant, C.S.; Banerjee, S. Synthesis, characterization, thermal and computational studies of novel tetra-azido esters as energetic plasticizers. Thermochim. Acta 2013, 562, 96–104. [Google Scholar] [CrossRef]
- Zhao, B.; Gao, F.; Wang, Y.; Liu, Y.; Chen, B.; Pan, Y. Azido Energetic Plasticizers for Gun and Rocket Propellants. Prog. Chem. 2019, 31, 475–490. [Google Scholar] [CrossRef]
- Nair, U.R.; Asthana, S.N.; Rao, A.S.; Gandhe, B.R. Advances in High Energy Materials. Def. Sci. J. 2010, 60, 137–151. [Google Scholar] [CrossRef]
- Amim, J., Jr.; Blachechen, L.S.; Petri, D.F.S. Effect of sorbitan-based surfactants on glass transition temperature of cellulose esters. J. Therm. Anal. Calorim. 2012, 107, 1259–1265. [Google Scholar] [CrossRef]
- Khanniche, S.; Mathieu, D.; Barthet, C.; Pereira, F.; Hairault, L. Molecular dynamics simulation of gaseous nitroaromatic compounds interacting with silica surfaces under various humidity conditions. Appl. Surf. Sci. 2018, 455, 533–542. [Google Scholar] [CrossRef]
- Mendonça, F.B.; Gonçalves, R.F.; Urgessa, G.S.; Iha, K.; Domingues, M.; Rocco, J.A. Computational Chemistry Employment in Verification and Validation of Detonation Pressure of Plastic Explosive-Pbx. Quim. Nova 2018, 41, 310–314. [Google Scholar] [CrossRef]
- Sadeghi, A.; Nazem, H.; Rezakazemi, M.; Shirazian, S. Predictive construction of phase diagram of ternary solutions containing polymer/solvent/nonsolvent using modified Flory-Huggins model. J. Mol. Liq. 2018, 263, 282–287. [Google Scholar] [CrossRef]
- Kundu, B.K.; Mobin, S.M.; Mukhopadhyay, S. Mechanistic and thermodynamic aspects of a pyrene-based fluorescent probe to detect picric acid. New J. Chem. 2019, 43, 11483–11492. [Google Scholar] [CrossRef]
- Dahiwale, S.; Bhongale, C.; Roy, S.; Navle, P.; Asthana, S. Studies on ballistic parameters of di-butyl phthalate-coated triple base propellant used in large caliber artillery gun ammunition. J. Energy Mater. 2019, 37, 98–109. [Google Scholar] [CrossRef]
- Singh, A.; Kumar, R.; Soni, P.K.; Singh, V. Compatibility and thermokinetics studies of octahydro-1, 3, 5, 7-tetranitro-1, 3, 5, 7-tetrazocine with polyether-based polyurethane containing different curatives. J. Energy Mater. 2019, 37, 141–153. [Google Scholar] [CrossRef]
- Ramanaiah, S.; Rani, P.R.; Sreekanth, T.; Reddy, K.S. Determination of Hansen solubility parameters for the solid surface of cellulose acetate butyrate by inverse gas chromatography. J. Macromol. Sci. Part B Phys. 2011, 50, 551–562. [Google Scholar] [CrossRef]
- Lindblad, M.S.; Keyes, B.M.; Gedvilas, L.M.; Rials, T.G.; Kelley, S.S. FTIR imaging coupled with multivariate analysis for study of initial diffusion of different solvents in cellulose acetate butyrate films. Cellulose 2008, 15, 23–33. [Google Scholar] [CrossRef]
- Cappello, M.; Lamia, P.; Mura, C.; Polacco, G.; Filippi, S. Azidated Ether-Butadiene-Ether Block Copolymers as Binders for Solid Propellants. J. Energy Mater. 2016, 34, 318–341. [Google Scholar] [CrossRef]
- Bafghi, S.M.A.T.; Kamalvand, M.; Morsali, A.; Bozorgmehr, M.R. Radial distribution function within the framework of the Tsallis statistical mechanics. Physical A 2018, 506, 857–867. [Google Scholar] [CrossRef]
- Larsen, M.L.; Shaw, R. A method for computing the three-dimensional radial distribution function of cloud particles from holographic images. Atmos. Meas. Tech. 2018, 11, 4261. [Google Scholar] [CrossRef]
- García-Negrón, V.; Oyedele, A.D.; Ponce, E.; Rios, O.; Harper, D.P.; Keffer, D.J. Evaluation of nano-and mesoscale structural features in composite materials through hierarchical decomposition of the radial distribution function. J. Appl. Crystallogr. 2018, 51, 76–86. [Google Scholar] [CrossRef]
- Liu, N.; Li, Y.N.; Zeman, S.; Shu, Y.J.; Wang, B.Z.; Zhou, Y.S.; Zhao, Q.L.; Wang, W.L. Crystal morphology of 3, 4-bis (3-nitrofurazan-4-yl) furoxan (DNTF) in a solvent system: Molecular dynamics simulation and sensitivity study. CrystEngComm 2016, 18, 2843–2851. [Google Scholar] [CrossRef]
- Chen, F.; Zhou, T.; Li, J.; Wang, X.L.; Cao, D.L.; Wang, J.L.; Yang, Z.J. Crystal morphology of dihydroxylammonium 5, 5′-bistetrazole-1, 1′-diolate (TKX-50) under solvents system with different polarity using molecular dynamics. Comput. Mater. Sci. 2019, 168, 48–57. [Google Scholar] [CrossRef]
- Shu, Y.; Zhang, S.W.; Shu, Y.J.; Liu, N.; Yi, Y.; Huo, J.C.; Ding, X.Y. Interactions and physical properties of energetic poly-(phthalazinone ether sulfone ketones)(PPESKs) and ε-hexanitrohexaazaisowurtzitane (ε-CL-20) based polymer bonded explosives: A molecular dynamics simulations. Struct. Chem. 2019, 30, 1041–1055. [Google Scholar] [CrossRef]
- Li, J.; Jin, S.S.; Lan, G.C.; Ma, X.; Ruan, J.; Zhang, B.; Chen, S.S.; Li, L.J. Morphology control of 3-nitro-1, 2, 4-triazole-5-one (NTO) by molecular dynamics simulation. CrystEngComm 2018, 20, 6252–6260. [Google Scholar] [CrossRef]
- Sekkar, V.; Alex, A.S.; Kumar, V.; Bandyopadhyay, G.G. Theoretical evaluation of crosslink density of chain extended polyurethane networks based on hydroxyl terminated polybutadiene and butanediol and comparison with experimental data. J. Energy Mater. 2018, 36, 38–47. [Google Scholar] [CrossRef]
- Lin, H.; Chen, J.F.; Cui, Y.M.; Zhang, Z.J.; Yang, D.D.; Zhu, S.G.; Li, H.Z. A DFT-D study on structural, electronic, thermodynamic, and mechanical properties of HMX/MPNO cocrystal under high pressure. J. Energy Mater. 2017, 35, 157–171. [Google Scholar] [CrossRef]
- Ahmadi, S.H.; Keshavarz, M.H.; Hafizi Atabak, H.R. Introducing Laser Induced Breakdown Spectroscopy (LIBS) as a Novel, Cheap and Non-destructive Method to Study the Changes of Mechanical Properties of Plastic Bonded Explosives (PBX). Z. Anorg. Allg. Chem. 2018, 644, 1667–1673. [Google Scholar] [CrossRef]
- Lan, G.C.; Jin, S.S.; Li, J.; Wang, J.Y.; Lu, Z.Y.; Wu, N.N.; Li, L.J.; Wang, D.X. Miscibility, glass transition temperature and mechanical properties of NC/DBP binary systems by molecular dynamics. Propellants Explos. Pyrotech. 2018, 43, 559–567. [Google Scholar] [CrossRef]
- Li, J.; Jin, S.S.; Lan, G.C.; Chen, S.S.; Li, L.J. Modelling. Molecular dynamics simulations on miscibility, glass transition temperature and mechanical properties of PMMA/DBP binary system. J. Mol. Graph. Model. 2018, 84, 182–188. [Google Scholar] [CrossRef]
- Shu, Y.; Yi, Y.; Huo, J.C.; Liu, N.; Wang, K.; Lu, Y.Y.; Wang, X.C.; Wu, Z.K.; Shu, Y.J.; Zhang, S.W. Interactions between poly-(phthalazinone ether sulfone ketone)(PPESK) and TNT or TATB in polymer bonded explosives: A molecular dynamic simulation study. J. Mol. Model. 2017, 23, 334. [Google Scholar] [CrossRef]
- Lu, Y.Y.; Shu, Y.J.; Liu, N.; Shu, Y.; Wang, K.; Wu, Z.K.; Wang, X.C.; Ding, X.Y. Theoretical simulations on the glass transition temperatures and mechanical properties of modified glycidyl azide polymer. Comput. Mater. Sci. 2017, 139, 132–139. [Google Scholar] [CrossRef]
- Hang, G.Y.; Yu, W.L.; Wang, T.; Wang, J.T.; Li, Z. Theoretical investigations on stabilities, sensitivity, energetic performance and mechanical properties of CL-20/NTO cocrystal explosives by molecular dynamics simulation. Theor. Chem. Acc. 2018, 137, 114. [Google Scholar] [CrossRef]
- Gumieniczek, A.; Galeza, J.; Berecka, A.; Mroczek, T.; Wojtanowski, K.; Lipska, K.; Skarbek, J. Chemical stability and interactions in a new antihypertensive mixture containing indapamide and dihydralazine using FT-IR, HPLC and LC-MS methods. RSC Adv. 2018, 8, 36076–36089. [Google Scholar] [CrossRef]
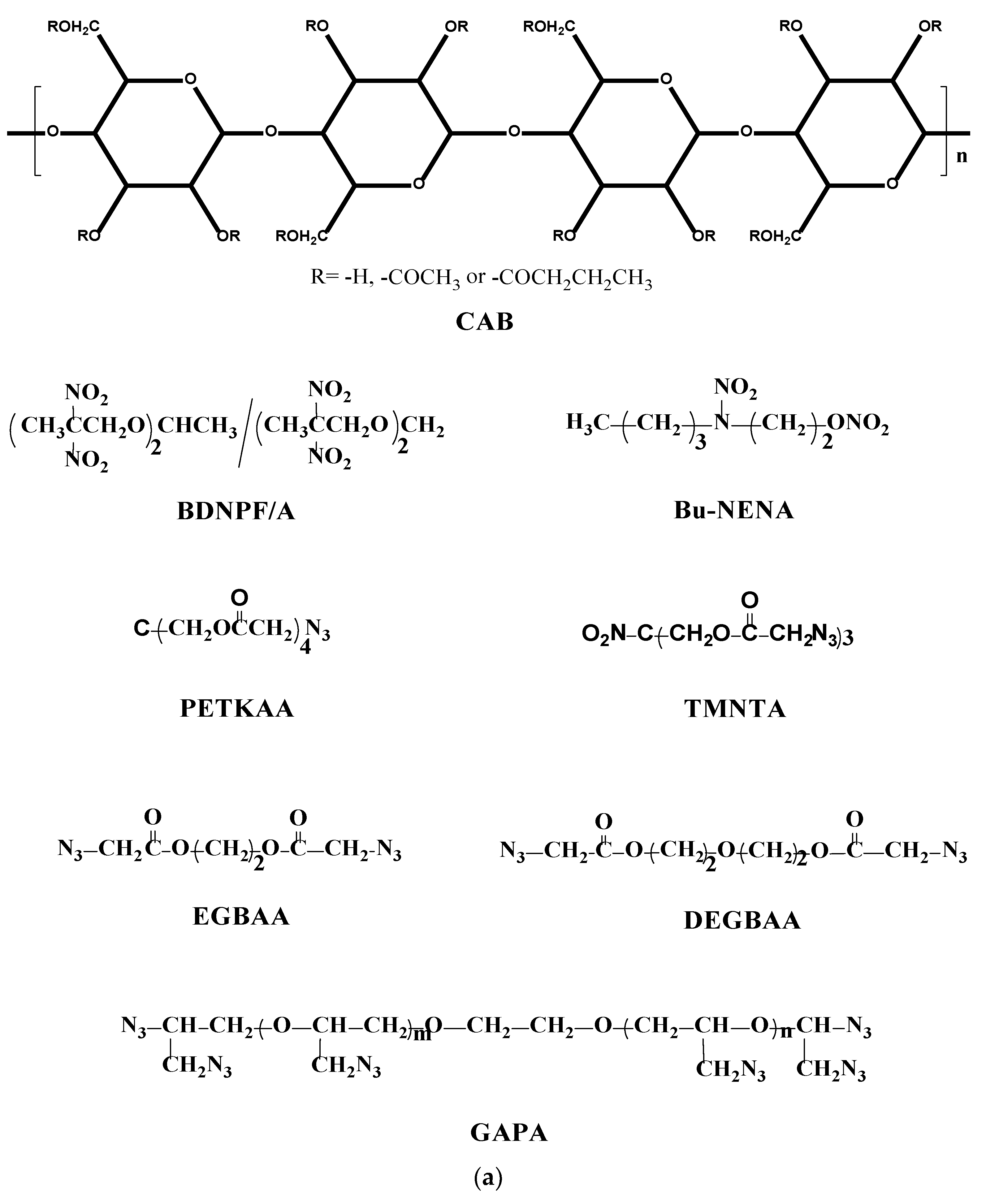
| Component | δMD/(J1/2·cm−3/2) | |ΔδMD|/(J1/2·cm−3/2) |
|---|---|---|
| CAB | 17.29 | 0 |
| A3 | 20.01 | 2.72 |
| GAPA | 20.56 | 3.27 |
| EGBAA | 23.59 | 6.20 |
| DEGBAA | 18.72 | 1.43 |
| TMNTA | 24.55 | 7.26 |
| Bu-NENA | 20.84 | 3.55 |
| PETKAA | 23.30 | 6.01 |
| System | Evalence/kcal·mol−1 | Evdw/kcal·mol−1 | Eelect/kcal·mol−1 | Ebind/kcal·mol−1 | Ebind’/kcal·g−1 |
|---|---|---|---|---|---|
| CAB/A3 | 0 | −448.44 | −149.96 | 598.40 | 0.71 |
| CAB/GAPA | 0 | −565.11 | −116.36 | 681.47 | 0.91 |
| CAB/PETKAA | 0 | −596.22 | −157.32 | 753.55 | 1.08 |
| CAB/EGBAA | 0 | −578.03 | −144.21 | 722.25 | 2.03 |
| CAB/Bu-NENA | 0 | −550.03 | −115.85 | 665.88 | 2.03 |
| CAB/TMNTA | 0 | −600.74 | −153.22 | 753.96 | 1.25 |
| CAB/DEGBAA | 0 | −562.56 | −138.11 | 700.67 | 1.65 |
| System | K/GPa | G/GPa | K/G | μ | E/GPa |
|---|---|---|---|---|---|
| CAB/A3 | 2.32 | 0.86 | 2.70 | 0.34 | 2.29 |
| CAB/GAPA | 2.50 | 0.78 | 3.20 | 0.36 | 2.13 |
| CAB/DEGBAA | 1.54 | 0.91 | 1.70 | 0.25 | 2.27 |
| CAB/Bu-NENA | 5.23 | 0.89 | 5.87 | 0.42 | 2.53 |
| CAB/TMNTA | 2.53 | 1.02 | 2.49 | 0.32 | 2.69 |
| CAB/PETKAA | 2.26 | 1.34 | 1.68 | 0.25 | 3.36 |
| CAB/EGBAA | 2.24 | 0.83 | 2.69 | 0.33 | 2.22 |
| System | ΔTp/°C | (ΔE/Ea)/% | Compatibility | |||
|---|---|---|---|---|---|---|
| DSC | DTA | DSC | DTA | DSC | DTA | |
| CAB/A3 | 1.57 | 1.74 | 17.25 | 19.48 | Very good | Very good |
| CAB/Bu-NENA | 1.88 | 1.98 | 16.62 | 11.82 | Very good | Very good |
| CAB/GAPA | 1.61 | 1.96 | 18.05 | 18.80 | Very good | Very good |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Li, L.; Jin, S.; Wang, Y.; Lan, G.; Chen, Y. Study on Cellulose Acetate Butyrate/Plasticizer Systems by Molecular Dynamics Simulation and Experimental Characterization. Polymers 2020, 12, 1272. https://doi.org/10.3390/polym12061272
Wang W, Li L, Jin S, Wang Y, Lan G, Chen Y. Study on Cellulose Acetate Butyrate/Plasticizer Systems by Molecular Dynamics Simulation and Experimental Characterization. Polymers. 2020; 12(6):1272. https://doi.org/10.3390/polym12061272
Chicago/Turabian StyleWang, Weizhe, Lijie Li, Shaohua Jin, Yalun Wang, Guanchao Lan, and Yu Chen. 2020. "Study on Cellulose Acetate Butyrate/Plasticizer Systems by Molecular Dynamics Simulation and Experimental Characterization" Polymers 12, no. 6: 1272. https://doi.org/10.3390/polym12061272
APA StyleWang, W., Li, L., Jin, S., Wang, Y., Lan, G., & Chen, Y. (2020). Study on Cellulose Acetate Butyrate/Plasticizer Systems by Molecular Dynamics Simulation and Experimental Characterization. Polymers, 12(6), 1272. https://doi.org/10.3390/polym12061272




