A Novel Simple Approach to Material Parameters from Commonly Accessible Rheometer Data
Abstract
:1. Introduction
- (1)
- A novel, yet simple, concept is suggested to directly reveal the constitutive equation of a material from rheological measurements. In particular, the constitutive equation in the form of a differential equation is directly accessed, relating stress σ and deformation ε.
- (2)
- Various rheological model systems are benchmarked to reveal the simplest and statistically most significant ones. The presented approach is applicable to Dynamic Mechanical Analysis (DMA; typically used symbols are σ for stress and ε for deformation) and shear rheology (τ for stress and γ for deformation).
- (3)
- We present a material independent approach that is suitable for further in-depth interpretation of frequency dependent material properties, known to be of major importance for a variety of industrial applications. The presented concept additionally allows the analysis of specific model parameters and their respective influences on the targeted applications. Hypothetically, one can correlate key processing parameters such as shape fidelity for additive manufacturing or sealing properties for rubbers to the resulting model parameters. It should be noted that huge amounts of data are required in order to reveal correlations between model and process parameters. This paper, however, will focus on the approach of generating necessary data for possible future correlations.
2. Materials and Methods
2.1. Theory/Strategy
2.2. Sample Preparation for Rheological Characterization
2.3. Shear Rheology
2.4. Printing of Alginate
3. Results and Discussion
3.1. Rheological Model Evaluation of Alginate
3.1.1. Single Parameter Model: Spring and Dashpot
3.1.2. Two Component Model Systems: Kelvin–Voigt and Maxwell
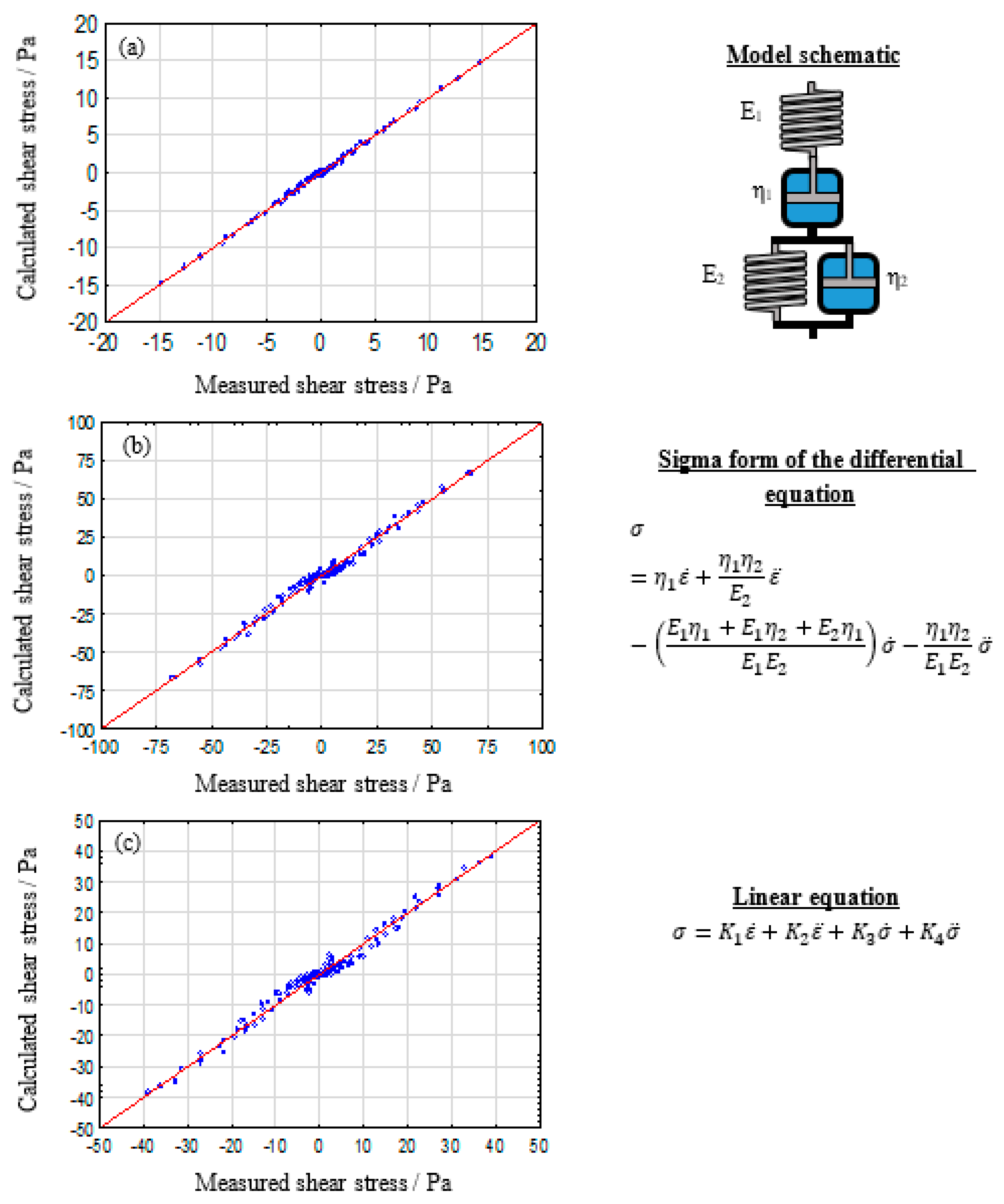
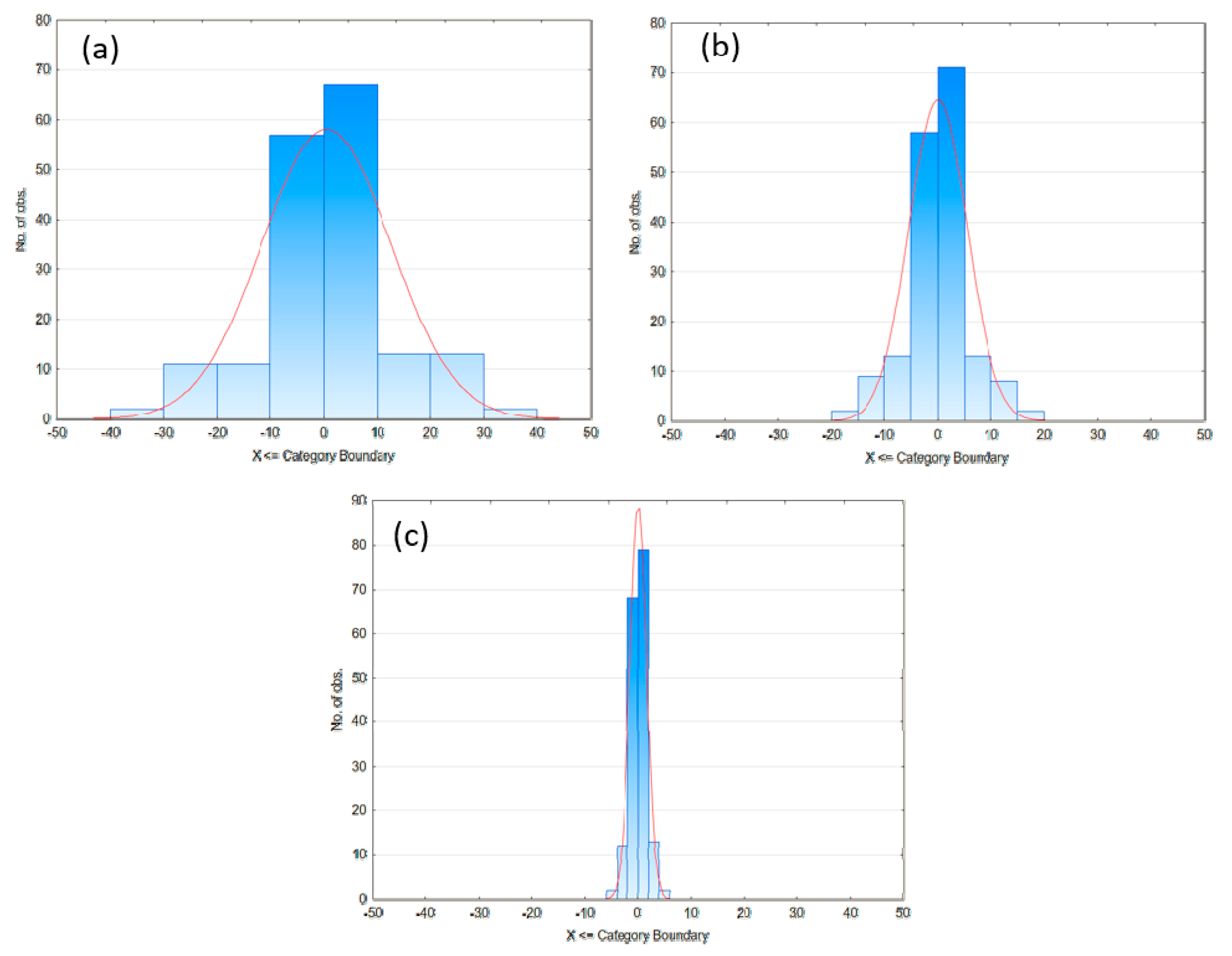
3.1.3. Four Parameter Model: The Burgers Model
3.1.4. Resulting Model Parameters for the Burgers Model
3.1.5. Correlation of Rheological Model Parameters and Key Processing Parameters
3.2. Rheological Model Evaluation of Further Materials
3.2.1. Analysis of Elastosil 7670
3.2.2. Analysis of TPU 1180A
3.2.3. Analysis of PCL Filled Alginate
3.3. Theoretical Comparison to Already Existing Methods for Model Parameter Determination
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Budday, S.; Sommer, G.; Haybaeck, J.; Steinmann, P.; Holzapfel, G.; Kuhl, E. Rheological characterization of human brain tissue. Acta Biomater. 2017, 60, 315–329. [Google Scholar] [CrossRef] [PubMed]
- Bird, R.; Giacomin, A.J. Polymer Fluid Dynamics: Continuum and Molecular Approaches. Annu. Rev. Chem. Biomol. Eng. 2016, 7, 479–507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luo, H.; Delshad, M.; Li, Z.-T.; Shahmoradi, A. Numerical simulation of the impact of polymer rheology on polymer injectivity using a multilevel local grid refinement method. Pet. Sci. 2015, 13, 110–125. [Google Scholar] [CrossRef] [Green Version]
- Fatahian, E.; Kordani, N.; Fatahian, H. The Application of Computational Fluid Dynamics (CFD) Method and Several Rheological Models of Blood Flow: A Review. Gazi Univ. J. Sci. 2018, 31, 1213–1227. [Google Scholar]
- Nakajima, A.; Sugawara, T. Fundamental Researches on Rheological Properties of Mastic Asphalt. Bull. Jpn. Pet. Inst. 1967, 9, 84–91. [Google Scholar] [CrossRef] [Green Version]
- Dey, A.; Basudhar, P.K. Applicability of Burger model in predicting the response of viscoelastic soil beds. In Proceedings of the GeoFlorida 2010: Advances in Analysis, Modeling & Design, Orlando, FL, USA, 20–24 February 2010; pp. 2611–2620. [Google Scholar] [CrossRef]
- Mazurek, G.; Iwański, M. Modelling of Asphalt Concrete Stiffness in the Linear Viscoelastic Region. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, 32029. [Google Scholar] [CrossRef]
- Xu, Q.; Solaimanian, M. Modelling linear viscoelastic properties of asphalt concrete by the Huet–Sayegh model. Int. J. Pavement Eng. 2009, 10, 401–422. [Google Scholar] [CrossRef]
- Mahiuddin, M.; Godhani, D.; Feng, L.; Liu, F.; Langrish, T.; Karim, M. Application of Caputo fractional rheological model to determine the viscoelastic and mechanical properties of fruit and vegetables. Postharvest Boil. Technol. 2020, 163, 111147. [Google Scholar] [CrossRef]
- Shi, A.; Wang, L.-J.; Li, N.; Adhikari, B. Characterization of starch films containing starch nanoparticles. Part 2: Viscoelasticity and creep properties. Carbohydr. Polym. 2013, 96, 602–610. [Google Scholar] [CrossRef]
- Meng, Y.C.; Sun, M.-H.; Fang, S.; Chen, J.; Li, Y.-H. Effect of sucrose fatty acid esters on pasting, rheological properties and freeze–thaw stability of rice flour. Food Hydrocoll. 2014, 40, 64–70. [Google Scholar] [CrossRef]
- Kundera, C.; Bochnia, J. Investigating the stress relaxation of photopolymer O-ring seal models. Rapid Prototyp. J. 2014, 20, 533–540. [Google Scholar] [CrossRef]
- Bagley, E.B. Large deformations in testing and processing of food materials. In Physical Properties of Foods; Avi Publishing Co.: Westport, CT, USA, 1983; pp. 325–341. [Google Scholar]
- Bhattacharyya, A.; Tobushi, H. Analysis of the isothermal mechanical response of a shape memory polymer rheological model. Polym. Eng. Sci. 2000, 40, 2498–2510. [Google Scholar] [CrossRef]
- Sun, X.; Koksel, F.; Nickerson, M.T.; Scanlon, M.G. Modeling the viscoelastic behavior of wheat flour dough prepared from a wide range of formulations. Food Hydrocoll. 2020, 98, 105129. [Google Scholar] [CrossRef]
- Okay, O. General properties of hydrogels. In Hydrogel Sensors and Actuators; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–14. [Google Scholar]
- Gómez-Díaz, D.; Navaza, J.M. Rheology of aqueous solutions of food additives. J. Food Eng. 2003, 56, 387–392. [Google Scholar] [CrossRef]
- Tønnesen, H.H.; Karlsen, J. Alginate in Drug Delivery Systems. Drug Dev. Ind. Pharm. 2002, 28, 621–630. [Google Scholar] [CrossRef]
- Qin, Y. Alginate fibres: An overview of the production processes and applications in wound management. Polym. Int. 2007, 57, 171–180. [Google Scholar] [CrossRef]
- Jia, J.; Richards, D.J.; Pollard, S.; Tan, Y.; Rodriguez, J.; Visconti, R.P.; Trusk, T.C.; Yost, M.J.; Yao, H.; Markwald, R.R.; et al. Engineering alginate as bioink for bioprinting. Acta Biomater. 2014, 10, 4323–4331. [Google Scholar] [CrossRef] [Green Version]
- Larsen, B.E.; Bjørnstad, J.; Pettersen, E.O.; Tønnesen, H.H.; Melvik, J.E. Rheological characterization of an injectable alginate gel system. BMC Biotechnol. 2015, 15, 29. [Google Scholar] [CrossRef] [Green Version]
- Paxton, N.; Smolan, W.; Böck, T.; Melchels, F.; Groll, J.; Jungst, T. Proposal to assess printability of bioinks for extrusion-based bioprinting and evaluation of rheological properties governing bioprintability. Biofabrication 2017, 9, 044107. [Google Scholar] [CrossRef]
- Rezende, R.A.; Bartolo, P.; Mendes, A.; Filho, R.M. Rheological behavior of alginate solutions for biomanufacturing. J. Appl. Polym. Sci. 2009, 113, 3866–3871. [Google Scholar] [CrossRef]
- Gao, T.; Gillispie, G.J.; Copus, J.S.; Pr, A.K.; Seol, Y.-J.; Atala, A.; Yoo, J.J.; Lee, S.J. Optimization of gelatin–alginate composite bioink printability using rheological parameters: A systematic approach. Biofabrication 2018, 10, 034106. [Google Scholar] [CrossRef]
- Lee, Y.E.; Wadsworth, L.C. Fiber and web formation of melt-blown thermoplastic polyurethane polymers. J. Appl. Polym. Sci. 2007, 105, 3724–3727. [Google Scholar] [CrossRef]
- Harris, C.G.; Jursik, N.J.S.; Rochefort, W.E.; Walker, T. Additive Manufacturing With Soft TPU—Adhesion Strength in Multimaterial Flexible Joints. Front. Mech. Eng. 2019, 5, 37. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Park, J.; Suh, J.H.; Kim, M.; Jeong, Y.; Park, I. 3D printing of multiaxial force sensors using carbon nanotube (CNT)/thermoplastic polyurethane (TPU) filaments. Sens. Actuators A Phys. 2017, 263, 493–500. [Google Scholar] [CrossRef]
- Krujatz, F.; Lode, A.; Seidel, J.; Bley, T.; Gelinsky, M.; Steingroewer, J. Additive Biotech—Chances, challenges, and recent applications of additive manufacturing technologies in biotechnology. New Biotechnol. 2017, 39, 222–231. [Google Scholar] [CrossRef]
- Xiao, J.; Gao, Y. The manufacture of 3D printing of medical grade TPU. Prog. Addit. Manuf. 2017, 40, 116–123. [Google Scholar] [CrossRef]
- Huang, P.; Xia, Z.; Cui, S. 3D printing of carbon fiber-filled conductive silicon rubber. Mater. Des. 2018, 142, 11–21. [Google Scholar] [CrossRef]
- Giffney, T.; Bejanin, E.; Kurian, A.S.; Travas-Sejdic, J.; Aw, K.C. Highly stretchable printed strain sensors using multi-walled carbon nanotube/silicone rubber composites. Sens. Actuators A Phys. 2017, 259, 44–49. [Google Scholar] [CrossRef]
- Boland, C.S.; Khan, U.; Backes, C.; O’Neill, A.; McCauley, J.; Duane, S.; Shanker, R.; Liu, Y.; Jurewicz, I.; Dalton, A.B.; et al. Sensitive, High-Strain, High-Rate Bodily Motion Sensors Based on Graphene–Rubber Composites. ACS Nano 2014, 8, 8819–8830. [Google Scholar] [CrossRef]
- Kim, M.H.; Lee, Y.W.; Jung, W.-K.; Oh, J.; Nam, S.Y. Enhanced rheological behaviors of alginate hydrogels with carrageenan for extrusion-based bioprinting. J. Mech. Behav. Biomed. Mater. 2019, 98, 187–194. [Google Scholar] [CrossRef]
- Schaffner, M.; Faber, J.A.; Pianegonda, L.; Rühs, P.A.; Coulter, F.; Studart, A.R. 3D printing of robotic soft actuators with programmable bioinspired architectures. Nat. Commun. 2018, 9, 878. [Google Scholar] [CrossRef] [PubMed]
- Zolfagharian, A.; Kouzani, A.Z.; Khoo, S.Y.; Moghadam, A.A.A.; Gibson, I.; Kaynak, A. Evolution of 3D printed soft actuators. Sens. Actuators A Phys. 2016, 250, 258–272. [Google Scholar] [CrossRef]
- McCoul, D.; Rosset, S.; Schlatter, S.; Shea, H. Inkjet 3D printing of UV and thermal cure silicone elastomers for dielectric elastomer actuators. Smart Mater. Struct. 2017, 26, 125022. [Google Scholar] [CrossRef] [Green Version]
- Mezger, T.G. The Rheology Handbook: For Users of Rotational and Oscillatory Rheometers, 2nd ed.; Vincentz Network GmbH & Co KG: Hannover, Germany, 2006; pp. 114–118. [Google Scholar]
- Mainardi, F.; Spada, G. Creep, relaxation and viscosity properties for basic fractional models in rheology. Eur. Phys. J. Spec. Top. 2011, 193, 133–160. [Google Scholar] [CrossRef] [Green Version]
- Linares-García, J.A.; Ramos-Ramírez, E.G.; Salazar-Montoya, J.A. Viscoelastic properties and textural characterisation of high methoxyl pectin of hawthorn (C rataegus pubescens) in a gelling system. Int. J. Food Sci. Technol. 2015, 50, 1484–1493. [Google Scholar] [CrossRef]
- Saha, D.; Bhattacharya, S. Hydrocolloids as thickening and gelling agents in food: A critical review. J. Food Sci. Technol. 2010, 47, 587–597. [Google Scholar] [CrossRef] [Green Version]
- Aktas, S.; Kalyon, D.M.; Marín-Santibáñez, B.M.; Pérez-González, J. Shear viscosity and wall slip behavior of a viscoplastic hydrogel. J. Rheol. 2014, 58, 513–535. [Google Scholar] [CrossRef]
- Cox, W.P.; Merz, E.H. Correlation of dynamic and steady flow viscosities. J. Polym. Sci. 1958, 28, 619–622. [Google Scholar] [CrossRef]
- Pahl, M.; Gleißle, W.; Laun, H.M. Praktische Rheologie der Kunststoffe und Elastomere, 4th ed.; VDI-Gesellschaft Kunststofftechnik: Düsseldorf, Germany, 1995; pp. 63–69. [Google Scholar]
- Münstedt, H.; Schwarzl, F.R. Deformation and Flow of Polymeric Materials; Springer: Berlin/Heidelberg, Germany, 2014; pp. 482–488. [Google Scholar]
- Piñeiro, G.; Perelman, S.; Guerschman, J.P.; Paruelo, J. How to evaluate models: Observed vs. predicted or predicted vs. observed? Ecol. Model. 2008, 216, 316–322. [Google Scholar] [CrossRef]
- Mitchell, J.R.; Blanshard, J.M.V. Rheological properties of alginate gels. J. Texture Stud. 1976, 7, 219–234. [Google Scholar] [CrossRef]
- Chejara, D.R.; Kondaveeti, S.; Prasad, K.; Siddhanta, A.K. Studies on the structure–property relationship of sodium alginate based thixotropic hydrogels. RSC Adv. 2013, 3, 15744–15751. [Google Scholar] [CrossRef]
- Lee, K.Y.; Mooney, D.J. Alginate: Properties and biomedical applications. Prog. Polym. Sci. 2012, 37, 106–126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chirila, T.V.; Hong, Y.E. Poly (1-vinyl-2-pyrrolidinone) hydrogels as vitreous substitutes: A rheological study. Polym. Int. 1998, 46, 183–195. [Google Scholar] [CrossRef]
- Kocen, R.; Gasik, M.; Gantar, A.; Novak, S. Viscoelastic behaviour of hydrogel-based composites for tissue engineering under mechanical load. Biomed. Mater. 2017, 12, 025004. [Google Scholar] [CrossRef] [PubMed]
- Schubert, D.W. Novel theoretical self-consistent mean-field approach to describe the conductivity of carbon fiber filled thermoplastics—PART III—Application of the concept to mechanical properties of composites and polymer solutions. Adv. Eng. Mater. 2020. [Google Scholar] [CrossRef]
- Korson, L.; Drost-Hansen, W.; Millero, F.J. Viscosity of water at various temperatures. J. Phys. Chem. 1969, 73, 34–39. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- De Gennes, P. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaka, NY, USA, 1979; p. 157. [Google Scholar]
- Oyen, M.L. Mechanical characterisation of hydrogel materials. Int. Mater. Rev. 2013, 59, 44–59. [Google Scholar] [CrossRef]
- Ribeiro, A.; Blokzijl, M.M.; Levato, R.; Visser, C.W.; Castilho, M.; Hennink, W.E.; Vermonden, T.; Malda, J. Assessing bioink shape fidelity to aid material development in 3D bioprinting. Biofabrication 2017, 10, 014102. [Google Scholar] [CrossRef] [PubMed]
- Daly, A.; Critchley, S.E.; Rencsok, E.M.; Kelly, D.J. A comparison of different bioinks for 3D bioprinting of fibrocartilage and hyaline cartilage. Biofabrication 2016, 8, 045002. [Google Scholar] [CrossRef]
- Kiyotake, E.A.; Douglas, A.W.; Thomas, E.E.; Nimmo, S.L.; Detamore, M.S. Development and quantitative characterization of the precursor rheology of hyaluronic acid hydrogels for bioprinting. Acta Biomater. 2019, 95, 176–187. [Google Scholar] [CrossRef]
- Schubert, D.W.; Schrüfer, S. An Analytical Model for One Dimensional Spreading and Its Application for Biofabrication; Erlangen, Germany, Unpublished Work.
- Härth, M.; Schubert, D.W. Simple Approach for Spreading Dynamics of Polymeric Fluids. Macromol. Chem. Phys. 2012, 213, 654–665. [Google Scholar] [CrossRef]
- Schrüfer, S.; Sonnleitner, D.; Lang, G.; Schubert, D.W. Erlangen, Bayreuth, Germany. Unpublished Work.







| …. | ….. | ….. | ….. | ….. | ….. | …. |
| …. | ….. | ….. | ….. | ….. | ….. | ….. |
| ………. | ………. | ………. | ………. | ………. | ………. | ………. |
| ………. | ………. | ………. | ………. | ………. | ………. | ………. |
| ………. | ………. | ………. | ………. | ………. | ………. | ………. |
| ………. | ………. | ………. | ………. | ………. | ………. |
| Model Name | Scheme | Linear Equation | |
|---|---|---|---|
| Maxwell | 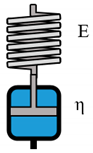 | ||
| Kelvin-Voigt | 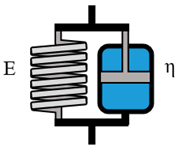 | ||
| Zener K | 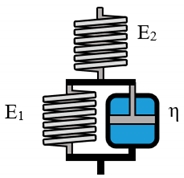 | ||
| Zener M | 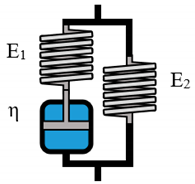 |
| Model Name | Scheme | Linear Equation | |
|---|---|---|---|
| Lethersich |  | ||
| Jeffreys | 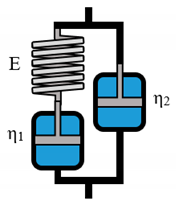 | ||
| Burgers | 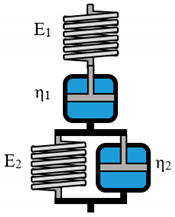 |
| Parameter in Burgers Model | E0/η0 (Pa/Pa∙s) | (g/l) | Exponent m/n |
|---|---|---|---|
| E1(c) | 1.18 ± 0.21 | 0.23 (fixed) | 2.37 ± 0.06 |
| E2(c) | 0.06 ± 0.01 | 0.11 (fixed) | 2.71 ± 0.03 |
| η1(c) | 0.001 (fixed) | 0.23 ± 0.02 | 3.49 ± 0.08 |
| η2(c) | 0.001 (fixed) | 0.11 ± 0.01 | 2.70 ± 0.04 |
| Parameter in Burgers Model | E0/η0 (Pa/Pa∙s) | (g/l) | Exponent m/n |
|---|---|---|---|
| E1(c) | 22.91 ± 5.67 | 1.45 ± 0.17 | 3 |
| E2(c) | 2.62 ± 0.71 | 0.63 ± 0.07 | 3 |
| η1(c) | 0.001 (fixed) | 0.14 ± 0.01 | 3 |
| η2(c) | 0.001 (fixed) | 0.16 ± 0.01 | 3 |
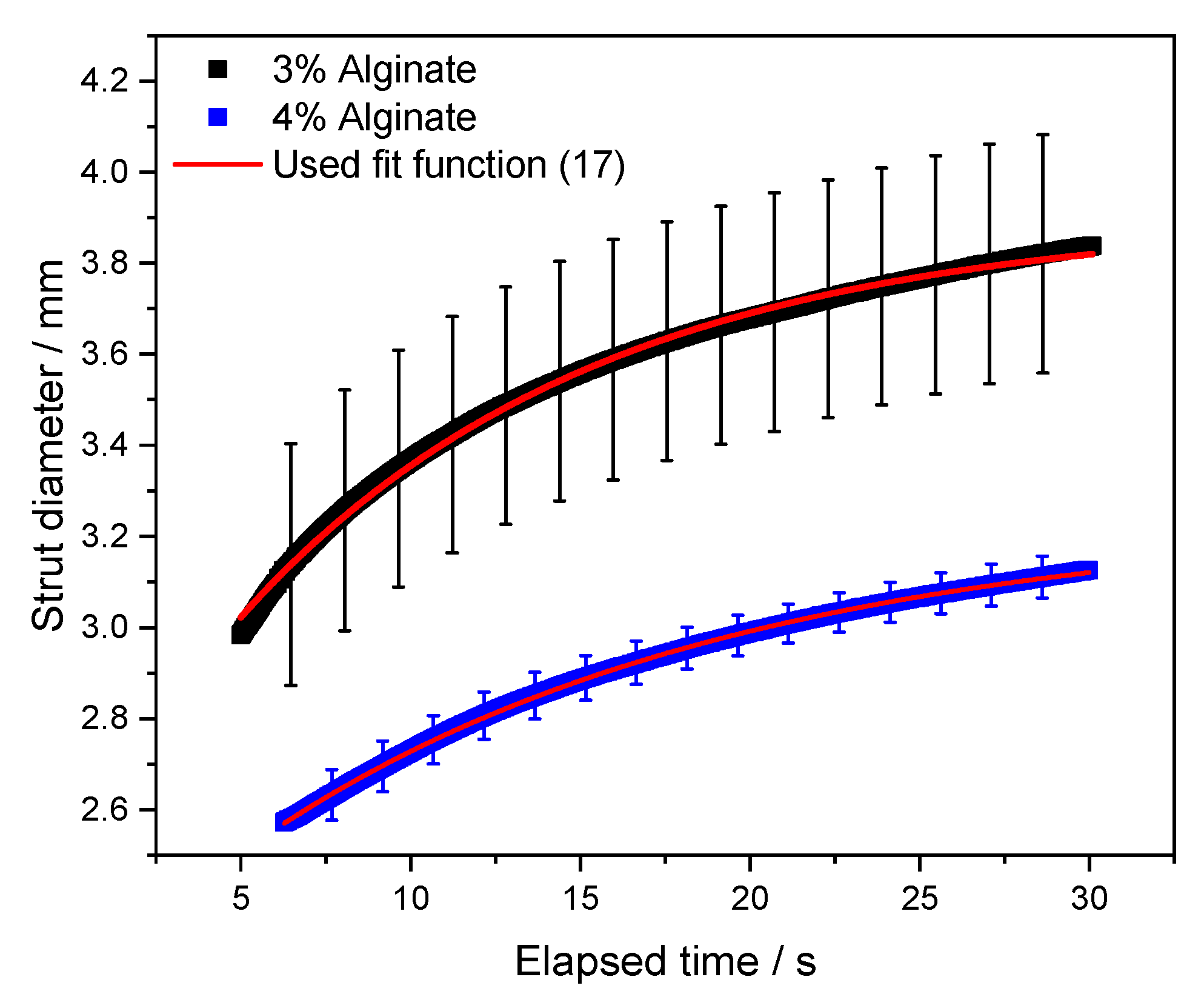
| Alginate Concentration | A (mm) | t0 (s) | τs (s) |
|---|---|---|---|
| 3% | 3.90 ± 0.002 | 10.65 ± 0.08 | 10.49 ± 0.05 |
| 4% | 3.24 ± 0.001 | 15.61 ± 0.05 | 13.92 ± 0.04 |
| Char. Time (s) | 3% Alginate | 4% Alginate | τ(4%)/τ(3%) | |
|---|---|---|---|---|
| Spreading | τs | 10.49 ± 0.52 | 13.93 ± 0.41 | 1.33 ± 0.01 |
| Maxwell-Part | τ1 | 0.016 ± 0.001 | 0.021 ± 0.001 | 1.29 ± 0.137 |
| Kelvin–Voigt-Part | τ2 | 0.017 ± 0.001 | 0.018 ± 0.001 | 1.06 ± 0.153 |
| Rheological Model System | Adjusted R2 |
|---|---|
| Maxwell | 0.286 |
| Kelvin–Voigt | 0.992 |
| Zener m/k | 0.996 |
| Lethersich/Jeffreys | 0.326 |
| Burgers | 0.457 |
| Rheological Model System | E1 | η | E2 |
|---|---|---|---|
| (Pa) | (Pa∙s) | (Pa) | |
| Kelvin–Voigt | 32,685.11 | 54.18 | / |
| Zener m | 6926.5 | 138.2 | 31,340.72 |
| Rheological Model System | Adjusted R2 |
|---|---|
| Maxwell | 0.997 |
| Kelvin–Voigt | 0.960 |
| Zener m/k | 0.997 |
| Lethersich/Jeffreys | 0.999 |
| Burgers | 0.999 |
| Model Parameter in Burgers Model | Elastollan 1180A |
|---|---|
| E1 (Pa) | 203,959.30 ± 5765.51 |
| E2 (Pa) | 116,297.58 ± 7.06 |
| η1 (Pa∙s) | 403.75 ± 0.48 |
| η2 (Pa∙s) | 1662.26 ± 27.00 |
| Rheological Model System | Adjusted R2 |
|---|---|
| Maxwell | 0.828 |
| Kelvin–Voigt | 0.639 |
| Zener m/k | 0.924 |
| Lethersich/Jeffreys | 0.859 |
| Burgers | 0.952 |
| Model Parameter | Pure 3% Alginate | 3% Alginate + 10 wt % PCL | Percentage Increase |
|---|---|---|---|
| E1 (Pa) | 697.69 ± 35.38 | 2916.71 ± 215.47 | 418% |
| E2 (Pa) | 511.27 ± 22.54 | 2611.20 ± 7.06 | 511% |
| η1 (Pa∙s) | 11.07 ± 0.12 | 139.74 ± 4.23 | 1262% |
| η2 (Pa∙s) | 8.38 ± 0.47 | 54.50 ± 3.26 | 650% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schrüfer, S.; Sonnleitner, D.; Lang, G.; Schubert, D.W. A Novel Simple Approach to Material Parameters from Commonly Accessible Rheometer Data. Polymers 2020, 12, 1276. https://doi.org/10.3390/polym12061276
Schrüfer S, Sonnleitner D, Lang G, Schubert DW. A Novel Simple Approach to Material Parameters from Commonly Accessible Rheometer Data. Polymers. 2020; 12(6):1276. https://doi.org/10.3390/polym12061276
Chicago/Turabian StyleSchrüfer, S., D. Sonnleitner, G. Lang, and D. W. Schubert. 2020. "A Novel Simple Approach to Material Parameters from Commonly Accessible Rheometer Data" Polymers 12, no. 6: 1276. https://doi.org/10.3390/polym12061276
APA StyleSchrüfer, S., Sonnleitner, D., Lang, G., & Schubert, D. W. (2020). A Novel Simple Approach to Material Parameters from Commonly Accessible Rheometer Data. Polymers, 12(6), 1276. https://doi.org/10.3390/polym12061276




