Introduction of a New In-Situ Measurement System for the Study of Touch-Feel Relevant Surface Properties
Abstract
:1. Introduction
2. Materials and Methods
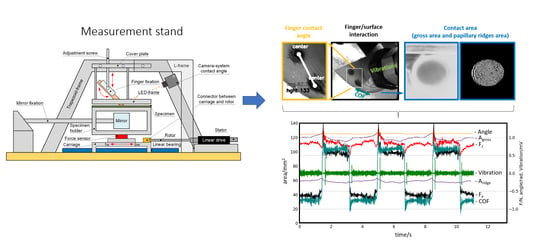
2.1. Experimental Setup
2.1.1. Description of the Haptic Tester
2.1.2. Tribological Parameters
2.1.3. Vibrational Parameters
2.1.4. Exploration Parameter—Angle Enclosed between the Human Finger and the Specimen Surface
2.1.5. Contact Area
2.1.6. Contact Area Extraction
2.2. Materials
2.2.1. Preparation of Soft Touch Coatings
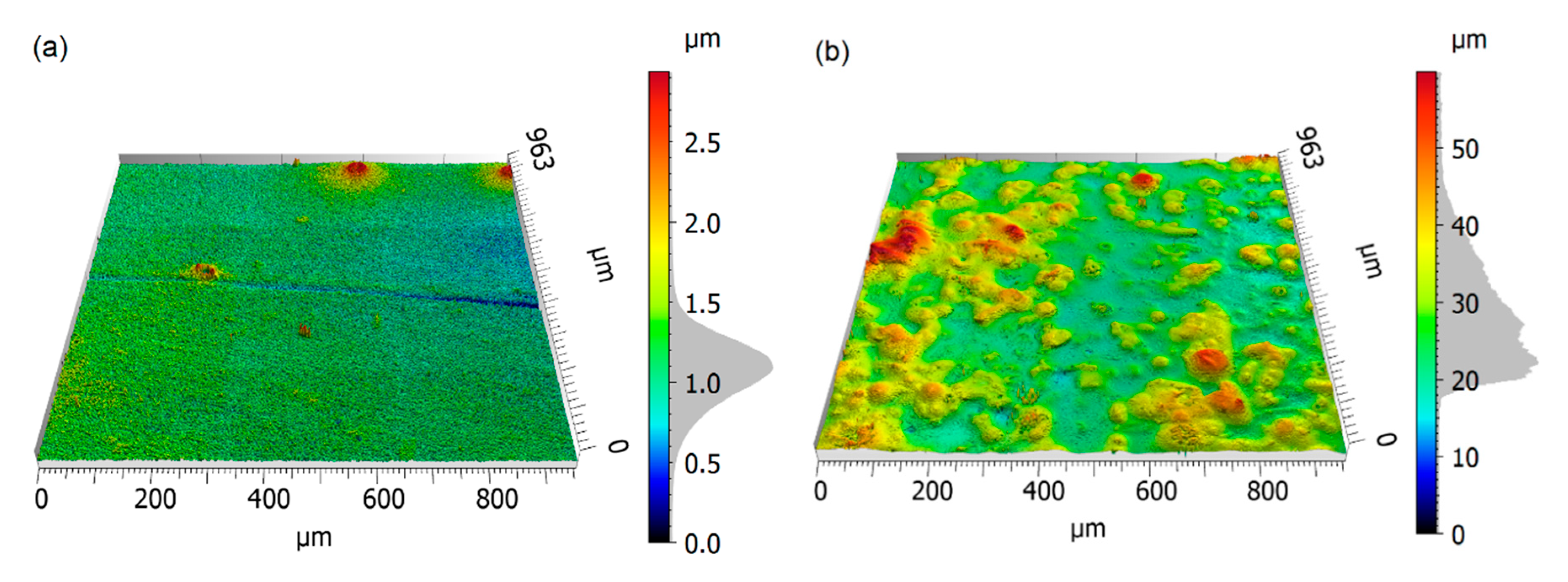
2.2.2. Topographical Characterization of the Specimen
3. Results and Discussion
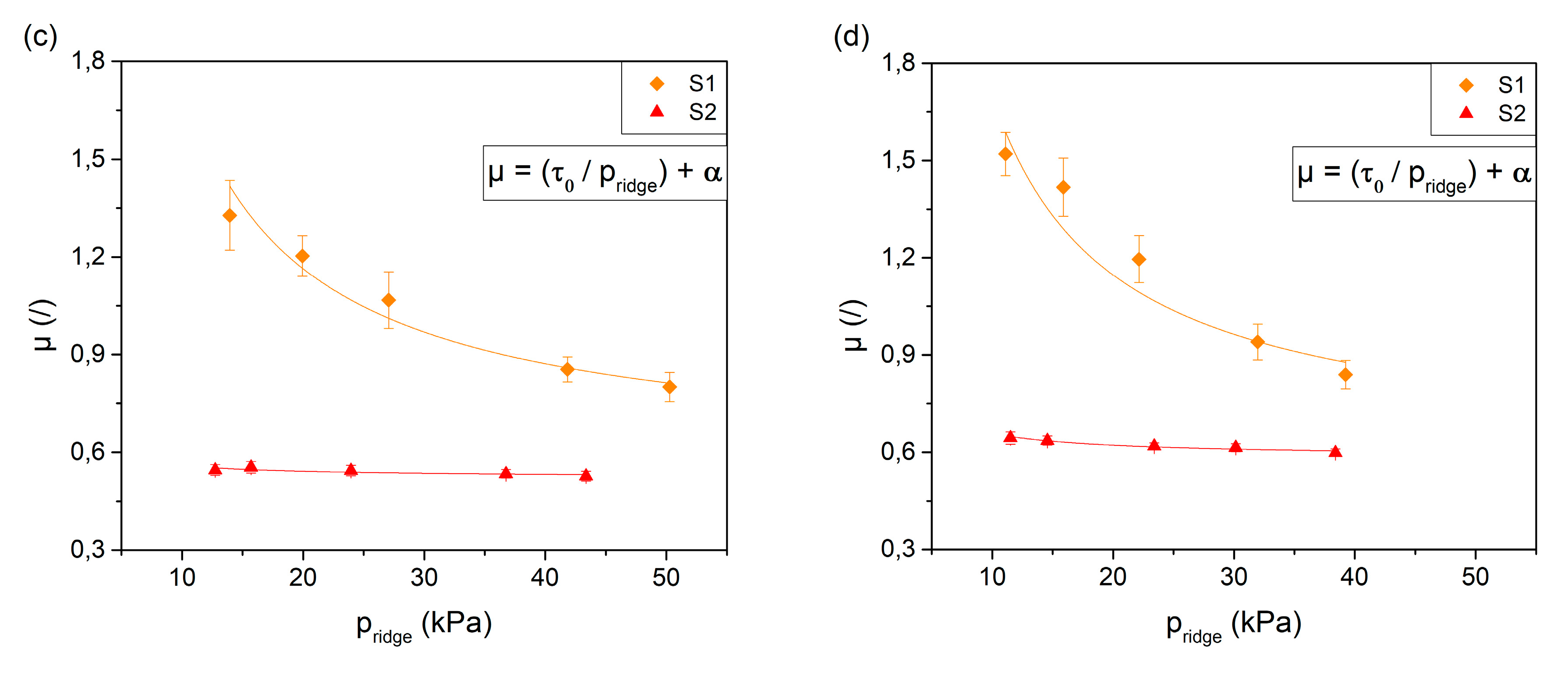
3.1. Friction
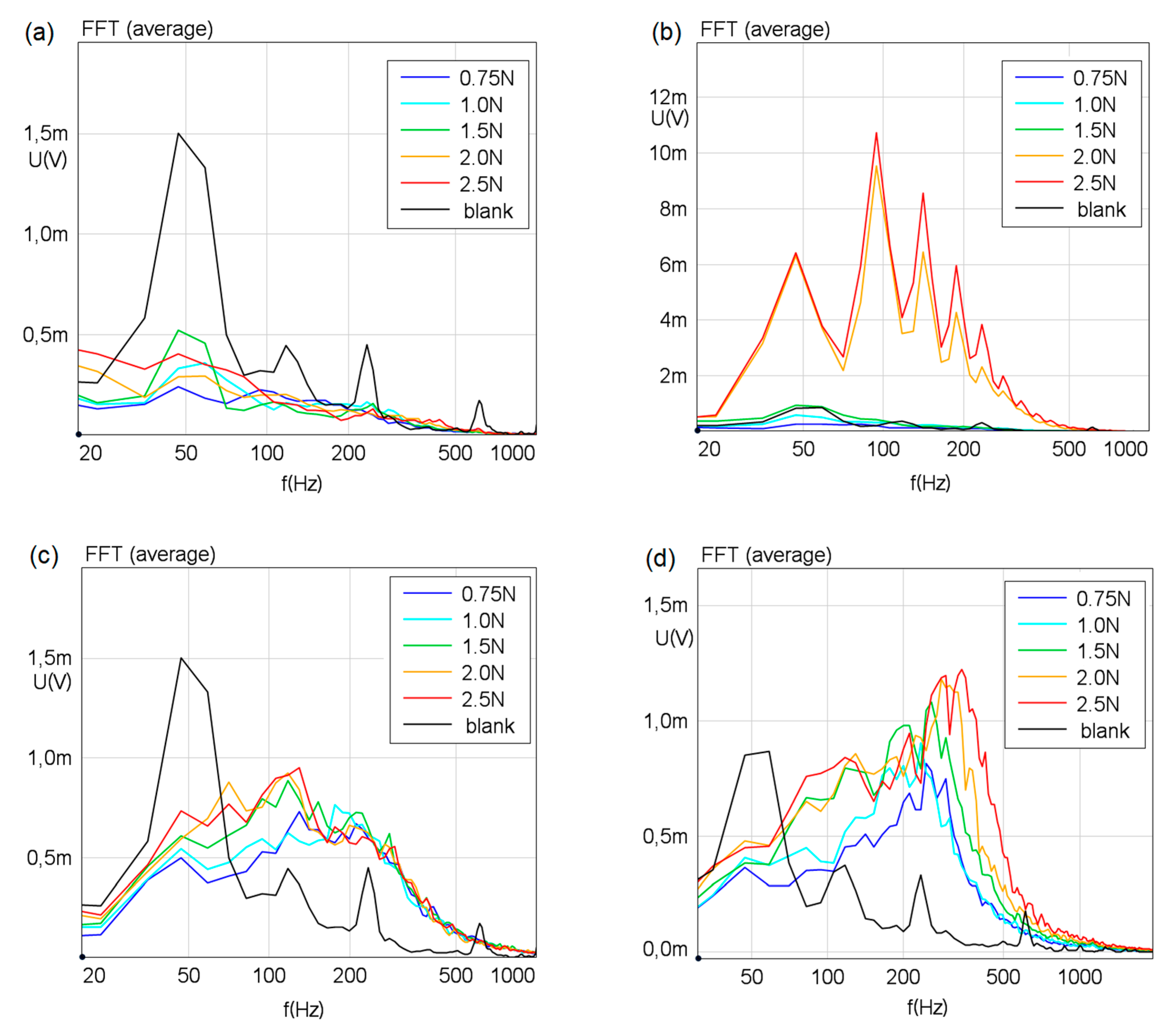
3.2. Vibrations
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Spence, C.; Gallace, A. Multisensory design: Reaching out to touch the consumer. Psychol. Mark. 2011, 28, 267–308. [Google Scholar] [CrossRef]
- Aktar, T.; Chen, J.; Ettelaie, R.; Holmes, M.; Henson, B. Human roughness perception and possible factors effecting roughness sensation. J. Texture Stud. 2017. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fagiani, R.; Barbieri, M. A contact mechanics interpretation of the duplex theory of tactile texture perception. Tribol. Int. 2016, 101, 49–58. [Google Scholar] [CrossRef]
- Manfredi, L.R.; Saal, H.P.; Brown, K.J.; Zielinski, M.C.; Dammann, J.F., III; Polashock, V.S.; Bensmaia, S.J. Natural scenes in tactile texture. J. Neurophysiol. 2014, 111, 1792–1802. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, Y.; Tiest, W.M.B.; Kappers, A.M.L.; Sano, A. Contact force and scanning velocity during active roughness perception. PLoS ONE 2014, 9, e93363. [Google Scholar] [CrossRef]
- Eck, J.; Kaas, A.L.; Mulders, J.L.J.; Goebel, R. Roughness perception of unfamiliar dot pattern textures. Acta Psychol. 2013, 143, 20–34. [Google Scholar] [CrossRef]
- Weber, A.I.; Saal, H.P.; Lieber, J.D.; Cheng, J.; Manfredi, L.R.; Dammann, J.F., III; Bensmaia, S.J. Spatial and temporal codes mediate the tactile perception of natural textures. Proc. Natl. Acad. Sci. USA 2013, 110, 17107–17112. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Ge, S. Experimental research on the tactile perception from fingertip skin friction. Wear 2017, 376, 305–314. [Google Scholar] [CrossRef]
- Ding, S.; Bhushan, B. Tactile perception of skin and skin cream by friction induced vibrations. J. Colloid Interface Sci. 2016, 481, 131–143. [Google Scholar] [CrossRef]
- Messaoud, W.B.; Bueno, M.A.; Lemaire-Semail, B. Relation between human perceived friction and finger friction characteristics. Tribol. Int. 2016, 98, 261–269. [Google Scholar] [CrossRef]
- Li, W.; Zhan, M.L.; Yu, Q.Y.; Zhang, B.Y.; Zhou, Z.R. Quantitative assessment of friction perception for fingertip touching with different roughness surface. Biosurf. Biotribol. 2015, 1, 278–286. [Google Scholar] [CrossRef] [Green Version]
- Schreiner, S.; Rechberger, M.; Bertling, J. Haptic perception of friction—Correlating friction measurements of skin against polymer surfaces with subjective evaluations of the surfaces’ grip. Tribol. Int. 2013, 63, 21–28. [Google Scholar] [CrossRef]
- Tiest, W.M.B.; Kappers, A.M.L. Tactile perception of thermal diffusivity. Atten. Percept. Psychophys. 2009, 71, 481–489. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jones, L.A.; Ho, H.N. Warm or Cool, Large or Small? The Challenge of Thermal Displays. IEEE Trans. Haptics 2008, 1, 53–70. [Google Scholar] [CrossRef]
- Hu, J.; Zhao, Q.; Jiang, R.; Wang, R.; Ding, X. Responses of cutaneous mechanoreceptors within fingerpad to stimulus information for tactile softness sensation of materials. Cogn. Neurodyn. 2013, 7, 441–447. [Google Scholar] [CrossRef] [Green Version]
- Friedman, R.M.; Hester, K.D.; Green, B.G.; LaMotte, R.H. Magnitude estimation of softness. Exp. Brain Res. 2008, 191, 133–142. [Google Scholar] [CrossRef] [Green Version]
- Tiest, W.M.B.; Kappers, A. Cues for Haptic Perception of Compliance. IEEE Trans. Haptics 2009, 2, 189–199. [Google Scholar] [CrossRef]
- Srinivasan, M.A.; LaMotte, R.H. Tactual discrimination of softness. J. Neurophysiol. 1995, 73, 88–101. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, S.; Nagano, H.; Yamada, Y. Psychophysical dimensions of tactile perception of textures. IEEE Trans. Haptics 2013, 6, 81–93. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Shao, F.; Barnes, C.; Childs, T.; Henson, B. Exploring Relationships between Touch Perception and Surface Physical Properties. Int. J. Des. 2009, 3, 67–76. [Google Scholar]
- Goodman, J.M.; Bensmaia, S.J. A Variation Code Accounts for the Perceived Roughness of Coarsely Textured Surfaces. Sci. Rep. 2017, 7, 46699. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hollins, M.; Bensmaia, S.J. The coding of roughness. Can. J. Exp. Psychol. 2007, 61, 184–195. [Google Scholar] [CrossRef] [PubMed]
- Fagiani, R.; Massi, F.; Chatelet, E.; Costes, J.P.; Berthier, Y. Contact of a Finger on Rigid Surfaces and Textiles: Friction Coefficient and Induced Vibrations. Tribol. Lett. 2012, 48, 145–158. [Google Scholar] [CrossRef]
- Saal, H.P.; Wang, X.; Bensmaia, S.J. Importance of spike timing in touch: An analogy with hearing? Curr. Opin. Neurobiol. 2016, 40, 142–149. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wandersman, E.; Candelier, R.; Debregeas, G.; Prevost, A. Texture-induced modulations of friction force: The fingerprint effect. Phys. Rev. Lett. 2011, 107, 164301. [Google Scholar] [CrossRef] [Green Version]
- Muniak, M.A.; Ray, S.; Hsiao, S.S.; Dammann, J.F.; Bensmaia, S.J. The neural coding of stimulus intensity: Linking the population response of mechanoreceptive afferents with psychophysical behavior. J. Neurosci. 2007, 27, 11687–11699. [Google Scholar] [CrossRef]
- Mackevicius, E.L.; Best, M.D.; Saal, H.P.; Bensmaia, S.J. Millisecond precision spike timing shapes tactile perception. J. Neurosci. 2012, 32, 15309–15317. [Google Scholar] [CrossRef] [Green Version]
- Fagiani, R.; Barbieri, M. Modelling of finger-surface contact dynamics. Tribol. Int. 2014, 74, 130–137. [Google Scholar] [CrossRef]
- Schwartz, D.; Magen, Y.K.; Levy, A.; Gefen, A. Effects of humidity on skin friction against medical textiles as related to prevention of pressure injuries. Int. Wound J. 2018, 15, 866–874. [Google Scholar] [CrossRef]
- Vilhena, L.; Ramalho, A. Friction of Human Skin against Different Fabrics for Medical Use. Lubricants 2016, 4, 6. [Google Scholar] [CrossRef]
- Rotaru, G.M.; Pille, D.; Lehmeier, F.K.; Stämpfli, R.; Scheel-Sailer, A.; Rossi, R.M.; Derler, S. Friction between human skin and medical textiles for decubitus prevention. Tribol. Int. 2013, 65, 91–96. [Google Scholar] [CrossRef]
- Gerhardt, L.C.; Strassle, V.; Lenz, A.; Spencer, N.D.; Derler, S. Influence of epidermal hydration on the friction of human skin against textiles. J. R. Soc. Interface 2008, 5, 1317–1328. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Johnson, S.A.; Gorman, D.M.; Adams, M.J.; Briscoe, B.J. The friction and lubrication of human stratum corneum. In Thin Films in Tribology, Proceedings of the 19th Leeds-Lyon Symposium on Tribology, Institute of Tribology, 8-11 September 1992, University of Leeds, Leeds, UK; Elsevier: Amsterdam, The Netherlands, 1993; Volume 25, pp. 663–672. [Google Scholar]
- Derler, S.; Gerhardt, L.C. Tribology of Skin: Review and Analysis of Experimental Results for the Friction Coefficient of Human Skin. Tribol. Lett. 2012, 45, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Adams, M.J.; Briscoe, B.J.; Johnson, S.A. Friction and lubrication of human skin. Tribol. Lett. 2007, 26, 239–253. [Google Scholar] [CrossRef]
- Briscoe, B.J.; Tabor, D. Shear Properties of Thin Polymeric Films. J. Adhes. 1978, 9, 145–155. [Google Scholar] [CrossRef]
- Tabor, D. The Role of Surface and Intermolecular Forces in Thin Film Lubrication. In Microscopic Aspects of Adhesion and Lubrication, Proceedings of the 34th International Meeting of the Société de Chimie Physique, 14-18 September 1981, Paris, France; Elsevier: Amsterdam, The Netherlands, 1981; Volume 7, pp. 651–682. [Google Scholar]
- Pasumarty, S.M.; Johnson, S.A.; Watson, S.A.; Adams, M.J. Friction of the Human Finger Pad: Influence of Moisture, Occlusion and Velocity. Tribol. Lett. 2011, 44, 117–137. [Google Scholar] [CrossRef]
- Adams, M.J.; Johnson, S.A.; Lefevre, P.; Levesque, V.; Hayward, V.; Andre, T.; Thonnard, J.L. Finger pad friction and its role in grip and touch. J. R. Soc. Interface 2013, 10, 20120467. [Google Scholar] [CrossRef] [Green Version]
- Hendriks, C.P.; Franklin, S.E. Influence of Surface Roughness, Material and Climate Conditions on the Friction of Human Skin. Tribol. Lett. 2010, 37, 361–373. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Tabor, D. The Friction of Hard Sliders on Lubricated Rubber: The Importance of Deformation Losses. Proc. Phys. Soc. 1958, 71, 989–1001. [Google Scholar] [CrossRef]
- Tomlinson, S.E.; Carré, M.J.; Lewis, R.; Franklin, S.E. Human finger contact with small, triangular ridged surfaces. Wear 2011, 271, 2346–2353. [Google Scholar] [CrossRef] [Green Version]
- Singer, I.L.; Pollock, H.M.; Adams, M.J. Friction of Granular Non-Metals. In Fundamentals of Friction: Macroscopic and Microscopic Processes; Springer Netherlands: Dordrecht, The Netherlands, 1992; Volume 220, pp. 183–209. [Google Scholar]
- Morales-Hurtado, M.; Vries, E.G.; de Peppelman, M.; Zeng, X.; van Erp, P.E.J.; van der Heide, E. On the role of adhesive forces in the tribo-mechanical performance of ex vivo human skin. Tribol. Int. 2017, 107, 25–32. [Google Scholar] [CrossRef]
- Derler, S.; Rossi, R.M.; Rotaru, G.M. Understanding the variation of friction coefficients of human skin as a function of skin hydration and interfacial water films. Proc. Inst. Mech. Eng. 2015, 229, 285–293. [Google Scholar] [CrossRef]
- Tomlinson, S.E.; Lewis, R.; Liu, X.; Texier, C.; Carré, M.J. Understanding the Friction Mechanisms Between the Human Finger and Flat Contacting Surfaces in Moist Conditions. Tribol. Lett. 2011, 41, 283–294. [Google Scholar] [CrossRef] [Green Version]
- Derler, S.; Gerhardt, L.C.; Lenz, A.; Bertaux, E.; Hadad, M. Friction of human skin against smooth and rough glass as a function of the contact pressure. Tribol. Int. 2009, 42, 1565–1574. [Google Scholar] [CrossRef]
- Dzidek, B.; Bochereau, S.; Johnson, S.A.; Hayward, V.; Adams, M.J. Why pens have rubbery grips. Proc. Natl. Acad. Sci. USA 2017, 114, 10864–10869. [Google Scholar] [CrossRef] [Green Version]
- Derler, S.; Preiswerk, M.; Rotaru, G.M.; Kaiser, J.-P.; Rossi, R.M. Friction mechanisms and abrasion of the human finger pad in contact with rough surfaces. Tribol. Int. 2015, 89, 119–127. [Google Scholar] [CrossRef]
- Archard, J.F. Elastic deformation and the laws of friction. Proc. R. Soc. Lond. A 1957, 243, 190–205. [Google Scholar] [CrossRef]
- Ciavarella, M.; Delfine, V.; Demelio, G. A “re-vitalized” Greenwood and Williamson model of elastic contact between fractal surfaces. J. Mech. Phys. Solids 2006, 54, 2569–2591. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of Nominally Flat Surfaces. Proc. R. Soc. A Math. Phys. Eng. Sci. 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Popov, V.L. Contact Mechanics and Friction: Physical Principles and Applications, 1st ed.; Springer: Berlin, Germany, 2010. [Google Scholar]
- Dzidek, B.M.; Adams, M.J.; Andrews, J.W.; Zhang, Z.; Johnson, S.A. Contact mechanics of the human finger pad under compressive loads. J. R. Soc. Interface 2017, 14, 20160935. [Google Scholar] [CrossRef]
- Liu, X.; Lu, Z.; Lewis, R.; Carré, M.J.; Matcher, S.J. Feasibility of using optical coherence tomography to study the influence of skin structure on finger friction. Tribol. Int. 2013, 63, 34–44. [Google Scholar] [CrossRef]
- Yi, Z.; Zhang, Y.; Peters, J. Bioinspired tactile sensor for surface roughness discrimination. Sens. Actuators A Phys. 2017, 255, 46–53. [Google Scholar] [CrossRef]
- Nawid, J.; Claude, S. IEEE International Conference on Robotics and Automation (ICRA), 2010, Anchorage, AK, USA, 3–8 May 2010; IEEE: Piscataway, NJ, USA, 2010. [Google Scholar]
- Takamuku, S.; Gomez, G.; Hosoda, K.; Pfeifer, R. Haptic discrimination of material properties by a robotic hand. In 2007 IEEE 6th International Conference on Development and Learning, IEEE 6th International Conference on: date, 11–13 July, 2007; IEEE Xplore: Piscataway, NJ, USA, 2007; pp. 1–6. [Google Scholar]
- Fishel, J.A.; Loeb, G.E. Bayesian exploration for intelligent identification of textures. Front. Neurorobotics 2012, 6, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, S.; Ge, S.; Tang, W.; Zhang, J.; Chen, N. Tactile perception of fabrics with an artificial finger compared to human sensing. Text. Res. J. 2015, 85, 2177–2187. [Google Scholar] [CrossRef]
- Ganguly, S.; Das, S.; Das, N. Chapter 16—Characterization tools and techniques of hydrogels. In Hydrogels Based on Natural Polymers; Elsevier: Amsterdam, The Netherlands, 2019; pp. 481–517. [Google Scholar] [CrossRef]
- Zahouani, H.; Mezghani, S.; Vargiolu, R.; Hoc, T.; Mansori, M.E.L. Effect of roughness on vibration of human finger during a friction test. Wear 2013, 301, 343–352. [Google Scholar] [CrossRef]
- Delhaye, B.; Barrea, A.; Edin, B.B.; Lefevre, P.; Thonnard, J.-L. Surface strain measurements of fingertip skin under shearing. J. R. Soc. Interface 2016, 13, 20150874. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Maiti, R.; Lu, Z.H.; Carré, M.J.; Matcher, S.J.; Lewis, R. New Non-invasive Techniques to Quantify Skin Surface Strain and Sub-surface Layer Deformation of Finger-pad during Sliding. Biotribology 2017, 12, 52–58. [Google Scholar] [CrossRef]
- Zimin, D.; Schmidt, K.; Lim, G.T.; Ranft, M.; Terrenoire, A.; Korb, H.; Sandler, J.; Fery, A.; Altstädt, V.; Krausch, G. Relating Haptic Perception of Polymer Surfaces to their Objective Properties. Zeitschrift Kunststofftechnik. Bd. 6. H. 1. München. Hanser. S. 50—64 2009. ISBN/ISSN 1864-2217. [Google Scholar]
- Yao, B.G.; Peng, Y.L.; Yang, Y.J. Mechanical Measurement System and Precision Analysis for Tactile Property Evaluation of Porous Polymeric Materials. Polymers 2018, 10, 373. [Google Scholar] [CrossRef] [Green Version]
- Gruber, D.P.; Winkler, G.; Resch, K. Comprehensive study on the light shielding potential of thermotropic layers for the development of new materials. Appl. Opt. 2015, 54, 150–156. [Google Scholar] [CrossRef]
- Anderson, R.R.; Parrish, J.A. The optics of human skin. J. Investig. Dermatol. 1981, 77, 13–19. [Google Scholar] [CrossRef] [Green Version]
- Van Rossum, G.; Drake, F.L.J. Python Tutorial; Centrum voor Wiskunde en Informatica: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Bradski, G. The OpenCV Library. Dr. Dobbs J. Softw. Tools 2000, 120, 122–125. [Google Scholar]
- Gadelmawlaa, E.S.; Kourab, M.M.; Maksoud, T.M.A.; Elewa, I.M.; Soliman, H.H. Roughness parameters. J. Mater. Process. Technol. 2002, 123, 133–145. [Google Scholar] [CrossRef]
- Dzidek, B.M.; Adams, M.; Zhang, Z.; Johnson, S.; Bochereau, S.; Hayward, V. Role of Occlusion in Non-Coulombic Slip of the Finger Pad. In Haptics: Neuroscience, Devices, Modeling, and Applications; Auvray, M., Duriez, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8618, pp. 109–116. [Google Scholar] [CrossRef]
- Hausberger, A.; Major, Z.; Theiler, G.; Gradt, T. Observation of the adhesive- and deformation-contribution to the friction and wear behaviour of thermoplastic polyurethanes. Wear 2018, 412, 14–22. [Google Scholar] [CrossRef]
- Xydas, N.; Kao, I. Modeling of Contact Mechanics and Friction Limit Surfaces for Soft Fingers in Robotics, with Experimental Results. Int. J. Robot. Res. 1999, 18, 941–950. [Google Scholar] [CrossRef]
- Fung, Y.C. Biomechanics: Mechanical Properties of Living Tissues, 2nd ed.; Springer: New York, NY, USA, 1993. [Google Scholar]
- Kinoshita, H.; Bäckström, L.; Flanagan, J.R.; Johansson, R.S. Tangential torque effects on the control of grip forces when holding objects with a precision grip. J. Neurophysiol. 1997, 78, 1619–1630. [Google Scholar] [CrossRef]
- Fagiani, R.; Massi, F.; Chatelet, E.; Berthier, Y.; Akay, A. Tactile perception by friction induced vibrations. Tribol. Int. 2011, 44, 1100–1110. [Google Scholar] [CrossRef]






| Formulation | Filler Type | Filler Concentration (wt.%) |
|---|---|---|
| S1 | - | - |
| S2 | Polyurethane (Decosoft® 60D) | 7.7 |
| Formulation | Sa (µm) | Ssk (/) | Sku (/) |
|---|---|---|---|
| S1 | 0.16 | 0.76 | 47.9 |
| S2 | 5.74 | 0.98 | 4.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ules, T.; Hausberger, A.; Grießer, M.; Schlögl, S.; Gruber, D.P. Introduction of a New In-Situ Measurement System for the Study of Touch-Feel Relevant Surface Properties. Polymers 2020, 12, 1380. https://doi.org/10.3390/polym12061380
Ules T, Hausberger A, Grießer M, Schlögl S, Gruber DP. Introduction of a New In-Situ Measurement System for the Study of Touch-Feel Relevant Surface Properties. Polymers. 2020; 12(6):1380. https://doi.org/10.3390/polym12061380
Chicago/Turabian StyleUles, Thomas, Andreas Hausberger, Michael Grießer, Sandra Schlögl, and Dieter P. Gruber. 2020. "Introduction of a New In-Situ Measurement System for the Study of Touch-Feel Relevant Surface Properties" Polymers 12, no. 6: 1380. https://doi.org/10.3390/polym12061380
APA StyleUles, T., Hausberger, A., Grießer, M., Schlögl, S., & Gruber, D. P. (2020). Introduction of a New In-Situ Measurement System for the Study of Touch-Feel Relevant Surface Properties. Polymers, 12(6), 1380. https://doi.org/10.3390/polym12061380