Interfacial Polarization in Thermoplastic Basalt Fiber-Reinforced Composites
Abstract
:1. Introduction
2. Materials and Methods
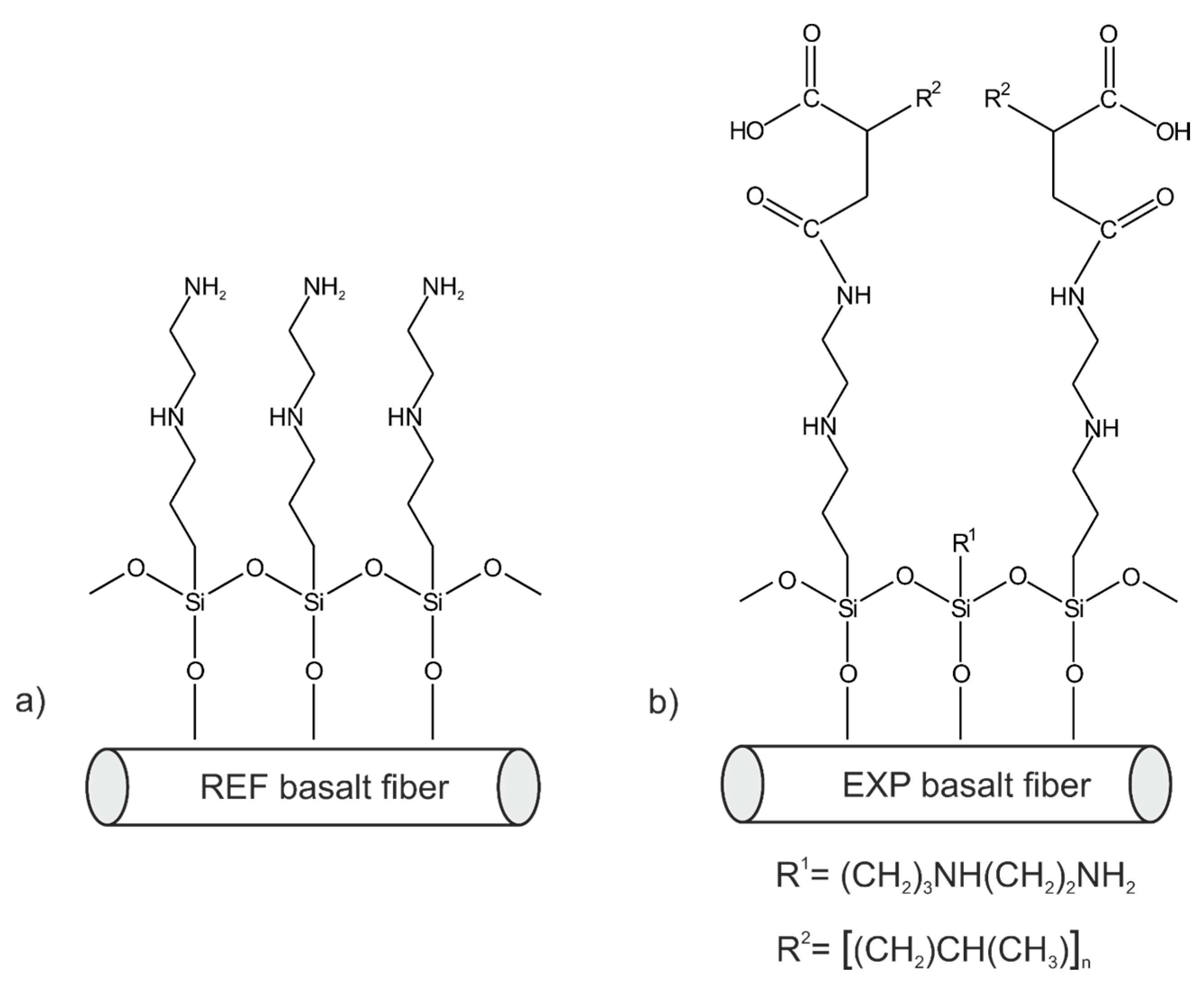
2.1. Materials
2.2. Methods
3. Results and Discussion
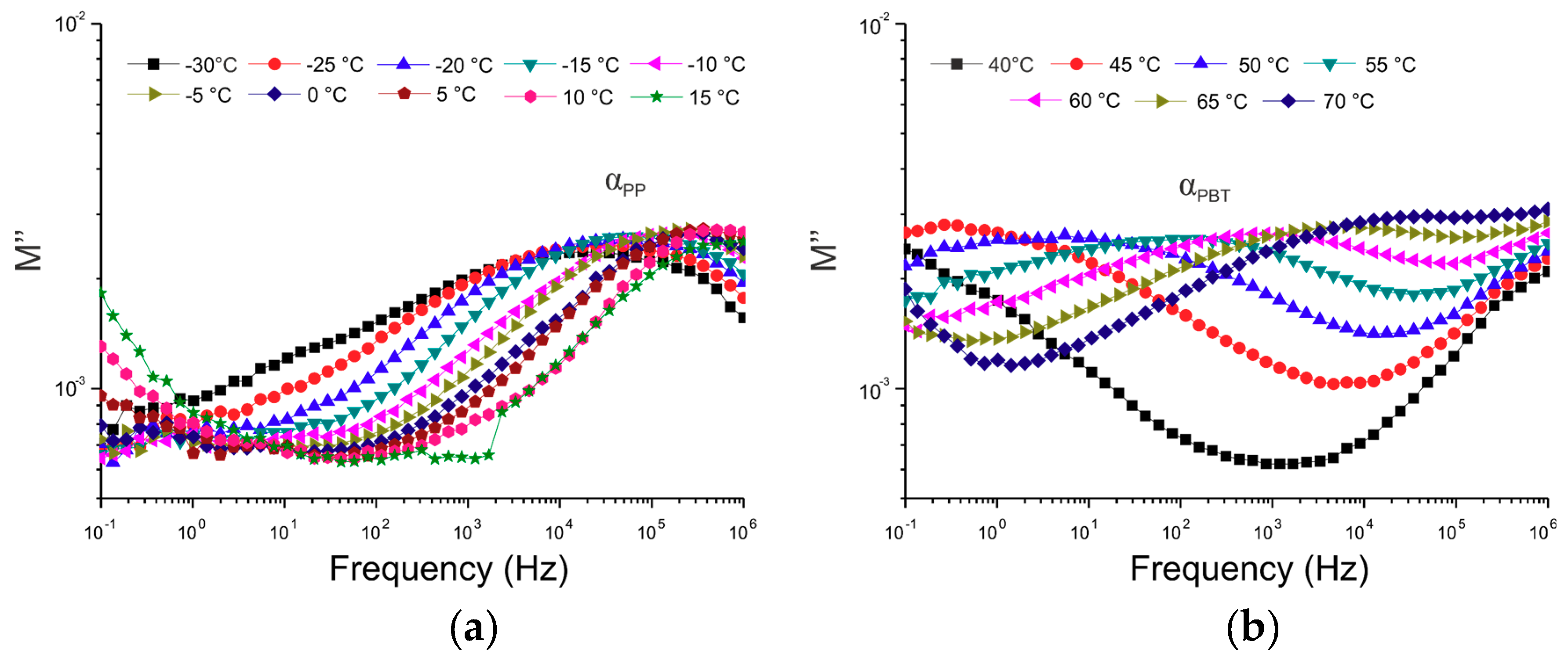
3.1. Thermal Properties
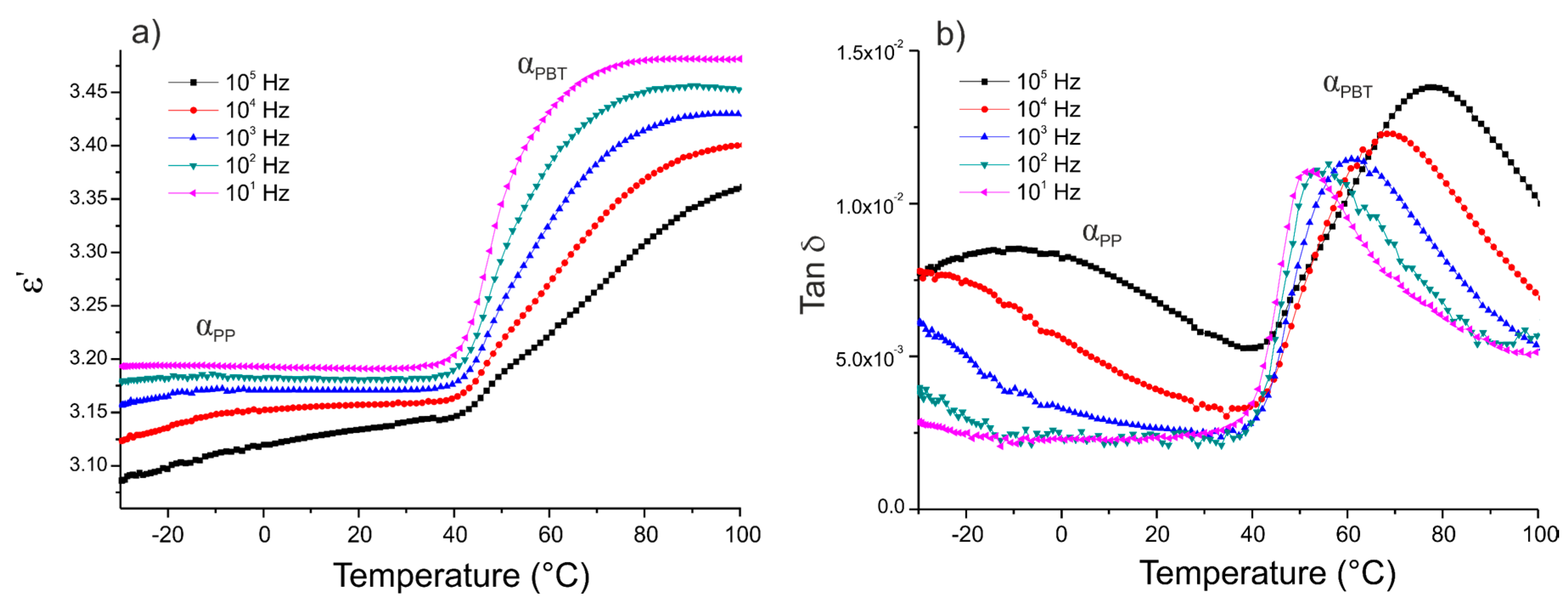
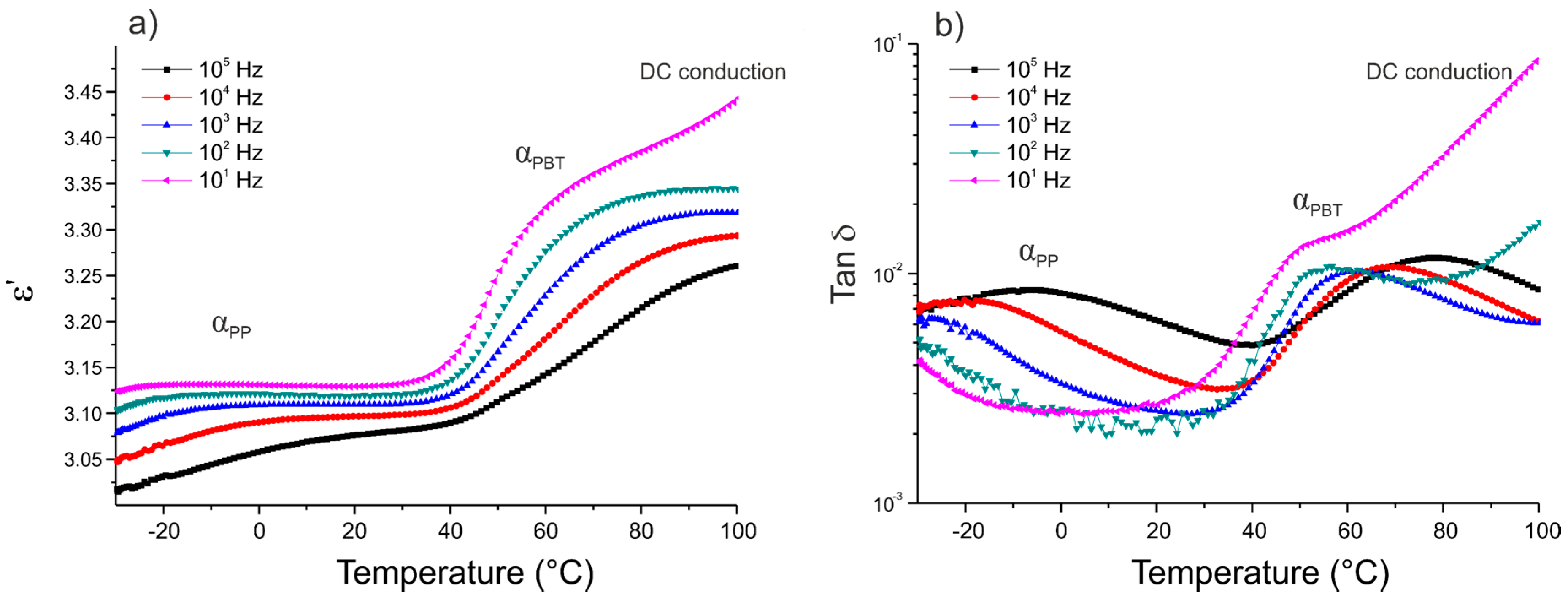
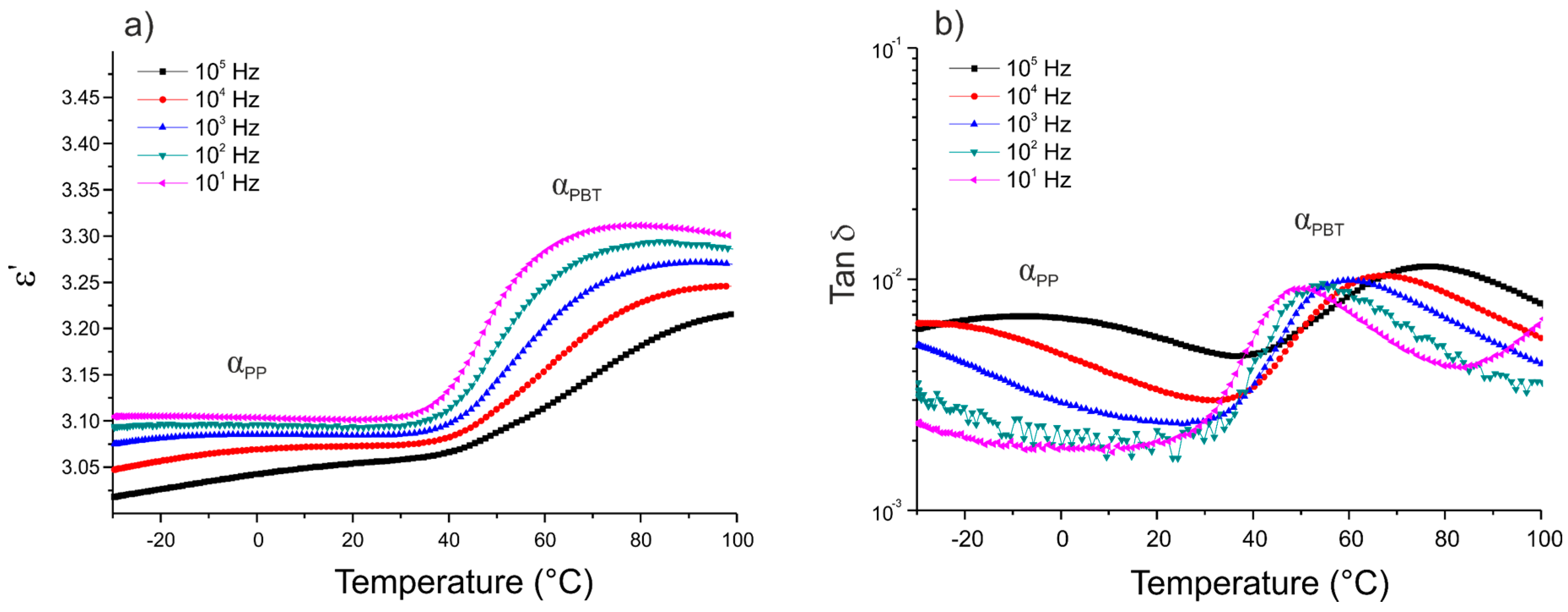
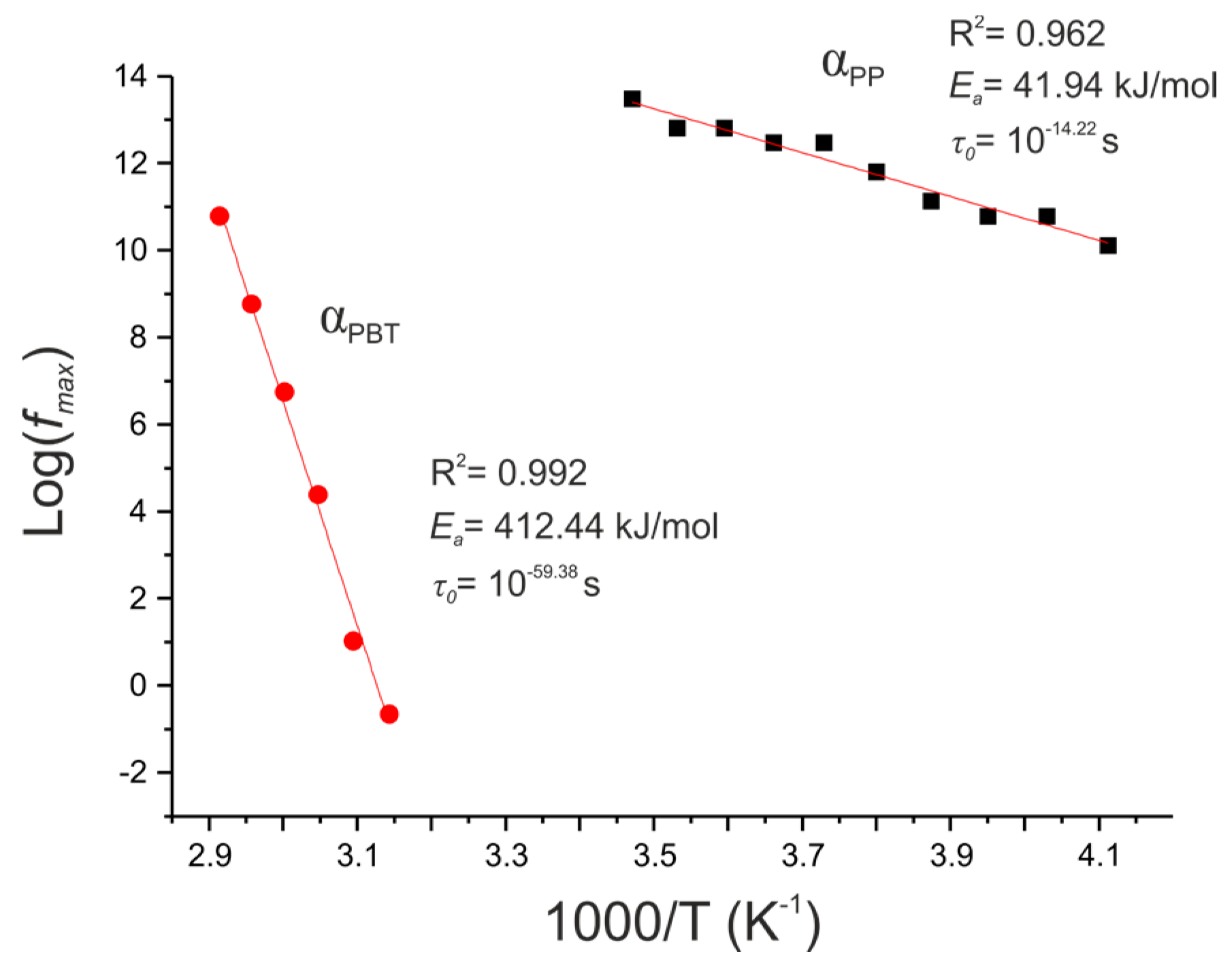
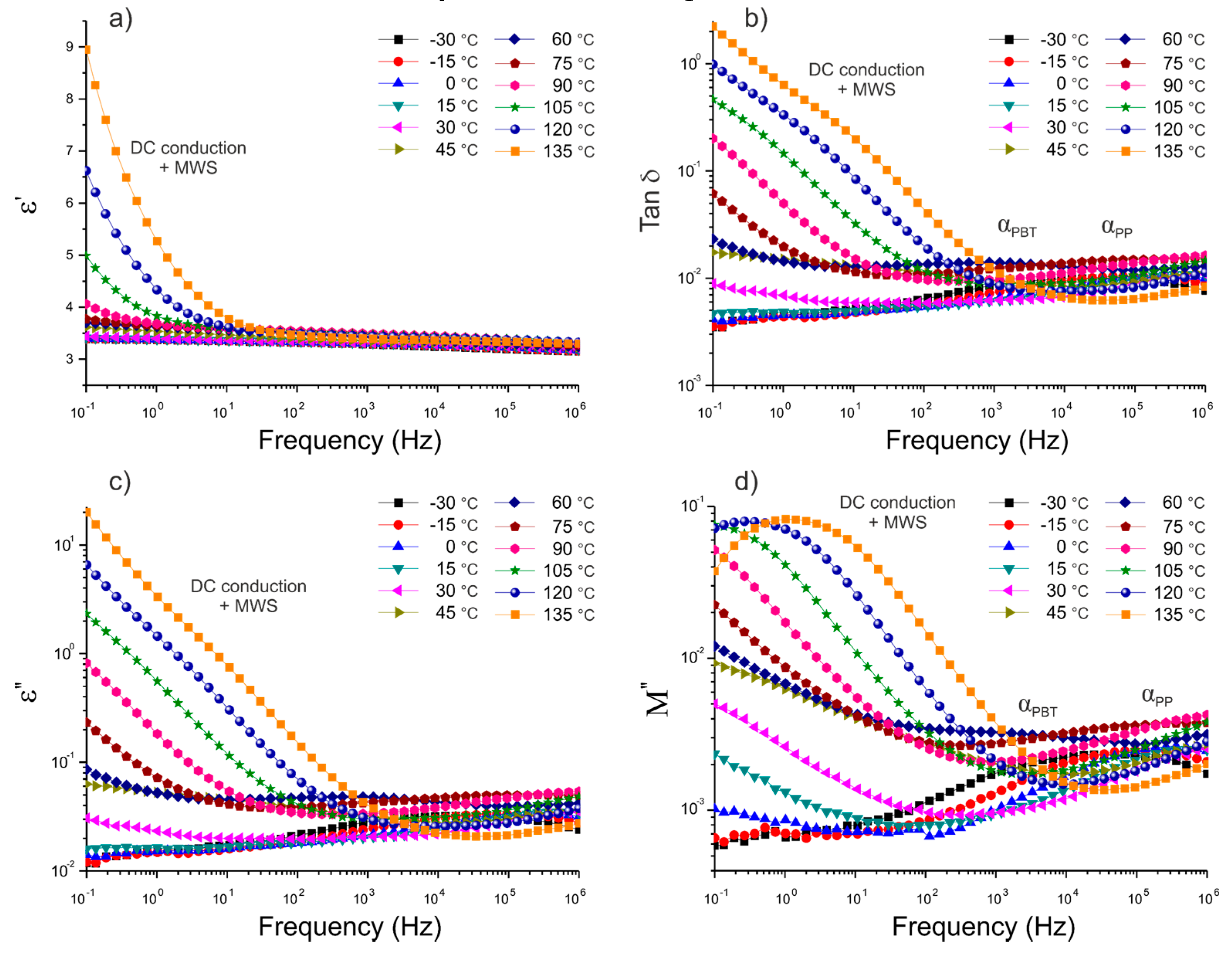
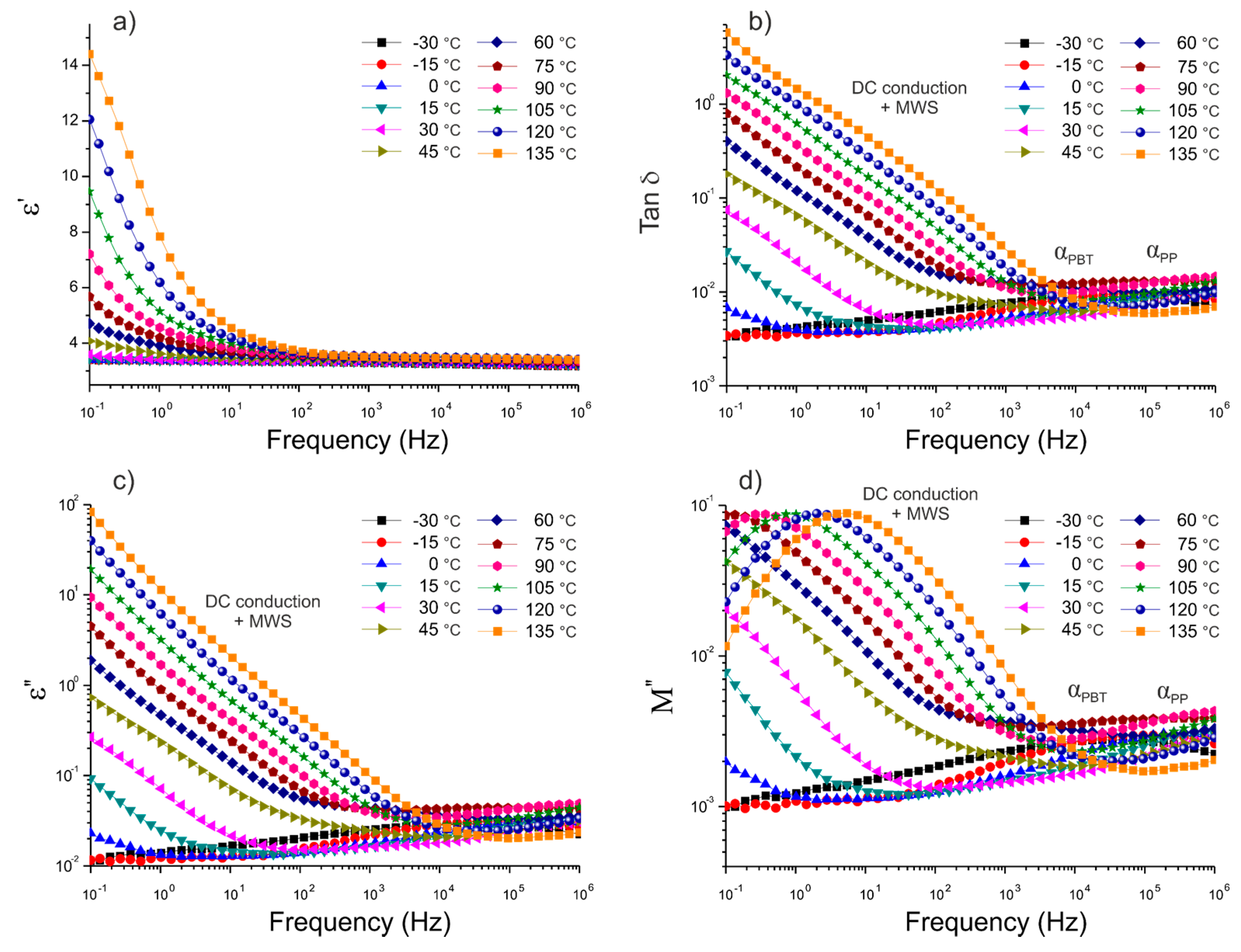
3.2. Dielectric Properties
3.3. Mechanical Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yin, M.; Liu, F.; He, J. Preparation and characterization of Bis-GMA free dental resin system with synthesized dimethacrylate monomer TDDMMA derived from tricyclo[5.2.1.0(2,6)]-decanedimethanol. J. Mech. Behav. Biomed. Mater. 2015, 57, 157–163. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wang, Y.; Gu, C.; Liu, J.; Liu, Y.; Li, M.; Lu, Y. Enhancement of the Mechanical Properties of Basalt Fiber-Wood-Plastic Composites via Maleic Anhydride Grafted High-Density Polyethylene (MAPE) Addition. Materials 2013, 6, 2483–2496. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Niemczyk, A.; Dziubek, K.; Sacher-Majewska, B.; Czaja, K.; Czech-Polak, J.; Oliwa, R.; Lenża, J.; Szołyga, M. Thermal Stability and Flame Retardancy of Polypropylene Composites Containing Siloxane-Silsesquioxane Resins. Polymers 2018, 10, 1019. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Noorunnisa Khanam, P.; AlMaadeed, M.A. Improvement of ternary recycled polymer blend reinforced with date palm fibre. Mater. Des. 2014, 60, 532–539. [Google Scholar] [CrossRef]
- Song, Y.; Shen, Y.; Liu, H.; Lin, Y.; Li, M.; Nan, C.-W. Improving the dielectric constants and breakdown strength of polymer composites: Effects of the shape of the BaTiO3 nanoinclusions, surface modification and polymer matrix. J. Mater. Chem. 2012, 22, 16491. [Google Scholar] [CrossRef]
- Kremer, F. Dielectric spectroscopy—Yesterday, today and tomorrow. J. Non-Cryst. Solids 2002, 305, 1–9. [Google Scholar] [CrossRef]
- Hammami, H.; Arous, M.; Lagache, M.; Kallel, A. Study of the interfacial MWS relaxation by dielectric spectroscopy in unidirectional PZT fibres/epoxy resin composites. J. Alloys Compd. 2007, 430, 1–8. [Google Scholar] [CrossRef]
- Liu, X.; Yu, L.; Nie, Y.; Skov, A.L. Silicone Elastomers with High-Permittivity Ionic Liquids Loading. Adv. Eng. Mater. 2019, 21, 1900481. [Google Scholar] [CrossRef] [Green Version]
- Banakar, P.; Shivanand, H.; Niranjan, H. Mechanical Properties of Angle Ply Laminated Composites-A Review. Int. J. Pure Appl. Sci. Technol. 2012, 9, 127–133. [Google Scholar]
- Deák, T.; Czigány, T.; Tamás, P.; Németh, C. Enhancement of interfacial properties of basalt fiber reinforced nylon 6 matrix composites with silane coupling agents. Express Polym. Lett. 2010, 4, 590–598. [Google Scholar] [CrossRef]
- Sim, J.; Park, C.; Moon, D.Y. Characteristics of basalt fiber as a strengthening material for concrete structures. Compos. Part B Eng. 2005, 36, 504–512. [Google Scholar] [CrossRef]
- Elmahdy, A.; Verleysen, P. Mechanical behavior of basalt and glass textile composites at high strain rates: A comparison. Polym. Test. 2020, 81, 106224. [Google Scholar] [CrossRef]
- Ralph, C.; Lemoine, P.; Archer, E.; McIlhagger, A. Mechanical properties of short basalt fibre reinforced polypropylene and the effect of fibre sizing on adhesion. Compos. Part B Eng. 2019, 176, 107260. [Google Scholar] [CrossRef]
- Arslan, C.; Dogan, M. The effects of silane coupling agents on the mechanical properties of basalt fiber reinforced poly(butylene terephthalate) composites. Compos. Part B Eng. 2018, 146, 145–154. [Google Scholar] [CrossRef]
- Kim, M.T.; Kim, M.H.; Rhee, K.Y.; Park, S.J. Study on an oxygen plasma treatment of a basalt fiber and its effect on the interlaminar fracture property of basalt/epoxy woven composites. Compos. Part B Eng. 2011, 42, 499–504. [Google Scholar] [CrossRef]
- Bashtadnik, P.I.; Kabak, A.I.; Yakovchuk, Y.Y. The Effect of Adhesion Interaction on the Mechanical Properties of Thermoplastic Basalt Plastics. Mech. Compos. Mater. 2003, 39, 85–88. [Google Scholar] [CrossRef]
- Botev, M.; Betchev, H.; Bikiaris, D.; Panayiotou, C. Mechanical properties and viscoelastic behavior of basalt fiber-reinforced polypropylene. J. Appl. Polym. Sci. 1999, 74, 523–531. [Google Scholar] [CrossRef]
- Czigány, T.; Pölöskei, K.; Karger-Kocsis, J. Fracture and failure behavior of basalt fiber mat-reinforced vinylester/epoxy hybrid resins as a function of resin composition and fiber surface treatment. J. Mater. Sci. 2005, 40, 5609–5618. [Google Scholar] [CrossRef]
- Lin, J.-H.; Huang, C.-L.; Liu, C.-F.; Chen, C.-K.; Lin, Z.-I.; Lou, C.-W. Polypropylene/Short Glass Fibers Composites: Effects of Coupling Agents on Mechanical Properties, Thermal Behaviors, and Morphology. Materials 2015, 8, 8279–8291. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lopresto, V.; Leone, C.; de Iorio, I. Mechanical characterisation of basalt fibre reinforced plastic. Compos. Part B Eng. 2011, 42, 717–723. [Google Scholar] [CrossRef]
- Arbelaiz, A.; Fernández, B.; Ramos, J.A.; Retegi, A.; Llano-Ponte, R.; Mondragon, I. Mechanical properties of short flax fibre bundle/polypropylene composites: Influence of matrix/fibre modification, fibre content, water uptake and recycling. Compos. Sci. Technol. 2005, 65, 1582–1592. [Google Scholar] [CrossRef]
- Dilsiz, N.; Wightman, J.P. Surface analysis of unsized and sized carbon fibers. Carbon 1999, 37, 1105–1114. [Google Scholar] [CrossRef]
- Zhao, F.M.; Takeda, N. Effect of interfacial adhesion and statistical fiber strength on tensile strength of unidirectional glass fiber/epoxy composites. Part. II: Comparison with prediction. Compos. Part A Appl. Sci. Manuf. 2000, 31, 1215–1224. [Google Scholar] [CrossRef]
- Ignaczak, W.; Sobolewski, P.; El Fray, M. Bio-Based PBT–DLA Copolyester as an Alternative Compatibilizer of PP/PBT Blends. Polymers 2019, 11, 1421. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- El Fray, M.; Słonecki, J. Multiblock terephthalate copolymer as impact modifier for poly(propylene)/poly(butylene terephthalate) blends. Die Angewandte Makromolekulare Chemie 1999, 266, 30–36. [Google Scholar] [CrossRef]
- Rybko, M.; El Fray, M. Study of structure and fatigue strength of thermoplastic elastomers modified with nanoparticles and radiation-crosslinked. Polimery 2014, 59, 400–408. [Google Scholar] [CrossRef]
- Ignaczak, W.; Sui, X.; Kellersztein, I.; Wagner, H.D.; El Fray, M. The effect of fibre sizing and compatibilizer of polypropylene/poly(butylene terephthalate) blends on the mechanical and interphase properties of basalt fibre reinforced composites. Polym. Int. 2018, 67, 414–421. [Google Scholar] [CrossRef]
- Bánhegyi, G.; Hedvig, P.; Petrović, Z.S.; Karasz, F.E. Applied Dielectric Spectroscopy of Polymeric Composites. Polym. Plast. Technol. Eng. 1991, 30, 183–225. [Google Scholar] [CrossRef]
- Jiang, S.; Li, Q.; Zhao, Y.; Wang, J.; Kang, M. Effect of surface silanization of carbon fiber on mechanical properties of carbon fiber reinforced polyurethane composites. Compos. Sci. Technol. 2015, 110, 87–94. [Google Scholar] [CrossRef]
- Shokoohi, S.; Arefazar, A.; Khosrokhavar, R. Silane Coupling Agents in Polymer-based Reinforced Composites: A Review. J. Reinf. Plast. Compos. 2008, 27, 473–485. [Google Scholar] [CrossRef]
- Silva, M.C.; Silva, G.G. A new composite from cellulose industrial waste and elastomeric polyurethane. J. Appl. Polym. Sci. 2005, 98, 336–340. [Google Scholar] [CrossRef]
- Umemura, T.; Suzuki, T.; Kashiwazaki, T. Impurity Effect of the Dielectric Properties of Isotactic Polypropylene. IEEE Trans. Electr. Insul. 1982, EI-17, 300–305. [Google Scholar] [CrossRef]
- Soccio, M.; Nogales, A.; Martín-Fabiani, I.; Lotti, N.; Munari, A.; Ezquerra, T.A. Relaxation dynamics and cold crystallization of poly(pentamethylene terephthalate) as revealed by dielectric spectroscopy. Polymer 2014, 55, 1552–1559. [Google Scholar] [CrossRef] [Green Version]
- Genovese, L.; Soccio, M.; Lotti, N.; Munari, A.; Szymczyk, A.; Paszkiewicz, S.; Linares, A.; Nogales, A.; Ezquerra, T.A. Effect of chemical structure on the subglass relaxation dynamics of biobased polyesters as revealed by dielectric spectroscopy: 2,5-furandicarboxylic acid vs. trans -1,4-cyclohexanedicarboxylic acid. Phys. Chem. Chem. Phys. 2018, 20, 15696–15706. [Google Scholar] [CrossRef] [PubMed]
- Drobny, J.G. Handbook of Thermoplastic Elastomers; William Andrew Publishing: Norwich, NY, USA, 2007; Volume 53, ISBN 978-0-8155-1549-4. [Google Scholar]
- Drobny, J.G. Chapter 5: Styrenic Block Copolymers. In Handbook of Thermoplastic Elastomers, 2nd ed.; William Andrew Publishing: Norwich, NY, USA, 2014; pp. 175–194. ISBN 9780323221368. [Google Scholar]
- Amin Omri, M.; Triki, A.; Ben Hassen, M.; Arous, M.; Bulou, A. Influence of wool and thermo-binder fibers relative fractions on the adhesion of non-woven Alfa fibers reinforced unsaturated polyester hybrid composites. Phys. E Low-Dimens. Syst. Nanostruct. 2016, 84, 316–323. [Google Scholar] [CrossRef]
- Steeman, P.A.M.; van Turnhout, J. Fine Structure in the Parameters of Dielectric and Viscoelastic Relaxations. Macromolecules 1994, 27, 5421–5427. [Google Scholar] [CrossRef]
- Triki, A.; Guicha, M.; Ben Hassen, M.; Arous, M. Comparative study of the dielectric properties of natural-fiber-matrix composites and E-glass-matrix composites. J. Appl. Polym. Sci. 2013, 129, 487–498. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, X.; Zhang, H. Influence of the relaxation of Maxwell-Wagner-Sillars polarization and dc conductivity on the dielectric behaviors of nylon 1010. J. Appl. Phys. 2006, 100, 054104. [Google Scholar] [CrossRef]
- Samet, M.; Levchenko, V.; Boiteux, G.; Seytre, G.; Kallel, A.; Serghei, A. Electrode polarization vs. Maxwell-Wagner-Sillars interfacial polarization in dielectric spectra of materials: Characteristic frequencies and scaling laws. J. Chem. Phys. 2015, 142, 194703. [Google Scholar] [CrossRef]
- Hernández, M.; Carretero-González, J.; Verdejo, R.; Ezquerra, T.A.; López-Manchado, M.A. Molecular Dynamics of Natural Rubber/Layered Silicate Nanocomposites As Studied by Dielectric Relaxation Spectroscopy. Macromolecules 2010, 43, 643–651. [Google Scholar] [CrossRef] [Green Version]
- Tsangaris, G.M.; Psarras, G.C.; Kouloumbi, N. Electric modulus and interfacial polarization in composite polymeric systems. J. Mater. Sci. 1998, 33, 2027–2037. [Google Scholar] [CrossRef]
- Ben Amor, I.; Rekik, H.; Kaddami, H.; Raihane, M.; Arous, M.; Kallel, A. Studies of dielectric relaxation in natural fiber–polymer composites. J. Electrost. 2009, 67, 717–722. [Google Scholar] [CrossRef]
- Ben Amor, I.; Rekik, H.; Kaddami, H.; Raihane, M.; Arous, M.; Kallel, A. Effect of Palm Tree Fiber Orientation on Electrical Properties of Palm Tree Fiber-reinforced Polyester Composites. J. Compos. Mater. 2010, 44, 1553–1568. [Google Scholar] [CrossRef]
- Havriliak, S.; Negami, S. A complex plane analysis of α-dispersions in some polymer systems. J. Polym. Sci. Part C Polym. Symp. 1966, 14, 99–117. [Google Scholar] [CrossRef]
- Havriliak, S.; Negami, S. A complex plane representation of dielectric and mechanical relaxation processes in some polymers. Polymer 1967, 8, 161–210. [Google Scholar] [CrossRef]
- Omri, M.A.; Triki, A.; Guicha, M.; Hassen, M.B.; Arous, M.; Bulou, A. Effect of wool fibers on thermal and dielectric properties of Alfa fibers reinforced polyester composite. Mater. Chem. Phys. 2016, 170, 312–318. [Google Scholar] [CrossRef]
- Ghallabi, Z.; Rekik, H.; Boufi, S.; Arous, M.; Kallel, A. Effect of the interface treatment on the dielectric behavior of composite materials of unsaturated polyester reinforced by Alfa fiber. J. Non-Cryst. Solids 2010, 356, 684–687. [Google Scholar] [CrossRef]
- Shinyashiki, N.; Miyara, M.; Nakano, S.; Yamamoto, W.; Ueshima, M.; Imoto, D.; Sasaki, K.; Kita, R.; Yagihara, S. Dielectric relaxation strength and magnitude of dipole moment of poly(vinyl pyrrolidone)in polar solutions. J. Mol. Liq. 2013, 181, 110–114. [Google Scholar] [CrossRef]
- Omri, M.A.; Sanjay, M.R.; Triki, A.; Yogesha, B.; Kallel, A. Dielectric properties and interfacial adhesion of jute, kenaf and E-glass fabrics reinforcing epoxy composites. Polym. Compos. 2019, 40, 2142–2153. [Google Scholar] [CrossRef]
- Greco, A.; Maffezzoli, A.; Casciaro, G.; Caretto, F. Mechanical properties of basalt fibers and their adhesion to polypropylene matrices. Compos. Part B Eng. 2014, 67, 233–238. [Google Scholar] [CrossRef]


| Matrix | Fiber | Tc1 (°C) | Tc2 (°C) | Tm1 (°C) | Tm2 (°C) | Tg1 (°C) | Tg2 (°C) |
|---|---|---|---|---|---|---|---|
| 50/50 | - | 122.9 | 193.3 | 160.6 | 223.3 | −6.3 | 44.0 |
| REF | 120.8 | 195.8 | 160.5 | 223.9 | −7.6 | 42.6 | |
| EXP | 120.7 | 194.5 | 161.8 | 225.0 | −9.3 | 43.0 | |
| 50/50 + PBT–DLA | − | 124.7 | 190.4 | 160.5 | 223.3 | −6.4 | 43.6 |
| REF | 123.3 | 193.7 | 161.0 | 223.5 | −7.5 | 43.4 | |
| EXP | 115.8 | 192.0 | 161.8 | 225.2 | −9.5 | 43.2 | |
| 50/50 + SEBS | − | 124.5 | 192.8 | 160.6 | 223.3 | −6.4 | 43.4 |
| REF | 123.1 | 193.9 | 160.3 | 224.3 | −8.8 | 43.7 | |
| EXP | 113.4 | 193.6 | 161.2 | 225.9 | −9.7 | 44.1 |
| PP/PBT Matrix | Relaxation | Ea (kJ/mol) | τ0 (s) |
|---|---|---|---|
| 50/50 | αPP | 51.97 | 10−17.83 |
| αPBT | 469.97 | 10−63.11 | |
| 50/50 + PBT–DLA | αPP | 41.94 | 10−14.22 |
| αPBT | 412.44 | 10−59.38 | |
| 50/50 + SEBS | αPP | 43.18 | 10−14.51 |
| αPBT | 429.58 | 10−61.16 |
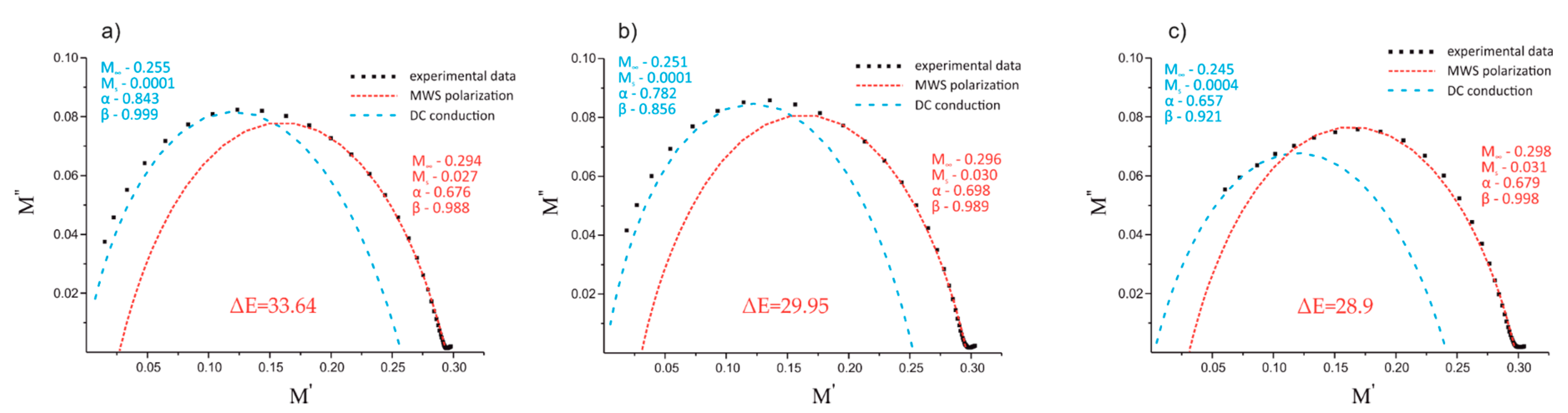
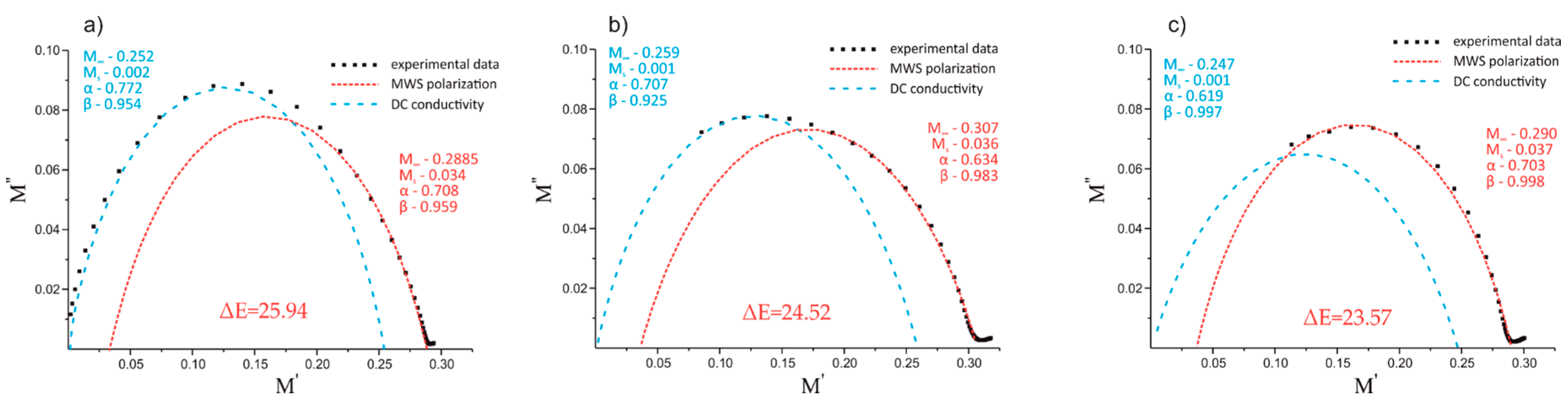
| PP/PBT Matrix | BF | Relaxation | α | β | ||
|---|---|---|---|---|---|---|
| 50/50 | REF | conduction | 0.843 | 0.999 | 0.0001 | 0.255 |
| MWS | 0.676 | 0.988 | 0.027 | 0.294 | ||
| EXP | conduction | 0.772 | 0.954 | 0.002 | 0.252 | |
| MWS | 0.708 | 0.959 | 0.034 | 0.2885 | ||
| 50/50 + PBT–DLA | REF | conduction | 0.782 | 0.856 | 0.0001 | 0.251 |
| MWS | 0.698 | 0.989 | 0.030 | 0.296 | ||
| EXP | conduction | 0.707 | 0.925 | 0.001 | 0.259 | |
| MWS | 0.634 | 0.983 | 0.036 | 0.307 | ||
| 50/50 + SEBS | REF | conduction | 0.657 | 0.921 | 0.0004 | 0.245 |
| MWS | 0.679 | 0.998 | 0.031 | 0.298 | ||
| EXP | conduction | 0.619 | 0.997 | 0.001 | 0.247 | |
| MWS | 0.703 | 0.998 | 0.037 | 0.290 |
| BF | PP/PBT Matrix | Δε | T (°C) |
|---|---|---|---|
| REF | 50/50 | 7.79 | 105 |
| 50/50 + PBT–DLA | 6.33 | ||
| 50/50 + SEBS | 6.02 | ||
| EXP | 50/50 | 6.83 | |
| 50/50 + PBT–DLA | 5.11 | ||
| 50/50 + SEBS | 5.22 | ||
| REF | 50/50 | 22.16 | 120 |
| 50/50 + PBT–DLA | 19.03 | ||
| 50/50 + SEBS | 18.65 | ||
| EXP | 50/50 | 17.44 | |
| 50/50 + PBT–DLA | 15.32 | ||
| 50/50 + SEBS | 15.16 | ||
| REF | 50/50 | 33.64 | 135 |
| 50/50 + PBT–DLA | 29.95 | ||
| 50/50 + SEBS | 28.9 | ||
| EXP | 50/50 | 25.94 | |
| 50/50 + PBT–DLA | 24.52 | ||
| 50/50 + SEBS | 23.57 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ignaczak, W.; Ladegaard Skov, A.; El Fray, M. Interfacial Polarization in Thermoplastic Basalt Fiber-Reinforced Composites. Polymers 2020, 12, 1486. https://doi.org/10.3390/polym12071486
Ignaczak W, Ladegaard Skov A, El Fray M. Interfacial Polarization in Thermoplastic Basalt Fiber-Reinforced Composites. Polymers. 2020; 12(7):1486. https://doi.org/10.3390/polym12071486
Chicago/Turabian StyleIgnaczak, Wojciech, Anne Ladegaard Skov, and Miroslawa El Fray. 2020. "Interfacial Polarization in Thermoplastic Basalt Fiber-Reinforced Composites" Polymers 12, no. 7: 1486. https://doi.org/10.3390/polym12071486
APA StyleIgnaczak, W., Ladegaard Skov, A., & El Fray, M. (2020). Interfacial Polarization in Thermoplastic Basalt Fiber-Reinforced Composites. Polymers, 12(7), 1486. https://doi.org/10.3390/polym12071486






