Tetrafunctional Epoxy Resin-Based Buoyancy Materials: Curing Kinetics and Properties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation
2.3. Characterization
3. Results and Discussion
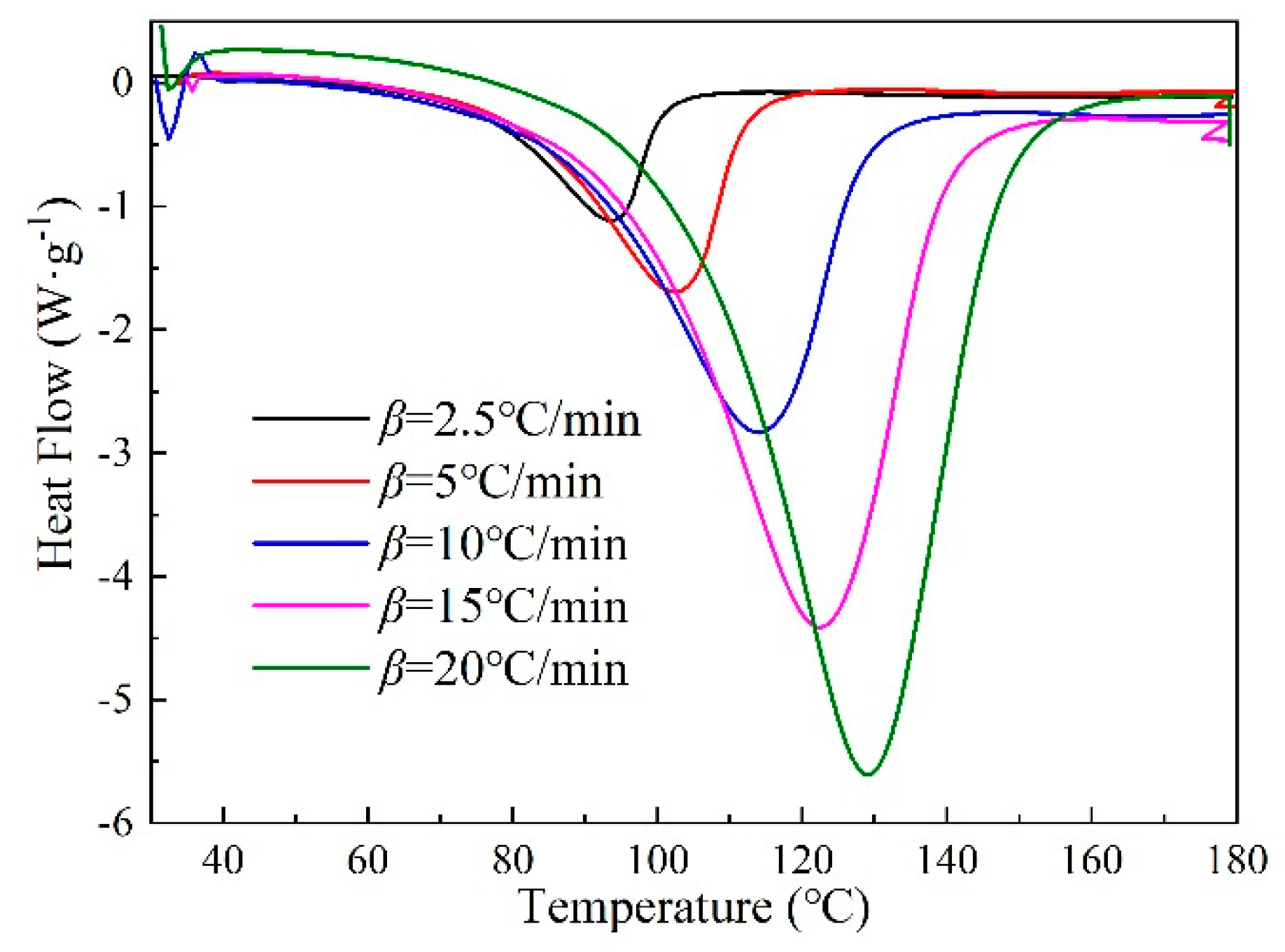
3.1. Curing Behaviors and Kinetics
3.2. Cross-Sectional Morphology Analysis
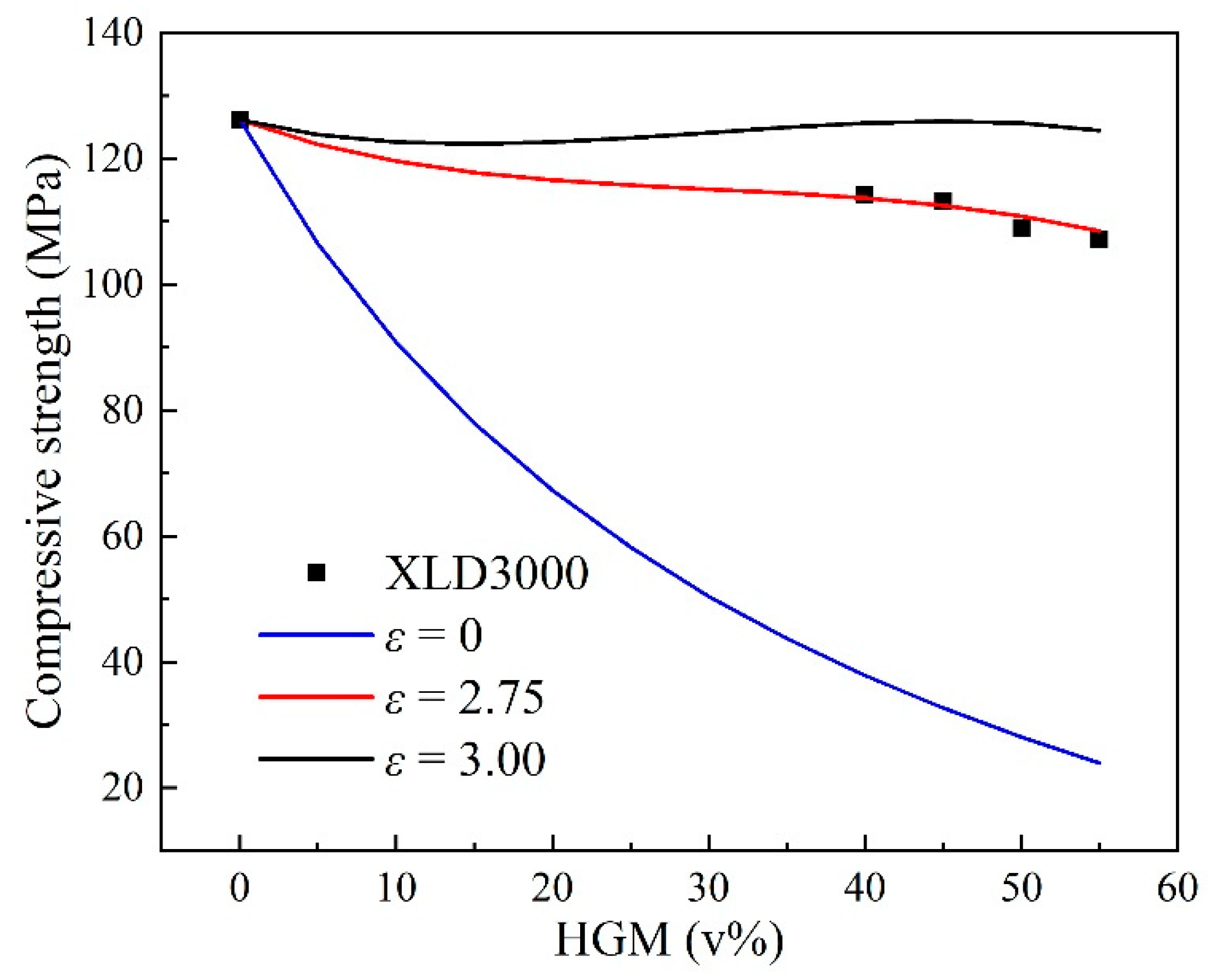
3.3. Properties of Buoyancy Materials
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gupta, N.; Zeltmann, S.E.; Shunmugasamy, V.C.; Pinisetty, D. Applications of polymer matrix syntactic foams. JOM 2014, 66, 245–254. [Google Scholar] [CrossRef]
- Liu, S.; Liu, C.; Dai, Y. Status and progress on researches and developments of deep ocean mining equipments. J. Mech. Eng. 2014, 50, 8–18. [Google Scholar] [CrossRef]
- Zheng, B.; Zhuang, M.M.; Guo, A.R.; Wang, M.C.; Ren, S.E.; Geng, H.T.; Liu, J.C. Buoyancy materials of aluminium borosilicate glass for high temperature resistance. Mater. Res. Innov. 2015, 19, S50–S53. [Google Scholar] [CrossRef]
- Cochran, J.K. Ceramic hollow spheres and their applications. Curr. Opin. Solid State Mater. Sci. 1998, 3, 474–479. [Google Scholar] [CrossRef]
- Li, L.; Yu, L.; Li, C.; Zhao, H.; Yu, J. Solid buoyancy material and research status on its properties. Mater. Rev. 2012, 26, 66–69. [Google Scholar]
- Ren, S.; Li, X.; Zhang, X.; Xu, X.; Dong, X.; Liu, J.; Du, H.; Guo, A. Mechanical properties and high-temperature resistance of the hollow glass microspheres/borosilicate glass composite with different particle size. J. Alloy. Compd. 2017, 722, 321–329. [Google Scholar] [CrossRef]
- Geng, H.; Hu, X.; Zhou, J.; Xu, X.; Wang, M.; Guo, A.; Du, H.; Liu, J. Fabrication and compressive properties of closed-cell alumina ceramics by binding hollow alumina spheres with high-temperature binder. Ceram. Int. 2016, 42, 16071–16076. [Google Scholar] [CrossRef]
- Wouterson, E.M.; Boey, F.Y.C.; Hu, X.; Wong, S.C. Specific properties and fracture toughness of syntactic foam: Effect of foam microstructures. Compos. Sci. Technol. 2005, 65, 1840–1850. [Google Scholar] [CrossRef]
- Ren, S.; Liu, J.; Guo, A.; Zang, W.; Geng, H.; Tao, X.; Du, H. Mechanical properties and thermal conductivity of a temperature resistance hollow glass microspheres/borosilicate glass buoyance material. Mater. Sci. Eng. A 2016, 674, 604–614. [Google Scholar] [CrossRef]
- Colombo, P.; Modesti, M. Silicon oxycarbide ceramic foams from a preceramic polymer. J. Am. Ceram. Soc. 1999, 82, 573–578. [Google Scholar] [CrossRef]
- Jeon, H.R.; Park, J.H.; Shon, M.Y. Corrosion protection by epoxy coating containing multi-walled carbon nanotubes. J. Ind. Eng. Chem. 2013, 19, 849–853. [Google Scholar] [CrossRef]
- Hong, I.K.; Yoon, Y.S.; Lee, S.B. Selection of thinner for epoxy type resins for neon transformer housing. J. Ind. Eng. Chem. 2012, 18, 1997–2003. [Google Scholar] [CrossRef]
- Vidil, T.; Tournilhac, F.; Musso, S.; Robisson, A.; Leibler, L. Control of reactions and network structures of epoxy thermosets. Prog. Polym. Sci. 2016, 62, 126–179. [Google Scholar] [CrossRef] [Green Version]
- Luft, J.H. Improvements in epoxy resin embedding methods. J. Biophys. Biochem. Cytol. 1961, 9, 409–414. [Google Scholar] [CrossRef]
- Li, Y.; Badrinarayanan, P.; Kessler, M.R. Liquid crystalline epoxy resin based on biphenyl mesogen: Thermal characterization. Polymer 2013, 54, 3017–3025. [Google Scholar] [CrossRef] [Green Version]
- Shafizadeh, J.E.; Guionnet, S.; Tillman, M.S.; Seferis, J.C. Synthesis and characterization of phenolic resole resins for composite applications. J. Appl. Polym. Sci. 1999, 73, 505–514. [Google Scholar] [CrossRef]
- Wang, P.; Yan, K.; Pan, S.; Zhang, J. Research development on solid buoyancy material for deep-sea application. J. Eng. Stud. 2016, 8, 223–229. [Google Scholar]
- Zhang, X.; Ya, B.; Huang, B.; Zhou, B.; Pei, L.; Jia, F. Study on preparation and properties of carbon nanotubes/hollow glass microspheres/epoxy syntactic foam. J. Polym. Eng. 2017, 37, 93–98. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Zhang, J.; Li, T.; Hu, Z.; Yu, Y. Effect of curing conversion on the water sorption, corrosion resistance and thermo-mechanical properties of epoxy resin. RSC Adv. 2015, 5, 11358–11370. [Google Scholar] [CrossRef]
- Li, L.; Yu, Y.; Wu, Q.; Zhan, G.; Li, S. Effect of chemical structure on the water sorption of amine-cured epoxy resins. Corros. Sci. 2009, 51, 3000–3006. [Google Scholar] [CrossRef]
- Vyazovkin, S. Thermal analysis. Anal. Chem. 2008, 80, 4301–4316. [Google Scholar] [CrossRef]
- Vyazovkin, S. Thermal analysis. Anal. Chem. 2002, 74, 2749–2762. [Google Scholar] [CrossRef]
- Cammenga, H.K.; Epple, M. Basic principles of thermoanalytical techniques and their applications in preparative chemistry. Angew. Chem., Int. Ed. 1995, 34, 1171–1187. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Perez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar]
- Yousefi, A.; Lafleur, P.G.; Gauvin, R. Kinetic studies of thermoset cure reactions: A review. Polym. Compos. 1997, 18, 157–168. [Google Scholar] [CrossRef]
- Wan, J.T.; Gan, B.; Li, C.; Molina-Aldareguia, J.; Kalali, E.N.; Wang, X.; Wang, D.Y. A sustainable, eugenol-derived epoxy resin with high biobased content, modulus, hardness and low flammability: Synthesis, curing kinetics and structure-property relationship. Chem. Eng. J. 2016, 284, 1080–1093. [Google Scholar] [CrossRef] [Green Version]
- Wan, J.; Li, C.; Bu, Z.-Y.; Xu, C.-J.; Li, B.-G.; Fan, H. A comparative study of epoxy resin cured with a linear diamine and a branched polyamine. Chem. Eng. J. 2012, 188, 160–172. [Google Scholar] [CrossRef]
- Wan, J.; Bu, Z.-Y.; Xu, C.-J.; Li, B.-G.; Fan, H. Preparation, curing kinetics, and properties of a novel low-volatile starlike aliphatic-polyamine curing agent for epoxy resins. Chem. Eng. J. 2011, 171, 357–367. [Google Scholar] [CrossRef]
- Lee, J.Y.; Shim, M.J.; Kim, S.W. Thermal decomposition kinetics of an epoxy resin with rubber-modified curing agent. J. Appl. Polym. Sci. 2001, 81, 479–485. [Google Scholar] [CrossRef]
- Natarajan, M.; Murugavel, S.C. Thermal stability and thermal degradation kinetics of bio-based epoxy resins derived from cardanol by thermogravimetric analysis. Polym. Bull. 2017, 74, 3319–3340. [Google Scholar] [CrossRef]
- Zabihi, O.; Khayyam, H.; Fox, B.L.; Naebe, M. Enhanced thermal stability and lifetime of epoxy nanocomposites using covalently functionalized clay: Experimental and modelling. New J. Chem. 2015, 39, 2269–2278. [Google Scholar] [CrossRef]
- Mustata, F.; Tudorachi, N. Thermal behavior of epoxy resin cured with aromatic dicarboxylic acids. J. Therm. Anal. Calorim. 2016, 125, 97–110. [Google Scholar] [CrossRef]
- Vyazovkin, S. A unified approach to kinetic processing of nonisothermal data. Int. J. Chem. Kinet. 1996, 28, 95–101. [Google Scholar] [CrossRef]
- Tao, Q.; Pinter, G.; Antretter, T.; Krivec, T.; Fuchs, P. Model free kinetics coupled with finite element method for curing simulation of thermosetting epoxy resins. J. Appl. Polym. Sci. 2018, 135, 46408. [Google Scholar] [CrossRef]
- Mustata, F.; Tudorachi, N. Curing kinetics and thermal characterization of epoxy resin cured with amidodicarboxylic acids. Appl. Therm. Eng. 2017, 125, 285–296. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Sbirrazzuoli, N. Mechanism and kinetics of epoxy-amine cure studied by differential scanning calorimetry. Macromolecules 1996, 29, 1867–1873. [Google Scholar] [CrossRef]
- Yu, S.Z.; Li, X.D.; Guo, X.Y.; Li, Z.R.; Zou, M.S. Curing and characteristics of N,N,N’,N’-tetraepoxypropyl-4,4’-diaminodiphenylmethane epoxy resin-based buoyancy material. Polymers 2019, 11, 1137. [Google Scholar] [CrossRef] [Green Version]
- Friedman, M.; Williams, L.D.; Masri, M.S. Reductive alkylation of proteins with aromatic-aldehydes and sodium cyanoborohydride. Int. J. Pept. Protein Res. 1974, 6, 183–185. [Google Scholar] [CrossRef]
- Skvara, F.; Sestak, J. Computer calculation of mechanism and associated kinetic data using a nonisothermal integral method. J. Therm. Anal. 1975, 8, 477–489. [Google Scholar]
- Du, X.; Li, X.; Zou, M.; Yang, R.; Pang, S.; Li, Y. Thermogravimetric analysis and kinetic study of 1-amino-1,2,3-triazolium nitrate. Thermochim. Acta 2013, 570, 59–63. [Google Scholar] [CrossRef]
- Ozawa, T. A new method of analyzing thermogravimetric data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef] [Green Version]
- Hu, R.Z.; Gao, S.L.; Zhao, F.Q.; Zhen, S.Q.; Zhang, T.L.; Zhang, J.J. Thermoanalysis Kinetics, 2nd ed.; Science Press: Beijing, China, 2008; p. 138. [Google Scholar]
- Deng, Y.; Yang, Y.Y.; Ge, L.Y.; Yang, W.Z.; Xie, K. Preparation of magnetic Ni-P amorphous alloy microspheres and their catalytic performance towards thermal decomposition of ammonium perchlorate. Appl. Surf. Sci. 2017, 425, 261–271. [Google Scholar] [CrossRef]
- Mozetic, M.; Vesel, A.; Primc, G.; Eisenmenger-Sittner, C.; Bauer, J.; Eder, A.; Schmid, G.H.S.; Ruzic, D.N.; Ahmed, Z.; Barker, D.; et al. Recent developments in surface science and engineering, thin films, nanoscience, biomaterials, plasma science, and vacuum technology. Thin Solid Films 2018, 660, 120–160. [Google Scholar] [CrossRef]
- Turcsanyi, B.; Pukanszky, B.; Tudos, F. Composition dependence of tensile yield stress in filled polymers. J. Mater. Sci. Lett. 1988, 7, 160–162. [Google Scholar] [CrossRef]

| α | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|
| Ea/kJ·mol−1 | 60.37 | 58.14 | 57.22 | 55.71 | 54.01 | 51.00 | 47.41 | 42.56 | 43.35 |
| Function Name | Mechanism | G(α) | f(α) | r2 |
|---|---|---|---|---|
| Jander equation | 3D, n = 1/2 | [1 − (1 − α)1/3]1/2 | 6(1 − α)2/3[1-(1 − α)1/3]1/2 | 0.9999 |
| Jander equation | 3D, D3, n = 2 | [1 − (1 − α)1/3]2 | 3/2(1 − α)2/3[1 − (1 − α)1/3]−1 | 0.9999 |
| Order of reaction | n = 1/4 | 1 − (1 − α)1/4 | 4(1 − α)3/4 | 0.9999 |
| Shrinkage spherical (volume) | R3, n = 1/3 | 1 − (1 − α)1/3 | 3(1 − α)2/3 | 0.9999 |
| G(α) | Ea (kJ·mol−1) | lgA | r2 |
|---|---|---|---|
| [1 − (1 − α)1/3]1/2 | 64.48 | 8.23 | 0.9999 |
| [1 − (1 − α)1/3]2 | 257.91 | 35.86 | 0.9999 |
| 1 − (1 − α)1/4 | 128.96 | 17.34 | 0.9999 |
| 1 − (1 − α)1/3 | 128.96 | 17.82 | 0.9999 |
| VH (v%) | 0 | 40 | 45 | 50 | 55 |
|---|---|---|---|---|---|
| ρ (g·cm−3) | 1.208 | 0.802 | 0.746 | 0.711 | 0.668 |
| ρcal (g·cm−3) | —— | 0.817 | 0.768 | 0.719 | 0.670 |
| VH/% | 0 | 40 | 45 | 50 | 55 |
|---|---|---|---|---|---|
| E/MPa | 126.14 | 114.20 | 113.27 | 108.99 | 107.07 |
| Ecal/MPa | —— | 113.68 | 112.53 | 110.87 | 108.46 |
| E/ρ | 104.42 | 142.29 | 151.84 | 153.29 | 160.28 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Li, X.; Zou, M.; Li, Z.; Wang, S.; Wang, D. Tetrafunctional Epoxy Resin-Based Buoyancy Materials: Curing Kinetics and Properties. Polymers 2020, 12, 1732. https://doi.org/10.3390/polym12081732
Yu S, Li X, Zou M, Li Z, Wang S, Wang D. Tetrafunctional Epoxy Resin-Based Buoyancy Materials: Curing Kinetics and Properties. Polymers. 2020; 12(8):1732. https://doi.org/10.3390/polym12081732
Chicago/Turabian StyleYu, Sizhu, Xiaodong Li, Meishuai Zou, Zhiren Li, Shuo Wang, and Danhui Wang. 2020. "Tetrafunctional Epoxy Resin-Based Buoyancy Materials: Curing Kinetics and Properties" Polymers 12, no. 8: 1732. https://doi.org/10.3390/polym12081732
APA StyleYu, S., Li, X., Zou, M., Li, Z., Wang, S., & Wang, D. (2020). Tetrafunctional Epoxy Resin-Based Buoyancy Materials: Curing Kinetics and Properties. Polymers, 12(8), 1732. https://doi.org/10.3390/polym12081732







