Theoretical and Numerical Analysis of Mechanical Behaviors of a Metamaterial-Based Shape Memory Polymer Stent
Abstract
:1. Introduction
2. Geometries of Expansion Model of SMP Stent with Vessel and Plaque
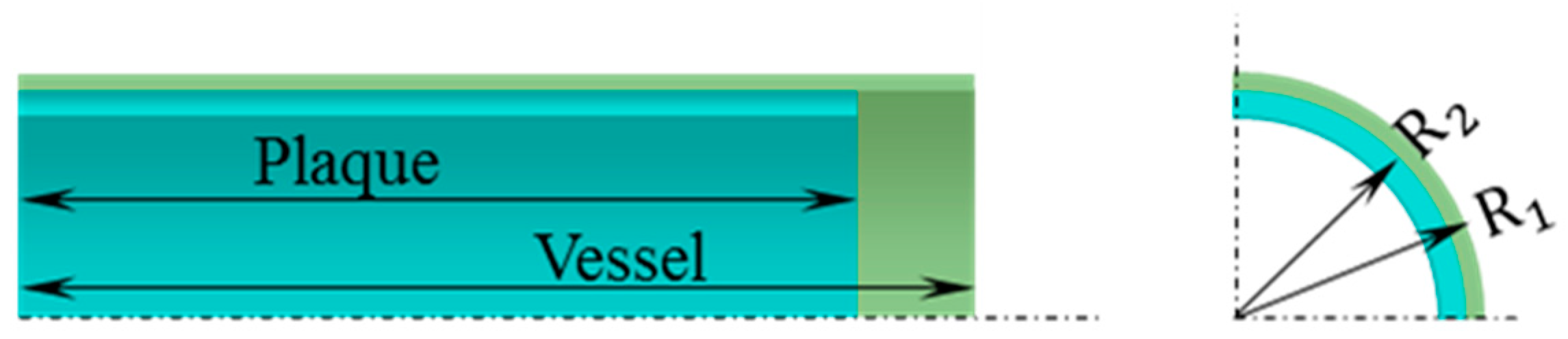
2.1. Geometric Model of Vessel with Plaque
2.2. Geometric Model of Stent Based on Metamaterial
3. Constitutive Models of the Vessel, Plaque, and SMP
3.1. Constitutive Models of the Vessel and Plaque
3.2. Constitutive Model of Shape Memory Polymer
4. Numerical Simulation for SMP Stent with Mechanical Metamaterial
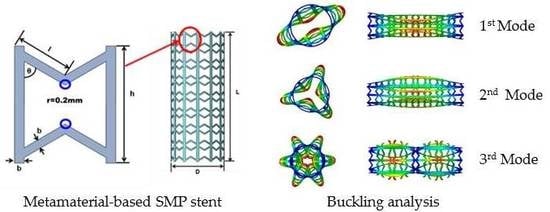
4.1. Buckling Analysis of SMP Stent
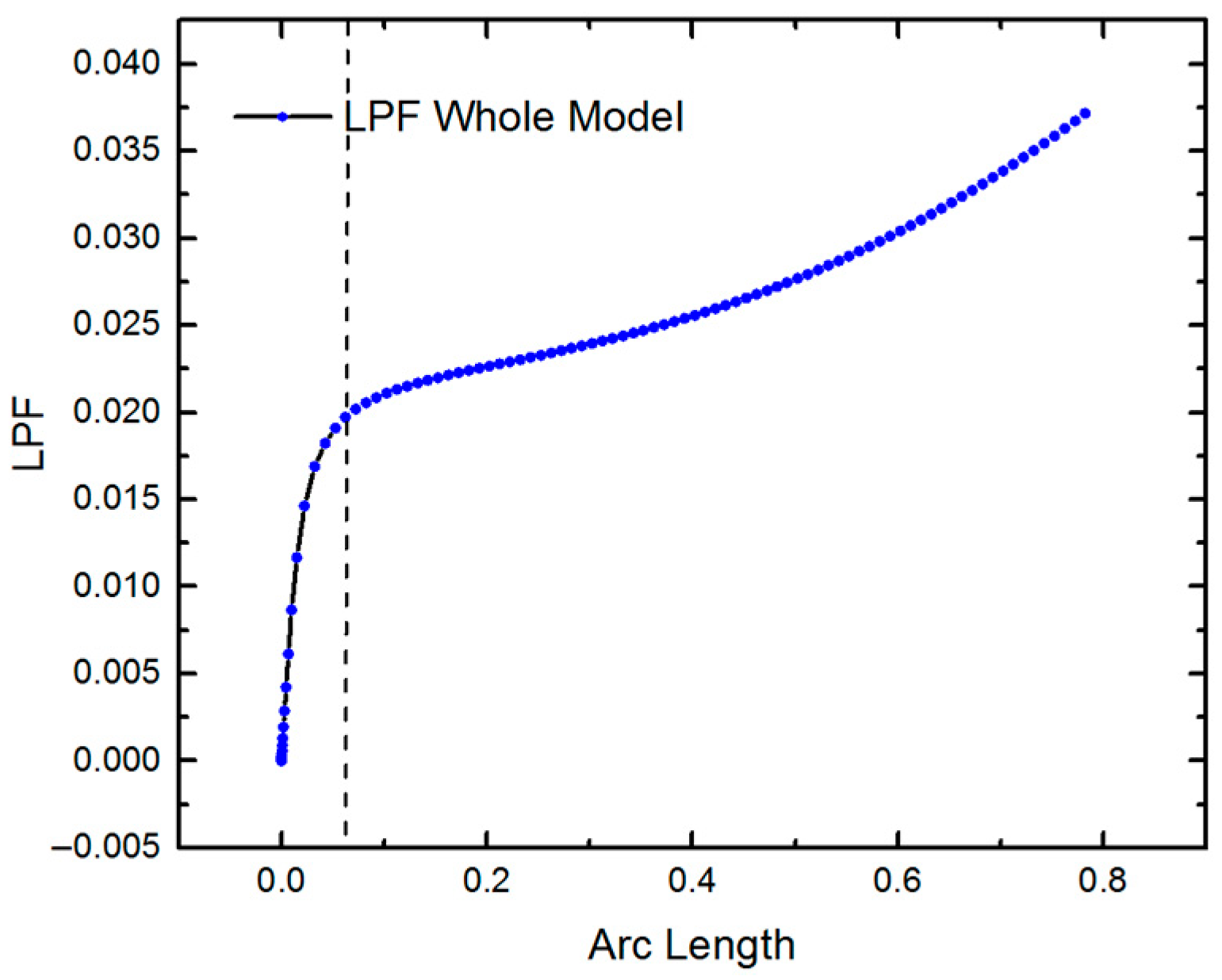
4.1.1. Eigenvalue Analysis
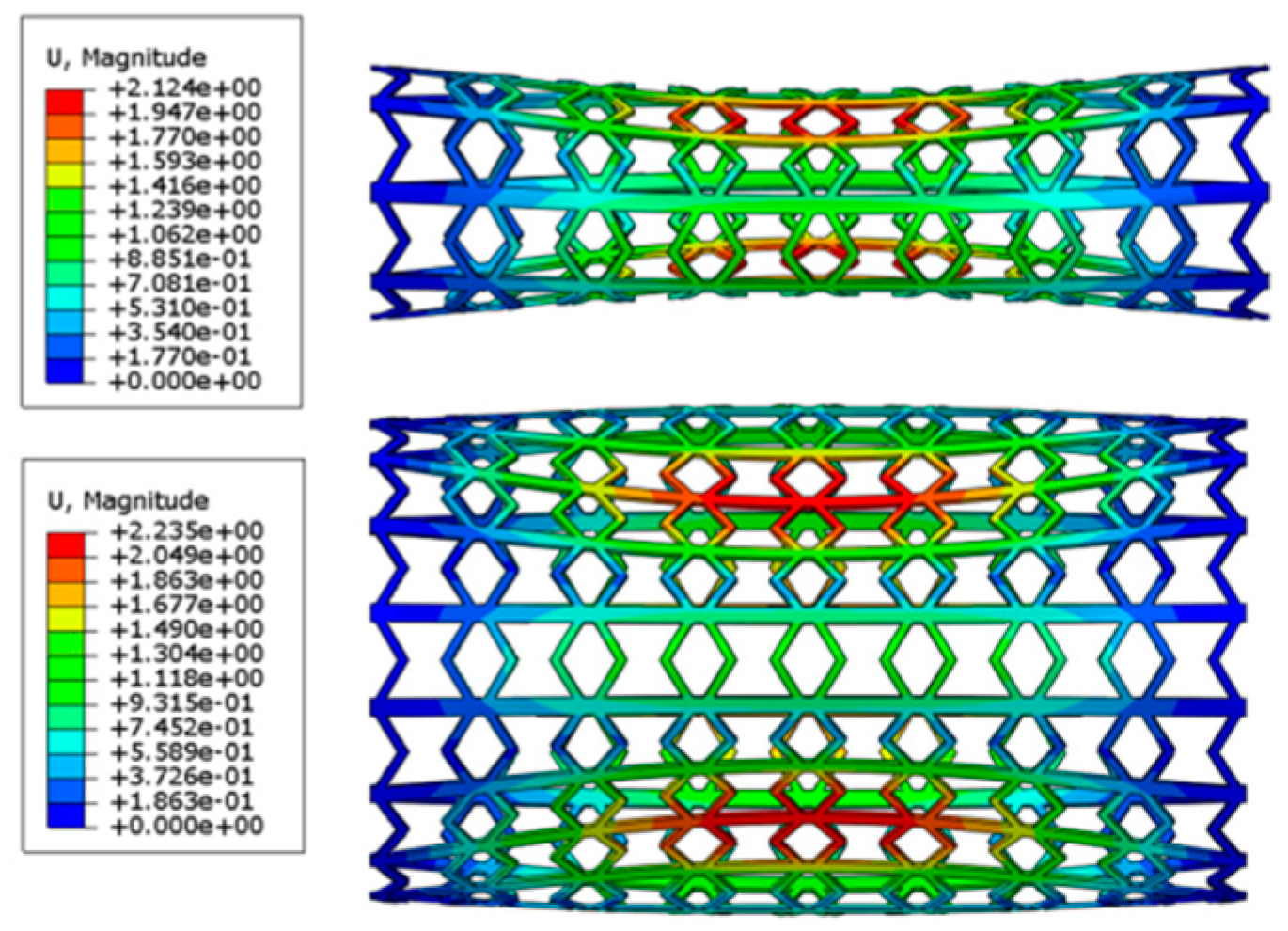
4.1.2. Nonlinear Buckling Analysis
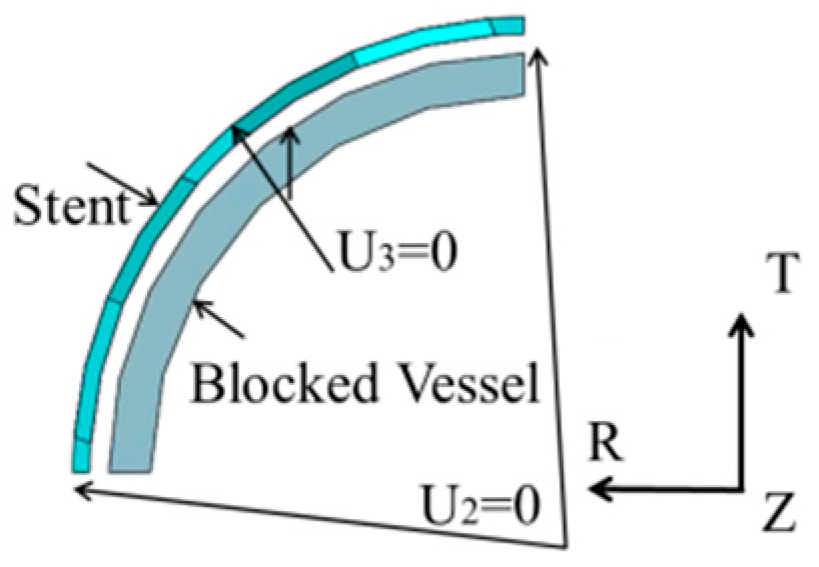
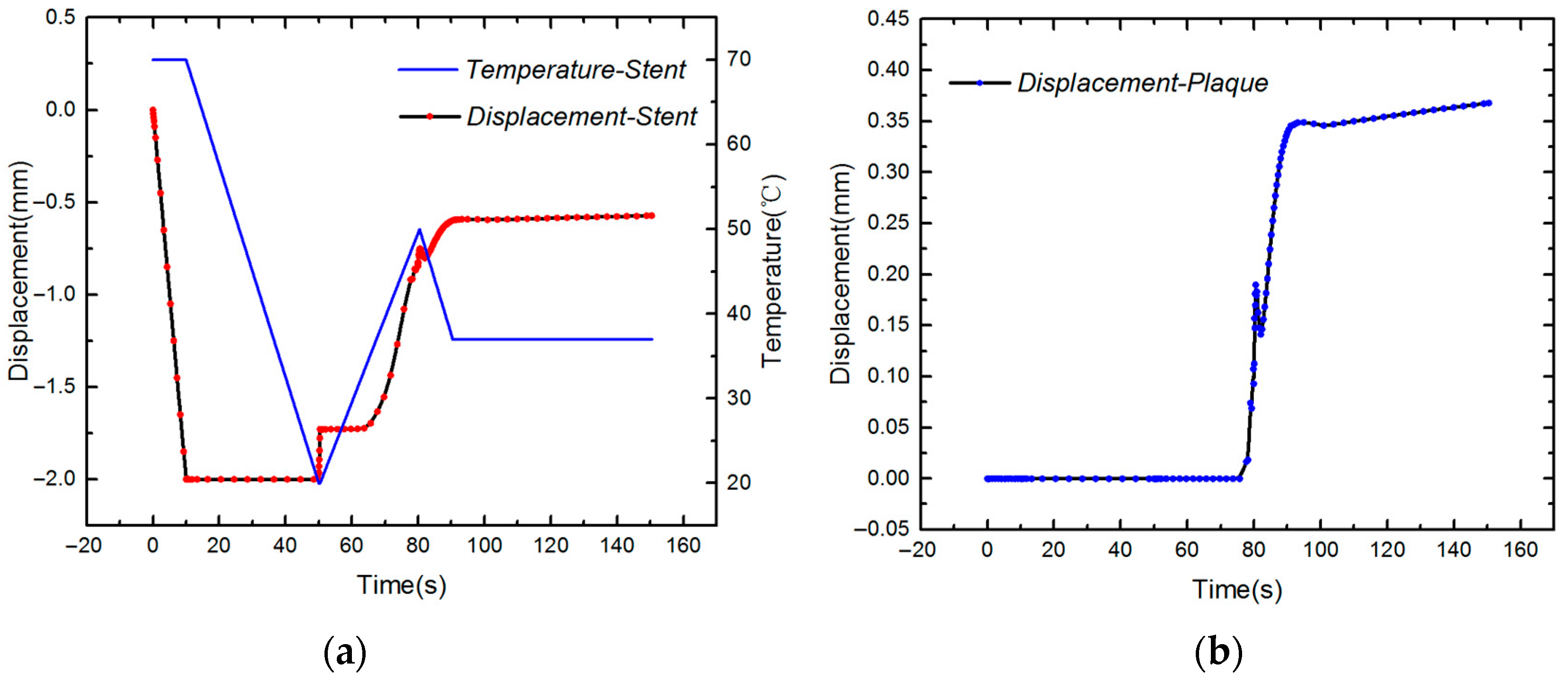
4.2. Expansion of SMP Stent with Metamaterial in a Blocked Vessel
- (1)
- Compress the stent to a smaller radius at a high temperature (T > Tg);
- (2)
- Cool the stent to temperature lower than Tg;
- (3)
- Release the load conducted on the stent;
- (4)
- Deliver the stent to the target vessel;
- (5)
- Stimuli the stent by heat, light, or magnetism;
- (6)
- Remove the stimuli and cool the stent to body temperature.
5. Analytical Model of Evaluating Radial Strength of SMP Stent
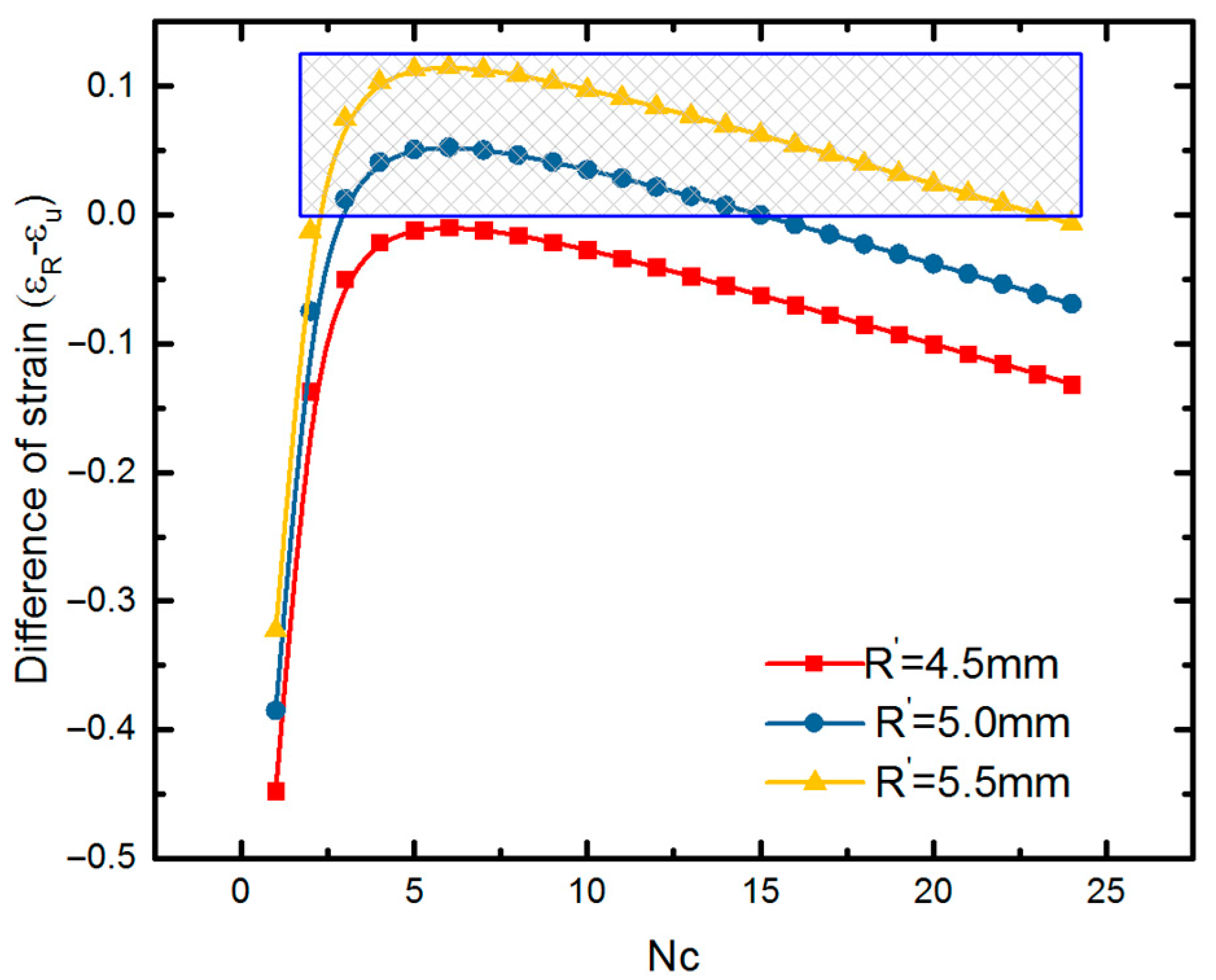
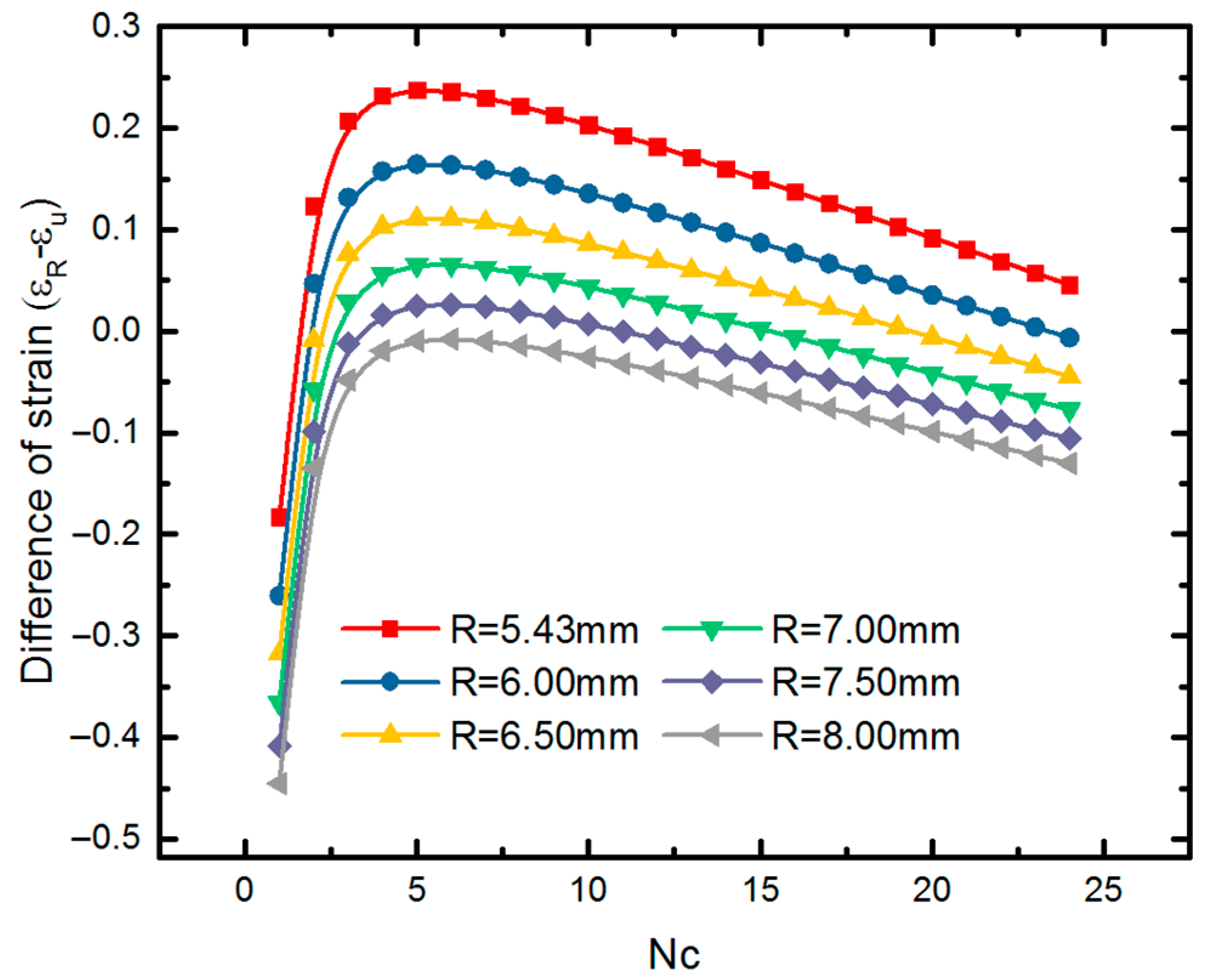
5.1. Mechanical Behavior of SMP Stent Unit Cell
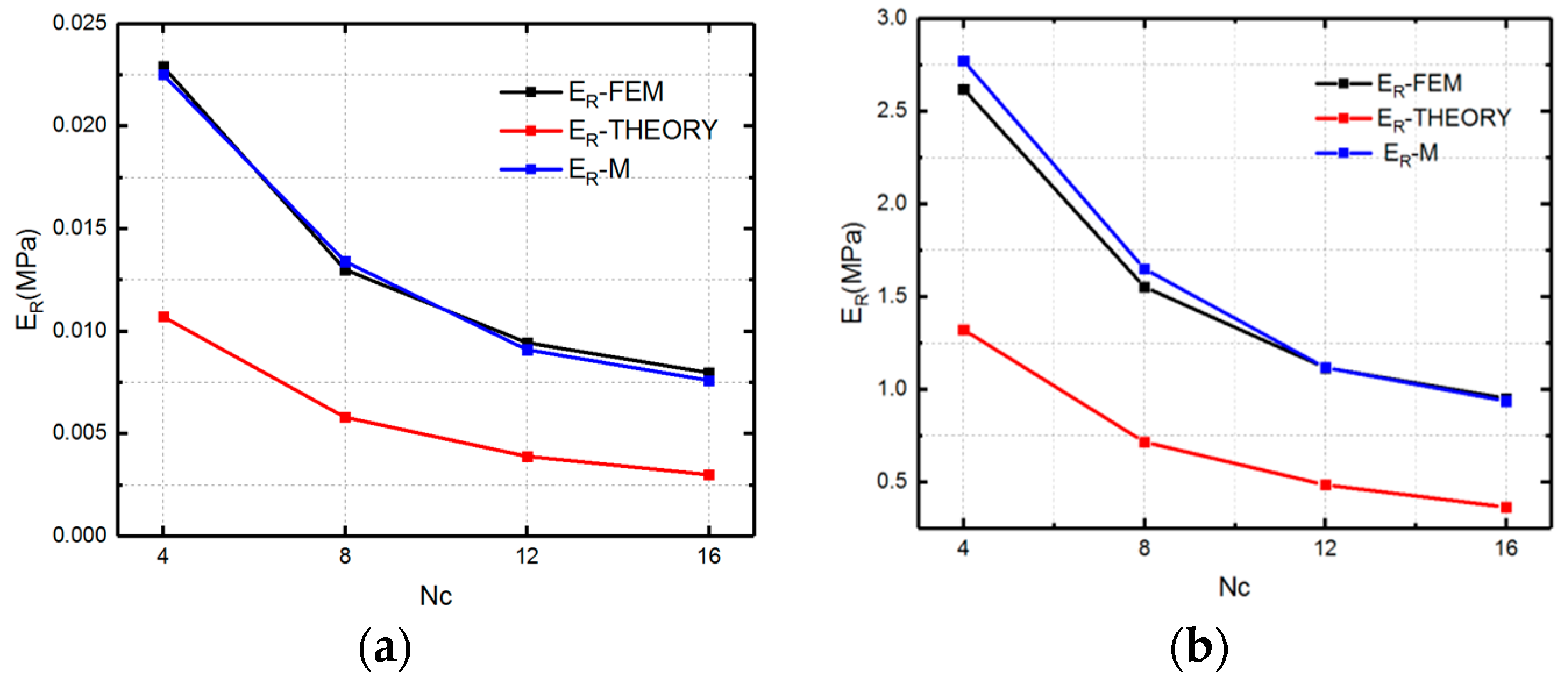
5.2. Mechanical Properties of SMP Stent through Analytical Approach
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Q.; Yan, D.; Zhang, K.; Hu, G. Pattern transformation of heat-shrinkable polymer by three-dimensional (3D) printing technique. Sci. Rep. 2015, 5, 8936. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Li, M.X.; Wang, Z.W.; Chen, C.; Ma, C.Q.; Yang, G. Highly tough, multi-stimuli-responsive and fast self-healing supramolecular networks toward strain sensor application. Chem. Eng. J. 2020, 389, 123468. [Google Scholar] [CrossRef]
- Lendlein, A.; Jiang, H.; Junger, O.; Langer, R. Light-induced shape-memory polymers. Nature 2005, 434, 879–882. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Gu, Y.; Hou, X.; Li, R.; Ke, H.; Xiao, X. Hybrid Nanocomposites of Cellulose/Carbon-Nanotubes/Polyurethane with Rapidly Water Sensitive Shape Memory Effect and Strain Sensing Performance. Polymers 2019, 11, 1586. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kunkel, R.; Laurence, D.; Wang, J.Y.; Robinson, D.; Scherrer, J.; Wu, Y.; Bohnstedt, B.; Chien, A.; Liu, T.J.; Lee, C. Synthesis and characterization of bio-compatible shape memory polymers with potential applications to endovascular embolization of intracranial aneurysms. J. Mech. Behav. Biomed. 2018, 88, 422–430. [Google Scholar] [CrossRef] [PubMed]
- Serrano, M.C.; Carbajal, L.; Ameer, G.A. Novel biodegradable shape-memory elastomers with drug-releasing capabilities. Adv. Mater. 2011, 23, 2211–2215. [Google Scholar] [CrossRef] [PubMed]
- Baker, R.M.; Tseng, L.F.; Iannolo, M.T.; Oest, M.E.; Henderson, J.H. Self-deploying shape memory polymer scaffolds for grafting and stabilizing complex bone defects: A mouse femoral segmental defect study. Biomaterials 2016, 76, 388–398. [Google Scholar] [CrossRef]
- Kai, D.; Prabhakaran, M.P.; Chan, B.Q.Y.; Liow, S.S.; Remakrising, S.; Xu, F.; Loh, X.J. Elastic poly (ε-caprolactone)-polydimethylsiloxane copolymer fibers with shape memory effect for bone tissue engineering. Biomed. Mater. 2016, 11, 015007. [Google Scholar] [CrossRef]
- Small, W., IV; Singhal, P.; Wilson, T.S.; Maitland, D.J. Biomedical applications of thermally activated shape memory polymers. J. Mater. Chem. 2010, 20, 3356–3366. [Google Scholar] [CrossRef]
- Govindarajan, T.; Shandas, R. A survey of surface modification techniques for next-generation shape memory polymer stent devices. Polymers 2014, 6, 2309–2331. [Google Scholar] [CrossRef]
- Xue, L.; Dai, S.; Li, Z. Biodegradable shape-memory block co-polymers for fast self-expandable stents. Biomaterials 2010, 31, 8132–8140. [Google Scholar] [CrossRef] [PubMed]
- Reese, S.; Böl, M.; Christ, D. Finite element-based multi-phase modelling of shape memory polymer stents. Comput. Method. Appl. Mech. Eng. 2010, 199, 1276–1286. [Google Scholar] [CrossRef]
- Liu, R.; Mcginty, S.; Cui, F.; Luo, X.; Liu, Z. Modelling and simulation of the expansion of a shape memory polymer stent. Eng. Comput. 2019, 36, 2726–2746. [Google Scholar] [CrossRef]
- Wache, H.M.; Tartakowska, D.J.; Hentrich, A.; Wagner, M.H. Development of a polymer stent with shape memory effect as a drug delivery system. J. Mater. Sci. Mater. Med. 2003, 14, 109–112. [Google Scholar] [CrossRef] [PubMed]
- Baer, G.M.; Small, W., IV; Wilson, T.S.; Benett, W.J.; Matthews, D.L.; Hartman, J.; Maitland, D.J. Fabrication and in vitro deployment of a laser-activated shape memory polymer vascular stent. Biomed. Eng. OnLine 2007, 6, 43–51. [Google Scholar] [CrossRef] [Green Version]
- Baer, G.M.; Wilson, T.S.; Small, W., IV; Hartman, J.; Benett, W.J.; Matthews, D.L.; Maitland, D.J. Thermomechanical Properties, Collapse Pressure, and Expansion of Shape Memory Polymer Neurovascular Stent Prototypes. J. Biomed. Mater. Res. Part B 2009, 90, 421–429. [Google Scholar] [CrossRef] [Green Version]
- Yakacki, C.M.; Shandas, R.; Lanning, C.; Rech, B.; Eckstein, A.; Gall, K. Unconstrained Recovery Characterization of Shape-Memory Polymer Networks for Cardiovascular Applications. Biomaterials 2007, 28, 2255–2263. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.H.; Kang, T.J.; Yu, W.R. Simulation of mechanical behavior of temperature-responsive braided stents made of shape memory polyurethanes. J. Biomech. 2010, 43, 632–643. [Google Scholar]
- Han, J.; Gu, S.Y.; Chang, K. 3D printed selfof temperature-responsive braidedbiodegradable shape memory polymer. Adv. Polym. Tech. 2018. [Google Scholar] [CrossRef]
- Ge, Q.; Sakhaei, A.; Lee, H.; Dunn, C.K.; Fang, N.; Dunn, M.L. Multimaterial 4D Printing with Tailorable Shape Memory Polymers. Sci. Rep. 2016, 6, 31110. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.J.; Zhang, F.H.; Liu, Y.J.; Leng, J.S. 4D printed shape memory polymers and their structures for biomedical applications. Sci. China Technol. Sci. 2020, 63, 545–560. [Google Scholar] [CrossRef] [Green Version]
- Dyet, J.F.; Watts, W.G.; Ettles, D.F.; Nicholson, A.A. Mechanical properties of metallic stents: How do these properties influence the choice of stent for specific lesions? Cardiovasc. Int. Rad. 2000, 23, 47–54. [Google Scholar] [CrossRef] [PubMed]
- Mccormick, C. Overview of cardiovascular stent designs. In Functionalised Cardiovascular Stents; Woodhead Publishing: San Diego, CA, USA, 2018; pp. 3–26. [Google Scholar]
- Hartung, O.; Grisoli, D.; Boufi, M.; Hakam, Z.; Barthelemy, P.; Alimi, Y.S. Endovascular stenting in the treatment of pelvic vein congestion caused by nutcracker syndrome: Lessons learned from the first five cases. J. Vasc. Surg. 2005, 42, 275–280. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khairy, S.A.; Neves, R.J.; Hartung, O.; O’Sullivan, G.J. Factors Associated with Contralateral Deep Venous Thrombosis after Iliocaval Venous Stenting. J. Vasc. Surg. 2018, 67, 358–359. [Google Scholar] [CrossRef]
- Lee, J.B.; Peng, S.; Yang, D.; Roh, Y.H.; Funabashi, H.; Park, N.; Rice, E.J.; Chen, L.; Long, R.; Wu, M.; et al. A mechanical metamaterial made from a DNA hydrogel. Nat. Nanotechnol. 2012, 7, 816. [Google Scholar]
- Brunet, T.; Leng, J.; Mondain-Monval, O. Soft acoustic metamaterials. Science 2013, 342, 323–324. [Google Scholar] [CrossRef]
- Jing, X.; Meng, Y.; Sun, X. Soft resonator of omnidirectional resonance for acoustic metamaterials with a negative bulk modulus. Sci. Rep. 2015, 5, 16110. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Ren, X.; Shen, J.; Ghaedizadeh, A.; Tain, H.; Xie, Y.M. A simple auxetic tubular structure with tuneable mechanical properties. Smart Mater. Struct. 2016, 25, 065012. [Google Scholar] [CrossRef]
- Geng, L.C.; Ruan, X.L.; Wu, W.W.; Xia, R.; Fang, D.N. Mechanical Properties of Selective Laser Sintering (SLS) Additive Manufactured Chiral Auxetic Cylindrical Stent. Exp. Mech. 2019, 59, 913–925. [Google Scholar] [CrossRef]
- Gatt, R.; Caruana-Gauci, R.; Attard, D.; Casha, A.R.; Wolak, W.; Dudek, K.; Mizzi, L.; Grima, J.N. On the properties of real finite-sized planar and tubular stent-like auxetic structures. Phys. Status Solidi B 2014, 251, 321–327. [Google Scholar] [CrossRef]
- Mizzi, L.; Attard, D.; Casha, A.; Grima, J.N.; Gatt, R. On the suitability of hexagonal honeycombs as stent geometries. Phys. Status Solidi B 2014, 251, 328–337. [Google Scholar] [CrossRef]
- Ali, M.N.; Busfield, J.J.C.; Rehman, I.U. Auxetic oesophageal stents: Structure and mechanical properties. J. Mater. Sci. Mater. Med. 2014, 25, 527–553. [Google Scholar] [CrossRef] [PubMed]
- Sedaghat, S.; van Sloten, T.T.; Laurent, S.; London, G.M.; Pannier, B.; Kavousi, M.; Mattace-Raso, F.; Franco, O.H.; Boutouyrie, P.; Ikram, M.A.; et al. Common carotid artery diameter and risk of cardiovascular events and mortality: Pooled analyses of four cohort studies. Hypertension 2018, 72, 85–92. [Google Scholar] [CrossRef] [PubMed]
- Snowhill, P.B.; Nosher, J.L.; Siegel, R.L.; Silver, F.H. Characterization of Radial Forces in Z Stents. Investig. Radiol. 2001, 36, 521–530. [Google Scholar] [CrossRef]
- Wang, R.; Zuo, H.; Yang, Y.M.; Yang, B.; Li, Q. Finite element simulation and optimization of radial resistive force for shape memory alloy vertebral body stent. J. Intell. Mater. Syst. Struct. 2017, 28, 2140–2150. [Google Scholar] [CrossRef]
- Gu, L.; Zhao, S.; Muttyam, A.; Hammel, J. The Relation Between the Arterial Stress and Restenosis Rate After Coronary Stenting. J. Med. Devices 2010, 4, 531–538. [Google Scholar] [CrossRef]
- Karnessis, N.; Burriesci, G. Uniaxial and buckling mechanical response of auxetic cellular tubes. Smart Mater. Struct. 2013, 22, 084008. [Google Scholar] [CrossRef]
- Olympic, K.R.; Gandhi, F. Zero Poisson’s Ratio Cellular Honeycombs for Flex Skins Undergoing One-Dimensional Morphing. J. Intell. Mater. Syst. Struct. 2010, 21, 1737–1753. [Google Scholar] [CrossRef]
- Huang, R.; Zheng, S.; Liu, Z.; Ng, T. Recent Advances of the Constitutive Models of Smart Materials-Hydrogels and Shape Memory Polymers. Int. J. Appl. Mech. 2020. [Google Scholar] [CrossRef] [Green Version]
- Tobushi, H.; Okumura, K.; Hayashi, S.; Ito, N. Thermomechanical constitutive model of shape memory polymer. Mech. Mater. 2001, 33, 545–554. [Google Scholar] [CrossRef]
- Pan, Z.; Liu, Z. A novel fractional viscoelastic constitutive model for shape memory polymers. J. Polym. Sci. Pol. Phys. 2018, 56, 1125–1134. [Google Scholar] [CrossRef]
- Liu, Y.; Gall, K.; Dunn, M.L.; Greenberg, A.R.; Diani, J. Thermomechanics of shape memory polymers: Uniaxial experiments and constitutive modeling. Int. J. Plast. 2006, 22, 279–313. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Z. A novel constitutive model of shape memory polymers combining phase transition and viscoelasticity. Polymer 2018, 143, 298–308. [Google Scholar] [CrossRef]
- Li, Y.; Liu, R.; Liu, Z.S.; Swaddiwudhipong, S. 3D phase-evolution-based thermomechanical constitutive model of shape memory polymer with finite element implementation. J. Mech. Mater. Struct. 2020, 15, 291–306. [Google Scholar] [CrossRef]
- He, Y.; Guo, S.; Liu, Z.; Liew, K.M. Pattern transformation of thermo-responsive shape memory polymer periodic cellular structures. Int. J. Solids Struct. 2015, 71, 194–205. [Google Scholar] [CrossRef]
- Diani, J.; Gilormini, P.; Frédy, C.; Rousseau, I. Predicting thermal shape memory of crosslinked polymer networks from linear viscoelasticity. Int. J. Solids Struct. 2012, 49, 793–799. [Google Scholar] [CrossRef] [Green Version]
- Migliavacca, F.; Gervaso, F.; Prosi, M.; Zunino, P.; Minisini, S.; Formaggia, L.; Dubini, G. Expansion and drug elution model of a coronary stent. Comput. Method Biomech. 2007, 10, 10–63. [Google Scholar] [CrossRef]
- Migliavacca, F.; Petrini, L.; Massarotti, P.; Schievano, S.; Auricchio, F.; Dubini, G. Stainless and shape memory alloy coronary stents: A computational study on the interaction with the vascular wall. Biomech. Model. mechanobiol. 2004, 2, 205–217. [Google Scholar] [CrossRef]
- Fung, Y.C. Mechanical Properties and Active Remodeling of Blood Vessels. Biomechanics 1993, 321–391. [Google Scholar] [CrossRef]
- Martufi, G.; Forneris, A.; Appoo, J.J.; Martino, E.S.D. Is there a role for biomechanical engineering in helping to elucidate the risk profile of the thoracic aorta? Ann. Thorac. Surg. 2005, 101, 390–398. [Google Scholar] [CrossRef] [Green Version]
- Timmins, L.H.; Miller, M.W.; Clubb, F.J.; Moore, J.E. Increased artery wall stress post-stenting leads to greater intimal thickening. Lab. Investig. 2011, 91, 955–967. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.; Gu, L.; Froemming, S.R. Effects of arterial strain and stress in the prediction of restenosis risk: Computer modeling of stent trials. Biomed. Eng. Lett. 2012, 2, 158–163. [Google Scholar] [CrossRef] [Green Version]
- Rieu, R.; Barragan, P.; Masson, C.; Fuseri, J.; Garitey, V.; Silvestri, M.; Roquebert, P.; Sainsous, J. Radial force of coronary stents: A comparative analysis. Catheter. Cardiovasc. Interv. 1999, 46, 380–391. [Google Scholar] [CrossRef]
- Mori, K.; Saito, T. Effects of stent structure on stent flexibility measurements. Ann. Biomed. Eng. 2005, 33, 733–742. [Google Scholar] [CrossRef]
- Choubey, R.K.; Pradhan, S.K. Prediction of strength and radial recoil of various stents using FE analysis. Mater. Today Proc. 2020, 27, 2254–2259. [Google Scholar] [CrossRef]
- Masters, I.G.; Evans, K.E. Models for the elastic deformation of honeycombs. Compos. Struct. 1996, 35, 403–422. [Google Scholar] [CrossRef]
- Omairey, S.L.; Dunning, P.D.; Srinivas, S. Development of an abaqus plugin tool for periodic rve homogenisation. Eng. Comput. 2019, 35, 567–577. [Google Scholar] [CrossRef] [Green Version]
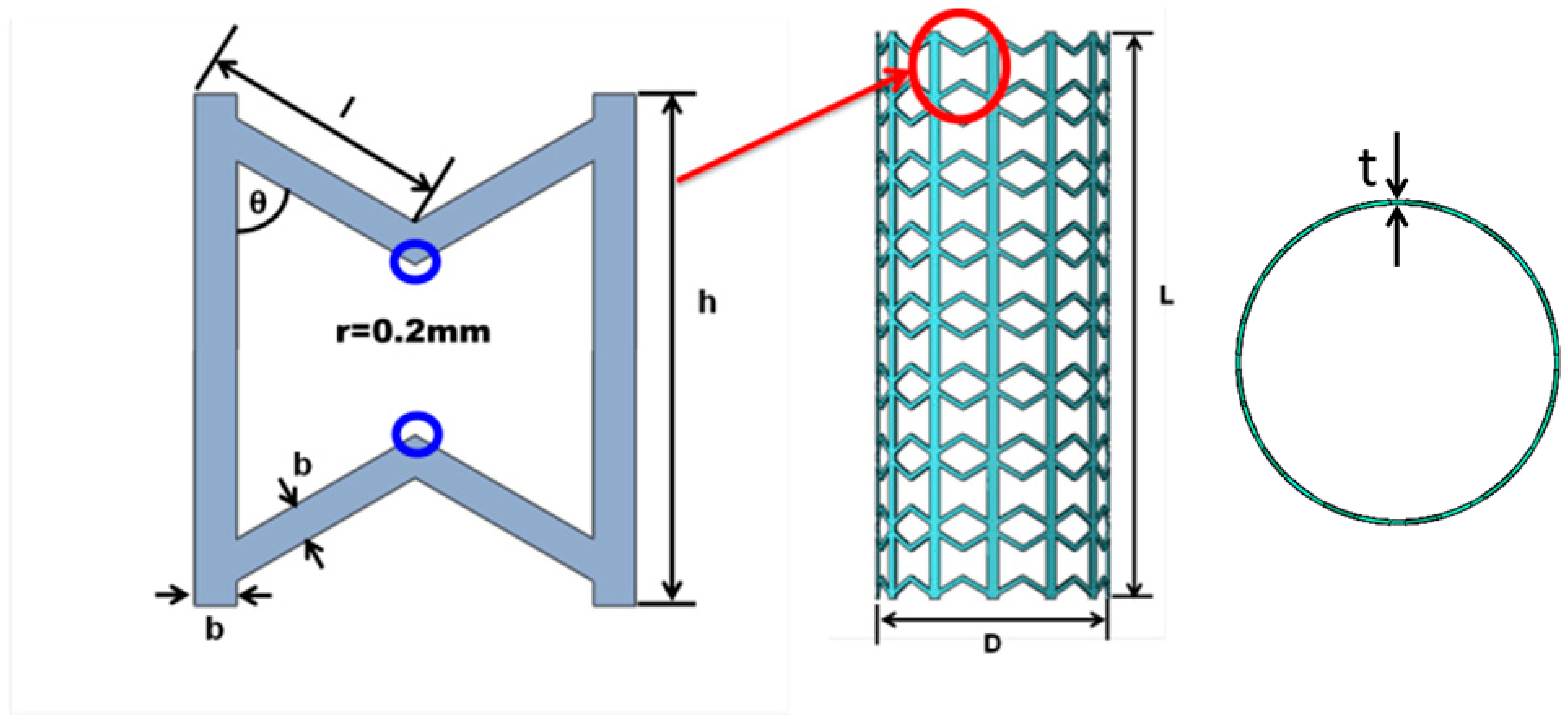

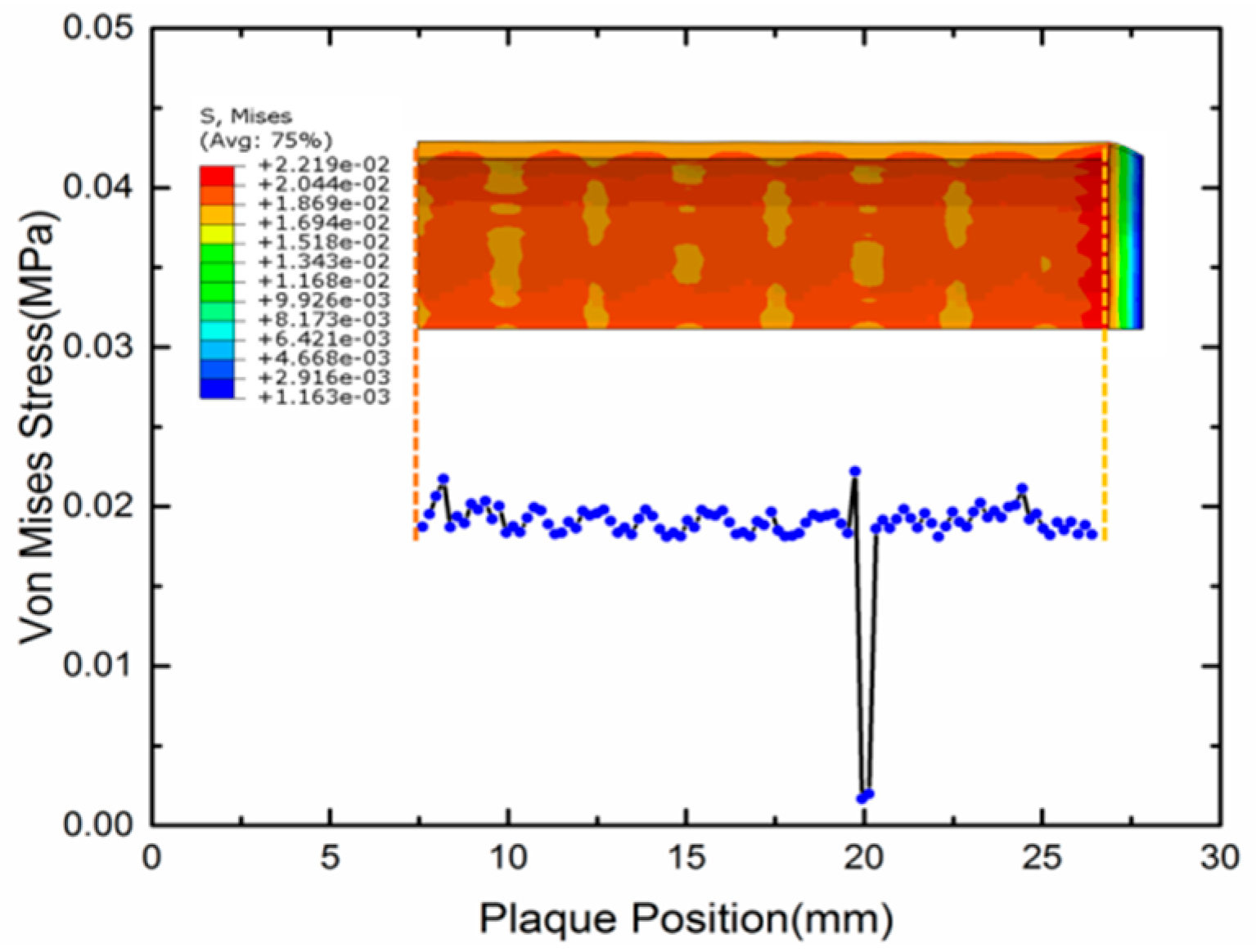

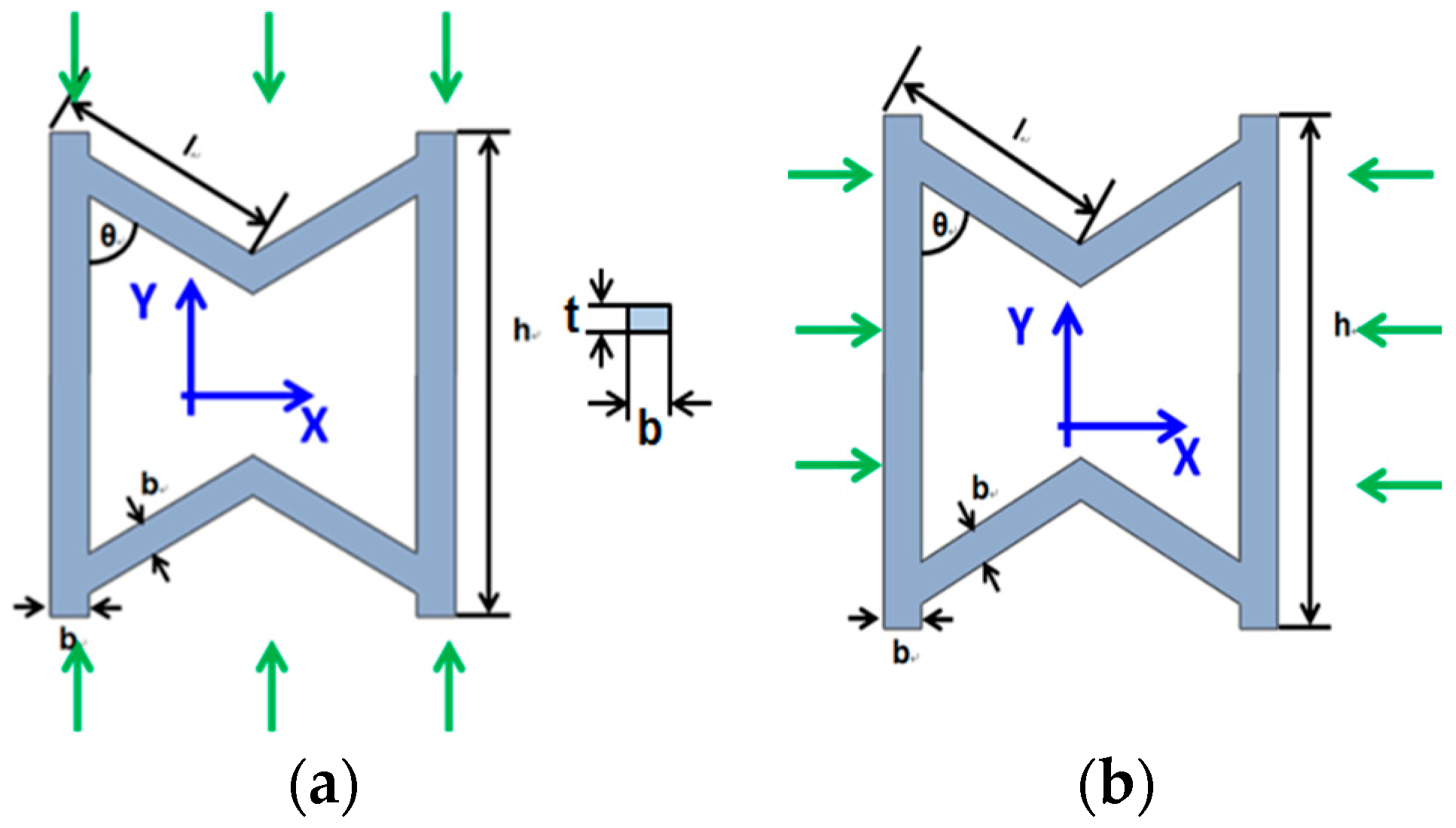

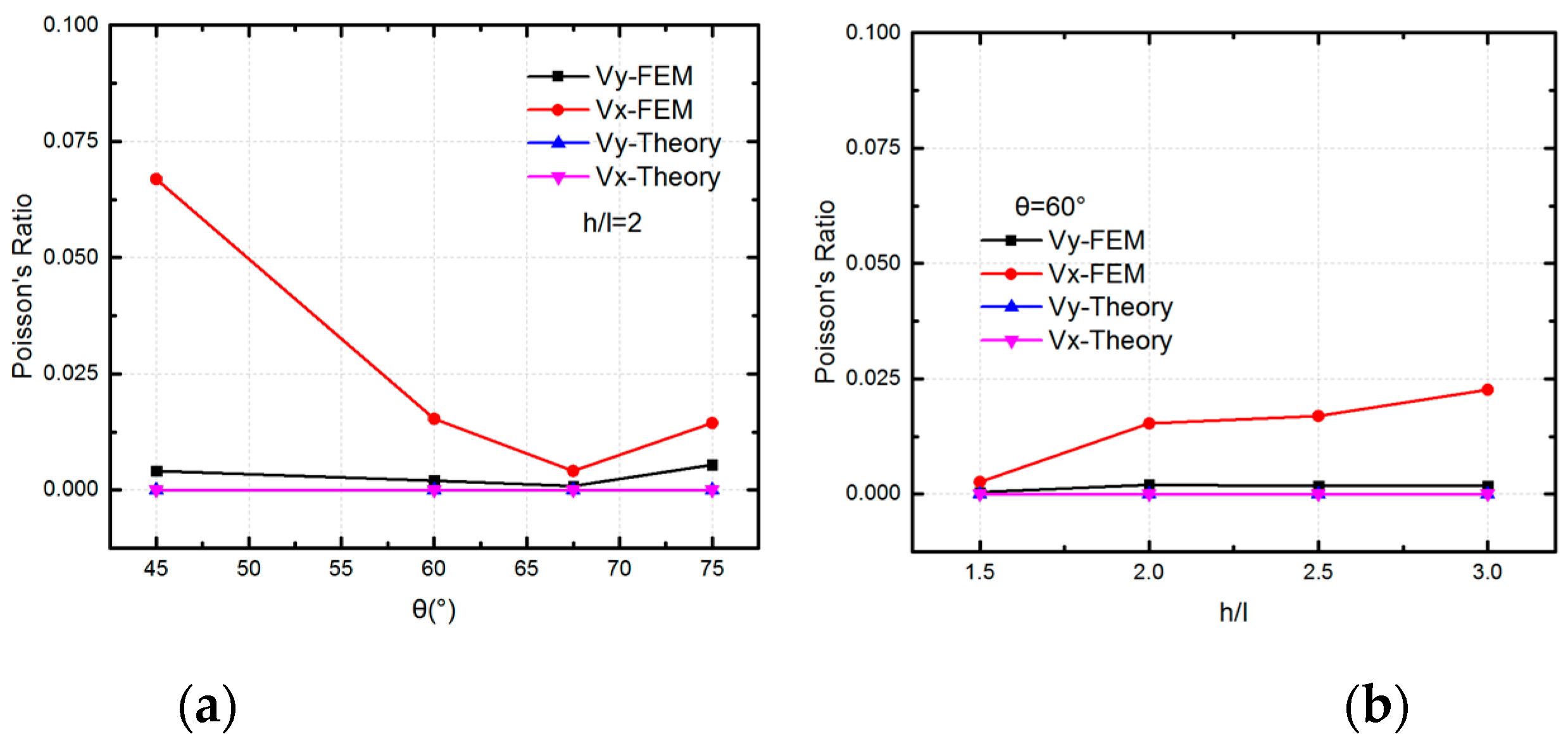

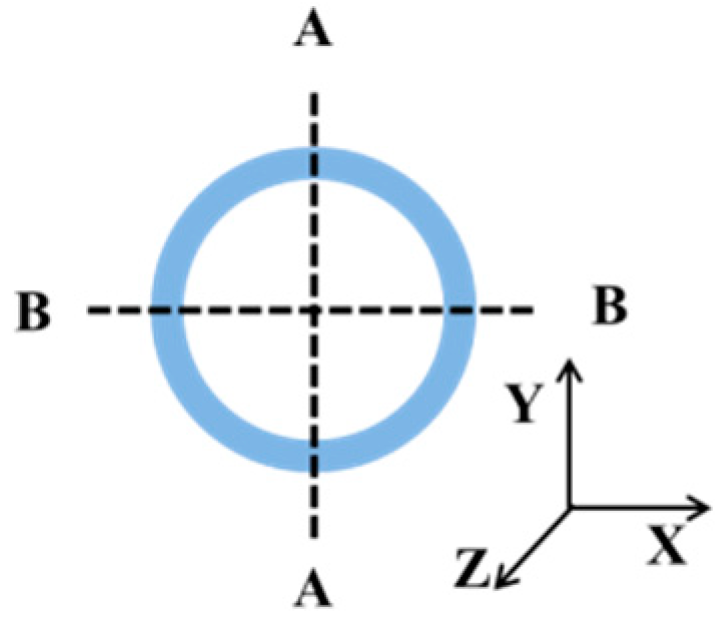

| l (mm) | θ (℃) | b (mm) | h (mm) | D (mm) | L (mm) | t (mm) |
|---|---|---|---|---|---|---|
| 2.4 | 60 | 0.4 | 4.8 | 7.939 | 38.4 | 0.2 |
| Mode 1 | Mode 2 | Mode 3 |
|---|---|---|
 |  |  |
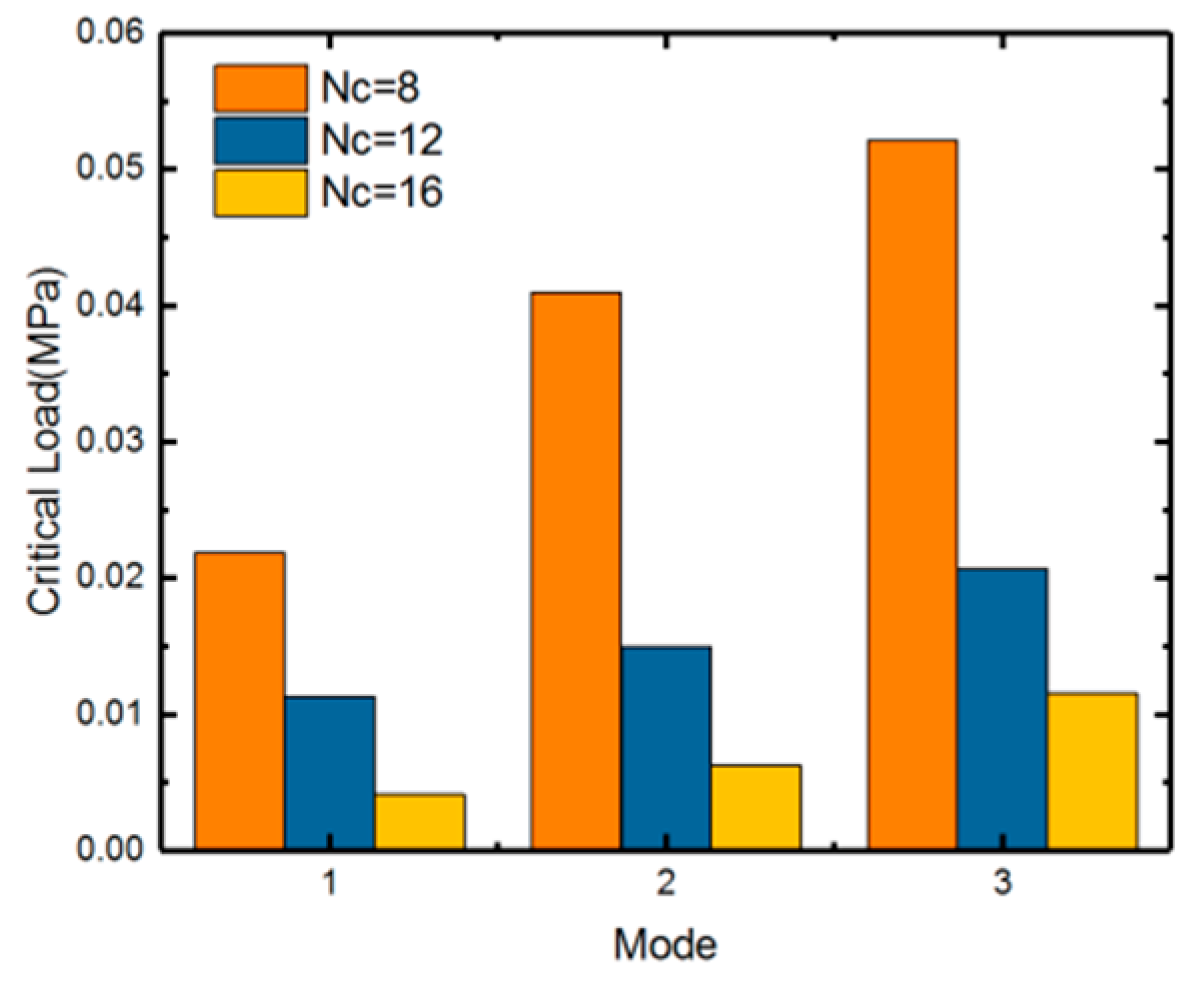
| Nc | 8 | 12 | 16 |
|---|---|---|---|
| Linear result (MPa) | 0.025153 | 0.015455 | 0.00876847 |
| Nonlinear Result (MPa) | 0.02 | 0.012 | 0.0076 |
| Nc | 4 | 8 | 12 | 16 |
|---|---|---|---|---|
| α | 0.3 | 0.35 | 0.35 | 0.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Xu, S.; Luo, X.; Liu, Z. Theoretical and Numerical Analysis of Mechanical Behaviors of a Metamaterial-Based Shape Memory Polymer Stent. Polymers 2020, 12, 1784. https://doi.org/10.3390/polym12081784
Liu R, Xu S, Luo X, Liu Z. Theoretical and Numerical Analysis of Mechanical Behaviors of a Metamaterial-Based Shape Memory Polymer Stent. Polymers. 2020; 12(8):1784. https://doi.org/10.3390/polym12081784
Chicago/Turabian StyleLiu, Ruoxuan, Shuai Xu, Xiaoyu Luo, and Zishun Liu. 2020. "Theoretical and Numerical Analysis of Mechanical Behaviors of a Metamaterial-Based Shape Memory Polymer Stent" Polymers 12, no. 8: 1784. https://doi.org/10.3390/polym12081784
APA StyleLiu, R., Xu, S., Luo, X., & Liu, Z. (2020). Theoretical and Numerical Analysis of Mechanical Behaviors of a Metamaterial-Based Shape Memory Polymer Stent. Polymers, 12(8), 1784. https://doi.org/10.3390/polym12081784