Analysis of Three-Phase Structure of Epoxy Resin/CNT/Graphene by Molecular Simulation
Abstract
1. Introduction
2. Simulation Method and Molecular Behavior
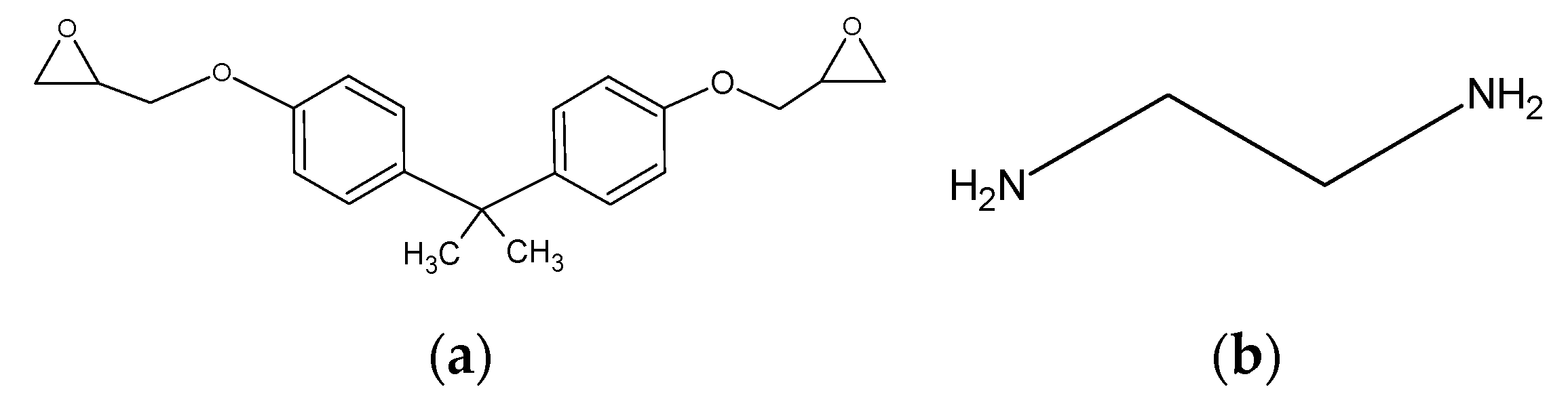
2.1. Modeling Each Molecule and Creating a Three-Phase Structure
2.2. Relaxation of the Three-Phase Structure
2.3. Molecular Analysis
3. Results
3.1. Results of Molecular Behavior
3.2. The Interaction Energy between One Molecule and Other Molecules
3.3. The Interaction Energy between Two Individual Molecules
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Santos, R.M.; Vale, D.; Rocha, J.; Martins, C.; Mould, S.T.; Rocha, N. Multiscale carbon fibre–reinforced polymer (CFRP) composites containing carbon nanotubes with tailored interfaces. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 1521–1533. [Google Scholar] [CrossRef]
- Sharma, M.; Gao, S.-L.; Mäder, E.; Sharma, H.; Wei, L.Y.; Bijwe, J. Carbon fiber surfaces and composite interphases. Compos. Sci. Technol. 2014, 102, 35–50. [Google Scholar] [CrossRef]
- Jones, C. The chemistry of carbon fibre surfaces and its effect on interfacial phenomena in fibre/epoxy composites. Compos. Sci. Technol. 1991, 42, 275–298. [Google Scholar] [CrossRef]
- Moniruzzaman, M.; Winey, K.I. Polymer Nanocomposites Containing Carbon Nanotubes. Macromolecules 2006, 39, 5194–5205. [Google Scholar] [CrossRef]
- Cheng, Q.; Wang, B.; Zhang, C.; Liang, R. Functionalized Carbon-Nanotube Sheet/Bismaleimide Nanocomposites: Mechanical and Electrical Performance Beyond Carbon-Fiber Composites. Small 2010, 6, 763–767. [Google Scholar] [CrossRef]
- Gandhi, R.A.; Jayaseelan, V.; Kumar, K.P.; Raghunath, B.; Krishnaraj, S. Effect of Carbon Nano Tubes (CNT) on Hardness of Polypropylene Matrix. In Proceedings of the 6th International Conference and Exhibition on Sustainable Energy and Advanced Materials; Springer: Singapore, 2019; pp. 261–270. [Google Scholar] [CrossRef]
- Bisht, A.; Dasgupta, K.; Lahiri, D. Effect of graphene and CNT reinforcement on mechanical and thermomechanical behavior of epoxy-A comparative study. J. Appl. Polym. Sci. 2017, 135, 46101. [Google Scholar] [CrossRef]
- Nomula, S.S.R.; Rathore, D.K.; Ray, B.C.; Prusty, R.K. Creep performance of CNT reinforced glass fiber/epoxy composites: Roles of temperature and stress. J. Appl. Polym. Sci. 2019, 136, 1–15. [Google Scholar] [CrossRef]
- Guo, B.; Du, Y.; Yan, N.; Song, M. Mechanical properties and microstructures of Al-10Mg-4.5Si matrix composites reinforced by carbon nanotubes. J. Alloy. Compd. 2019, 792, 860–868. [Google Scholar] [CrossRef]
- Panchagnula, K.K.; Kuppan, P. Improvement in the mechanical properties of neat GFRPs with multi-walled CNTs. J. Mater. Res. Technol. 2019, 8, 366–376. [Google Scholar] [CrossRef]
- Rao, Y.A.; Ramji, K.; Rao, P.S.; Srikanth, I. Effect of A-MWCNTs and ETBN toughener on impact, compression and damping properties of carbon fiber reinforced epoxy composites. J. Mater. Res. Technol. 2019, 8, 896–903. [Google Scholar] [CrossRef]
- Sanchez, M.; Campo, M.; Suárez, A.J.; Ureña, A. Effect of the carbon nanotube functionalization on flexural properties of multiscale carbon fiber/epoxy composites manufactured by VARIM. Compos. Part B Eng. 2013, 45, 1613–1619. [Google Scholar] [CrossRef]
- Shi, H.; Wang, X.; Hu, X.; Meng, L.; Leng, X.; Wu, K. Interfacial Modification Using Matrix Alloying in Mg/CNT Composites for Improved Mechanical Performance. J. Mater. Eng. Perform. 2019, 28, 3041–3047. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, X.; Liu, P.; Li, W.; Ma, F.; He, D.; Li, J. Effect of yttrium on the electrical and mechanical properties of in situ synthesized CNTs/CuCr composites. J. Mater. Res. 2019, 34, 2590–2599. [Google Scholar] [CrossRef]
- Shekar, K.C.; Prasad, B.A.; Singaravel, B.; Prasad, N.E. Effect of CNTs addition on the fracture behaviour of neat epoxy and epoxy-carbon fiber-reinforced composites. AIP Conf. Proc. 2019, 2057, 020043. [Google Scholar] [CrossRef]
- Shekar, K.C.; Priya, M.S.; Subramanian, P.K.; Kumar, A.; Prasad, B.A.; Prasad, N.E. Processing, structure and flexural strength of CNT and carbon fibre reinforced, epoxy-matrix hybrid composite. Bull. Mater. Sci. 2014, 37, 597–602. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. Analysis of the Connecting Effectiveness of the Interphase Zone on the Tensile Properties of Carbon Nanotubes (CNT) Reinforced Nanocomposite. Polymers 2020, 12, 896. [Google Scholar] [CrossRef]
- Badakhsh, A.; An, K.-H.; Kim, B.-J. Enhanced Surface Energetics of CNT-Grafted Carbon Fibers for Superior Electrical and Mechanical Properties in CFRPs. Polymers 2020, 12, 1432. [Google Scholar] [CrossRef]
- Zare, Y.; Rhee, K.Y. Development of Expanded Takayanagi Model for Tensile Modulus of Carbon Nanotubes Reinforced Nanocomposites Assuming Interphase Regions Surrounding the Dispersed and Networked Nanoparticles. Polymers 2020, 12, 233. [Google Scholar] [CrossRef]
- Koyanagi, J.; Itano, N.; Yamamoto, M.; Mori, K.; Ishida, Y.; Bazhirov, T. Evaluation of the mechanical properties of carbon fiber/polymer resin interfaces by molecular simulation. Adv. Compos. Mater. 2019, 28, 639–652. [Google Scholar] [CrossRef]
- Fankhänel, J.; Arash, B.; Rolfes, R. Elastic interphase properties of nanoparticle/epoxy nanocomposites: A molecular dynamics study. Compos. Part B Eng. 2019, 176, 107211. [Google Scholar] [CrossRef]
- Al Mahmud, H.; Radue, M.S.; Chinkanjanarot, S.; Pisani, W.A.; Gowtham, S.; Odegard, G.M. Multiscale modeling of carbon fiber- graphene nanoplatelet-epoxy hybrid composites using a reactive force field. Compos. Part B Eng. 2019, 172, 628–635. [Google Scholar] [CrossRef]
- Sun, R.; Li, L.; Feng, C.; Kitipornchai, S.; Yang, J. Tensile property enhancement of defective graphene/epoxy nanocomposite by hydrogen functionalization. Compos. Struct. 2019, 224, 111079. [Google Scholar] [CrossRef]
- Sahraei, A.A.; MokariZadeh, A.H.; George, D.; Rodrigue, D.; Baniassadi, M.; Foroutan, M. Insights into interphase thickness characterization for graphene/epoxy nanocomposites: A molecular dynamics simulation. Phys. Chem. Chem. Phys. 2019, 21, 19890–19903. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Kwon, S.; Lee, M.Y.; Cho, M. Molecular dynamics and micromechanics study of hygroelastic behavior in graphene oxide-epoxy nanocomposites. Compos. Part B Eng. 2019, 164, 425–436. [Google Scholar] [CrossRef]
- Rahman, R.; Haque, A. Molecular modeling of crosslinked graphene–epoxy nanocomposites for characterization of elastic constants and interfacial properties. Compos. Part B Eng. 2013, 54, 353–364. [Google Scholar] [CrossRef]
- Yang, M.; Koutsos, V.; Zaiser, M. Interactions between Polymers and Carbon Nanotubes: A Molecular Dynamics Study. J. Phys. Chem. B 2005, 109, 10009–10014. [Google Scholar] [CrossRef]
- Park, C.; Jung, J.; Yun, G.J. Thermomechanical properties of mineralized nitrogen-doped carbon nanotube/polymer nanocomposites by molecular dynamics simulations. Compos. Part B Eng. 2019, 161, 639–650. [Google Scholar] [CrossRef]
- Rahimian-Koloor, S.M.; Hashemianzadeh, S.M.; Shokrieh, M.M. Effect of CNT structural defects on the mechanical properties of CNT/Epoxy nanocomposite. Phys. B Condens. Matter 2018, 540, 16–25. [Google Scholar] [CrossRef]
- Wang, H.; Jin, K.; Wang, C.; Guo, X.; Chen, Z.; Tao, J. Effect of fiber surface functionalization on shear behavior at carbon fiber/epoxy interface through molecular dynamics analysis. Compos. Part A Appl. Sci. Manuf. 2019, 126, 105611. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Wang, Q. Enhancement of tribological properties of polymer composites reinforced by functionalized graphene. Compos. Part B Eng. 2017, 120, 83–91. [Google Scholar] [CrossRef]
- Khare, K.S.; Khare, R. Effect of Carbon Nanotube Dispersion on Glass Transition in Cross-Linked Epoxy–Carbon Nanotube Nanocomposites: Role of Interfacial Interactions. J. Phys. Chem. B 2013, 117, 7444–7454. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Sharma, K.; Dixit, A.R. A review on the mechanical and thermal properties of graphene and graphene-based polymer nanocomposites: Understanding of modelling and MD simulation. Mol. Simul. 2019, 46, 136–154. [Google Scholar] [CrossRef]
- Koloor, S.S.R.; Karimzadeh, A.; Hamdi, M.; Petrů, M.; Tamin, M.N.; Rahimian-Koloor, S.M. Nano-Level Damage Characterization of Graphene/Polymer Cohesive Interface under Tensile Separation. Polymers. 2019, 11, 1435. [Google Scholar] [CrossRef] [PubMed]
- Shiu, S.-C.; Tsai, J.-L. Characterizing thermal and mechanical properties of graphene/epoxy nanocomposites. Compos. Part B Eng. 2014, 56, 691–697. [Google Scholar] [CrossRef]
- Jin, Y.; Duan, F.; Mu, X. Functionalization enhancement on interfacial shear strength between graphene and polyethylene. Appl. Surf. Sci. 2016, 387, 1100–1109. [Google Scholar] [CrossRef]
- Arash, B.; Wang, Q.; Varadan, V.K. Mechanical properties of carbon nanotube/polymer composites. Sci. Rep. 2014, 4, 6479. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Wang, Q.; Xing, M. A comparison study on mechanical properties of polymer composites reinforced by carbon nanotubes and graphene sheet. Compos. Part B Eng. 2018, 133, 35–41. [Google Scholar] [CrossRef]
- Yu, B.; Fu, S.; Wu, Z.; Bai, H.; Ning, N.; Fu, Q. Molecular dynamics simulations of orientation induced interfacial enhancement between single walled carbon nanotube and aromatic polymers chains. Compos. Part A Appl. Sci. Manuf. 2015, 73, 155–165. [Google Scholar] [CrossRef]
- Thakuria, R.; Nath, N.K.; Saha, B.K. The Nature and Applications of π–π Interactions: A Perspective. Cryst. Growth Des. 2019, 19, 523–528. [Google Scholar] [CrossRef]
- Sinnokrot, M.O.; Sherrill, C.D.; Sherrill, C.D. High-Accuracy Quantum Mechanical Studies of π−π Interactions in Benzene Dimers. J. Phys. Chem. A 2006, 110, 10656–10668. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Zhuang, X.; Muthu, J.S.; Mabrouki, T.; Fontaine, M.; Gong, Y.; Rabczuk, T. Load transfer of graphene/carbon nanotube/polyethylene hybrid nanocomposite by molecular dynamics simulation. Compos. Part B Eng. 2014, 63, 27–33. [Google Scholar] [CrossRef]
- Sun, S.; Chen, S.; Weng, X.; Shan, F.; Hu, S. Effect of Carbon Nanotube Addition on the Interfacial Adhesion between Graphene and Epoxy: A Molecular Dynamics Simulation. Polymers 2019, 11, 121. [Google Scholar] [CrossRef] [PubMed]
- Mayo, S.L.; Olafson, B.D.; Goddard, W.A. DREIDING: A generic force field for molecular simulations. J. Phys. Chem. 1990, 94, 8897–8909. [Google Scholar] [CrossRef]





| Model | Dimensions of Simulation Cell (x, y, z) (Å) | CNT Diameter (nm) | Number of CNTs | Arrangements of CNTs | Temperature Changes (K) |
|---|---|---|---|---|---|
| (a) Two CNT (4,4) | (44.32, 38.38, 160.0) | 0.542 | 2 | - | - |
| (b) Three CNT (4,4) | (44.32, 38.38, 160.0) | 0.542 | 3 | - | - |
| (c) Two CNT (8,8) | (44.32, 38.38, 190.0) | 1.084 | 2 | - | - |
| (d) Two CNT (8,8) considering temperature changes | (44.32, 38.38, 190.0) | 1.084 | 2 | - | 600→300 |
| (e) Four CNT (8,8) parallel arrangements | (44.32, 38.38, 190.0) | 1.084 | 4 | parallel | -- |
| (f) Four CNT (8,8) vertical arrangements | (44.32, 38.38, 190.0) | 1.084 | 4 | vertical |
| Etotal (kJ/mol) | EG (kJ/mol) | EC/E (kJ/mol) | EG−(C/E) (kJ/mol) | |
|---|---|---|---|---|
| (a) Two CNT (4,4) | 4.579 × 105 | 3.401 × 104 | 4.288 × 105 | 4848 |
| (b) Three CNT (4,4) | 4.813 × 105 | 3.402 × 104 | 4.524 × 105 | 5200 |
| (c) Two CNT (8,8) | 4.738 × 105 | 3.402 × 104 | 4.450 × 105 | 5192 |
| (d) Two CNT (8,8) considering temperature changes | 4.726 × 105 | 3.402 × 104 | 4.440 × 105 | 5378 |
| (e) Four CNT (8,8) parallel arrangements | 5.375 × 105 | 3.404 × 104 | 5.088 × 105 | 5297 |
| (f) Four CNT (8,8) vertical arrangements | 7.261 × 105 | 3.406 × 104 | 6.966 × 105 | 4504 |
| Etotal (kJ/mol) | EE (kJ/mol) | EC/G (kJ/mol) | EE−(C/G) (kJ/mol) | |
|---|---|---|---|---|
| (a) Two CNT (4,4) | 4.580 × 105 | 3.819 × 105 | 8.108 × 104 | 5030 |
| (b) Three CNT (4,4) | 4.813 × 105 | 3.823 × 105 | 1.042 × 105 | 5265 |
| (c) Two CNT (8,8) | 4.738 × 105 | 3.817 × 105 | 9.755 × 104 | 5462 |
| (d) Two CNT (8,8) considering temperature changes | 4.726 × 105 | 3.811 × 105 | 9.744 × 104 | 5917 |
| (e) Four CNT (8,8) parallel arrangements | 5.375 × 105 | 3.823 × 105 | 1.616 × 105 | 6350 |
| (f) Four CNT (8,8) vertical arrangements | 7.261 × 105 | 3.953 × 105 | 3.363 × 105 | 5437 |
| Etotal (kJ/mol) | EC (kJ/mol) | EG/E (kJ/mol) | EC−(E/G) (kJ/mol) | |
|---|---|---|---|---|
| (a) Two CNT (4,4) | 4.579 × 105 | 4.823 × 104 | 4.122 × 105 | 2518 |
| (b) Three CNT (4,4) | 4.813 × 105 | 7.191 × 104 | 4.129 × 105 | 3576 |
| (c) Two CNT (8,8) | 4.738 × 105 | 6.522 × 104 | 4.122 × 105 | 3666 |
| (d) Two CNT (8,8) considering temperature changes | 4.726 × 105 | 6.509 × 104 | 4.114 × 105 | 3871 |
| (e) Four CNT (8,8) parallel arrangements | 5.375 × 105 | 1.302 × 105 | 4.136 × 105 | 6287 |
| (f) Four CNT (8,8) vertical arrangements | 7.261 × 105 | 3.041 × 105 | 4.267 × 105 | 4632 |
| EE−G (kJ/mol) | EC−G (kJ/mol) | EE−C (kJ/mol) | |
|---|---|---|---|
| (a) Two CNT (4,4) | 3681 | 1168 | 1350 |
| (b) Three CNT (4,4) | 3445 | 1755 | 1820 |
| (c) Two CNT (8,8) | 3494 | 1698 | 1968 |
| (d) Two CNT (8,8) considering temperature changes | 3712 | 1666 | 2205 |
| (e) Four CNT (8,8) parallel arrangements | 2688 | 2622 | 3662 |
| (f) Four CNT (8,8) vertical arrangements | 2655 | 1849 | 2783 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naito, S.; Koyanagi, J.; Komukai, T.; Uno, T. Analysis of Three-Phase Structure of Epoxy Resin/CNT/Graphene by Molecular Simulation. Polymers 2020, 12, 1821. https://doi.org/10.3390/polym12081821
Naito S, Koyanagi J, Komukai T, Uno T. Analysis of Three-Phase Structure of Epoxy Resin/CNT/Graphene by Molecular Simulation. Polymers. 2020; 12(8):1821. https://doi.org/10.3390/polym12081821
Chicago/Turabian StyleNaito, Shun, Jun Koyanagi, Takuji Komukai, and Toshikazu Uno. 2020. "Analysis of Three-Phase Structure of Epoxy Resin/CNT/Graphene by Molecular Simulation" Polymers 12, no. 8: 1821. https://doi.org/10.3390/polym12081821
APA StyleNaito, S., Koyanagi, J., Komukai, T., & Uno, T. (2020). Analysis of Three-Phase Structure of Epoxy Resin/CNT/Graphene by Molecular Simulation. Polymers, 12(8), 1821. https://doi.org/10.3390/polym12081821






