Next Article in Journal
Block Copolymers of Poly(ω-Pentadecalactone) in Segmented Polyurethanes: Novel Biodegradable Shape Memory Polyurethanes
Previous Article in Journal
Synthesis of Antibacterial Gelatin/Sodium Alginate Sponges and Their Antibacterial Activity
Previous Article in Special Issue
Effect of Fibre Orientation and Hostile Solutions on Stress Relaxation of Glass/Polyamide Composites
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Polymers
Volume 12
Issue 9
10.3390/polym12091927
polymers-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effect of Post-Cure on the Static and Viscoelastic Properties of a Polyester Resin

by
Marco P. Silva
1,
Paulo Santos
1,
João M. Parente
1,
Sara Valvez
1,
Paulo N. B. Reis
1 and
Ana P. Piedade
2,*
1
C-MAST, Department of Electromechanical Engineering, University of Beira Interior, Calçada Fonte do Lameiro, 6201-100 Covilha, Portugal
2
University of Coimbra, CEMMPRE, Department of Mechanical Engineering, 3030-788 Coimbra, Portugal
*
Author to whom correspondence should be addressed.
Polymers 2020, 12(9), 1927; https://doi.org/10.3390/polym12091927
Submission received: 22 July 2020 / Revised: 8 August 2020 / Accepted: 24 August 2020 / Published: 26 August 2020
(This article belongs to the Special Issue Viscoelastic Behavior of Polymer–Matrix Composites)
Browse Figures
Versions Notes

Abstract

:
This work intends to study the effect of the curing parameters on the mechanical properties of a polyester resin without a complete curing reaction process. For this purpose, cures at room temperature, 40 °C, and 60 °C, and post-cures at 40 °C and 60 °C, with different exposure times, were considered. Three-point bending tests were performed to assess the bending properties and both stress relaxation and creep behavior. The degree of crosslinking was estimated by evaluating the C = C ester bond, by Fourier infrared spectroscopy and complemented with the thermal characterization made by differential scanning calorimetry. The results showed that higher curing temperatures are preferable to methods involving curing and post-curing, which can be confirmed by the higher degree of conversion of unsaturated ester bonds at 60 °C. Compared to the resin cured at room temperature, the bending strength increased by 36.5% at 40 °C and 88.6% at 60 °C. A similar effect was observed for bending stiffness. In terms of stress relaxation and creep strain, the lowest values were obtained for samples cured at 60 °C.

Graphical Abstract

1. Introduction

Thermosetting resins are extensively used in diverse areas ranging from boats, consumer goods, aircraft, automotive components, and several industrial applications. Regarding the polyester resins, for example, they are the most widely used resins in polymer matrix composites, particularly in the maritime and automotive industries, and represent about 75% of total resin used in the composites industry. They are the most economical resin systems used in engineering applications that, simultaneously, combine low viscosity, adequate resistance to water and variety of chemicals, adequate resistance to weathering and ageing, good wetting to glass fibers, and relatively low shrinkage between 4 and 8% during curing. Nerveless, polyester resins have limited use in high-performance composites [1,2,3].
Regardless of their excellent aptitude for different manufacturing processes, such as compression molding, injection molding, resin transfer molding, and hand lay-up process [1,2], the main problem is related to their curing process [4,5,6]. The complexity of the problem is considerable, mainly in the quality control of the cure, because the process is affected by numerous factors, including ambient temperature, quality, and quantity of catalysts, the volume of the cured portion, and heat removal from the curing area. Therefore, both mechanical performance and surface appearance will be dramatically affected by the quality of the cure, a problem that is transversal to the various types of thermosetting resins [7,8].
The curing process of unsaturated polyester is exothermic due to a polymerization reaction that causes crosslinking among individual linear polymer chains [9,10,11,12]. Therefore, as polymerization by free radicals, the curing reaction of unsaturated polyester can be initiated by either the thermal or reduction–oxidation (redox) initiation system. Moreover, organic peroxides (initiators) can also initiate the reaction by adding metallic salts or amines (initiator + promoter system) at room temperature (RT). Unlike other thermosetting resins, no byproducts are formed during the curing reaction, and these resins can be molded, cast, and laminated at low pressures and temperatures [13,14,15,16]. However, many of the processing problems arise precisely in this curing process, which are generally ignored in the production planning phase. In this context, it is essential to have the curing data to correctly understand the final properties of polymers and/or composites and, thus, to ensure safe applications.
According to the open literature, different parameters define the post-cure process, but the post-cure temperature is considered the most important factor that influences the extent of crosslinking [8]. Senthilkumar et al. [17], for example, developed works about the temperature effect on the mechanical properties of sisal fiber reinforced polyester composites. For this purpose, composites were produced for different curing temperatures ranging from 60 to 100 °C in steps of 10 with a hot compression molding process. The best tensile and impact strength was obtained for composites cured at 100 °C. Kumar et al. [18] studied the post-curing temperature and time on the interlaminar shear strength (ILSS) and glass transition temperature (Tg) of glass fiber reinforced polymer (GFRP) composites. Three different temperatures (80 °C, 110 °C, and 140 °C) and four different periods (2 h, 4 h, 6 h, 8 h, and 12 h) were analyzed. They concluded that post-curing at 140 °C for 6 h gave better thermal and mechanical properties as compared to post-curing at different temperatures and periods. For example, in terms of ILSS, a drastic increase was observed between 2 and 6 h, but, when the maximum was reached after 6 h, this property remains constant (a negligible effect was observed). According to the authors, the energy available at lower post-curing temperatures may not be enough to enhance further the wettability at the fiber/matrix interface.
In contrast, on the highest temperature, the energy received by the system is reasonably high for activating the monomers to crosslink further. Campana et al. [19] studied the effect of post-cure on flax fiber reinforced epoxy composites, and the following conditions were analyzed: composite cured at 80 °C for 24 h, 2 h at 100 °C, 120 °C, and 150 °C. They observed a crosslinking degree of 92% and a Tg of 121 °C for 24 h of curing at 80 °C. Nevertheless, when the resin was post-cured 2 h at 150 °C, these values increased to 100% and 165 °C, respectively. This trend was expected because the goal of post-cure is to achieve a crosslinking rate of 100%. After post-cure, the molecular mobility within the resin is reduced, leading to a higher Tg. It was also noticed that the resin and composite followed the same trend, but, while the Tg of the composite was lower when cured at 80 °C for 24 h, all conditions that involved post-cured promoted higher values. This behavior is explained by a change in specific heat or thermal conductivity when the fibers were introduced [20,21]. Finally, Elleuch et al. [22] confirmed that a woven glass-polyester composite’s mechanical properties increased with the post-cure. The low crosslinking density effect increases the resin ductility and the failure strain. Therefore, a rigid interface (brittle failure) was obtained in the case of post-cure and a weak interface (progressive failure) in the case of post-cure absence.
Therefore, the main goal of the present work is to study the curing parameters of a polyester resin usually used on surf boards to understand their effects on mechanical properties. Moreover, due to some degree of ductility required for the specific application of this polyester resin, the curing and post-curing processes are recommended, by the manufacturer, to occur at much lower temperatures than the ones usually reported in the literature. Therefore, special attention will be given to the viscoelastic behavior of the resin because, due to its inherent viscoelasticity, composites will be prone to creep and stress relaxation, constituting a significant challenge when used in long-term applications.

2. Materials and Methods

A polyester resin (AROPOL FS 1962, SF Composites, Mauguio, France) was mixed with 1% peroxide (MEKP-50, SF Composites, Mauguio, France), and, after mixing, the system was degassed in a vacuum oven to remove any potential air bubbles. According to the manufacture, the resin presents low reactivity, which implies that after curing is almost inert towards other chemical species, and it is formulated with additives: a preaccelerating compound (enabling faster polymerization), and an UV stabilizer. The main properties/characteristics are (at RT): a viscosity of 550 mPa.s, a styrene content of 34%, and a geltime with 1.5% of MEKP-50 of 12 minutes. The crosslinking agent (or hardener) is a methyl ethyl ketone peroxide (MEKP-50) 33% (v/v) in dimethyl phthalate with a viscosity of 20 mPa.s, a peroxide content of 33%, and active oxygen content between 8.8 and 9%. After being degassed, the mixture was poured into a rectangular cardboard mold, with dimensions of 100 × 100 × 3 mm3, and between acetate sheets to both facilitate its removal after curing and obtaining an excellent surface finish. After unmolding the plates, they were submitted to different post-cures that are summarized in Table 1. Different temperatures were considered based on the supplier’s datasheet and the post-cure time based on the different values suggested in the literature [18,19]. Finally, the specimens were cut from those plates, with the final dimensions of 100 × 10 × 3 mm3, using a diamond saw and a moving speed chosen to reduce the heat in the specimen (Figure 1).
The analysis of the chemical functional groups of the resin, crosslinker, and cured samples was performed using Fourier transform infrared spectroscopy (FTIR) in the reflectance mode, using the non-destructive attenuated total reflectance (ATR) sampling technique.
The infrared spectrum (4000–550 cm−1) of the samples at room temperature was recorded using a Perkin Elmer Frontier spectrometer (FT NIR/MIR, PerkinElmer, Waltham, MA, USA), equipped with an FR-DTGS detector and a KBr beam splitter. Spectrum registration was performed with a 4.0 cm−1 resolution with 16 accumulations. A Perkin Elmer sampling accessory, universal ATR module (UATR universal attenuated total reflectance, PerkinElmer, Waltham, MA, USA) with diamond crystal/ZnSe, was used, and a constant 80 N force was applied throughout the spectrum register. The specimens were analyzed without any treatment and three repetitions of each specimen were performed to access the homogeneity of the prepared samples. For the analysis of the chemical functional groups of interest, a deconvolution was made in the original spectra through Origin® software (version 6.1, OriginLab, Northampton, MA, USA). Due to the use of the same force all spectra were normalized and the area of specific bands used for the determination of the degree of conversion of the double bonds.
The thermal events of the specimens, especially Tg, were determined by differential scanning calorimetry (DSC, TA Instruments, Newcastle, USA) in a DSC Q100 V9.9 equipment, with a heating rate of 10 °C.min−1 and with a constant nitrogen flow of 50 mL.min−1. The Tg values were determined through the maximal height of the 1st derivative of each obtained curve.
Three-point bending (3PB) static tests were performed with the spam of 40 mm, according to ASTM Standard D 7264/D 7264M-07 [23], and a Shimadzu AG-10 universal testing machine (Shimadzu Corp., Kyoto, Japan) equipped with a 10 kN load cell was used. For each condition, at least five specimens were tested at room temperature and a rate of 2 mm.min−1.
The flexural properties were also obtained according to ASTM Standard D 7264/D 7264M-07 [23] and, for example, while the flexural strength was calculated as the nominal stress at the middle span section, using the maximum value of the load Equation (1), the bending stiffness modulus was obtained by linear regression of the load–displacement curves considering the interval in the linear segment and according to Equation (2). A correlation factor more significant than 95% was used. Finally, the flexural strain (ε) was calculated according to Equation (3).
σ = 3   P   L 2   b   h 2
E = Δ P ⋅ L 3 48 Δ u ⋅ I
ε f = 6 × S × h L 2
where P is the load, S the deflexion, L the span length, b the width, h the thickness of the specimen, I the moment of inertia of the cross-section and ∆P as well as ∆u, respectively, the load range and flexural displacement range in the middle span for an interval in the linear region of the load versus displacement plot.
The same equipment (Shimadzu AG-10) was used to carry out stress relaxation (SR) and creep tests at room temperature and with similar specimens to those shown in Figure 1. In the first case, all experimental procedure was supported by ASTM D6048-07 [24], where a fixed strain was applied (correspondent to around 51.5 MPa for all configurations) and the stress recorded during the loading time of 10,800 s. For this study, only specimens cured at room temperature (method 1) and with post-cure at 40 °C for 24 h (method 5) and 60 °C for 24 h (method 6) were analyzed. Finally, this bending strain value was selected to guarantee that all SR tests were carried out in the elastic regime of all conditions studied. The creep tests were carried out according to the procedures described in ASTM D7337M-12 [25], at room temperature, for constant stress of 20 MPa, and the displacement recorded during the loading time. In both cases, the data were analyzed according to the respective ASTM standards. On the other hand, and as reported in the open literature [26,27,28], these short-term tests reveal to be an easy, fast, and reliable method to predict long-term behavior. In fact, due to the main costs incurred with long-term test programs, in addition to the fact that long periods between the development of new or improved materials and their applications are not allowed, it is highly desirable that the design data could be obtained by extrapolating the results obtained by short-term tests.

3. Results and Discussion

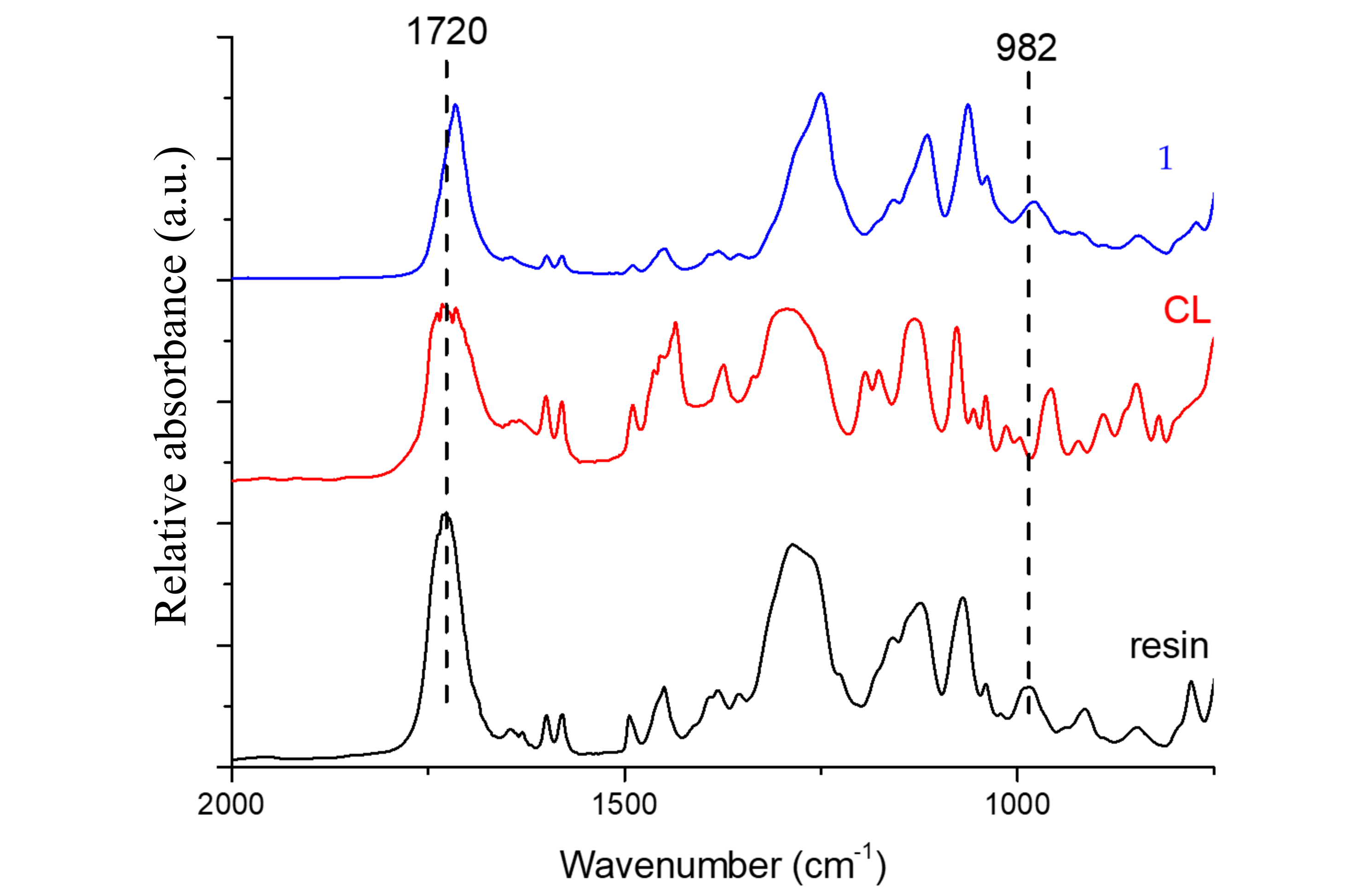
An analysis of the chemical modifications was carried out, considering the different curing parameters. Figure 2 shows the FTIR spectra of the polyester resin, crosslinker agent (CL), and curing process at room temperature (method 1). Only the absorptions bands of the stretching mode of carbonyl groups (>C = O) at 1720 cm−1, and the polyester C = C bonds (982 cm−1), as assigned by other researchers [12,29,30,31], will be considered.
The normalized ratio of the absorption between the mentioned peaks, taking the peak of the carbonyl group as an internal reference, after curing (Figure 3), allows estimating the degree of conversion of the C = C from polyester bonds (X), according to previous studies [32]. The results are displayed in Figure 4 and can provide a rough approximation of the conversion of double bonds. However, it must be highlighted that the covalent bond between adjacent macromolecules can occur via other chemical reactions that do not involve the polyester unsaturated C = C bonds.
It is possible to conclude that a higher degree of conversion was obtained when a higher temperature was used at the beginning of the curing process, as suggested by the comparison between the values from methods 1, 6, and 11. The use of the first step of 24 h curing at room temperature followed by different curing times at higher temperatures (specimens 2–5 and 7–10), induced an almost linear increase of the degree of conversion. These results suggest that the RT induced an increase of the mixture viscosity that makes the evolution of further crosslinking in the post-curing stage difficult. The results suggest that to obtain a higher degree of conversion of the double bonds it is preferable to start with a higher temperature of the curing reaction, instead of a lower temperature followed by higher temperatures in the post-curing step.
In the literature, at least for the last three decades, DSC studies are used to more accurately calculate the percentage of the crosslinking degree [33,34,35,36]. However, the reported studies usually refer to the system with a complete crosslinking reaction, which, as stated before, will not occur for the used resin nor for the tested temperatures. Nevertheless, in this work the DSC values provided additional information through the Tg determination (Table 2 and Figure 5).
The results indicate that when the curing process was made at room temperature, a Tg1 around 16 °C always appeared. This indicates that the system presents free styrene molecules that are not crosslinked. They contribute to a high free volume of the system [33], which, consequently, presents a low (Tg1). Even with a post-cure step at 40 °C (specimens 2–5) this endothermal transition occurred. For higher times of post-curing at 40 °C the system began to present a Tg value, around 144 °C (Tg3), which is the main indicator of the crosslinking reaction. This first Tg disappeared when the curing process was made at 40 or 60 °C with or without subsequently post-curing (specimens 6–11) indicating the low crosslinking efficiency of the process when the curing step was made at room temperatures. These results reinforce the observations made after the FTIR characterization and, according to the literature the process is limited by the decrease of the diffusion of the reactive species, because radicals are trapped and the propagation reaction is stopped [36]. For the system that begins with the curing temperature of 60 °C the post-cure procedure has very little effect on the crosslinking percentage, as the Tg3 increased for 0 h or 24 h of post-curing, at RT, was not significant.
Flexural static tests were performed to obtain the bending properties against the different cure procedures (different exposure times and temperatures). In this context, Figure 6 presents typical bending stress versus strain curves obtained for each condition, which are representative of all other methods.
Even though Figure 6a represents the results obtained for curing parameters 4 (post-curing at 40 °C for 12 h), it is representative of all the specimens that involved the curing temperature of 40 °C. In this case, (Figure 6a) all curves present two distinct regions: a linear behavior up to around 4–5% of the bending strain, followed by a non-linear region in which the maximum bending stress occurs. These two regions appeared in all samples cured or post-cured at 40 °C, where the strain corresponding to the maximum bending stress occurred between 2% and 4%. However, the bending failure strain reached values above 10% due to the low crosslinking density [19,22]. According to Figure 4, the complete crosslinking has not yet been reached and, consequently, a certain level of molecular mobility is expected.
On the other hand, for specimens where the curing temperature of 60 °C was involved, all curves show a nearly fragile behavior. In these conditions, a linear region up to the maximum load was observed, followed by a significant drop, due to reduced molecular mobility promoted by the high density of crosslinking [19,22]. As reported in Figure 4 and Table 2, and comparatively to the value obtained at room temperature, the degree of conversion was around 1.4 times higher for 40 °C and 1.6 times higher for 60 °C. Therefore, a higher degree of conversion was obtained for higher temperatures and, in this case, the bending failure strain coincided with the maximum bending stress, typical behavior of a brittle material.
Figure 7 presents the maximum bending stress against the curing parameters in terms of average values (marks), and the dispersion bands indicate the maximum and minimum values for each condition. It is possible to observe that the curing parameters had a significant influence on the maximum flexural strength of the polyester resin.
From Figure 7a, for example, it is noticed that the use of higher temperatures in the curing process, and without post-cure (specimens 6 and 11), was responsible for higher bending strengths. Compared to the resin cured at room temperature (specimen 1), the bending strength increased around 36.5% for 40 °C (specimen 6) and 88.6% for 60 °C (specimen 11) due to the higher degree of conversion of unsaturated C = C bonds. Therefore, the lower molecular mobility, promoted by the higher conversion of double bonds, is responsible for the higher bending strengths [19,22].
On the other hand, in the case of post-cures effect, the viscosity induced by the crosslinking at RT makes further reticulation when the temperature is increased during the second stage of the process difficult. This behavior is explained by the diffusion problems of the crosslinking agent within the reticulated structure. Regardless of the curing temperatures, Figure 7b confirms what was observed in Figure 4, and a linear increase in bending strength was observed as a function of the exposure time. A higher degree of conversion was achieved for higher exposure times, which, in principle, implies lower molecular mobility [19,22]. For example, the bending strength obtained for a post-cure at 40 °C for 24 h was 73.9% higher than the value obtained at 40 °C for 3 h. At 60 °C post-cure temperature, the increase was around 46.1%.
Figure 8 shows the post-cure effect on bending stiffness, and a behavior very similar to that obtained for bending strength was observed.
In more detail, from Figure 8a, it is possible to observe that, for methods without post-cures (methods 1, 6, and 11), an increase in temperature was responsible for higher bending stiffness values. Bending stiffness was about two times higher for 40 °C (method 6) and three times higher for 60 °C (method 11), compared to the value obtained at room temperature. As reported above, and according to Figure 4 and Table 2, the lower molecular mobility due to a higher density of crosslinking explains these improvements [19,22]. However, when the post-cure effect was analyzed separately in Figure 8b, one more time, a linear increase was observed as a function of the exposure time. Higher exposure times promote a higher degree of conversion of the unsaturated ester bonds, and, consequently, less molecular mobility [19,22]. The bending stiffness obtained for a post-cure at 40 °C for 24 h was 73.3% higher than the value obtained at 40 °C for 3 h, and for the same comparison at 60 °C this value was only 5.5% higher. It is noticed that the exposure time was less expressive in this property with increasing temperature. A brief comparison with the study developed by Gudapati et al. [37], carried out with a cure of 24 h at RT followed by 2 h at 80 °C, evidences a bending modulus similar to the value obtained with method 3 (24 h at RT followed by a post-cure performed at 40 °C for 6 h). In this context, it is noticed the post-cure temperature effect on the crosslinking and, consequently, on the mechanical properties. As reported above, it is the most important factor that influences the extent of cross linking [8]. However, in terms of flexural strength, these authors obtained lower values.
Considering the viscoelastic behavior, Figure 9 presents the stress relaxation curves only for the methods without the post-cure. This figure plots the average bending stress versus time, where σ is the bending stress at any given moment of the test, and σ0 is the initial bending stress. The final bands represent the maximum and minimum values obtained for each condition analyzed.
In general, the stress decreased over time to one value expected to be constant, but in the present work, this constant bending stress was not achieved because it focuses on short-term tests. These tests represent an easy, fast, and reliable method to predict long-term behavior [26,27,28]. Another similarity with the open literature is the existence of an initial stage, in which the stress decreases considerably with the remaining time [38,39,40]. The duration of this initial stage depends significantly on the material. In the present case, for example, considering the values obtained for method 11, stress decreased around 29.5% after 50 minutes, but this value reached 17.7% in the last 130 minutes. Regarding method 6, these values were 50.2% and 27.5%, while for method 1 they were 52.3% and 27.9%, respectively. This result was clear evidence that the bending stress was tending to a constant value, as reported above.
The curing process’ effect was also analyzed at the level of difference observed between the initial bending stress value and the final one after 3 hours. It was possible to conclude that, for curing at room temperature, the bending stress decreased around 65.6% concerning the initial value. However, this value was 63.9% for 40 °C and 42% for 60 °C. This decrease is well reported in the open literature, which is based on physical phenomena (molecular rearrangements that require little formation or rupture of primary bonds) and/or chemical phenomena (chain scission, crosslink scission, or crosslink formation) [41,42,43]. Both were expected in this study, but it is possible to conclude that higher curing temperatures decrease stress relaxation behavior. As reported in the static properties, also the best performance in terms of stress relaxation was obtained for a temperature of 60 °C. The degree of conversion, as shown in Figure 4, was 1.2 times higher than the one observed at 40 °C, and, consequently, this resin system had less molecular mobility.
The reasons that explain the stress relaxation behavior are the same that support the creep curves shown in Figure 10, where ε represents the strain value obtained at any instant of the test, and ε0 is the initial instantaneous strain (value obtained immediately after application of the respective load). The final bands represent the maximum and minimum values obtained for each condition analyzed. It is possible to observe that all curves present an instantaneous strain, followed by the primary and secondary creep regimes that characterize the typical creep curves. In this study, the third regime was expected to occur only for higher stress values or longer times. Finally, the strain increased with time; however, this behavior became less pronounced with the increasing of curing temperature. For example, while for control samples (method 1), the initial strain was around 3.2 times higher concerning its initial value, this value decreased to 2.9 times for 40 °C and to 2 times for 60 °C. In this case, the curing temperature of 60 °C promoted a decrease of the creep strain, after 180 mm, around 37.5% concerning the resin cured at room temperature.
The creep phenomenon in polymers occurs even at room temperature and for stresses below their ultimate strength due to the molecular motion in the backbone polymer arrangement [44,45,46,47]. Therefore, the degree of conversion 1.4 times higher for 40 °C and 1.6 times for 60 °C, when compared to the value obtained at room temperature, explains the higher crosslinking rate and, consequently, the lower molecular mobility in the resin. In such a context, lower creep strain values are expected/obtained.
Finally, the ability to model the viscoelastic behavior of polymer-based materials is determined to predict their long-term structural behavior. In terms of stress relaxation, for example, literature reports complex models to the detriment of those based on spring-dashpot systems, because the data are not fitted by a linear function. Therefore, the Kohlrausch–Williams–Watts (KWW) function, an empirical “stretched exponential” function, is suggested by the open literature as an appropriate methodology to model the stress relaxation [27,28,39,40,48,49]. According with this model, the relaxation function ∅ as a function of time is given by Equation (4):
∅ =   σ t σ 0 = e − t τ β
where σ(t) and σ0 are the stress at time t and at t = 0, respectively, β a fractional power exponent (known as non-exponential factor), and τ the KWW relaxation time.
Figure 11 compares the experimental results against the theoretical ones obtained with the KWW model for samples cured by Method 1. These curves are representative of all conditions and, apparently, the Kohlrausch–Williams–Watts (KWW) function fits the data successfully. Table 3 reports all parameters of the KWW model and its accuracy, where the errors observed between the average experimental curve and the KWW prediction were less than 8.9% (in absolute value) after 3 h of testing. Therefore, it is possible to conclude that the model fits to the data successfully.
Regarding the creep behavior, the Findley power law model is one of the most widely used to describe this phenomenon in composite materials and has been recommended, inclusively, by the ASCE Structural Plastics Design Manual to analyze and design the long-term strength [50]. The Findley’s power law is given by Equation (5):
ε t = ε 0   +   A t n
where ε(t) is the creep displacement at time t, ε0 is the instantaneous elastic displacement or time-independent, A is the amplitude of transient creep (time-dependent), and n is a constant independent of the stress and generally less than one [51]. Several studies can be found in the open literature, where the Findley’s power law was also applied to short-term creep data [27,28,51,52,53].
Therefore, similar to the previous figure, Figure 12 compares the experimental results against the theoretical ones obtained with the Findley power law model for samples cured by method 1. These curves are representative of all the conditions studied, and it is noticed that the Findley model fits the data successfully. Table 4 reports all parameters of the Findley power law model and its accuracy after 3 h of testing. The maximum error observed between the average experimental curves and the predicted ones was less than 7.1%, for all conditions studied, which confirms that the model fits the experimental data successfully.

4. Conclusions

The main goal of this study was to analyze the effect of the curing parameters on the mechanical properties of a polyester resin usually used in surfboards. For this purpose, the curing temperature was lower than the normally used with this type of resins, for other applications, in order to obtain lower percentages of curing and evaluate their influence on the mechanical properties. Moreover, the use of lower temperatures also has a beneficial impact both to the economic and environmental aspects. Three-point bending tests were performed to assess the bending properties and both stress relaxation and creep behavior.
The polymer if cured at room temperature, even when followed by short times of post-curing at 40 °C, presents unreacted macromolecules according to the DSC characterization. The higher percentages of crosslinking were obtained when the curing process was made at 60 °C for 24 h.
In terms of static properties, it was also possible to conclude that using higher curing temperatures, without post-curing, is preferable to the approach that involves curing followed by post-curing, because the exposure time at room temperature induces a percentage of conversion of double bonds that difficult further crosslinking in the second process step (post-cure). Therefore, the maximum bending strength and modulus were obtained at 60 °C for 24 h. Finally, it was also noticed that, when a post-cure was applied, these properties increased linearly with the exposure time due to a higher degree of conversion achieved.
Finally, the viscoelastic behavior was evaluated, and both stress relaxation and creep strain presented the lowest values for samples cured at 60 °C. The degree of conversion was higher for 60 °C, and, consequently, this resin system had less molecular mobility due to its higher crosslinking. The Kohlrausch–Williams–Watts (KWW) equation and the Findley power law model were used to predict the viscoelastic behavior, and good accuracy was obtained between the experimental results and those predicted by the proposed models.

Author Contributions

P.N.B.R. conceived and designed the study, P.S., J.M.P. and S.V. conducted the experiments related with mechanical characterization, A.P.P. conducted the chemical experiments. M.P.S., P.N.B.R. and A.P.P. analyzed the results. M.P.S. and A.P.P. wrote the paper. All authors read and approved the final manuscript.

Funding

This work was supported by the project Centro-01-0145-FEDER-000017—EMaDeS—Energy, Materials and Sustainable Development, co-financed by the Portugal 2020 Program (PT 2020), within the Regional Operational Program of the Center (CENTRO 2020) and the European Union through the European Regional Development Fund (ERDF).

Acknowledgments

This work was partially supported by the project UIDB/EMS/00285/2020 from Fundação para a Ciência e a Tecnologia, Portugal.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Devi, L.U.; Bhagawan, S.S.; Thomas, S. Mechanical properties of pineapple leaf fiber-reinforced polyester composites. J. Appl. Polym. Sci. 1997, 64, 1739–1748. [Google Scholar] [CrossRef]
  2. Vilas, J.L.; Laza, J.M.; Garay, M.T. Unsaturated polyester resins cure: Kinetic, rheologic, and mechanical dynamical analysis. II. The glass transition in the mechanical dynamical spectrum of polyester networks. J. Polym. Sci. B Polym. Phys. 2001, 39, 146–152. [Google Scholar] [CrossRef]
  3. Mohd Nurazzi, N.; Khalina, A.; Sapuan, S.M.; Dayang Laila, A.M.; Rahmah, M. Curing behaviour of unsaturated polyester resin and interfacial shear stress of sugar palm fibre. J. Mech. Eng. Sci. 2017, 11, 2650–2664. [Google Scholar] [CrossRef]
  4. de la Caba, K.; Guerrero, P.; Eceiza, A.; Mondragon, I. Kinetic and rheological studies of an unsaturated polyester cured with different catalyst amounts. Polymer 1996, 37, 275–280. [Google Scholar] [CrossRef]
  5. Huang, Y.J.; Leu, J.S. Curing of unsaturated polyester resins. Effects of temperature and initiator: 1. Low temperature reactions. Polymer 1993, 34, 295–304. [Google Scholar] [CrossRef]
  6. Crawford, R.J. Plastics Engieneering, 2nd ed.; Pergamon Press: New York, NY, USA, 1987. [Google Scholar]
  7. Stark, W. Investigation of the curing behaviour of carbon fibre epoxy prepreg by Dynamic Mechanical Analysis DMA. Polym. Test. 2013, 32, 231–239. [Google Scholar] [CrossRef]
  8. Aruniit, A.; Kers, J.; Krumme, A.; Poltimäe, T.; Tall, K. Preliminary study of the influence of post curing parameters to the particle reinforced composite’s mechanical and physical properties. Mater. Sci. 2012, 18, 256–261. [Google Scholar] [CrossRef] [Green Version]
  9. Ramis, X.; Salla, J.M. Theoretical and experimental conversion in the curing of unsaturated polyester resins with styrene as a crosslinking agent. J. Appl. Polym. Sci. 1992, 45, 227–236. [Google Scholar] [CrossRef]
  10. Salla, J.M.; Ramis, X. Comparative study of the cure kinetics of an unsaturated polyester resin using different procedures. Polym. Eng. Sci. 1996, 36, 835–851. [Google Scholar] [CrossRef]
  11. Ramis, X.; Salla, J.M. Effect of the initiator content and temperature on the curing of an unsaturated polyester resin. J. Polym. Sci. B Polym. Phys. 1999, 37, 751–768. [Google Scholar] [CrossRef]
  12. de la Caba, K.; Guerrero, P.; Mondragon, I.; Kenny, J.M. Comparative study by DSC and FTIR techniques of an unsaturated polyester resin cured at different temperatures. Polym. Int. 1998, 45, 333–338. [Google Scholar] [CrossRef]
  13. Xu, X.; Zhou, Q.; Song, N.; Ni, Q.; Ni, L. Kinetic analysis of isothermal curing of unsaturated polyester resin catalyzed with tert-butyl peroxybenzoate and cobalt octoate by differential scanning calorimetry. J. Therm. Anal. Calorim. 2017, 129, 843–850. [Google Scholar] [CrossRef]
  14. Worzakowska, M. The influence of tertiary aromatic amines on the BPO initiated cure of unsaturated epoxy polyesters with styrene studied by non-isothermal DSC. J. Therm. Anal. Calorim. 2011, 105, 987–994. [Google Scholar] [CrossRef]
  15. Poorabdollah, M.; Beheshty, M.H.; Vafayan, M. Kinetic modeling of nanoclay-reinforced unsaturated polyester resin. Polym. Compos. 2011, 32, 1265–1273. [Google Scholar] [CrossRef]
  16. Martin, J.L. Kinetic analysis of two DSC peaks in the curing of an unsaturated polyester resin catalyzed with methylethylketone peroxide and cobalt octoate. Polym. Eng. Sci. 2007, 47, 62–70. [Google Scholar] [CrossRef]
  17. Senthilkumar, K.; Siva, I.; Chandrasekar, M.; Rajini, N.; Kalusuraman, G.; Karthikeyan, S.; Vishnuteja, B.; Mallikarjuna, B. Influence of curing temperature on the mechanical and free vibration properties of sisal fiber reinforced polyester composites. In AIP Conference Proceedings, Proceedings of The 3rd International Conference on Automotive Innovation and Green Energy Vehicle, Kuantan, Malaysia, 25–26 July 2018; AIP Publishing: New York, NY, USA, 2018; p. 020066. [Google Scholar]
  18. Kumar, D.S.; Shukla, M.J.; Mahato, K.K.; Rathore, D.K.; Prusty, R.K.; Ray, B.C. Effect of post-curing on thermal and mechanical behavior of GFRP composites. In IOP Conference Series: Materials Science and Engineering, Proceedings of the 4th National Conference on Processing and Characterization of Materials, Rourkela, India, 5–6 December 2014; IOP Publishing Ltd.: Bristol, UK, 2015; Volume 75, p. 012012. [Google Scholar]
  19. Campana, C.; Leger, R.; Sonnier, R.; Ferry, L.; Ienny, P. Effect of post curing temperature on mechanical properties of a flax fiber reinforced epoxy composite. Compos. Part A Appl. Sci. Manuf. 2018, 107, 171–179. [Google Scholar] [CrossRef]
  20. Nicolais, L.; Landel, R.F.; Giordano-Orsini, P. The Glass Transition Temperature of Poly(phenylene oxide): Annealing and Filler Effects. Polym. J. 1975, 7, 259–263. [Google Scholar] [CrossRef]
  21. Crowson, R.J.; Arridge, R.G.C. The elastic properties in bulk and shear of a glass bead-reinforced epoxy resin composite. J. Mater. Sci. 1977, 12, 2154–2164. [Google Scholar] [CrossRef]
  22. Elleuch, R.; Zidi, M.; Bradai, C. Effects of post-cure on the mechanical properties of woven glass-polyester composite by macro and micro-mechanical methods. Sci. Eng. Compos. Mater. 1999, 8, 25–34. [Google Scholar] [CrossRef]
  23. ASTM. D7264/D7264M—07 Standard Test Method for Flexural Properties of Polymer Matrix Composite Materials; ASTM: West Conshohocken, PA, USA, 2015. [Google Scholar]
  24. ASTM. D6048—07(2018) Standard Practice for Stress Relaxation Testing of Raw Rubber, Unvulcanized Rubber Compounds, and Thermoplastic Elastomers; ASTM: West Conshohocken, PA, USA, 2018. [Google Scholar]
  25. ASTM. D7337/D7337M—12(2019) Standard Test Method for Tensile Creep Rupture of Fiber Reinforced Polymer Matrix Composite Bars; ASTM: West Conshohocken, PA, USA, 2019. [Google Scholar]
  26. Lim, S.D.; Rhee, J.M.; Nah, C.; Lee, S.H.; Lyu, M.Y. Predicting the long-term creep behavior of plastics using the short-term creep test. In International Polymer Processing; Carl Hanser Verlag: Munich, Germany, 2004; Volume 19, pp. 313–319. [Google Scholar]
  27. Reis, P.N.B.; Silva, M.P.; Santos, P.; Parente, J.M.; Bezazi, A. Viscoelastic behaviour of composites with epoxy matrix filled by cork powder. Compos. Struct. 2020, 234, 111669. [Google Scholar] [CrossRef]
  28. Reis, P.N.B.; Silva, M.P.; Santos, P.; Parente, J.M.; Valvez, S.; Bezazi, A. Mechanical performance of an optimized cork agglomerate core-glass fibre sandwich panel. Compos. Struct. 2020, 245, 112375. [Google Scholar] [CrossRef]
  29. Yang, Y.S.; Lee, L.J. Polymerization of Polyurethane-Polyester Interpenetrating Polymer Network (IPN). Macromolecules 1987, 20, 1490–1495. [Google Scholar] [CrossRef]
  30. Yang, Y.; Lee, L.J. Rheokinetic Studies of Unsaturated Polyester Resins; Dekker: New York, NY, USA, 1988. [Google Scholar]
  31. Yang, Y.S.; Lee, L.J. Comparison of thermal and infrared spectroscopic analyses in the formation of polyurethane, unsaturated polyester, and their blends. J. Appl. Polym. Sci. 1988, 36, 1325–1342. [Google Scholar] [CrossRef]
  32. Rahmat, A.R.; Day, R.J. Curing Characteristics of Unsaturated Polyester/aramid Reinforced Composite: Microwave vs. Thermal Energy. J. Teknol. 2003, 39, 83–96. [Google Scholar] [CrossRef] [Green Version]
  33. Ma, S.C.; Lin, H.L.; Yu, T.L. Glass Transition Temperature, Free Volume, and Curing Kinetics of Unsaturated Polyester. Polym. J. 1993, 25, 897–907. [Google Scholar] [CrossRef] [Green Version]
  34. Lucas, J.C.; Borrajo, J.; Williams, R.J.J. Cure of unsaturated polyester resins: 1. Heat of copolymerization and glass transition temperature. Polymer 1993, 34, 3216–3219. [Google Scholar] [CrossRef]
  35. Yu, T. Glass Transition Temperature Profile of the Curing Reaction of Unsaturated Polyester Resin. Polym. J. 1996, 28, 965–969. [Google Scholar] [CrossRef]
  36. Delaite, C.; Bistac, S.; Dreyer, E.; Schuller, A.-S. Influence of glass transition temperature of crosslinked unsaturated polyester resin/styrene formulations on the final conversion after an isothermal curing at 100 °C. Polym. Adv. Technol. 2020, 1–7. [Google Scholar] [CrossRef]
  37. Gudapati, S.P.K.; Krishna, C.V.; Prasad, A.V.R. Effect of nano clay on tensile and flexural properties of vakka fiber polyester composites. Mater. Today Proc. 2019, 18, 2032–2035. [Google Scholar] [CrossRef]
  38. Ferreira, J.A.M.; Costa, J.D.M.; Reis, P.N.B. Static and fatigue behaviour of glass-fibre-reinforced polypropylene composites. Theor. Appl. Fract. Mec. 1999, 31, 67–74. [Google Scholar] [CrossRef] [Green Version]
  39. Reis, P.N.B.; Gorbatikh, L.; Ivens, J.; Lomov, S.V. Strain-rate sensitivity and stress relaxation of hybrid self-reinforced polypropylene composites under bending loads. Compos. Struct. 2019, 209, 802–810. [Google Scholar] [CrossRef]
  40. Reis, P.N.B.; Silva, M.P.; Santos, P. Stress Relaxation in Delaminated Carbon/Epoxy Composites. Fibers Polym. 2019, 20, 1284–1289. [Google Scholar] [CrossRef]
  41. Varghese, S.; Kuriakose, B.; Thomas, S. Stress relaxation in short sisal-fiber-reinforced natural rubber composites. J. Appl. Polym. Sci. 1994, 53, 1051–1060. [Google Scholar] [CrossRef]
  42. George, J.; Sreekala, M.S.; Thomas, S.; Bhagawan, S.S.; Neelakantan, N.R. Stress Relaxation Behavior of Short Pineapple Fiber Reinforced Polyethylene Composites. J. Reinf. Plast. Comp. 1998, 17, 651–672. [Google Scholar] [CrossRef]
  43. Sreekala, M.S.; Kumaran, M.G.; Joseph, R.; Thomas, S. Stress-relaxation behaviour in composites based on short oil-palm fibres and phenol formaldehyde resin. Compos. Sci. Technol. 2001, 61, 1175–1188. [Google Scholar] [CrossRef]
  44. Park, B.-D.; Balatinecz, J.J. Short term flexural creep behavior of wood-fiber/polypropylene composites. Polym. Compos. 1998, 19, 377–382. [Google Scholar] [CrossRef]
  45. Houshyar, S.; Shanks, R.A.; Hodzic, A. Tensile creep behaviour of polypropylene fibre reinforced polypropylene composites. Polym. Test. 2005, 24, 257–264. [Google Scholar] [CrossRef]
  46. Koubaa, A.; Perré, P.; Cloutier, A. Creep behaviour of HDPE/wood particle composites. Int. J. Microstruct. Mater. Prop. 2013, 8, 225–238. [Google Scholar]
  47. Wang, W.-H.; Huang, H.-B.; Du, H.-H.; Wang, H. Effects of fiber size on short-term creep behavior of wood fiber/HDPE composites. Polym. Eng. Sci. 2015, 55, 693–700. [Google Scholar] [CrossRef]
  48. Fancey, K.S. A mechanical model for creep, recovery and stress relaxation in polymeric materials. J. Mater. Sci. 2005, 40, 4827–4831. [Google Scholar] [CrossRef]
  49. Vaidyanathan, T.K.; Vaidyanathan, J. Validity of predictive models of stress relaxation in selected dental polymers. Dent. Mater. 2015, 31, 799–806. [Google Scholar] [CrossRef] [PubMed]
  50. Scott, D.W.; Lai, J.S.; Zureick, A.H. Creep behavior of fiber-reinforced polymeric composites: A review of the technical literature. J. Reinf. Plast. Compos. 1995, 14, 588–617. [Google Scholar] [CrossRef]
  51. Almeida, J.H.S.; Ornaghi, H.L.; Lorandi, N.P.; Bregolin, B.P.; Amico, S.C. Creep and interfacial behavior of carbon fiber reinforced epoxy filament wound laminates. Polym. Compos. 2018, 39, E2199–E2206. [Google Scholar] [CrossRef]
  52. Georgiopoulos, P.; Kontou, E.; Christopoulos, A. Short-term creep behavior of a biodegradable polymer reinforced with wood-fibers. Compos. Part B Eng. 2015, 80, 134–144. [Google Scholar] [CrossRef]
  53. Gupta, V.B.; Lahiri, J. Non linear viscoelastic behavior of polypropylene and glass reinforced polypropylene in creep. J. Compos. Mater. 1980, 14, 286–296. [Google Scholar] [CrossRef]
Polymers 12 01927 g001 550
Figure 1. (a) Specimens geometry (dimensions in mm) and (b) schematic view of the three-point bending apparatus. All dimensions in mm.
Figure 1. (a) Specimens geometry (dimensions in mm) and (b) schematic view of the three-point bending apparatus. All dimensions in mm.
Polymers 12 01927 g001
Polymers 12 01927 g002 550
Figure 2. FTIR spectra of the resin, crosslinker (CL) and sample subjected to curing parameter 1.
Figure 2. FTIR spectra of the resin, crosslinker (CL) and sample subjected to curing parameter 1.
Polymers 12 01927 g002
Polymers 12 01927 g003 550
Figure 3. FTIR spectra of samples cured according to parameters 1, 6, and 11.
Figure 3. FTIR spectra of samples cured according to parameters 1, 6, and 11.
Polymers 12 01927 g003
Polymers 12 01927 g004 550
Figure 4. Degree of conversion of C = C polyester bonds (X) according to the curing parameters.
Figure 4. Degree of conversion of C = C polyester bonds (X) according to the curing parameters.
Polymers 12 01927 g004
Polymers 12 01927 g005 550
Figure 5. DSC heat flows and derivatives of specimens 1 (a) and 11 (b), showing the Tg values determination.
Figure 5. DSC heat flows and derivatives of specimens 1 (a) and 11 (b), showing the Tg values determination.
Polymers 12 01927 g005
Polymers 12 01927 g006 550
Figure 6. Flexural stress versus strain for: (a) post-cure at 40 °C for 12 h (specimen 4) and (b) post-cure at 60 °C for 6 h (specimen 8).
Figure 6. Flexural stress versus strain for: (a) post-cure at 40 °C for 12 h (specimen 4) and (b) post-cure at 60 °C for 6 h (specimen 8).
Polymers 12 01927 g006
Polymers 12 01927 g007a 550Polymers 12 01927 g007b 550
Figure 7. (a) Effect of the curing parameters on the bending stress and (b) effect of the post-cure on the bending stress.
Figure 7. (a) Effect of the curing parameters on the bending stress and (b) effect of the post-cure on the bending stress.
Polymers 12 01927 g007aPolymers 12 01927 g007b
Polymers 12 01927 g008a 550Polymers 12 01927 g008b 550
Figure 8. (a) Effect of the curing parameters on bending stiffness and (b) effect of the post-cure on bending stiffness.
Figure 8. (a) Effect of the curing parameters on bending stiffness and (b) effect of the post-cure on bending stiffness.
Polymers 12 01927 g008aPolymers 12 01927 g008b
Polymers 12 01927 g009 550
Figure 9. Stress relaxation curves obtained for the specimens 1, 6, and 11 (bending strain correspondent to 51.5 MPa).
Figure 9. Stress relaxation curves obtained for the specimens 1, 6, and 11 (bending strain correspondent to 51.5 MPa).
Polymers 12 01927 g009
Polymers 12 01927 g010 550
Figure 10. Creep curves obtained for the methods 1, 6, and 11 (bending stress of 20 MPa).
Figure 10. Creep curves obtained for the methods 1, 6, and 11 (bending stress of 20 MPa).
Polymers 12 01927 g010
Polymers 12 01927 g011 550
Figure 11. Comparison between the experimental average curve and theoretical curve obtained with the Kohlrausch–Williams–Watts (KWW) model for samples cured by method 1 (bending strain correspondent to 51.5 MPa).
Figure 11. Comparison between the experimental average curve and theoretical curve obtained with the Kohlrausch–Williams–Watts (KWW) model for samples cured by method 1 (bending strain correspondent to 51.5 MPa).
Polymers 12 01927 g011
Polymers 12 01927 g012 550
Figure 12. Comparison between experimental average curve and theoretical curve obtained with the Findley power law model for samples cured by method 1 (bending stress of 20 MPa).
Figure 12. Comparison between experimental average curve and theoretical curve obtained with the Findley power law model for samples cured by method 1 (bending stress of 20 MPa).
Polymers 12 01927 g012
Table
Table 1. Summary of cure and post-cure conditions.
Table 1. Summary of cure and post-cure conditions.
Cure MethodCurePost-Cure
Time (h)Temperature (°C)Time (h)Temperature (°C)
1360RT--
224RT340
324RT640
424RT1240
524RT2440
62440--
724RT360
824RT660
924RT1260
1024RT2460
112460--
RT = Room temperature.
Table
Table 2. Average and standard deviation values of Tg calculated from differential scanning calorimetry (DSC).
Table 2. Average and standard deviation values of Tg calculated from differential scanning calorimetry (DSC).
Curing ParametersTg Values (°C)
Tg1Tg2Tg3
119.5 ± 0.866.8 ± 0.2n.d.
218.7 ± 1.5 66.4 ± 0.3n.d.
318.0 ± 0.766.6 ± 0.6 n.d.
417.7 ± 1.055.8 ± 0.2n.d.
517.8 ± 1.063.5 ± 0.3143.7 ± 2.0
6n.d.62.6 ± 0.3159.1 ± 0.1
7n.d.62.1 ± 0.5162.0 ± 1.0
8n.d.58.3 ± 0.9162.8 ± 0.7
9n.d.62.3 ± 0.3163.3 ± 0.3
10n.d.62.5 ± 1.0 165.2 ± 0.8
11n.d.62.1 ± 0.0157.4 ± 0.2
n.d. = not detected.
Table
Table 3. Parameters of the KWW model for stress relaxation.
Table 3. Parameters of the KWW model for stress relaxation.
Curing MethodβτBending Stress after 3 h (MPa)
Experimental ValueKWW ValueError (%)
10.3721.29 × 10217.716. 66.2
60.3932.83 × 10219.421.38.9
110.4097.12 × 10229.929.12.7
Table
Table 4. Parameters of the Findley power law model for creep.
Table 4. Parameters of the Findley power law model for creep.
Curing Methodε0AnDisplacement after 3 h (MPa)
Experimental ValueFindley ValueError (%)
10.2290.3970.2183.33.23.0
60.2310.3780.1992.52.63.8
110.1770.2500.1661.41.37.1

Share and Cite

MDPI and ACS Style

Silva, M.P.; Santos, P.; Parente, J.M.; Valvez, S.; Reis, P.N.B.; Piedade, A.P. Effect of Post-Cure on the Static and Viscoelastic Properties of a Polyester Resin. Polymers 2020, 12, 1927. https://doi.org/10.3390/polym12091927

AMA Style

Silva MP, Santos P, Parente JM, Valvez S, Reis PNB, Piedade AP. Effect of Post-Cure on the Static and Viscoelastic Properties of a Polyester Resin. Polymers. 2020; 12(9):1927. https://doi.org/10.3390/polym12091927

Chicago/Turabian Style

Silva, Marco P., Paulo Santos, João M. Parente, Sara Valvez, Paulo N. B. Reis, and Ana P. Piedade. 2020. "Effect of Post-Cure on the Static and Viscoelastic Properties of a Polyester Resin" Polymers 12, no. 9: 1927. https://doi.org/10.3390/polym12091927

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop