Diffraction and Polarization Properties of Electrically–Tunable Nematic Liquid Crystal Grating
Abstract
1. Introduction
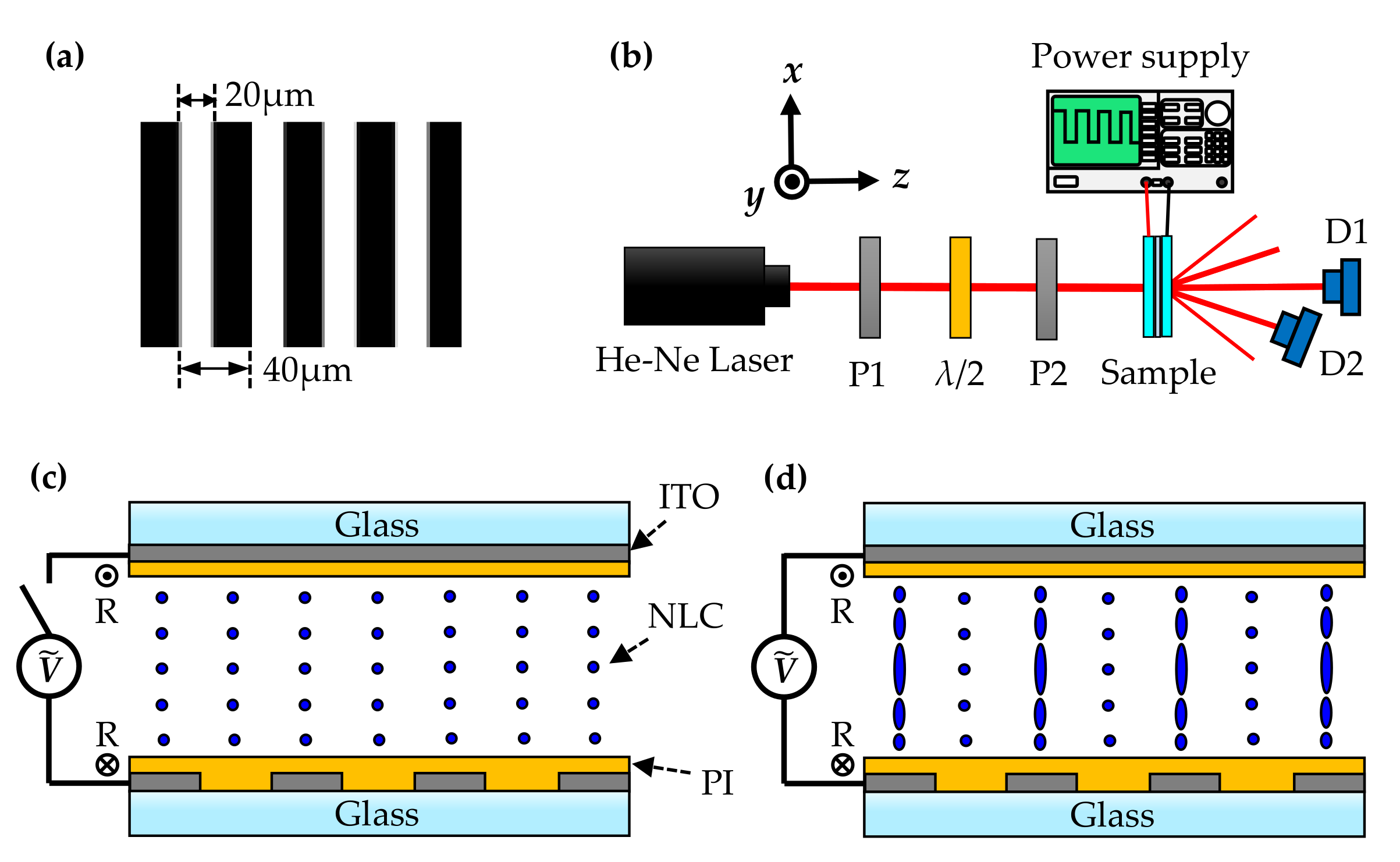
2. Materials and Methods
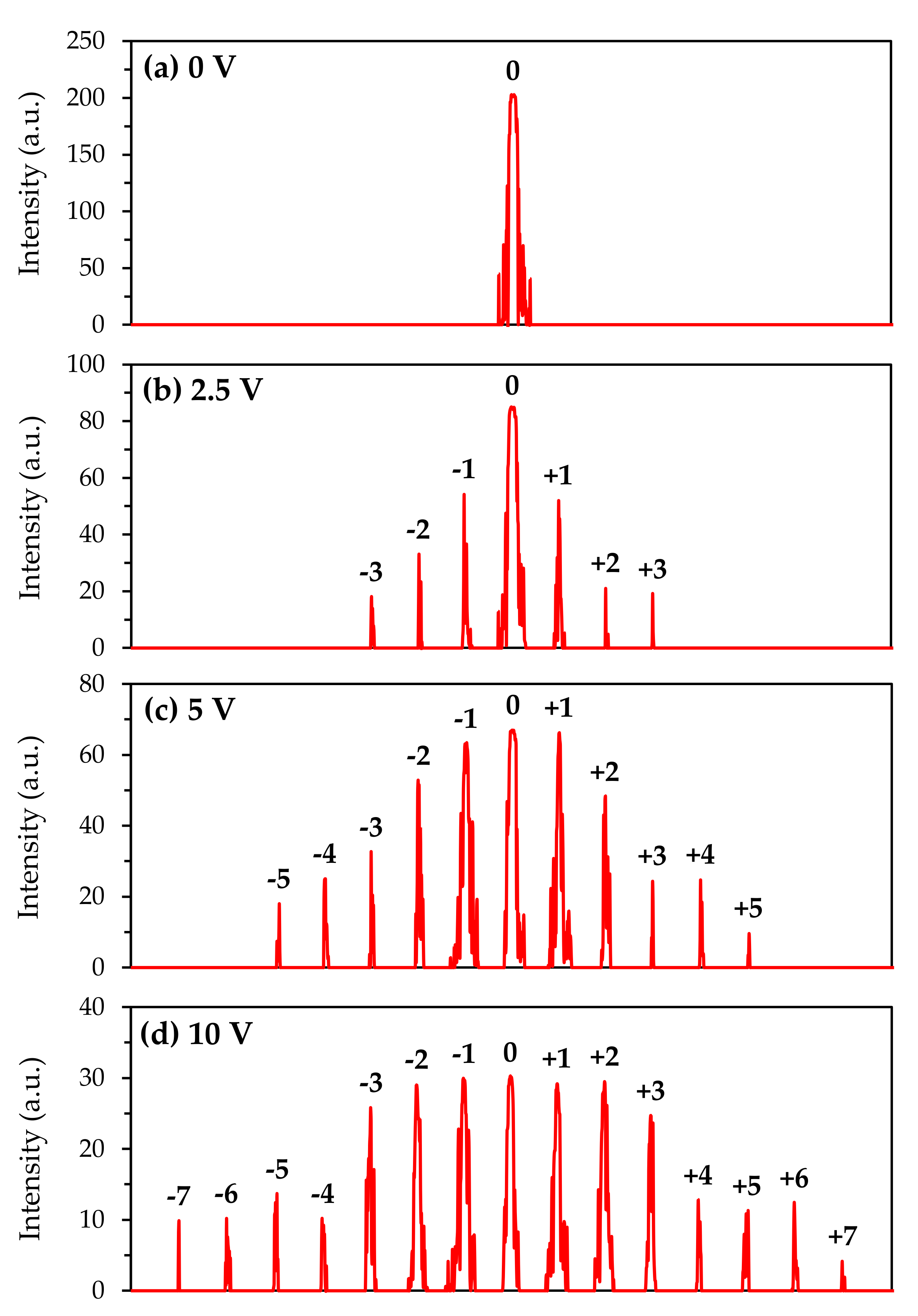
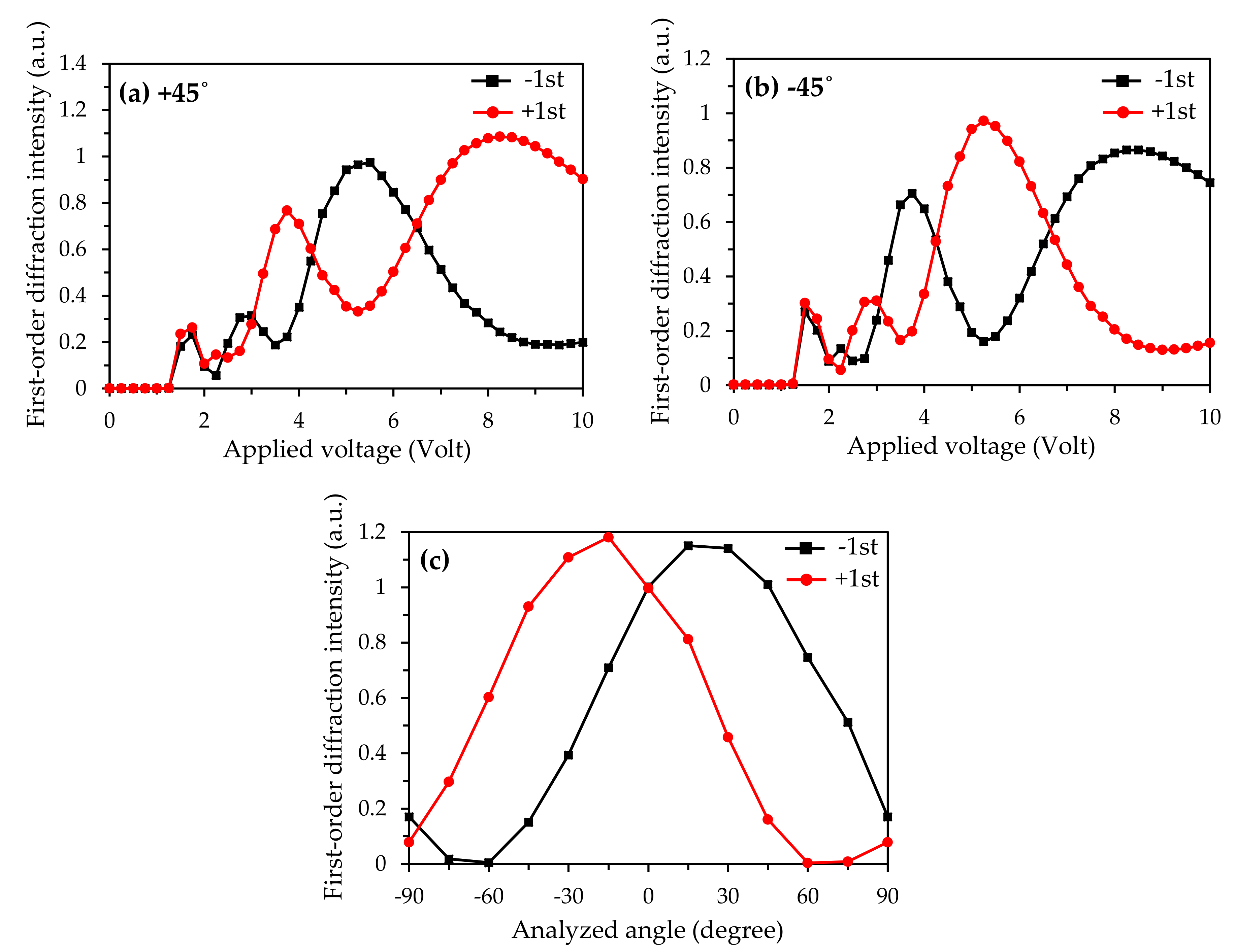
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hecht, E. Optics, 4th ed.; Addison-Wesley: San Francisco, FL, USA, 2001; ISBN 978-0805385663. [Google Scholar]
- Wang, Q.-H.; Ji, C.-C.; Li, L.; Deng, H. Dual-view integral imaging 3D display by using orthogonal polarizer array and polarization switcher. Opt. Express 2016, 24, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Weng, Y.; Xu, D.; Tabiryan, N.V.; Wu, S.-T. Beam steering for virtual/augmented reality displays with a cycloidal diffractive waveplate. Opt. Express 2016, 24, 7287–7298. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.-H.; Yin, K.; Wu, S.-T. Reflective polarization volume gratings for high efficiency waveguide-coupling augmented reality displays. Opt. Express 2017, 25, 27008. [Google Scholar] [CrossRef]
- Chen, H.-W.; Lee, J.-H.; Lin, B.-Y.; Chen, S.; Wu, S.-T. Liquid crystal display and organic light-emitting diode display: Present status and future perspectives. Light. Sci. Appl. 2017, 7, 17168. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-H.; Chen, H.-S. Electrically tunable-focusing and polarizer-free liquid crystal lenses for ophthalmic applications. Opt. Express 2013, 21, 9428–9436. [Google Scholar] [CrossRef]
- Galstian, T.; Asatryan, K.; Presniakov, V.; Zohrabyan, A. Electrically variable liquid crystal lenses for ophthalmic distance accommodation. Opt. Express 2019, 27, 18803–18817. [Google Scholar] [CrossRef]
- Algorri, J.F.; Zografopoulos, D.C.; Urruchi, V.; Sanchez-Pena, J.M.; Pena, S.-. Recent Advances in Adaptive Liquid Crystal Lenses. Cryst. 2019, 9, 272. [Google Scholar] [CrossRef]
- Chen, P.; Lu, Y.-Q.; Hu, W. Beam shaping via photopatterned liquid crystals. Liq. Cryst. 2016, 43, 2051–2061. [Google Scholar] [CrossRef]
- Jiang, M.; Yu, H.; Feng, X.; Guo, Y.; Chaganava, I.; Turiv, T.; Lavrentovich, O.D.; Wei, Q.-H. Liquid Crystal Pancharatnam-Berry Micro-Optical Elements for Laser Beam Shaping. Adv. Opt. Mater. 2018, 6, 1800961. [Google Scholar] [CrossRef]
- Ma, H.; Zhou, P.; Wang, X.; Ma, Y.; Xi, F.; Xu, X.; Liu, Z. Near-diffraction-limited annular flattop beam shaping with dual phase only liquid crystal spatial light modulators. Opt. Express 2010, 18, 8251–8260. [Google Scholar] [CrossRef]
- Guzmaán, O.; Abbott, N.L.; De Pablo, J.J. Quenched disorder in a liquid-crystal biosensor: Adsorbed nanoparticles at confining walls. J. Chem. Phys. 2005, 122, 184711. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.-J.; Lee, W. Liquid crystal-based capacitive, electro-optical and dielectric biosensors for protein quantitation. Liq. Cryst. 2019, 1–9. [Google Scholar] [CrossRef]
- Fan, Y.-J.; Chen, F.-L.; Liou, J.-C.; Huang, Y.-W.; Chen, C.-H.; Hong, Z.-Y.; Lin, J.-D.; Hsiao, Y.-C. Label-Free Multi-Microfluidic Immunoassays with Liquid Crystals on Polydimethylsiloxane Biosensing Chips. Polymers 2020, 12, 395. [Google Scholar] [CrossRef] [PubMed]
- Kneubuhl, F. Diffraction Grating Spectroscopy. Appl. Opt. 1969, 8, 505–519. [Google Scholar] [CrossRef]
- Laude, J.-P.; Lerner, J.M. Wavelength Division Multiplexing/Demultiplexing (WDM) Using Diffraction Gratings. In Proceedings of the 28th Annual Technical Symposium, San Diego, CA, USA, 12 December 1984; Volume 503, pp. 22–28. [Google Scholar] [CrossRef]
- Harvey, K.C.; Myatt, C.J. External-cavity diode laser using a grazing-incidence diffraction grating. Opt. Lett. 1991, 16, 910–912. [Google Scholar] [CrossRef]
- Simoni, F.; Bloisi, F.; Vicari, L. Transient Amplitude Grating in Polymer Dispersed Liquid Crystals. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. A. Mol. Cryst. Liq. Cryst. 1992, 223, 169–179. [Google Scholar] [CrossRef]
- Huang, S.-Y.; Wu, S.-T.; Fuh, A.Y.-G. Optically switchable twist nematic grating based on a dye-doped liquid crystal film. Appl. Phys. Lett. 2006, 88, 41104. [Google Scholar] [CrossRef]
- Tien, C.-L.; Lin, R.-J.; Kang, C.-C.; Huang, B.-Y.; Kuo, C.-T.; Huang, S.-Y. Electrically Controlled Diffraction Grating in Azo Dye-Doped Liquid Crystals. Polym. 2019, 11, 1051. [Google Scholar] [CrossRef]
- Shen, Y.; Xu, Y.-C.; Ge, Y.-H.; Jiang, R.-G.; Wang, X.-Z.; Li, S.-S.; Chen, L. Photoalignment of dye-doped cholesteric liquid crystals for electrically tunable patterns with fingerprint textures. Opt. Express 2018, 26, 1422–1432. [Google Scholar] [CrossRef]
- Chin, H.-K.; Kuo, H.-Y.; Zheng, Y.-C.; Lin, J.-D.; Lee, C.-R. Circular Polarization and Wavelength Selective Gratings Based on Holographic Cholesteric Liquid Crystal Templates. Adv. Condens. Matter Phys. 2018, 2018, 1–8. [Google Scholar] [CrossRef]
- Kogelnik, H. Coupled Wave Theory for Thick Hologram Gratings. Bell Syst. Tech. J. 1969, 48, 2909–2947. [Google Scholar] [CrossRef]
- He, Z.; Nose, T.; Sato, S. Diffraction and Polarization Properties of a Liquid Crystal Grating. Jpn. J. Appl. Phys. 1996, 35, 3529–3530. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S.-Y.; Huang, B.-Y.; Kang, C.-C.; Kuo, C.-T. Diffraction and Polarization Properties of Electrically–Tunable Nematic Liquid Crystal Grating. Polymers 2020, 12, 1929. https://doi.org/10.3390/polym12091929
Huang S-Y, Huang B-Y, Kang C-C, Kuo C-T. Diffraction and Polarization Properties of Electrically–Tunable Nematic Liquid Crystal Grating. Polymers. 2020; 12(9):1929. https://doi.org/10.3390/polym12091929
Chicago/Turabian StyleHuang, Shuan-Yu, Bing-Yau Huang, Chi-Chung Kang, and Chie-Tong Kuo. 2020. "Diffraction and Polarization Properties of Electrically–Tunable Nematic Liquid Crystal Grating" Polymers 12, no. 9: 1929. https://doi.org/10.3390/polym12091929
APA StyleHuang, S.-Y., Huang, B.-Y., Kang, C.-C., & Kuo, C.-T. (2020). Diffraction and Polarization Properties of Electrically–Tunable Nematic Liquid Crystal Grating. Polymers, 12(9), 1929. https://doi.org/10.3390/polym12091929



