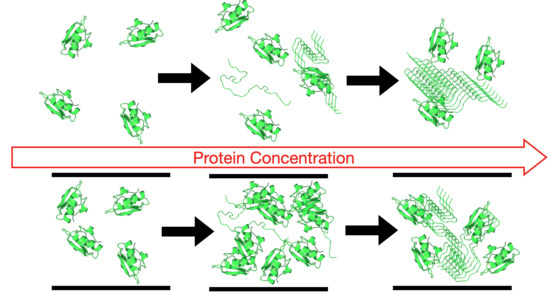
Protein Unfolding and Aggregation near a Hydrophobic Interface
Abstract
:1. Introduction
2. Model
2.1. Franzese–Stanley Water Model
2.2. Protein and Interface Model
2.3. The Hydrophobic Surface
2.4. The Model’s Parameters
3. Method
3.1. The Protein
3.2. The Monte Carlo Simulation
- We choose randomly a global protein-move among shift, rotation, crankshaft, or pivot [51]. Then, we pick at random one of the proteins, and we attempt the selected global move. We repeat the random selection for times, updating on average all the proteins.
- We choose a random number m between 1 and . For m times, we select one of the cells. If it includes an amino acid, we attempt a corner flip, i.e., the local protein-move [51]. If it includes a water molecule, we select one of its four -variables and attempt to change its state, hence, breaking or forming a HB.
- We attempt a global change of the system volume.
3.3. The Observables
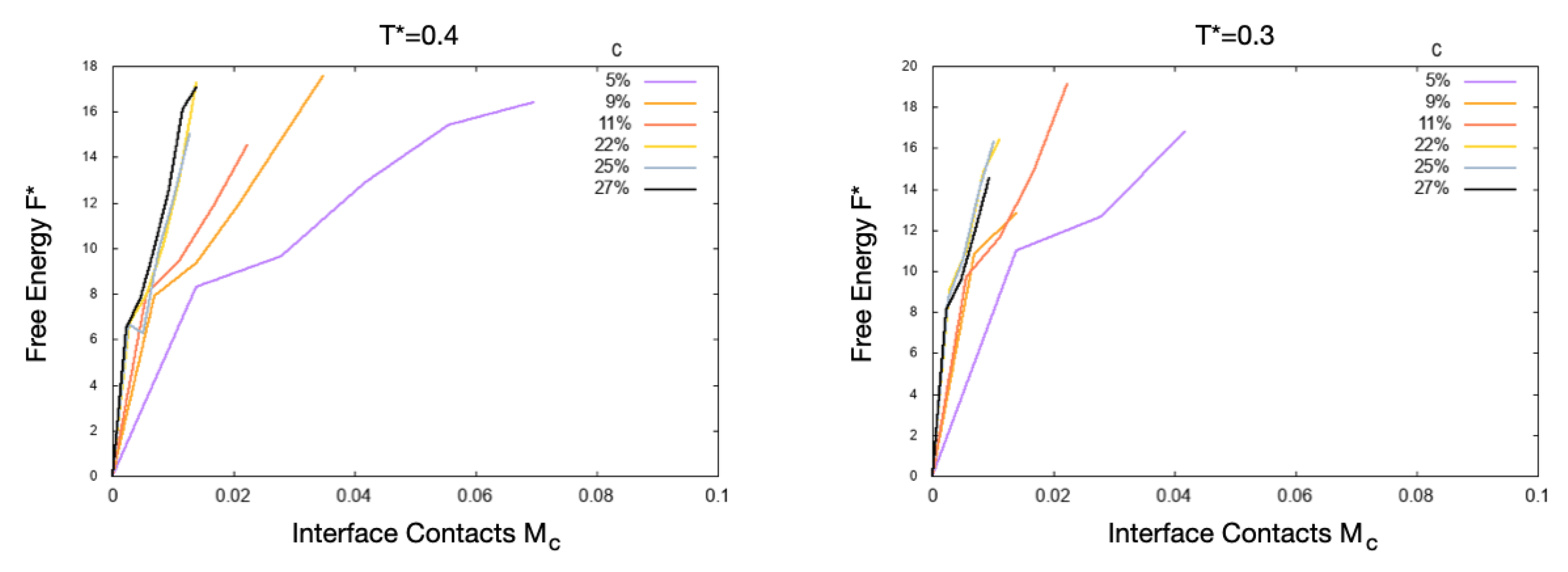
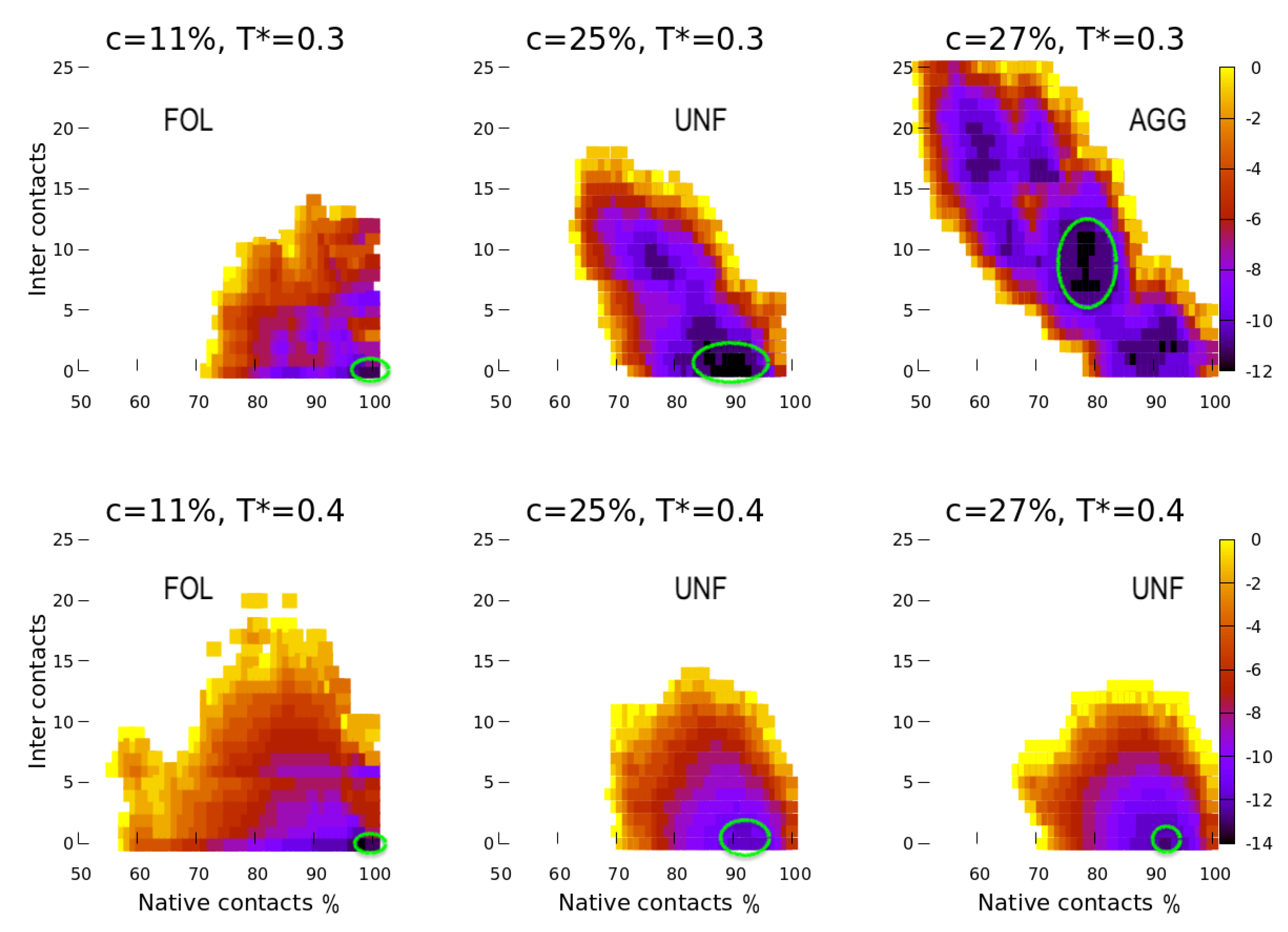
4. Results
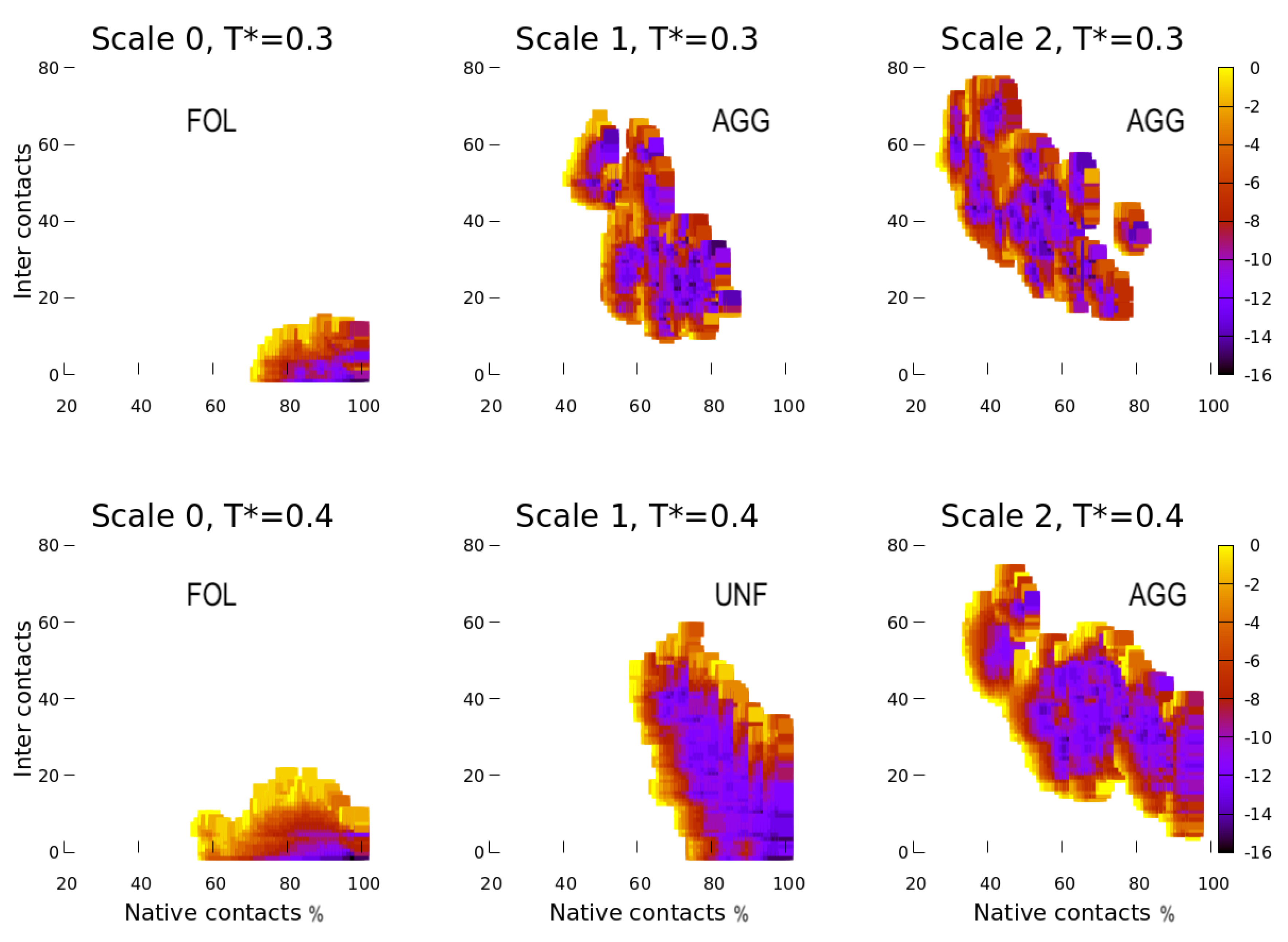
4.1. Scale 0
4.2. Scale 1 and Scale 2
5. Discussion
5.1. Effect of the Hydrophobic Walls
5.2. Effect of the Temperature
5.3. Effect of the HB Strength near a Hydrophobic Interface
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AGG | Aggregated |
| FOL | Folded |
| HB | Hydrogen Bond |
| MC | Monte Carlo |
| PBC | Periodic Boundary Conditions |
| UNF | Unfolded |
| Hydrophobic | |
| Hydrophilic | |
| Mixed |
References
- Finkelstein, A.V.; Ptitsyn, O.B. Protein Physics, 2nd ed.; Academic Press: Amsterdam, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Kiefhaber, T.; Rudolph, R.; Kohler, H.H.; Buchner, J. Protein Aggregation in vitro and in vivo: A Quantitative Model of the Kinetic Competition between Folding and Aggregation. BioTechnology 1991, 9, 825–829. [Google Scholar] [CrossRef] [PubMed]
- Eliezer, D.; Chiba, K.; Tsuruta, H.; Doniach, S.; Hodgson, K.O.; Kihara, H. Evidence of an associative intermediate on the myoglobin refolding pathway. Biophys. J. 1993, 65, 912–917. [Google Scholar] [CrossRef]
- Fink, A.L. Protein aggregation: Folding aggregates, inclusion bodies and amyloid. Fold. Des. 1998, 3, R9–R23. [Google Scholar] [CrossRef]
- Roberts, C.J. Non-native protein aggregation kinetics. Biotechnol. Bioeng. 2007, 98, 927–938. [Google Scholar] [CrossRef]
- Neudecker, P.; Robustelli, P.; Cavalli, A.; Walsh, P.; Lundström, P.; Zarrine-Afsar, A.; Sharpe, S.; Vendruscolo, M.; Kay, L.E. Structure of an Intermediate State in Protein Folding and Aggregation. Science 2012, 336, 362–366. [Google Scholar] [CrossRef]
- De Simone, A.; Kitchen, C.; Kwan, A.H.; Sunde, M.; Dobson, C.M.; Frenkel, D. Intrinsic disorder modulates protein self-assembly and aggregation. Proc. Natl. Acad. Sci. USA 2012, 109, 6951–6956. [Google Scholar] [CrossRef]
- Tartaglia, G.G.; Vendruscolo, M. Correlation between mRNA expression levels and protein aggregation propensities in subcellular localisations. Mol. BioSyst. 2009, 5, 1873–1876. [Google Scholar] [CrossRef]
- Schröder, M.; Schäfer, R.; Friedl, P. Induction of protein aggregation in an early secretory compartment by elevation of expression level. Biotechnol. Bioeng. 2002, 78, 131–140. [Google Scholar] [CrossRef]
- Tartaglia, G.G.; Pechmann, S.; Dobson, C.M.; Vendruscolo, M. Life on the edge: A link between gene expression levels and aggregation rates of human proteins. Trends Biochem. Sci. 2007, 32, 204–206. [Google Scholar] [CrossRef]
- Ross, C.A.; Poirier, M.A. Opinion: What is the role of protein aggregation in neurodegeneration? Nat. Reviews. Mol. Cell Biol. 2005, 6, 891–898. [Google Scholar] [CrossRef]
- Chiti, F.; Dobson, C.M. Protein Misfolding, Functional Amyloid, and Human Disease. Annu. Rev. Biochem. 2006, 75, 333–366. [Google Scholar] [CrossRef] [PubMed]
- Aguzzi, A.; O’Connor, T. Protein aggregation diseases: Pathogenicity and therapeutic perspectives. Nat. Reviews. Drug Discov. 2010, 9, 237–248. [Google Scholar] [CrossRef] [PubMed]
- Knowles, T.P.J.; Vendruscolo, M.; Dobson, C.M. The amyloid state and its association with protein misfolding diseases. Nat. Rev. Mol. Cell Biol. 2014, 15, 384–396. [Google Scholar] [CrossRef] [PubMed]
- Roberts, C.J. Protein aggregation and its impact on product quality. Curr. Opin. Biotechnol. 2014, 30, 211–217. [Google Scholar] [CrossRef] [PubMed]
- Zaman, M.; Ahmad, E.; Qadeer, A.; Rabbani, G.; Khan, R.H. Nanoparticles in relation to peptide and protein aggregation. Int. J. Nanomed. 2014, 9, 899–912. [Google Scholar] [CrossRef]
- Howes, P.D.; Chandrawati, R.; Stevens, M.M. Colloidal nanoparticles as advanced biological sensors. Science 2014, 346. [Google Scholar] [CrossRef]
- Vilanova, O.; Mittag, J.J.; Kelly, P.M.; Milani, S.; Dawson, K.A.; Rädler, J.O.; Franzese, G. Understanding the Kinetics of Protein–Nanoparticle Corona Formation. ACS Nano 2016, 10, 10842–10850. [Google Scholar] [CrossRef]
- Meesaragandla, B.; García, I.; Biedenweg, D.; Toro-Mendoza, J.; Coluzza, I.; Liz-Marzán, L.M.; Delcea, M. H-Bonding-mediated binding and charge reorganization of proteins on gold nanoparticles. Phys. Chem. Chem. Phys. 2020, 22, 4490–4500. [Google Scholar] [CrossRef]
- Dobrovolskaia, M.A.; McNeil, S.E. Immunological properties of engineered nanomaterials. Nat. Nanotechnol. 2007, 2, 469–478. [Google Scholar] [CrossRef]
- Jiao, Q.; Li, L.; Mu, Q.; Zhang, Q. Immunomodulation of Nanoparticles in Nanomedicine Applications. BioMed Res. Int. 2014, 2014, 426028. [Google Scholar] [CrossRef]
- Höök, F.; Rodahl, M.; Kasemo, B.; Brzezinski, P. Structural changes in hemoglobin during adsorption to solid surfaces: Effects of pH, ionic strength, and ligand binding. Proc. Natl. Acad. Sci. USA 1998, 95, 12271. [Google Scholar] [CrossRef] [PubMed]
- Henry, M.; Dupont-Gillain, C.; Bertrand, P. Conformation Change of Albumin Adsorbed on Polycarbonate Membranes as Revealed by ToF-SIMS. Langmuir 2003, 19, 6271–6276. [Google Scholar] [CrossRef]
- Lacerda, S.H.D.P.; Park, J.J.; Meuse, C.; Pristinski, D.; Becker, M.L.; Karim, A.; Douglas, J.F. Interaction of Gold Nanoparticles with Common Human Blood Proteins. ACS Nano 2010, 4, 365–379. [Google Scholar] [CrossRef] [PubMed]
- Cañaveras, F.; Madueño, R.; Sevilla, J.; Blázquez, M.; Pineda, T. Role of the Functionalization of the Gold Nanoparticle Surface on the Formation of Bioconjugates with Human Serum Albumin. J. Phys. Chem. C 2012, 116, 10430–10437. [Google Scholar] [CrossRef]
- Zhang, C.; Myers, J.N.; Chen, Z. Elucidation of molecular structures at buried polymer interfaces and biological interfaces using sum frequency generation vibrational spectroscopy. Soft Matter 2013, 9, 4738–4761. [Google Scholar] [CrossRef]
- Wei, S.; Ahlstrom, L.S.; Brooks III, C.L. Exploring Protein–Nanoparticle Interactions with Coarse-Grained Protein Folding Models. Small 2017, 13, 1603748. [Google Scholar] [CrossRef]
- Cellmer, T.; Bratko, D.; Prausnitz, J.M.; Blanch, H.W. Protein aggregation in silico. Trends Biotechnol. 2007, 25, 254–261. [Google Scholar] [CrossRef]
- Nasica-Labouze, J.; Nguyen, P.H.; Sterpone, F.; Berthoumieu, O.; Buchete, N.V.; Coté, S.; De Simone, A.; Doig, A.J.; Faller, P.; Garcia, A.; et al. Amyloid β Protein and Alzheimer’s Disease: When Computer Simulations Complement Experimental Studies. Chem. Rev. 2015, 115, 3518–3563. [Google Scholar] [CrossRef]
- Bianco, V.; Franzese, G.; Coluzza, I. In Silico Evidence That Protein Unfolding is a Precursor of Protein Aggregation. ChemPhysChem 2020, 21, 377–384. [Google Scholar] [CrossRef]
- Bianco, V.; Alonso-Navarro, M.; Di Silvio, D.; Moya, S.; Cortajarena, A.L.; Coluzza, I. Proteins are Solitary! Pathways of Protein Folding and Aggregation in Protein Mixtures. J. Phys. Chem. Lett. 2019, 10, 4800–4804. [Google Scholar] [CrossRef]
- Franzese, G.; Bianco, V.; Iskrov, S. Water at Interface with Proteins. Food Biophys. 2011, 6, 186–198. [Google Scholar] [CrossRef]
- Bianco, V.; Iskrov, S.; Franzese, G. Understanding the role of hydrogen bonds in water dynamics and protein stability. J. Biol. Phys. 2012, 38, 27–48. [Google Scholar] [CrossRef] [PubMed]
- Franzese, G.; Bianco, V. Water at Biological and Inorganic Interfaces. Food Biophys. 2013, 8, 153–169. [Google Scholar] [CrossRef]
- Bianco, V.; Franzese, G. Contribution of Water to Pressure and Cold Denaturation of Proteins. Phys. Rev. Lett. 2015, 115, 108101. [Google Scholar] [CrossRef]
- Bianco, V.; Pagès-Gelabert, N.; Coluzza, I.; Franzese, G. How the stability of a folded protein depends on interfacial water properties and residue-residue interactions. J. Mol. Liq. 2017, 245, 129–139. [Google Scholar] [CrossRef]
- Bianco, V.; Franzese, G.; Dellago, C.; Coluzza, I. Role of Water in the Selection of Stable Proteins at Ambient and Extreme Thermodynamic Conditions. Phys. Rev. X 2017, 7, 021047. [Google Scholar] [CrossRef]
- Franzese, G.; Stokely, K.; Chu, X.Q.; Kumar, P.; Mazza, M.G.; Chen, S.H.; Stanley, H.E. Pressure effects in supercooled water: Comparison between a 2D model of water and experiments for surface water on a protein. J. Phys. Condens. Matter 2008, 20, 494210. [Google Scholar] [CrossRef]
- Stokely, K.; Mazza, M.G.; Stanley, H.E.; Franzese, G. Effect of hydrogen bond cooperativity on the behavior of water. Proc. Natl. Acad. Sci. USA 2010, 107, 1301–1306. [Google Scholar] [CrossRef]
- Mazza, M.G.; Stokely, K.; Pagnotta, S.E.; Bruni, F.; Stanley, H.E.; Franzese, G. More than one dynamic crossover in protein hydration water. Proc. Natl. Acad. Sci. USA 2011, 108, 19873–19878. [Google Scholar] [CrossRef]
- De los Santos, F.; Franzese, G. Understanding Diffusion and Density Anomaly in a Coarse-Grained Model for Water Confined between Hydrophobic Walls. J. Phys. Chem. B 2011, 115, 14311–14320. [Google Scholar] [CrossRef]
- Bianco, V.; Franzese, G. Critical behavior of a water monolayer under hydrophobic confinement. Sci. Rep. 2014, 4, 4440. [Google Scholar] [CrossRef] [PubMed]
- Bianco, V.; Franzese, G. Hydrogen bond correlated percolation in a supercooled water monolayer as a hallmark of the critical region. J. Mol. Liq. 2019, 285, 727–739. [Google Scholar] [CrossRef]
- Gopinadhan, K.; Hu, S.; Esfandiar, A.; Lozada-Hidalgo, M.; Wang, F.C.; Yang, Q.; Tyurnina, A.V.; Keerthi, A.; Radha, B.; Geim, A.K. Complete steric exclusion of ions and proton transport through confined monolayer water. Science 2019, 363, 145–148. [Google Scholar] [CrossRef] [PubMed]
- Calero, C.; Franzese, G. Water under extreme confinement in graphene: Oscillatory dynamics, structure, and hydration pressure explained as a function of the confinement width. J. Mol. Liq. 2020, 317, 114027. [Google Scholar] [CrossRef]
- Coronas, L.E.; Bianco, V.; Zantop, A.; Franzese, G. Liquid-Liquid Critical Point in 3D Many-Body Water Model. arXiv 2016, arXiv:1610.00419. [Google Scholar]
- Luzar, A.; Chandler, D. Effect of Environment on Hydrogen Bond Dynamics in Liquid Water. Phys. Rev. Lett. 1996, 76, 928–931. [Google Scholar] [CrossRef]
- Coronas, L.E.; Vilanova, O.; Bianco, V.; de los Santos, F.; Franzese, G. Properties of Water from Numerical and Experimental Perspectives; Chapter The Franzese-Stanley Coarse Grained Model for HydrationWater; Martelli, F., Ed.; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Miyazawa, S.; Jernigan, R.L. Estimation of effective interresidue contact energies from protein crystal structures: Quasi-chemical approximation. Macromolecules 1985, 18, 534–552. [Google Scholar] [CrossRef]
- Sarupria, S.; Garde, S. Quantifying Water Density Fluctuations and Compressibility of Hydration Shells of Hydrophobic Solutes and Proteins. Phys. Rev. Lett. 2009, 103, 037803. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understand Molecular Simulations; Academic Press: San Diego, CA, USA; London, UK, 2002. [Google Scholar]
- Brini, E.; Simmerling, C.; Dill, K. Protein storytelling through physics. Science 2020, 370. [Google Scholar] [CrossRef]
- Mathieu, C.; Pappu, R.V.; Taylor, J.P. Beyond aggregation: Pathological phase transitions in neurodegenerative disease. Science 2020, 370, 56. [Google Scholar] [CrossRef]
- Vilanova, O.; Bianco, V.; Franzese, G. Multi-Scale Approach for Self-Assembly and Protein Folding. In Design of Self-Assembling Materials; Coluzza, I., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 107–128. [Google Scholar] [CrossRef]

| Scale | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 4 | 0.48 | ||||||
| 1 | 2 | 4 | 0.24 | ||||||
| 2 | 2 | 4 | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
March, D.; Bianco, V.; Franzese, G. Protein Unfolding and Aggregation near a Hydrophobic Interface. Polymers 2021, 13, 156. https://doi.org/10.3390/polym13010156
March D, Bianco V, Franzese G. Protein Unfolding and Aggregation near a Hydrophobic Interface. Polymers. 2021; 13(1):156. https://doi.org/10.3390/polym13010156
Chicago/Turabian StyleMarch, David, Valentino Bianco, and Giancarlo Franzese. 2021. "Protein Unfolding and Aggregation near a Hydrophobic Interface" Polymers 13, no. 1: 156. https://doi.org/10.3390/polym13010156
APA StyleMarch, D., Bianco, V., & Franzese, G. (2021). Protein Unfolding and Aggregation near a Hydrophobic Interface. Polymers, 13(1), 156. https://doi.org/10.3390/polym13010156