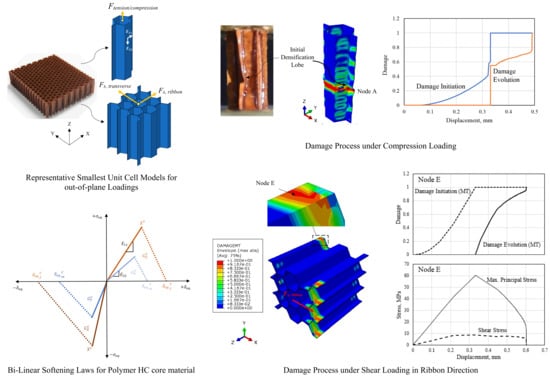
Representative Cell Analysis for Damage-Based Failure Model of Polymer Hexagonal Honeycomb Structure under the Out-of-Plane Loadings
Abstract
:1. Introduction
2. Framework for FE Simulation of Damage and Failure of Honeycomb Core Structure
2.1. Representative Unit Cell Models
2.2. Materials, Properties, and Damage Models
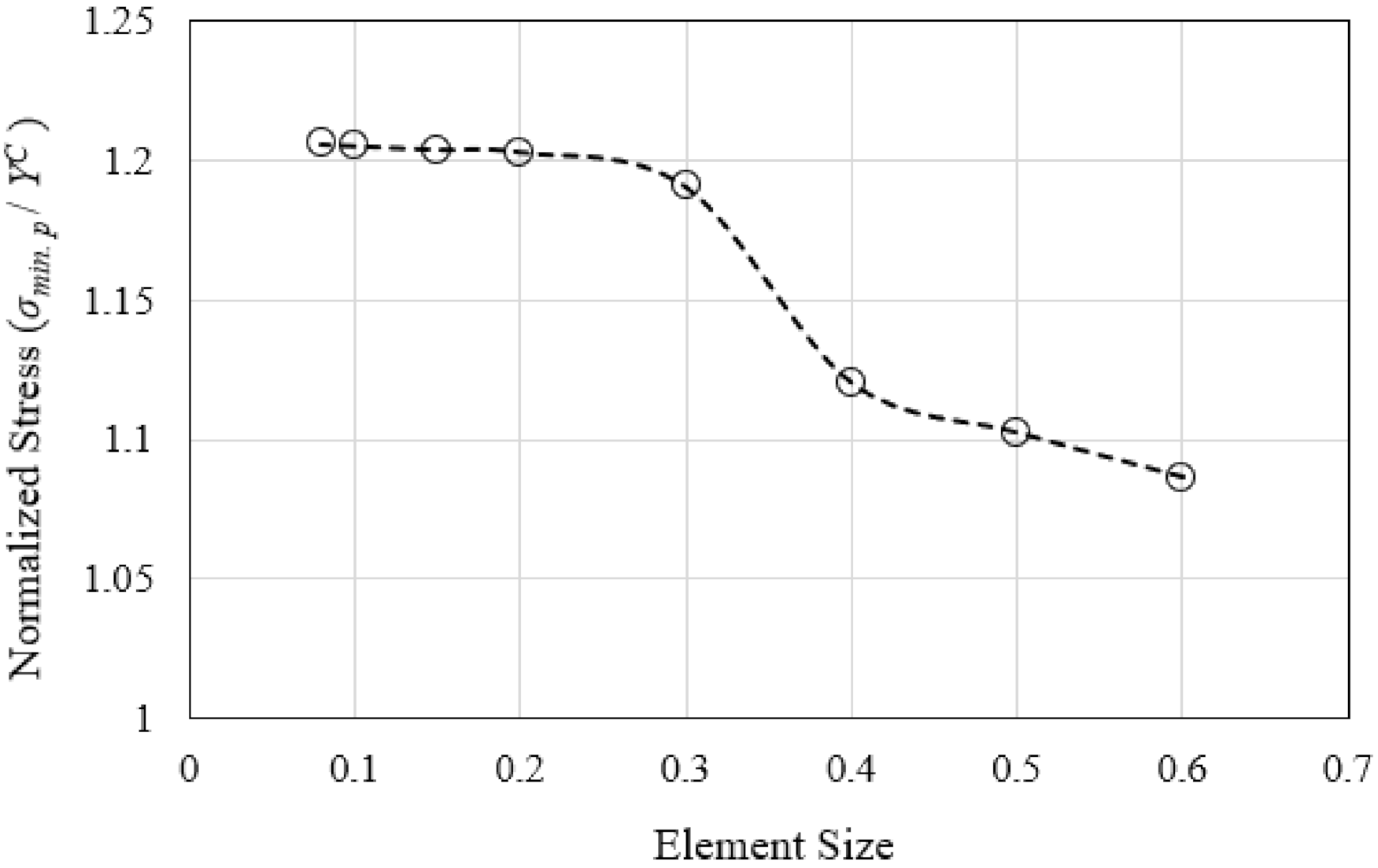
2.3. Finite Element Simulation of the Failure Process
3. Results and Discussion
3.1. Out-of-Plane Tensile Response
3.2. Out-of-Plane Compressive Failure
3.3. Out-of-Plane Shear Responses
3.4. Summary of the Results
4. Conclusions
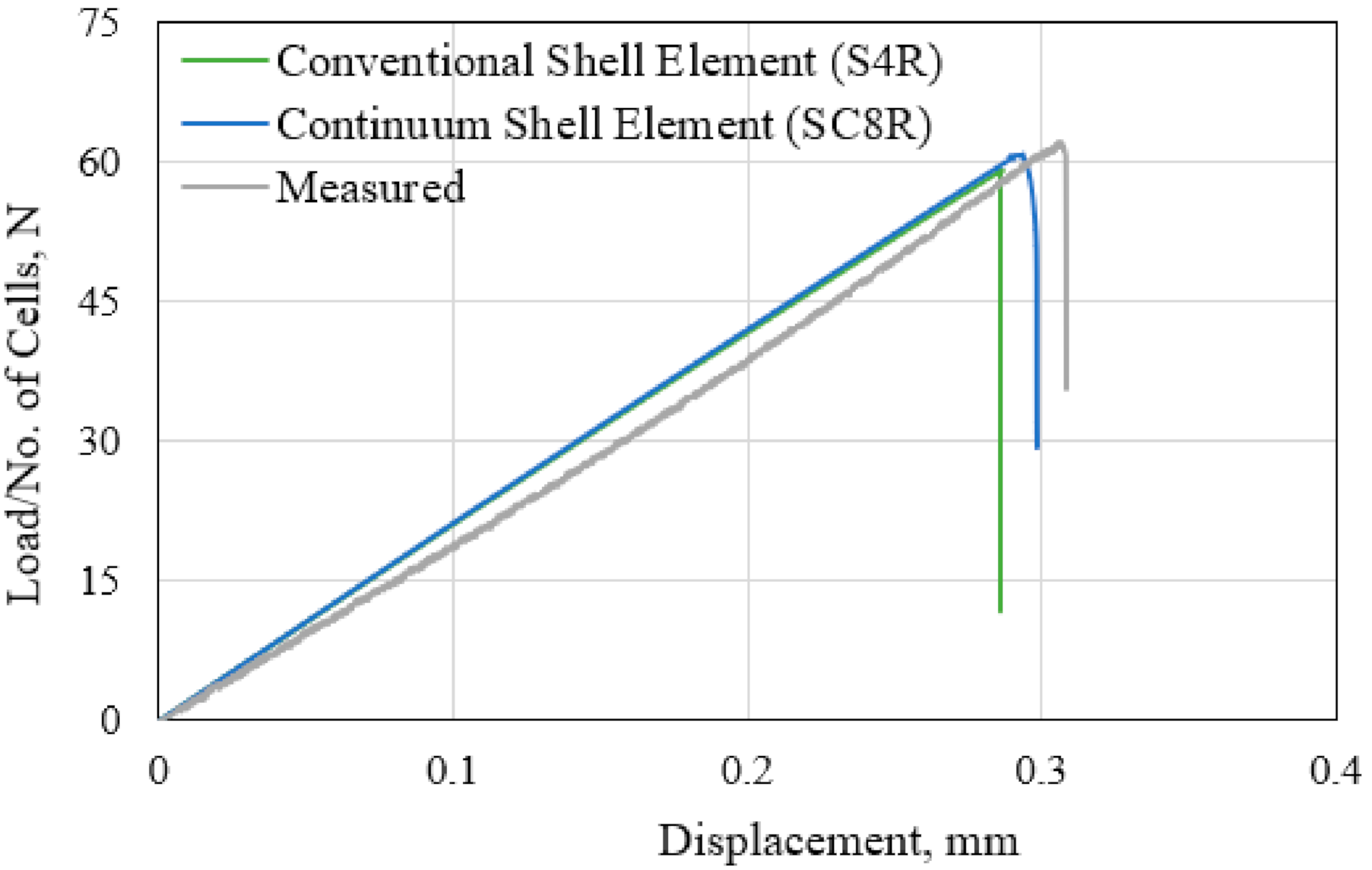
- The single-cell FE model with continuum shell elements offers a closer prediction of the peak load to the measured tensile load level at fracture, compared to the model with the conventional shell elements. However, the 17.2% greater number of the unknown variables resulted in a 63.6% longer wall-clock time, rendering it computationally less efficient.
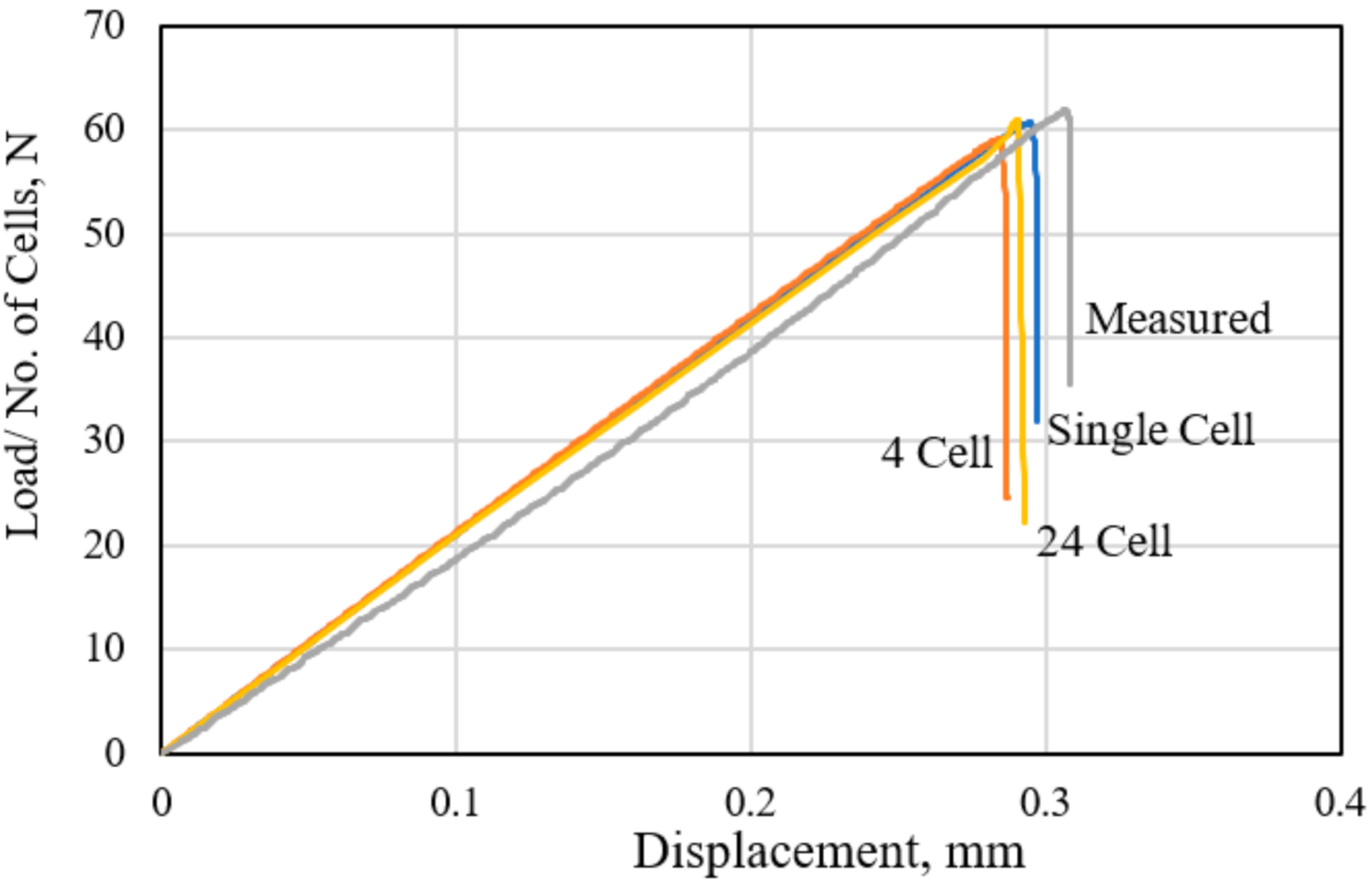
- The single-cell model is adequate in representing the out-of-plane tensile and compressive responses of the HC core structure with less than 5.0% difference in the measured stiffness and strength, compared with the 4-cell and 24-cell model.
- The smallest representative polymer hexagonal HC core model for the out-of-plane shear in the transverse and ribbon direction is a six-cell model. The predicted shear stiffness and load at the shear failure are within 9.0% and 3.0% variation, respectively, from the measured values.
- The onset of damage and the characteristic damage evolution of the critical cell wall material were shown to accurately manifest in the observed localized failure mechanism and the global stiffness degradation of the polymer hexagonal HC core structure.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

References
- Grediac, M. A finite element study of the transverse shear in honeycomb cores. Int. J. Solids Struct. 1993, 30, 1777–1788. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, X.; Li, P.; Huang, G.; Feng, S.; Shen, C.; Han, B.; Zhang, X.; Jin, F.; Xu, F. Bioinspired engineering of honeycomb structure—Using nature to inspire human innovation. Prog. Mater. Sci. 2015, 74, 332–400. [Google Scholar] [CrossRef]
- Ashab, A.; Ruan, D.; Lu, G.; Xu, S.; Wen, C. Experimental investigation of the mechanical behavior of aluminum honeycombs under quasi-static and dynamic indentation. Mater. Des. 2015, 74, 138–149. [Google Scholar] [CrossRef]
- Cote, F.; Deshpande, V.; Fleck, N.; Evans, A. The out-of-plane compressive behavior of metallic honeycombs. Mater. Sci. Eng. A 2004, 380, 272–280. [Google Scholar] [CrossRef] [Green Version]
- Nomoto, K. Aramid Honeycombs and a Method for Producing the Same. U.S. Patent No. 6,544,622, 8 April 2003. [Google Scholar]
- Roy, R.; Park, S.-J.; Kweon, J.-H.; Choi, J.-H. Characterization of Nomex honeycomb core constituent material mechanical properties. Compos. Struct. 2014, 117, 255–266. [Google Scholar] [CrossRef]
- Soltani, A.; Noroozi, R.; Bodaghi, M.; Zolfagharian, A.; Hedayati, R. 3D printing on-water sports boards with bio-inspired core designs. Polymers 2020, 12, 250. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zaharia, S.M.; Enescu, L.A.; Pop, M.A. Mechanical Performances of lightweight sandwich structures produced by material extrusion-based additive manufacturing. Polymers 2020, 12, 1740. [Google Scholar] [CrossRef]
- Saad, N.A.; Sabah, A. An investigation of new design of light weight structure of (ABS/PLA) by using of three dimensions printing. In Proceedings of the 13th International Conference Standardization, Prototypes and Quality: A Means of Balkan Countries’ Collaboration, Brasov, Romania, 15–17 September 2016; pp. 3–4. [Google Scholar]
- Lee, H.S.; Hong, S.H.; Lee, J.R.; Kim, Y.K. Mechanical behavior and failure process during compressive and shear deformation of honeycomb composite at elevated temperatures. J. Mater. Sci. 2002, 37, 1265–1272. [Google Scholar] [CrossRef]
- Aminanda, Y.; Castanié, B.; Barrau, J.-J.; Thevenet, P. Experimental analysis and modeling of the crushing of honeycomb cores. Appl. Compos. Mater. 2005, 12, 213–227. [Google Scholar] [CrossRef]
- Asprone, D.; Auricchio, F.; Menna, C.; Morganti, S.; Prota, A.; Reali, A. Statistical finite element analysis of the buckling behavior of honeycomb structures. Compos. Struct. 2013, 105, 240–255. [Google Scholar] [CrossRef]
- Foo, C.; Chai, G.; Seah, L. A model to predict low-velocity impact response and damage in sandwich composites. Compos. Sci. Technol. 2008, 68, 1348–1356. [Google Scholar] [CrossRef]
- Akour, S.; Maaitah, H. Finite element analysis of loading area effect on sandwich panel behaviour beyond the yield limit. In Finite Element Analysis—New Trends and Developments; Ebrahimi, F., Ed.; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Heimbs, S. Virtual testing of sandwich core structures using dynamic finite element simulations. Comput. Mater. Sci. 2009, 45, 205–216. [Google Scholar] [CrossRef]
- Aktay, L.; Johnson, A.F.; Kröplin, B.-H. Numerical modelling of honeycomb core crush behaviour. Eng. Fract. Mech. 2008, 75, 2616–2630. [Google Scholar] [CrossRef]
- Becker, W. The in-plane stiffnesses of a honeycomb core including the thickness effect. Arch. Appl. Mech. 1998, 68, 334–341. [Google Scholar] [CrossRef]
- Giglio, M.; Manes, A.; Gilioli, A. Investigations on sandwich core properties through an experimental–numerical approach. Compos. Part B Eng. 2012, 43, 361–374. [Google Scholar] [CrossRef]
- Castanié, B.; Bouvet, C.; Aminanda, Y.; Barrau, J.-J.; Thévenet, P. Modelling of low-energy/low-velocity impact on Nomex honeycomb sandwich structures with metallic skins. Int. J. Impact Eng. 2008, 35, 620–634. [Google Scholar] [CrossRef] [Green Version]
- Roy, R.; Kweon, J.; Choi, J. Meso-scale finite element modeling of NomexTM honeycomb cores. Adv. Compos. Mater. 2014, 23, 17–29. [Google Scholar] [CrossRef]
- Fischer, S.; Drechsler, K.; Kilchert, S.; Johnson, A. Mechanical tests for foldcore base material properties. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1941–1952. [Google Scholar] [CrossRef]
- Liu, L.; Meng, P.; Wang, H.; Guan, Z. The flatwise compressive properties of Nomex honeycomb core with debonding imperfections in the double cell wall. Compos. Part B Eng. 2015, 76, 122–132. [Google Scholar] [CrossRef]
- Liu, L.; Wang, H.; Guan, Z. Experimental and numerical study on the mechanical response of Nomex honeycomb core under transverse loading. Compos. Struct. 2015, 121, 304–314. [Google Scholar] [CrossRef]
- Seemann, R.; Krause, D. Numerical modelling of nomex honeycomb cores for detailed analyses of sandwich panel joints. In Proceedings of the 11th World Congress on Computational Mechanics (WCCM XI), Barcelona, Spain, 20–25 July 2014. [Google Scholar]
- Pan, S.-D.; Wu, L.-Z.; Sun, Y.-G.; Zhou, Z.-G.; Qu, J.-L. Longitudinal shear strength and failure process of honeycomb cores. Compos. Struct. 2006, 72, 42–46. [Google Scholar] [CrossRef]
- Gornet, L.; Marguet, S.; Marckmann, G. Finite Element modeling of Nomex® honeycomb cores: Failure and effective elastic properties. Int. J. Comput. Mater. Contin. Tech. Sci. 2006, 1, 11–22. [Google Scholar]
- Kaman, M.O.; Solmaz, M.Y.; Turan, K. Experimental and numerical analysis of critical buckling load of honeycomb sandwich panels. J. Compos. Mater. 2010, 44, 2819–2831. [Google Scholar] [CrossRef]
- Malek, S.; Gibson, L. Effective elastic properties of periodic hexagonal honeycombs. Mech. Mater. 2015, 91, 226–240. [Google Scholar] [CrossRef]
- Płatek, P.; Rajkowski, K.; Cieplak, K.; Sarzyński, M.; Małachowski, J.; Woźniak, R.; Janiszewski, J. Deformation Process of 3D Printed Structures Made from Flexible Material with Different Values of Relative Density. Polymers 2020, 12, 2120. [Google Scholar] [CrossRef]
- Hashin, Z. Failure criteria for unidirectional fiber composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Li, S.; Sitnikova, E.; Liang, Y.; Kaddour, A.-S. The Tsai-Wu failure criterion rationalised in the context of UD composites. Compos. Part A Appl. Sci. Manuf. 2017, 102, 207–217. [Google Scholar] [CrossRef]
- Fuchs, C.; Bhattacharyya, D.; Fakirov, S. Microfibril reinforced polymer–polymer composites: Application of Tsai-Hill equation to PP/PET composites. Compos. Sci. Technol. 2006, 66, 3161–3171. [Google Scholar] [CrossRef]
- Sun, C.; Tao, J. Prediction of failure envelopes and stress/strain behaviour of composite laminates. Compos. Sci. Technol. 1998, 58, 1125–1136. [Google Scholar] [CrossRef]
- Jaafar, M.; Atlati, S.; Makich, H.; Nouari, M.; Moufki, A.; Julliere, B. A 3D FE modeling of machining process of Nomex® honeycomb core: Influence of the cell structure behaviour and specific tool geometry. Procedia Cirp 2017, 58, 505–510. [Google Scholar] [CrossRef]
- Yang, G. Experimental investigation of strength criteria for S-glass, E-glass and graphite fiber composite plate. Theor. Appl. Fract. Mech. 1994, 20, 59–66. [Google Scholar] [CrossRef]
- Koloor, S.; Khosravani, M.R.; Hamzah, R.; Tamin, M. FE model-based construction and progressive damage processes of FRP composite laminates with different manufacturing processes. Int. J. Mech. Sci. 2018, 141, 223–235. [Google Scholar] [CrossRef]
- Rahimian Koloor, S.S.; Karimzadeh, A.; Yidris, N.; Petrů, M.; Ayatollahi, M.R.; Tamin, M.N. An energy-based concept for yielding of multidirectional FRP composite structures using a mesoscale lamina damage model. Polymers 2020, 12, 157. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giunta, G.; Catapano, A.; Belouettar, S. Failure indentation analysis of composite sandwich plates via hierarchical models. J. Sandw. Struct. Mater. 2013, 15, 45–70. [Google Scholar] [CrossRef]
- Lee, S.M.; Tsotsis, T.K. Indentation failure behavior of honeycomb sandwich panels. Compos. Sci. Technol. 2000, 60, 1147–1159. [Google Scholar] [CrossRef]
- Rodríguez-Ramírez, J.d.D.; Castanié, B.; Bouvet, C. Damage Mechanics Modelling of the shear nonlinear behavior of Nomex honeycomb core. Application to sandwich beams. Mech. Adv. Mater. Struct. 2020, 27, 80–89. [Google Scholar] [CrossRef] [Green Version]
- Venkatesan, K.R.R.; Rai, A.; Stoumbos, T.G.; Inoyama, D.; Chattopadhyay, A. Finite element based damage and failure analysis of honeycomb core sandwich composite structures for space applications. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 0249. [Google Scholar]
- Aborehab, A.; Kassem, M.; Nemnem, A.; Kamel, M. Miscellaneous Modeling Approaches and Testing of a Satellite Honeycomb Sandwich Plate. J. Appl. Comput. Mech. 2019. [Google Scholar] [CrossRef]
- Li, Z.; Ma, J. Experimental Study on Mechanical Properties of the sandwich composite structure reinforced by basalt fiber and nomex honeycomb. Materials 2020, 13, 1870. [Google Scholar] [CrossRef]
- Hähnel, F.; Wolf, K. Evaluation of the material properties of resin-impregnated Nomex paper as basis for the simulation of the impact behaviour of honeycomb sandwich. In Proceedings of the 3rd International Conference on Composites Testing and Model Identification, Porto, Portugal, 10–12 April 2006; pp. 1–2. [Google Scholar]
- Khan, M.S.; Koloor, S.S.R.; Tamin, M.N. Effects of cell aspect ratio and relative density on deformation response and failure of honeycomb core structure. Mater. Res. Express 2020, 7, 015332. [Google Scholar] [CrossRef]


















| Elastic Constants | Constitutive Damage Model Parameters | ||
|---|---|---|---|
| , (MPa) | 3768 | Longitudinal tensile strength, XT (MPa) | 86.57 |
| , (MPa) | 2879 | Longitudinal compression strength, XC (MPa) | 95.37 |
| , (MPa) | 2647 | Transverse tensile strength, YT (MPa) | 51.79 |
| , (MPa) | 1367 | Transverse compression strength, YC (MPa) | 78.5 |
| , (MPa) | 1318 | Longitudinal shear strength, SL (MPa) | 82 |
| , (MPa) | 1140 | Transverse shear strength, ST (MPa) | 40.7 |
| v12 | 0.21 | Longitudinal tensile fracture energy, GXT (N/mm) | 2.18 |
| v13 | 0.21 | Longitudinal compression fracture energy, GXC (N/mm) | 2.54 |
| v23 | 0.21 | Transverse tensile fracture energy, GYT (N/mm) | 1.45 |
| Transverse compression fracture energy, GYC (N/mm) | 2.17 | ||
| Computational Variables | Shell Element Type | |
|---|---|---|
| Conventional Shell (S4R) | Continuum Shell (SC8R) | |
| Number. of elements | 4662 | 5402 |
| Number of nodes | 4865 | 11,249 |
| Total unknown variables (DOF 1) | 29,190 | 34,206 |
| Total CPU 2 time (s) | 2554.4 | 3386 |
| Wall clock time (s) | 748 | 1224 |
| Elastic Moduli (MPa) | Strength (MPa) | ||||
|---|---|---|---|---|---|
| Load Case | FE Model | Measured | FE Model | Measured | |
| Tension | Single-cell | 144.5 | 137.5 | 3.4 | 3.47 |
| 4-cell | 147.2 | 3.32 | |||
| 24-cell | 147.6 | 3.38 | |||
| Compression | Single-cell | 142.7 | 140.74 | 4.06 | 4.01 |
| 4-cell | 143.8 | 4.06 | |||
| 24-cell | 144.5 | 4.27 | |||
| Shear (transverse) | 6-cell | 29.3 | 25.07 | 1.12 | 1.09 |
| Shear (ribbon) | 6-cell | 44.5 | 42.5 | 1.65 | 1.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.S.; Abdul-Latif, A.; Koloor, S.S.R.; Petrů, M.; Tamin, M.N. Representative Cell Analysis for Damage-Based Failure Model of Polymer Hexagonal Honeycomb Structure under the Out-of-Plane Loadings. Polymers 2021, 13, 52. https://doi.org/10.3390/polym13010052
Khan MS, Abdul-Latif A, Koloor SSR, Petrů M, Tamin MN. Representative Cell Analysis for Damage-Based Failure Model of Polymer Hexagonal Honeycomb Structure under the Out-of-Plane Loadings. Polymers. 2021; 13(1):52. https://doi.org/10.3390/polym13010052
Chicago/Turabian StyleKhan, Muhammad Salman, Ainullotfi Abdul-Latif, Seyed Saeid Rahimian Koloor, Michal Petrů, and Mohd Nasir Tamin. 2021. "Representative Cell Analysis for Damage-Based Failure Model of Polymer Hexagonal Honeycomb Structure under the Out-of-Plane Loadings" Polymers 13, no. 1: 52. https://doi.org/10.3390/polym13010052
APA StyleKhan, M. S., Abdul-Latif, A., Koloor, S. S. R., Petrů, M., & Tamin, M. N. (2021). Representative Cell Analysis for Damage-Based Failure Model of Polymer Hexagonal Honeycomb Structure under the Out-of-Plane Loadings. Polymers, 13(1), 52. https://doi.org/10.3390/polym13010052