Theoretical and Experimental Investigation of Bonded Patch Repairs of a Rubber Reinforced Composite Conveyor Belt
Abstract
:1. Introduction
2. Experimental Method
2.1. Material
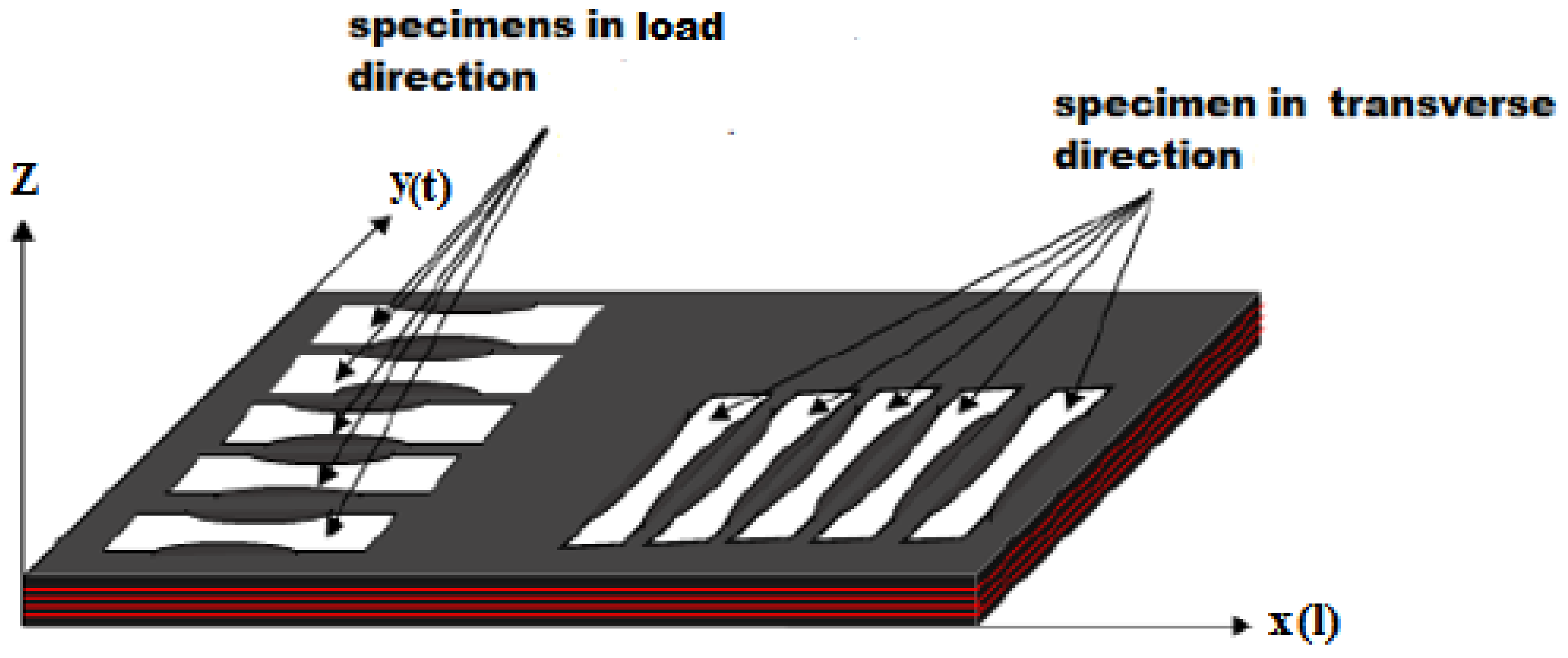
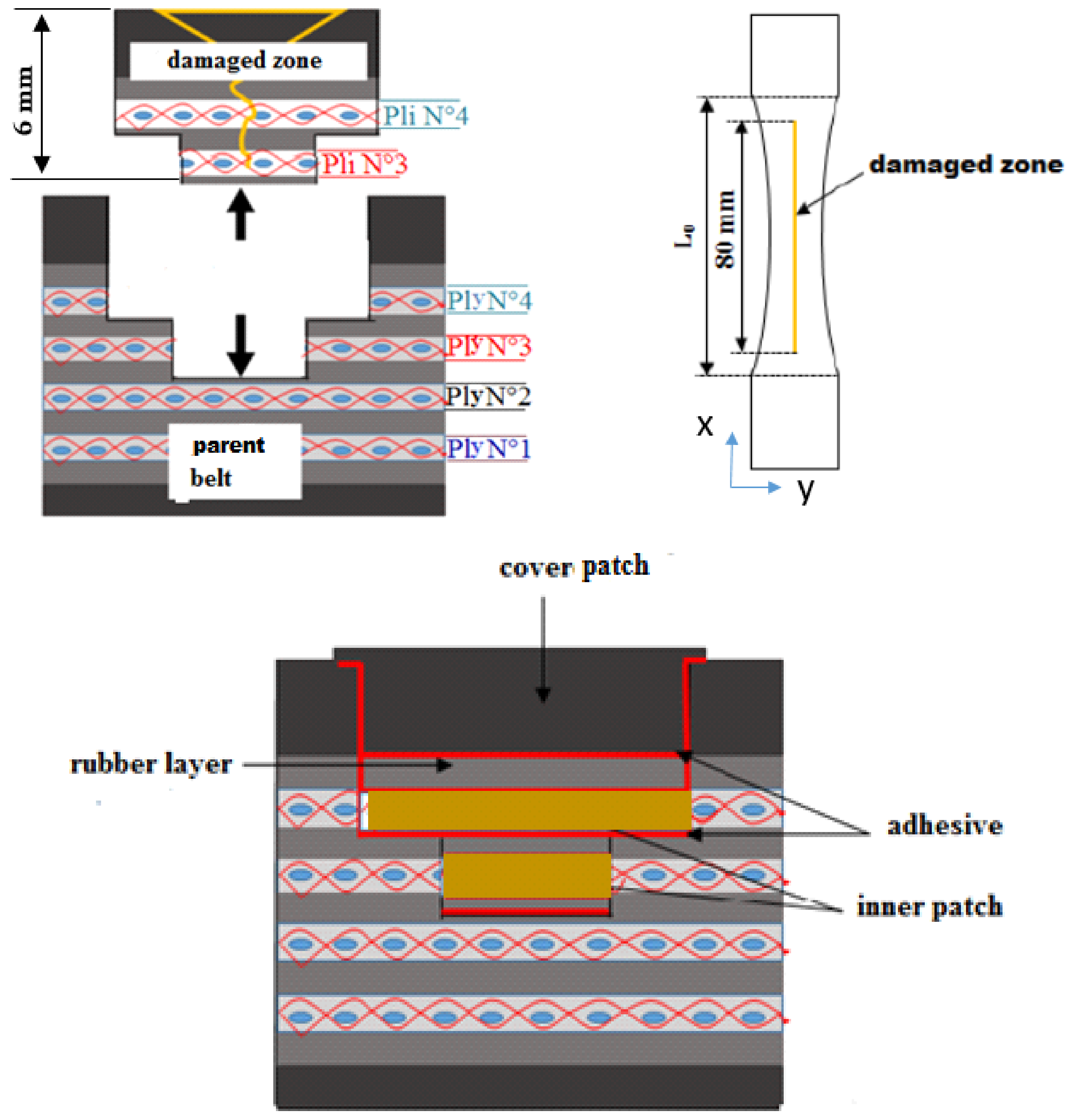
2.2. Repaired Specimen Manufacturing
2.3. Adhesive Specimen Manufacturing
2.4. Mechanical Test
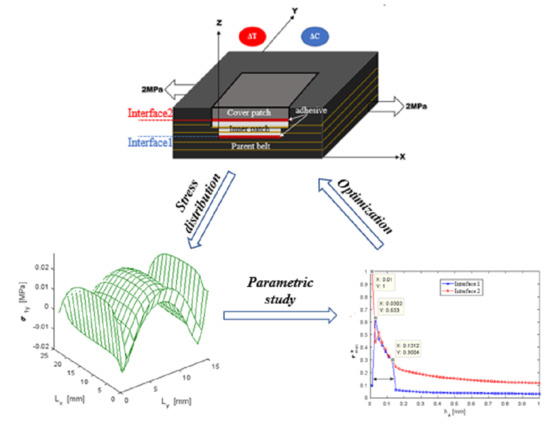
3. Bidirectional Hygro-Thermomechanical Modelling
4. Results and Discussion
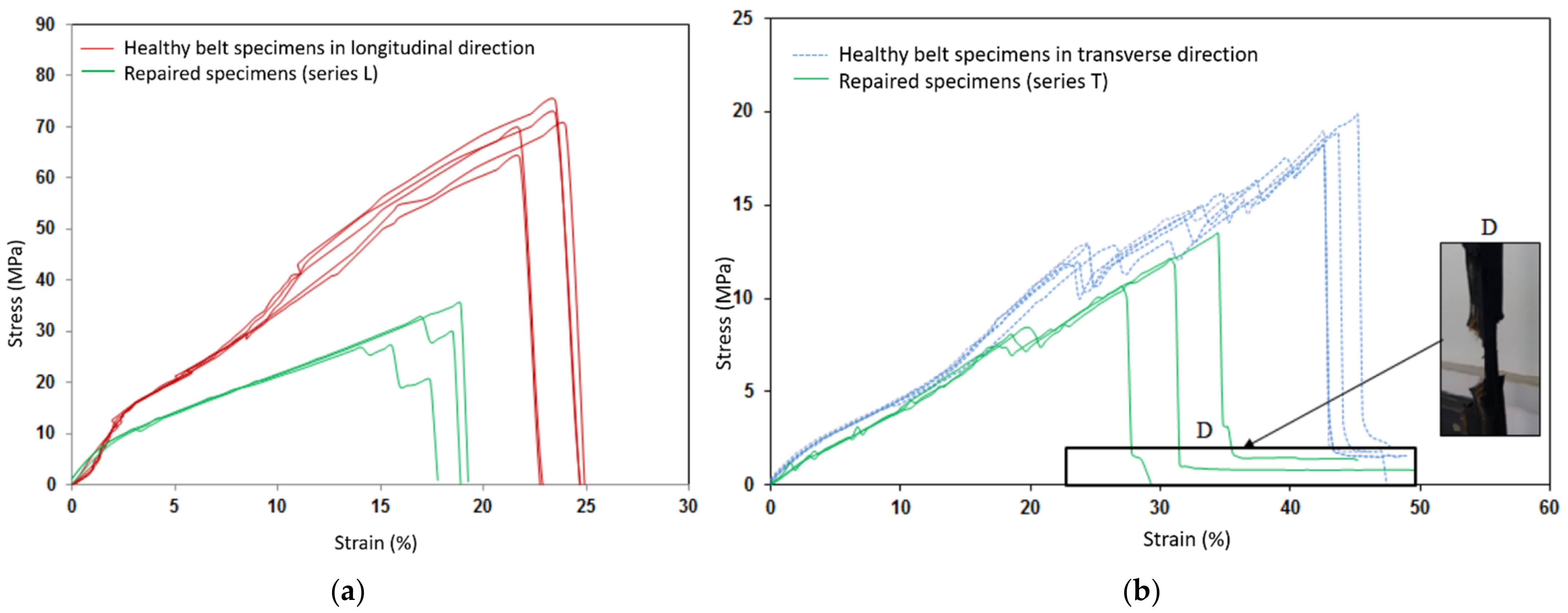
4.1. Experiment Test Results
- The stress-strain curves obtained on the two sets of repaired specimens by the polymerization process presented the same behavior as those on the healthy specimens. However, a loss of tensile strength in the repaired structure was estimated at 57% for series (L) and at 39% for series (T) as listed in Table 6.
- An attenuation of the director coefficient in the elastic domain was observed. Consequently, the reduction of the Young’s modulus of the repaired structure was estimated at 20% for series (L) and at 13% for series (T).
- On the curves, an important decrease of the director coefficient in the elastic and plastic domains was observed for series (L) of the repaired specimens because of the concentration of high stresses located in the joint’s interfaces, which favored the important damage in the repaired specimens and led to premature failure.
- Series (T) repairs using the [90]2 stacking sequence have the best performance in terms of resistance, which was up to 68.73% (Table 6) while repairs of series (L) by means of the most rigid patch [0]2 seemed the least effective. It was then observed that the performance of the repairs by the polymerization process decreased when the rigidity of the plies and test specimen increased. The repair was not perfect if the inner patch was too soft or too rigid. Therefore, optimization of the inner patch was necessary to achieve the best repair performance.
- For series (T), the cover patch was still attached to the parent belt as shown in Figure 11 even if the fibers were broken and completely separated from the parent belt. This implied that the cover patch in the parent belt, which was adjacent to the top adhesive layer, was particularly not damaged and the hyper-elastic behavior led to the absorption of the transfer shear stress. The observation of the covered patch in domain D proved that the orientation of the specimens relative to the stacking sequence and the rigidity of the inner patch had a significant effect on the rupture mechanism and the mode of repaired specimen damage.
4.2. Bidirectional Analysis
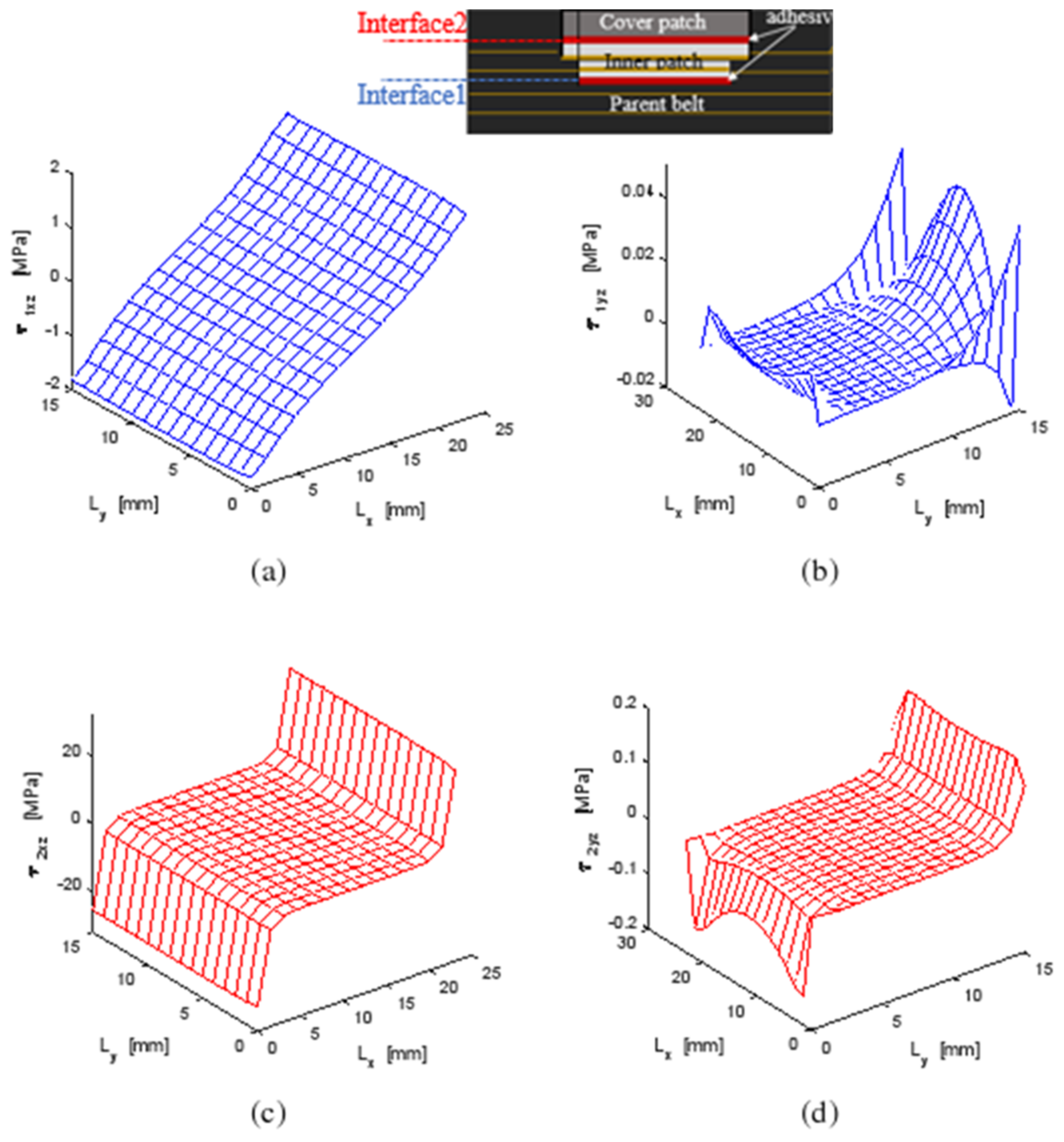
4.2.1. Shear Stress Distribution
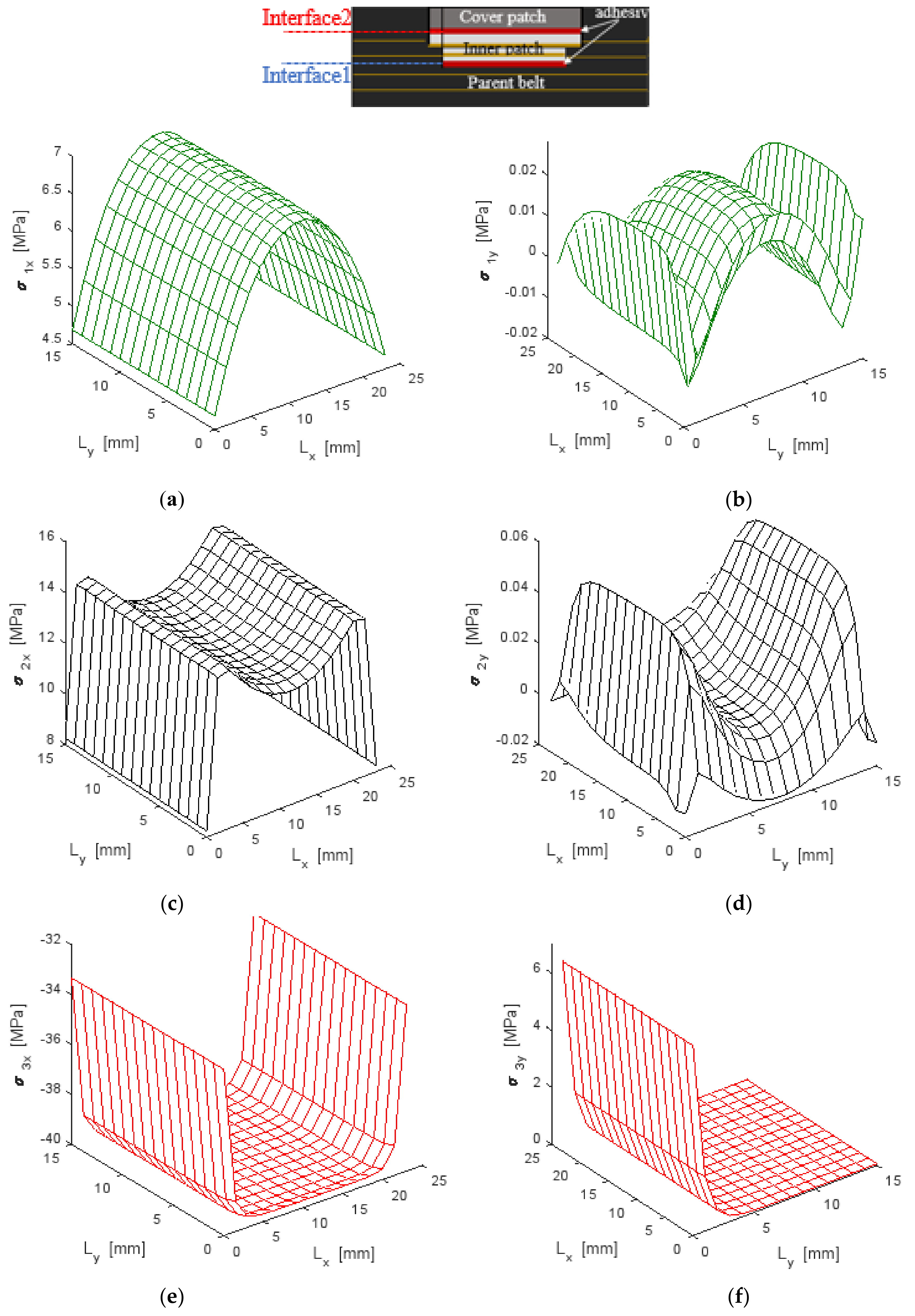
4.2.2. Normal Stress Distribution
4.3. Parametric Study
- Zone 1: at the center of the parent belt.
- Zone 2: near the transverse edges of the inner patch.
- Zone 3: near the longitudinal edges of the inner patch.
- Zone 4: at the longitudinal edges of the covered patch.
- Zone 5: at the longitudinal edges of the interface between the inner and cover patches.
- Zone 6: at the transverse edges of the interface between the inner and cover patches.
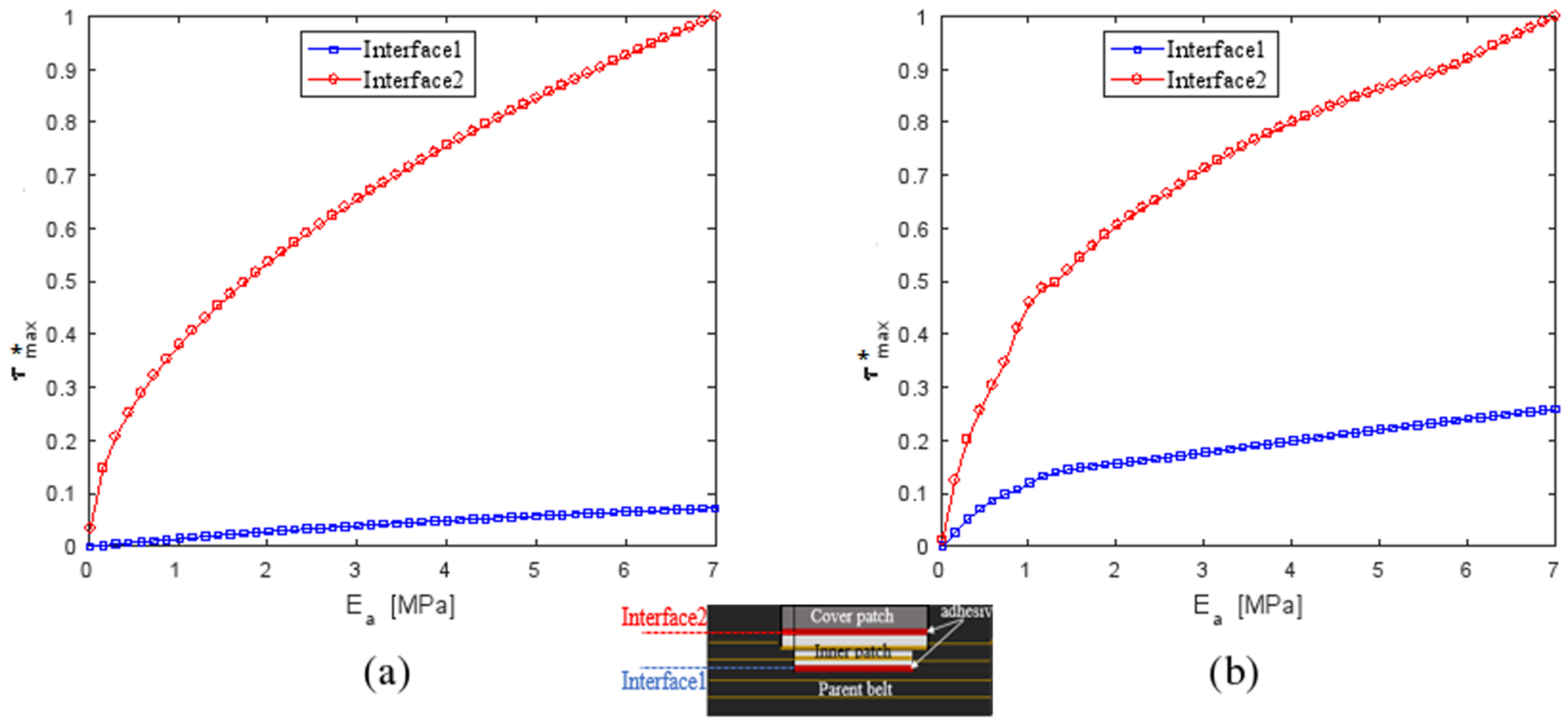
4.3.1. Influence of Young’s Modulus of the Adhesive Ea
4.3.2. Influence of the Thickness Adhesive ha
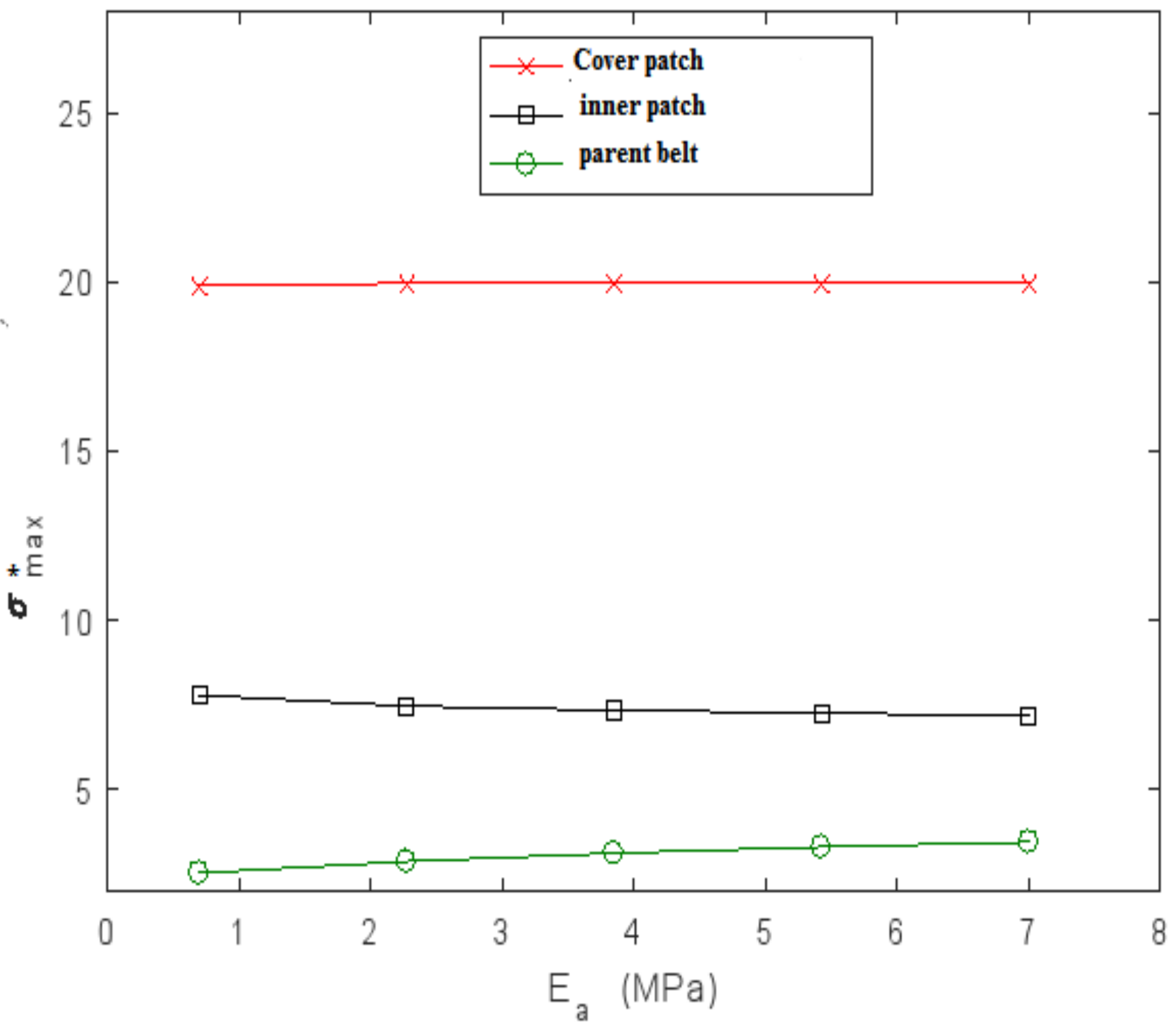
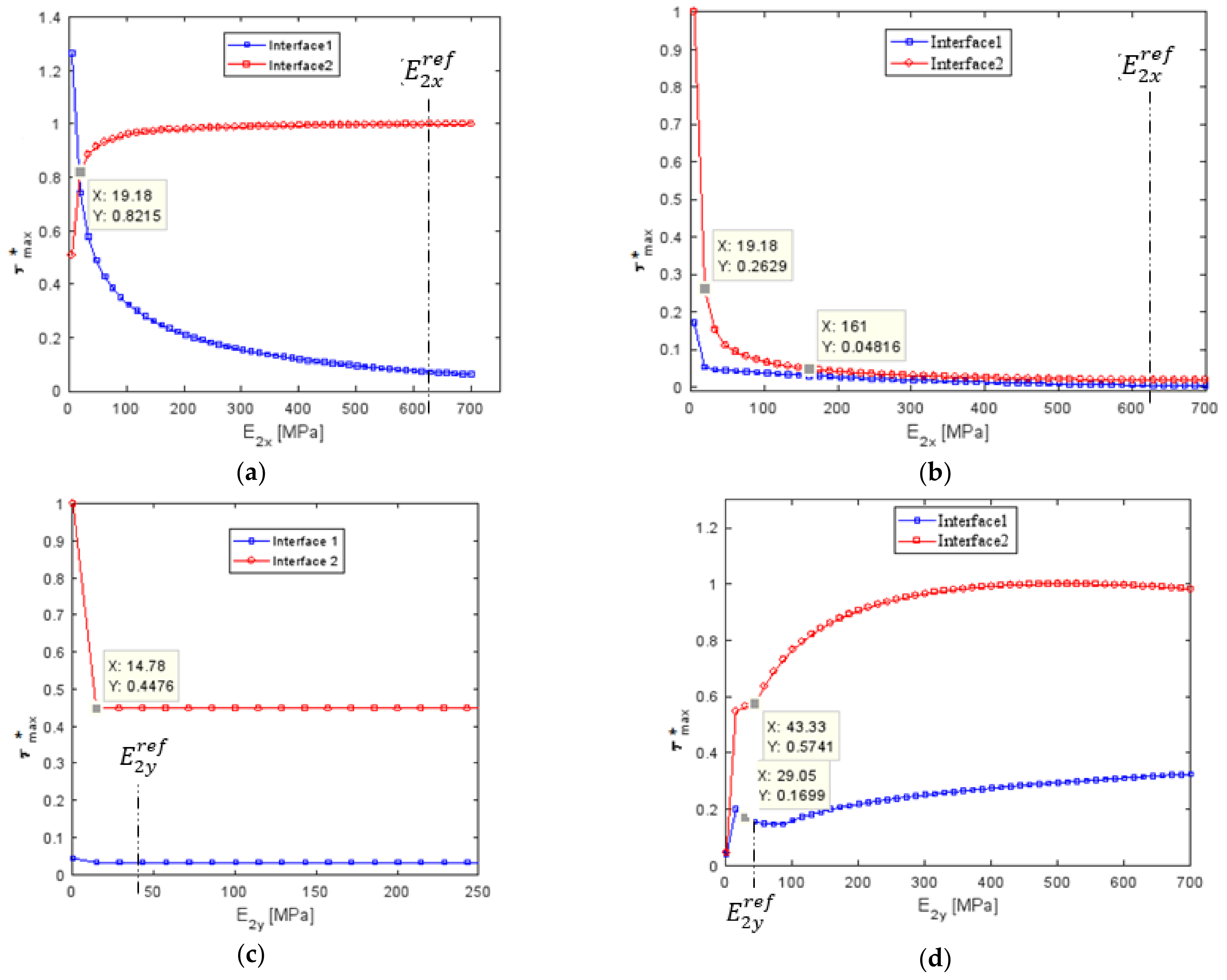
4.3.3. Influence of Young’s Modulus of the Composite Patch
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jones, R.; Chiu, W.; Smith, R. Airworthiness of composite repairs: Failure mechanisms. Eng. Fail. Anal. 1995, 2, 117–128. [Google Scholar] [CrossRef]
- Marioli-Riga, Z.P.; Xenos, D. Reparability and cost analysis criteria for typical composite patch repairs. Facta Univ. Ser. Mech. Autom. Control Robot. 2003, 14, 951–962. [Google Scholar]
- Yala, A.A.; Megueni, A. Optimisation of composite patches repairs with the design of experiments method. Mater. Des. 2009, 30, 200–205. [Google Scholar] [CrossRef]
- Khalili, S.M.R.; Shiravi, M.; Nooramin, A.S. Mechanical Behavior of Notched Plate Repaired with Polymer Composite and Smart Patches Experimental Study. J. Reinf. Plast. Compos. 2010, 29, 3021–3037. [Google Scholar] [CrossRef]
- Errouane, H.; Sereir, Z.; Chateauneuf, A. Numerical model for optimal design of composite patch repair of cracked aluminum plates under tension. Int. J. Adhes. Adhes. 2014, 49, 64–72. [Google Scholar] [CrossRef]
- Tran, T.Q.; Lee, J.K.Y.; Chinnappan, A.; Jayathilaka, W.; Ji, D.; Kumar, V.V.; Ramakrishna, S. Strong, lightweight, and highly conductive CNT/Au/Cu wires from sputtering and electroplating methods. J. Mater. Sci. Technol. 2020, 40, 99–106. [Google Scholar] [CrossRef]
- Serrano-Garcia, W.; Jayathilaka, W.A.D.M.; Chinnappan, A.; Tran, T.Q.; Baskar, C.; Thomas, S.W.; Ramakrishna, S. Nanocomposites for electronic applications that can be embedded for textiles and wearables. Sci. China Ser. E Technol. Sci. 2019, 62, 895–902. [Google Scholar] [CrossRef]
- Mohammadi, S.; Yousefi, M.; Khazaei, M. A review on composite patch repairs and the most important parameters affecting its efficiency and durability. J. Reinf. Plast. Compos. 2020, 40, 1–13. [Google Scholar] [CrossRef]
- Standard NF EN ISO 283. Textile Conveyor Belts—Full Thickness Tensile Testing—Part 1: Determination of Tensile Strength, Elongation at Break and Elongation at the Reference Load. 2000. Available online: https://www.iso.org/standard/22088.html (accessed on 15 October 2020).
- Standard NF ISO 37:2011 Caoutchouc Vulcanisé ou Thermoplastique—Détermination des Caractéristiques de Con-Trainte-Déformation en Traction. 2018. Available online: https://www.iso.org/fr/standard/53023.html (accessed on 12 December 2018).
- Kessentini, R.; Klinkova, O.; Tawfiq, I.; Haddar, M. Transient hygro-thermo-mechanical stresses analysis in multi-layers bonded structure with coupled bidirectional model. Int. J. Mech. Sci. 2019, 150, 188–201. [Google Scholar] [CrossRef]
- Kessentini, R.; Klinkova, O.; Tawfiq, I.; Haddar, M. Modeling the moisture diffusion and hygroscopic swelling of a textile reinforced conveyor belt. Polym. Test. 2019, 75, 159–166. [Google Scholar] [CrossRef]
- Gong, X.-J.; Cheng, P.; Aivazzadeh, S.; Xiao, X. Design and optimization of bonded patch repairs of laminated composite structures. Compos. Struct. 2015, 123, 292–300. [Google Scholar] [CrossRef]
- Kessentini, R.; Klinkova, O.; Tawfiq, I.; Haddar, M. Techniques de Réparation Structurale des Bandes de Convoyeurs. Patent TN2020/0075, 2020. [Google Scholar]



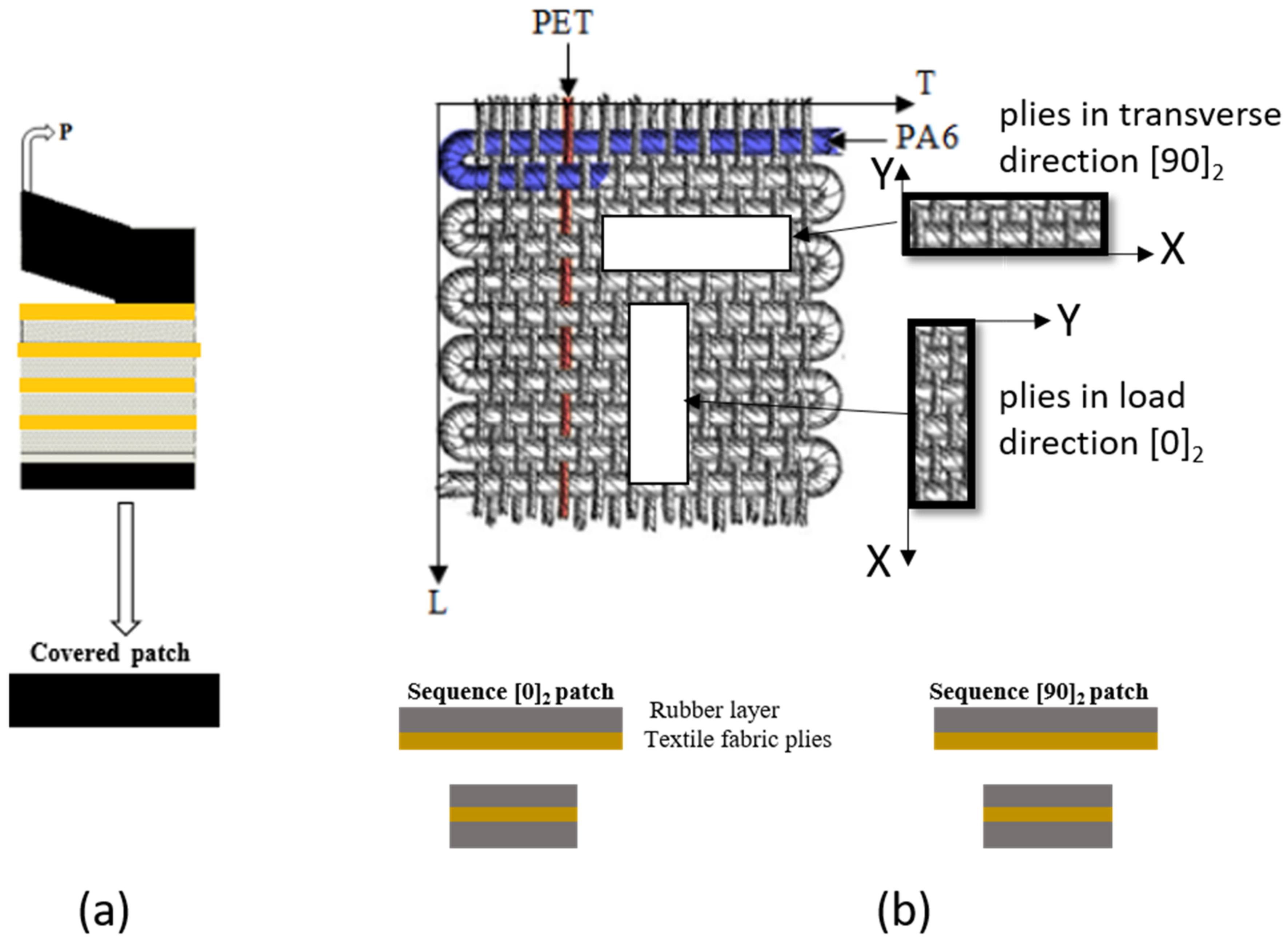






| Materials | Belt | Textile Carcass PET/Pa6 | Cover Rubber | ELASTOGLUE 2000 | |
|---|---|---|---|---|---|
| Properties | |||||
| Ex (MPa) | 550.77 | 626.05 | 3.42 | 7.11 | |
| Ey, Ez (MPa) | 41.85 | 46.54 | - | - | |
| νxy | 0.38 | 0.38 | 0.33 | 0.4 | |
| Re,x (MPa) | 10 | 10.12 | - | - | |
| Re,y (MPa) | 1.29 | 1.34 | - | - | |
| Parameters | Dimension [mm] |
|---|---|
| Overlap length Lx | 25 |
| Overlap width Ly | 15 |
| Belt thickness eb | 10 |
| Covered patch thickness h3 | 3 |
| Inner patch thickness h2 | 2.42 |
| Adhesive thickness ec | 0.15 |
| Parent belt thickness h1 | 4.27 |
| Materials | CTE (×10−6) |
|---|---|
| Polyester (PET) | 25 |
| Polyamide (Pa6) | 15 |
| Rubber | 10 |
| Model | D1 (× 10−11 m2/s) | D2 (× 10−14 m2/s) | C1∞ = C∞R (%) | C∞ (%) | (s1/2) |
|---|---|---|---|---|---|
| SDF | 2.14 | 5.25 | 5.32 | 37.89 | 380 |
| Materials | β (%−1) |
|---|---|
| Upper covering rubber | 0.00530 |
| Belt in the longitudinal direction (PET) | 0.00265 |
| Carcass in the longitudinal direction (PET) | 0.00165 |
| Carcass in the transverse direction (PA6) | 0.00136 |
| Specimens | Patch Stacking Sequence | Young’s Modulus (MPa) | Failure Resistance (MPa) | (%) | (%) |
|---|---|---|---|---|---|
| L-1 | [0]2 | 440.9 | 33.96 | 48.53 | 80.05 |
| L-2 | 439.4 | 24.96 | 35.66 | 79.77 | |
| L-3 | 439.47 | 31.3 | 44.71 | 79.79 | |
| Average for L | 439.92 | 30.07 | 42.96 | 79.87 | |
| T-1 | [90]2 | 34.89 | 9.77 | 52.07 | 83.35 |
| T-2 | 37.84 | 11.18 | 59.59 | 90.4 | |
| T-3 | 36.34 | 12.9 | 68.73 | 86.82 | |
| Average for T | 36.35 | 11.28 | 60.13 | 86.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kessentini, R.; Klinkova, O.; Tawfiq, I.; Haddar, M. Theoretical and Experimental Investigation of Bonded Patch Repairs of a Rubber Reinforced Composite Conveyor Belt. Polymers 2021, 13, 1710. https://doi.org/10.3390/polym13111710
Kessentini R, Klinkova O, Tawfiq I, Haddar M. Theoretical and Experimental Investigation of Bonded Patch Repairs of a Rubber Reinforced Composite Conveyor Belt. Polymers. 2021; 13(11):1710. https://doi.org/10.3390/polym13111710
Chicago/Turabian StyleKessentini, Rawdha, Olga Klinkova, Imad Tawfiq, and Mohamed Haddar. 2021. "Theoretical and Experimental Investigation of Bonded Patch Repairs of a Rubber Reinforced Composite Conveyor Belt" Polymers 13, no. 11: 1710. https://doi.org/10.3390/polym13111710
APA StyleKessentini, R., Klinkova, O., Tawfiq, I., & Haddar, M. (2021). Theoretical and Experimental Investigation of Bonded Patch Repairs of a Rubber Reinforced Composite Conveyor Belt. Polymers, 13(11), 1710. https://doi.org/10.3390/polym13111710