Thermo-Mechanical Behavior of Poly(ether ether ketone): Experiments and Modeling
Abstract
1. Introduction
2. Materials and Methods
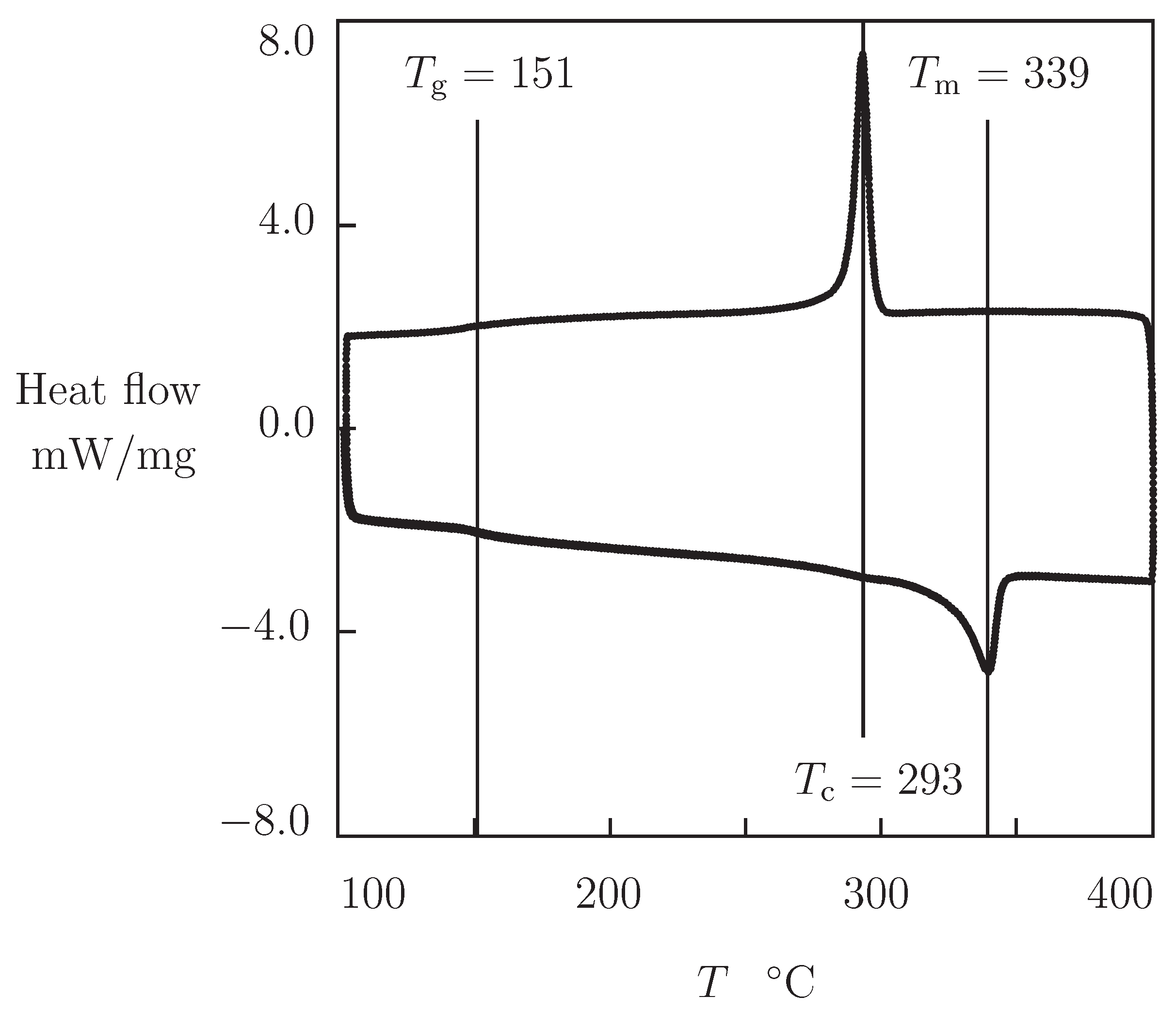
3. Results and Discussion
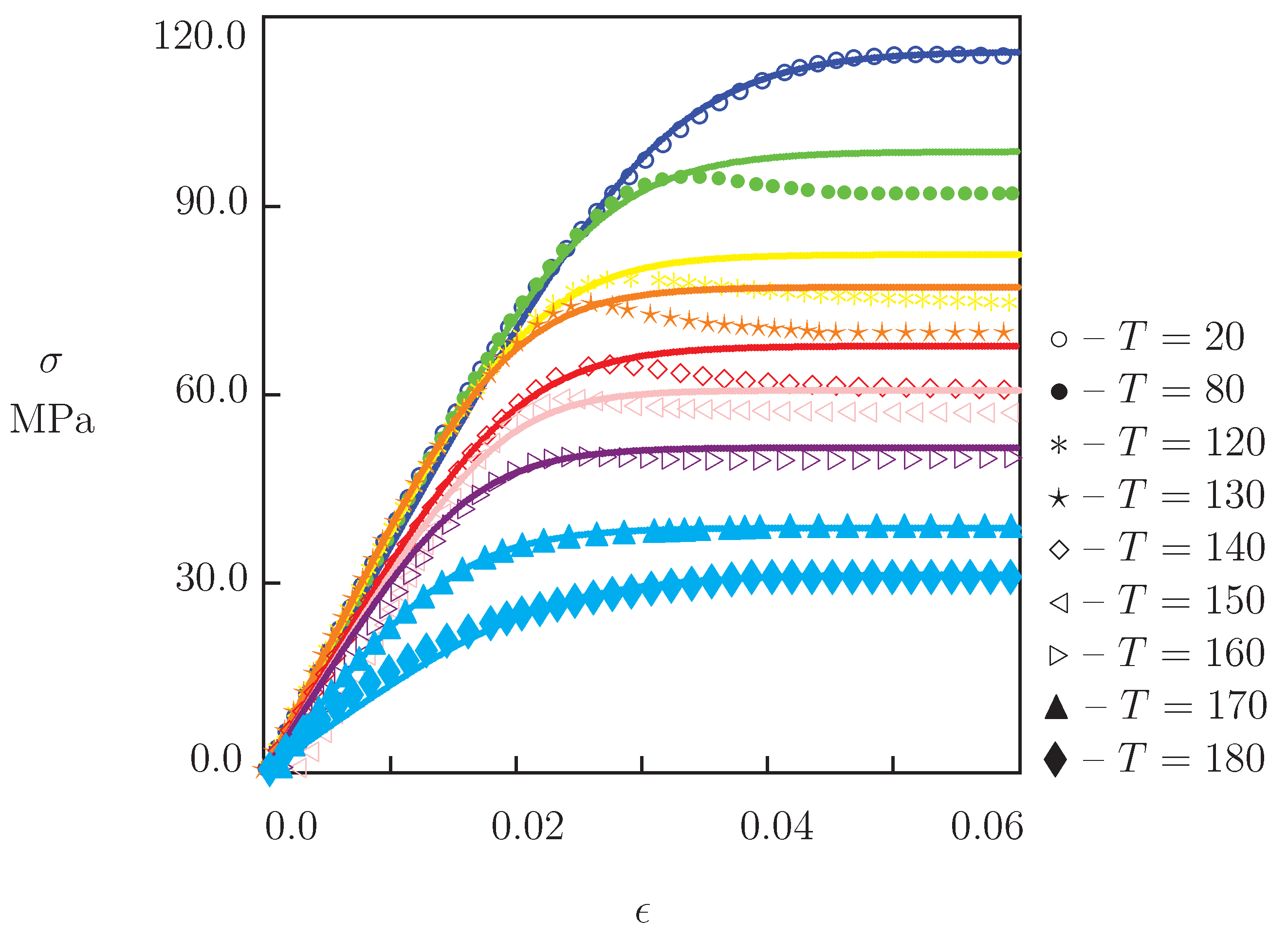
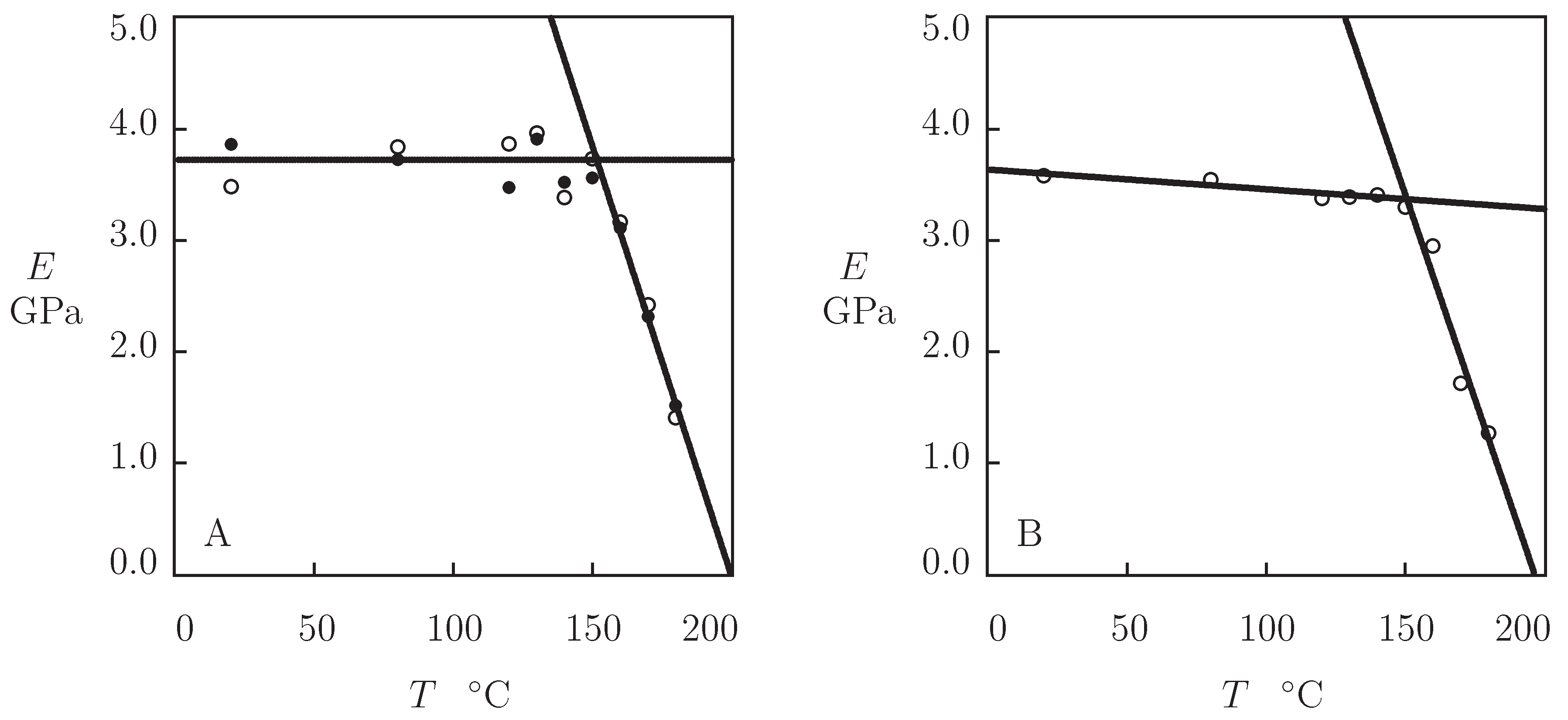
3.1. Thermo–Elastoplasticity
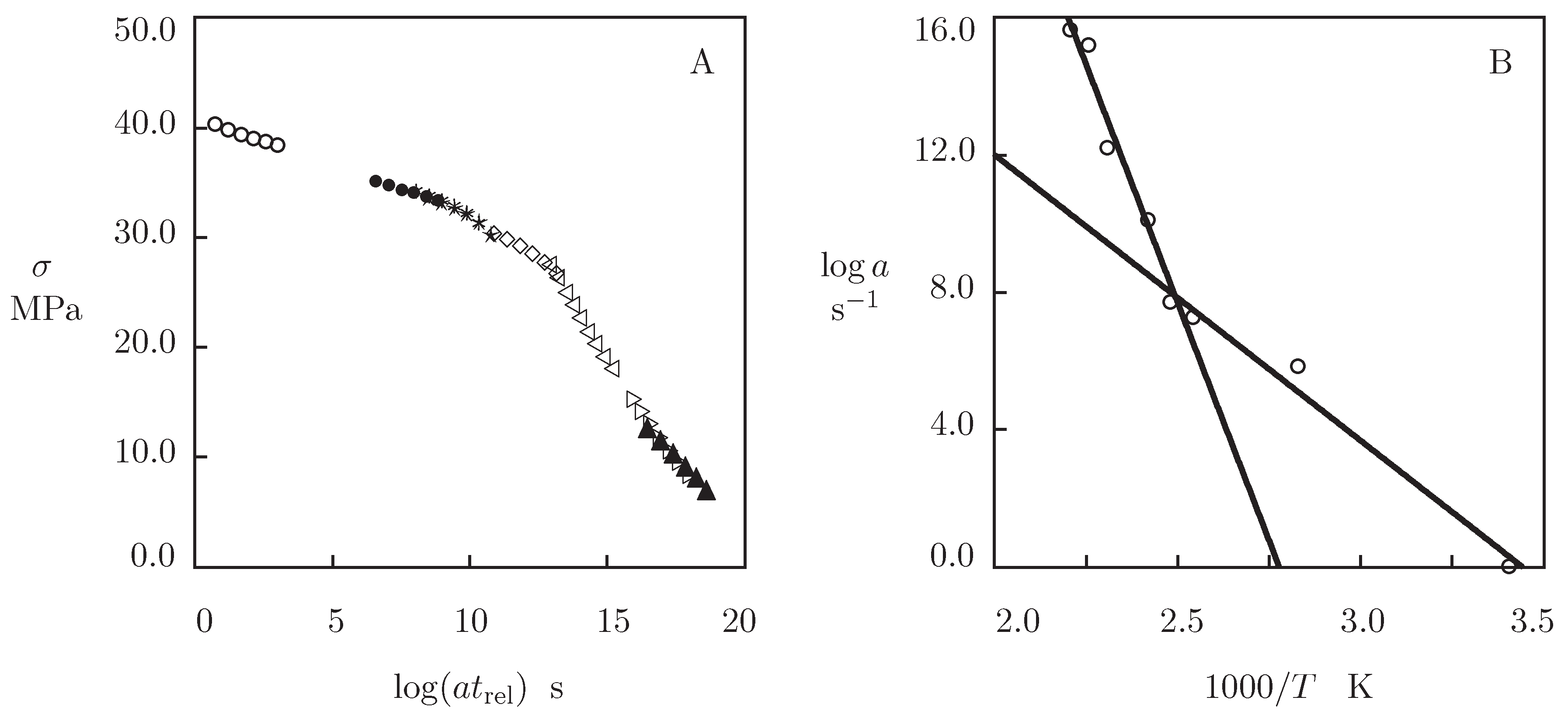
3.2. Thermo–Viscoelasticity
3.3. Thermo–Viscoelastoplasticity
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Diez-Pascual, A.M.; Naffakh, M.; Marco, C.; Ellis, G.; Gomez-Fatou, M.A. High-performance nanocomposites based on polyetherketones. Prog. Mater. Sci. 2012, 57, 1106–1190. [Google Scholar] [CrossRef]
- Flanagan, M.; Grogan, D.M.; Goggins, J.; Appel, S.; Doyle, K.; Leen, S.B.; O’Bradaigh, C.M. Permeability of carbon fibre PEEK composites for cryogenic storage tanks of future space launchers. Composites A 2017, 101, 173–184. [Google Scholar] [CrossRef]
- Kalra, S.; Munjal, B.S.; Singh, V.R.; Mahajan, M.; Bhattacharya, B. Investigations on the suitability of PEEK material under space environment conditions and its application in a parabolic space antenna. Adv. Space Res. 2019, 63, 4039–4045. [Google Scholar] [CrossRef]
- Lin, L.; Schlarb, A.K. Effect of the varied load conditions on the tribological performance and the thermal characteristics of PEEK-based hybrid composites. Tribol. Int. 2016, 101, 218–225. [Google Scholar] [CrossRef]
- Kim, D.J.; Lee, B.-N.; Nam, S.Y. Characterization of highly sulfonated PEEK based membrane for the fuel cell application. Int. J. Hydrogen Energy 2017, 42, 23768–23775. [Google Scholar] [CrossRef]
- Lei, L.; Zhu, X.; Xu, J.; Qian, H.; Zou, Z.; Yang, H. Highly stable ionic-covalent cross-linked sulfonated poly(ether ether ketone) for direct methanol fuel cells. J. Power Sources 2017, 350, 41–48. [Google Scholar] [CrossRef]
- Panayotov, I.V.; Orti, V.; Cuisinier, F.; Yachouh, J. Polyetheretherketone (PEEK) for medical applications. J. Mater. Sci. Mater. Med. 2016, 27, 2–11. [Google Scholar] [CrossRef] [PubMed]
- Verma, S.; Sharma, N.; Kango, S.; Sharma, S. Developments of PEEK (polyetheretherketone) as a biomedical material: A focused review. Eur. Polym. J. 2021, 147, 110295. [Google Scholar] [CrossRef]
- Krishnaswamy, R.K.; Kalika, D.S. Dynamic mechanical relaxation properties of poly(ether ether ketone). Polymer 1994, 35, 1157–1165. [Google Scholar] [CrossRef]
- Rae, P.J.; Brown, E.N.; Orler, E.B. The mechanical properties of poly(ether-ether-ketone) (PEEK) with emphasis on the large compressive strain response. Polymer 2007, 48, 598–615. [Google Scholar] [CrossRef]
- Guo, Y.; Bradshaw, R.D. Isothermal physical aging characterization of polyether-ether-ketone (PEEK) and polyphenylene sulfide (PPS) films by creep and stress relaxation. Mech. Time-Depend. Mater. 2007, 11, 61–89. [Google Scholar] [CrossRef]
- Yuan, M.; Galloway, J.A.; Hoffman, R.J.; Bhatt, S. Influence of molecular weight on rheological, thermal, and mechanical properties of PEEK. Polym. Eng. Sci. 2011, 51, 94–102. [Google Scholar] [CrossRef]
- Garcia-Leiner, M.; Reitman, M.T.F.; El-Hibri, M.J.; Roeder, R.K. Structure-property relationships in commercial polyetheretherketone resins. Polym. Eng. Sci. 2017, 57, 955–964. [Google Scholar] [CrossRef]
- Abbasnezhad, N.; Khavandi, A.; Fitoussi, J.; Arabi, H.; Shirinbayan, M.; Tcharkhtchi, A. Influence of loading conditions on the overall mechanical behavior of polyether-ether-ketone (PEEK). Int. J. Fatigue 2018, 109, 83–92. [Google Scholar] [CrossRef]
- Ha, S.Y.; Ang, Q.; Chang, F.-K. Modeling the viscoplastic behavior of fiber-reinforced thermoplastic matrix composites at elevated temperatures. J. Compos. Mater. 1991, 25, 334–374. [Google Scholar] [CrossRef]
- Hamdan, S.; Swallowe, G.M. The strain-rate and temperature dependence of the mechanical properties of polyetherketone and polyetheretherketone. J. Mater. Sci. 1996, 31, 1415–1423. [Google Scholar] [CrossRef]
- Chen, F.; Ou, H.; Gatea, S.; Long, H. Hot tensile fracture characteristics and constitutive modelling of polyether-ether-ketone (PEEK). Polym. Test. 2017, 63, 168–179. [Google Scholar] [CrossRef]
- Zheng, B.; Wang, H.; Huang, Z.; Zhang, Y.; Zhou, H.; Li, D. Experimental investigation and constitutive modeling of the deformation behavior of poly-ether-ether-ketone at elevated temperatures. Polym. Test. 2017, 63, 349–359. [Google Scholar] [CrossRef]
- Barba, D.; Arias, A.; Garcia-Gonzalez, D. Temperature and strain rate dependences on hardening and softening behaviours in semi-crystalline polymers: Application to PEEK. Int. J. Solids Struct. 2020, 182–183, 205–217. [Google Scholar] [CrossRef]
- El-Qoubaa, Z.; Othman, R. Characterization and modelling of the strain rate sensitivity of polyetheretherketones compressive yield stress. Mater. Des. 2015, 66, 336–345. [Google Scholar] [CrossRef]
- El-Qoubaa, Z.; Othman, R. Strain rate sensitivity of polyetheretherketones compressive yield stress at low and high temperatures. Mech. Mater. 2016, 95, 15–27. [Google Scholar] [CrossRef]
- Chen, F.; Ou, H.; Lu, B.; Long, H. A constitutive model of polyether-ether-ketone (PEEK). J. Mech. Behav. Biomed. Mater. 2016, 53, 427–433. [Google Scholar] [CrossRef]
- Turner, J.A.; Menary, G.H.; Martin, P.J. Biaxial characterization of poly(ether-ether-ketone) for thermoforming: A comparison between bulge and in-plane biaxial testing. Polym. Eng. Sci. 2019, 59, 1853–1865. [Google Scholar] [CrossRef]
- Turner, J.A.; Menary, G.H.; Martin, P.J.; Yan, S. Modelling the temperature dependent biaxial response of poly(ether-ether-ketone) above and below the glass transition for thermoforming applications. Polymers 2019, 11, 1042. [Google Scholar] [CrossRef] [PubMed]
- Sobieraj, M.C.; Murphy, J.E.; Brinkman, J.G.; Kurtz, S.M.; Rimnac, C.M. Notched fatigue behavior of PEEK. Biomaterials 2010, 31, 9156–9162. [Google Scholar] [CrossRef] [PubMed]
- Berer, M.; Tscharnuter, D.; Pinter, G. Dynamic mechanical response of polyetheretherketone (PEEK) exposed to cyclic loads in the high stress tensile regime. Int. J. Fatigue 2015, 80, 397–405. [Google Scholar] [CrossRef]
- Shrestha, R.; Simsiriwong, J.; Shamsaei, N.; Moser, R.D. Cyclic deformation and fatigue behavior of polyether ether ketone (PEEK). Int. J. Fatigue 2016, 82, 411–427. [Google Scholar] [CrossRef]
- Shrestha, R.; Simsiriwong, J.; Shamsaei, N. Mean strain effects on cyclic deformation and fatigue behavior of polyether ether ketone (PEEK). Polym. Test. 2016, 55, 69–77. [Google Scholar] [CrossRef]
- Li, W.; Gazonas, G.; Brown, E.N.; Rae, P.J.; Negahban, M. Thermomechanical model for monotonic and cyclic loading of PEEK. Mech. Mater. 2019, 129, 113–138. [Google Scholar] [CrossRef]
- Kemmish, D.J.; Hay, J.N. The effect of physical ageing on the properties of amorphous PEEK. Polymer 1985, 26, 905–912. [Google Scholar] [CrossRef]
- Millett, J.C.F.; Bournel, N.K.; Stevens, G.S. Taylor impact of polyether ether ketone. Int. J. Impact Eng. 2006, 32, 1086–1094. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, D.; Rusinek, A.; Jankowiak, T.; Arias, A. Mechanical impact behavior of polyether-ether-ketone (PEEK). Compos. Struct. 2015, 124, 88–99. [Google Scholar] [CrossRef]
- Bourne, N.K.; Garcea, S.C.; Eastwood, D.S.; Parry, S.; Rau, C.; Withers, P.J.; McDonald, S.A.; Brown, E.N. On compression and damage evolution in two thermoplastics. Proc. R. Soc. A 2017, 473, 20160495. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y. Sensitivity of nanoindentation strain rate in poly(ester-ester-ketone) using atomic force microscopy. Polym. Test. 2016, 53, 85–88. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Samadi-Dooki, A.; Malekmotiei, L. Nanoindentation of high performance semicrystalline polymers: A case study on PEEK. Polym. Test. 2017, 61, 57–64. [Google Scholar] [CrossRef]
- Kim, W.; Sun, C.T. Modeling relaxation of a polymeric composite during loading and unloading. J. Compos. Mater. 2002, 36, 745–755. [Google Scholar] [CrossRef]
- Jiang, Z.; Liu, P.; Sue, H.-J.; Bremner, T. Effect of annealing on the viscoelastic behavior of poly(ether-ether-ketone). Polymer 2019, 160, 231–237. [Google Scholar] [CrossRef]
- Ogale, A.A.; McCullough, R.L. Influence of microstructure on elastic and viscoelastic properties of polyether ether ketone. Compos. Sci. Technol. 1987, 30, 185–201. [Google Scholar] [CrossRef]
- Xiao, X.R.; Hiel, C.C.; Cardon, A.H. Characterization and modeling of nonlinear viscoelastic response of PEEK resin and PEEK composites. Compos. Eng. 1994, 4, 681–702. [Google Scholar] [CrossRef]
- Katouzian, M.; Bruller, O.S.; Horoschenkoff, A. On the effect of temperature on the creep behavior of neat and carbon fiber reinforced PEEK and epoxy resin. J. Compos. Mater. 1995, 29, 372–387. [Google Scholar] [CrossRef]
- Drozdov, A.D.; Gupta, R.K. Constitutive equations in finite viscoplasticity of semicrystalline polymers. Int. J. Solids Struct. 2003, 40, 6217–6243. [Google Scholar] [CrossRef]
- Drozdov, A.D.; Klitkou, R.; Christiansen, J.D. Cyclic viscoplasticity of semicrystalline polymers with finite deformations. Mech. Mater. 2013, 56, 53–64. [Google Scholar] [CrossRef]
- Yu, C.; Kang, G.; Chen, K.; Lu, F. A thermo-mechanically coupled nonlinear viscoelastic-viscoplastic cyclic constitutive model for polymeric materials. Mech. Mater. 2017, 105, 1–15. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, D.; Zaera, R.; Arias, A. A hyperelastic–thermoviscoplastic constitutive model for semi-crystalline polymers: Application to PEEK under dynamic loading conditions. Int. J. Plast. 2016, 88, 27–52. [Google Scholar] [CrossRef]
- Chang, B.; Wang, X.; Long, Z.; Li, Z.; Gu, J.; Ruan, S.; Shen, C. Constitutive modeling for the accurate characterization of the tension behavior of PEEK under small strain. Polym. Test. 2018, 69, 514–521. [Google Scholar] [CrossRef]
- Lei, M.; Hamel, C.M.; Chen, K.; Zhao, Z.; Lu, H.; Yu, K.; Qi, H.J. Thermomechanical behaviors of polyether ether ketone (PEEK) with stretch-induced anisotropy. J. Mech. Phys. Solids 2021, 148, 104271. [Google Scholar] [CrossRef]
- Iulianelli, A.; Basile, A. Sulfonated PEEK based polymers in PEMFC and DMFC applications: A review. Int. J. Hydrogen Energy 2012, 37, 15241–15255. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, H.; Wang, J.; Xu, Y.; Pan, C.; Li, Q.; He, R. Dual cross-linked polymer electrolyte membranes based on poly(aryl ether ketone) and poly(styrene-vinylimidazole-divinylbenzene) for high temperature proton exchange membrane fuel cells. J. Power Sources 2020, 480, 228859. [Google Scholar] [CrossRef]
- Liu, D.; Dong, B.; Zhang, H.; Xie, Y.; Pang, J.; Jiang, Z. High methanol resistant polyelectrolyte membrane based on semi-crystalline poly(ether ketone) with densely sulfonated side chain for direct methanol fuel cell. J. Power Sources 2021, 482, 228982. [Google Scholar] [CrossRef]
- Wu, G.; Lin, S.-J.; Hsu, I.-C.; Su, J.-Y.; Chen, D.W. Study of high performance sulfonated polyether ether ketone composite electrolyte membranes. Polymers 2019, 11, 1177. [Google Scholar] [CrossRef] [PubMed]
- Haleem, A.; Javaid, M. Polyether ether ketone (PEEK) and its 3D printed implants applications in medical field: An overview. Clin. Epidemiol. Glob. Health 2019, 7, 571–577. [Google Scholar] [CrossRef]
- Singh, S.; Prakash, C.; Ramakrishna, S. 3D printing of polyether-ether-ketone for biomedical applications. Eur. Polym. J. 2019, 114, 234–248. [Google Scholar] [CrossRef]
- Song, X.; Shi, D.; Song, P.; Han, X.; Wei, Q.; Huang, C. Fused deposition modeling of poly(ether ether ketone) scaffolds. High Temp. Mater. Process. 2021, 40, 1–11. [Google Scholar] [CrossRef]
- Bauwens-Crowet, C.; Bauwens, J.C.; Homes, G. The temperature dependence of yield of polycarbonate in uniaxial compression and tensile tests. J. Mater. Sci. 1972, 7, 176–183. [Google Scholar] [CrossRef]
- Richeton, J.; Ahzi, S.; Vecchio, K.S.; Jiang, F.C.; Adharapurapu, R.R. Influence of temperature and strain rate on the mechanical behavior of three amorphous polymers: Characterization and modeling of the compressive yield stress. Int. J. Solids Struct. 2006, 43, 2318–2335. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Haraya, K.; Hattori, S.; Sasuga, T. Evaluation of polymer free volume by positron annihilation and gas diffusivity measurements. Polymer 1994, 35, 925–928. [Google Scholar] [CrossRef]
- Jean, Y.C.; Nakanishi, H.; Hao, L.Y.; Sandreczki, T.C. Anisotropy of free-volume-hole dimensions in polymers probed by positron-annihilation spectroscopy. Phys. Rev. B 1990, 42, 9705–9708. [Google Scholar] [CrossRef]
- Nakanishi, H.; Jean, Y.C. Dynamics of excess free volume in semicrystalline PEEK studied by positron annihilation. Macromolecules 1991, 24, 6618–6621. [Google Scholar] [CrossRef]
- Drozdov, A.D. Effect of temperature on the viscoelastic and viscoplastic behavior of polypropylene. Mech. Time-Depend. Mater. 2010, 14, 411–434. [Google Scholar] [CrossRef]
- Drozdov, A.D.; Christiansen, J.D. Modeling non-isothermal viscoelastic response of glassy polymers. Acta Mech. 2018, 229, 1137–1156. [Google Scholar] [CrossRef]
- Sauer, B.B.; Avakian, P.; Starkweather, H.W.; Hsiao, B.S. Thermally stimulated current and dielectric studies of poly(aryl ether ketone ketone). Macromolecules 1990, 23, 5119–5126. [Google Scholar] [CrossRef]
- Goodwin, A.A.; Hay, J.N. Dielectric and dynamic mechanical relaxation studies on poly(aryl ether ketone)s. J. Polym. Sci. B Polym. Phys. 1998, 36, 851–859. [Google Scholar] [CrossRef]
- Drozdov, A.D.; Kalamkarov, A.L. A constitutive model for nonlinear viscoelastic behavior of polymers. Polym. Eng. Sci. 1996, 36, 1907–1919. [Google Scholar] [CrossRef]
- Henann, D.L.; Anand, L. A large deformation theory for rate-dependent elastic-plastic materials with combined isotropic and kinematic hardening. Int. J. Plast. 2009, 25, 1833–1878. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drozdov, A.D.; deClaville Christiansen, J. Thermo-Mechanical Behavior of Poly(ether ether ketone): Experiments and Modeling. Polymers 2021, 13, 1779. https://doi.org/10.3390/polym13111779
Drozdov AD, deClaville Christiansen J. Thermo-Mechanical Behavior of Poly(ether ether ketone): Experiments and Modeling. Polymers. 2021; 13(11):1779. https://doi.org/10.3390/polym13111779
Chicago/Turabian StyleDrozdov, A. D., and J. deClaville Christiansen. 2021. "Thermo-Mechanical Behavior of Poly(ether ether ketone): Experiments and Modeling" Polymers 13, no. 11: 1779. https://doi.org/10.3390/polym13111779
APA StyleDrozdov, A. D., & deClaville Christiansen, J. (2021). Thermo-Mechanical Behavior of Poly(ether ether ketone): Experiments and Modeling. Polymers, 13(11), 1779. https://doi.org/10.3390/polym13111779







