Predictions of Moisture Diffusion Behavior of Cellulose-Fiber-Reinforced Plain Weave Epoxy Composites
Abstract
:1. Introduction
2. Method and Experiment
2.1. Theoretical Method
2.1.1. Geometry of Plain Weave Composite
2.1.2. Superposition Method for Moisture Diffusion of Plain Weave Composite
- Minimum equivalence. If we directly ensure that the area of the upper triangular resin phase is equal to the equivalent model, i.e., the thickness of the upper resin in the equivalent model is 4/a, the moisture diffusion will be underestimated because moisture diffusion in the cellulose fiber tow is not enough to be considered. We will later prove this phenomenon; this model is named the minimum equivalence model, as shown in Figure 3c.
- Maximum equivalence. If the thickness of the upper resin phase is 0, as depicted in Figure 3d, the moisture diffusion will be obviously overestimated. This model is named the maximum equivalence model.
- Approximate equivalence. As illustrated in Figure 3e, the moisture uptake of half of part 4 is actually situated between minimum equivalence and minimum equivalence. The thickness of the upper resin phase is τa. This model is named the approximate equivalence model.
2.1.3. Three-Phase Diffusion Equation
2.2. Experiment
2.2.1. Experimental Material and Setup
2.2.2. Water Absorption Experiment
3. Results and Discussion
3.1. Validation of Three-Phase Diffusion Model
3.2. Comparison with FEA
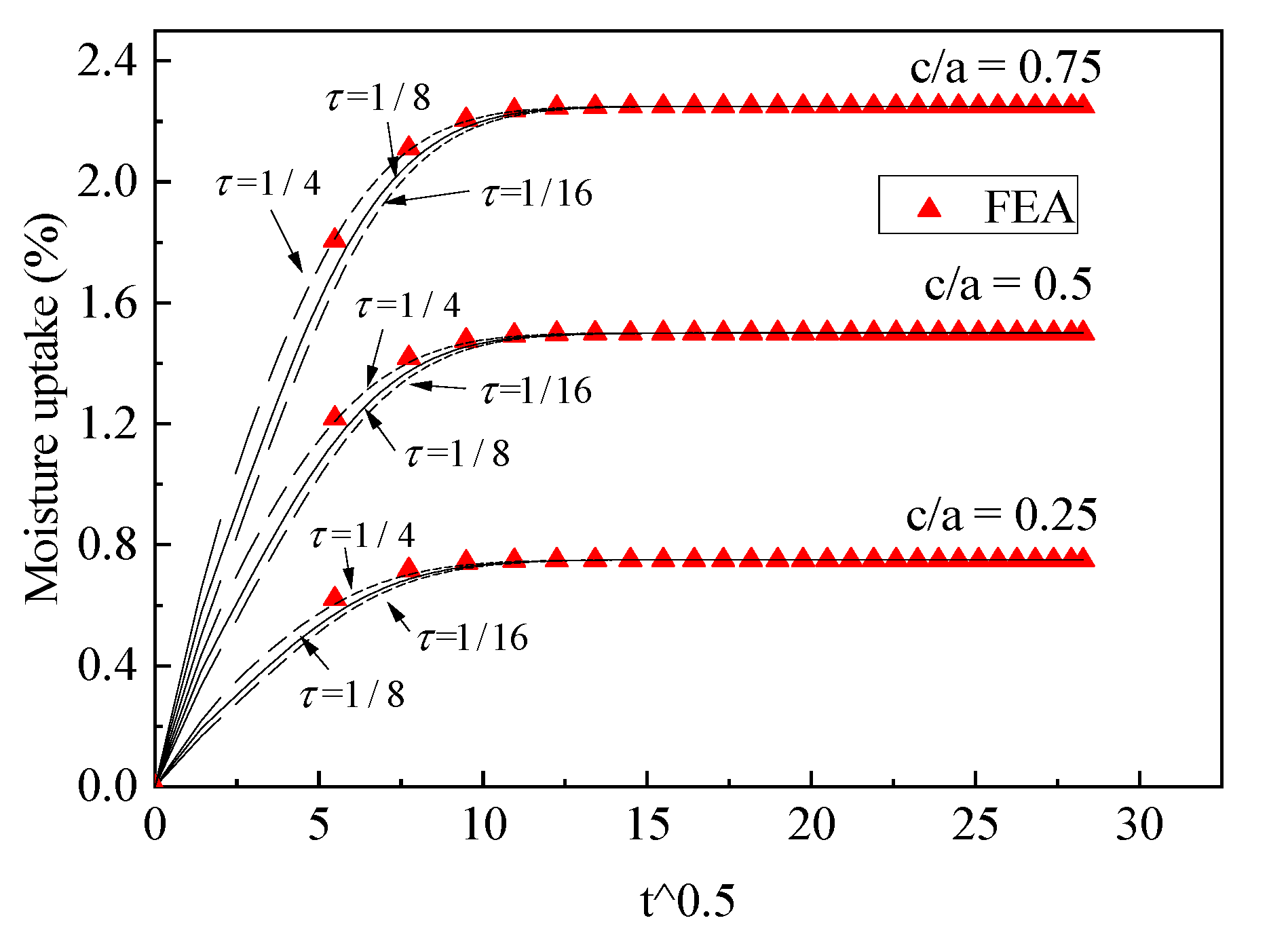
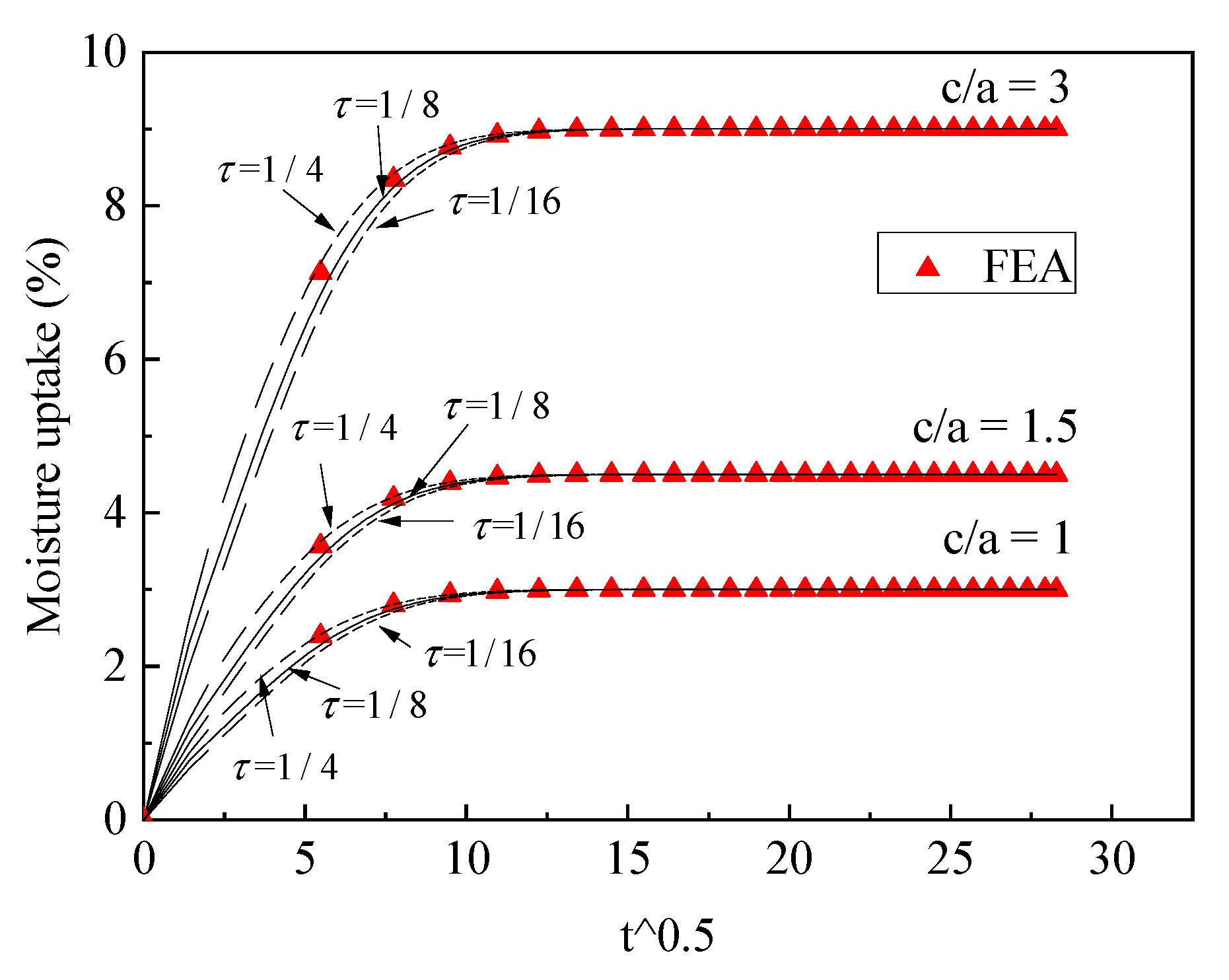
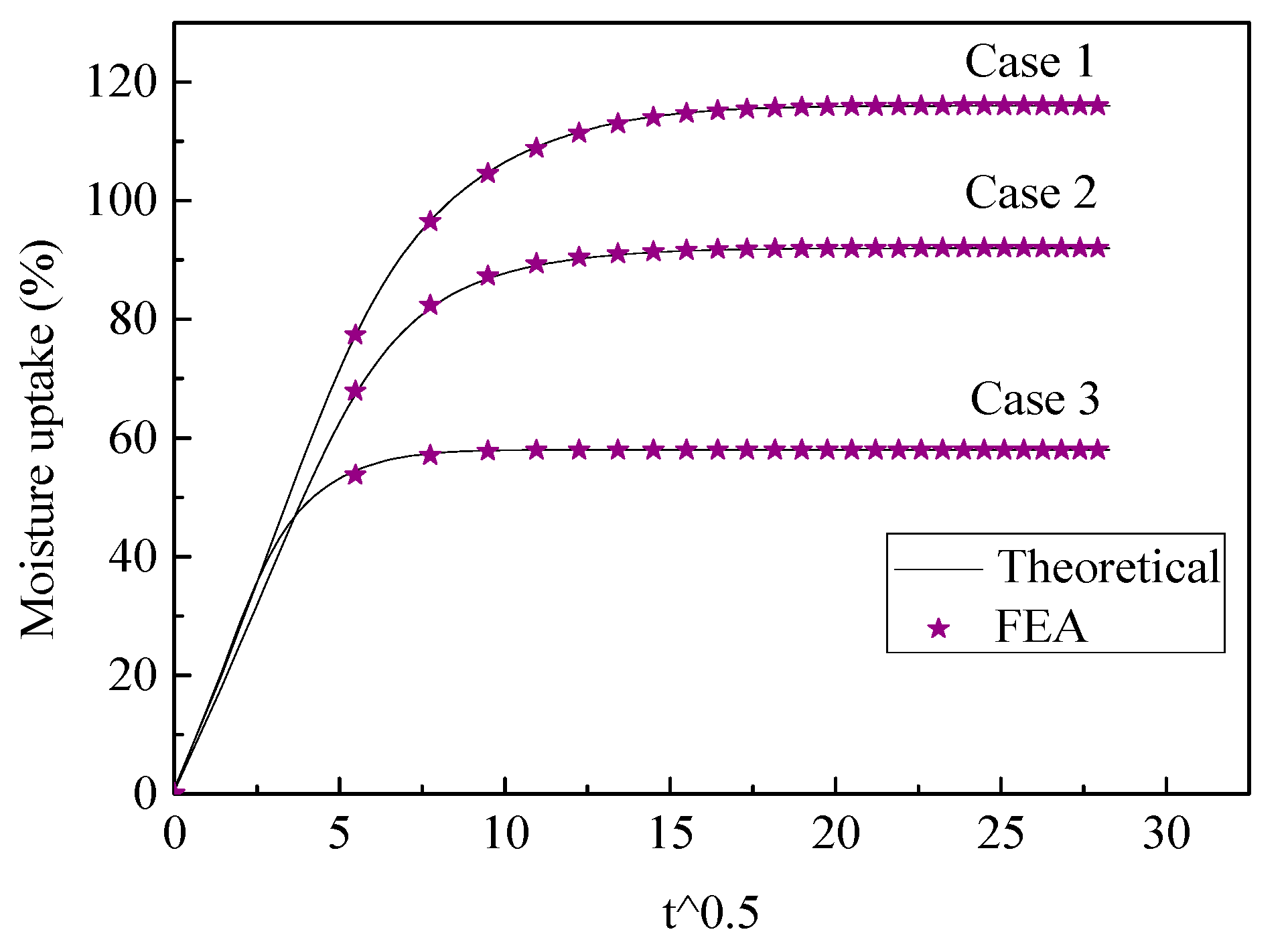
3.2.1. The Determination of Value τ
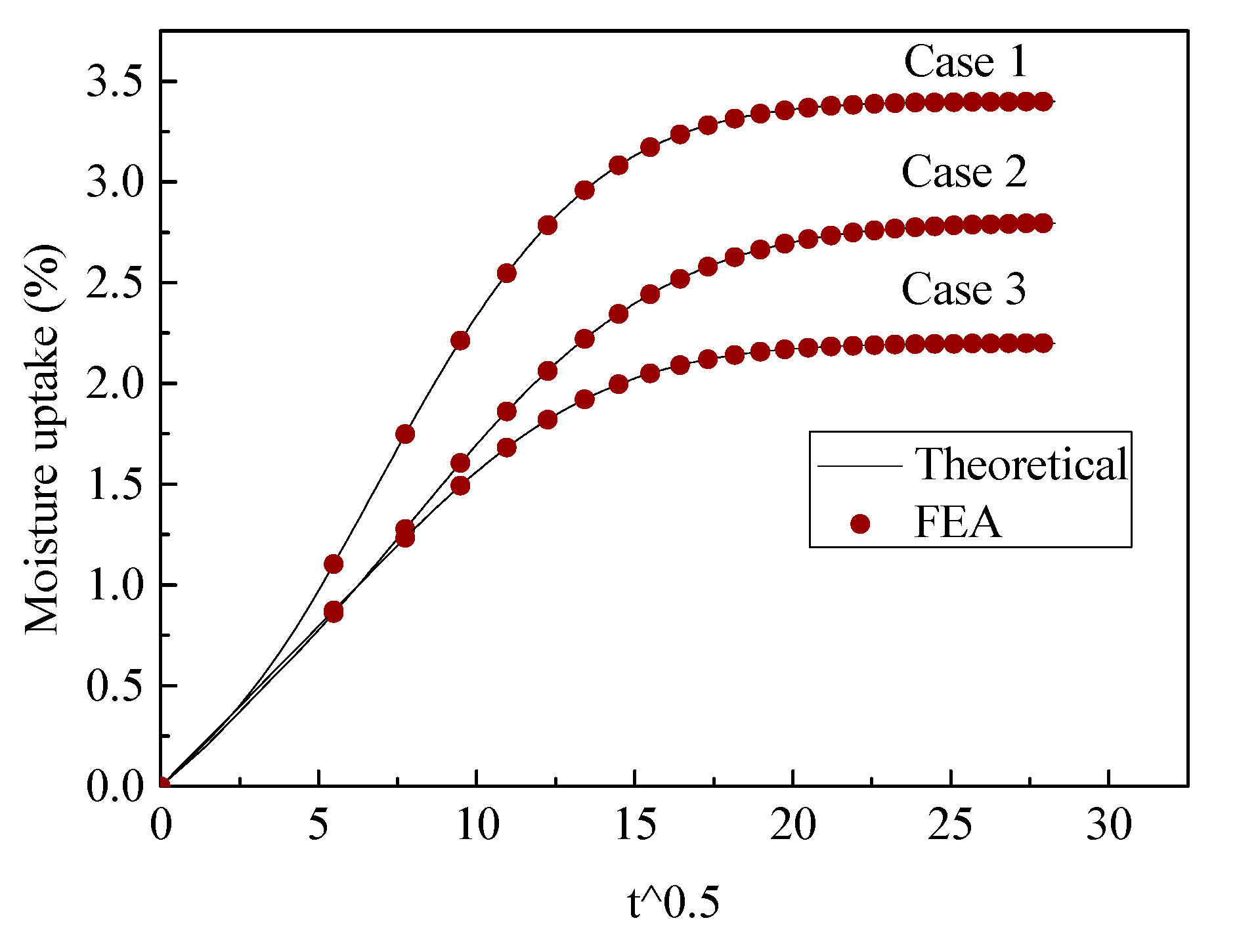
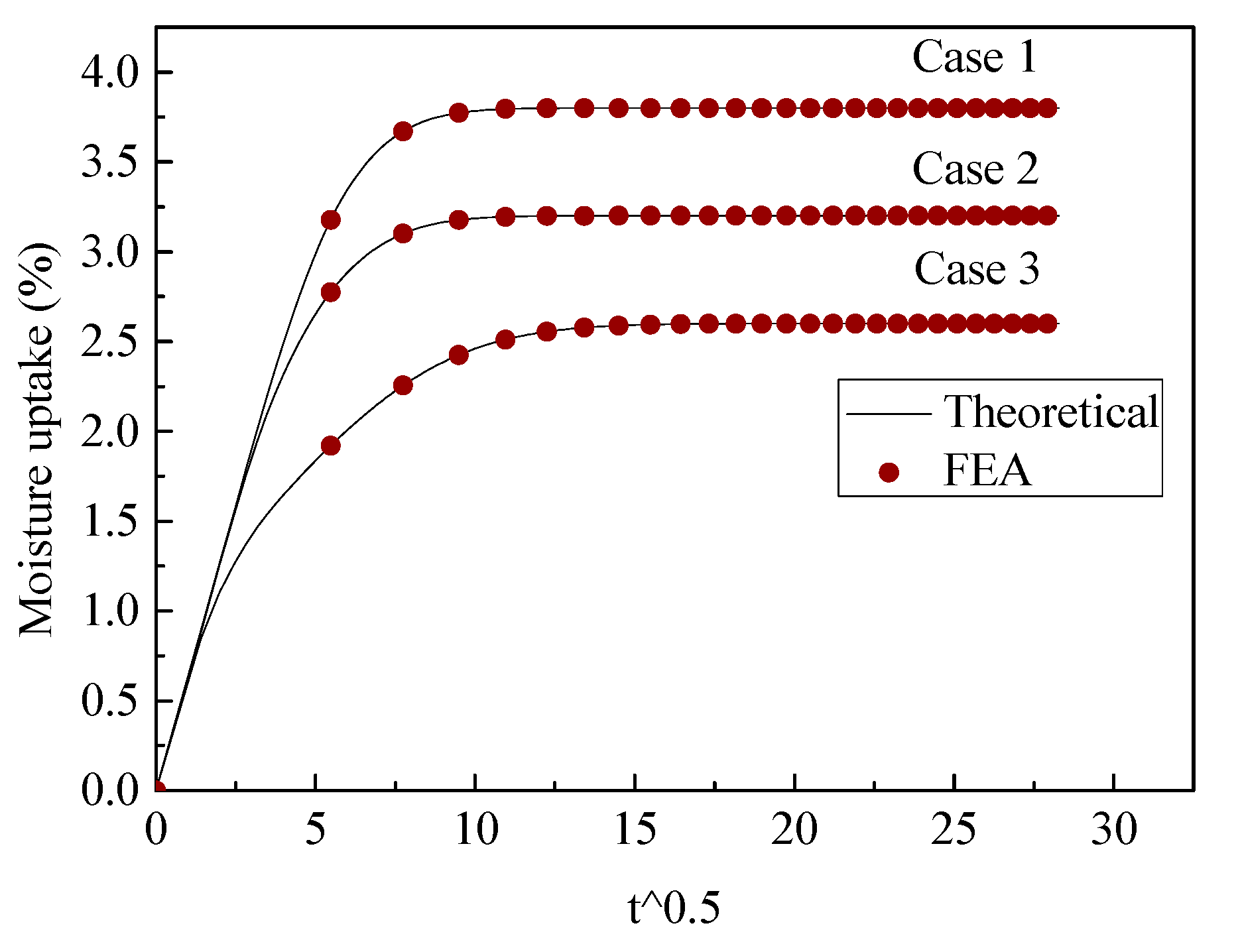
3.2.2. Moisture Uptake of the Whole Unit Cell
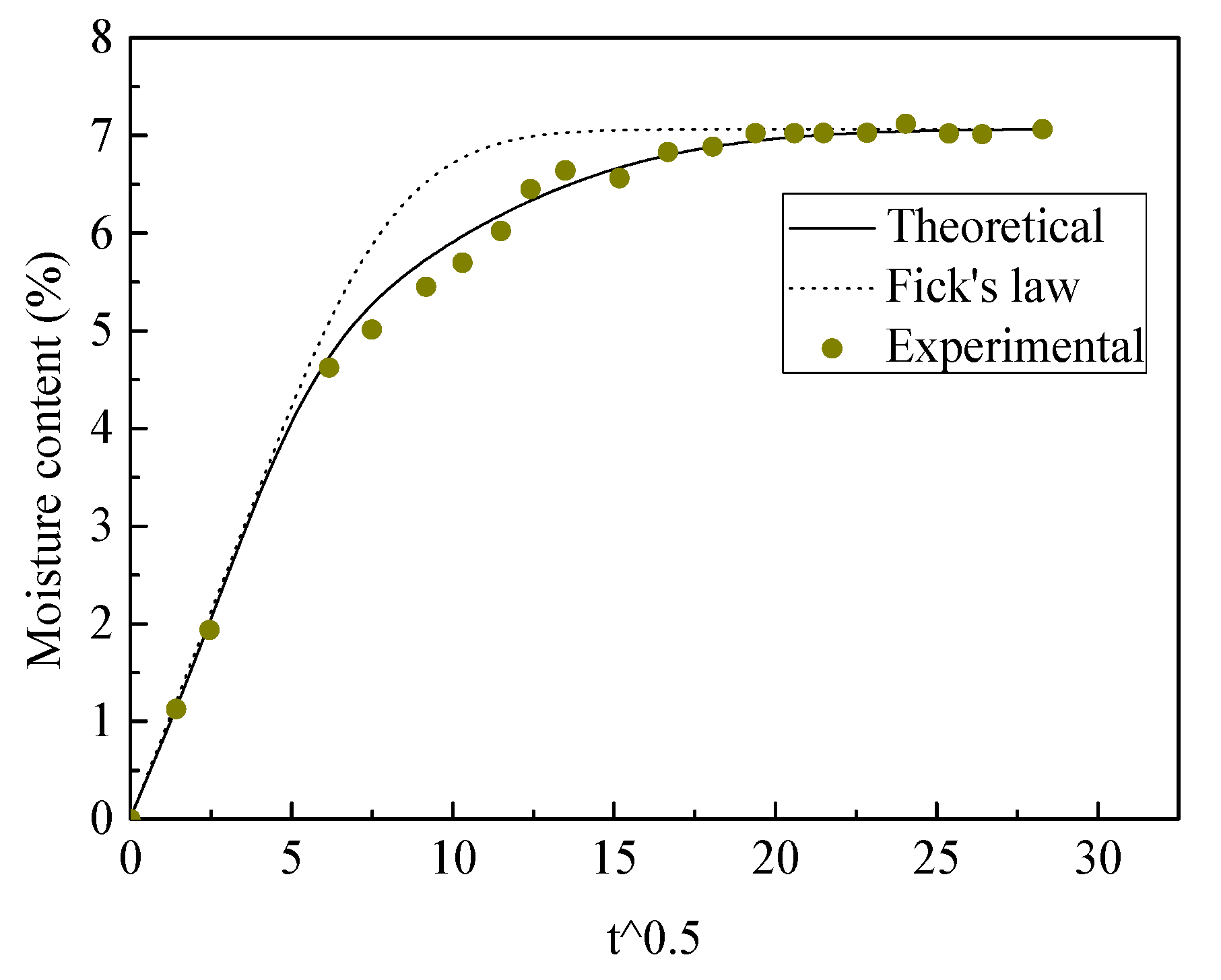
3.3. Experimental Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Junior, J.H.S.A.; Amico, S.C.; Botelho, E.; Amado, F. Hybridization effect on the mechanical properties of curaua/glass fiber composites. Compos. Part B 2013, 55, 492–497. [Google Scholar]
- Raghavendra, G.; Ojha, S.; Acharya, S.; Pal, S. Jute fiber reinforced epoxy composites and comparison with the glass and neat epoxy composites. J. Compos. Mater. 2013, 48, 2537–2547. [Google Scholar] [CrossRef]
- Silva, H.; Júnior, H.; Júnior, J.H.S.A.; Zattera, A.J.; Amico, S.C. Mechanical behavior and correlation between dynamic fragility and dynamic mechanical properties of curaua fiber composites. Polym. Compos. 2014, 35, 1078–1086. [Google Scholar] [CrossRef]
- Pickering, K.L.; Efendy, M.A.; Le, T.M. A review of recent developments in natural fibre composites and their mechanical performance. Compos. Part A Appl. Sci. Manuf. 2016, 83, 98–112. [Google Scholar] [CrossRef] [Green Version]
- Saba, N.; Jawaid, M.; Alothman, O.Y.; Paridah, M.T. A review on dynamic mechanical properties of natural fibre reinforced polymer composites. Constr. Build. Mater. 2016, 106, 149–159. [Google Scholar] [CrossRef]
- Dicker, M.P.; Duckworth, P.F.; Baker, A.B.; Francois, G.; Hazzard, M.K.; Weaver, P.M. Green composites: A review of material attributes and complementary applications. Compos. Part A Appl. Sci. Manuf. 2014, 56, 280–289. [Google Scholar] [CrossRef]
- Shahzad, A. Hemp fiber and its composites–a review. J. Compos. Mater. 2012, 46, 973–986. [Google Scholar] [CrossRef]
- Jeannin, T.; Gabrion, X.; Ramasso, E.; Placet, V. About the fatigue endurance of unidirectional flax-epoxy composite laminates. Compos. Part B Eng. 2019, 165, 690–701. [Google Scholar] [CrossRef] [Green Version]
- Aliotta, L.; Gigante, V.; Coltelli, M.B.; Cinelli, P.; Seggiani, M. Thermo-Mechanical Properties of PLA/Short Flax Fiber Biocomposites. Appl. Sci. 2019, 9, 3797. [Google Scholar] [CrossRef] [Green Version]
- Chandrasekar, M.; Ishak, M.; Sapuan, S.; Leman, Z.; Jawaid, M. A review on the characterisation of natural fibres and their composites after alkali treatment and water absorption. Plast. Rubber Compos. 2017, 46, 119–136. [Google Scholar] [CrossRef]
- Maslinda, A.; Majid, M.A.; Ridzuan, M.; Afendi, M.; Gibson, A. Effect of water absorption on the mechanical properties of hybrid interwoven cellulosic-cellulosic fibre reinforced epoxy composites. Compos. Struct. 2017, 167, 227–237. [Google Scholar] [CrossRef]
- Sepe, R.; Bollino, F.; Boccarusso, L.; Caputo, F. Influence of chemical treatments on mechanical properties of hemp fiber reinforced composites. Compos. Part B Eng. 2018, 133, 210–217. [Google Scholar] [CrossRef]
- Yan, L.; Chouw, N.; Jayaraman, K. Flax fibre and its composites–A review. Compos. Part B Eng. 2014, 56, 296–317. [Google Scholar] [CrossRef]
- Ali, A.; Shaker, K.; Nawab, Y.; Jabbar, M.; Hussain, T.; Militky, J.; Baheti, V. Hydrophobic treatment of natural fibers and their composites—A review. J. Ind. Text. 2018, 47, 2153–2183. [Google Scholar] [CrossRef]
- Kabir, M.; Wang, H.; Lau, K.; Cardona, F. Chemical treatments on plant-based natural fibre reinforced polymer composites: An overview. Compos. Part B Eng. 2012, 43, 2883–2892. [Google Scholar] [CrossRef]
- Zhou, Y.; Fan, M.; Chen, L. Interface and bonding mechanisms of plant fibre composites: An overview. Compos. Part B Eng. 2016, 101, 31–45. [Google Scholar] [CrossRef] [Green Version]
- Ghasemzadeh-Barvarz, M.; Duchesne, C.; Rodrigue, D. Mechanical, Water absorption, and aging properties of polypropylene/flax/glass fiber hybrid composites. J. Compos. Mater. 2015, 49, 3781–3798. [Google Scholar] [CrossRef]
- Cherif, Z.; Poilâne, C.; Vivet, A.; Doudou, B.B.; Chen, J. About optimal architecture of plant fibre textile composite for mechanical and sorption properties. Compos. Struct. 2016, 140, 240–251. [Google Scholar] [CrossRef]
- Bao, L.-R.; Yee, A.F. Moisture diffusion and hygrothermal aging in bismaleimide matrix carbon fiber composites: Part II—woven and hybrid composites. Compos. Sci. Technol. 2002, 62, 2111–2119. [Google Scholar] [CrossRef]
- Chilali, A.; Zouari, W.; Assarar, M.; Kebir, H.; Ayad, R. Effect of water ageing on the load-unload cyclic behaviour of flax fibre-reinforced thermoplastic and thermosetting composites. Compos. Struct. 2018, 183, 309–319. [Google Scholar] [CrossRef]
- Sanjay, M.; Madhu, P.; Jawaid, M.; Senthamaraikannan, P.; Senthil, S.; Pradeep, S. Characterization and properties of natural fiber polymer composites: A comprehensive review. J. Clean. Prod. 2018, 172, 566–581. [Google Scholar] [CrossRef]
- Li, Y.; Xue, B. Hydrothermal ageing mechanisms of unidirectional flax fabric reinforced epoxy composites. Polym. Degrad. Stab. 2016, 126, 144–158. [Google Scholar] [CrossRef]
- Saidane, E.H.; Scida, D.; Assarar, M.; Ayad, R. Assessment of 3D moisture diffusion parameters on flax/epoxy composites. Compos. Part A 2016, 80, 53–60. [Google Scholar] [CrossRef]
- Almeida, J.; Souza, S.; Botelho, E.C.; Amico, S.C. Carbon fiber-reinforced epoxy filament-wound composite laminates exposed to hygrothermal conditioning. J. Mater. Sci. 2016, 51, 4697–4708. [Google Scholar] [CrossRef] [Green Version]
- Perrier, A.; Touchard, F.; Chocinski-Arnault, L.; Mellier, D. Quantitative analysis by micro-CT of damage during tensile test in a woven hemp/epoxy composite after water ageing. Compos. Part A Appl. Sci. Manuf. 2017, 102, 18–27. [Google Scholar] [CrossRef]
- Tang, X.; Whitcomb, J.D.; Li, Y.; Sue, H.-J. Micromechanics modeling of moisture diffusion in woven composites. Compos. Sci. Technol. 2005, 65, 817–826. [Google Scholar] [CrossRef]
- Eggers, F.; Jr, J.; Lisba, T.V.; Amico, S.C. Creep and Residual Properties of Filament-Wound Composite Rings under Radial Compression in Harsh Environments. Polymers 2020, 13, 33. [Google Scholar] [CrossRef]
- Yu, H.; Zhou, C. Sandwich diffusion model for moisture absorption of flax/glass fiber reinforced hybrid composite. Compos. Struct. 2017, 188, 1–6. [Google Scholar] [CrossRef]
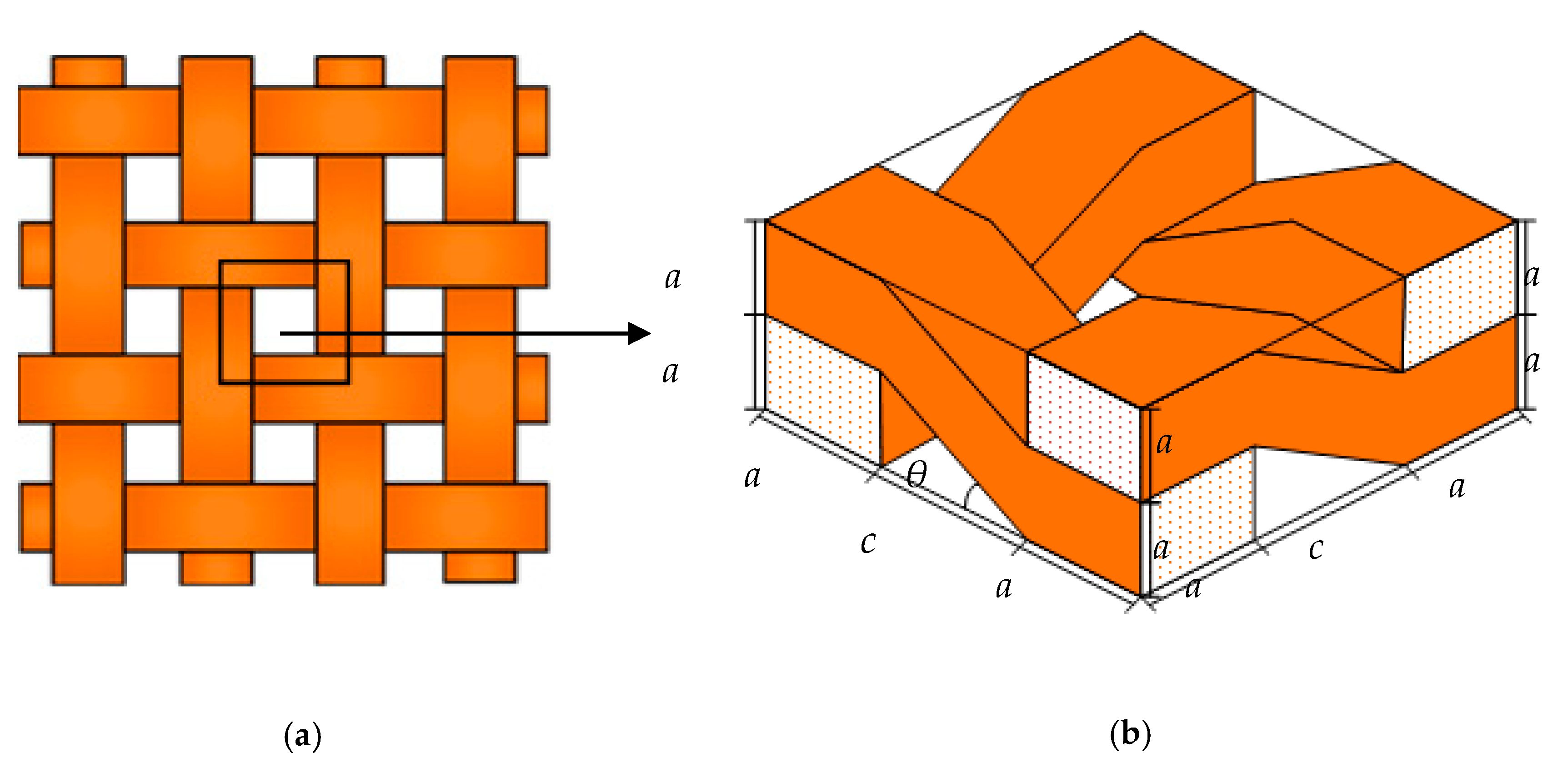
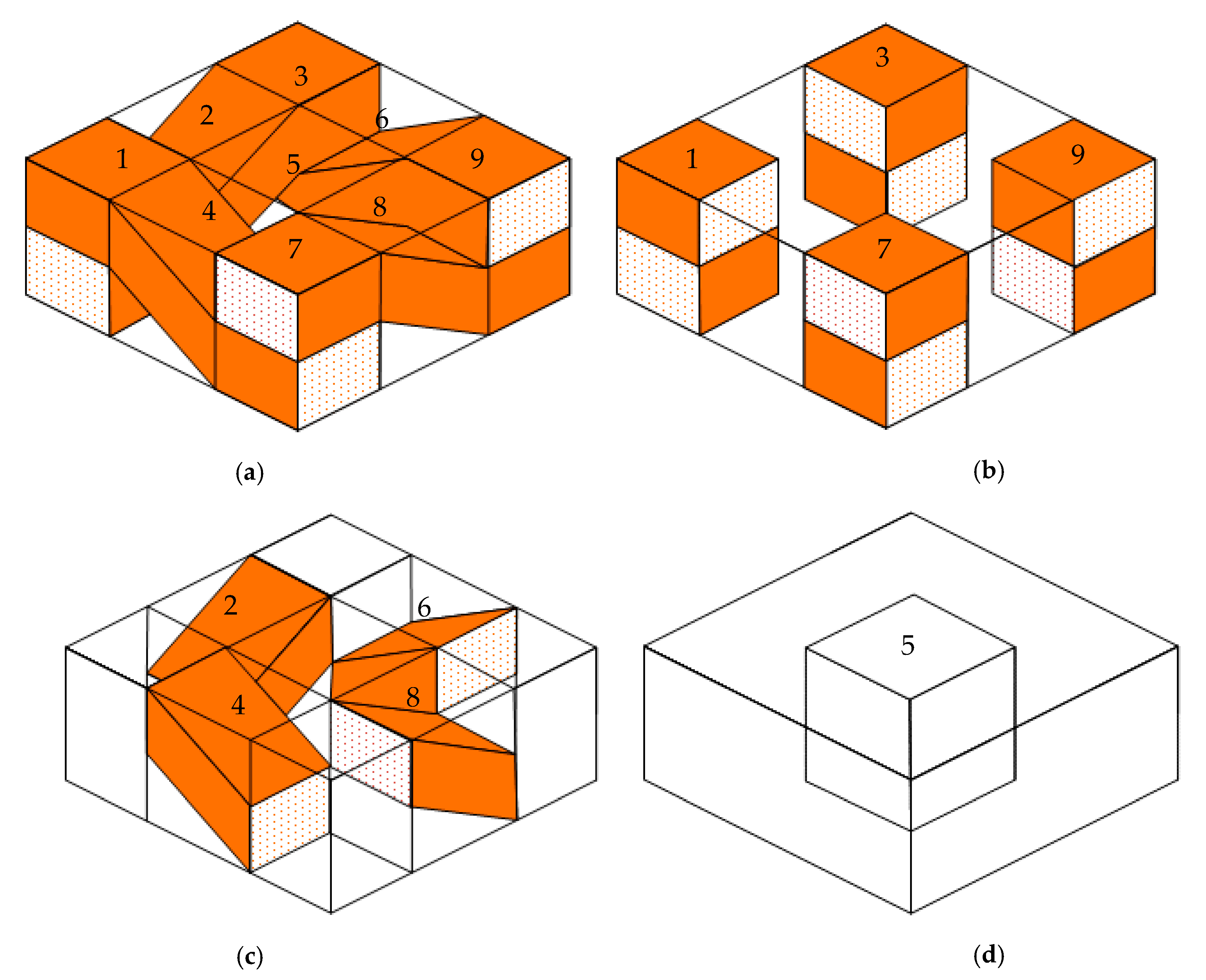
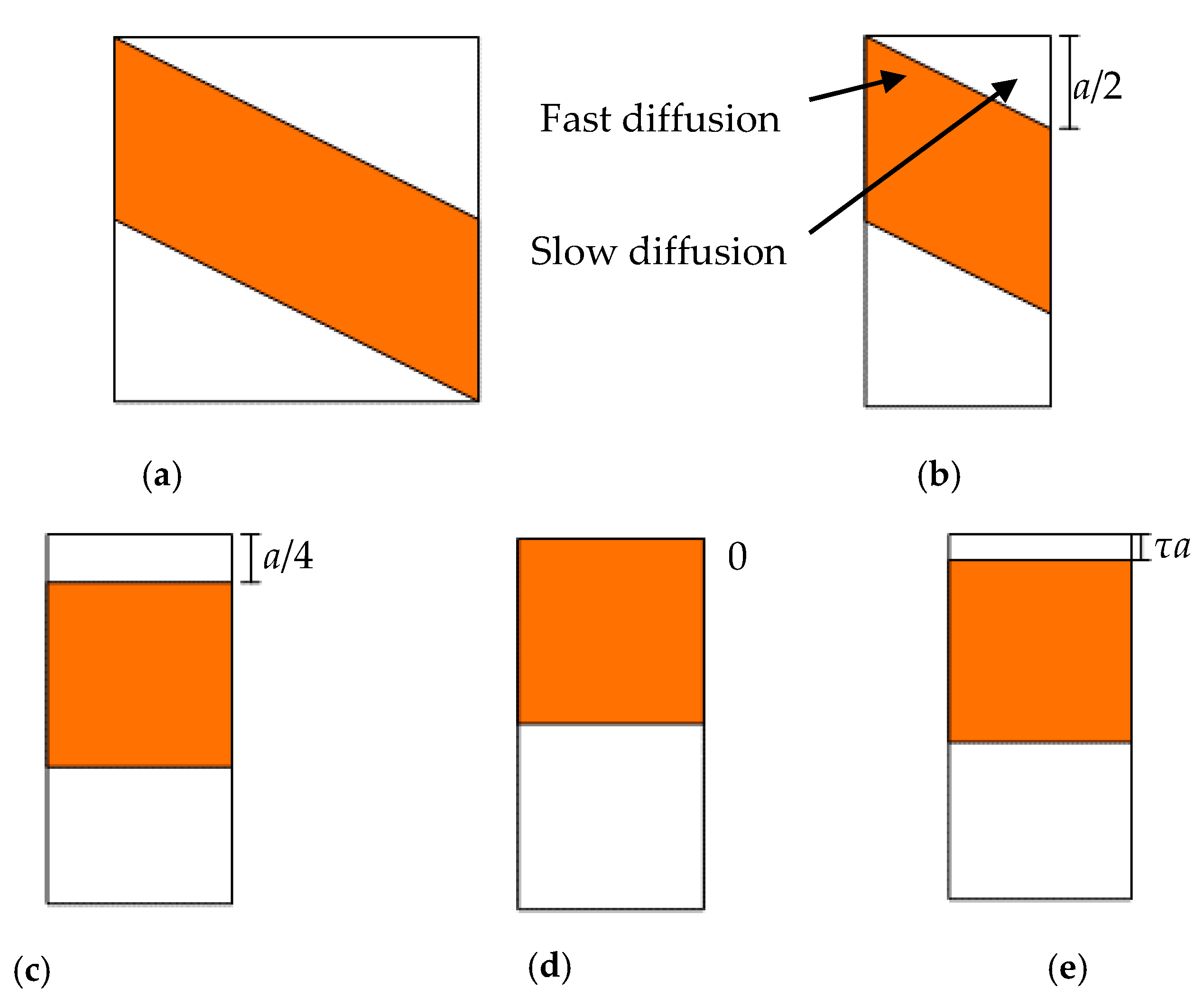
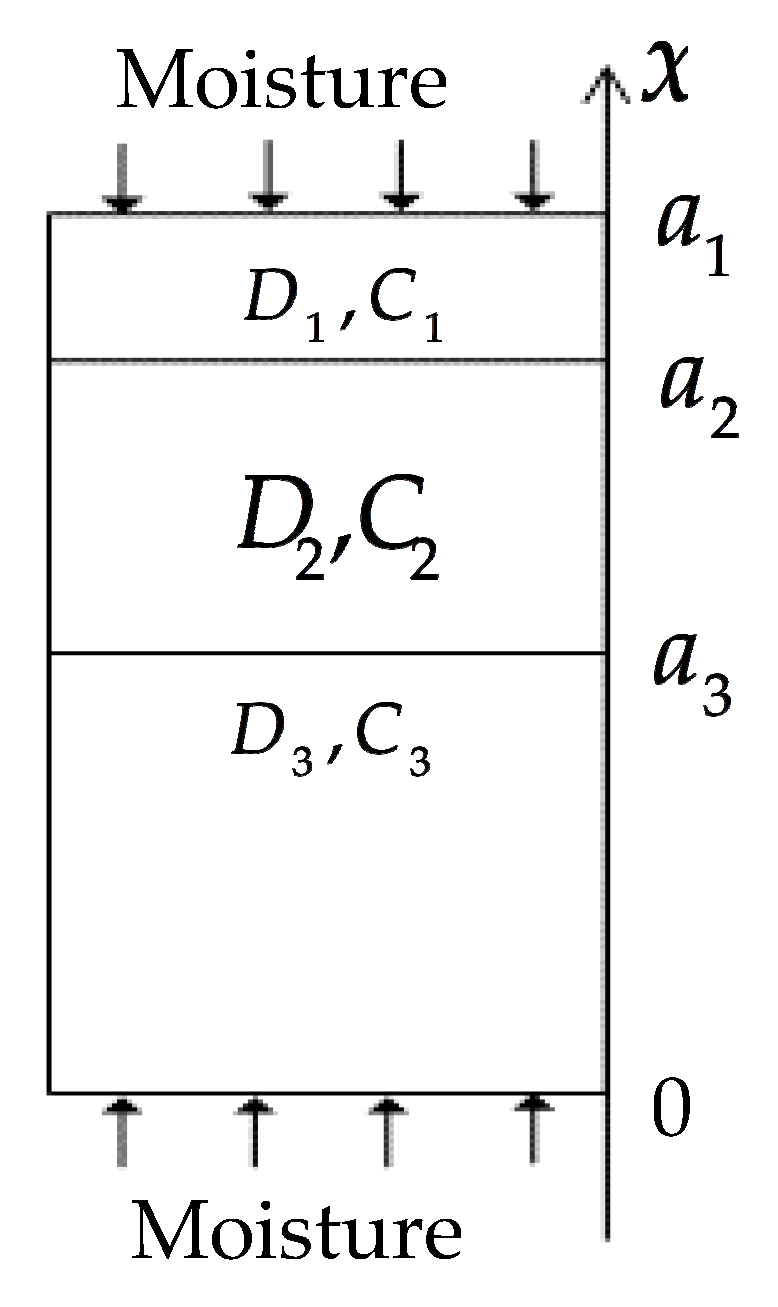



| Dimension | a (mm) | b (mm) | c (mm) | d (mm) |
|---|---|---|---|---|
| Plain a | 0.852 | 1.514 | 1.926 | 1.926 |
| Plain b | 0.852 | 1.514 | 2.628 | 2.628 |
| Case | a1–a2 | a2–a3 | a3 |
|---|---|---|---|
| 1 | 0.2 | 1.4 | 0.4 |
| 2 | 0.6 | 0.8 | 0.6 |
| 3 | 1 | 0.2 | 0.8 |
| Case | a | b | c |
|---|---|---|---|
| 1 | 1 | 3 | 2 |
| 2 | 1 | 3 | 1 |
| 3 | 0.5 | 3 | 2 |
| Parameters | |||||
|---|---|---|---|---|---|
| Composite | 0.0216 | 0.0165 | 0.0045 | 8.6 | 1.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Yang, J. Predictions of Moisture Diffusion Behavior of Cellulose-Fiber-Reinforced Plain Weave Epoxy Composites. Polymers 2021, 13, 2347. https://doi.org/10.3390/polym13142347
Yu H, Yang J. Predictions of Moisture Diffusion Behavior of Cellulose-Fiber-Reinforced Plain Weave Epoxy Composites. Polymers. 2021; 13(14):2347. https://doi.org/10.3390/polym13142347
Chicago/Turabian StyleYu, Hang, and Jie Yang. 2021. "Predictions of Moisture Diffusion Behavior of Cellulose-Fiber-Reinforced Plain Weave Epoxy Composites" Polymers 13, no. 14: 2347. https://doi.org/10.3390/polym13142347
APA StyleYu, H., & Yang, J. (2021). Predictions of Moisture Diffusion Behavior of Cellulose-Fiber-Reinforced Plain Weave Epoxy Composites. Polymers, 13(14), 2347. https://doi.org/10.3390/polym13142347







