Prediction of Residual Curing Capacity of Melamine-Formaldehyde Resins at an Early Stage of Synthesis by In-Line FTIR Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Resin Preparation
2.3. Experimental Design
2.4. Differential Scanning Calorimetry (DSC)
2.5. Inline Infrared Spectroscopic Analysis
2.6. Multivariate Data Analysis
3. Results and Discussion
3.1. Spectral Time Course of MF Resin Synthesis and Infrared Band Assignment
3.2. Process Trajectories of MF Resin Synthesis
3.2.1. Time Course of Entire MF Resin Synthesis
3.2.2. Time Course of the Condensation Reaction in Homogenous Medium (Phase 3 of MF Resin Synthesis)
3.3. Predicting Residual Curing Capacity of MF Resin Using PLS-Regression
3.3.1. PLS-Regression in the Spectral Range from 1750 to 750 cm−1
3.3.2. PLS-Regression Using a Reduced Data Set and Concept for a Low-Cost Process Spectrometer
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rätzsch, M.; Bucka, H.; Ivanchev, S.; Pavlyuchenko, V.; Leitner, P.; Primachenko, O.N. The reaction mechanism of the transetherification and crosslinking of melamine resins. Macromol. Symp. 2004, 217, 431–443. [Google Scholar] [CrossRef]
- Chai, Y.; Zhao, Y.; Yan, N. Synthesis and characterization of biobased melamine formaldehyde resins from bark extractives. Ind. Eng. Chem. Res. 2014, 53, 11228–11238. [Google Scholar] [CrossRef]
- Kohlmayr, M.; Eder, F.; Hölbling, B.; Muralt, S.; Kandelbauer, A. Direkt beschichtete abriebfeste Aminoplast-Oberflächen. Holztechnologie 2010, 51, 30–35. [Google Scholar]
- Kandelbauer, A.; Petek, P.; Medved, S.; Pizzi, A.; Teischinger, A. On the performance of a melamine-urea-formaldehyde resin for decorative paper coatings. Eur. J. Wood Wood Prod. 2010, 68, 63–75. [Google Scholar] [CrossRef]
- Pizzi, A.; Mittal, K.L. Handbook of Adhesive Technology, 2nd ed.; Marcel Dekker: New York, NY, USA, 2003; ISBN 0824709861. [Google Scholar]
- Dunky, M.; Niemz, P. Holzwerkstoffe und Leime; Teil 2.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Becker, G.W.; Braun, D.; Woebcken, W. Duroplaste-Kunststoff Handbuch 10; Carl Hanser Verlag: München, Germany, 2006; ISBN 3446220178. [Google Scholar]
- Gordon, M.; Halliwell, A.; Wilson, T. Kinetics of the addition stage in the melamine–formaldehyde reaction. J. Appl. Polym. Sci. 1966, 10, 1153–1170. [Google Scholar] [CrossRef]
- Sato, K.; Naito, T. Studies on melamine resin. VII. Kinetics of the acid-catalyzed condensation of Di- and trimethylolmelamine. Polym. J. 1973, 5, 144–157. [Google Scholar] [CrossRef][Green Version]
- Tomita, B. Melamine-formaldehyde resins: Molecular species distributions of methylolmelamines and some kinetics of methylolation. J. Polym. Sci. 1977, 15, 2347–2365. [Google Scholar] [CrossRef]
- Lavrič, S.; Kočar, D.; Mihelič, I.; Braybrook, C. Accurate mass determination of melamine-formaldehyde synthetic polymers after separation on preparative HPLC. Prog. Org. Coat. 2015, 81, 27–34. [Google Scholar] [CrossRef]
- Kandelbauer, A.; Wuzella, G.; Mahendran, A.; Taudes, I.; Widsten, P. Model-free kinetic analysis of melamine-formaldehyde resin cure. Chem. Eng. J. 2009, 152, 556–565. [Google Scholar] [CrossRef]
- Ogata, Y.; Okano, M. Kinetics of the condensation of melamine with formaldehyde. J. Am. Chem. Soc. 1951, 72, 1459–1461. [Google Scholar] [CrossRef]
- Nastke, R.; Dietrich, K.; Reinisch, G.; Rafler, G.; Gajewski, H. The initial stage of the reaction of melamine with formaldehyde. J. Macromol. Sci. Part A Chem. Pure Appl. Chem. 1986, 23, 579–596. [Google Scholar] [CrossRef]
- Kumar, A.; Katiyar, V. Modeling and experimental investigation of melamine–formaldehyde polymerization. Macromolecules 1990, 23, 3729–3736. [Google Scholar] [CrossRef]
- Mijatovic, J.; Binder, W.H.; Kubel, F.; Kantner, W. Studies on the stability of MF resin solutions: Investigations on network formation. Macromol. Symp. 2002, 181, 373–382. [Google Scholar] [CrossRef]
- Kessler, R.W. Process analytics in science and industry. Anal. Bioanal. Chem. 2017, 409, 629–630. [Google Scholar] [CrossRef] [PubMed]
- Rathore, A.S.; Bhambure, R.; Ghare, V. Process analytical technology (PAT) for biopharmaceutical products. Anal. Bioanal. Chem. 2010, 398, 137–154. [Google Scholar] [CrossRef] [PubMed]
- Kohlmayr, M.; Stultschnik, J.; Teischinger, A.; Kandelbauer, A. Drying and curing behaviour of melamine formaldehyde resin impregnated papers. J. Appl. Polym. Sci. 2014, 131, 39860. [Google Scholar] [CrossRef]
- Weiss, S.; Seidl, R.; Kessler, W.; Kessler, R.W.; Zikulnig-Rusch, E.M.; Kandelbauer, A. Multivariate process trajectories for molecular description of MF thermal curing and correlation with hydrolytic stability. J. Appl. Polym. Sci. 2021, 12. [Google Scholar] [CrossRef]
- Weiss, S.; Seidl, R.; Kessler, W.; Kessler, R.W.; Zikulnig-Rusch, E.M.; Kandelbauer, A. Unravelling the phases of melamine formaldehyde resin cure by infrared spectroscopy (FTIR) and multivariate curve resolution (MCR). Polymers 2020, 12, 2569. [Google Scholar] [CrossRef]
- Weiss, S.; Seidl, R.; Kessler, W.; Kessler, R.W.; Zikulnig-Rusch, E.M.; Kandelbauer, A. Multivariate curve resolution (MCR) of real-time infrared spectra for analyzing the curing behavior of solid MF thermosetting resin. Int. J. Adhes. Adhes. 2021, 110, 102956. [Google Scholar] [CrossRef]
- Seidl, R.; Weiss, S.; Zikulnig-Rusch, E.M.; Kandelbauer, A. Response surface optimization for improving the processing behaviour of melamine formaldehyde impregnation resins. J. Appl. Polym. Sci. 2021, 138, 1–17. [Google Scholar] [CrossRef]
- Box, G.E.P.; Hunter, J.S.; Hunter, W.G. Statistics for Experimenters, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005; ISBN 9780471718130. [Google Scholar]
- Kessler, W. Multivariate Datenanalyse; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2007; ISBN 9783527312627. [Google Scholar]
- Basilevsky, A. Statistical Factor Analysis and Related Methods; John Wiley & Sons: New York, NY, USA, 1997; ISBN 9780471570820. [Google Scholar]
- Esposito Vinzi, V.; Chin, W.W.; Henseler, J.; Wang, H. Handbook of Partial Least Squares; Springer: New York, NY, USA, 2011; ISBN 9783540328254. [Google Scholar]
- Weiss, S.; Urdl, K.; Mayer, H.A.; Zikulnig-Rusch, E.M.; Kandelbauer, A. IR spectroscopy: Suitable method for determination of curing degree and crosslinking type in melamine–formaldehyde resins. J. Appl. Polym. Sci. 2019, 136, 47691. [Google Scholar] [CrossRef]
- Socrates, G. Infrared and Raman Characteristic Group Frequencies, 3rd ed.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2001; ISBN 978-0-470-09307-8. [Google Scholar]
- Gottwald, W.; Wachter, G. IR-Spektroskopie für Anwender; Wiley-VCH Verlag: Weinheim, Germany, 1997; ISBN 978-3-527-28749-9. [Google Scholar]
- Bogomolov, A. Multivariate process trajectories: Capture, resolution and analysis. Chemom. Intell. Lab. Syst. 2011, 108, 49–63. [Google Scholar] [CrossRef]
- Scheepers, M.L.; Adriaensens, P.J.; Gelan, J.M.; Carleer, R.A.; Vanderzande, D.J.; De Vries, N.K.; Brandts, P.M. Demonstration of methylene-ether bridge formation in melamine-formaldehyde resins. J. Polym. Sci. Part A Polym. Chem. 1995, 33, 915–920. [Google Scholar] [CrossRef]
- Mircescu, N.E.; Oltean, M.; Chis, V.; Leopold, N. FTIR, FT-Raman, SERS and DFT study on melamine. Vib. Spectrosc. 2012, 62, 165–171. [Google Scholar] [CrossRef]
- Luisi, M. Characterizing the Measurement Uncertainty of a High-Temperature Heat Flux Differential Scanning Calorimeter. Ph.D. Thesis, Graz University of Technology, Graz, Austria, 2014. [Google Scholar]
- Gatta, G.D.; Richardson, M.J.; Sarge, S.M.; Stolen, S. Standards, calibration, and guidelines in microcalorimetry. Part 2. Calibration for differential scanning calorimetry (IUPAC Technical Report). Pure Appl. Chem. 2006, 78, 1455–1476. [Google Scholar] [CrossRef]
- Dekking, F.M.; Kraaikamp, C.; Lopuhaä, H.P.; Meester, L.E. A Modern Introduction to Probability and Statistics; Springer: London, UK, 2005; ISBN 9788578110796. [Google Scholar]
- Steinbach, J.C.; Schneider, M.; Hauler, O.; Lorenz, G.; Rebner, K.; Kandelbauer, A. A process analytical concept for in-line FTIR monitoring of polysiloxane formation. Polymers 2020, 12, 2473. [Google Scholar] [CrossRef]


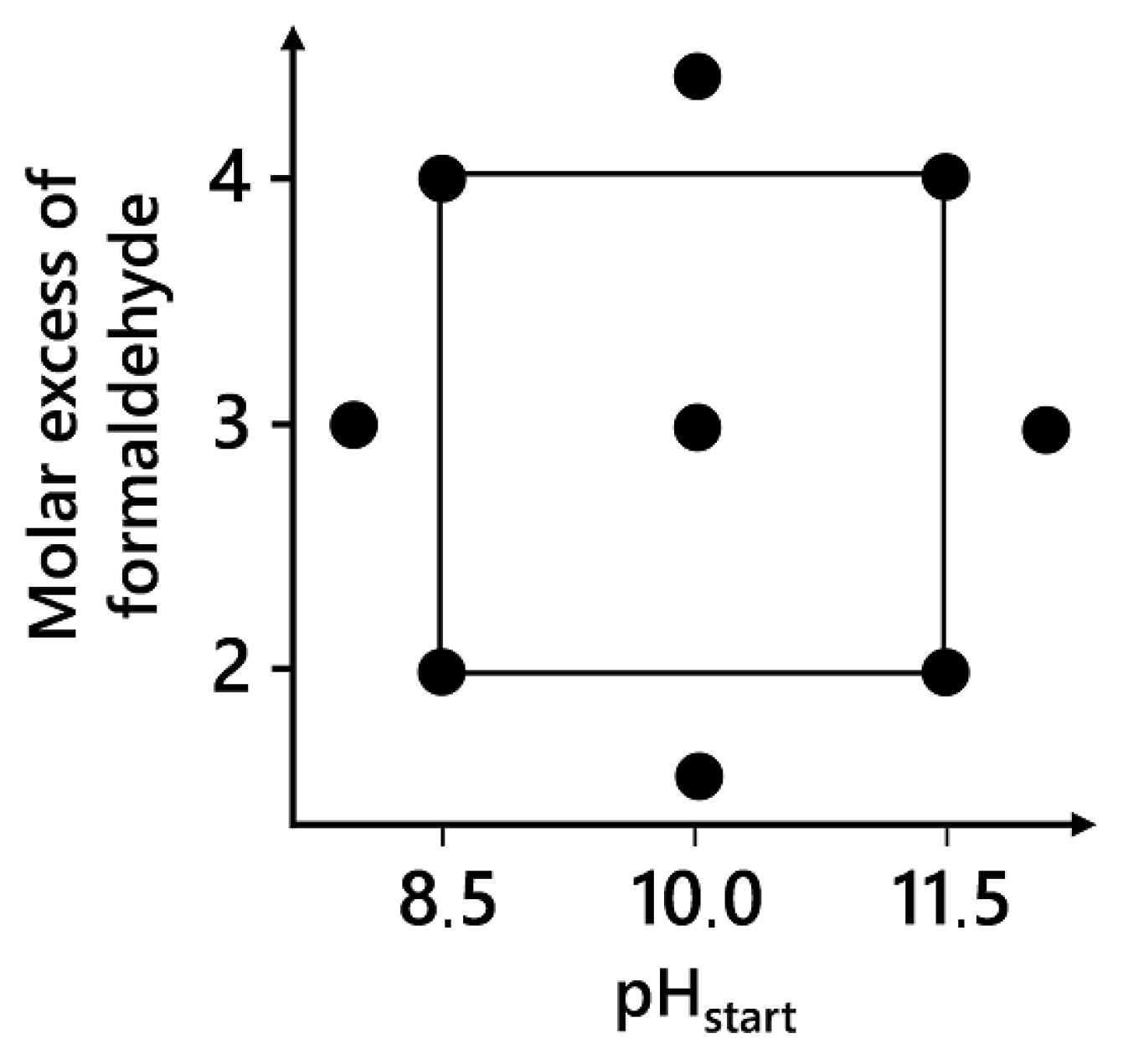
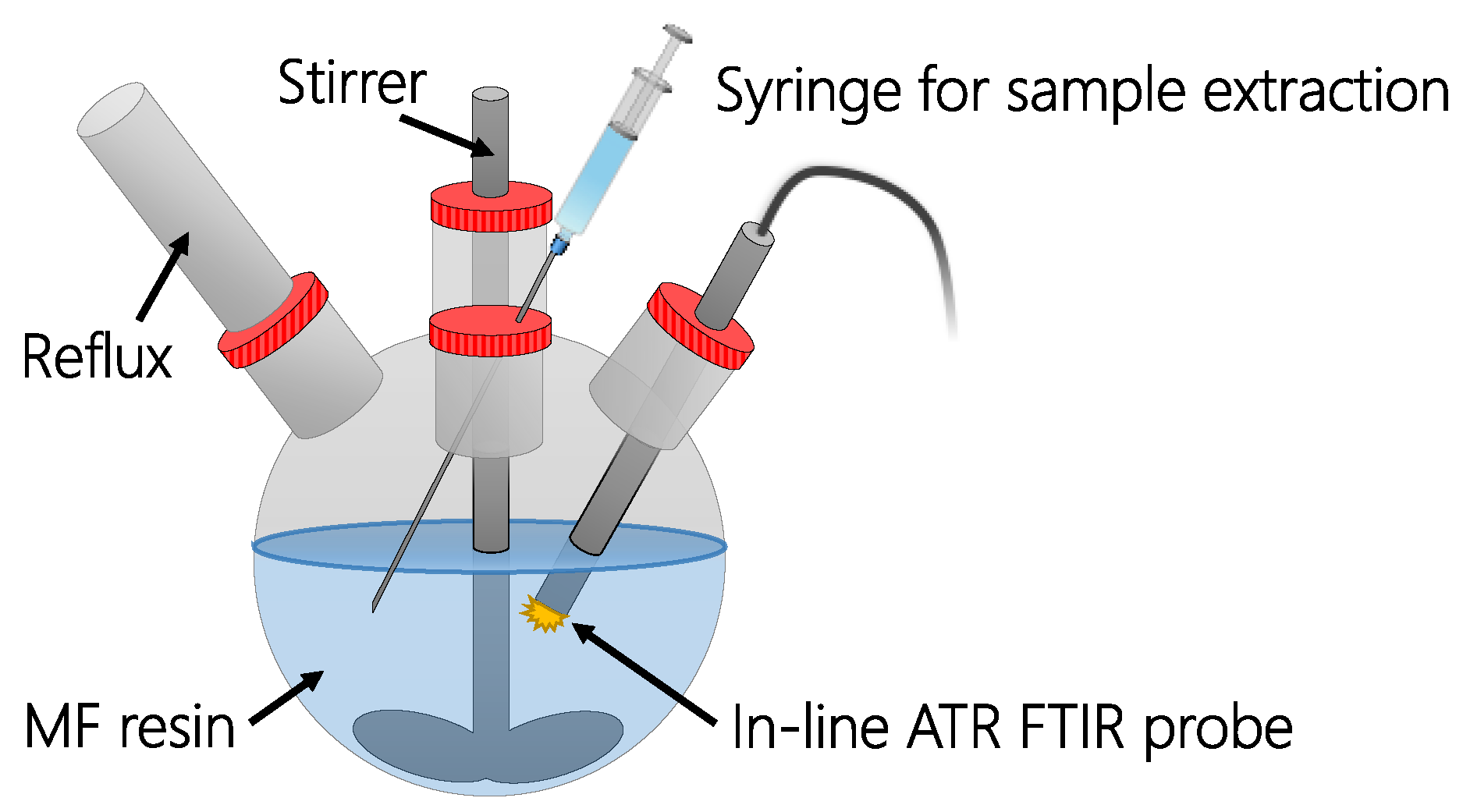


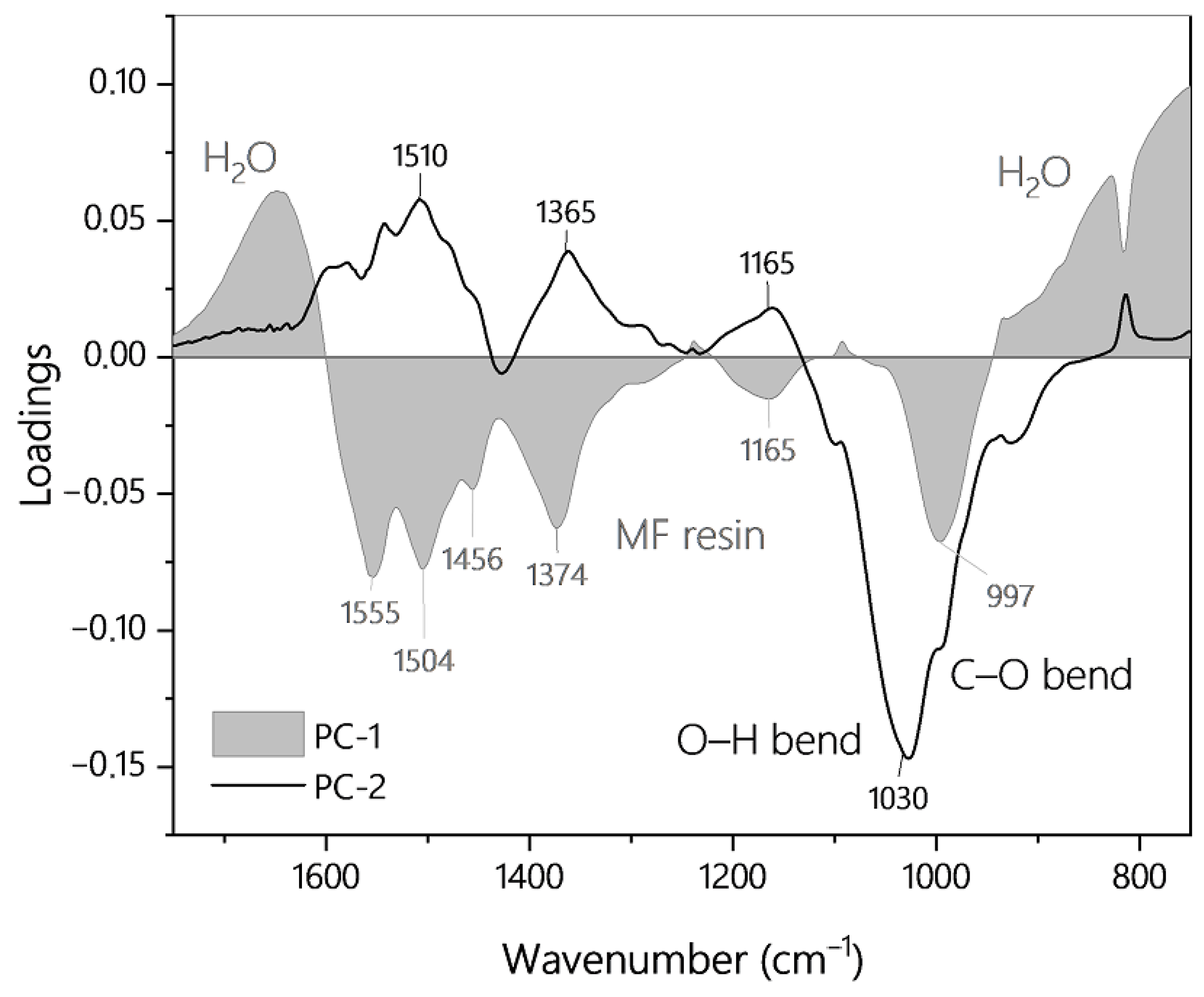

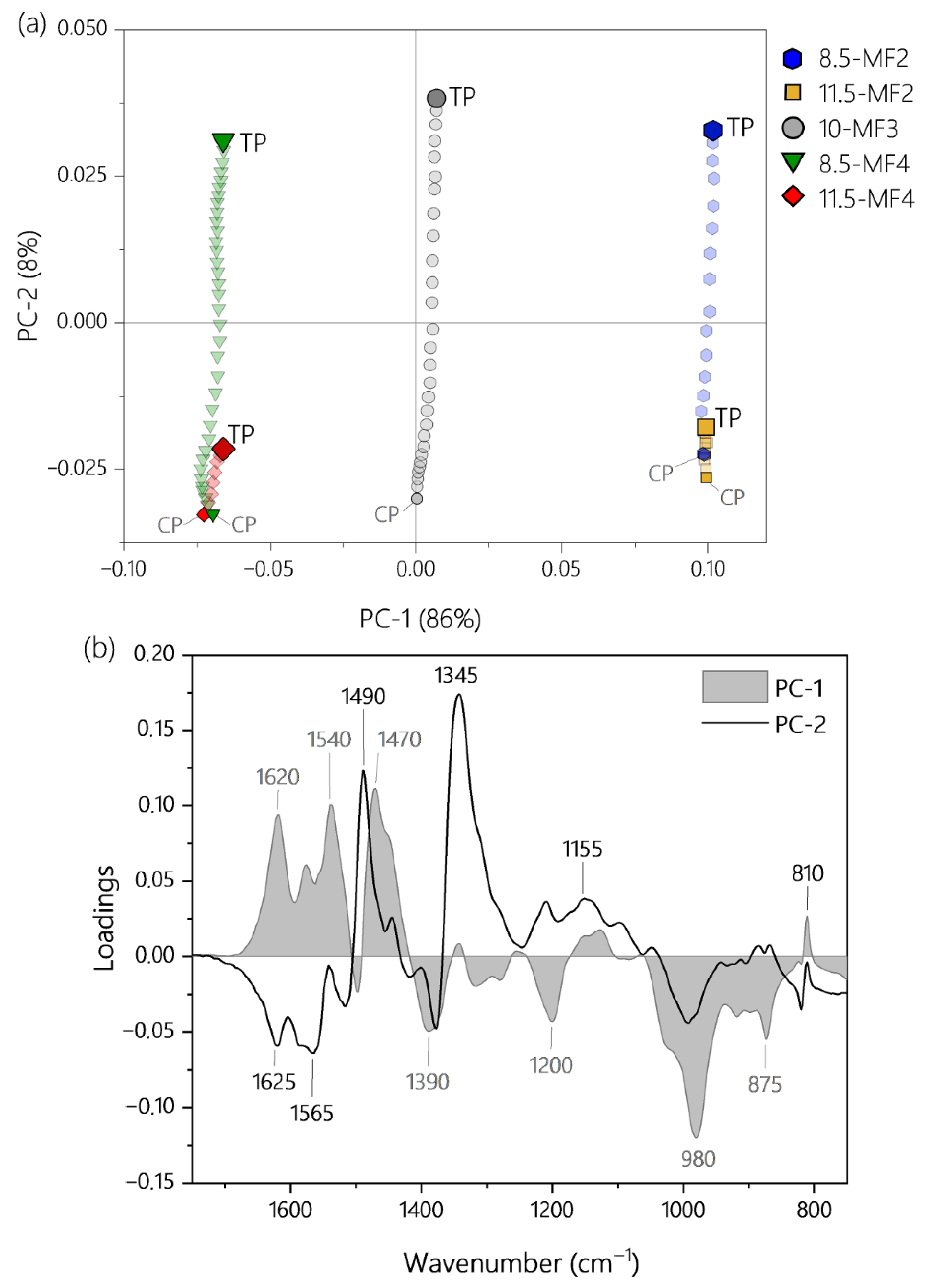


| Resin | Factors | Response | Use in PLS Model | |
|---|---|---|---|---|
| pHstart | M:F Ratio | Enthalpy H (J/g) | ||
| 8.5-MF2 | 8.5 | 1:2.0 | 62.56 | cal |
| 11.5-MF2 | 11.5 | 1:2.0 | 74.01 | cal |
| 8.5-MF4 | 8.5 | 1:4.0 | 37.41 | cal |
| 11.5-MF4 | 11.5 | 1:4.0 | 42.15 | cal |
| 7.9-MF3 | 7.9 | 1:3.0 | 42.65 | cal |
| 12.1-MF3 | 12.1 | 1:3.0 | 68.30 | cal |
| 10-MF1.5 | 10.0 | 1:1.5 | 82.97 | cal |
| 10-MF4.5 | 10.0 | 1:4.5 | 47.37 | cal |
| 10-MF3 a | 10.0 | 1:3.0 | 50.16 | val |
| 10-MF3 b | 10.0 | 1:3.0 | 49.39 | val |
| 10-MF3 c | 10.0 | 1:3.0 | 43.62 | val |
| 10-MF3 d | 10.0 | 1:3.0 | 61.08 | val |
| 10-MF3 avg | 10.0 | 1:3.0 | 51.06 | cal |
| y Reference (Enthalpy H) | y Predicted (Spectral Information) | |
|---|---|---|
| Mean value | 51.06 | 48.34 |
| SD | 6.31 | 0.80 |
| SE | 3.16 | 0.40 |
| Stage of Synthesis Used | Model Based On | Wavenumbers (cm−1) | R2cal | RMSEC |
|---|---|---|---|---|
| TP | Entire spectral range | 1750–750 | 0.89 | 4.98 |
| TP | 6 single wavenumbers | 1620, 1540, 1390, 1160, 1050, 985 | 0.92 | 4.20 |
| TP | 3 single wavenumbers | 1620, 1540, 985 | 0.82 | 6.86 |
| CP | Entire spectral range | 1750–750 | 0.85 | 5.87 |
| CP | 6 single wavenumbers | 1620, 1540, 1390, 1160, 1050, 985 | 0.85 | 5.77 |
| CP | 3 single wavenumbers | 1620, 1540, 985 | 0.90 | 5.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seidl, R.; Weiss, S.; Kessler, R.W.; Kessler, W.; Zikulnig-Rusch, E.M.; Kandelbauer, A. Prediction of Residual Curing Capacity of Melamine-Formaldehyde Resins at an Early Stage of Synthesis by In-Line FTIR Spectroscopy. Polymers 2021, 13, 2541. https://doi.org/10.3390/polym13152541
Seidl R, Weiss S, Kessler RW, Kessler W, Zikulnig-Rusch EM, Kandelbauer A. Prediction of Residual Curing Capacity of Melamine-Formaldehyde Resins at an Early Stage of Synthesis by In-Line FTIR Spectroscopy. Polymers. 2021; 13(15):2541. https://doi.org/10.3390/polym13152541
Chicago/Turabian StyleSeidl, Regina, Stephanie Weiss, Rudolf W. Kessler, Waltraud Kessler, Edith M. Zikulnig-Rusch, and Andreas Kandelbauer. 2021. "Prediction of Residual Curing Capacity of Melamine-Formaldehyde Resins at an Early Stage of Synthesis by In-Line FTIR Spectroscopy" Polymers 13, no. 15: 2541. https://doi.org/10.3390/polym13152541
APA StyleSeidl, R., Weiss, S., Kessler, R. W., Kessler, W., Zikulnig-Rusch, E. M., & Kandelbauer, A. (2021). Prediction of Residual Curing Capacity of Melamine-Formaldehyde Resins at an Early Stage of Synthesis by In-Line FTIR Spectroscopy. Polymers, 13(15), 2541. https://doi.org/10.3390/polym13152541








