Optimization of a Totally Fiber-Reinforced Plastic Composite Sandwich Construction of Helicopter Floor for Weight Saving, Fuel Saving and Higher Safety
Abstract
:1. Introduction
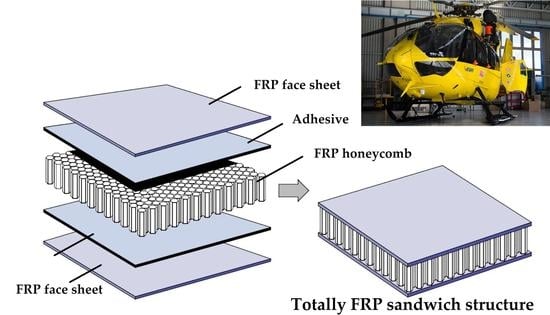
- FRP sandwich structures are some of the most widely applied structural elements in engineering applications. FRP sandwich structures are built from FRP face sheets (e.g., laminated plates) and core materials (e.g., honeycomb, foam). These structures provide a high strength and stiffness, easy assembly, and excellent tailorability [24,25,26].
- Many relevant publications are available on the design and optimization procedures of composite sandwich structures to construct optimal structures that provide a high stiffness and strength, in addition to a low weight and cost [27,28,29]. Heimbs et al. found that the mechanical behavior of the sandwich construction consists of a folded core made of carbon fiber-reinforced plastic; furthermore, they discussed the development of the folded core models in the LS-DYNA FE software. The validation of models was performed by optimizing the LS-OPT software concerning core manufacturer experimental data [30,31]. Bisagni et al. elaborated an optimization method under crashworthiness conditions for a typical helicopter subfloor made of aluminum alloy [32]. Adel and Steven minimized the single-objective function and multi-objective functions for foam sandwich plates with hybrid composite face sheets subjected to bending and torsional stiffness constraints [33].
- Some articles discussed experimental and computational analysis to assess foam-formed materials’ sound insulation capabilities and applied the gray relational analysis method and multi-objective particle swarm optimization algorithm to develop the acoustic performances of foam composites [34,35,36]. Khan et al. described the improvement models of the smallest cell for quantifying the deformation and failure modes for a core structure under static loadings [37].
- Different techniques and methods have been introduced in the literature to solve optimization problems in various composite structures [38,39,40,41]. Furthermore, many software applications (e.g., Matlab, Abaqus) have become common for structural optimization. The finite element software applications are often used to numerically solve differential equations during structural analysis [42,43,44]. Khalkhali et al. used a modified genetic algorithm to solve the weight and the deflection functions of sandwich panels with a corrugated core [45]. Corvino et al. introduced a procedure for multi-objective optimization based on genetic algorithms with the ANSYS software [46].
- Based on the synthesis of the existing literature, it can be concluded that although there are several design and optimization methods available for optimization of sandwich structures, no method can be found relating to a totally FRP sandwich (both the face sheets and the honeycomb core are FRP materials) construction. Therefore, the newly elaborated optimization method fills a gap in this research field.
2. Materials and Methods—Structure and Material Constituents of the Newly Designed Helicopter Floor
2.1. Structure of the Newly Designed Helicopter Floor Panel
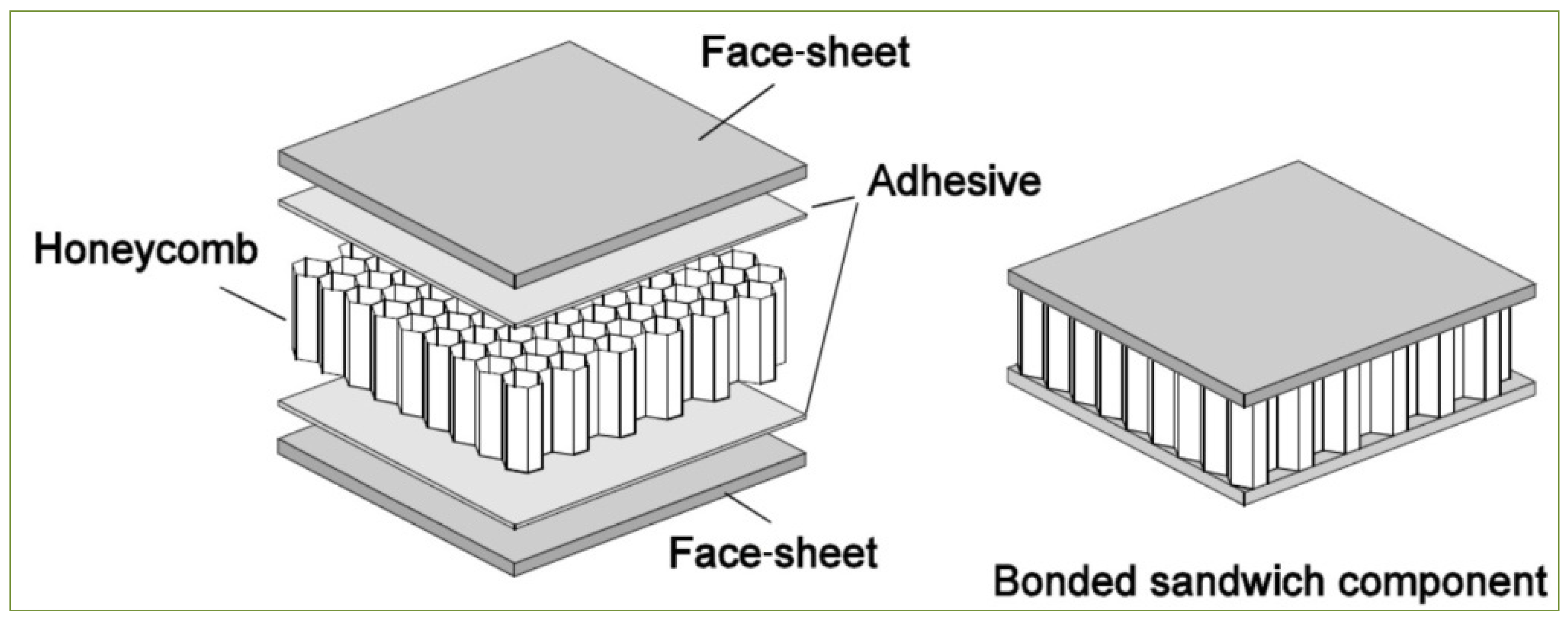
2.1.1. Face Sheets of the Sandwich Plate
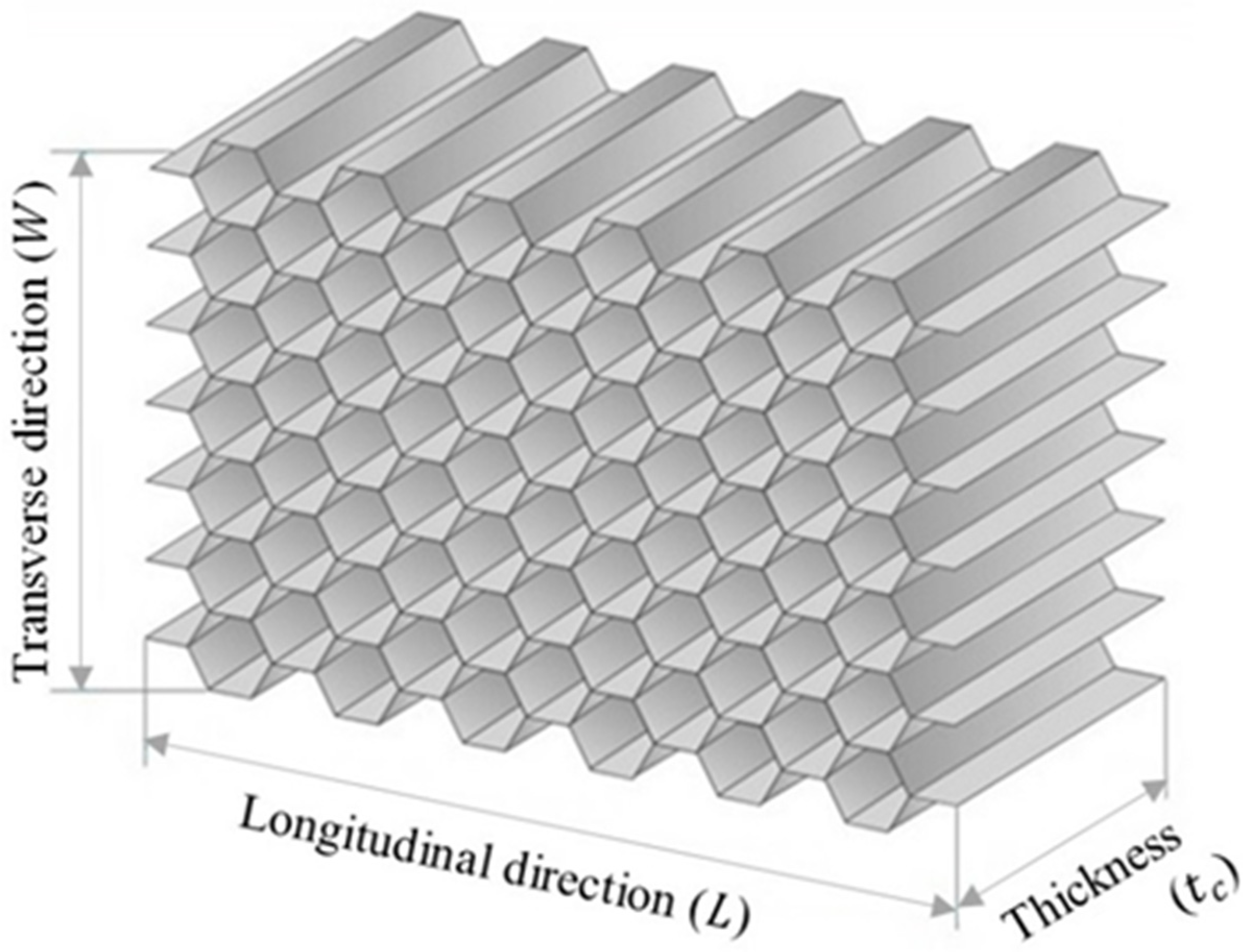
2.1.2. Honeycomb Core of the Sandwich Plate
3. Single-Objective Optimization Methods
3.1. Weight Objective Function
3.2. Design Variables
3.3. Design Constraints
3.3.1. Stiffness
3.3.2. Deflection
3.3.3. Skin Stress
3.3.4. Core Shear Stress
3.3.5. Facing Stress (End Loading)
3.3.6. Buckling
3.3.7. Shear Crimping
3.3.8. Skin Wrinkling
3.3.9. Intracell Buckling (Face Sheet Dimpling)
4. Results—Case Study for the Optimization of Helicopter Floor
4.1. Weight Objective Optimization by Applying the Excel Solver Software for Sandwich Structure of the Helicopter Floor
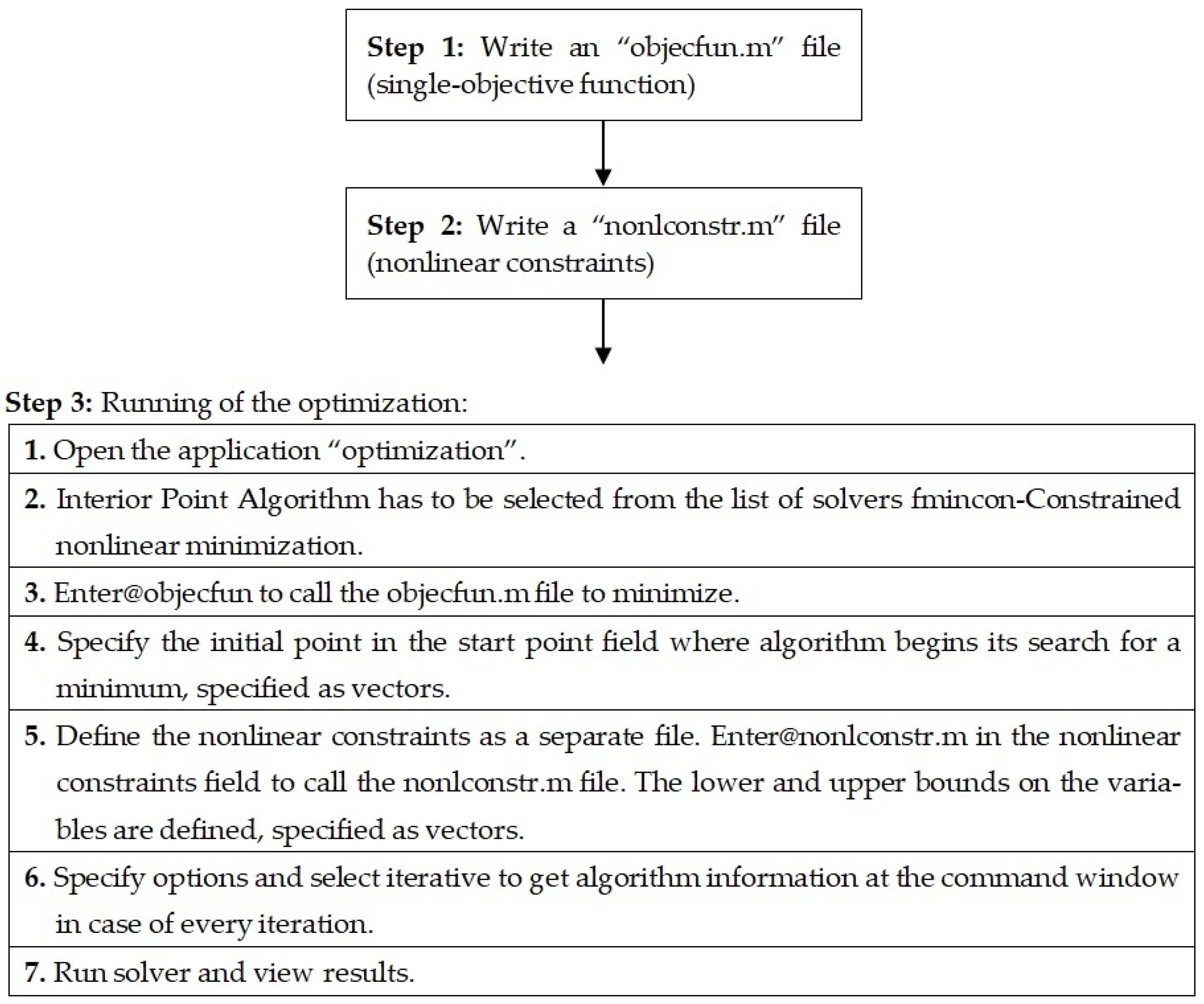
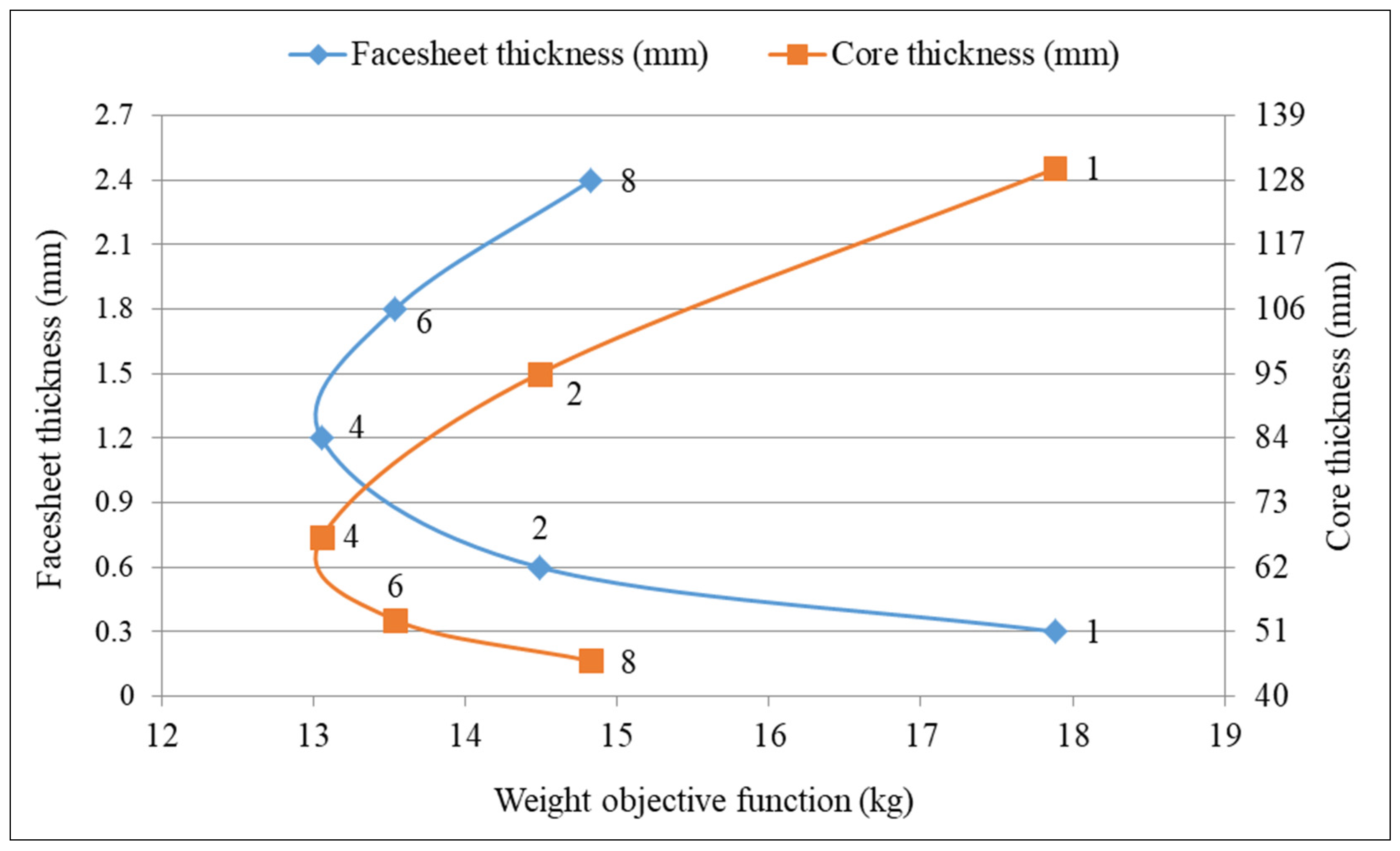
4.2. Weight Objective Optimization by Applying the Matlab Software for Sandwich Structure of the Helicopter Floor
4.3. Evaluation of the Optimization Results Achieved by Applying the Matlab and Excel Solver Software
- The actual caltulated values for the optimal construction have to be less than the relevant maximum allowable values in the case of the following four design constraints to fulfill the requirements.
- Deflection ()—maximum allowable value: 25 mm/calculated value: 24.949 mm;
- Skin stress ()—maximum allowable value: 785.5 MPa/calculated value: 211.7 MPa;
- Core shear stress ()—maximum allowable value: 2.28 MPa/calculated value: 0.338 MPa;
- Facing stress ()—maximum allowable value: 687 MPa/calculated value: 54 MPa.
- The actual caltulated values for the optimal construction have to be higher than the relevant minimum allowable values in the case of the following five design constraints to fulfill the requirements.
- 5.
- Stiffness ()—minimum allowable value: 174.6 kN·m/calculated value: 179.4 kN·m;
- 6.
- Buckling ()—minimum allowable value: 64.86 kN/m/calculated value: 766.61 kN/m;
- 7.
- Shear crimping ()—minimum allowable value: 53.51 kN/calculated value: 7064.12 kN;
- 8.
- Skin wrinkling ()—minimum allowable value: 64.86 kN/m/calculated value: 285.72 kN/m;
- 9.
- Intracell buckling ()—minimum allowable value: 785.2 MPa/calculated value 1296.9 MPa.
5. Further Advantages of the Newly Developed Totally Composite Sandwich Structure of the Helicopter Floor
5.1. Safety Factors Relating to the Design Constraints
5.2. Annual Fuel and Carbon Savings
6. Numerical Analysis for Optimum Sandwich Plate of Helicopter Floor Using the Digimat-HC Program
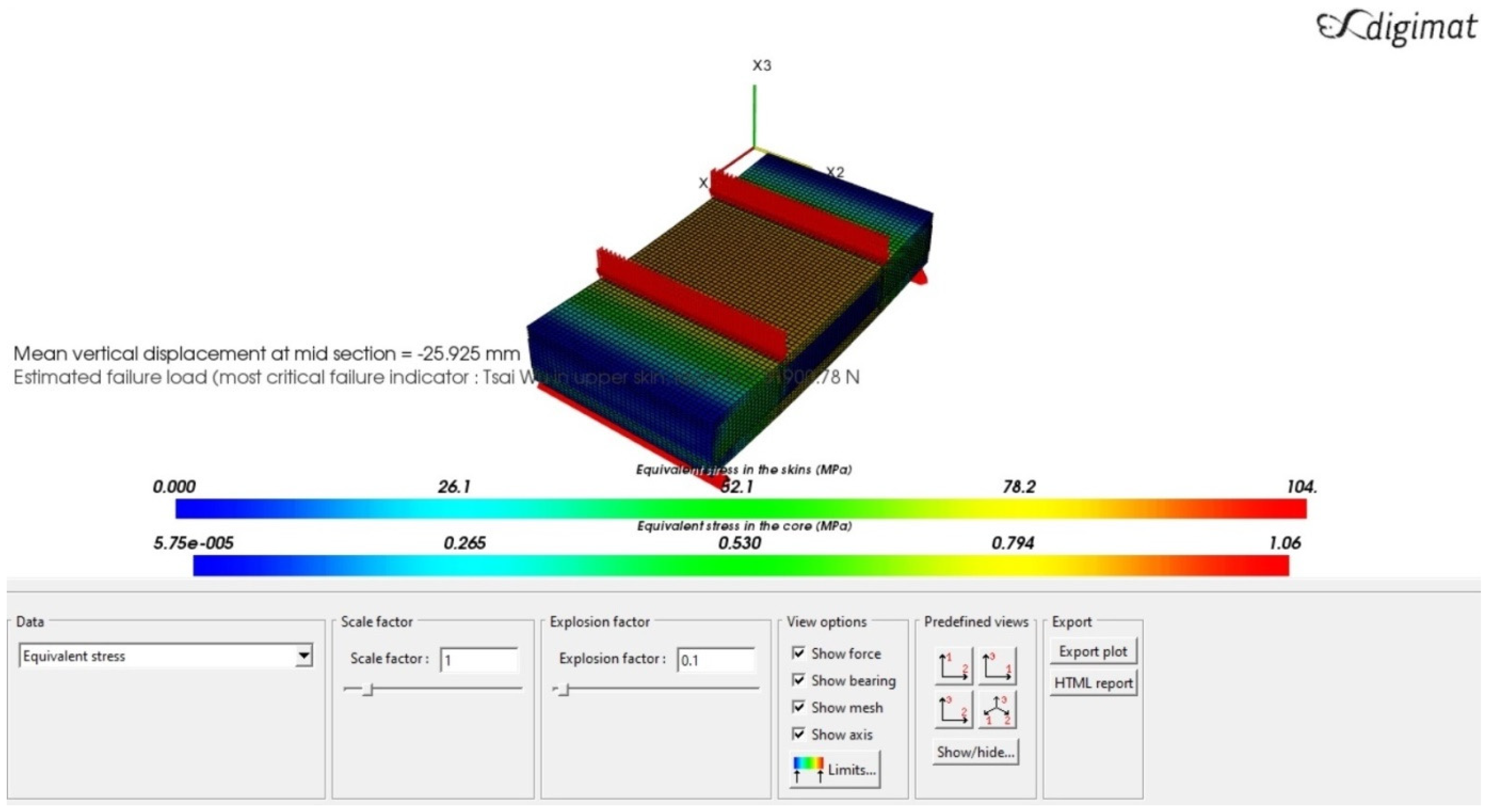
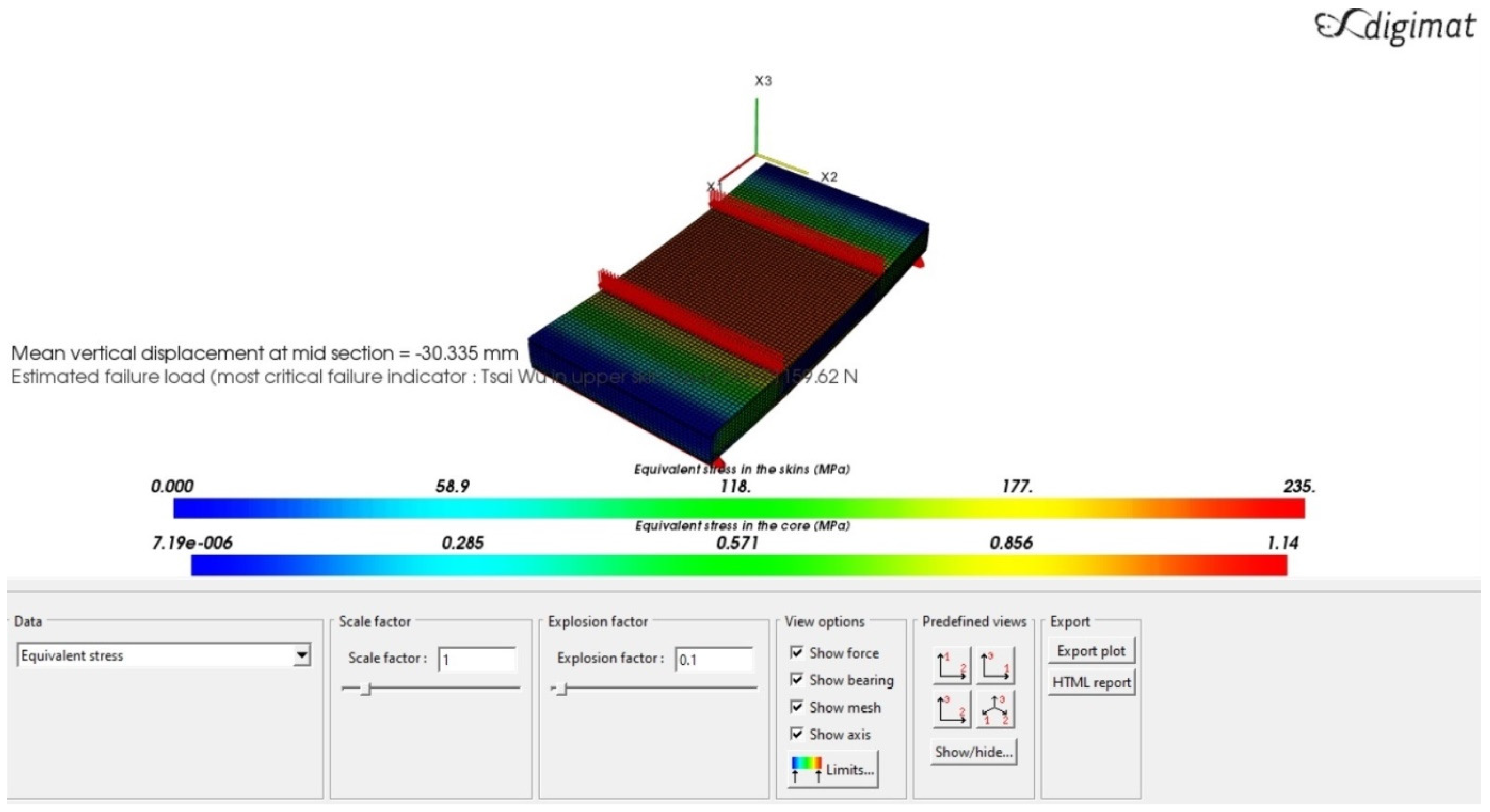
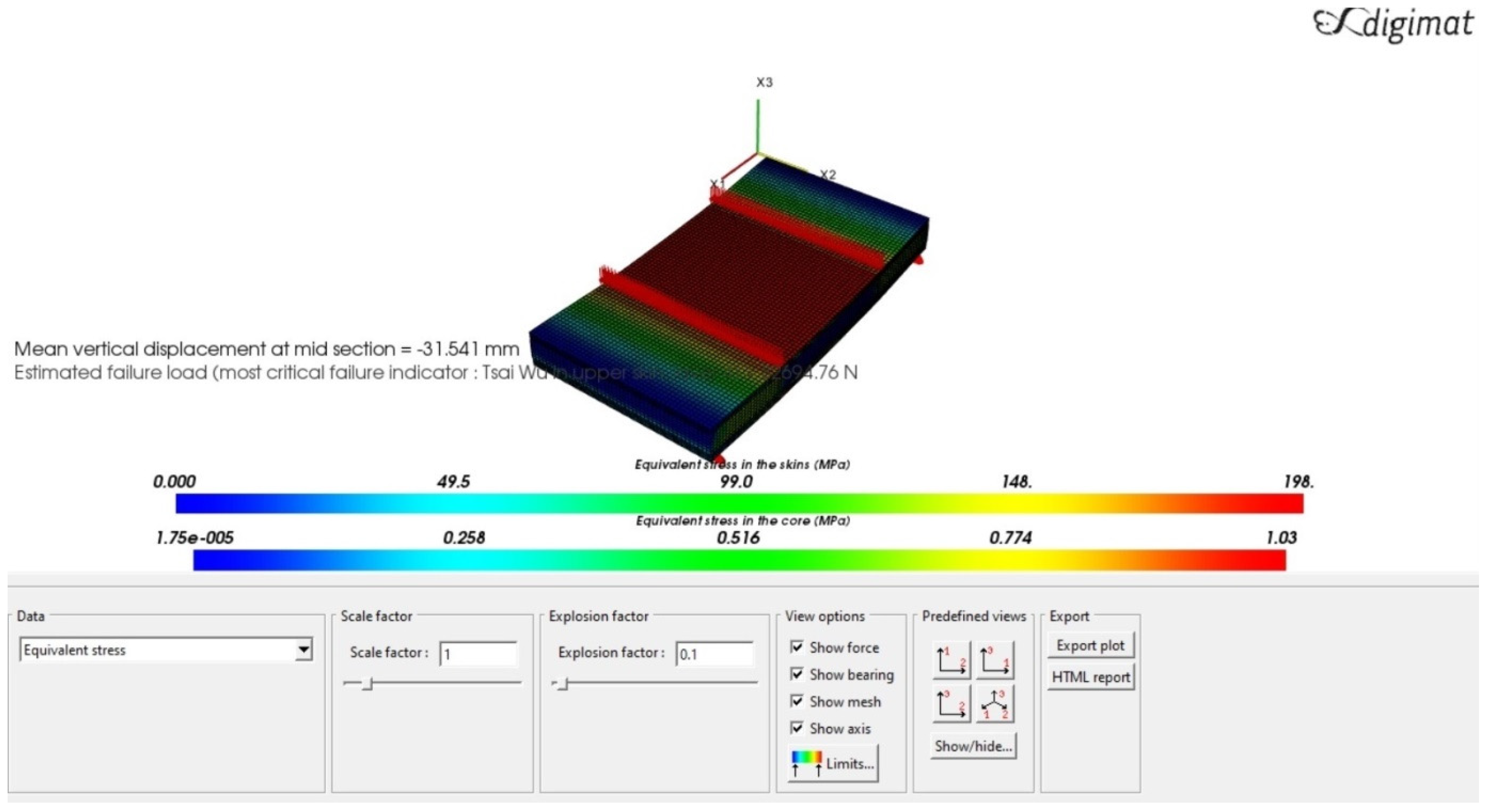
- The four-point bending test was performed by applying the Digimat-HC software. The results of the simulation are the evaluation of the following parameters for the optimum sandwich plates of the helicopter floor and are shown in Table 10 (see Figure A1, Figure A2, Figure A3 and Figure A4 in Appendix B):
- -
- : vertical displacement of the structure at the mid-section;
- -
- : equivalent skin stress;
- -
- : equivalent core shear stress.
7. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. List of Symbols
| Width | mm | |
| Distance between facing skin centers | mm | |
| Bending stiffness in the global coordinate | N·m | |
| Minimum stiffness of a sandwich structure | N·m | |
| Young’s modulus of elasticity of the core | GPa | |
| Average modulus of elasticity | GPa | |
| Young’s modulus of elasticity of composite face sheet in direction | GPa | |
| Young’s modulus of elasticity of composite face sheet in direction | GPa | |
| Maximum shear force | N | |
| g | Acceleration | m/sec2 |
| Core shear modulus | GPa | |
| Core shear modulus in direction (longitudinal direction) | GPa | |
| Core shear modulus in direction (transverse direction) | GPa | |
| Bending deflection coefficient | - | |
| Shear deflection coefficient | - | |
| Length | mm | |
| Maximum bending moment | N·m | |
| Number of epoxy woven carbon fiber laminates | piece | |
| Number of epoxy woven glass fiber laminates | piece | |
| Number of layers in the laminate | piece | |
| The optimum number of layers in the laminate | piece | |
| Load per unit area | MPa | |
| Applied load | N | |
| Overall critical buckling load | N | |
| Critical shear crimping load | N | |
| Skin wrinkling critical load | N | |
| Span | mm | |
| Shear stiffness of a composite sandwich structure | N/m | |
| Core thickness | mm | |
| Optimum core thickness | mm | |
| Lamina thickness of epoxy woven carbon fiber face sheet | mm | |
| Thickness of one layer | mm | |
| Face sheet thickness | mm | |
| Optimum face sheet thickness | mm | |
| Lamina thickness of epoxy woven glass fiber face sheet | mm | |
| Lamina thickness | mm | |
| Core weight | kg | |
| Face sheet weight | kg | |
| Weight of epoxy woven carbon fiber face sheets | kg | |
| Weight of epoxy woven glass fiber face sheets | kg | |
| Minimum weight | kg | |
| Total weight | kg | |
| Buckling factor | - | |
| Deflection | mm | |
| Maximum deflection | mm | |
| Fiber orientation angle | degree | |
| Core density | kg/m3 | |
| The density of epoxy woven carbon fiber | kg/m3 | |
| Face sheet density | kg/m3 | |
| The density of epoxy woven glass fiber | kg/m3 | |
| Skin stress | MPa | |
| Intracell buckling critical stress | MPa | |
| Typical yield strength of the composite face sheet in the direction | MPa | |
| Typical yield strength of the composite face sheet in the direction | MPa | |
| Numerical stress | MPa | |
| Equivalent skin stress | MPa | |
| Skin wrinkling critical stress | MPa | |
| Core shear stress | MPa | |
| Typical shear stress of the core material in the transverse direction | MPa | |
| Core Poisson’s ratio | - | |
| Face sheet Poisson’s ratio | - |
Appendix B

References
- Koberg, E.; Longoni, A. A systematic review of sustainable supply chain management in global supply chains. J. Clean. Prod. 2019, 207, 1084–1098. [Google Scholar] [CrossRef]
- Grondys, K.; Androniceanu, A.; Dacko-Pikiewicz, Z. Energy management in the operation of enterprises in the light of the applicable provisions of the energy efficiency directive (2012/27/EU). Energies 2020, 13, 4338. [Google Scholar] [CrossRef]
- Yildirim, C.; Sevil Oflaç, B.; Yurt, O. The doer effect of failure and recovery in multi-agent cases: Service supply chain perspective. J. Serv. Theory Pract. 2018, 28, 274–297. [Google Scholar] [CrossRef] [Green Version]
- Rushton, A.; Croucher, P.; Baker, P. The Handbook of Logistics & Distribution Management; Kogan Page Limited: London, UK, 2010. [Google Scholar]
- Kot, S. Sustainable supply chain management in small and medium enterprises. Sustainability 2018, 10, 1143. [Google Scholar] [CrossRef] [Green Version]
- Kovács, G.; Illés, B. Development of an optimization method and software for optimizing global supply chains for increased efficiency, competitiveness, and sustainability. Sustainability 2019, 11, 1610. [Google Scholar] [CrossRef] [Green Version]
- Teodorović, D.; Janić, M. Transportation Engineering: Theory, Practice and Modeling; Butterworth-Heinemann: Oxford, UK, 2016. [Google Scholar]
- Kovács, G. Innovative mathematical methods and new software applications for cost-effective, profitable and environmentally friendly freight transport. Pol. J. Environ. Stud. 2019, 28, 2659–2671. [Google Scholar] [CrossRef]
- Astori, P.; Zanella, M.; Bernardini, M. Validation of numerical models of a rotorcraft crashworthy seat and subfloor. Aerospace 2020, 7, 174. [Google Scholar] [CrossRef]
- Todor, M.P.; Kiss, I. Systematic approach on materials selection in the automotive industry for making vehicles lighter, safer and more fuel-efficient. Appl. Eng. Lett. 2016, 1, 91–97. [Google Scholar]
- Hajela, P.; Lee, E. Topological optimization of rotorcraft subfloor structures for crashworthiness considerations. Comp. Struct. 1997, 64, 65–76. [Google Scholar] [CrossRef]
- Zheng, J.; Xiang, J.; Luo, Z.; Ren, Y. Crashworthiness design of transport aircraft subfloor using polymer foams. Int. J. Crashworth. 2011, 16, 375–383. [Google Scholar] [CrossRef]
- Astori, P.; Impari, F. Crash response optimisation of helicopter seat and subfloor. Int. J. Crashworth. 2013, 18, 570–578. [Google Scholar] [CrossRef]
- Yang, X.; Ma, J.; Wen, D.; Yang, J. Crashworthy design and energy absorption mechanisms for helicopter structures: A Systematic literature review. Prog. Aeros. Sci. 2020, 114, 100618. [Google Scholar] [CrossRef]
- Hollaway, L.C. A review of the present and future utilisation of FRP composites in the civil infrastructure with reference to their important in-service properties. Constr. Build. Mater. 2010, 24, 2419–2445. [Google Scholar] [CrossRef]
- Todor, M.P.; Bulei, C.; Kiss, I. An overview on fiber-reinforced composites used in the automotive industry. Ann. Fac. Eng. Huned. Int. J. Eng. 2017, 15, 181–184. [Google Scholar]
- Ferreira, A.D.B.L.; Nóvoa, P.R.O.; Marques, A.T. Multifunctional Material Systems: A state-of-the-art review. Compos. Struct. 2016, 151, 3–35. [Google Scholar] [CrossRef]
- Callister, W.D.; Rethwisch, D.G. Materials Science and Engineering: An Introduction, 8th ed.; John Wiley & Sons: New York, NY, USA, 2018. [Google Scholar]
- Kollár, L.P.; Springer, G.S. Mechanics of Composite Structures; Cambridge University Press: London, UK, 2003. [Google Scholar]
- Sarika, P.R.; Nancarrow, P.; Khansaheb, A.; Ibrahim, T. Bio-based alternatives to phenol and formaldehyde for the production of resins. Polymers 2020, 12, 2237. [Google Scholar] [CrossRef]
- Culkova, K.; Khouri, S.; Straka, M.; Rosova, A. Ecological and economic savings of fly ash using as geopolymer. Rocz. Ochr. Sr. 2018, 20, 73–88. [Google Scholar]
- Dong, C.; Davies, I.J. Optimal design for the flexural behavior of glass and carbon fiber reinforced polymer hybrid composites. Mater. Des. 2012, 37, 450–457. [Google Scholar] [CrossRef]
- Smith, W.F.; Hashemi, J. Foundations of Materials Science and Engineering, 6th ed.; McGraw-Hill Education: New York, NY, USA, 2019. [Google Scholar]
- Zaharia, S.M.; Enescu, L.A.; Pop, M.A. Mechanical performances of lightweight sandwich structures produced by material extrusion-based additive manufacturing. Polymers 2020, 12, 1740. [Google Scholar] [CrossRef]
- Baca Lopez, D.M.; Ahmad, R. Tensile mechanical behaviour of multi-polymer sandwich structures via fused deposition modelling. Polymers 2020, 12, 651. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Wang, G.; Li, Q.; Zhang, L.; Yan, J.D.; Chen, C.; Fang, Z. A comparative study on damage mechanism of sandwich structures with different core materials under lightning strikes. Energies 2017, 10, 1594. [Google Scholar] [CrossRef] [Green Version]
- Nayak, S.K.; Singh, A.K.; Belegundu, A.D.; Yen, C.F. Process for design optimization of honeycomb core sandwich panels for blast load mitigation. Struct. Multidiscip. Optim. 2013, 47, 749–763. [Google Scholar] [CrossRef]
- Xiang, L.; Gangyan, L.; Chun, H.W.; Min, Y. Optimum design of composite sandwich structures subjected to combined torsion and bending loads. Appl. Compos. Mater. 2012, 19, 315–331. [Google Scholar]
- Nikbakt, S.; Kamarian, S.; Shakeri, M. A review on optimization of composite structures Part I: Laminated composites. Compos. Struct. 2018, 195, 158–185. [Google Scholar] [CrossRef]
- Heimbs, S.; Mehrens, T.; Middendorf, P.; Maier, M.; Schumacher, A. Numerical Determination of the Nonlinear Effective Mechanical Properties of Folded Core Structures for Aircraft Sandwich Panels. In Proceedings of the 6th European LS-DYNA Users’ Conference, Gothenburg, Sweden, 29–30 May 2007. [Google Scholar]
- Heimbs, S.; Middendorf, P.; Hampf, C.; Hähnel, F.; Wolf, K. Aircraft Sandwich Structures with Folded Core under Impact Load. In Proceedings of the International Conference on Sandwich Structures, Porto, Portugal, 6–8 May 2008. [Google Scholar]
- Bisagni, C.; Lanzi, L.; Ricci, S. Size and Topological Optimization for Crashworthiness Design of Helicopter Subfloor. In Proceedings of the 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, Georgia, 4–6 September 2002. [Google Scholar]
- Adel, I.S.; Steven, L.D. Weight and cost multi-objective optimization of hybrid composite sandwich structures. Int. J. Comp. Met. Exp. Meas. 2017, 5, 200–210. [Google Scholar]
- Hambric, S.A.; Shepherd, M.R.; Schiller, N.H.; Snider, R.; May, C. Quieting a rib-framed honeycomb-core sandwich panel for a rotorcraft roof. J. Am. Helicopter Soc. 2017, 62, 1–10. [Google Scholar] [CrossRef]
- Debeleac, C.; Nechita, P.; Nastac, S. Computational investigations on soundproof applications of foam-formed cellulose materials. Polymers 2019, 11, 1223. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Zhu, W.; Cheng, Y. Multi-objective optimization of acoustic performances of polyurethane foam composites. Polymers 2018, 10, 788. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.S.; Abdul-Latif, A.; Koloor, S.S.R.; Petrů, M.; Tamin, M.N. Representative cell analysis for damage-based failure model of polymer hexagonal honeycomb structure under the out-of-plane loadings. Polymers 2021, 13, 52. [Google Scholar] [CrossRef]
- Sohouli, A.; Yildiz, M.; Suleman, A. Design optimization of thin-walled composite structures based on material and fiber orientation. Compos. Struct. 2017, 176, 1081–1095. [Google Scholar] [CrossRef]
- Gillet, A.; Francescato, P.; Saffre, P. Single-and multi-objective optimization of composite structures: The influence of design variables. J. Compos. Mater. 2010, 44, 457–480. [Google Scholar] [CrossRef]
- Ghafil, H.N.; Jármai, K. Dynamic differential annealed optimization: New metaheuristic optimization algorithm for engineering applications. Appl. Soft Comput. 2020, 93, 106392. [Google Scholar] [CrossRef]
- Houmat, A. Optimal lay-up design of variable stiffness laminated composite plates by a layer-wise optimization technique. Eng. Optimiz. 2018, 50, 205–217. [Google Scholar] [CrossRef]
- Virág, Z.; Szirbik, S. Finite element modal analysis of a hybrid stiffened plate. Ann. Univ. Petroşani Mech. Eng. 2019, 21, 115–120. [Google Scholar]
- Delgado, S.D.R.; Kostal, P.; Cagánová, D.; Cambál, M. On the possibilities of intelligence implementation in manufacturing: The role of simulation. Appl. Mech. Mater. 2013, 309, 96–104. [Google Scholar] [CrossRef]
- Kundrák, J.; Karpuschewski, B.; Pálmai, Z.; Felhő, C.; Makkai, T.; Borysenko, D. The energetic characteristics of milling with changing cross-section in the definition of specific cutting force by FEM method. CIRP J. Manuf. Sci. Technol. 2021, 32, 61–69. [Google Scholar] [CrossRef]
- Khalkhali, A.; Khakshournia, S.; Nariman-Zadeh, N. A hybrid method of FEM, modified NSGAII and TOPSIS for structural optimization of sandwich panels with corrugated core. J. Sandw. Struct. Mater. 2014, 16, 398–417. [Google Scholar] [CrossRef]
- Corvino, M.; Iuspa, L.; Riccio, A.; Scaramuzzino, F. Weight and cost oriented multi-objective optimization of impact damage resistant stiffened composite panels. Comp. Struct. 2009, 87, 1033–1042. [Google Scholar] [CrossRef]
- Available online: https://commons.wikimedia.org/wiki/File:Inaer_Airbus_Helicopters_EC145_T2_JP7991183.jpg (accessed on 10 June 2021).
- Zenkert, D. An Introduction to Sandwich Construction; Engineering Materials Advisory Services (EMAS): London, UK; Stockholm, Sweden, 1995. [Google Scholar]
- Hexcel Composites Publication No. AGU 075b, Honeycomb Sandwich Design Technology. 2000. Available online: https://www.hexcel.com/user_area/content_media/raw/Honeycomb_Sandwich_Design_Technology.pdf (accessed on 10 June 2021).
- Product Data of Fibreglass/Phenolic Honeycomb Publication ATU 122b. 2007. Available online: https://www.hexcel.com/user_area/content_media/raw/HRP_eu.pdf (accessed on 23 April 2021).


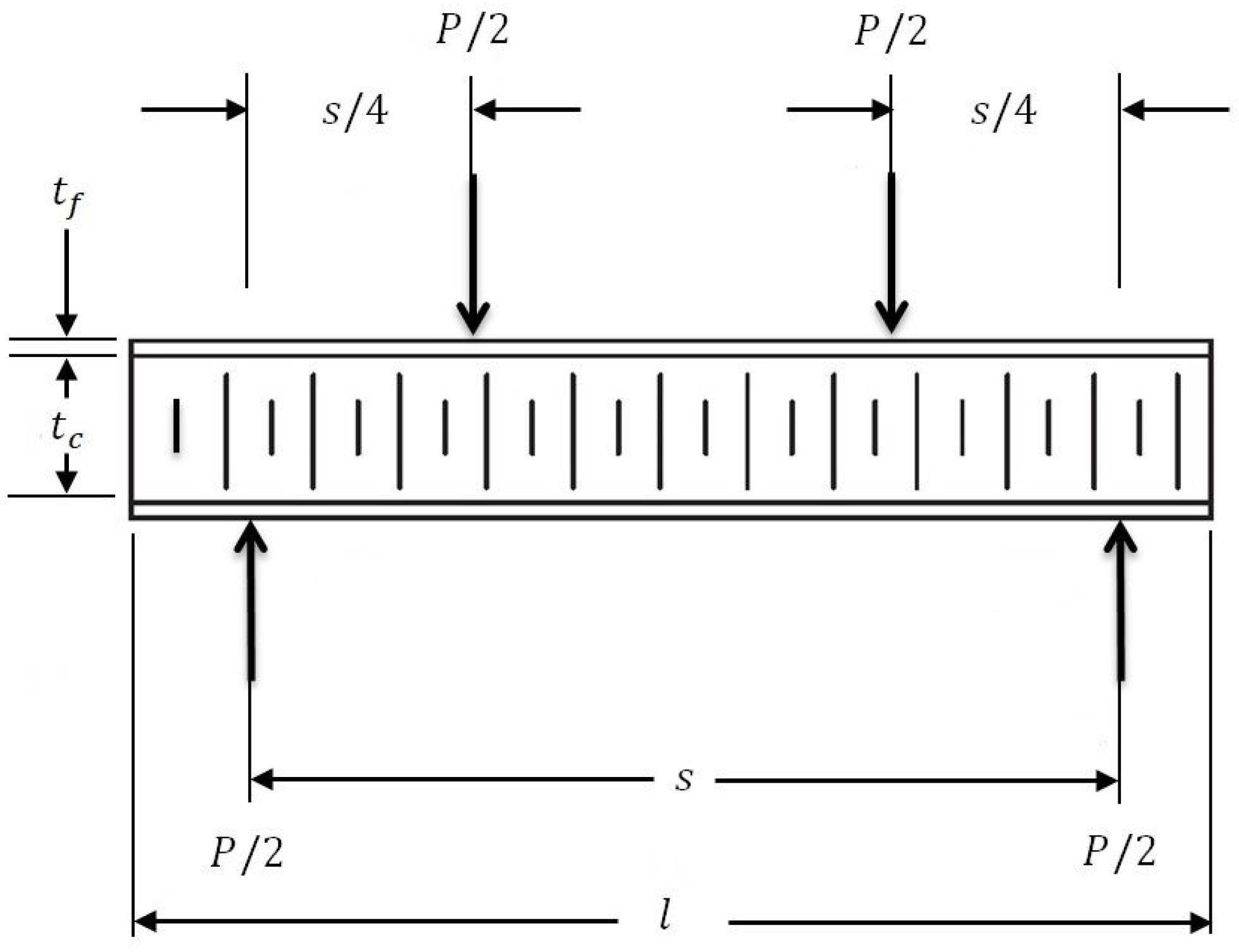
| Length | Width | Deflection | Acceleration | Maximum Load | |
|---|---|---|---|---|---|
| g | |||||
| (mm) | (mm) | (mm) | (m/sec2) | (N) | (Pa) |
| 1500 | 825 | 25 | 9.81·4.5 | 53510 | 66217.5 |
| Coefficient for Bending Deflection | Coefficient for Shear Deflection | Moment for Maximum Bending | Force for Maximum Shear | Factor for Buckling |
|---|---|---|---|---|
| Type of Layers | Tension/Compression Strength (MPa) | Tension/Compression Modulus of Elasticity (GPa) | Poisson’s Ratio (–) | Cured Ply Thickness (mm) | Weight/Ply (kg/m2) |
|---|---|---|---|---|---|
| Woven Glass Fiber Phenolic Resin | 400/360 | 20/17 | 0.13 | 0.25 | 0.47 |
| Woven Glass Fiber Epoxy Resin | 600/550 | 20/17 | 0.13 | 0.25 | 0.47 |
| Woven Carbon Fiber Epoxy Resin | 800/700 | 70/60 | 0.05 | 0.3 | 0.45 |
| Characteristics | Compression | Plate Shear | |||||
|---|---|---|---|---|---|---|---|
| Density | Cell Dimension | Stabilized | Longitudinal Direction | Transverse Direction | |||
| Strength | Modulus | Strength | Modulus | Strength | Modulus | ||
| (kg/m3) | (mm) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) |
| 104.12 | 6.35 | 8.14 | 828 | 4 | 159 | 2.28 | 90 |
| Type of Face Sheets: | (1) Phenolic Woven Glass Fiber | |||
|---|---|---|---|---|
| Layers’ Number and Fiber Orientations: | kg | mm | mm | |
| 4 (0°, 90°, 90°, 0°) Optimum value | 22.133 | 1 | 136 | |
| Type of face sheets: | (2) Epoxy woven glass fiber | |||
| Layers’ number and fiber orientations: | kg | mm | mm | |
| 4 (0°, 90°, 90°, 0°) Optimum value | 22.133 | 1 | 136 | |
| Type of face sheets: | (3) Epoxy woven carbon fiber | |||
| Layers’ number and fiber orientations: | kg | mm | mm | |
| 2 (0°, 90°) Optimum value | 14.486 | 0.6 | 95 | |
| Type of face sheets: | (4) Hybrid composite | |||
| Layers’ number and fiber orientations: | kg | mm | mm | |
| 4 (0°, 90°, 90°, 0°) Optimum value | 15.475 | 1.1 | 85 | |
| Type of Face Sheets: | (1) Phenolic Woven Glass Fiber | |||
|---|---|---|---|---|
| Layers’ Number and Fiber Orientations: | kg | mm | mm | |
| 4 (0°, 90°, 90°, 0°) Optimum value | 22.127 | 1 | 136 | |
| Type of face sheets: | (2) Epoxy woven glass fiber | |||
| Layers’ number and fiber orientations: | kg | mm | mm | |
| 4 (0°, 90°, 90°, 0°) Optimum value | 22.127 | 1 | 136 | |
| Type of face sheets: | (3) Epoxy woven carbon fiber | |||
| Layers’ number and fiber orientations: | kg | mm | mm | |
| 2 (0°, 90°) Optimum value | 14.473 | 0.6 | 95 | |
| Type of face sheets: | (4) Hybrid composite | |||
| Layers’ number and fiber orientations: | kg | mm | mm | |
| 4 (0°, 90°, 90°, 0°) Optimum value | 15.475 | 1.1 | 85 | |
| Constraints | Factor of Safety (FoS) Relating to the 4 Different Face Sheets | |||
|---|---|---|---|---|
| Phenolic Woven Glass Fiber (0°, 90°, 90°, 0°) | Epoxy Woven Glass Fiber (0°, 90°, 90°, 0°) | Epoxy Woven Carbon Fiber (0°, 90°) | Hybrid Composite (0°, 90°, 90°, 0°) | |
| 1.018 | 1.018 | 1.027 | 1.03 | |
| 1 | 1 | 1 | 1 | |
| 4.173 | 6.258 | 3.71 | 4.05 | |
| 9.608 | 9.608 | 6.731 | 3.984 | |
| 10.302 | 15.741 | 12.71 | 15.582 | |
| Not Active Constraint | ||||
| 1.812 | 1.208 | 1.3 | 1.585 | |
| 2.808 | 1.671 | 1.652 | 3.995 | |
| 1.812 | 1.208 | 1.3 | 1.585 | |
| 1. Fuel Saving | Price | Unit |
|---|---|---|
| Weight of fuel desired to transport added 1 kg/h | 0.04 | kg |
| Weight of fuel desired to transport added 1 kg/1 year | 200 | kg |
| Fuel cost/1000 kg | 993 | USD |
| Fuel cost to transport added 1 kg/1 year | 199 | USD |
| Weight of lightweight sandwich plate of a helicopter floor | 14.473 | kg |
| 2. Carbon Savings | ||
| Carbon generated/1 kg of fuel | 3.1 | kg |
| Carbon generated to transport 1 kg/1 year | 620 | kg |
| Cost of carbon per ton | 40 | USD |
| Dimensions | Length | Span | Width | Thickness of Honeycomb Core | Thickness of Face Sheet | Load |
|---|---|---|---|---|---|---|
| Face Sheets | ||||||
| (mm) | (mm) | (mm) | (mm) | (mm) | (N) | |
| Phenolic Woven Glass Fiber (0°, 90°, 90°, 0°) | 1500 | 1400 | 825 | 136 | 1 | 53,510 |
| Epoxy Woven Glass Fiber (0°, 90°, 90°, 0°) | 136 | 1 | ||||
| Epoxy Woven Carbon Fiber (0°, 90°) | 95 | 0.6 | ||||
| Hybrid Composite (0°, 90°, 90°, 0°) | 85 | 1.1 |
| Optimal Forms of Different Face Sheets | |||
|---|---|---|---|
| (mm) | (MPa) | (MPa) | |
| (1) Phenolic Woven Glass Fiber | 25.925 | 104 | 1.06 |
| (2) Epoxy Woven Glass Fiber | 25.925 | 104 | 1.06 |
| (3) Epoxy Woven Carbon Fiber | 30.335 | 235 | 1.14 |
| (4) Hybrid Composite | 31.541 | 198 | 1.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Fatlawi, A.; Jármai, K.; Kovács, G. Optimization of a Totally Fiber-Reinforced Plastic Composite Sandwich Construction of Helicopter Floor for Weight Saving, Fuel Saving and Higher Safety. Polymers 2021, 13, 2735. https://doi.org/10.3390/polym13162735
Al-Fatlawi A, Jármai K, Kovács G. Optimization of a Totally Fiber-Reinforced Plastic Composite Sandwich Construction of Helicopter Floor for Weight Saving, Fuel Saving and Higher Safety. Polymers. 2021; 13(16):2735. https://doi.org/10.3390/polym13162735
Chicago/Turabian StyleAl-Fatlawi, Alaa, Károly Jármai, and György Kovács. 2021. "Optimization of a Totally Fiber-Reinforced Plastic Composite Sandwich Construction of Helicopter Floor for Weight Saving, Fuel Saving and Higher Safety" Polymers 13, no. 16: 2735. https://doi.org/10.3390/polym13162735
APA StyleAl-Fatlawi, A., Jármai, K., & Kovács, G. (2021). Optimization of a Totally Fiber-Reinforced Plastic Composite Sandwich Construction of Helicopter Floor for Weight Saving, Fuel Saving and Higher Safety. Polymers, 13(16), 2735. https://doi.org/10.3390/polym13162735