Dynamics of Opposing Polymer Brushes: A Computer Simulation Study
Abstract
:1. Introduction
2. Materials and Methods
- The generation of random vector field of motion attempts. A unit vector, pointed towards one of the nearest neighboring lattice sites, represents the direction along which the object attempts to move;
- The identification of groups of vectors forming closed loops, indicating ways of possible successful cooperative rearrangement. The rest of the objects are immobilized at the given time step. Additionally, if the movement realized in a given loop would lead to the break of a bond between segments in the polymer chain, then the loop is immobilized;
- The rearrangement of objects along these closed paths by displacing them to the neighboring sites according to the vector generated in step 1.
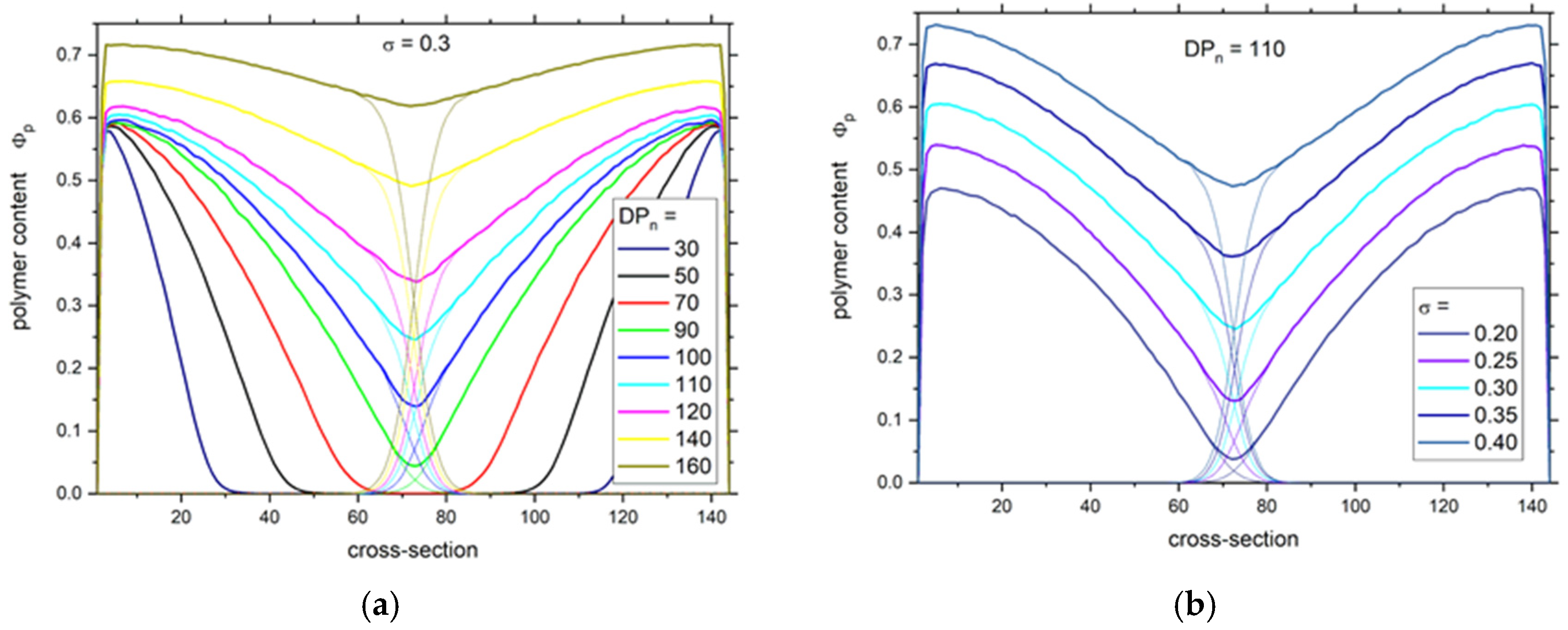
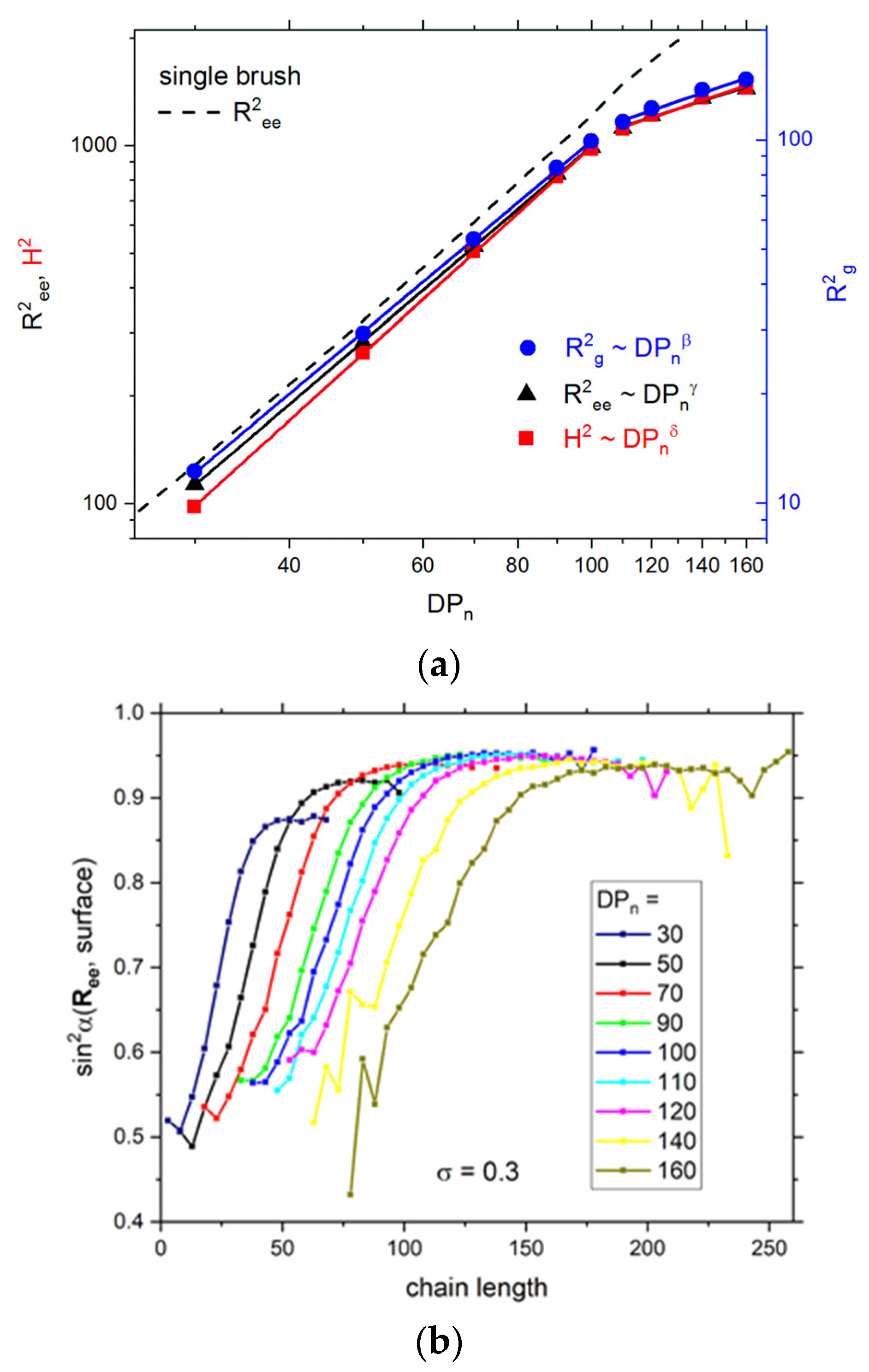
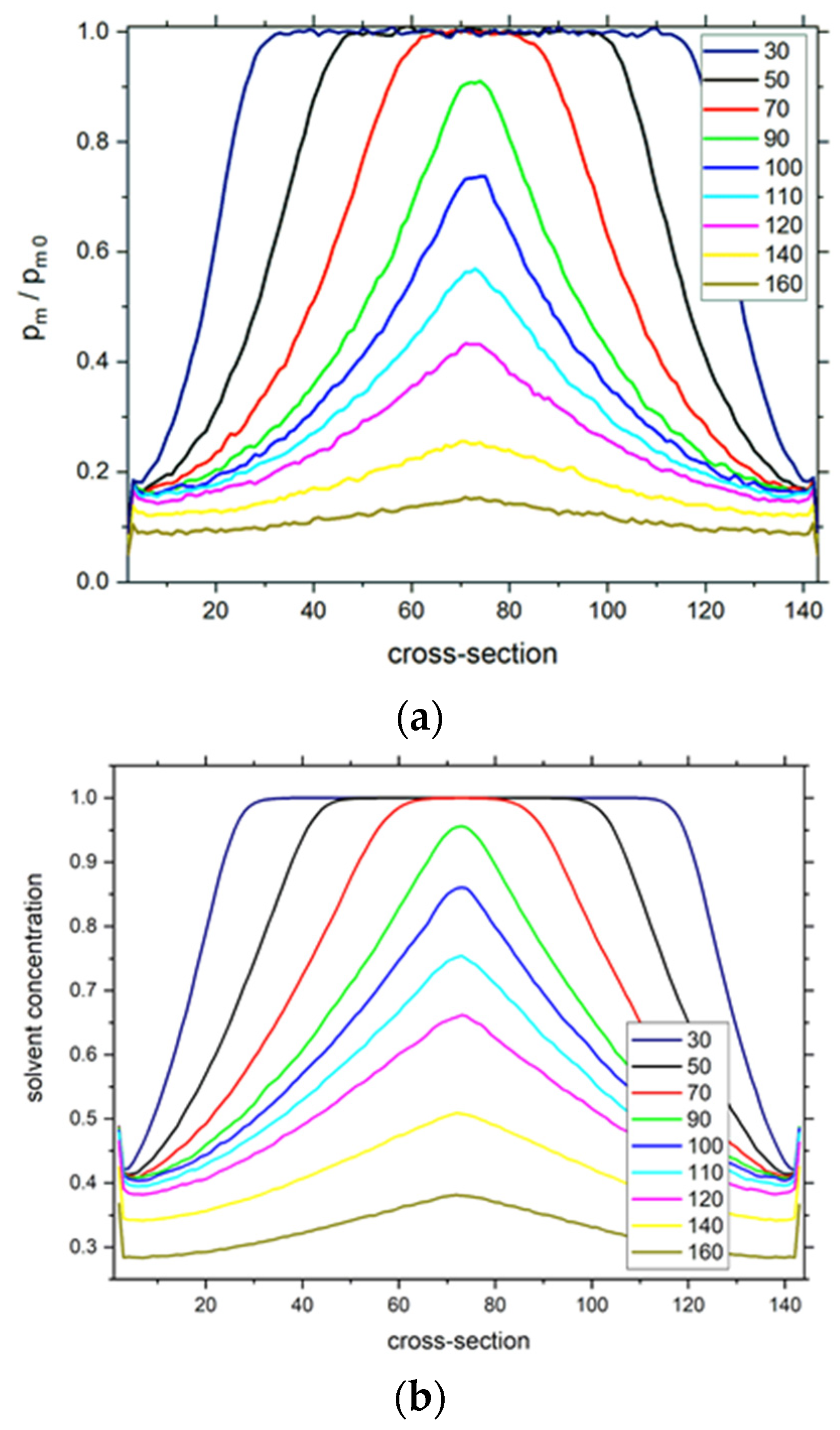
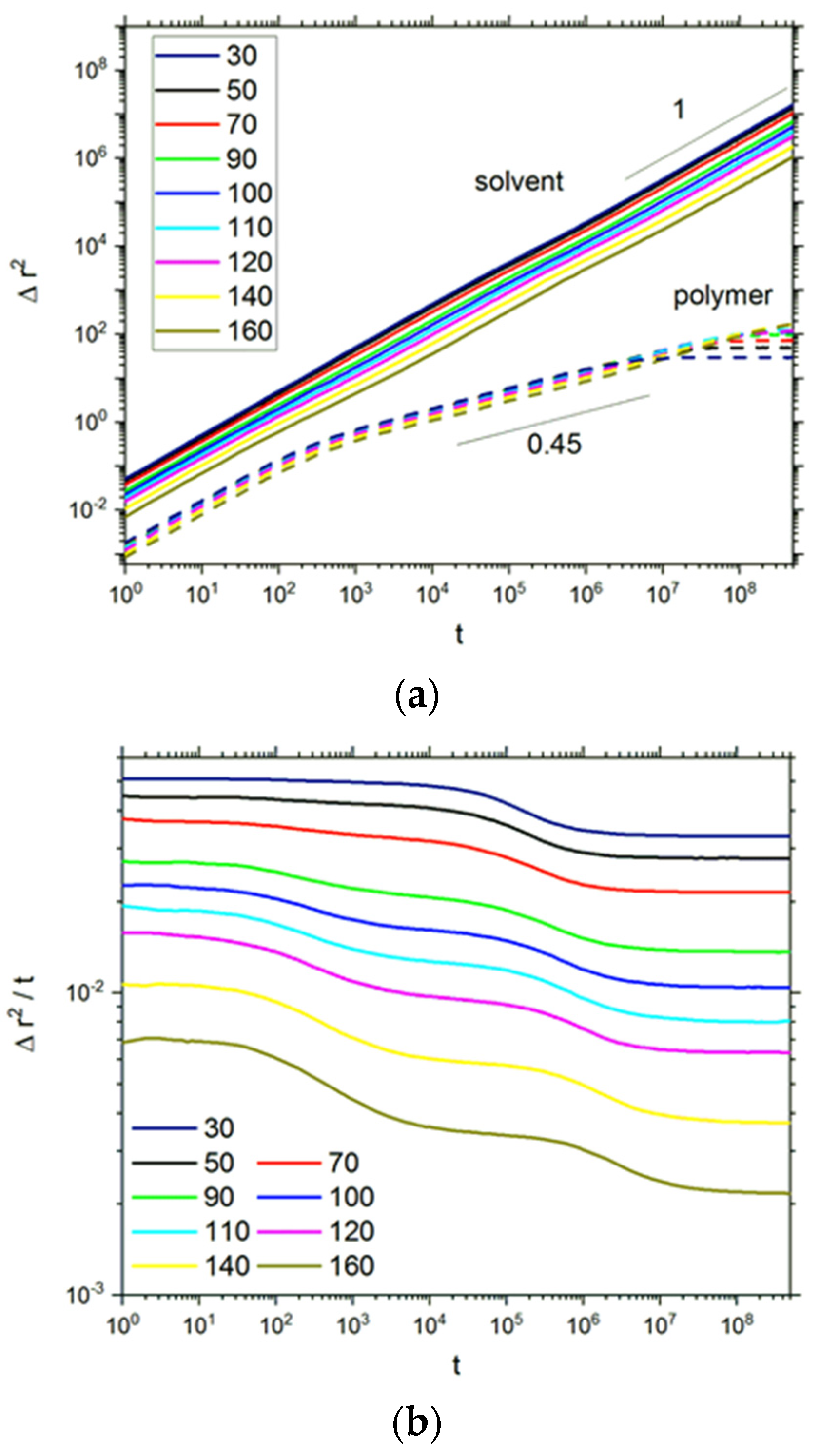
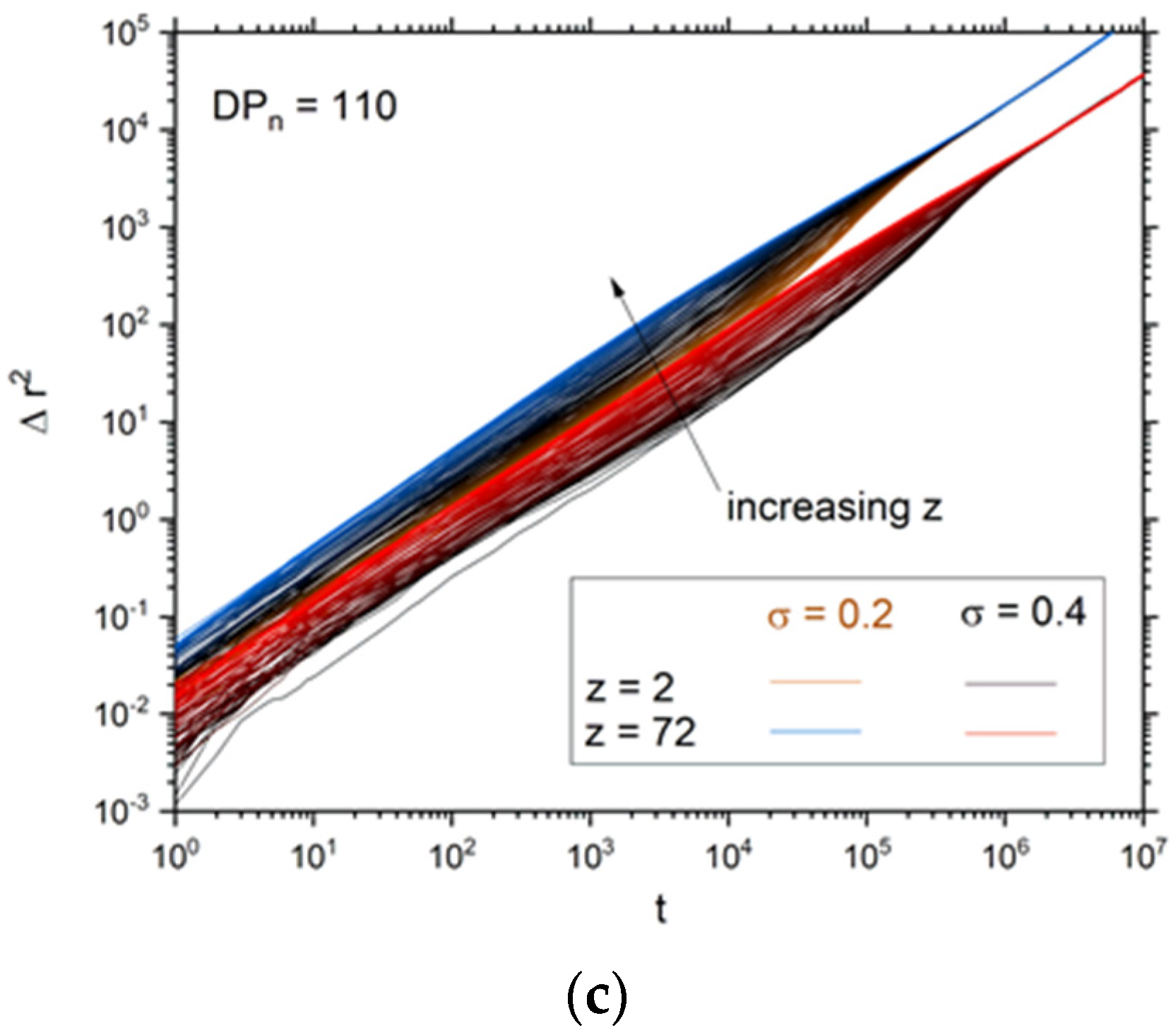
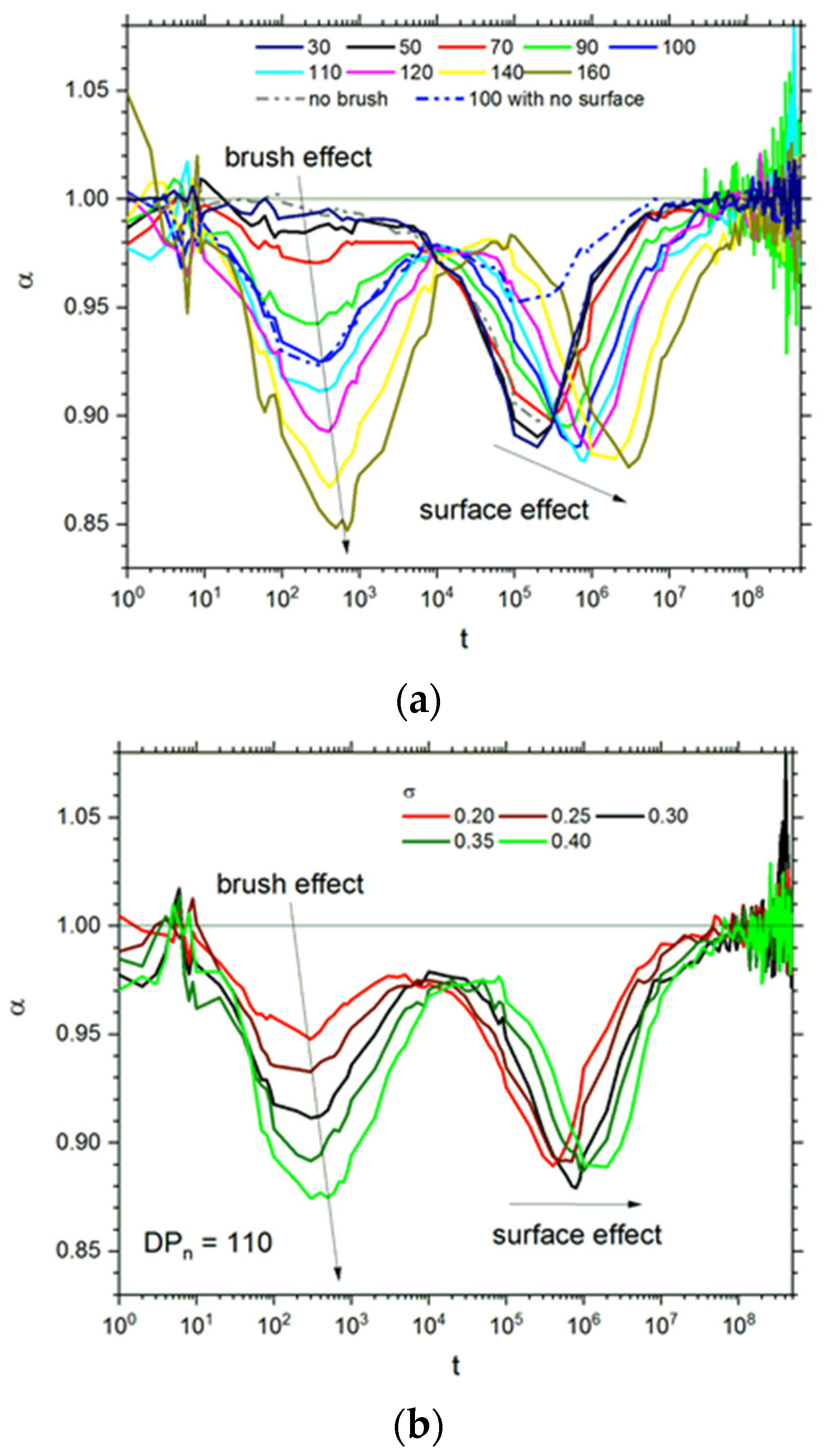
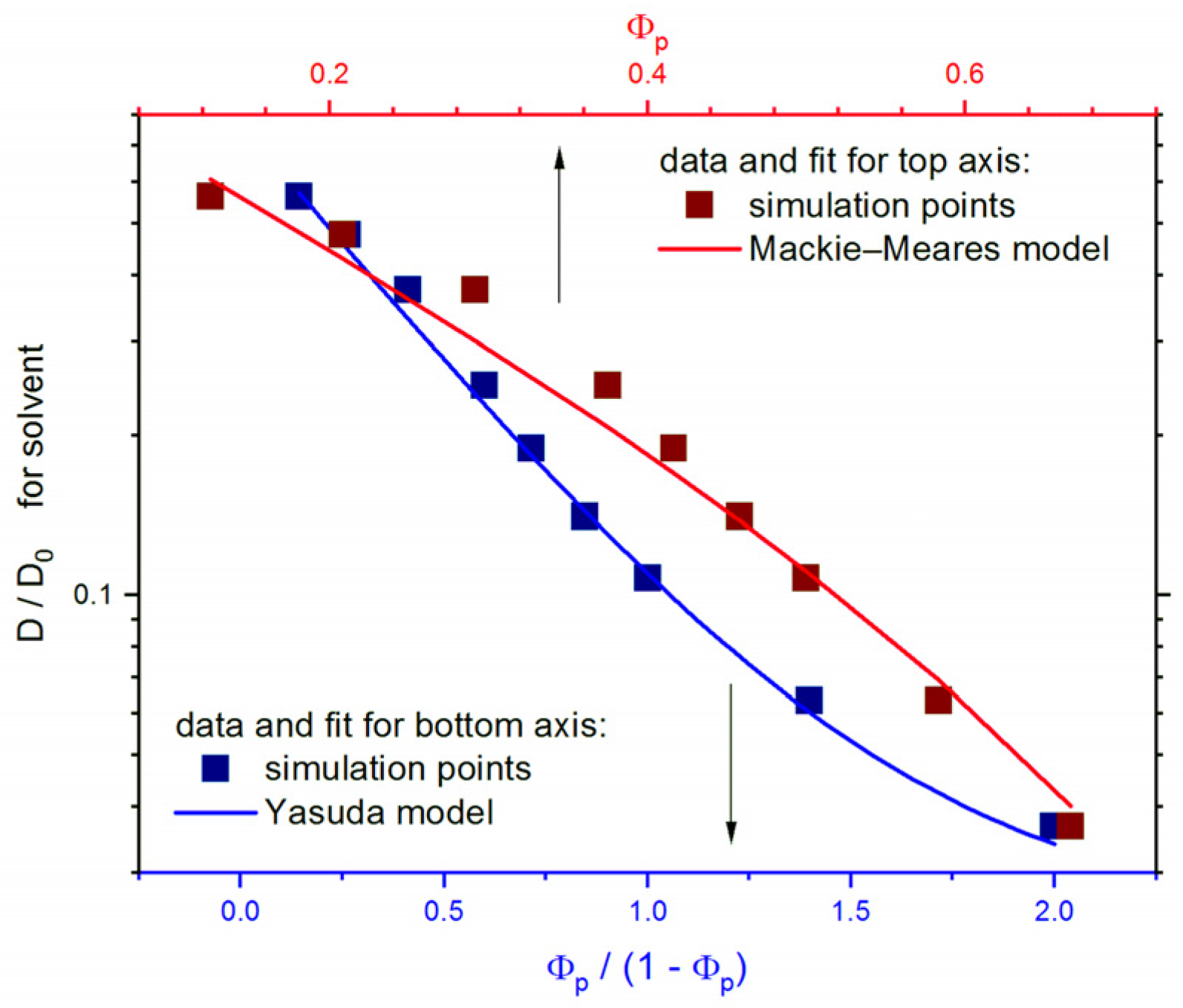
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eisenriegler, E. Polymers Near Surfaces; World Scientific: Singapore, 1993. [Google Scholar]
- Teraoka, I. Polymer solutions in confining geometries. Prog. Polym. Sci. 1996, 21, 89–149. [Google Scholar] [CrossRef]
- Chen, W.-L.; Cordero, R.; Tran, H.; Ober, C.K. 50th anniversary perspective: Polymer brushes: Novel surfaces for future materials. Macromolecules 2017, 50, 4089–4113. [Google Scholar] [CrossRef]
- Brittain, W.J.; Minko, S. A structural definition of polymer brushes. J. Polym. Sci. Part A Polym. Chem. 2007, 45, 3505–3512. [Google Scholar] [CrossRef]
- Zhao, B.; Brittain, W.J. Polymer brushes: Surface-immobilized macromolecules. Prog. Polym. Sci. 2000, 25, 677–710. [Google Scholar] [CrossRef]
- Zoppe, J.O.; Ataman, N.C.; Mocny, P.; Wang, J.; Moraes, J.; Klok, H.-A. Surface-initiated controlled radical polymerization: State-of-art, opportunities, and challenges in surface and interface engineering with polymer brushes. Chem. Rev. 2017, 117, 1105–1318. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Bockstaller, M.R.; Matyjaszewski, K. Brush-modified materials: Control of molecular architecture, assembly behavior, properties and applications. Prog. Polym. Sci. 2020, 100, 101180. [Google Scholar] [CrossRef]
- Binder, K.; Milchev, A. Polymer brushes on flat and curved surfaces: How computer simulations can help to test theories and to interpret experiments. J. Polym. Sci. Part B Polym. Phys. 2012, 50, 1516–1555. [Google Scholar] [CrossRef]
- Reith, D.; Milchev, A.; Virnau, P.; Binder, K. Computer simulation studies of chain dynamics in polymer brushes. Macromolecules 2012, 45, 4381–4393. [Google Scholar] [CrossRef]
- Deng, B.; Palermo, E.F.; Shi, Y. Comparison of chain-growth polymerization in solution versus on surface using reactive coarse-grained simulations. Polymer 2017, 129, 105–118. [Google Scholar] [CrossRef]
- Elliot, I.G.; Kuhl, T.L.; Faller, R. Molecular simulation study of the structure of high density polymer brushes in good solvent. Macromolecules 2010, 43, 9131–9138. [Google Scholar] [CrossRef]
- Murat, M.; Grest, G.S. Structure of a grafted polymer brush: A molecular dynamics simulation. Macromolecules 1989, 22, 4054–4059. [Google Scholar] [CrossRef]
- Malfreyt, P.; Tildesley, D.J. Dissipative Particle Dynamics simulations of grafted polymer chains between two walls. Langmuir 2000, 16, 4732–4740. [Google Scholar] [CrossRef]
- Pakula, T.; Zhulina, E.B. Computer simulations of polymers in thin layers. II. Structure of polymer melt layers consisting of end-to-end grafted chains. J. Chem. Phys. 1991, 95, 4691–4697. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Pakula, T. Structure of dense polymer layers between end-grafting and end-adsorbing walls. Macromolecules 1992, 25, 754–758. [Google Scholar] [CrossRef]
- Kuznetsov, D.V.; Balazs, A.C. Phase behavior of end-functionalized polymers confined between two surfaces. J. Chem. Phys. 2000, 113, 2479–2483. [Google Scholar] [CrossRef]
- Lai, P.Y.; Binder, K. Structure and dynamics of grafted polymer layers—A Monte Carlo simulation. J. Chem. Phys. 1991, 95, 9288–9299. [Google Scholar] [CrossRef]
- Lai, P.Y.; Binder, K. Structure and dynamics of polymer brushes near the theta point—A Monte Carlo simulation. J. Chem. Phys. 1992, 97, 586–595. [Google Scholar] [CrossRef]
- Stadler, C.; Schmid, F. Phase behavior of grafted chain molecules: Influence of head size and chain length. J. Chem. Phys. 1999, 110, 9697–9705. [Google Scholar] [CrossRef] [Green Version]
- Stadler, C.; Lange, H.; Schmid, F. Short grafted chains: Monte Carlo simulations of a model for monolayers of amphiphiles. Phys. Rev. E 1999, 59, 4248–4257. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Jiang, W.; Han, S. Dynamic Monte Carlo simulation on the polymer chain with one end grafted on a flat surface. Macromol. Theory Simul. 2001, 10, 339–342. [Google Scholar] [CrossRef]
- Polanowski, P.; Hałagan, K.; Pietrasik, J.; Jeszka, J.K.; Matyjaszewski, K. Growth of polymer brushes by “grafting from” via ATRP—Monte Carlo simulations. Polymer 2017, 130, 267–279. [Google Scholar] [CrossRef]
- Genzer, J. In silico polymerization: Computer simulation of controlled radical polymerization in bulk and on flat surfaces. Macromolecules 2006, 39, 7157–7169. [Google Scholar] [CrossRef]
- Turgman-Cohen, S.; Genzer, J. Computer simulation of controlled radical polymerization: Effect of chain confinement due to initiator grafting density and solvent quality in “grafting from” method. Macromolecules 2010, 43, 9567–9577. [Google Scholar] [CrossRef]
- Turgman-Cohen, S.; Genzer, J. Computer simulation of concurrent bulk- and surface-initiated living polymerization. Macromolecules 2012, 45, 2128–2137. [Google Scholar] [CrossRef]
- Jalili, K.; Abbasi, F.; Milchev, A. Dynamic compression of in situ grown living polymer brush: Simulation and experiment. Macromolecules 2012, 45, 9827–9840. [Google Scholar] [CrossRef] [Green Version]
- Milchev, A.; Wittmer, J.P.; Landau, D.P. Formation and equilibrium properties of living polymer brushes. J. Chem. Phys. 2000, 112, 1606–1615. [Google Scholar] [CrossRef] [Green Version]
- Binder, K. Scaling concepts for polymer brushes and their test with computer simulation. Eur. Phys. J. E 2002, 9, 293–298. [Google Scholar] [CrossRef]
- Netz, R.R.; Schick, M. Polymer brushes: From self-consistent field theory to classical theory. Macromolecules 1998, 31, 5105–5122. [Google Scholar] [CrossRef]
- Milner, S.T.; Witten, T.A.; Cates, M.E. Theory of the grafted polymer brush. Macromolecules 1988, 21, 2610–2619. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Borisov, O.V.; Pryamitsyn, V.A.; Birshtein, T.M. Coil globule type transitions in polymers. 1. Collapse of layers of grafted polymer-chains. Macromolecules 1991, 24, 140–149. [Google Scholar] [CrossRef]
- Wittmer, J.; Johner, A.; Joanny, J.F.; Binder, K. Some dynamic properties of grafted polymer layers. Colloids Surf. A Physicochem. Eng. Asp. 1994, 86, 85–89. [Google Scholar] [CrossRef]
- de Vos, W.M.; Leermakers, F.A.M. Modeling the structure of a polydisperse polymer brush. Polymer 2009, 50, 305–316. [Google Scholar] [CrossRef]
- Matsen, M.W. Field theoretic approach for block polymer melts: SCFT and FTS. J. Chem. Phys. 2020, 152, 110901. [Google Scholar] [CrossRef] [Green Version]
- Milner, S.T. Polymer brushes. Science 1991, 251, 905–914. [Google Scholar] [CrossRef] [PubMed]
- Kreer, T. Polymer-brush lubrication: A review of recent theoretical advances. Soft Matter 2016, 12, 3479–3501. [Google Scholar] [CrossRef]
- Klushin, L.I.; Skvortsov, A.M.; Qi, S.; Kreer, T.; Schmid, F. Polydispersity effects on interpenetration in compressed brushes. Macromolecules 2019, 52, 1810–1820. [Google Scholar] [CrossRef]
- Galuschko, A.; Spirin, L.; Kreer, T.; Johner, A.; Pastorino, C.; Wittmer, J.; Baschnagel, J. Frictional forces between strongly compressed, nonentangled polymer brushes: Molecular dynamics simulations and scaling theory. Langmuir 2010, 26, 6418–6429. [Google Scholar] [CrossRef]
- Desai, P.R.; Sinha, S.; Das, S. Compression of polymer brushes in the weak interpenetration regime: Scaling theory and molecular dynamics simulations. Soft Matter 2017, 13, 4159–4166. [Google Scholar] [CrossRef]
- Tai, C.-H.; Pan, G.-T.; Yu, H.-Y. Entropic effects in solvent-free bidisperse polymer brushes investigated using Density Functional Theories. Langmuir 2019, 35, 16835–16849. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Rubinstein, M. Lubrication by polyelectrolyte brushes. Macromolecules 2014, 47, 5825–5838. [Google Scholar] [CrossRef] [Green Version]
- Romiszowski, P.; Sikorski, A. Properties of polymer sandwich brushes. Colloids Surf. A Physicochem. Eng. Asp. 2008, 321, 254–257. [Google Scholar] [CrossRef]
- Romiszowski, P.; Sikorski, A. The Monte Carlo dynamics of polymer chains in sandwich brushes. Rheol. Acta 2008, 47, 565–569. [Google Scholar] [CrossRef]
- Mendonça, A.; Goujon, F.; Malfreyt, P.; Tildedsley, D.J. Monte Carlo simulations of the static friction between two grafted polymer brushes. Phys. Chem. Chem. Phys. 2016, 18, 6164–6174. [Google Scholar] [CrossRef]
- Murat, M.; Grest, G.S. Interaction between grafted polymeric brushes: A molecular-dynamics study. Phys. Rev. Lett. 1989, 63, 1074–1077. [Google Scholar] [CrossRef]
- Goujon, F.; Ghoufi, A.; Malfreyt, P.; Tildesley, D.J. Frictional forces in polyelectrolyte brushes: Effects of sliding velocity, solvent quality and salt. Soft Matter 2012, 8, 4635–4644. [Google Scholar] [CrossRef]
- Goujon, F.; Ghoufi, A.; Malfreyt, P.; Tildesley, D.J. The kinetic friction coefficient of neutral and charged polymer brushes. Soft Matter 2013, 9, 2966–2972. [Google Scholar] [CrossRef]
- Hehmeyer, O.J.; Stevens, M.J. Molecular dynamics simulations of grafted polyelectrolytes on two apposing walls. J. Chem. Phys. 2005, 122, 134909. [Google Scholar] [CrossRef] [PubMed]
- Pakula, T. Simulation on the Completely Occupied Lattices. In Simulation Methods for Polymers; Kotelyanskii, M., Theodorou, D.N., Eds.; Marcel Dekker: New York, NY, USA, 2004. [Google Scholar]
- Polanowski, P.; Sikorski, A. Simulation of diffusion in a crowded environment. Soft Matter 2014, 10, 3597–3607. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.; Polanowski, P.; Matyjaszewski, K. Gelation in living copolymerization of monomer and divinyl cross linker: Comparison of ATRP experiments with Monte Carlo simulations. Macromolecules 2009, 42, 5925–5932. [Google Scholar] [CrossRef]
- Polanowski, P.; Jeszka, J.K.; Matyjaszewski, K. Modeling of branching and gelation in living copolymerization of monomer and divinyl cross-linker using dynamic lattice liquid model (DLL) and Flory–Stockmayer model. Polymer 2010, 51, 6084–6092. [Google Scholar] [CrossRef]
- Polanowski, P.; Jeszka, J.K.; Krysiak, K.; Matyjaszewski, K. Influence of intramolecular crosslinking on gelation in living copolymerization of monomer and divinyl cross-linker. Monte Carlo simulation studies. Polymer 2015, 79, 171–178. [Google Scholar] [CrossRef]
- Kozanecki, M.; Halagan, K.; Saramak, J.; Matyjaszewski, K. Diffusive properties of solvent molecules in the neighborhood of a polymer chain as seen by Monte-Carlo simulations. Soft Matter 2016, 12, 5519–5528. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matyjaszewski, K.; Dong, H.; Jakubowski, W.; Pietrasik, J.; Kusumo, A. Grafting from surfaces for “everyone”: ARGET ATRP in the presence of air. Langmuir 2007, 23, 4528–4531. [Google Scholar] [CrossRef] [PubMed]
- Matyjaszewski, K.; Miller, P.J.; Shukla, N.; Immaraporn, B.; Gelman, A.; Luokala, B.B.; Silovan, T.M.; Kickelbick, G.; Vallant, T.; Hoffmann, H.; et al. Polymers at interfaces: Using atom transfer radical polymerization in the controlled growth of homopolymers and block copolymers from silicon surfaces in the absence of untethered sacrificial initiator. Macromolecules 1999, 32, 8716–8724. [Google Scholar] [CrossRef]
- Tsuji, Y.; Ohno, K.; Yamamoto, S.; Goto, A.; Fukuda, T. Structure and properties of high-density polymer brushes prepared by surface-initiated living radical polymerization. Adv. Polym. Sci. 2006, 197, 1–45. [Google Scholar]
- Khabibullin, A.; Mastan, E.; Matyjaszewski, K.; Zhu, S. Surface-initiated atom transfer radical polymerization. Adv. Polym. Sci. 2016, 270, 29–76. [Google Scholar]
- Polanowski, P.; Jeszka, J.K.; Matyjaszewski, K. Polymer brush relaxation during and after polymerization—Monte Carlo simulation study. Polymer 2019, 173, 190–196. [Google Scholar] [CrossRef]
- Kiełbik, R.; Hałagan, K.; Zatorski, W.; Jung, J.; Ulański, J.; Napieralski, A.; Rudnicki, K.; Amrozik, P.; Jabłoński, G.; Stożek, D.; et al. ARUZ–Large-scale, Massively parallel FPGA-based Analyzer of Real Complex Systems. Comput. Phys. Commun. 2018, 232, 22–34. [Google Scholar] [CrossRef]
- Jung, J.; Polanowski, P.; Kiełbik, R.; Zatorski, W.; Ulański, J.; Napieralski, A.; Pakuła, T.; Hałagan, K. A Parallel Machine Having Operational Cells Located at Nodes of a Face Centered Lattice. European Patent EP3079073A1, 12 October 2016. [Google Scholar]
- Jung, J.; Polanowski, P.; Kiełbik, R.; Zatorski, W.; Ulański, J.; Napieralski, A.; Pakuła, T.; Hałagan, K. A Parallel Machine with Reduced Number of Connections between Logical Circuits. European Patent EP3079072A1, 12 October 2016. [Google Scholar]
- Jung, J.; Polanowski, P.; Kielbik, R.; Halagan, K.; Zatorski, W.; Ulański, J.; Napieralski, A.; Pakula, T. System of Electronic Modules Having a Redundant Configuration. European Patent EP3079066B1, 23 August 2017. [Google Scholar]
- Jung, J.; Polanowski, P.; Kielbik, R.; Halagan, K.; Zatorski, W.; Ulański, J.; Napieralski, A.; Pakula, T. A Panel with Electronic Circuits and a Set of Panels. European Patent EP3079071B1, 1 August 2018. [Google Scholar]
- Jung, J.; Kiełbik, R.; Hałagan, K.; Polanowski, P.; Sikorski, A. Technology of Real-World Analyzers (TAUR) and its practical application. Comput. Methods Sci. Technol. 2020, 26, 69–75. [Google Scholar]
- Teraoka, I. Polymer Solutions. An Introduction to Physical Properties; Wiley-Interscience: New York, NY, USA, 2002. [Google Scholar]
- Baschnagel, J.; Paul, W.; Tries, V.; Binder, K. Statics and dynamics of bidisperse polymer melt. A Monte Carlo study of the Bond-Fluctuation-Model. Macromolecules 1998, 31, 3856–3867. [Google Scholar] [CrossRef]
- Polanowski, P.; Pakula, T. Studies of mobility, interdiffusion, and self-diffusion in two-component mixtures using the dynamic lattice liquid model. J. Chem. Phys. 2003, 118, 11139–11146. [Google Scholar] [CrossRef]
- Ben-Avraham, D.; Havlin, S. Diffusion and Reactions in Fractals and Disordered Systems; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Wedemeier, A.; Merlitz, H.; Langowski, J. Anomalous diffusion in the presence of mobile obstacles. Europhys. Lett. 2009, 88, 38004. [Google Scholar] [CrossRef]
- Vilaseca, E.; Isvoran, A.; Madurga, S.; Pastor, L.; Garcés, J.L.; Mas, F. New insights into diffusion in 3D crowded media by Monte Carlo simulations: Effect of size, mobility and spatial distribution of obstacles. Phys. Chem. Chem. Phys. 2011, 13, 7396. [Google Scholar] [CrossRef] [Green Version]
- Eslami, H.; Müller-Plathe, F. How thick is the interphase in an ultrathin polymer film? Coarse-grained molecular dynamics simulations of polyamide-6,6 on graphene. J. Phys. Chem. C 2013, 117, 5249–5257. [Google Scholar] [CrossRef]
- Eslami, H.; Rahimi, M.; Müller-Plathe, F. Molecular dynamics simulation of a silica nanoparticle in oligomeric poly(methyl methacrylate): A model system for studying the interphase thickness in a polymer−nanocomposite via different properties. Macromolecules 2013, 46, 8680–8692. [Google Scholar] [CrossRef]
- Polanowski, P.; Sikorski, A. Diffusion of small particles in polymer films. J. Chem. Phys. 2017, 147, 014902. [Google Scholar] [CrossRef] [PubMed]
- Masaro, L.; Zhu, X.X. Physical models of diffusion for polymer solutions, gels and solids. Prog. Polym. Sci. 1999, 24, 731–775. [Google Scholar] [CrossRef]
- Mackie, J.S.; Meares, P. The diffusion of electrolytes in a cation-exchange resin membrane I. Theoretical. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1955, 232, 498–509. [Google Scholar]
- Yasuda, H.; Lamaze, C.E.; Ikenberry, L.D. Permeability of solutes through hydrated polymer membranes. Part I. Diffusion of sodium chloride. Makromol. Chem. 1968, 118, 19–35. [Google Scholar]
- Eslami, H.; Müller-Plathe, F. Structure and mobility of poly(ethylene terephthalate): A Molecular dynamics simulation study. Macromolecules 2009, 42, 8241–8250. [Google Scholar] [CrossRef]
- Golmohammadi, N.; Boland-Hemmat, M.; Barahmand, S.; Eslami, H. Coarse-grained molecular dynamics simulations of poly(ethylene terephthalate). J. Chem. Phys. 2020, 152, 114901. [Google Scholar] [CrossRef] [PubMed]
- Lang, M.; Werner, M.; Dockhorn, R.; Kreer, T. Arm retraction dynamics in dense polymer brushes. Macromolecules 2016, 49, 5190–5201. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hałagan, K.; Banaszak, M.; Jung, J.; Polanowski, P.; Sikorski, A. Dynamics of Opposing Polymer Brushes: A Computer Simulation Study. Polymers 2021, 13, 2758. https://doi.org/10.3390/polym13162758
Hałagan K, Banaszak M, Jung J, Polanowski P, Sikorski A. Dynamics of Opposing Polymer Brushes: A Computer Simulation Study. Polymers. 2021; 13(16):2758. https://doi.org/10.3390/polym13162758
Chicago/Turabian StyleHałagan, Krzysztof, Michał Banaszak, Jarosław Jung, Piotr Polanowski, and Andrzej Sikorski. 2021. "Dynamics of Opposing Polymer Brushes: A Computer Simulation Study" Polymers 13, no. 16: 2758. https://doi.org/10.3390/polym13162758
APA StyleHałagan, K., Banaszak, M., Jung, J., Polanowski, P., & Sikorski, A. (2021). Dynamics of Opposing Polymer Brushes: A Computer Simulation Study. Polymers, 13(16), 2758. https://doi.org/10.3390/polym13162758








