Thermal Behavior of Mixed Plastics at Different Heating Rates: I. Pyrolysis Kinetics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Thermal Decomposition Experiments
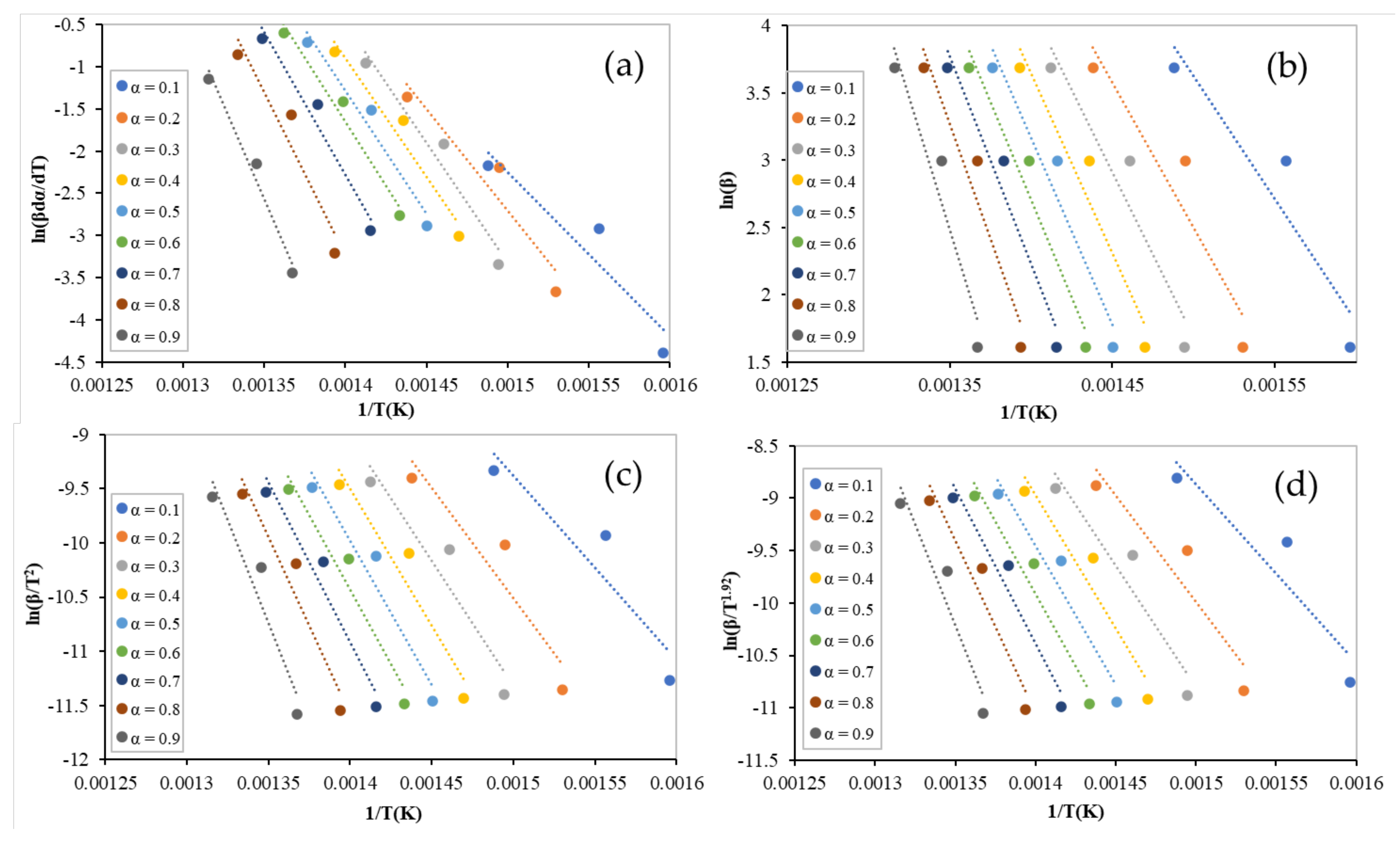
2.3. Kinetic Theory
3. Results and Discussion
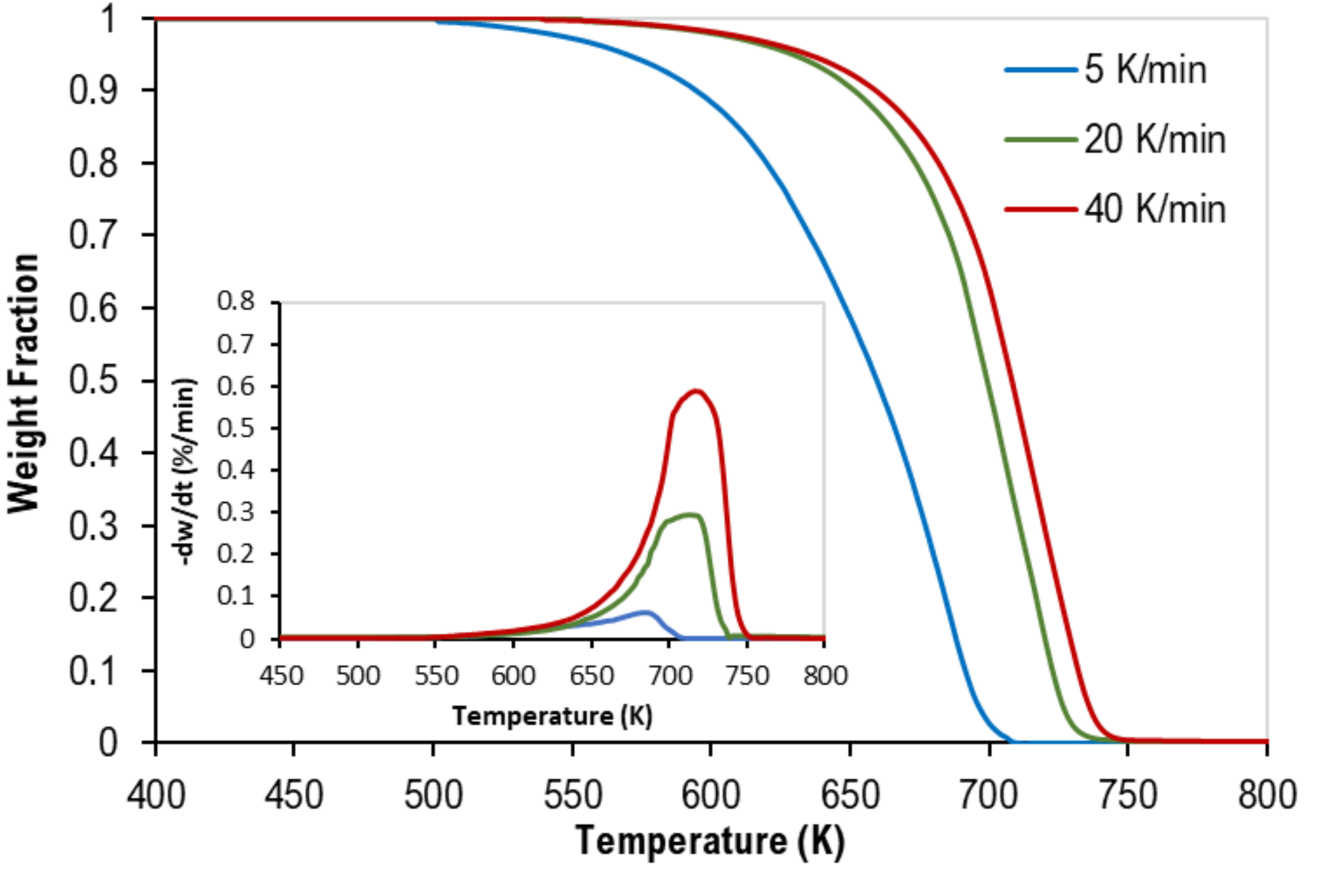
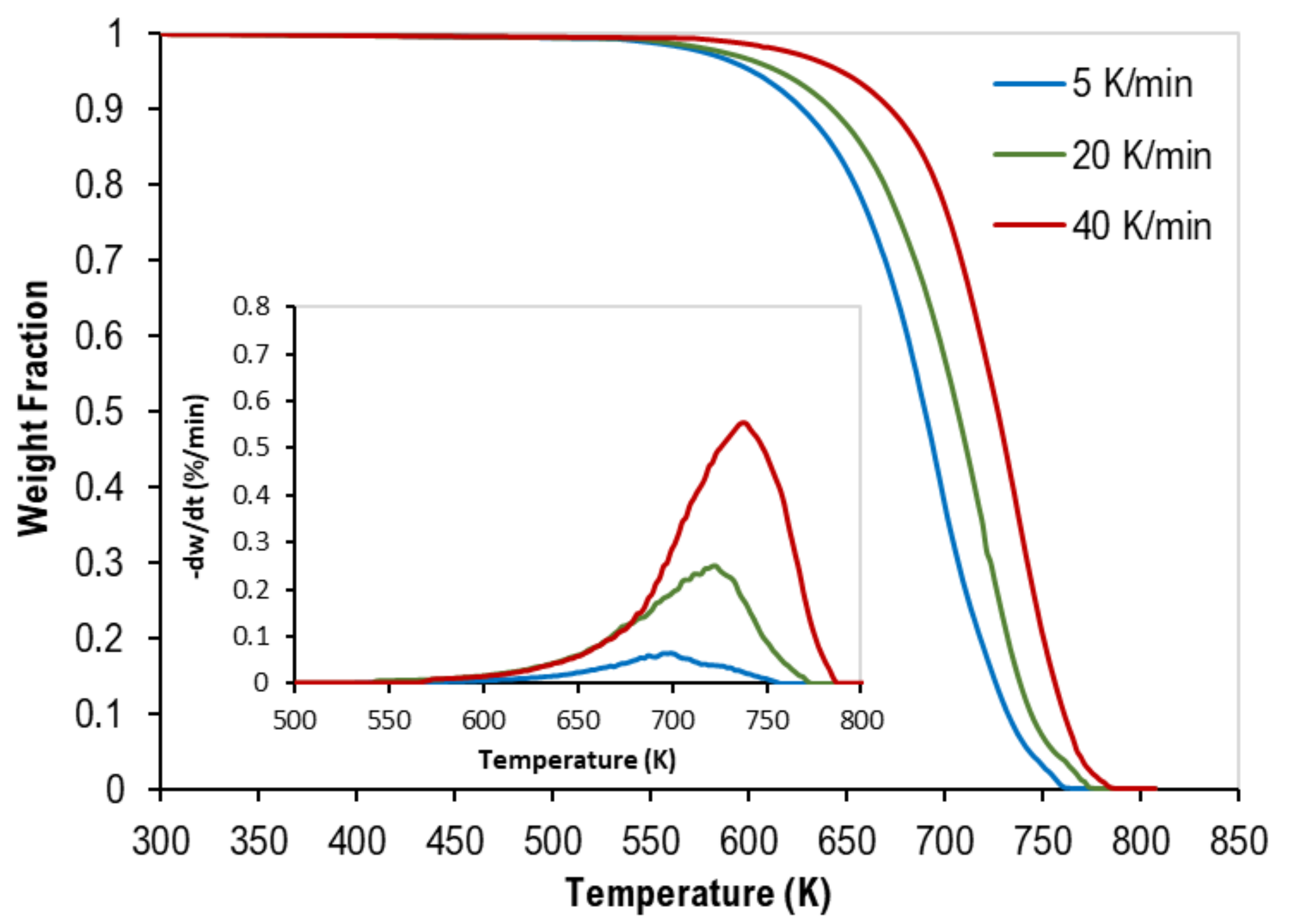
3.1. Thermogravimetric Analysis
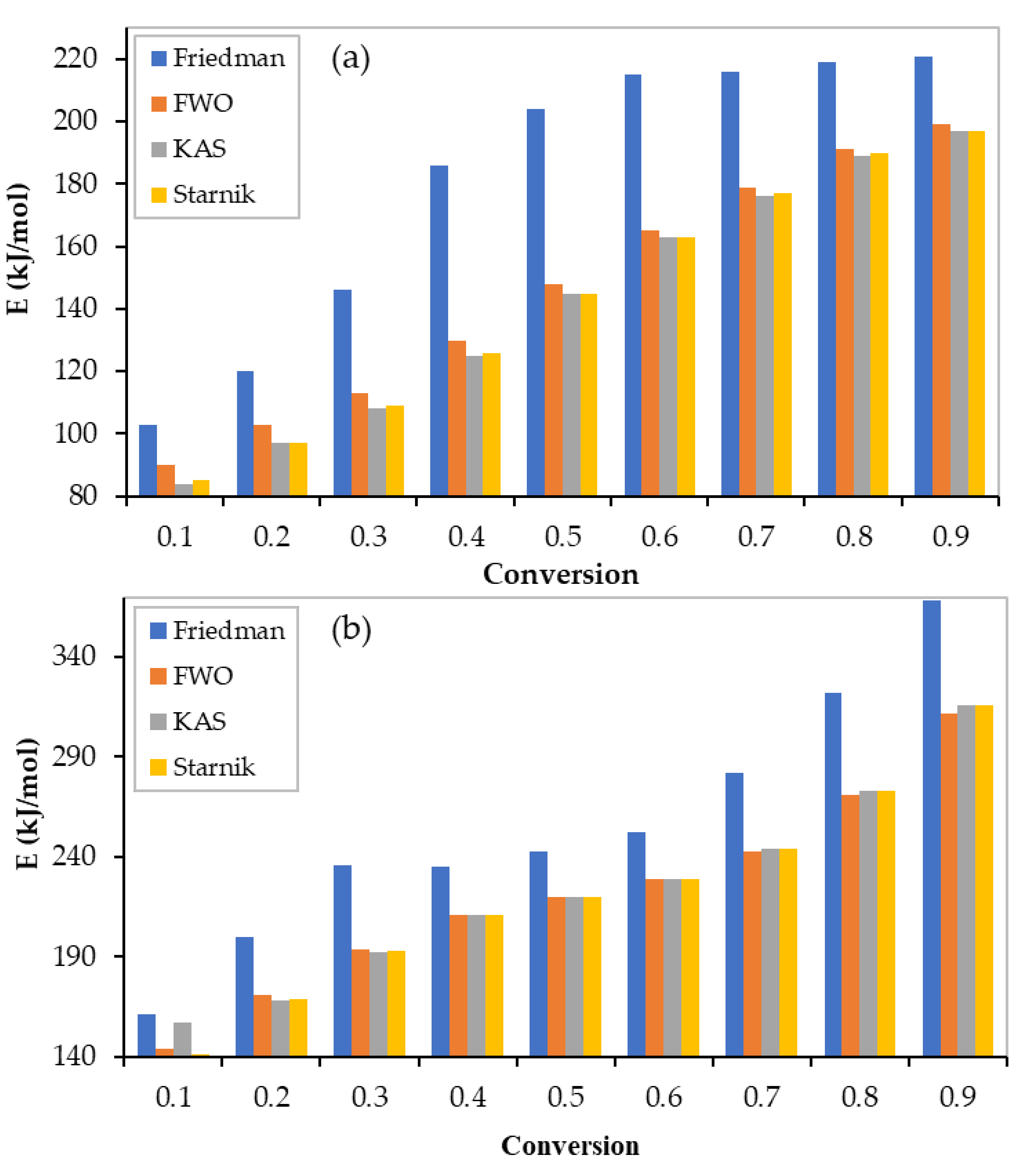
3.2. Activation Energy Determination
3.3. Reaction Mechanism Determination
3.4. Pre-Exponential Factor Determination
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Diaz Silvarrey, L.S.; Phan, A.N. Kinetic study of municipal plastic waste. Int. J. Hydrog. Energy 2016, 41, 16352–16364. [Google Scholar] [CrossRef] [Green Version]
- Thompson, R.C.; Moore, C.J.; Fvom Saal, F.S.; Swan, S.H. Plastics, the environment and human health: Current consensus and future trends. Philos. Trans. R. Soc. B Biol. Sci. 2009, 364, 2153–2166. [Google Scholar] [CrossRef] [PubMed]
- Hopewell, J.; Dvorak, R.; Kosior, E. Plastics recycling: Challenges and opportunities. Philos. Trans. R. Soc. B Biol. Sci. 2009, 364, 2115–2126. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, I.I.; Gupta, A.K. Hydrogen production from polystyrene pyrolysis and gasification: Characteristics and kinetics. Int. J. Hydrog. Energy 2009, 34, 6253–6264. [Google Scholar] [CrossRef]
- Arandes, J.; Abajo, I.; Lopez-Valerio, D.; Fernandez, I.; Azkoiti, M.J.; Olazar, M.; Bilbao, J. Transformation of several plastic wastes into fuels by catalytic cracking. Ind. Eng. Chem. Res. 1997, 36, 4523–4529. [Google Scholar] [CrossRef]
- Kaminsky, W.; Schlesselmann, B.; Simon, C.M. Thermal degradation of mixed plastic waste to aromatic and gas. Poly. Degrad. Stab. 1996, 53, 189–197. [Google Scholar] [CrossRef]
- Aguado, J.; Serrano, D.P.; San Miguel, G.; Castro, M.C.; Madrid, S. Feedstock recycling of polyethylene in a two-step thermo-catalytic reaction system. J. Anal. Appl. Pyrolysis 2007, 79, 415–423. [Google Scholar] [CrossRef]
- Rasul Jan, M.; Shah, J.; Gulab, H. Catalytic conversion of waste high-density polyethylene into useful hydrocarbons. Fuel 2013, 105, 595–602. [Google Scholar] [CrossRef]
- Wu, C.H.; Chang, C.Y.; Hor, J.L.; Shih, S.M.; Chen, L.W.; Chang, F.W. On The Thermal Treatment of Plastic Mixtures of MSW: Pyrolysis Kinetics. Waste Manag. 1993, 13, 221–235. [Google Scholar] [CrossRef]
- Chowlu, A.C.K.; Reddy, P.K.; Ghoshal, A.K. Pyrolytic decomposition and model-free kinetics analysis of mixture of polypropylene (PP) and low-density polyethylene (LDPE). Thermochim. Acta 2009, 485, 20–25. [Google Scholar] [CrossRef]
- Aboulkas, A.; El Harfi, K.; Bouadili, A. Thermal degradation behaviors of polyethylene and polypropylene. Part I: Pyrolysis Kinetics and Mechanisms. Energy Convers. Manag. 2010, 51, 1363–1369. [Google Scholar] [CrossRef]
- Yu, J.; Sun, L.; Ma, C.; Qiao, Y.; Yao, H. Thermal degradation of PVC: A review. Waste Manag. 2016, 48, 300–314. [Google Scholar] [CrossRef] [PubMed]
- Anene, A.F.; Fredriksen, S.B.; Sætre, K.A.; Tokheim, L.A. Experimental Study of Thermal and Catalytic Pyrolysis of Plastic Waste Components. Sustainability 2018, 10, 3979. [Google Scholar] [CrossRef] [Green Version]
- Mumbach, G.D.; Alves, J.L.F.; Silva, J.C.G.D.; Sena, R.F.D.; Marangoni, C.; Machado, R.A.F.; Bolzan, A. Thermal investigation of plastic solid waste pyrolysis via the deconvolution technique using the asymmetric double sigmoidal function: Determination of the kinetic triplet, thermodynamic parameters, thermal lifetime and pyrolytic oil composition for clean energy recovery. Energy Convers. Manag. 2019, 200, 112031. [Google Scholar] [CrossRef]
- Dubdub, I.; Al-Yaari, M. Pyrolysis of mixed plastic waste: I. Kinetic study. Materials 2020, 13, 4912. [Google Scholar] [CrossRef] [PubMed]
- Dubdub, I.; Al-Yaari, M. Pyrolysis of low density polyethylene: Kinetic study using TGA data and ANN prediction. Polymers 2020, 12, 891. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Al-Yaari, M.; Dubdub, I. Application of Artificial Neural Networks to Predict the Catalytic Pyrolysis of HDPE Using Non-Isothermal TGA Data. Polymers 2020, 12, 1813. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Wight, C.A. Model-free and model-fitting approaches to kinetic analysis of isothermal and nonisothermal data. Thermochim. Acta 1999, 340, 53–68. [Google Scholar] [CrossRef]
- Özsin, G.; Pütün, A.E. TGA/MS/FT-IR study for kinetic evaluation and evolved gas analysis of a biomass/PVC co-pyrolysis process. Energy Convers. Manag. 2019, 182, 143–153. [Google Scholar] [CrossRef]
- Xu, F.; Wang, B.; Yang, D.; Hao, J.; Qiao, Y.; Tian, Y. Thermal degradation of typical plastics under high heating rate conditions by TG-FTIR: Pyrolysis behaviors and kinetic analysis. Energy Convers. Manag. 2018, 171, 1106–1115. [Google Scholar] [CrossRef]
- Chen, R.; Li, Q.; Zhang, Y.; Xu, X.; Zhang, D. Pyrolysis kinetics and mechanism of typical industrial non-tyre rubber wastes by peak-differentiating analysis and multi kinetics methods. Fuel 2019, 235, 1224–1237. [Google Scholar] [CrossRef]
- Dubdub, I.; Al-Yaari, M. Pyrolysis of Mixed Plastic Waste: II. An Artificial Neural Networks Prediction and Sensitivity Analysis. Appl. Sci. 2021, 11, 8456. [Google Scholar] [CrossRef]


| Plastic | Proximate Analysis, wt% | Ultimate Analysis, wt% | |||||
|---|---|---|---|---|---|---|---|
| Moisture | Volatile | Ash | C | H | N | S | |
| PP | 0.08 | 99.63 | 0.29 | 85.00 | 14.73 | 0.04 | 0.23 |
| PS | 0.24 | 99.59 | 0.17 | 90.47 | 9.43 | 0.00 | 0.08 |
| LDPE | 0.20 | 99.65 | 0.15 | 83.00 | 16.75 | 0.00 | 0.25 |
| Test No. | Heating Rate (K/min) | Weight % | ||
|---|---|---|---|---|
| PP | PS | LDPE | ||
| 1 | 5 | 50 | 50 | 0 |
| 2 | 20 | 50 | 50 | 0 |
| 3 | 40 | 50 | 50 | 0 |
| 4 | 5 | 33.3 | 33.3 | 33.3 |
| 5 | 20 | 33.3 | 33.3 | 33.3 |
| 6 | 40 | 33.3 | 33.3 | 33.3 |
| Reaction Mechanism | ||
|---|---|---|
| Reaction-Order Models | ||
| First order (F1) | 1-α | |
| Second order (F2) | ||
| Third order (F3) | ||
| Diffusion Models | ||
| One-dimensional (D1) | ||
| Two-dimensional (D2) | ||
| Three-dimensional (D3) | ||
| Nucleation Models | ||
| Two-dimensional nucleation (A2) | ||
| Three-dimensional nucleation (A3) | ||
| Four-dimensional nucleation (A4) | ||
| Geometrical Contraction Models | ||
| Prout–Tompkins (R1) | 1 | |
| Contracting cylinder (R2) | ||
| Contracting sphere (R3) | ||
| Power Law Models | ||
| Power law (P2) | ||
| Power law (P3) | ||
| Power law (P4) |
| Test No. | Heating Rate (K/min) | Weight % | Onset Temp. (K) | Peak Temp. (K) | Final Temp. (K) | ||
|---|---|---|---|---|---|---|---|
| PP | PS | LDPE | |||||
| 1 | 5 | 50 | 50 | 0 | 500 | 686 | 708 |
| 2 | 20 | 50 | 50 | 0 | 550 | 720 | 734 |
| 3 | 40 | 50 | 50 | 0 | 560 | 730 | 750 |
| 4 | 5 | 33.3 | 33.3 | 33.3 | 540 | 690 | 760 |
| 5 | 20 | 33.3 | 33.3 | 33.3 | 610 | 720 | 775 |
| 6 | 40 | 33.3 | 33.3 | 33.3 | 630 | 735 | 785 |
| Conversion | Differential Method | Integral Methods | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Friedman | FWO | KAS | Starink | Average Values | ||||||
| R2 | R2 | R2 | R2 | R2 | ||||||
| 0.1 | 103 | 0.9663 | 90 | 0.9458 | 84 | 0.9329 | 85 | 0.9335 | 86 | 0.9374 |
| 0.2 | 120 | 0.9668 | 103 | 0.9525 | 97 | 0.9423 | 97 | 0.9428 | 99 | 0.9459 |
| 0.3 | 146 | 0.9803 | 113 | 0.9562 | 108 | 0.9476 | 109 | 0.948 | 110 | 0.9506 |
| 0.4 | 186 | 0.9911 | 130 | 0.9641 | 125 | 0.9579 | 126 | 0.9582 | 127 | 0.9601 |
| 0.5 | 204 | 0.9887 | 148 | 0.9709 | 145 | 0.9665 | 145 | 0.9667 | 146 | 0.9680 |
| 0.6 | 215 | 0.9915 | 165 | 0.9756 | 163 | 0.9723 | 163 | 0.9724 | 164 | 0.9734 |
| 0.7 | 216 | 0.9852 | 179 | 0.9783 | 176 | 0.9755 | 177 | 0.9756 | 177 | 0.9765 |
| 0.8 | 219 | 0.9888 | 191 | 0.9724 | 189 | 0.9691 | 190 | 0.9693 | 190 | 0.9703 |
| 0.9 | 221 | 0.995 | 199 | 0.9867 | 197 | 0.9852 | 197 | 0.9852 | 198 | 0.9857 |
| Average | 181 | 0.9837 | 146 | 0.9669 | 142 | 0.961 | 143 | 0.9613 | 144 | 0.9631 |
| Conversion | Differential Method | Integral Methods | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Friedman | FWO | KAS | Starink | Average Values | ||||||
| E (kJ/mol) | R2 | R2 | R2 | R2 | R2 | |||||
| 0.1 | 161 | 0.8895 | 144 | 0.8859 | 157 | 0.8696 | 141 | 0.8703 | 147 | 0.8753 |
| 0.2 | 200 | 0.9164 | 171 | 0.898 | 168 | 0.8852 | 169 | 0.8858 | 169 | 0.8897 |
| 0.3 | 236 | 0.9549 | 194 | 0.9164 | 192 | 0.9069 | 193 | 0.9073 | 193 | 0.9102 |
| 0.4 | 235 | 0.9561 | 211 | 0.9363 | 211 | 0.9294 | 211 | 0.9297 | 211 | 0.9318 |
| 0.5 | 243 | 0.9645 | 220 | 0.948 | 220 | 0.9424 | 220 | 0.9427 | 220 | 0.9444 |
| 0.6 | 252 | 0.9731 | 229 | 0.9562 | 229 | 0.9516 | 229 | 0.9518 | 229 | 0.9532 |
| 0.7 | 282 | 0.9608 | 243 | 0.9563 | 244 | 0.952 | 244 | 0.9522 | 244 | 0.9535 |
| 0.8 | 322 | 0.9232 | 271 | 0.9395 | 273 | 0.9342 | 273 | 0.9344 | 272 | 0.9360 |
| 0.9 | 368 | 0.9749 | 312 | 0.9265 | 316 | 0.921 | 316 | 0.9212 | 315 | 0.9229 |
| Average | 255 | 0.9459 | 222 | 0.9292 | 223 | 0.9213 | 222 | 0.9217 | 222 | 0.9241 |
| Reaction Mechanism | 5 K/min | 20 K/min | 40 K/min | Average Values | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | R2 | R2 | R2 | |||||
| F1 | 87 | 0.9998 | 182 | 0.9992 | 188 | 0.9997 | 152 | 0.9996 |
| F2 | 110 | 0.9981 | 259 | 0.9933 | 271 | 0.9945 | 213 | 0.9953 |
| F3 | 137 | 0.9941 | 352 | 0.9837 | 372 | 0.9863 | 287 | 0.9880 |
| D1 | 144 | 0.9976 | 258 | 0.995 | 261 | 0.9958 | 221 | 0.9961 |
| D2 | 156 | 0.9989 | 292 | 0.9977 | 297 | 0.9983 | 248 | 0.9983 |
| D3 | 170 | 0.9996 | 333 | 0.9992 | 341 | 0.9997 | 281 | 0.9995 |
| A2 | 38 | 0.9998 | 85 | 0.9991 | 88 | 0.9996 | 70 | 0.9995 |
| A3 | 22 | 0.9997 | 53 | 0.999 | 55 | 0.9996 | 43 | 0.9994 |
| A4 | 14 | 0.9995 | 37 | 0.9989 | 38 | 0.9996 | 30 | 0.9993 |
| R1 | 67 | 0.9972 | 123 | 0.9945 | 125 | 0.9954 | 105 | 0.9957 |
| R2 | 76 | 0.9992 | 151 | 0.9986 | 154 | 0.9992 | 127 | 0.9990 |
| R3 | 80 | 0.9996 | 161 | 0.9992 | 165 | 0.9997 | 135 | 0.9995 |
| P2 | 28 | 0.9957 | 56 | 0.9932 | 56 | 0.9943 | 47 | 0.9944 |
| P3 | 15 | 0.9931 | 33 | 0.9914 | 34 | 0.9928 | 27 | 0.9924 |
| P4 | 9 | 0.9877 | 22 | 0.9888 | 22 | 0.9906 | 18 | 0.9890 |
| Reaction Mechanism | 5 K/min | 20 K/min | 40 K/min | Average Values | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | R2 | R2 | R2 | |||||
| F1 | 120 | 0.9996 | 114 | 0.9992 | 143 | 0.9999 | 126 | 0.9996 |
| F2 | 176 | 0.9962 | 152 | 0.9962 | 181 | 0.9993 | 170 | 0.9972 |
| F3 | 244 | 0.9903 | 196 | 0.9924 | 224 | 0.9971 | 221 | 0.9933 |
| D1 | 165 | 0.9955 | 176 | 0.9998 | 233 | 0.998 | 191 | 0.9978 |
| D2 | 190 | 0.9979 | 195 | 1 | 253 | 0.9989 | 213 | 0.9989 |
| D3 | 220 | 0.9994 | 217 | 0.9998 | 275 | 0.9996 | 237 | 0.9996 |
| A2 | 54 | 0.9996 | 51 | 0.9991 | 66 | 0.9999 | 57 | 0.9995 |
| A3 | 32 | 0.9995 | 30 | 0.9989 | 40 | 0.9998 | 34 | 0.9994 |
| A4 | 21 | 0.9993 | 20 | 0.9986 | 27 | 0.9998 | 23 | 0.9992 |
| R1 | 77 | 0.9948 | 82 | 0.9997 | 111 | 0.9977 | 90 | 0.9974 |
| R2 | 97 | 0.9987 | 97 | 0.9999 | 126 | 0.9993 | 107 | 0.9993 |
| R3 | 104 | 0.9993 | 103 | 0.9998 | 132 | 0.9996 | 113 | 0.9996 |
| P2 | 33 | 0.9926 | 35 | 0.9996 | 49 | 0.9971 | 39 | 0.9964 |
| P3 | 18 | 0.9889 | 20 | 0.9994 | 29 | 0.9961 | 22 | 0.9948 |
| P4 | 11 | 0.9817 | 12 | 0.999 | 19 | 0.9947 | 14 | 0.9918 |
| Conversion | ln (A) (ln min−1) | |||
|---|---|---|---|---|
| Friedman | FWO | KAS | Starink | |
| 0.1 | 16.58 | 14.09 | 13.41 | 14.00 |
| 0.2 | 19.81 | 16.58 | 15.82 | 16.41 |
| 0.3 | 24.70 | 18.72 | 17.92 | 18.52 |
| 0.4 | 31.85 | 21.81 | 20.97 | 21.57 |
| 0.5 | 34.81 | 25.28 | 24.42 | 25.02 |
| 0.6 | 36.71 | 28.39 | 27.50 | 28.10 |
| 0.7 | 36.79 | 30.71 | 29.80 | 30.40 |
| 0.8 | 37.44 | 32.98 | 32.06 | 32.66 |
| 0.9 | 37.96 | 34.28 | 33.34 | 33.94 |
| Average | 30.74 | 24.76 | 23.92 | 24.52 |
| Conversion | ln (A) (ln min−1) | |||
|---|---|---|---|---|
| Friedman | FWO | KAS | Starink | |
| 0.1 | 27.19 | 23.22 | 23.32 | 23.92 |
| 0.2 | 34.13 | 27.96 | 27.99 | 28.59 |
| 0.3 | 40.38 | 32.04 | 32.03 | 32.63 |
| 0.4 | 40.21 | 35.12 | 35.07 | 35.68 |
| 0.5 | 41.66 | 36.57 | 36.50 | 37.10 |
| 0.6 | 43.50 | 38.15 | 38.06 | 38.66 |
| 0.7 | 48.80 | 40.67 | 40.55 | 41.16 |
| 0.8 | 55.84 | 45.41 | 45.26 | 45.87 |
| 0.9 | 64.05 | 52.45 | 52.28 | 52.89 |
| Average | 43.97 | 36.84 | 36.78 | 37.39 |
| Mixture | Binary | Ternary | |||
|---|---|---|---|---|---|
| Polymers | PS | PP | PS | PP | LDPE |
| Composition (wt %) | 50 | 50 | 33.3 | 33.3 | 33.3 |
| Reaction Mechanism | F1 | F3 | |||
| (kJ/mol) | |||||
| Differential Model (Friedman) | 181 | 255 | |||
| Integral Models (FWO, KAS, and Starink) | 144 ± 2 * | 222.3 ± 0.6 * | |||
| ln A (ln min−1) | |||||
| Differential Model (Friedman) | 30.74 | 43.97 | |||
| Integral Models (FWO, KAS, and Starink) | 24.4 ± 0.4 * | 37 ± 0.3 * | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dubdub, I.; Al-Yaari, M. Thermal Behavior of Mixed Plastics at Different Heating Rates: I. Pyrolysis Kinetics. Polymers 2021, 13, 3413. https://doi.org/10.3390/polym13193413
Dubdub I, Al-Yaari M. Thermal Behavior of Mixed Plastics at Different Heating Rates: I. Pyrolysis Kinetics. Polymers. 2021; 13(19):3413. https://doi.org/10.3390/polym13193413
Chicago/Turabian StyleDubdub, Ibrahim, and Mohammed Al-Yaari. 2021. "Thermal Behavior of Mixed Plastics at Different Heating Rates: I. Pyrolysis Kinetics" Polymers 13, no. 19: 3413. https://doi.org/10.3390/polym13193413
APA StyleDubdub, I., & Al-Yaari, M. (2021). Thermal Behavior of Mixed Plastics at Different Heating Rates: I. Pyrolysis Kinetics. Polymers, 13(19), 3413. https://doi.org/10.3390/polym13193413








