Computational Modeling of Chromatin Fiber to Characterize Its Organization Using Angle-Resolved Scattering of Circularly Polarized Light
Abstract
:1. Introduction
2. Materials and Method
2.1. Computational Method
2.2. Chromatin Fiber Model
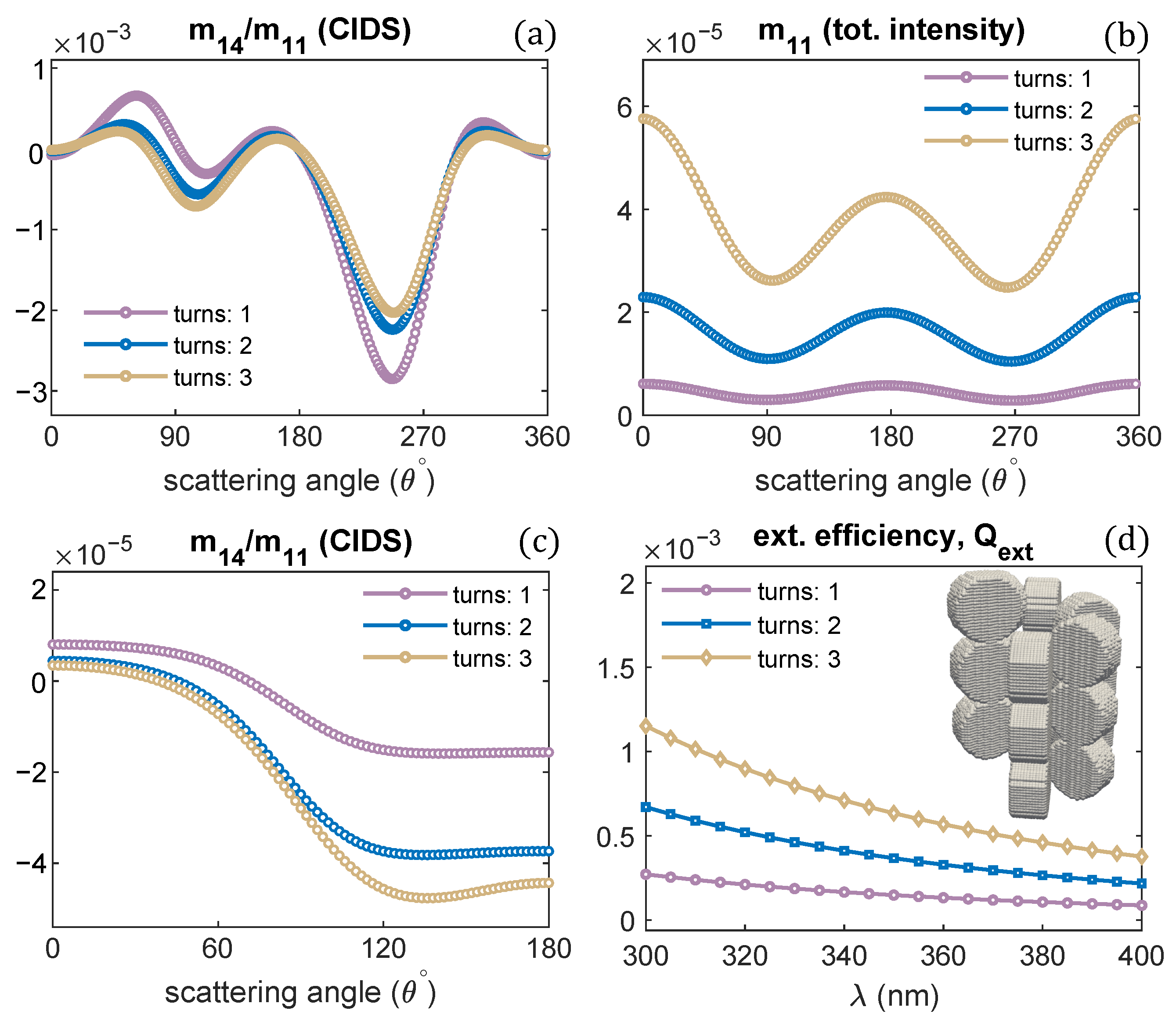
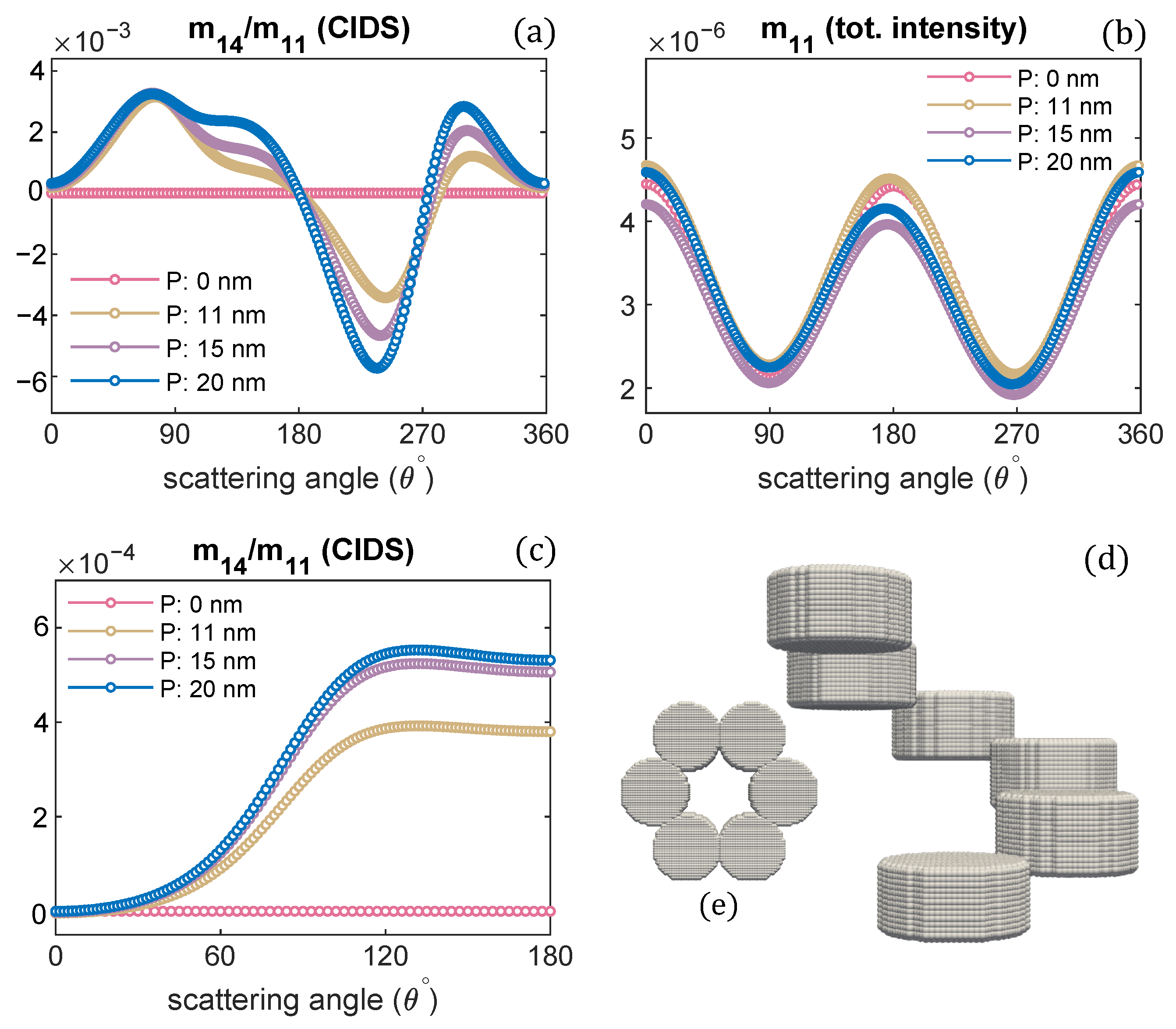
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CIDS | Circular intensity differential scattering |
| CD | Circular dichroism |
| DDA | Discrete dipole approximation |
| ADDA | DDA code |
| LCP | Left circularly polarized |
| RCP | Right circularly polarized |
References
- Kornberg, R.D.; Lorch, Y. Twenty-five years of the nucleosome, fundamental particle of the eukaryote chromosome. Cell 1999, 98, 285–294. [Google Scholar] [CrossRef] [Green Version]
- Luger, K.; Dechassa, M.L.; Tremethick, D.J. New insights into nucleosome and chromatin structure: An ordered state or a disordered affair? Nat. Rev. Mol. Cell. Biol. 2012, 13, 436–447. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Horng, D.O.; Phan, S.; Deerinck, T.J.; Thor, A.; Ellisman, M.H.; O’Shea, C.C. ChromEMT: Visualizing 3D chromatin structure and compaction in interphase and mitotic cells. Science 2017, 357, eaag0025. [Google Scholar]
- Ma, Y.; Kanakousaki, K.; Buttitta, L. How the cell cycle impacts chromatin architecture and influences cell fate. Front. Genet. 2015, 6, 19. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Groth, A.; Rocha, W.; Verreault, A.; Almouzni, G. Chromatin challenges during DNA replication and repair. Cell 2007, 128, 721–733. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cainero, I.; Cerutti, E.; Faretta, M.; Dellino, G.I.; Pelicci, P.G.; Bianchini, P.; Vicidomini, G.; Diaspro, A.; Lanzanò, L. Chromatin investigation in the nucleus using a phasor approach to structured illumination microscopy. Biophys. J. 2021, 120, 2566–2576. [Google Scholar] [CrossRef]
- Schermelleh, L.; Ferrand, A.; Huser, T.; Eggeling, C.; Sauer, M.; Biehlmaier, O.; Drummen, G.P. Super-resolution microscopy demystified. Nat. Cell Biol. 2019, 21, 72–84. [Google Scholar] [CrossRef]
- Dong, B.; Almassalha, L.M.; Stypula-Cyrus, Y.; Urban, B.E.; Chandler, J.E.; Nguyen, T.Q.; Sun, C.; Zhang, H.F.; Backman, V. Superresolution intrinsic fluorescence imaging of chromatin utilizing native, unmodified nucleic acids for contrast. Proc. Natl. Acad. Sci. USA 2016, 113, 9716–9721. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, F.; Chen, P.; Sun, D.; Wang, M.; Dong, L.; Liang, D.; Xu, R.M.; Zhu, P.; Li, G. Cryo-EM Study of the chromatin fiber reveals a double Helix twisted by tetranucleosomal Units. Science 2014, 344, 376–380. [Google Scholar] [CrossRef]
- Eltsov, M.; MacLellan, K.M.; Maeshima, K.; Frangakis, A.S.; Dubochet, J. Analysis of cryo-electron microscopy images does not support the existence of 30-nm chromatin fibers in mitotic chromosomes in situ. Proc. Natl. Acad. Sci. USA 2008, 105, 19732–19737. [Google Scholar] [CrossRef] [Green Version]
- Kostiuk, G.; Bucevičius, J.; Gerasimaitė, R.; Lukinavičius, G. Application of STED imaging for chromatin studies. J. Phys. D Appl. Phys. 2019, 52, 504003. [Google Scholar] [CrossRef] [Green Version]
- Lukinavičius, G.; Umezawa, K.; Olivier, N.; Honigmann, A.; Yang, G.; Plass, T.; Mueller, V.; Reymond, L.; Corrêa, I.R., Jr.; Luo, Z.G. A near-infrared fluorophore for live-cell super-resolution microscopy of cellular proteins. Nat. Chem. 2013, 5, 132–139. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Hovenier, J.W.; Travis, L.E. Light Scattering by Nonspherical Particles Theory, Measurements, and Applications; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Yao, F.; Yu, W.; Liu, C.; Su, Y.; You, Y.; Ma, H.; Qiao, R.; Wu, C.; Ma, C.; Gao, P.; et al. Complete structural characterization of single carbon nanotubes by Rayleigh scattering circular dichroism. Nat. Nanotechnol. 2021. [Google Scholar] [CrossRef] [PubMed]
- Tuchin, V.V. Polarized light interaction with tissues. J. Biomed. Opt. 2016, 21, 071114. [Google Scholar] [CrossRef] [Green Version]
- Diaspro, A.; Bertolotto, M.; Vergani, L.; Nicolini, C. Polarized light scattering of nucleosomes and polynucleosomes-in situ and in vitro studies. IEEE. Trans. Biomed. Eng. 1991, 38, 670–678. [Google Scholar] [CrossRef] [PubMed]
- Alali, S.; Vitkin, A. Polarized light imaging in biomedicine: Emerging Mueller matrix methodologies for bulk tissue assessment. J. Biomed. Opt. 2015, 20, 061104. [Google Scholar] [CrossRef] [PubMed]
- Le Gratiet, A.; Lanzano, L.; Bendandi, A.; Marongiu, R.; Bianchini, P.; Sheppard, C.; Diaspro, A. Phasor approach of Mueller matrix optical scanning microscopy for biological tissue imaging. Biophys. J. 2021, 120, 3112–3125. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.R.; Saytashev, I.; Du Le, V.N.; Mahendroo, M.; Ramella-Roman, J.; Novikova, T. Mueller matrix imaging for collagen scoring in mice model of pregnancy. Sci. Rep. 2021, 11, 15621. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley and Sons: New York, NY, USA, 1998. [Google Scholar]
- Roy-Brehonnet, F.L.; Jeune, B.L. Utilization of Mueller matrix formalism to obtain optical targets depolarization and polarization properties. Prog. Quantum. Electron. 1997, 21, 109–151. [Google Scholar] [CrossRef]
- Qi, J.; Elson, D.S. Mueller polarimetric imaging for surgical and diagnostic applications: A review. J. Biophotonics 2017, 10, 950–982. [Google Scholar] [CrossRef] [Green Version]
- Lu, S.Y.; Chipman, R.A. Interpretation of Mueller matrices based on polar decomposition. J. Opt. Soc. Am. A 1996, 13, 1106–1113. [Google Scholar] [CrossRef]
- He, H.; Liao, R.; Zeng, N.; Li, P.; Chen, Z.; Liu, X.; Ma, H. Mueller matrix polarimetry—An emerging new tool for characterizing the microstructural feature of complex biological specimen. J. Light. Technol. 2019, 37, 2534–2548. [Google Scholar] [CrossRef]
- Dong, Y.; Liu, S.; Shen, Y.; He, H.; Ma, H. Probing variations of fibrous structures during the development of breast ductal carcinoma tissues via Mueller matrix imaging. Biomed. Opt. Express 2020, 11, 4960–4975. [Google Scholar] [CrossRef] [PubMed]
- Bagge, L.E.; Kenton, A.C.; Lyons, B.A.; Wehling, M.F.; Goldstein, D.H. Mueller matrix characterizations of circularly polarized reflections from golden scarab beetles. Appl. Opt. 2020, 59, F85–F93. [Google Scholar] [CrossRef] [PubMed]
- Ray, S.K.; Chandel, S.; Singh, A.K.; Kumar, A.; Mandal, A.; Misra, S.; Mitra, P.; Ghosh, N. Polarization-tailored fano interference in plasmonic crystals: A Mueller matrix model of anisotropic fano resonance. ACS Nano 2017, 11, 1641–1648. [Google Scholar] [CrossRef] [Green Version]
- Fricke, D.; Becker, A.; Heratizadeh, A.; Knigge, S.; Jütte, L.; Wollweber, M.; Werfel, T.; Roth, B.W.; Glasmacher, B. Mueller Matrix Analysis of Collagen and Gelatin Containing Samples Towards More Objective Skin Tissue Diagnostics. Polymers 2020, 12, 1400. [Google Scholar] [CrossRef]
- Tinoco, I.J.; Mickols, W.; Maestre, M.F.; Bustamante, C. Absorption, scattering, and imaging of biomolecular structures with polarized light. Annu. Rev. Phys. Chem. 1987, 16, 319–349. [Google Scholar] [CrossRef]
- Bustamante, C.; Tinoco, I.; Maestre, M.F. Circular differential scattering can be an important Part of the circular dichroism of macromolecules. Proc. Natl. Acad. Sci. USA 1983, 80, 3568–3572. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.; Campbell, A.; Leoni, J.; Theng, Y.; Markus, C.; Lakhwan, M. Circular intensity differential scattering reveals the internal structure of polymer fibrils. J. Phys. Chem. Lett. 2019, 10, 7547–7553. [Google Scholar] [CrossRef]
- Ashraf, M.W.; Ranjan, R.; Diaspro, A. Circular intensity differential scattering of light to characterize the coronavirus particles. J. Opt. Soc. Am. B 2021, 38, 1702–1709. [Google Scholar] [CrossRef]
- Diaspro, A.; Radicchi, G.; Nicolini, C. Polarized light scattering: A biophysical method for studying bacterial cells. IEEE. Trans. Biomed. Eng. 1995, 42, 1038–1043. [Google Scholar] [CrossRef]
- Le Gratiet, A.; Marongiu, R.; Diaspro, A. Circular intensity differential scattering for label-free chromatin characterization: A review for optical microscopy. Polymers 2020, 12, 2428. [Google Scholar] [CrossRef] [PubMed]
- Diaspro, A.; Nicolini, C.A. Circular intensity differential scattering and chromatin-DNA structure. Cell Biophy. 1987, 10, 45–60. [Google Scholar] [CrossRef] [PubMed]
- Singham, S.B.; Patterson, C.W.; Salzman, G.C. Polarizabilities for light scattering from chiral particles. J. Chem. Phys. 1986, 85, 763–770. [Google Scholar] [CrossRef]
- Shapiro, D.B.; Maestre, M.F.; McClain, W.M.; Hull, P.G.; Shi, Y.; Quinby-Hunt, M.S.; Hearst, J.E.; Hunt, A.J. Determination of the average orientation of DNA in the octopus sperm eledone cirrhossa through polarized light scattering. Appl. Opt. 1994, 33, 5733–5744. [Google Scholar] [CrossRef] [PubMed]
- Kaczmarczyk, A.; Meng, H.; Ordu, O.; Noort, J.V.; Dekker, N.H. Chromatin fibers stabilize nucleosomes under torsional stress. Nat. Commun. 2020, 11, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Le Gratiet, A.; Pesce, L.; Oneto, M.; Marongiu, R.; Zanini, G.; Bianchini, P.; Diaspro, A. Circular intensity differential scattering (CIDS) scanning microscopy to image chromatin-DNA nuclear organization. OSA Contin. 2018, 1, 1068–1078. [Google Scholar] [CrossRef] [Green Version]
- Bustamante, C.; Tinoco, I.; Maestre, M.F. Circular intensity differential scattering of light. IV. Randomly oriented species. J. Chem. Phys. 1982, 76, 3440–3446. [Google Scholar] [CrossRef] [Green Version]
- Ye, L.; Yang, L.; Zheng, X.; Mukamel, S. Enhancing circular dichroism signals with vector beams. Phys. Rev. Lett. 2021, 126, 123001. [Google Scholar] [CrossRef]
- Lasa-Alonso, J.; Abujetas, D.R.; Nodar, Á.; Dionne, J.A.; Sáenz, J.J.; Molina-Terriza, G.; Aizpurua, J.; García-Etxarri, A. Surface-enhanced circular dichroism spectroscopy on periodic dual nanostructures. ACS Photonics 2020, 7, 2978–2986. [Google Scholar] [CrossRef]
- Lazzari, F.; Manfredi, A.; Alongi, J.; Mendichi, R.; Ganazzoli, F.; Raffaini, G.; Ferruti, P.; Ranucci, E. Self-Structuring in Water of Polyamidoamino Acids with Hydrophobic Side Chains Deriving from Natural α-Amino Acids. Polymers 2018, 10, 1261. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hirose, D.; Nozaki, S.; Kanoh, S.; Maeda, K. Synthesis of Amphiphilic Block Copolymers Containing Chiral Polythiophene Chains and Their Micelle Formation and Chiroptical Properties. Polymers 2018, 10, 718. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mohebi, A.; Le Gratiet, A.; Marongiu, R.; Callegari, F.; Bianchini, P.; Diaspro, A. Combined approach using circular intensity differential scattering microscopy under phasor map data analysis. Appl. Opt. 2021, 60, 1558–1565. [Google Scholar] [CrossRef] [PubMed]
- Marongiu, R.; Le Gratiet, A.; Pesce, L.; Bianchini, P.; Diaspro, A. ExCIDS: A combined approach coupling Expansion Microscopy (ExM) and Circular Intensity Differential Scattering (CIDS) for chromatin-DNA imaging. OSA Contin. 2020, 3, 1770–1780. [Google Scholar] [CrossRef]
- Draine, B.T.; Flatau, P.J. Discrete-dipole approximation for scattering calculations. J. Opt. Soc. Am. A 1994, 11, 1491–1499. [Google Scholar] [CrossRef]
- Loke, V.L.Y.; Mengüç, M.P.; Nieminen, T.A. Discrete-dipole approximation with surface interaction: Computational toolbox for MATLAB. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 1711–1725. [Google Scholar] [CrossRef]
- Yurkin, M.A.; Hoekstra, A.G. The discrete dipole approximation: An overview and recent developments. J. Quant. Spectrosc. Radiat. Transf. 2007, 106, 558–589. [Google Scholar] [CrossRef] [Green Version]
- Yurkin, M.A.; Hoekstra, A.G. The discrete-dipole-approximation code ADDA: Capabilities and known limitations. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 2234–2247. [Google Scholar] [CrossRef]
- Antti, P.; Zubko, E.; Lumme, K.; Muinonen, K.; Yurkin, M.A.; Draine, B.; Rahola, J.; Hoekstra, A.G.; Shkuratov, Y. Comparison between discrete dipole implementations and exact techniques. J. Quant. Spectrosc. Radiat. Transf. 2007, 106, 417–436. [Google Scholar]
- Konokhova, A.I.; Yurkin, M.A.; Moskalensky, A.E.; Chernyshev, A.V.; Tsvetovskaya, G.A.; Chikova, E.D.; Maltsev, V.P. Light-scattering flow cytometry for identification and characterization of blood microparticles. J. Biomed. Opt. 2012, 17, 057006. [Google Scholar] [CrossRef]
- Jain, P.K.; Lee, K.S.; El-Sayed, I.H.; El-Sayed, M.A. Calculated absorption and scattering properties of gold nanoparticles of different size, shape, and composition: Applications in biological imaging and biomedicine. J. Phys. Chem. B 2006, 110, 7238–7248. [Google Scholar] [CrossRef] [Green Version]
- Dong, J.; Zhang, W.; Liu, L. Discrete dipole approximation method for electromagnetic scattering by particles in an absorbing host medium. Opt. Express 2021, 29, 7690–7705. [Google Scholar] [CrossRef] [PubMed]
- Sakaguchi, N.; Matsumoto, S.; Kunisada, Y.; Ueda, M. Interaction of localized surface plasmons of a silver nanosphere dimer embedded in a uniform medium: Scanning transmission electron microscopy electron energy-loss spectroscopy and discrete dipole approximation simulation. J. Phys. Chem. C 2019, 123, 6735–6744. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, A.Q.; Li, H.J.; Qian, D.J.; Chen, M. Synthesis, study, and discrete dipole approximation simulation of Ag-Au bimetallic nanostructures. Nanoscale Res. Lett. 2016, 11, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baker, M.; Liu, W.; McLeod, E. Accurate and fast modeling of scattering from random arrays of nanoparticles using the discrete dipole approximation and angular spectrum method. Opt. Express 2021, 29, 22761–22777. [Google Scholar] [CrossRef] [PubMed]
- Schuh, R. Arbitrary particle shape modeling in DDSCAT and validation of simulation results. In Proceedings of the DDA-Workshop, Bremen, Germany, 23 March 2007; pp. 22–24. [Google Scholar]
- Olins, D.E.; Olins, A.L. Chromatin history: Our view from the bridge. Nat. Rev. Mol. Cell Biol. 2003, 4, 809–814. [Google Scholar] [CrossRef] [PubMed]
- Kepper, N.; Foethke, D.; Stehr, R.; Wedemann, G.; Rippe, K. Nucleosome geometry and internucleosomal interactions control the chromatin fiber conformation. Biophys. J. 2008, 95, 3692–3705. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fierz, B.; Poirier, M.G. Biophysics of chromatin dynamics. Annu. Rev. Biophys. 2019, 48, 321–345. [Google Scholar] [CrossRef]
- Oudet, P.; Gross-Bellard, M.; Chambon, P. Electron microscopic and biochemical evidence that chromatin structure is a repeating unit. Cell 1975, 4, 281–300. [Google Scholar] [CrossRef]
- Nicolini, C. Biophysics and Cancer; Springer, Plenum Press: New York, NY, USA, 1986. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ashraf, M.W.; Le Gratiet, A.; Diaspro, A. Computational Modeling of Chromatin Fiber to Characterize Its Organization Using Angle-Resolved Scattering of Circularly Polarized Light. Polymers 2021, 13, 3422. https://doi.org/10.3390/polym13193422
Ashraf MW, Le Gratiet A, Diaspro A. Computational Modeling of Chromatin Fiber to Characterize Its Organization Using Angle-Resolved Scattering of Circularly Polarized Light. Polymers. 2021; 13(19):3422. https://doi.org/10.3390/polym13193422
Chicago/Turabian StyleAshraf, Muhammad Waseem, Aymeric Le Gratiet, and Alberto Diaspro. 2021. "Computational Modeling of Chromatin Fiber to Characterize Its Organization Using Angle-Resolved Scattering of Circularly Polarized Light" Polymers 13, no. 19: 3422. https://doi.org/10.3390/polym13193422






