Morphology Evolution, Molecular Simulation, Electrical Properties, and Rheology of Carbon Nanotube/Polypropylene/Polystyrene Blend Nanocomposites: Effect of Molecular Interaction between Styrene-Butadiene Block Copolymer and Carbon Nanotube
Abstract
:1. Introduction
2. Materials and Methods
2.1. Gaussian Molecular Simulation
2.2. Materials and Composites Preparation
2.3. Materials Characterization
3. Results and Discussion
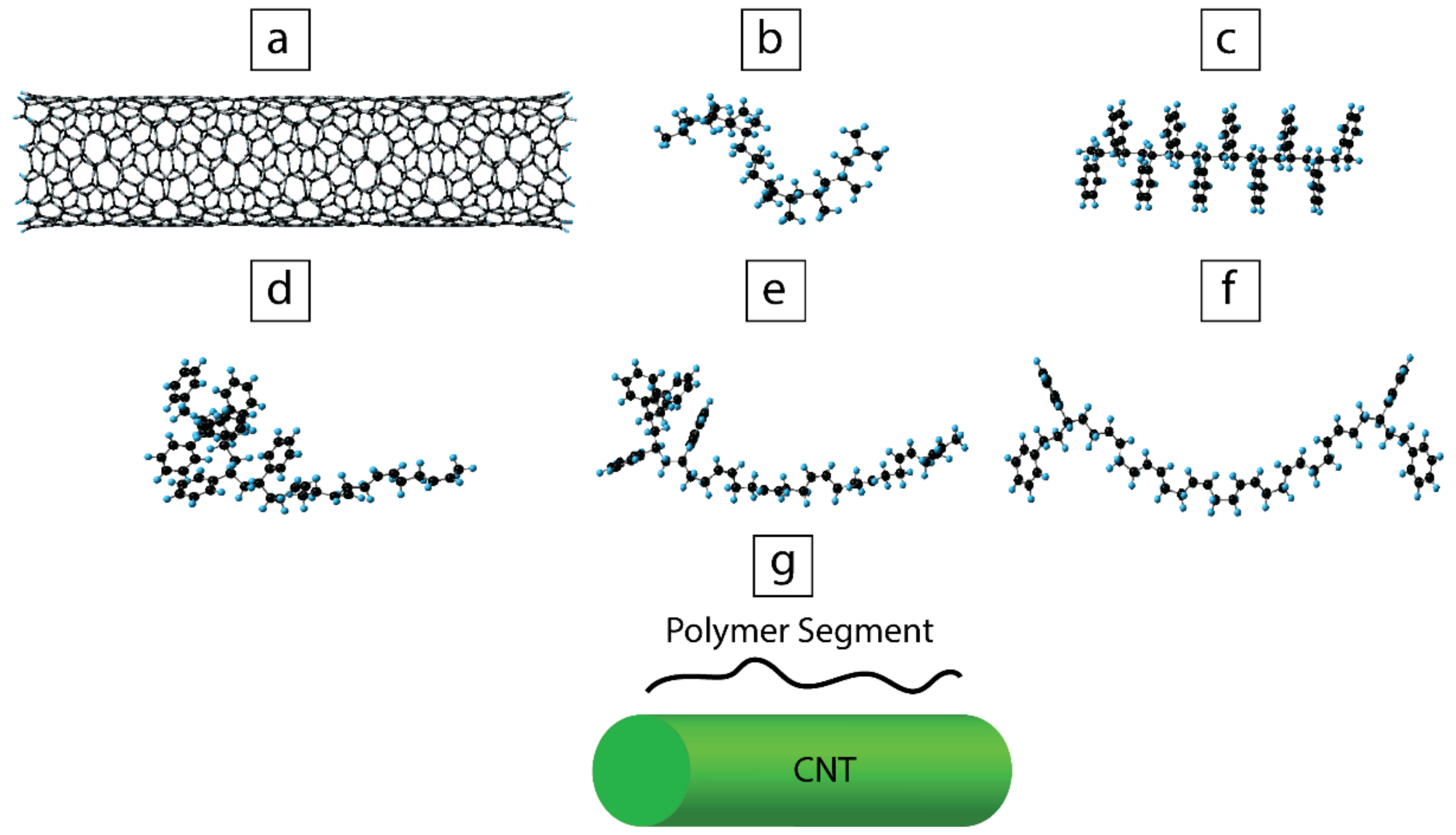
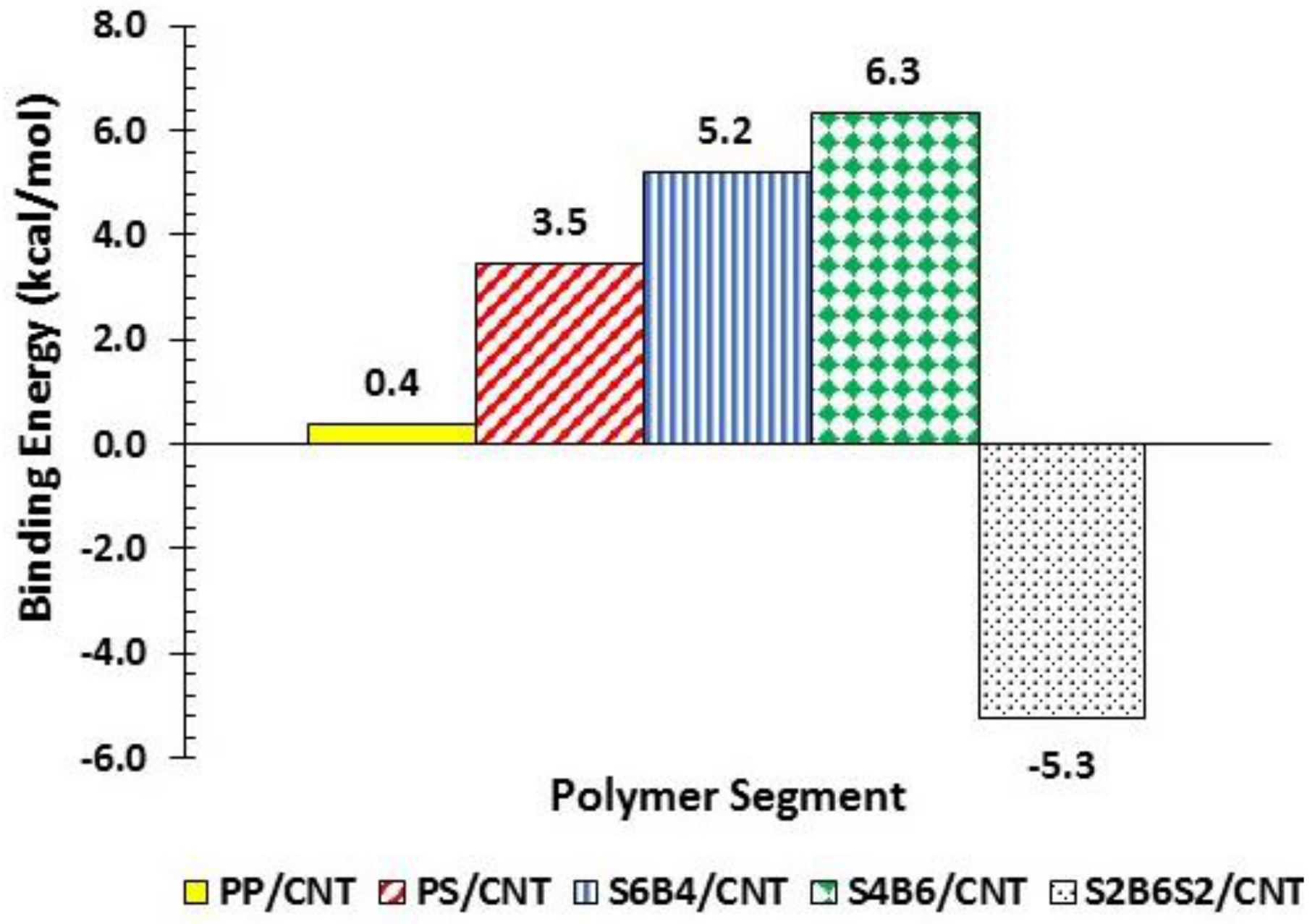
3.1. Molecular Simulation
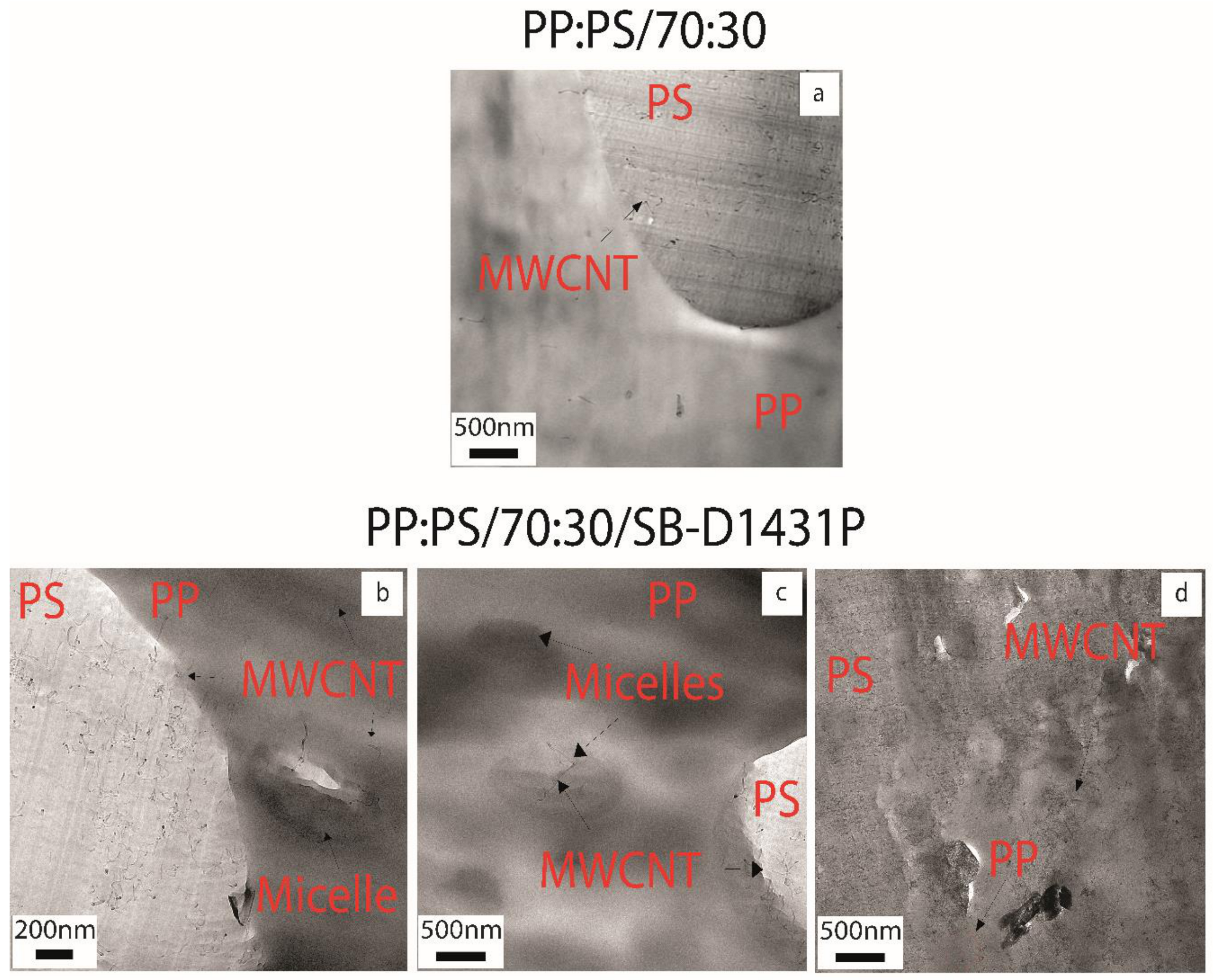
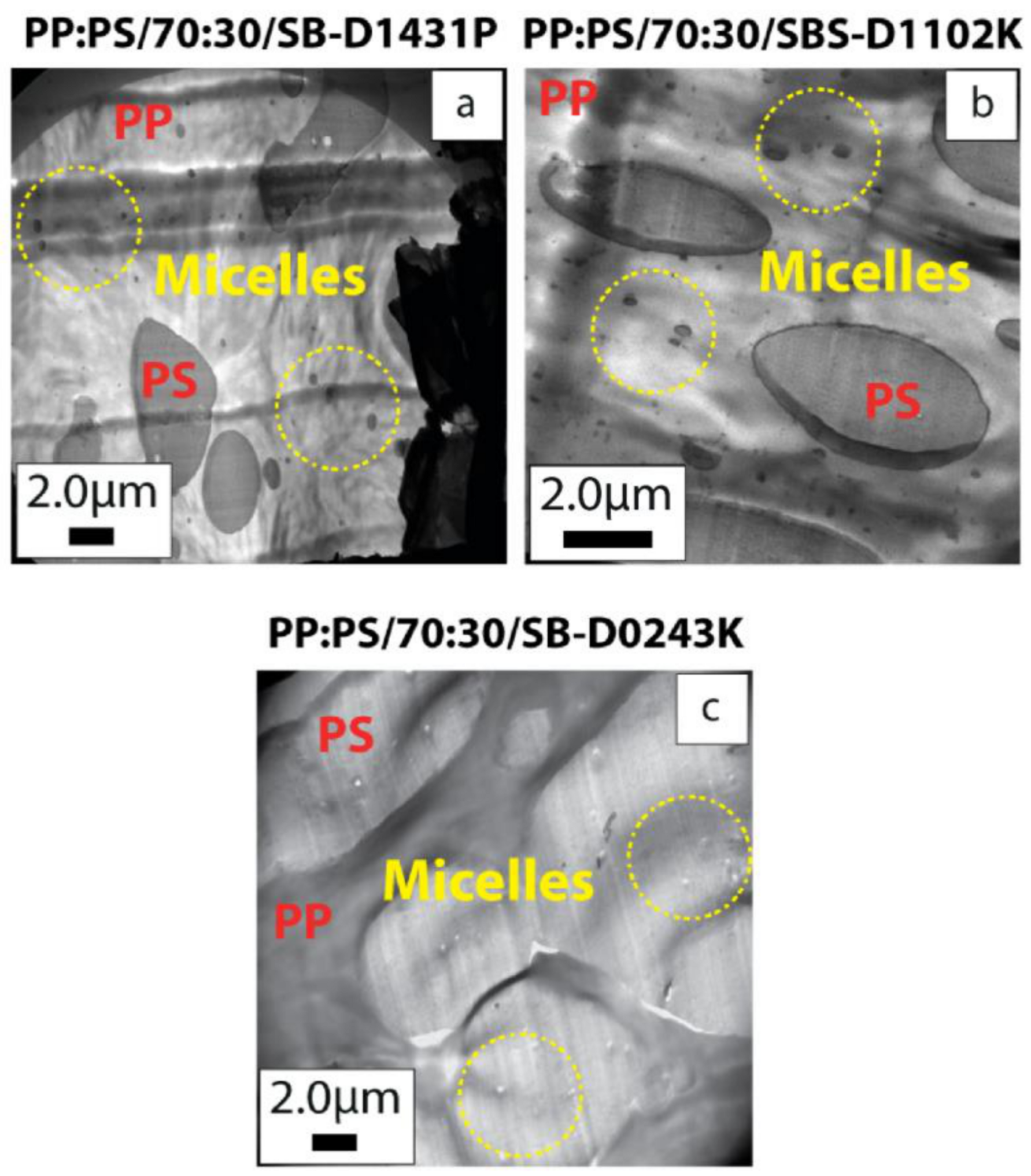
3.2. MWCNT Localization
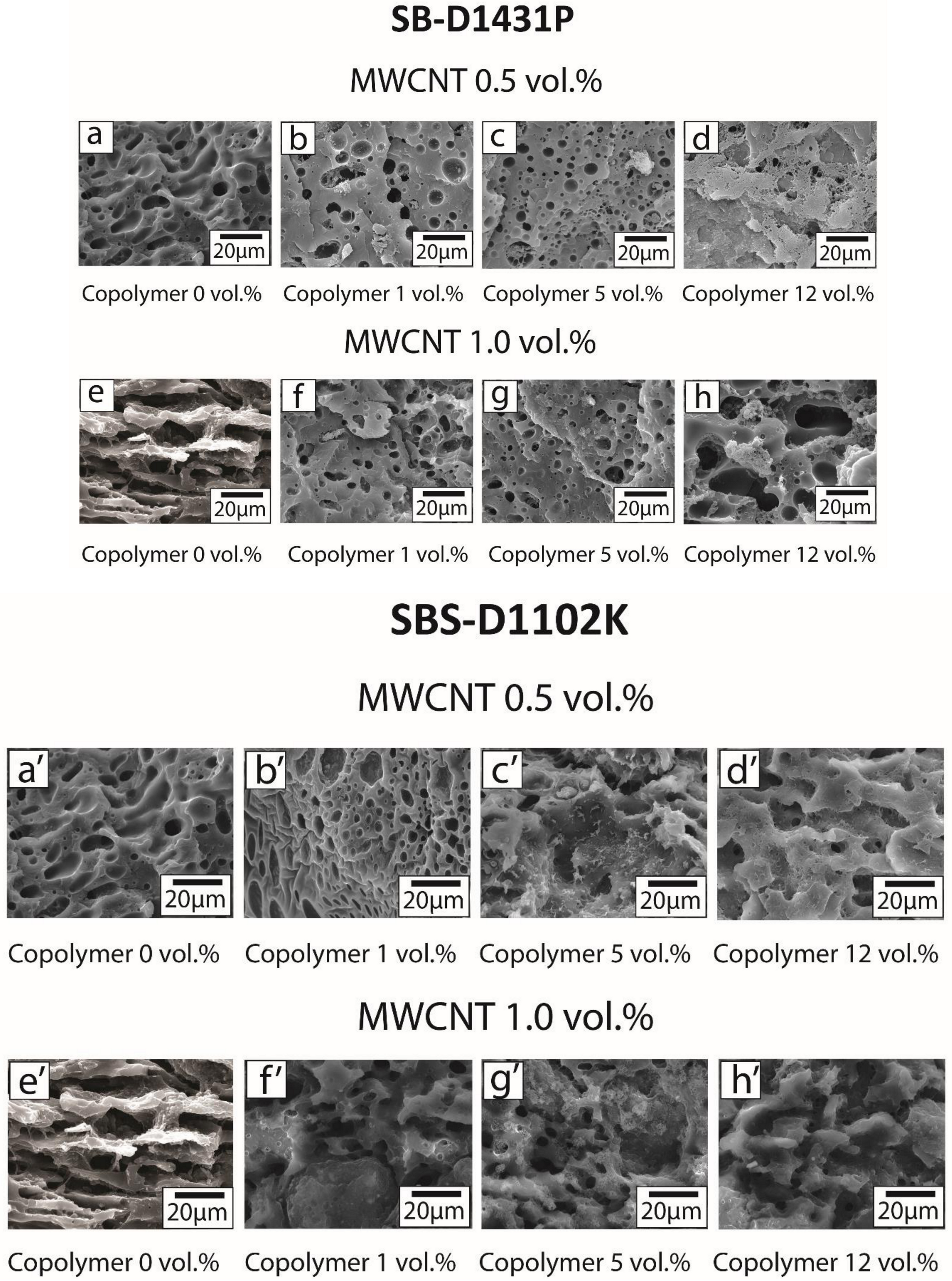
3.3. Morphology Observation
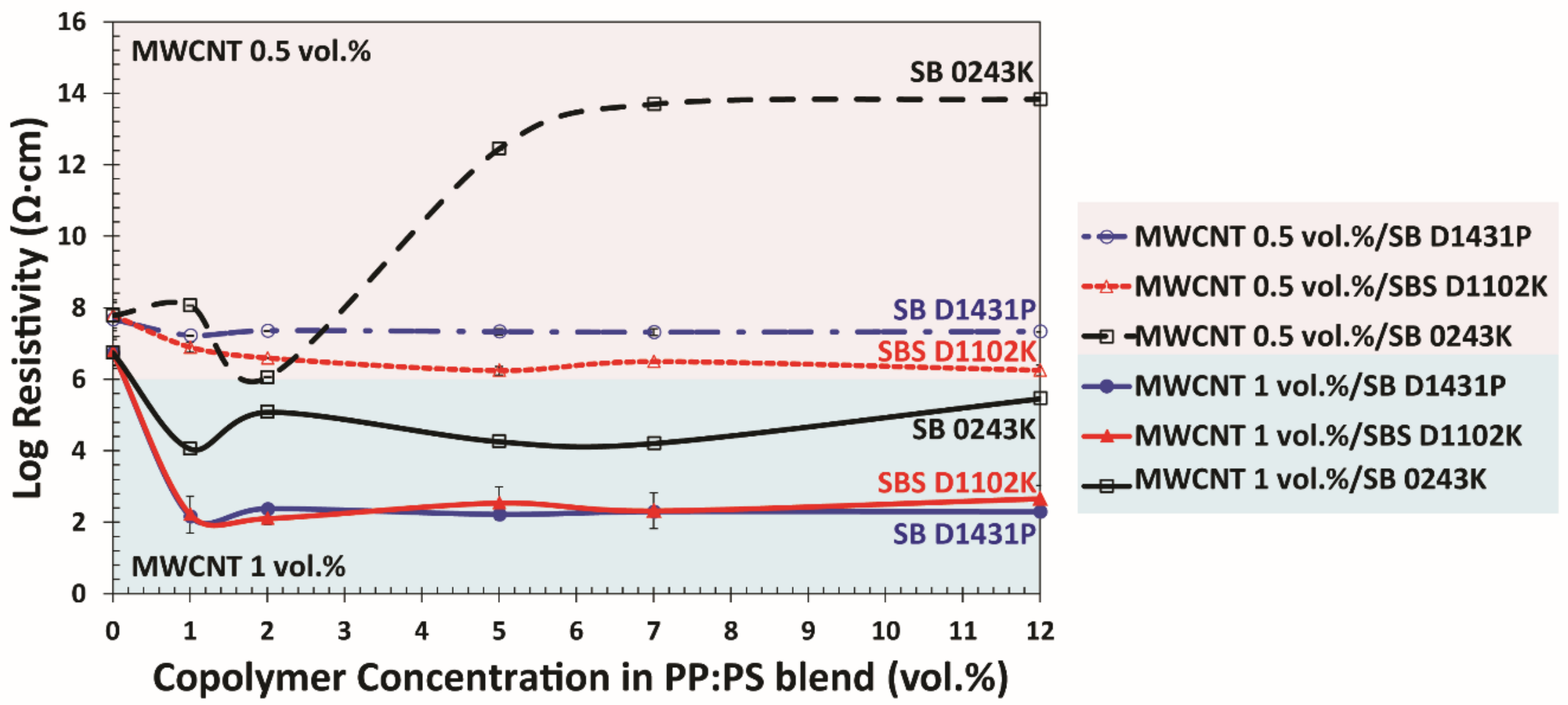
3.4. Electrical Properties
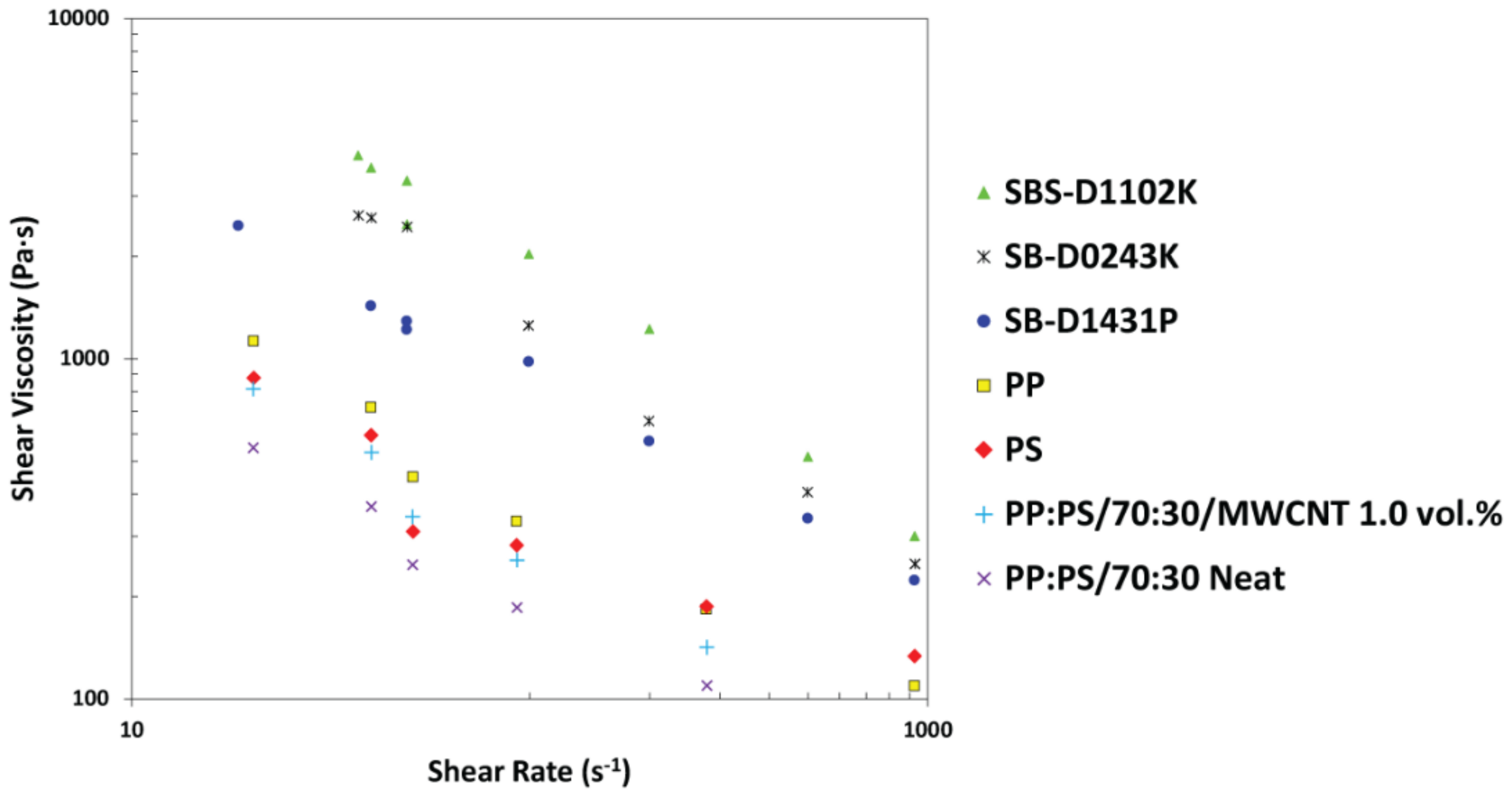
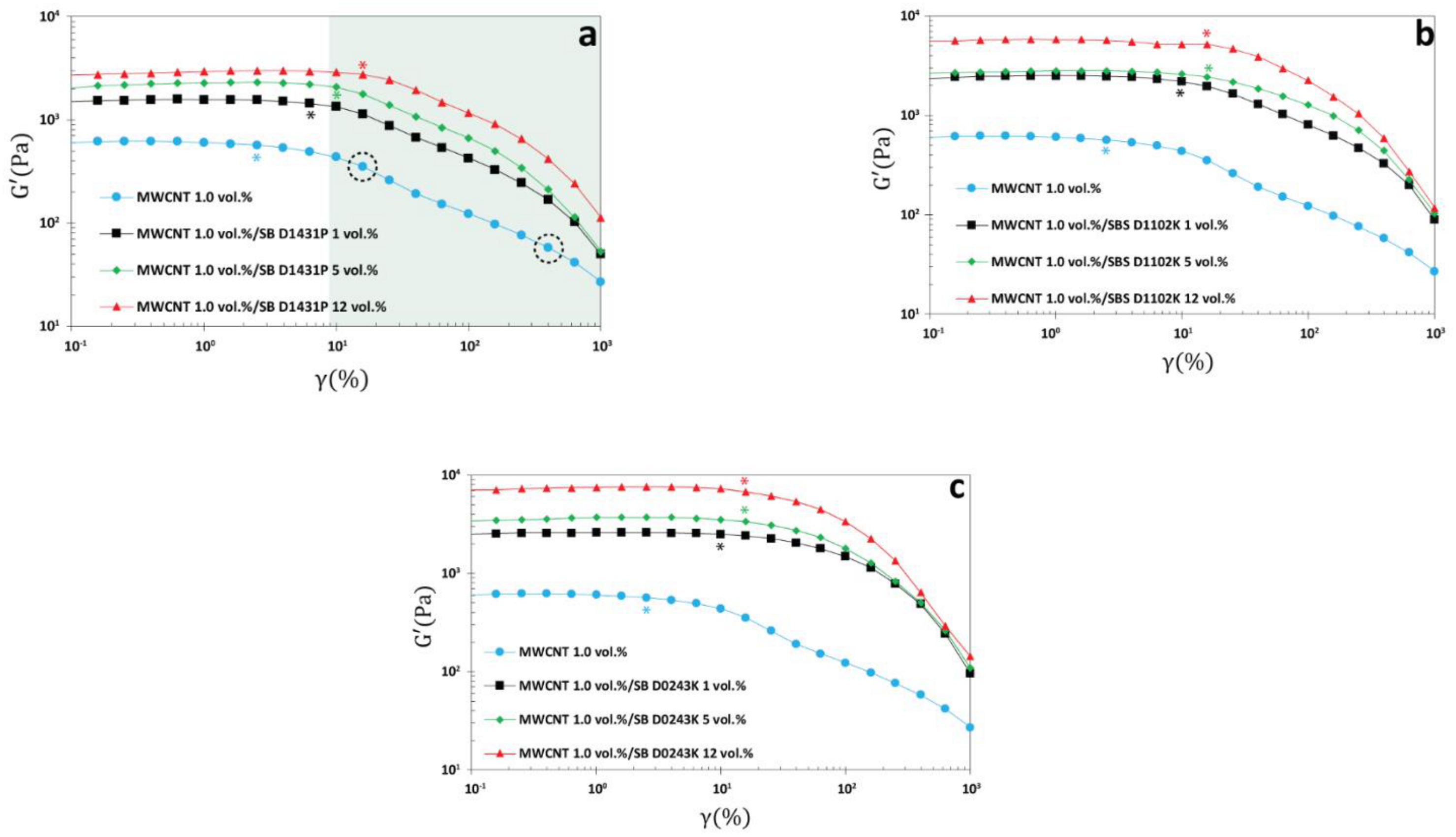
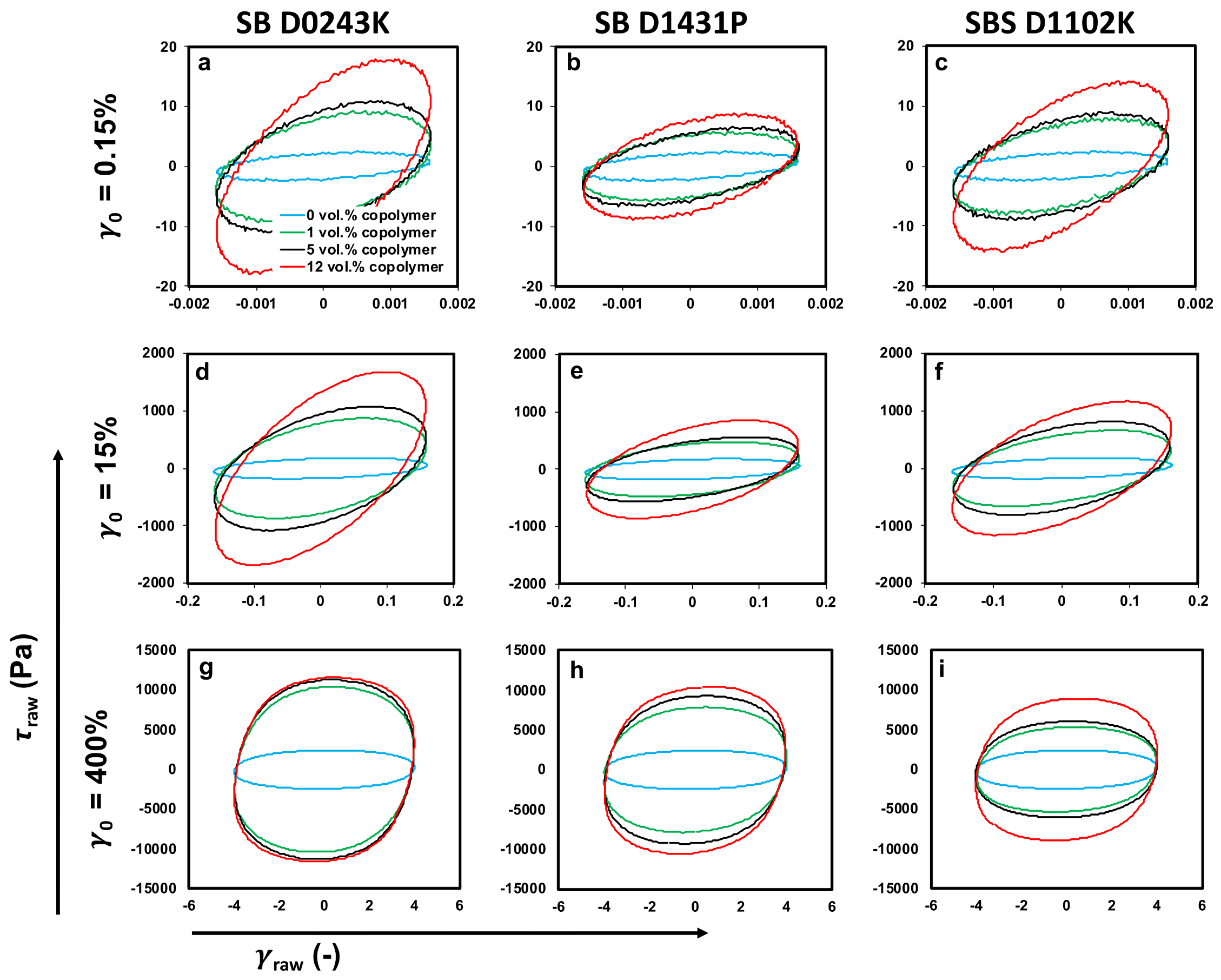
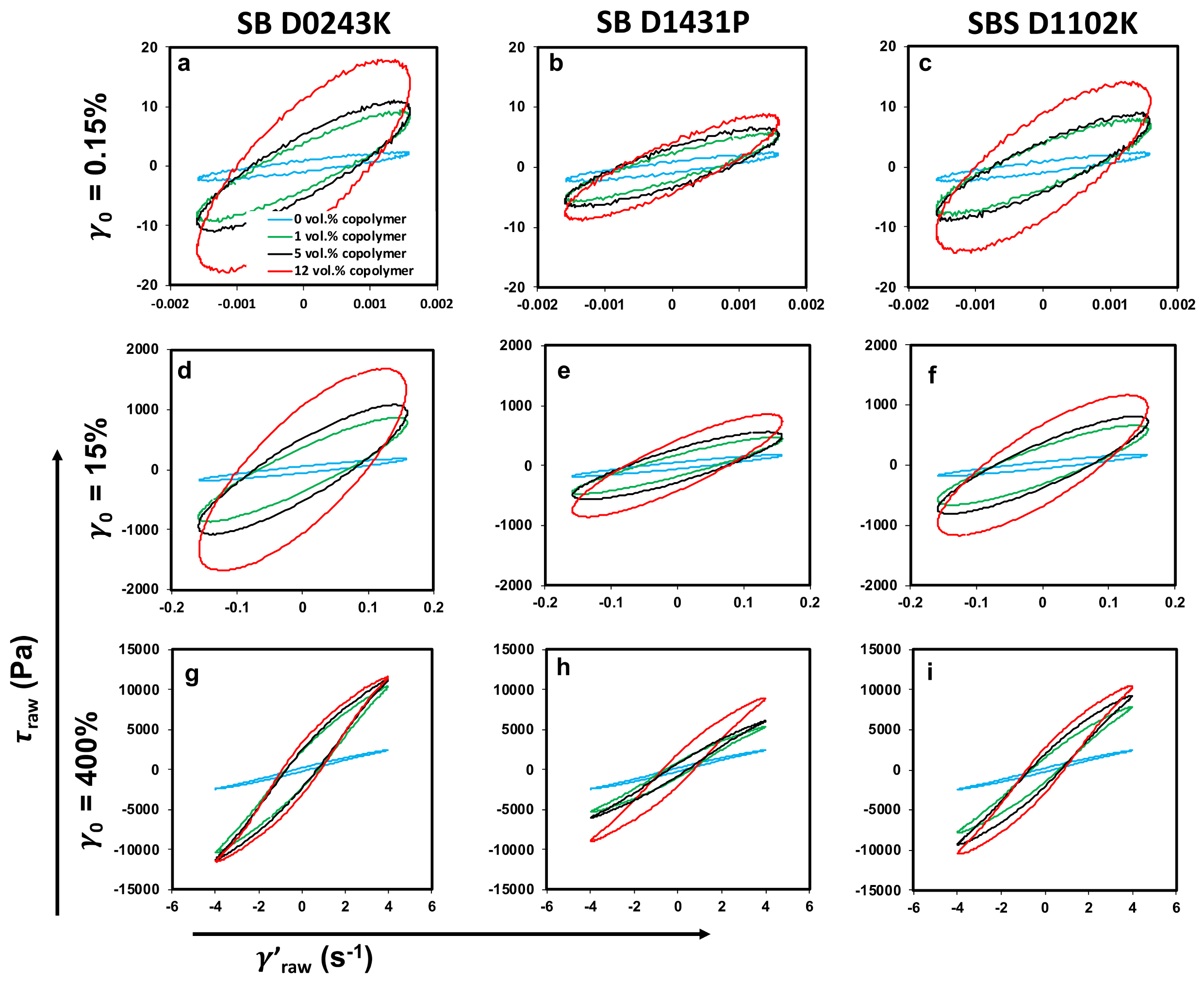
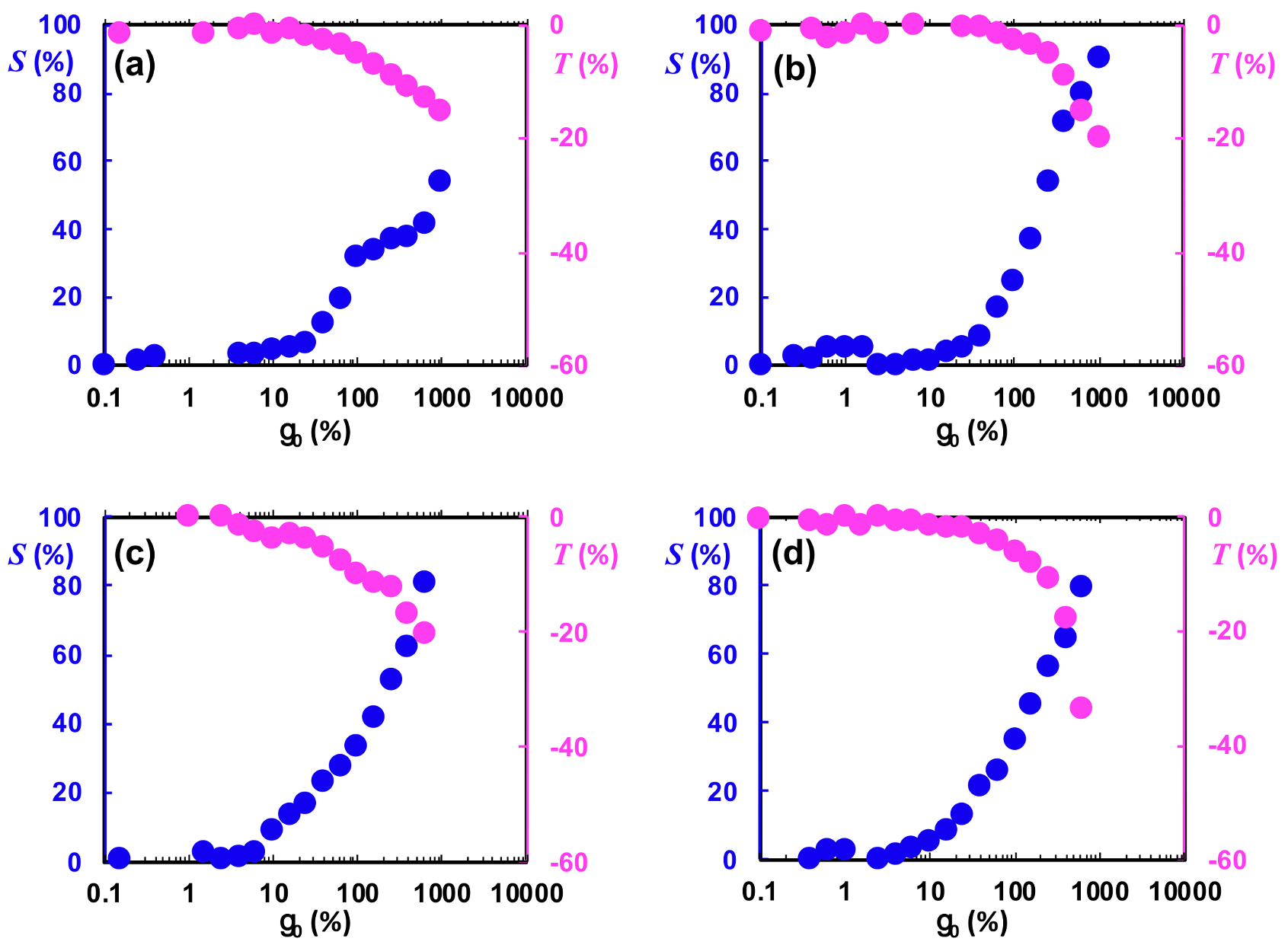
3.5. Rheology
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Robeson, L.M. Fundamentals of Polymer Blends. In Polymer Blends: A Comprehensive Review; Hanser Publications: Munich, Germany, 2007; pp. 11–19. [Google Scholar]
- Sundararaj, U.; Macosko, C.W.; Rolando, R.J.; Chan, H.T. Morphology development in polymer blends. Polym. Eng. Sci. 1992, 32, 1814–1823. [Google Scholar] [CrossRef]
- Sundararaj, U.; Dori, Y.; Macosko, C.W. Sheet formation in immiscible polymer blends: Model experiments on initial blend morphology. Polymer 1995, 36, 1957–1968. [Google Scholar] [CrossRef]
- Ghodgaonkar, P.G.; Sundararaj, U. Prediction of dispersed phase drop diameter in polymer blends: The effect of elasticity. Polym. Eng. Sci. 1996, 36, 1656–1665. [Google Scholar] [CrossRef]
- Sundararaj, U.; Macosko, C.W. Drop Breakup and Coalescence in Polymer Blends: The Effects of Concentration and Compatibilization. Macromolecules 1995, 28, 2647–2657. [Google Scholar] [CrossRef]
- Utracki, L.A. Development of Polymer Blends. In Commercial Polymer Blends; Springer: Boston, MA, USA, 1998; p. 658. [Google Scholar]
- Zaikin, A.E.; Zharinova, E.A.; Bikmullin, R.S. Specifics of localization of carbon black at the interface between polymeric phases. Polym. Sci. Ser. A 2007, 49, 328–336. [Google Scholar] [CrossRef]
- Al-Saleh, M.H.; Sundararaj, U. An innovative method to reduce percolation threshold of carbon black filled immiscible polymer blends. Compos. Part A Appl. Sci. Manuf. 2008, 39, 284–293. [Google Scholar] [CrossRef]
- Cohen, E.; Zonder, L.; Ophir, A.; Kenig, S.; McCarthy, S.; Barry, C.; Mead, J. Hierarchical Structures Composed of Confined Carbon Nanotubes in Cocontinuous Ternary Polymer Blends. Macromolecules 2013, 46, 1851–1859. [Google Scholar] [CrossRef]
- Van Puyvelde, P.; Moldenaers, P. Rheology and Morphology Development in Immiscible Polymer Blends; The British Society of Rheology: Aberystwyth, UK, 2005; pp. 101–145. [Google Scholar]
- Sundararaj, U.; Macosko, C.W.; Shih, C.-K. Evidence for inversion of phase continuity during morphology development in polymer blending. Polym. Eng. Sci. 1996, 36, 1769–1781. [Google Scholar] [CrossRef]
- Kim, J.K.; Son, H.W.; Lee, Y.; Kim, J. The effect of phase-separated morphology on the rheological properties of polystyrene/poly(vinyl methyl ether) blend. J. Polym. Sci. Part B Polym. Phys. 1999, 37, 889–906. [Google Scholar] [CrossRef]
- Li, H.; Sundararaj, U. Morphology Development of Polymer Blends in Extruder: The Effects of Compatibilization and Rotation Rate. Macromol. Chem. Phys. 2009, 210, 852–863. [Google Scholar] [CrossRef]
- Sumita, M.; Sakata, K.; Hayakawa, Y.; Asai, S.; Miyasaka, K.; Tanemura, M. Double percolation effect on the electrical conductivity of conductive particles filled polymer blends. Colloid Polym. Sci. 1992, 270, 134–139. [Google Scholar] [CrossRef]
- Gubbels, F.; Blacher, S.; Vanlathem, E.; Jérôme, R.; Deltour, R.; Brouers, F.; Teyssié, P. Design of Electrical Composites: Determining the Role of the Morphology on the Electrical Properties of Carbon Black Filled Polymer Blends. Macromolecules 1995, 28, 1559–1566. [Google Scholar] [CrossRef]
- Elias, L.; Fenouillot, F.; Majesté, J.-C.; Martin, G.; Cassagnau, P. Migration of nanosilica particles in polymer blends. J. Polym. Sci. Part B Polym. Phys. 2008, 46, 1976–1983. [Google Scholar] [CrossRef]
- Yuan, J.; Yao, S.-H.; Sylvestre, A.; Bai, J. Biphasic Polymer Blends Containing Carbon Nanotubes: Heterogeneous Nanotube Distribution and Its Influence on the Dielectric Properties. J. Phys. Chem. C 2012, 116, 2051–2058. [Google Scholar] [CrossRef]
- Gubbels, F.; Jerome, R.; Teyssie, P.; Vanlathem, E.; Deltour, R.; Calderone, A.; Parente, V.; Brebdas, J.L. Selective Localization of Carbon Black in Immiscible Polymer Blends: A Useful Tool To Design Electrical Conductive Composites. Macromolecules 1994, 27, 1972–1974. [Google Scholar] [CrossRef]
- Göldel, A.; Marmur, A.; Kasaliwal, G.R.; Pötschke, P.; Heinrich, G. Shape-Dependent Localization of Carbon Nanotubes and Carbon Black in an Immiscible Polymer Blend during Melt Mixing. Macromolecules 2011, 44, 6094–6102. [Google Scholar] [CrossRef]
- Maiti, S.; Shrivastava, N.K.; Khatua, B.B. Reduction of percolation threshold through double percolation in melt-blended polycarbonate/acrylonitrile butadiene styrene/multiwall carbon nanotubes elastomer nanocomposites. Polym. Compos. 2013, 34, 570–579. [Google Scholar] [CrossRef]
- Poyekar, A.V.; Bhattacharyya, A.R.; Panwar, A.S.; Simon, G.P. Evolution of phase morphology and ‘network-like’ structure of multiwall carbon nanotubes in binary polymer blends during melt-mixing. Polym. Eng. Sci. 2015, 55, 429–442. [Google Scholar] [CrossRef]
- Sultana, S.M.N.; Pawar, S.P.; Kamkar, M.; Sundararaj, U. Tailoring MWCNT dispersion, blend morphology and EMI shielding properties by sequential mixing strategy in immiscible PS/PVDF blends. J Electron. Mater. 2020, 49, 1588–1600. [Google Scholar] [CrossRef]
- Dil, E.J.; Arjmand, M.; Li, Y.; Sundararaj, U.; Favis, B.D. Assembling copper nanowires at the interface and in discrete phases in PLA-based polymer blends. Eur. Polym. J. 2016, 85, 187–197. [Google Scholar] [CrossRef]
- Otero-Navas, I.; Arjmand, M.; Sundararaj, U. Carbon nanotube induced double percolation in polymer blends: Morphology, rheology and broadband dielectric properties. Polymer 2017, 114, 122–134. [Google Scholar] [CrossRef]
- Elias, L.; Fenouillot, F.; Majeste, J.; Cassagnau, P. Morphology and rheology of immiscible polymer blends filled with silica nanoparticles. Polymer 2007, 48, 6029–6040. [Google Scholar] [CrossRef]
- Vermant, J.; Vandebril, S.; Dewitte, C.; Moldenaers, P. Particle-stabilized polymer blends. Rheol. Acta 2008, 47, 835–839. [Google Scholar] [CrossRef]
- Thareja, P.; Moritz, K.; Velankar, S.S. Interfacially active particles in droplet/matrix blends of model immiscible homopolymers: Particles can increase or decrease drop size. Rheol. Acta 2010, 49, 285–298. [Google Scholar] [CrossRef]
- Navas, I.O.; Arjmand, M.; Sundararaj, U. Effect of carbon nanotubes on morphology evolution of polypropylene/polystyrene blends: Understanding molecular interactions and carbon nanotube migration mechanisms. RSC Adv. 2017, 7, 54222–54234. [Google Scholar] [CrossRef] [Green Version]
- Wu, G.; Li, B.; Jiang, J. Carbon black self-networking induced co-continuity of immiscible polymer blends. Polymer 2010, 51, 2077–2083. [Google Scholar] [CrossRef]
- Nuzzo, A.; Bilotti, E.; Peijs, T.; Acierno, D.; Filippone, G. Nanoparticle-induced co-continuity in immiscible polymer blends—A comparative study on bio-based PLA-PA11 blends filled with organoclay, sepiolite, and carbon nanotubes. Polymer 2014, 55, 4908–4919. [Google Scholar] [CrossRef]
- López-Barrón, C.R.; Macosko, C.W. Rheology of compatibilized immiscible blends with droplet-matrix and cocontinuous morphologies during coarsening. J. Rheol. 2014, 58, 1935–1953. [Google Scholar] [CrossRef]
- Gubbels, F.; Jerome, R.; Vanlathem, E.; Deltour, R.; Blacher, S.; Brouers, F. Kinetic and Thermodynamic Control of the Selective Localization of Carbon Black at the Interface of Immiscible Polymer Blends. Chem. Mater. 1998, 10, 1227–1235. [Google Scholar] [CrossRef]
- Persson, A.L.; Bertilsson, H. Viscosity difference as distributing factor in selective absorption of aluminium borate whiskers in immiscible polymer blends. Polymer 1998, 39, 5633–5642. [Google Scholar] [CrossRef]
- Radonjič, G.; Musil, V.; Šmit, I. Compatibilization of polypropylene/polystyrene blends with poly(styrene-b-butadiene-b-styrene) block copolymer. J. Appl. Polym. Sci. 1998, 69, 2625–2639. [Google Scholar] [CrossRef]
- Macaúbas, P.; Demarquette, N. Morphologies and interfacial tensions of immiscible polypropylene/polystyrene blends modified with triblock copolymers. Polymer 2001, 42, 2543–2554. [Google Scholar] [CrossRef]
- Utracki, L.A. Compatibilization of Polymer Blends. Can. J. Chem. Eng. 2002, 80, 1008–1016. [Google Scholar] [CrossRef] [Green Version]
- Lin, B.; Mighri, F.; Huneault, M.A.; Sundararaj, U. Effect of premade compatibilizer and reactive polymers on polystyrene drop deformation and breakup in simple shear. Macromolecules 2005, 38, 5609–5616. [Google Scholar] [CrossRef]
- Brostow, W.; Grgurić, T.H.; Olea-Mejia, O.; Pietkiewicz, D.; Rek, V. Polypropylene + Polystyrene Blends with a Compatibilizer. Part 2. Tribological and Mechanical Properties. e-Polymers 2008, 8, 364–375. [Google Scholar] [CrossRef] [Green Version]
- Lyu, S.; Jones, T.D.; Bates, F.S.; Macosko, C.W. Role of Block Copolymers on Suppression of Droplet Coalescence. Macromolecules 2002, 35, 7845–7855. [Google Scholar] [CrossRef]
- Cristini, V.; Bławzdziewicz, J.; Loewenberg, M. Near-contact motion of surfactant-covered spherical drops. J. Fluid Mech. 1998, 366, 259–287. [Google Scholar] [CrossRef]
- Nowak, E.; Kovalchuk, N.M.; Che, Z.; Simmons, M.J. Effect of surfactant concentration and viscosity of outer phase during the coalescence of a surfactant-laden drop with a surfactant-free drop. Colloids Surf. A Physicochem. Eng. Asp. 2016, 505, 124–131. [Google Scholar] [CrossRef] [Green Version]
- Lepers, J.-C.; Favis, B.D. Interfacial tension reduction and coalescence suppression in compatibilized polymer blends. AIChE J. 1999, 45, 887–895. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03. 2016; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007, 13, 1173–1213. [Google Scholar] [CrossRef] [Green Version]
- Arjmand, M.; Apperley, T.; Okoniewski, M.; Sundararaj, U. Comparative study of electromagnetic interference shielding properties of injection molded versus compression molded multi-walled carbon nanotube/polystyrene composites. Carbon 2012, 50, 5126–5134. [Google Scholar] [CrossRef]
- Mahmoodi, M.; Arjmand, M.; Sundararaj, U.; Park, S.S. The electrical conductivity and electromagnetic interference shielding of injection molded multi-walled carbon nanotube/polystyrene composites. Carbon 2012, 50, 1455–1464. [Google Scholar] [CrossRef]
- Gelves, G.A.; Lin, B.; Sundararaj, U.; Haber, J.A. Low Electrical Percolation Threshold of Silver and Copper Nanowires in Polystyrene Composites. Adv. Funct. Mater. 2006, 16, 2423–2430. [Google Scholar] [CrossRef]
- Bousmina, M.; Ait-Kadi, A.; Faisant, J.B. Determination of shear rate and viscosity from batch mixer data. J. Rheol. 1999, 43, 415–433. [Google Scholar] [CrossRef]
- Mezger, T.G. The Rheology Handbook: For Users of Rotational and Oscillatory Rheometers; Coatings compendia; Vincentz Network: Hanover, Germany, 2006. [Google Scholar]
- Luo, Y.; Wang, R.; Zhao, S.; Chen, Y.; Su, H.; Zhao, X.; Chan, T.W.; Wu, S. Experimental study and molecular dynamics simulation of dynamic properties and interfacial bonding characteristics of graphene/solution-polymerized styrene-butadiene rubber composites. RSC Adv. 2016, 6, 58077–58087. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, R.; Wang, W.; Zhao, X.; Wu, S. Molecular Dynamics Simulation Insight Into Two-Component Solubility Parameters of Graphene and Thermodynamic Compatibility of Graphene and Styrene Butadiene Rubber. J. Phys. Chem. C 2017, 121, 10163–10173. [Google Scholar] [CrossRef]
- De Rosa, C.; Auriemma, F.; Di Girolamo, R.; Romano, L.; De Luca, M.R. A New Mesophase of Isotactic Polypropylene in Copolymers of Propylene with Long Branched Comonomers. Macromolecules 2010, 43, 8559–8569. [Google Scholar] [CrossRef]
- Chang, K.; Macosko, C.W.; Morse, D.C. Interfacial Tension Measurement and Micellization in a Polymer Blend with Copolymer Surfactant: A False Critical Micelle Concentration. Macromolecules 2015, 48, 8154–8168. [Google Scholar] [CrossRef]
- Koning, C. Strategies for compatibilization of polymer blends. Prog. Polym. Sci. 1998, 23, 707–757. [Google Scholar] [CrossRef]
- Van Krevelen, D.W. Properties of Polymers: Their Correlation with Chemical Structure; Their Numerical Estimation and Prediction from Additive Group Contributions, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Lee, K.; Lim, H.J.; Yang, S.J.; Kim, Y.S.; Park, C.R. Determination of solubility parameters of single-walled and double-walled carbon nanotubes using a finite-length model. RSC Adv. 2013, 3, 4814–4820. [Google Scholar] [CrossRef]
- Bergin, S.D.; Sun, Z.; Rickard, D.; Streich, P.V.; Hamilton, J.P.; Coleman, J.N. Multicomponent Solubility Parameters for Single-Walled Carbon Nanotube−Solvent Mixtures. ACS Nano 2009, 3, 2340–2350. [Google Scholar] [CrossRef] [PubMed]
- Clark, M.D.; Krishnamoorti, R. Dispersion of Functionalized Multiwalled Carbon Nanotubes. J. Phys. Chem. C 2009, 113, 20861–20868. [Google Scholar] [CrossRef]
- Detriche, S.; Zorzini, G.; Colomer, J.-F.; Fonseca, A.; Nagy, J.B. Application of the Hansen Solubility Parameters Theory to Carbon Nanotubes. J. Nanosci. Nanotechnol. 2008, 8, 6082–6092. [Google Scholar] [CrossRef] [PubMed]
- Molau, G.E. Heterogeneous polymer systems. II. Mechanism of stabilization of polymeric oil-in-oil emulsions. J. Polym. Sci. Part A Gen. Pap. 1965, 3, 4235–4242. [Google Scholar] [CrossRef]
- Jaensson, N. Modeling Interfaces and Particles in Viscoelastic Fluids; Eindhoven University of Technology: Eindhoven, The Netherlands, 2016; p. 181. [Google Scholar]
- Williams, P.; Phillips, G.O. Gums and Stabilisers for the Food Industry 12; Royal Society of Chemistry: London, UK, 2004. [Google Scholar]
- Cigana, P.; Favis, B.D.; Jerome, R. Diblock copolymers as emulsifying agents in polymer blends: Influence of molecular weight, architecture, and chemical composition. J. Polym. Sci. Part B Polym. Phys. 1996, 34, 1691–1700. [Google Scholar] [CrossRef]
- Matos, M.; Favis, B.; Lomellini, P. Interfacial modification of polymer blends—The emulsification curve: 1. Influence of molecular weight and chemical composition of the interfacial modifier. Polymer 1995, 36, 3899–3907. [Google Scholar] [CrossRef]
- Ruzette, A.-V.; Leibler, L. Block copolymers in tomorrow’s plastics. Nat. Mater. 2005, 4, 19–31. [Google Scholar] [CrossRef]
- Adedeji, A.; Lyu, S.; Macosko, C.W. Block Copolymers in Homopolymer Blends: Interface vs Micelles. Macromolecules 2001, 34, 8663–8668. [Google Scholar] [CrossRef]
- Hlavatá, D.; Horák, Z.; Hromádková, J.; Lednický, F.; Pleska, A. Compatabilization of polystyrene/polypropylene blends by styrene–butadiene block copolymers with differing polystyrene block lengths. J. Polym. Sci. Part B Polym. Phys. 1999, 37, 1647–1656. [Google Scholar] [CrossRef]
- Liu, X.; Pan, Y.; Zheng, G.; Schubert, D.W. Rheological and electrical behavior of poly(methyl methacrylate)/carbon black composites as investigated by creep recovery in shear. Compos. Sci. Technol. 2016, 128, 1–7. [Google Scholar] [CrossRef]
- Garzón, C.; Palza, H. Electrical behavior of polypropylene composites melt mixed with carbon-based particles: Effect of the kind of particle and annealing process. Compos. Sci. Technol. 2014, 99, 117–123. [Google Scholar] [CrossRef]
- Mohamed, M.G.; Kuo, S.-W. Functional Silica and Carbon Nanocomposites Based on Polybenzoxazines. Macromol. Chem. Phys. 2019, 220, 1800306. [Google Scholar] [CrossRef]
- Samy, M.M.; Mohamed, M.G.; Kuo, S.-W. Pyrene-functionalized tetraphenylethylene polybenzoxazine for dispersing single-walled carbon nanotubes and energy storage. Compos. Sci. Technol. 2020, 199, 108360. [Google Scholar] [CrossRef]
- López-Barrón, C.R.; Tsou, A.H. Strain Hardening of Polyethylene/Polypropylene Blends via Interfacial Reinforcement with Poly(ethylene-cb-propylene) Comb Block Copolymers. Macromolecules 2017, 50, 2986–2995. [Google Scholar] [CrossRef]
- Salehiyan, R.; Song, H.Y.; Kim, M.; Choi, W.J.; Hyun, K. Morphological Evaluation of PP/PS Blends Filled with Different Types of Clays by Nonlinear Rheological Analysis. Macromolecules 2016, 49, 3148–3160. [Google Scholar] [CrossRef]
- Kamkar, M.; Aliabadian, E.; Zeraati, A.S.; Sundararaj, U. Application of nonlinear rheology to assess the effect of secondary nanofiller on network structure of hybrid polymer nanocomposites. Phys. Fluids 2018, 30, 023102. [Google Scholar] [CrossRef]
- Aliabadian, E.; Kamkar, M.; Chen, Z.; Sundararaj, U. Prevention of network destruction of partially hydrolyzed polyacrylamide (HPAM): Effects of salt, temperature, and fumed silica nanoparticles. Phys. Fluids 2019, 31, 013104. [Google Scholar] [CrossRef]
- Kamkar, M.; Sultana, S.N.; Pawar, S.P.; Eshraghian, A.; Erfanian, E.; Sundararaj, U. The key role of processing in tuning nonlinear viscoelastic properties and microwave absorption in CNT-based polymer nanocomposites. Mater. Today Commun. 2020, 24, 101010. [Google Scholar] [CrossRef]
- Moud, A.A.; Kamkar, M.; Nezhad, A.S.; Hejazi, S.H.; Sundararaj, U. Nonlinear viscoelastic characterization of charged cellulose nanocrystal network structure in the presence of salt in aqueous media. Cellulose 2020, 27, 5729–5743. [Google Scholar] [CrossRef]
- Kamkar, M.; Sadeghi, S.; Arjmand, M.; Sundararaj, U. Structural Characterization of CVD Custom-Synthesized Carbon Nanotube/Polymer Nanocomposites in Large-Amplitude Oscillatory Shear (LAOS) Mode: Effect of Dispersion Characteristics in Confined Geometries. Macromolecules 2019, 52, 1489–1504. [Google Scholar] [CrossRef]
- Kamkar, M.; Sadeghi, S.; Arjmand, M.; Aliabadian, E.; Sundararaj, U. Intra-Cycle Elastic Nonlinearity of Nitrogen-Doped Carbon Nanotube/Polymer Nanocomposites under Medium Amplitude Oscillatory Shear (MAOS) Flow. Nanomaterials 2020, 10, 1257. [Google Scholar] [CrossRef] [PubMed]
- Moud, A.A.; Kamkar, M.; Nezhad, A.S.; Hejazi, S.H.; Sundararaj, U. Viscoelastic properties of poly (vinyl alcohol) hydrogels with cellulose nanocrystals fabricated through sodium chloride addition: Rheological evidence of double network formation. Colloids Surf. A Physicochem. Eng. Asp. 2020, 609, 125577. [Google Scholar] [CrossRef]
- Cho, K.S.; Hyun, K.; Ahn, K.H.; Lee, S.J. A geometrical interpretation of large amplitude oscillatory shear response. J. Rheol. 2005, 49, 747–758. [Google Scholar] [CrossRef]
- Yziquel, F.; Carreau, P.J.; Tanguy, P.A. Non-linear viscoelastic behavior of fumed silica suspensions. Rheol. Acta 1999, 38, 14–25. [Google Scholar] [CrossRef]
- Ewoldt, R.H.; Hosoi, A.E.; McKinley, G.H. New measures for characterizing nonlinear viscoelasticity in large amplitude oscillatory shear. J. Rheol. 2008, 52, 1427–1458. [Google Scholar] [CrossRef] [Green Version]
- Filipe, S.; Cidade, M.T.; Wilhelm, M.; Maia, J. Evolution of the morphological and rheological properties along the extruder length for compatibilized blends of a commercial liquid-crystalline polymer and polypropylene. J. Appl. Polym. Sci. 2005, 99, 347–359. [Google Scholar] [CrossRef]





| Polymer | Reference | Manufacturer | Styrene Content wt.% | Shear Viscosity at 200 °C & 40 s−1 (Pa∙s) | Specific Gravity |
|---|---|---|---|---|---|
| SBS | D1102K | Kraton | 26.8–30 | 3640 | 0.94 |
| SB | D0243K | Kraton | 31–36 | 2600 | 0.94 |
| SB | D1431P | Kraton | 75 | 1430 | 1.01 |
| Polymer | Hildebrand Solubility (δ)(cal1/2 cm−3/2) |
|---|---|
| PP | 8.7 [55] |
| PS | 8.9 [55] |
| PBD | 8.4 [55] |
| SWCNT | Theoretical: Zigzag (6,0) 8.3–Zigzag (15,0) 9.6 [56] Experimental: HiPCO SWCNT 11.4 [57] |
| DWCNT | Theoretical: 11.1 [56] |
| MWCNT | Theoretical: 10.5–11.3 [56] Experimental: Arc produced CNT: 10.5–11.2 [58] Experimental: CVD produced CNT (Nanocyl NC7000): 10.3 [59] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otero Navas, I.; Kamkar, M.; Arjmand, M.; Sundararaj, U. Morphology Evolution, Molecular Simulation, Electrical Properties, and Rheology of Carbon Nanotube/Polypropylene/Polystyrene Blend Nanocomposites: Effect of Molecular Interaction between Styrene-Butadiene Block Copolymer and Carbon Nanotube. Polymers 2021, 13, 230. https://doi.org/10.3390/polym13020230
Otero Navas I, Kamkar M, Arjmand M, Sundararaj U. Morphology Evolution, Molecular Simulation, Electrical Properties, and Rheology of Carbon Nanotube/Polypropylene/Polystyrene Blend Nanocomposites: Effect of Molecular Interaction between Styrene-Butadiene Block Copolymer and Carbon Nanotube. Polymers. 2021; 13(2):230. https://doi.org/10.3390/polym13020230
Chicago/Turabian StyleOtero Navas, Ivonne, Milad Kamkar, Mohammad Arjmand, and Uttandaraman Sundararaj. 2021. "Morphology Evolution, Molecular Simulation, Electrical Properties, and Rheology of Carbon Nanotube/Polypropylene/Polystyrene Blend Nanocomposites: Effect of Molecular Interaction between Styrene-Butadiene Block Copolymer and Carbon Nanotube" Polymers 13, no. 2: 230. https://doi.org/10.3390/polym13020230
APA StyleOtero Navas, I., Kamkar, M., Arjmand, M., & Sundararaj, U. (2021). Morphology Evolution, Molecular Simulation, Electrical Properties, and Rheology of Carbon Nanotube/Polypropylene/Polystyrene Blend Nanocomposites: Effect of Molecular Interaction between Styrene-Butadiene Block Copolymer and Carbon Nanotube. Polymers, 13(2), 230. https://doi.org/10.3390/polym13020230







