Channels with Helical Modulation Display Stereospecific Sensitivity for Chiral Superstructures
Abstract
1. Introduction
2. Materials and Methods
2.1. Model of DNA Chain
2.2. Molecular Topology
2.3. Channels
3. Results and Discussion
3.1. Preliminary Measures of Pulled Knots in Free Spaces Do Not Exhibit Chiral Differences
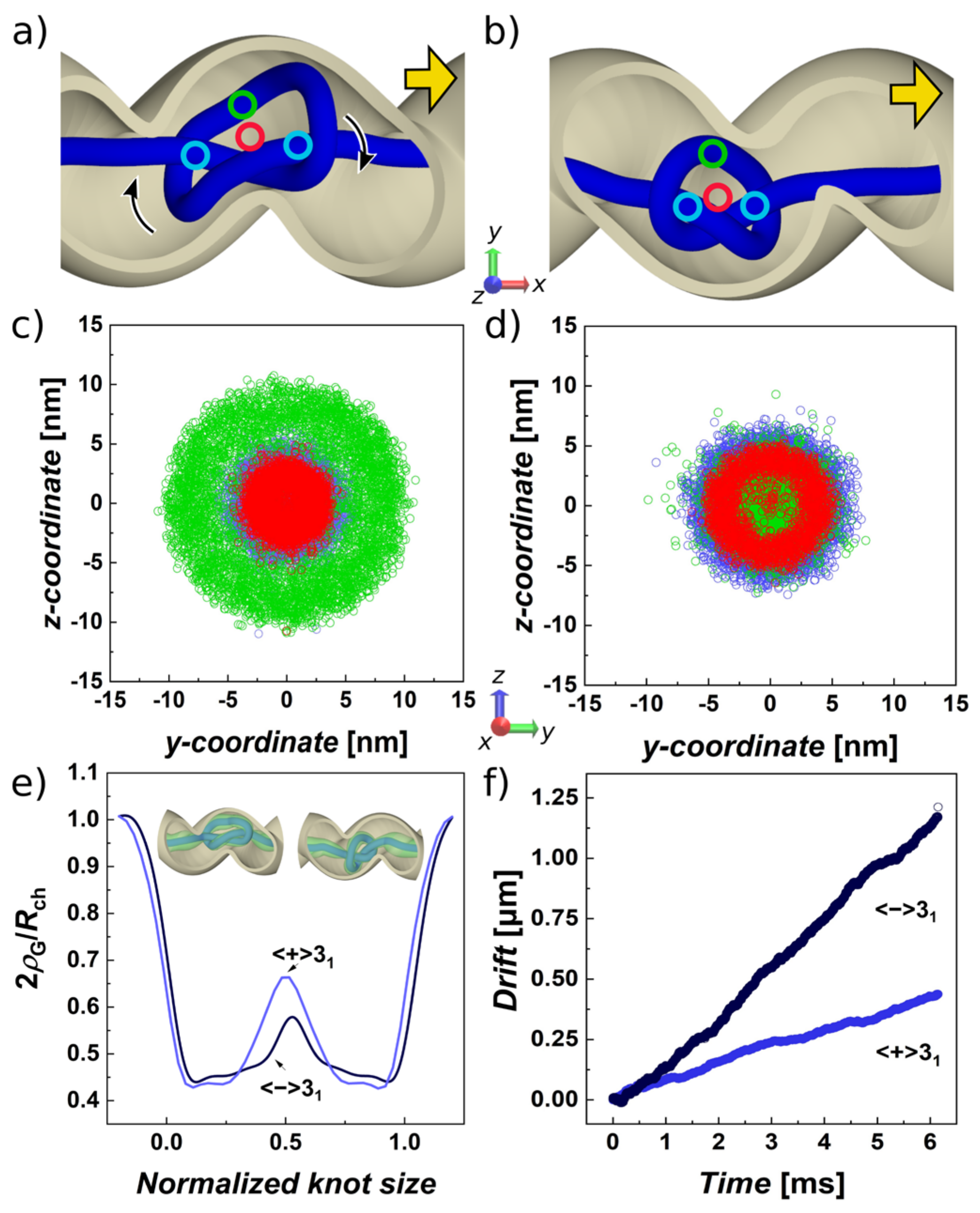
3.2. Pulled Trefoil Knot in the Helical Confinement Shows Symmetry Breaking
3.3. Effect of Helical Radius, Pitch and Pulling Force on Separation of Knots
3.4. Different Chiral Knot Types Show Symmetry Breaking in Helical Channels, While Achiral Knots Do Not
3.5. Helical Channels Can Separate Chiral Knots Embedded on Circular Polymers
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Young, R.J.; Lovell, P.A. Introduction to Polymers, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2011; ISBN 978-0-8493-3929-5. [Google Scholar]
- Tezuka, Y.; Oike, H. Topological Polymer Chemistry. Prog. Polym. Sci. 2002, 27, 1069–1122. [Google Scholar] [CrossRef]
- Flory, P.J. Molecular Size Distribution in Three Dimensional Polymers. VI. Branched Polymers Containing A—R—Bf-1 Type Units. J. Am. Chem. Soc. 1952, 74, 2718–2723. [Google Scholar] [CrossRef]
- Burchard, W. Static and Dynamic Light Scattering from Branched Polymers and Biopolymers. In Light Scattering from Polymers; Springer: Berlin/Heidelberg, Germany, 1983; pp. 1–124. [Google Scholar]
- Ren, J.M.; McKenzie, T.G.; Fu, Q.; Wong, E.H.H.; Xu, J.; An, Z.; Shanmugam, S.; Davis, T.P.; Boyer, C.; Qiao, G.G. Star Polymers. Chem. Rev. 2016, 116, 6743–6836. [Google Scholar] [CrossRef]
- Wijesinghe, S.; Perahia, D.; Grest, G.S. Polymer Topology Effects on Dynamics of Comb Polymer Melts. Macromolecules 2018, 51, 7621–7628. [Google Scholar] [CrossRef]
- Haque, F.M.; Grayson, S.M. The Synthesis, Properties and Potential Applications of Cyclic Polymers. Nat. Chem. 2020, 12, 433–444. [Google Scholar] [CrossRef]
- Dietrich-Buchecker, C.; Rapenne, G.; Sauvage, J.-P. Molecular Knots—From Early Attempts to High-Yield Template Syntheses. In Molecular Catenanes, Rotaxanes and Knots; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1999; pp. 107–142. ISBN 978-3-527-61372-4. [Google Scholar]
- Ayme, J.-F.; Beves, J.; Campbell, C.; Leigh, D. Template Synthesis of Molecular Knots. Chem. Soc. Rev. 2012, 42, 1700–1712. [Google Scholar] [CrossRef] [PubMed]
- Frisch, H.L.; Wasserman, E. Chemical Topology1. J. Am. Chem. Soc. 1961, 83, 3789–3795. [Google Scholar] [CrossRef]
- Rybenkov, V.V.; Cozzarelli, N.R.; Vologodskii, A.V. Probability of DNA Knotting and the Effective Diameter of the DNA Double Helix. Proc. Natl. Acad. Sci. USA 1993, 90, 5307. [Google Scholar] [CrossRef]
- Lim, N.; Jackson, S. Molecular Knots in Biology and Chemistry. J. Phys. Condens. Matter Inst. Phys. J. 2015, 27, 354101. [Google Scholar] [CrossRef]
- Meluzzi, D.; Smith, D.E.; Arya, G. Biophysics of Knotting. Annu. Rev. Biophys. 2010, 39, 349–366. [Google Scholar] [CrossRef]
- Kirkegaard, K.; Wang, J.C. Escherichia Coli DNA Topoisomerase I Catalyzed Linking of Single-Stranded Rings of Complementary Base Sequences. Nucleic Acids Res. 1978, 5, 3811–3820. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Krasnow, M.A.; Stasiak, A.; Spengler, S.J.; Dean, F.; Koller, T.; Cozzarelli, N.R. Determination of the Absolute Handedness of Knots and Catenanes of DNA. Nature 1983, 304, 559–560. [Google Scholar] [CrossRef]
- Deibler, R.W.; Mann, J.K.; Sumners, D.W.L.; Zechiedrich, L. Hin-Mediated DNA Knotting and Recombining Promote Replicon Dysfunction and Mutation. BMC Mol. Biol. 2007, 8, 44. [Google Scholar] [CrossRef] [PubMed]
- Weber, C.; Stasiak, A.; De Los Rios, P.; Dietler, G. Numerical Simulation of Gel Electrophoresis of DNA Knots in Weak and Strong Electric Fields. Biophys. J. 2006, 90, 3100–3105. [Google Scholar] [CrossRef]
- Juette, M.F.; Terry, D.S.; Wasserman, M.R.; Zhou, Z.; Altman, R.B.; Zheng, Q.; Blanchard, S.C. The Bright Future of Single-Molecule Fluorescence Imaging. Curr. Opin. Chem. Biol. 2014, 20, 103–111. [Google Scholar] [CrossRef] [PubMed]
- Riveline, D. “Single Molecule”: Theory and Experiments, an Introduction. J Nanobiotechnol. 2013, 11 (Suppl. 1), S1. [Google Scholar] [CrossRef][Green Version]
- Tang, J.; Du, N.; Doyle, P.S. Compression and Self-Entanglement of Single DNA Molecules under Uniform Electric Field. Proc. Natl. Acad. Sci. USA 2011, 108, 16153. [Google Scholar] [CrossRef]
- Bao, X.R.; Lee, H.J.; Quake, S.R. Behavior of Complex Knots in Single DNA Molecules. Phys. Rev. Lett. 2003, 91, 265506. [Google Scholar] [CrossRef]
- Arai, Y.; Yasuda, R.; Akashi, K.; Harada, Y.; Miyata, H.; Kinosita, K.; Itoh, H. Tying a Molecular Knot with Optical Tweezers. Nature 1999, 399, 446–448. [Google Scholar] [CrossRef]
- Plesa, C.; Verschueren, D.; Pud, S.; van der Torre, J.; Ruitenberg, J.W.; Witteveen, M.J.; Jonsson, M.P.; Grosberg, A.Y.; Rabin, Y.; Dekker, C. Direct Observation of DNA Knots Using a Solid-State Nanopore. Nat. Nanotechnol. 2016, 11, 1093–1097. [Google Scholar] [CrossRef] [PubMed]
- Gal, J.; Cintas, P. Early History of the Recognition of Molecular Biochirality. In Biochirality: Origins, Evolution and Molecular Recognition; Cintas, P., Ed.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2013; pp. 1–40. ISBN 978-3-642-37626-9. [Google Scholar]
- Lukin, O.; Vögtle, F. Knotting and Threading of Molecules: Chemistry and Chirality of Molecular Knots and Their Assemblies. Angew. Chem. Int. Ed. 2005, 44, 1456–1477. [Google Scholar] [CrossRef]
- Leigh, D.A.; Pirvu, L.; Schaufelberger, F. Stereoselective Synthesis of Molecular Square and Granny Knots. J. Am. Chem. Soc. 2019, 141, 6054–6059. [Google Scholar] [CrossRef]
- Adams, C.C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots; American Mathematical Society: Providence, RI, USA, 2004; ISBN 978-0-8218-3678-1. [Google Scholar]
- Silver, D.S. Knot Theory’s Odd Origins: The Modern Study of Knots Grew out an Attempt by Three 19th-Century Scottish Physicists to Apply Knot Theory to Fundamental Questions about the Universe. Am. Sci. 2006, 94, 158–165. [Google Scholar]
- Hoste, J.; Thistlethwaite, M.; Weeks, J. The First 1,701,936 Knots. Math. Intell. 1998, 20, 33–48. [Google Scholar] [CrossRef]
- Fielden, S.D.P.; Leigh, D.A.; Woltering, S.L. Molecular Knots. Angew. Chem. Int. Ed. 2017, 56, 11166–11194. [Google Scholar] [CrossRef] [PubMed]
- Horie, K.; Kitano, T.; Matsumoto, M.; Suzuki, M. A Partial Order on the Set of Prime Knots with up to 11 Crossings. J. Knot Theory Ramif. 2011, 20, 275–303. [Google Scholar] [CrossRef]
- Vaughan, F.R. Jones A Polynomial Invariant for Knots via von Neumann Algebras. Bull. Am. Math. Soc. 1985, 12, 103–111. [Google Scholar]
- Bates, A.D.; Maxwell, A. DNA Topology; Oxford University Press: Oxford, UK; New York, NY, USA, 1993; ISBN 978-0-19-963349-4. [Google Scholar]
- Morrow, S.M.; Bissette, A.J.; Fletcher, S.P. Transmission of Chirality through Space and across Length Scales. Nat. Nanotechnol. 2017, 12, 410–419. [Google Scholar] [CrossRef]
- Smrek, J.; Chubak, I.; Likos, C.N.; Kremer, K. Active Topological Glass. Nat. Commun. 2020, 11, 26. [Google Scholar] [CrossRef]
- Smrek, J.; Kremer, K.; Rosa, A. Threading of Unconcatenated Ring Polymers at High Concentrations: Double-Folded vs Time-Equilibrated Structures. ACS Macro Lett. 2019, 8, 155–160. [Google Scholar] [CrossRef] [PubMed]
- Vargas-Lara, F.; Pazmiño Betancourt, B.A.; Douglas, J.F. Influence of Knot Complexity on Glass-Formation in Low Molecular Mass Ring Polymer Melts. J. Chem. Phys. 2019, 150, 101103. [Google Scholar] [CrossRef]
- Kolesov, G.; Virnau, P.; Kardar, M.; Mirny, L.A. Protein Knot Server: Detection of Knots in Protein Structures. Nucleic Acids Res 2007, 35, W425–W428. [Google Scholar] [CrossRef]
- Dabrowski-Tumanski, P.; Rubach, P.; Goundaroulis, D.; Dorier, J.; Sułkowski, P.; Millett, K.; Rawdon, E.; Stasiak, A.; Sulkowska, J. KnotProt 2.0: A Database of Proteins with Knots and Other Entangled Structures. Nucleic Acids Res. 2018, 47, D367–D375. [Google Scholar] [CrossRef]
- Portugal, J.; Rodríguez-Campos, A. T7 RNA Polymerase Cannot Transcribe through a Highly Knotted DNA Template. Nucleic Acids Res. 1996, 24, 4890–4894. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, L.A.; He, H.; Pham-Huy, C. Chiral Drugs: An Overview. Int. J. Biomed. Sci. 2006, 2, 85–100. [Google Scholar]
- Liu, L.F.; Wang, J.C. Supercoiling of the DNA Template during Transcription. Proc. Natl. Acad. Sci. USA 1987, 84, 7024–7027. [Google Scholar] [CrossRef] [PubMed]
- Valdés, A.; Martinez-Garcia, B.; Segura, J.; Dyson, S.; Díaz-Ingelmo, O.; Roca, J. Quantitative Disclosure of DNA Knot Chirality by High-Resolution 2D-Gel Electrophoresis. Nucleic Acids Res. 2019, 47, e29. [Google Scholar] [CrossRef]
- Goundaroulis, D.; Lieberman Aiden, E.; Stasiak, A. Chromatin Is Frequently Unknotted at the Megabase Scale. Biophys. J. 2020, 118, 2268–2279. [Google Scholar] [CrossRef]
- Dolgin, E. DNA’s Secret Weapon against Knots and Tangles. Nature 2017, 544, 284–286. [Google Scholar] [CrossRef] [PubMed]
- Dorier, J.; Goundaroulis, D.; Benedetti, F.; Stasiak, A. Knoto-ID: A Tool to Study the Entanglement of Open Protein Chains Using the Concept of Knotoids. Bioinformatics 2018, 34, 3402–3404. [Google Scholar] [CrossRef] [PubMed]
- Turaev, V. Knotoids. Osaka J. Math. 2012, 49, 195–223. [Google Scholar]
- Gügümcü, N.; Kauffman, L. New Invariants of Knotoids. Eur. J. Comb. 2017, 65, 186–229. [Google Scholar] [CrossRef]
- Vologodskii, A. Brownian Dynamics Simulation of Knot Diffusion along a Stretched DNA Molecule. Biophys. J. 2006, 90, 1594–1597. [Google Scholar] [CrossRef]
- Metzler, R.; Reisner, W.; Riehn, R.; Austin, R.; Tegenfeldt, J.O.; Sokolov, I.M. Diffusion Mechanisms of Localised Knots along a Polymer. Europhys. Lett. 2006, 76, 696–702. [Google Scholar] [CrossRef]
- Liu, L.; Liu, C.; Alberts, B. Type II DNA Topoisomerases: Enzymes That Can Unknot a Topologically Knotted DNA Molecule via a Reversible Double-Strand Break. Cell 1980, 19, 697–707. [Google Scholar] [CrossRef]
- Dean, F.B.; Stasiak, A.; Koller, T.; Cozzarelli, N.R. Duplex DNA Knots Produced by Escherichia Coli Topoisomerase I. Structure and Requirements for Formation. J. Biol. Chem. 1985, 260, 4975–4983. [Google Scholar] [CrossRef]
- Rybenkov, V.V.; Ullsperger, C.; Vologodskii, A.V.; Cozzarelli, N.R. Simplification of DNA Topology Below Equilibrium Values by Type II Topoisomerases. Science 1997, 277, 690. [Google Scholar] [CrossRef]
- Witz, G.; Dietler, G.; Stasiak, A. Tightening of DNA Knots by Supercoiling Facilitates Their Unknotting by Type II DNA Topoisomerases. Proc. Natl. Acad. Sci. USA 2011, 108, 3608. [Google Scholar] [CrossRef]
- Racko, D.; Benedetti, F.; Dorier, J.; Burnier, Y.; Stasiak, A. Generation of Supercoils in Nicked and Gapped DNA Drives DNA Unknotting and Postreplicative Decatenation. Nucleic Acids Res. 2015, 43, 7229–7236. [Google Scholar] [CrossRef] [PubMed]
- Racko, D.; Benedetti, F.; Goundaroulis, D.; Stasiak, A. Chromatin Loop Extrusion and Chromatin Unknotting. Polymers 2018, 10, 1126. [Google Scholar] [CrossRef]
- Orlandini, E.; Marenduzzo, D.; Michieletto, D. Synergy of Topoisomerase and Structural-Maintenance-of-Chromosomes Proteins Creates a Universal Pathway to Simplify Genome Topology. Proc. Natl. Acad. Sci. USA 2019, 116, 8149. [Google Scholar] [CrossRef]
- Rawdon, E.J.; Dorier, J.; Racko, D.; Millett, K.C.; Stasiak, A. How Topoisomerase IV Can Efficiently Unknot and Decatenate Negatively Supercoiled DNA Molecules without Causing Their Torsional Relaxation. Nucleic Acids Res. 2016, 44, 4528–4538. [Google Scholar] [CrossRef]
- Bonato, A.; Marenduzzo, D.; Michieletto, D. Simplifying Topological Entanglements by Entropic Competition of Slip-Links. arXiv 2020, arXiv:2010.16205. [Google Scholar]
- Millett, K.C.; Rawdon, E.J.; Tran, V.T.; Stasiak, A. Symmetry-Breaking in Cumulative Measures of Shapes of Polymer Models. J. Chem. Phys. 2010, 133, 154113. [Google Scholar] [CrossRef] [PubMed]
- Arsuaga, J.; Vazquez, M.; McGuirk, P.; Trigueros, S.; Sumners, D.W.; Roca, J. DNA Knots Reveal a Chiral Organization of DNA in Phage Capsids. Proc. Natl. Acad. Sci. USA 2005, 102, 9165. [Google Scholar] [CrossRef]
- Stone, M.D.; Bryant, Z.; Crisona, N.J.; Smith, S.B.; Vologodskii, A.; Bustamante, C.; Cozzarelli, N.R. Chirality Sensing by Escherichia Coli Topoisomerase IV and the Mechanism of Type II Topoisomerases. Proc. Natl. Acad. Sci. USA 2003, 100, 8654. [Google Scholar] [CrossRef] [PubMed]
- Milchev, A. Single-Polymer Dynamics under Constraints: Scaling Theory and Computer Experiment. J. Phys. Condens. Matter 2011, 23, 103101. [Google Scholar] [CrossRef]
- Ha, B.-Y.; Jung, Y. Polymers under Confinement: Single Polymers, How They Interact, and as Model Chromosomes. Soft Matter 2015, 11, 2333–2352. [Google Scholar] [CrossRef]
- Palyulin, V.V.; Ala-Nissila, T.; Metzler, R. Polymer Translocation: The First Two Decades and the Recent Diversification. Soft Matter 2014, 10, 9016–9037. [Google Scholar] [CrossRef]
- Szymczak, P. Translocation of Knotted Proteins through a Pore. Eur. Phys. J. Spec. Top. 2014, 223, 1805–1812. [Google Scholar] [CrossRef]
- Matthews, R.; Louis, A.A.; Yeomans, J.M. Knot-Controlled Ejection of a Polymer from a Virus Capsid. Phys. Rev. Lett. 2009, 102, 088101. [Google Scholar] [CrossRef]
- Liu, L.F.; Perkocha, L.; Calendar, R.; Wang, J.C. Knotted DNA from Bacteriophage Capsids. Proc. Natl. Acad. Sci. USA 1981, 78, 5498. [Google Scholar] [CrossRef]
- Suma, A.; Micheletti, C. Pore Translocation of Knotted DNA Rings. Proc. Natl. Acad. Sci. USA 2017, 114, E2991. [Google Scholar] [CrossRef]
- Ma, Z.; Dorfman, K.D. Diffusion of Knots along DNA Confined in Nanochannels. Macromolecules 2020, 53, 6461–6468. [Google Scholar] [CrossRef]
- Grosberg, A.; Rabin, Y. Metastable Tight Knots in a Wormlike Polymer. Phys. Rev. Lett. 2007, 99, 217801. [Google Scholar] [CrossRef]
- Dai, L.; Renner, C.B.; Doyle, P.S. Metastable Knots in Confined Semiflexible Chains. Macromolecules 2015, 48, 2812–2818. [Google Scholar] [CrossRef]
- Di Stefano, M.; Tubiana, L.; Di Ventra, M.; Micheletti, C. Driving Knots on DNA with AC/DC Electric Fields: Topological Friction and Memory Effects. Soft Matter 2014, 10, 6491–6498. [Google Scholar] [CrossRef]
- Trigueros, S.; Arsuaga, J.; Vazquez, M.E.; Sumners, D.W.; Roca, J. Novel Display of Knotted DNA Molecules by Two-Dimensional Gel Electrophoresis. Nucleic Acids Res. 2001, 29, e67. [Google Scholar] [CrossRef] [PubMed]
- Shaw, S.Y.; Wang, J.C. Chirality of DNA Trefoils: Implications in Intramolecular Synapsis of Distant DNA Segments. Proc. Natl. Acad. Sci. USA 1997, 94, 1692. [Google Scholar] [CrossRef] [PubMed]
- Witz, G.; Stasiak, A. Chapter 8: Structure and Dynamics of Supercoiled DNA Knots and Catenanes. RSC Biomol. Sci. 2012, 2, 179–197. [Google Scholar] [CrossRef]
- Rosa, A.; Di Ventra, M.; Micheletti, C. Topological Jamming of Spontaneously Knotted Polyelectrolyte Chains Driven Through a Nanopore. Phys. Rev. Lett. 2012, 109, 118301. [Google Scholar] [CrossRef] [PubMed]
- Michieletto, D.; Marenduzzo, D.; Orlandini, E. Topological Patterns in Two-Dimensional Gel Electrophoresis of DNA Knots. Proc. Natl. Acad. Sci. USA 2015, 112, E5471. [Google Scholar] [CrossRef] [PubMed]
- Marenda, M.; Orlandini, E.; Micheletti, C. Sorting Ring Polymers by Knot Type with Modulated Nanochannels. Soft Matter 2017, 13, 795–802. [Google Scholar] [CrossRef]
- Weiss, L.B.; Marenda, M.; Micheletti, C.; Likos, C.N. Hydrodynamics and Filtering of Knotted Ring Polymers in Nanochannels. Macromolecules 2019, 52, 4111–4119. [Google Scholar] [CrossRef]
- Wang, X.; Llopis, P.M.; Rudner, D.Z. Organization and Segregation of Bacterial Chromosomes. Nat. Rev. Genet. 2013, 14, 191–203. [Google Scholar] [CrossRef] [PubMed]
- Stagno, J.; Ma, B.; Li, J.; Altieri, A.; Byrd, R.A.; Ji, X. Crystal Structure of a Plectonemic RNA Supercoil. Nat. Commun. 2012, 3, 901. [Google Scholar] [CrossRef]
- Gier, T.E.; Bu, X.; Feng, P.; Stucky, G.D. Synthesis and Organization of Zeolite-like Materials with Three-Dimensional Helical Pores. Nature 1998, 395, 154–157. [Google Scholar] [CrossRef]
- Zhang, J.; Albelda, M.T.; Liu, Y.; Canary, J.W. Chiral Nanotechnology. Chirality 2005, 17, 404–420. [Google Scholar] [CrossRef]
- Zhang, C.; Deng, X.; Wang, C.; Bao, C.; Yang, B.; Zhang, H.; Qi, S.; Dong, Z. Helical Supramolecular Polymer Nanotubes with Wide Lumen for Glucose Transport: Towards the Development of Functional Membrane-Spanning Channels. Chem. Sci. 2019, 10, 8648–8653. [Google Scholar] [CrossRef]
- Limbach, H.J.; Arnold, A.; Mann, B.A.; Holm, C. ESPResSo—an Extensible Simulation Package for Research on Soft Matter Systems. Comput. Phys. Commun. 2006, 174, 704–727. [Google Scholar] [CrossRef]
- Arnold, A.; Lenz, O.; Kesselheim, S.; Weeber, R.; Fahrenberger, F.; Roehm, D.; Košovan, P.; Holm, C. ESPResSo 3.1: Molecular Dynamics Software for Coarse-Grained Models. In Meshfree Methods for Partial Differential Equations VI; Griebel, M., Schweitzer, M.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–23. [Google Scholar]
- Langowski, J. Polymer Chain Models of DNA and Chromatin. Eur. Phys. J. E 2006, 19, 241–249. [Google Scholar] [CrossRef]
- Lu, Y.; Weers, B.; Stellwagen, N.C. DNA Persistence Length Revisited. Biopolymers 2002, 61, 261–275. [Google Scholar] [CrossRef] [PubMed]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of Repulsive Forces in Determining the Equilibrium Structure of Simple Liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Racko, D.; Benedetti, F.; Dorier, J.; Burnier, Y.; Stasiak, A. Molecular Dynamics Simulation of Supercoiled, Knotted, and Catenated DNA Molecules, Including Modeling of Action of DNA Gyrase. Methods Mol. Biol. 2017, 1624, 339–372. [Google Scholar] [PubMed]
- Bar-Natan, D.; Morrison, S. The Knot Atlas. Available online: http://katlas.org (accessed on 3 July 2015).
- Tubiana, L.; Polles, G.; Orlandini, E.; Micheletti, C. KymoKnot: A Web Server and Software Package to Identify and Locate Knots in Trajectories of Linear or Circular Polymers. Eur. Phys. J. E 2018, 41, 72. [Google Scholar] [CrossRef] [PubMed]
- Brasher, R.; Scharein, R.; Vázquez, M. New Biologically Motivated Knot Table. Biochem. Soc. Trans. 2013, 41, 606–611. [Google Scholar] [CrossRef]
- Rolfsen, D. Knots and Links; AMS Chelsea Publishing: New York, NY, USA, 2003; Volume 346.H, ISBN 978-0-8218-3436-7. [Google Scholar]
- Portillo, J.; Diao, Y.; Scharein, R.; Arsuaga, J.; Vazquez, M. On the Mean and Variance of the Writhe of Random Polygons. J. Phys. A Math. Theor. 2011, 44, 275004. [Google Scholar] [CrossRef]
- Lu, X.-J.; Olson, W. 3DNA: A Software Package for the Analysis, Rebuilding and Visualization of Three-Dimensional Nucleic Acid Structures. Nucleic Acids Res. 2003, 31, 5108–5121. [Google Scholar] [CrossRef] [PubMed]
- Račko, D.; Cifra, P. Segregation of Semiflexible Macromolecules in Nanochannel. J. Chem. Phys. 2013, 138, 184904. [Google Scholar] [CrossRef]
- Rawdon, E.J.; Kern, J.C.; Piatek, M.; Plunkett, P.; Stasiak, A.; Millett, K.C. Effect of Knotting on the Shape of Polymers. Macromolecules 2008, 41, 8281–8287. [Google Scholar] [CrossRef]
- Klenin, K.; Langowski, J. Computation of Writhe in Modeling of Supercoiled DNA. Biopolymers 2000, 54, 307–317. [Google Scholar] [CrossRef]
- Benedetti, F. Polymer Public Library at Github. 2016. Available online: https://github.com/fbenedett/polymer-libraries (accessed on 26 May 2017).
- Klotz, A.R.; Soh, B.W.; Doyle, P.S. Motion of Knots in DNA Stretched by Elongational Fields. Phys. Rev. Lett. 2018, 120, 188003. [Google Scholar] [CrossRef]
- Bechinger, C.; Di Leonardo, R.; Löwen, H.; Reichhardt, C.; Volpe, G.; Volpe, G. Active Particles in Complex and Crowded Environments. Rev. Mod. Phys. 2016, 88, 045006. [Google Scholar] [CrossRef]
- Ao, X.; Ghosh, P.; Li, Y.; Schmid, G.; Hänggi, P.; Marchesoni, F. Active Brownian Motion in a Narrow Channel. Eur. Phys. J. Spec. Top. 2014, 223, 3227–3242. [Google Scholar] [CrossRef]
- Chávez, Y.; Chacón-Acosta, G.; Dagdug, L. Unbiased Diffusion of Brownian Particles in a Helical Tube. J. Chem. Phys. 2018, 148, 214106. [Google Scholar] [CrossRef]
- Gonzalez, O.; Maddocks, J.H. Global Curvature, Thickness, and the Ideal Shapes of Knots. Proc. Natl. Acad. Sci. USA 1999, 96, 4769. [Google Scholar] [CrossRef] [PubMed]
- Benedetti, F.; Japaridze, A.; Dorier, J.; Racko, D.; Kwapich, R.; Burnier, Y.; Dietler, G.; Stasiak, A. Effects of Physiological Self-Crowding of DNA on Shape and Biological Properties of DNA Molecules with Various Levels of Supercoiling. Nucleic Acids Res. 2015, 43, 2390–2399. [Google Scholar] [CrossRef] [PubMed]
- Shen, L.; Chen, Z. Critical Review of the Impact of Tortuosity on Diffusion. Chem. Eng. Sci. 2007, 62, 3748–3755. [Google Scholar] [CrossRef]
- Ogawa, N. Diffusion in a Curved Tube. Phys. Lett. A 2013, 377, 2465–2471. [Google Scholar] [CrossRef]
- Valero, C.; Herrera, R. Fick-Jacobs Equation for Channels over Three-Dimensional Curves. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2014, 90, 052141. [Google Scholar] [CrossRef] [PubMed]
- Zwanzig, R. Diffusion Past an Entropy Barrier. J. Phys. Chem. 1992, 96, 3926–3930. [Google Scholar] [CrossRef]
- Burada, P.; Schmid, G.; Reguera, D.; Rubi, J.; Hänggi, P. Biased Diffusion in Confined Media: Test of the Fick-Jacobs Approximation and Validity Criteria. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2007, 75, 051111. [Google Scholar] [CrossRef]
- Reimann, P.; Van den Broeck, C.; Linke, H.; Hänggi, P.; Rubi, J.; Pérez-Madrid, A. Diffusion in Tilted Periodic Potentials: Enhancement, Universality, and Scaling. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2002, 65, 031104. [Google Scholar] [CrossRef] [PubMed]
- Muthukumar, M. Communication: Charge, Diffusion, and Mobility of Proteins through Nanopores. J. Chem. Phys. 2014, 141, 081104. [Google Scholar] [CrossRef]
- Shi, Y.; Lee, Y.T.; Kim, A. Knudsen Diffusion Through Cylindrical Tubes of Varying Radii: Theory and Monte Carlo Simulations. Transp. Porous Media 2012, 93, 517–541. [Google Scholar] [CrossRef]
- Jamroz, M.; Niemyska, W.; Rawdon, E.J.; Stasiak, A.; Millett, K.C.; Sułkowski, P.; Sulkowska, J.I. KnotProt: A Database of Proteins with Knots and Slipknots. Nucleic Acids Res. 2015, 43, D306–D314. [Google Scholar] [CrossRef] [PubMed]
- Sogo, J.; Stasiak, A.; Martínez-Robles, M.; Krimer, D.; Hernd_ndez, P.; Schvartzman, J. Formation of Knots in Partially Replicated DNA Molecules. J. Mol. Biol. 1999, 286 3, 637–643. [Google Scholar] [CrossRef]
- Suma, A.; Rosa, A.; Micheletti, C. Pore Translocation of Knotted Polymer Chains: How Friction Depends on Knot Complexity. ACS Macro Lett. 2015, 4, 1420–1424. [Google Scholar] [CrossRef]
- Narsimhan, V.; Renner, C.B.; Doyle, P.S. Translocation Dynamics of Knotted Polymers under a Constant or Periodic External Field. Soft Matter 2016, 12, 5041–5049. [Google Scholar] [CrossRef] [PubMed]





| Knotoid | Knot | ΔWr | Rg | Lk | A | P | vdrift | D |
|---|---|---|---|---|---|---|---|---|
| [nm] | [nm] | [μm·s−1] | [μm2·s−1] | |||||
| 3_1m | <+> 31 | 3.27 | 7.7 ± 0.1 | 79.5 ± 0.5 | 0.11 | −0.32 | 312 ± 14 | 16.94 |
| 3_1 | <−> 31 | −3.27 | 7.8 ± 0.1 | 80.1 ± 0.6 | 0.11 | −0.33 | 316 ± 5 | 17.58 |
| 4_1|11n_19 | 41 | 0 | 9.0 ± 0.0 | 102.6 ± 0.2 | 0.16 | 0.41 | 239 ± 7 | 13.05 |
| 5_1m|10_132m | <+> 51 | 6.1 | 8.6 ± 0.0 | 115.1 ± 0.0 | 0.09 | −0.36 | 307 ± 5 | 15.63 |
| 5_1|10_132 | <−> 51 | −6.10 | 8.9 ± 0.1 | 117.6 ± 0.0 | 0.09 | −0.39 | 302 ± 5 | 16.79 |
| 5_2|11n_57m | <+> 52 | 4.56 | 10.6 ± 0.1 | 128.9 ± 0.9 | 0.17 | 0.69 | 304 ± 15 | 17.08 |
| |12n_475m | ||||||||
| 5_2m|11n_57 | <−> 52 | −4.57 | 10.9 ± 0.5 | 132.3 ± 4.3 | 0.16 | 0.67 | 302 ± 7 | 16.71 |
| |12n_475 | ||||||||
| 6_1 | <+> 61 | 1.17 | 12.8 ± 0.1 | 158.0 ± 0.6 | 0.21 | 0.84 | 265 ± 6 | 14.68 |
| 6_1m | <−> 61 | −1.18 | 12.5 ± 0.2 | 156.8 ± 2.6 | 0.2 | 0.77 | 276 ± 16 | 15.22 |
| 7_1m|12n_749 | <+> 71 | 8.77 | 11.5 ± 0.1 | 172.3 ± 4.5 | 0.1 | 0.14 | 334 ± 7 | 19 |
| 7_1|12n_749m | <−> 71 | −8.82 | 11.3 ± 0.1 | 164.5 ± 4.5 | 0.12 | 0.37 | 313 ± 7 | 17.39 |
| 10_124 | <+>10124 | 10.7 | 10.0 ± 0.3 | 167.9 ± 3.5 | 0.07 | −0.42 | 359 ± 6 | 18.26 |
| 10_124m | <−>10124 | −10.71 | 9.8±0.3 | 161.8 ± 3.5 | 0.07 | −0.41 | 347 ± 6 | 19.61 |
 3_1m |  4_1|11n_19 |  5_1| 10_132 |  5_2|11n_57m|12n_475m |  6_1 |  7_1m| 12n_749 |  10_124 | ||
| System | Knot | ΔWr | Rg [nm] | Lk [nm] | A | P | vdrift [μm·s−1] | D [μm2·s−1] |
|---|---|---|---|---|---|---|---|---|
| Antichiral | <+>31 (m) | 3.24 | 6.8 ± 0.0 | 73.0 ± 0.3 | 0.12 | 0.10 | 87 ± 4 | 3.94 ± 0.22 |
| Equichiral | <–>31 | −3.43 | 6.3 ± 0.0 | 69.6 ± 0.4 | 0.11 | 0.22 | 188 ± 5 | 10.29 ± 0.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rusková, R.; Račko, D. Channels with Helical Modulation Display Stereospecific Sensitivity for Chiral Superstructures. Polymers 2021, 13, 3726. https://doi.org/10.3390/polym13213726
Rusková R, Račko D. Channels with Helical Modulation Display Stereospecific Sensitivity for Chiral Superstructures. Polymers. 2021; 13(21):3726. https://doi.org/10.3390/polym13213726
Chicago/Turabian StyleRusková, Renáta, and Dušan Račko. 2021. "Channels with Helical Modulation Display Stereospecific Sensitivity for Chiral Superstructures" Polymers 13, no. 21: 3726. https://doi.org/10.3390/polym13213726
APA StyleRusková, R., & Račko, D. (2021). Channels with Helical Modulation Display Stereospecific Sensitivity for Chiral Superstructures. Polymers, 13(21), 3726. https://doi.org/10.3390/polym13213726








