Abstract
The bandwidth of multimode W-type plastic optical fibers (POFs) with graded-index (GI) core distribution is investigated by solving the time-dependent power flow equation. The multimode W-type GI POF is designed from a multimode single-clad (SC) GI POF fiber upon modification of the cladding layer of the latter. Results show how the bandwidth in W-type GI POFs can be enhanced by increasing the wavelength for different widths of the intermediate layer and refractive indices of the outer cladding. These fibers are characterized according to their apparent efficiency to reduce modal dispersion and increase bandwidth.
1. Introduction
In the last three decades, data traffic demand has increased exponentially for access and backbone networks. The growth was accelerated by streaming transmissions and cloud computing. This concept also becomes a strong approach for use in optical networking strategies for automotive communications systems, given the advances in both intelligent driving systems and multimedia services. These systems usually use multimode POFs (Poly(methyl methacrylate), or PMMA, optical fibers) thanks to their easy connection and strength in tight curves.
Transmission characteristics of multimode POFs strongly depend upon the differential mode-attenuation and mode coupling [1]. The latter represents power transfer between neighboring modes caused by fiber impurities and inhomogeneities introduced during the fiber manufacturing process (such as microscopic bends, irregularity of the core-cladding boundary and refractive index distribution fluctuations) [2]. Mode coupling increases fiber bandwidth in data networks by reducing modal dispersion [3]. In practice, when installing a POF-based link, the cable has to be repeatedly bent, thus increasing the strength of mode coupling and radiation losses [4]. It has been shown that organic glass-clad PMMA fibers show a similar strength of mode coupling compared to standard POFs but stronger mode coupling than do the plastic-clad silica fibers [5].
Studies have been reported using geometric optics (ray approximation) to investigate transmission in optical fibers [6,7]. By employing the time-independent power flow equation [2,8] as well as the Fokker–Planck and Langevin equations [9], far-field patterns in SI POFs have been predicted as a function of the launch conditions and fiber length. By employing the time-dependent power flow equation, the bandwidth of GI POF has been obtained for different radial launch conditions [10].
In terms of the number of functional cover layers, multimode optical fibers are usually SC fibers. Special detection [11], modulation [12], equalization [13] and compensation for modal-dispersion [14] can improve the bandwidth and attenuation properties of SC fiber. Since the structure of fiber can influence its features significantly, different POFs (double-clad fibers) of the step-index (SI), GI and W types were proposed [15,16,17]. Due to their progressively decreased core refractive index with a radial distance from the fiber axis, GI POFs have a much lower modal dispersion than SI POFs [18]. Since the dispersion of the W-type fiber is smaller than that of SC fiber [19], W-type fiber has a larger bandwidth and lower bending losses compared to a corresponding fiber of SC. The glass optical fiber’s bandwidth-distance product is approximately 30 MHz·km for SC and approximately 50 MHz·km for W-type fiber. The POFs have a bandwidth-distance product of approximately 15 MHz·km for the SC and approximately 200 MHz·km for the W-type fibers [15,17,20].
The intermediate layer of a W-type fiber (inner cladding) decreases the dispersion and enlarges the bandwidth, thereby lowering the number of guided modes that are held closer to the core [20,21]. Optical power is transferred between modes because of the mode coupling [2]. Methods are needed for calculating modal attenuation and coupling to loss modes of W-type fiber’s intermediate layer, and for optimizing the fiber’s refractive index profile in order to minimize the group delay difference between modes in the output field [20,22]. In this study, we examined how the wavelength influences the bandwidth for various W-type GI POF configurations. It should be noted that our calculations include modal attenuation, mode coupling and modal dispersion.
2. Time-Dependent Power Flow Equation
Consider a W-type GI fiber with refractive index profile, as shown in Figure 1b. The refractive index profile of W-type optical fibers with GI distribution of the core may be expressed as [8,23]:
where g is the core index exponent, a is the core radius, δa is the intermediate layer width, b is the fiber diameter, n0(λ) is the maximum index of the core (measured at the fiber axis), nq and np are refractive indices of the intermediate layer and cladding respectively, and is the relative index difference between the core and intermediate layer.
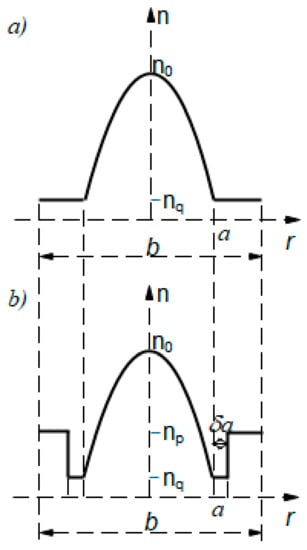
Figure 1.
Refractive index profile of (a) SC GI POF and (b) W-type GI POF.
The time-dependent power flow equation for multimode optical fibers with GI core distribution is:
where P(m,λ,z,ω) is the power in the m—the principal mode (modal group), z is the coordinate along the fiber axis from the input fiber end, α(m,) = is the attenuation of the mode m, where α0 represents conventional losses due to absorption and scattering (the term α0 leads only to a multiplier exp(−α0z) in the solution and is thus neglected, the term in the expansion of is dominant for higher-order modes), d(m,) is the coupling coefficient of the mode m, ω = 2πf is the baseband angular frequency and is delay time per unit length of mode m, which can be determined as:
where c is the free-space velocity of light and:
The maximum principal mode number, M(λ), can be obtained as [24]:
where is the free-space wave number. Gaussian launch-beam distribution, P0(θ,,z = 0), can be converted to P0(m,,z = 0) (one needs P0(m,,z = 0) to solve the power flow equation numerically (2)), using the following relationship [25]:
where r0 is radial distance (radial offset) between the launch beam position and the core center and θ is the propagation angle with respect to the core axis.
The relative refractive index difference, , between the core and intermediate layer is larger than the difference between the core and cladding. Modes propagating along with subcritical angles m < mq are guided. The same is true for those propagating through the complete W-fiber, with m below the critical value mp. On the other hand, modes with angles between mp and mq ≡ M are transformed into leaky modes [10]. The leaky mode attenuation constants are provided as:
One can see from Equation (7) that for thick intermediate layer widths, δ, the lower leaky modes are substantially guided because of the low leaky modes’ losses. Experiments in a SC GI fiber reveal that attenuation remains constant throughout the guided-mode region (m ≤ ) and rises quite steeply in the radiation-mode region [26]. As a result, in a W-type GI POF, the modal attenuation can be expressed as:
A W-type fiber can be thought of as a combination of SCq fiber with cladding. In the SCq fiber, modes m < can be guided. When the SCq fiber is coupled with surrounding medium of index np, the lower-order modes m < remain guided, while the higher-order modes m () are transformed into leaky modes. Due to the strong dependence of αL(m) on the intermediate layer width δa (Equation (7)), it is expected that characteristics of a W-type GI fiber also depend on δa and coincide with those of SCp and SCq GI fibers in the limits of δ→0 and δ→∞, respectively [20,27].
It is obvious that P(m,,z,ω) is complex. By separating P into the real part Pr and imaginary part Pi, Equation (2) can be rewritten as the following simultaneous partial differential equations:
where P = Pr + jPi. Assuming a constant coupling coefficient d ≡ D, Equations (9) and (10) can be written as:
Using the EFDM, discretization of Equations (11) and (12) leads to:
where and refer to the discretization step lengths Δm and Δz for the mode m and length z respectively, i.e., and .
If Pr and Pi are obtained by solving Equations (13) and (14), the transmission characteristics can be calculated. Thus, the frequency response of fiber at length z is:
where the factor 2m denotes degeneracy of modal group m. The frequency responses for a specific fiber can be determined over a wide range of lengths, revealing the bandwidth dependence with distance. The modal power distribution, , and the spatial transient of power, , can be obtained by:
One should note here that the numerical solution of the time-dependent power flow equation as well as the calculation of the frequency response and bandwidth in the analyzed W-type GI POF have been obtained by employing our FORTRAN90 code. This enabled us to determine the relationship between the transmission length and bandwidth in the W-type GI POF.
3. Numerical Results and Discussion
In this research, we investigated the bandwidth at various wavelengths in a differently constructed W-type GI POF designed from the SC GI POF (Figure 1a), which we experimentally investigated in our previously published works [8,10]. For the structure shown in Figure 1b, a W-shape refractive index model is adopted. SC GI POF (OM Giga, Fiber FinTM) had the following characteristics: The fiber’s core diameter was 2a = 0.9 mm (fiber diameter was b = 1 mm), the core’s refractive index measured along the fiber axis was n0 = 1.522 and the intermediate layer (inner cladding) cladding’s refractive index was nq = 1.492. The maximum principal mode number for the examined SC GI POF was M = 656 at wavelength λ = 633 nm, g = 1.80101 and ∆q= (n0 − nq)/n0 = 0.019711. The W-type GI POF with GI distribution of the core is designed from this SC GI POF in such a way that the W-type GI POF’s inner cladding retains the distribution of the SC GI POF’s cladding, while the W-type GI POF’s outer cladding has a refractive index, np, that is higher than the inner cladding’s refractive index, nq (Figure 1b). In the modeling, three values of the outer cladding refractive index, np, were used: np = 1.51366 (mp = 346), np = 1.51065 (mp = 404) and np = 1.50718 (mp = 461). The normalized intermediate layer widths of δ = 0.001, δ = 0.002 and δ = 0.003 (actual width is δ·a mm) were used. In the calculations, the constant coupling coefficient ≡ was employed [8]. At λ = 476, 522, 568 and 633 nm, the maximum principal mode number in such proposed W-type GI POFs is M = 872, 795, 731 and 656, respectively. In the numerical calculations, a Gaussian beam, P(θ,z), is assumed to be launched with ⟨θ⟩ = 0° and standard deviation σθ = 1.3° (FWHM = 3.06°). The width of the launched beam measured at the end of a single-mode optical fiber, which is butt-coupled to the SC GI POF examined in our earlier experimental work [8], is described by this standard deviation. The numerical calculations have been performed for radial offset ∆r = 0 µm.
Figure 2 shows our numerical solution to the time-dependent power flow equation. It depicts the evolution of the W-type GI POF’s bandwidth at 30 m with wavelength for varied widths of intermediate layer, δ, in three inserts corresponding to three outer cladding refractive indices: np = 1.51366 (mp = 346), np = 1.51065 (mp = 404) and np = 1.50718 (mp = 461). Figure 2 shows that the influence of wavelength on bandwidth is less noticeable for the smallest width of the intermediate layer (δ = 0.001). This is due to large leaky mode losses (Figure 3), and as these modes are practically not guided along the fiber, modal dispersion (bandwidth) changes very little. There is a wavelength-dependent drop in bandwidth as the width of the intermediate layer increases. At short wavelengths, this decrease is more pronounced because leaky mode losses are reduced (Figure 3), resulting in a rise in modal dispersion and a fall in fiber bandwidth.
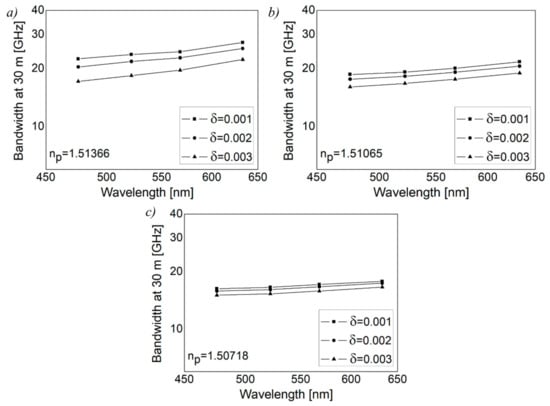
Figure 2.
Numerical results for bandwidth for W-type GI POF at 30 m as a function of wavelength for (a) np = 1.51366, (b) np = 1.51065 and (c) np = 1.50718, where (FWHM)z=0 = 3.06°, δ = 0.001, 0.002 and 0.003 and .
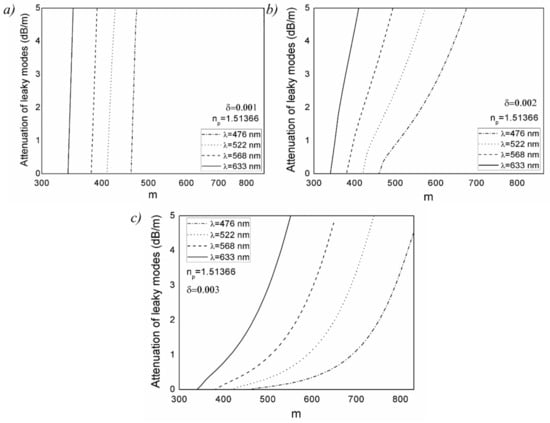
Figure 3.
Leaky mode losses for W-type GI POF as a function of wavelength, for (a) δ = 0.001, (b) δ = 0.002 and (c) δ = 0.003, and np = 1.51366.
When the refractive index of the outer cladding, np, is increased, leaky mode losses increase, resulting in the maximum bandwidth values in the case of δ = 0.001. The improvement in the bandwidth of W-type GI POFs is more noticeable at longer fiber lengths, as seen in Figure 2. Since a narrow launch beam distribution is assumed in the calculations, only guided modes are excited at the input fiber length. As a result, for short fiber lengths, leaky modes play a less important role. More leaky modes are filtered out with longer fiber lengths due to mode coupling, resulting in the significant improvement of the bandwidth of the W-type GI POF [28].
4. Conclusions
For W-type GI POFs with a variable width of the intermediate layer and refractive index of the outer cladding, bandwidth was determined using the time-dependent power flow equation over a variety of light wavelengths. The bandwidth of W-fibers broadened with larger wavelengths for all intermediate layer widths, as shown in this study. Higher leaky mode losses and the resulting decline in modal dispersion caused this broadening of the bandwidth. Since leaky mode losses grow as the outer cladding’s refractive index rises, the bandwidth rises as well. These findings can be used to design and implement a W-type GI POF at various operating wavelengths.
Author Contributions
Conceptualization, A.S.; methodology, software, A.S. and B.D.; writing—original draft preparation, A.S. and S.S.; writing—review and editing, A.D. and R.M.; supervision, S.S.; project administration, funding acquisition, R.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (62003046, 6211101138), the Strategic Research Grant of City University of Hong Kong (Project No. CityU 7004600), a grant from the Serbian Ministry of Education, Science and Technological Development (Agreement No. 451-03-68/2020-14/200122), a grant from the Science Fund of the Republic of Serbia (Agreement No. CTPCF-6379382), the Guangdong Basic and Applied Basic Research Foundation (2021A1515011997), a special project in key field of Guangdong Provincial Department of Education (2021ZDZX1050) and The Innovation Team Project of Guangdong Provincial Department of Education (2021KCXTD014).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ziemann, O.; Krauser, J.; Zamzow, P.E.; Daum, W. Optical Short Range Transmission Systems. In POF Handbook; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-76629-2. [Google Scholar]
- Gloge, D. Optical power flow in multimode fibers. Bell Syst. Tech. J. 1972, 51, 1767–1783. [Google Scholar] [CrossRef]
- Gloge, D. Impulse response of clad optical multomode fibers. Bell Syst. Tech. J. 1973, 52, 801–816. [Google Scholar] [CrossRef]
- Savović, S.; Djordjevich, A. Mode coupling in strained and unstrained step-index plastic optical fibers. Appl. Opt. 2006, 45, 6775–6780. [Google Scholar] [CrossRef]
- Savović, S.; Djordjevich, A. Mode Coupling in Plastic-Clad Silica Fibers and Organic Glass-Clad PMMA Fibers. J. Lightwave Technol. 2014, 32, 1290–1294. [Google Scholar] [CrossRef]
- Eve, M.; Hannay, J.H. Ray theory and random mode coupling in an optical fibre waveguide, I. Opt. Quantum Electron. 1976, 8, 503–508. [Google Scholar] [CrossRef]
- Borecki, M. Light behaviour in polymer optical fibre bend-a new analysis method. Opt. Appl. 2003, 33, 191–204. [Google Scholar]
- Savović, S.; Simović, A.; Drljača, B.; Djordjevich, A.; Stepniak, G.; Bunge, C.A.; Bajić, J. Power flow in graded index plastic optical fibers. J. Lightwave Technol. 2019, 37, 4985–4990. [Google Scholar] [CrossRef]
- Savović, S.; Djordjevich, A. Solution of mode coupling in step-index optical fibers by the Fokker-Planck equation and the Langevin equation. Appl. Opt. 2002, 41, 2826–2830. [Google Scholar] [CrossRef]
- Simović, A.; Djordjevich, A.; Drljača, B.; Savović, S.; Min, R. Investigation of bandwidth in multimode graded index plastic optical fibers. Opt. Express 2021, 29, 29587–29594. [Google Scholar] [CrossRef] [PubMed]
- Patel, K.M.; Ralph, S.E. Enhanced multimode fiber link performance using a spatially resolved receiver. IEEE Photon. Technol. Lett. 2002, 14, 393–395. [Google Scholar] [CrossRef]
- Tyler, E.J.; Webster, M.; Penty, R.V.; White, I.H.; Yu, S.; Rorison, J. Subcarrier modulated transmission of 2.5 Gb/s over 300 m of 62.5-μm-core diameter multimode fiber. IEEE Photon. Technol. Lett. 2002, 14, 1743–1745. [Google Scholar] [CrossRef]
- Zhao, X.; Choa, F.S. Demonstration of 10 Gb/s transmission over 1.5-km-long multimode fiber using equalization techniques. IEEE Photon. Technol. Lett. 2002, 14, 1187–1189. [Google Scholar] [CrossRef]
- Abbott, J.S.; Smith, G.E.; Truesdale, C.M. Multimode Fiber Link Dispersion Compensator. U.S. Patent 6,363,195, 26 March 2002. [Google Scholar]
- Yamashita, T.; Kagami, M. Fabrication of light-induced self-written waveguides with a W-shaped refractive index profile. J. Lightwave Technol. 2005, 23, 2542–2548. [Google Scholar] [CrossRef]
- Asai, M.; Inuzuka, Y.; Koike, K.; Takahashi, S.; Koike, Y. High-bandwidth graded-index plastic optical fiber with low-attenuation, high-bending ability, and high-thermal stability for home-networks. J. Lightvawe Technol. 2011, 29, 1620–1626. [Google Scholar] [CrossRef]
- Mikoshiba, K.; Kajioka, H. Transmission characteristics of multimode W-type optical fiber: Experimental study of the effect of the intermediate layer. Appl. Opt. 1978, 17, 2836–2841. [Google Scholar] [CrossRef] [PubMed]
- Koike, Y.; Koike, K. Progress in low-loss and high-bandwidth plastic optical fibers. J. Polym. Sci. B 2011, 49, 2–17. [Google Scholar] [CrossRef]
- Takahashi, K.; Ishigure, T.; Koike, Y. Index profile design for high-bandwidth W-shaped plastic optical fiber. J. Lightwave Technol. 2006, 24, 2867–2876. [Google Scholar] [CrossRef]
- Tanaka, T.; Yamada, S.; Sumi, M.; Mikoshiba, K. Microbending losses of doubly clad (W-type) optical fibers. Appl. Opt. 1977, 18, 2391–2394. [Google Scholar] [CrossRef]
- Simović, A.; Savović, S.; Drljača, B.; Djordjevich, A. Influence of the fiber design and launch beam on transmission characteristics of W-type optical fibers. Opt. Laser Technol. 2015, 68, 151–159. [Google Scholar] [CrossRef]
- Savović, S.; Simović, A.; Djordjevich, A. Explicit finite difference solution of the power flow equation in W-type optical fibers. Opt. Laser Techn. 2012, 44, 1786–1790. [Google Scholar] [CrossRef]
- Kitayama, K.; Seikai, S.; Uchida, N. Impulse response prediction based on experimental mode coupling coefficient in a 10-km long graded-index fiber. IEEE J. Quant. Electron. 1980, 16, 356–362. [Google Scholar] [CrossRef]
- Olshansky, R. Mode coupling effects in graded-index optical fibers. Appl. Opt. 1975, 14, 935–945. [Google Scholar] [CrossRef] [PubMed]
- Nagano, K.; Kawakami, S. Measurements of mode conversion coefficients in graded-index fibers. Appl. Opt. 1980, 19, 2426–2434. [Google Scholar] [CrossRef]
- Yabre, G. Comprehensive theory of dispersion in graded-index optical fibers. J. Lightwave Technol. 2000, 18, 166–177. [Google Scholar] [CrossRef] [Green Version]
- Ishigure, T.; Endo, H.; Ohdoko, K.; Takahashi, K.; Koike, Y. Modal bandwidth enhancement in a plastic optical fiber by W-refractive index profile. J. Lightwave Technol. 2005, 23, 1754–1762. [Google Scholar] [CrossRef]
- Simović, A.; Djordjevich, A.; Drljača, B.; Savović, S. Power flow in W-type plastic optical fibers with graded index core distribution. Opt. Laser Technol. 2021, 143, 107295. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).