Analysis and Calculation of Stability Coefficients of Cross-Laminated Timber Axial Compression Member
Abstract
:1. Introduction
2. Stability Coefficient Calculation Formulae in Selected Countries
2.1. Stability Coefficient Formulae in Canada
2.2. Stability Coefficient Formulae in Europe
2.3. Stability Coefficient Formulae in the USA
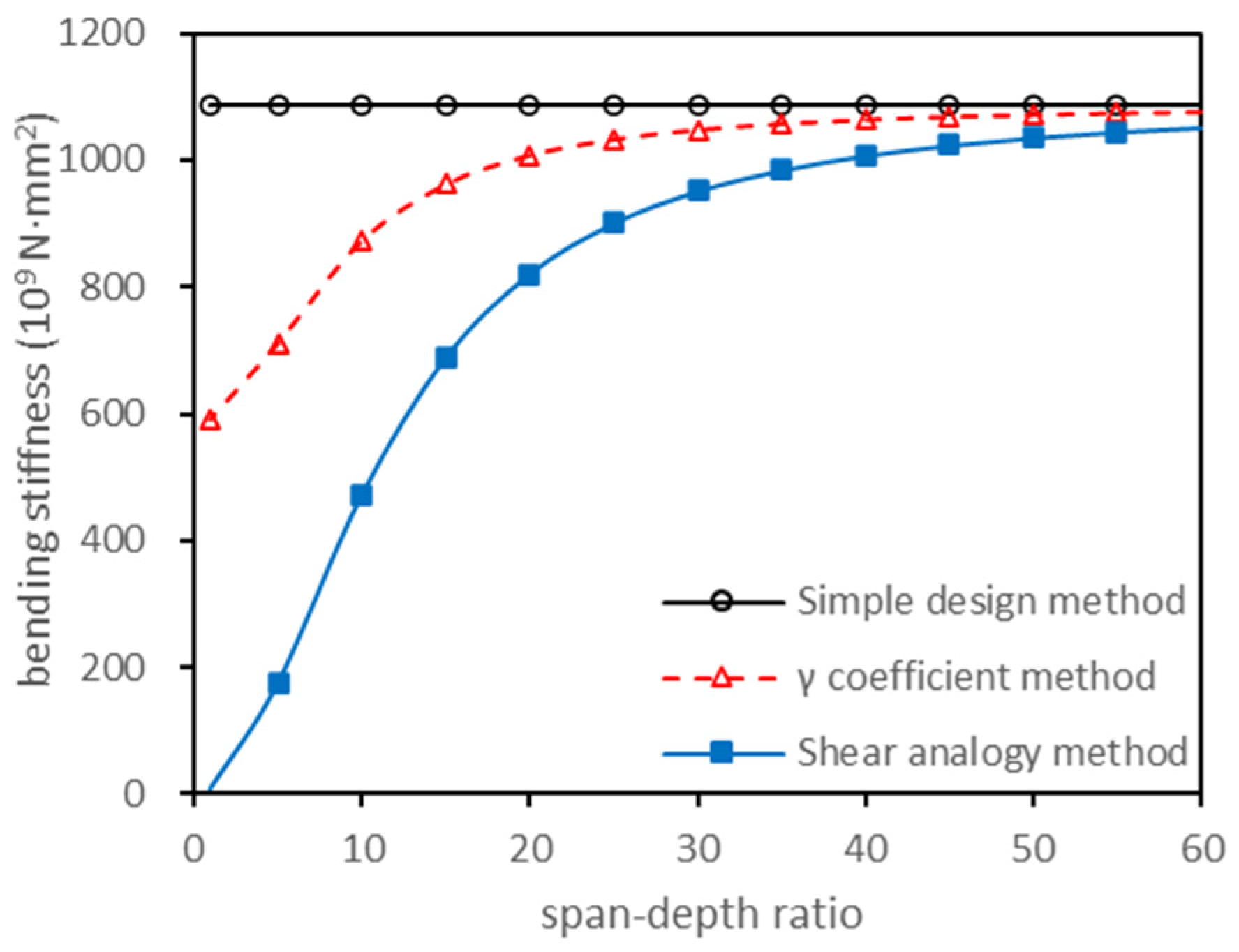
2.4. Modification Based on Formulae in Selected Countries
3. Establishment of Stability Coefficient Calculation Formulae in China
3.1. Slenderness Ratio Formula
3.2. Stability Coefficient Formulae
3.3. Stability Coefficient Parameters
4. Materials and Methods
4.1. Materials
4.2. Compression Test
5. Results and Discussion
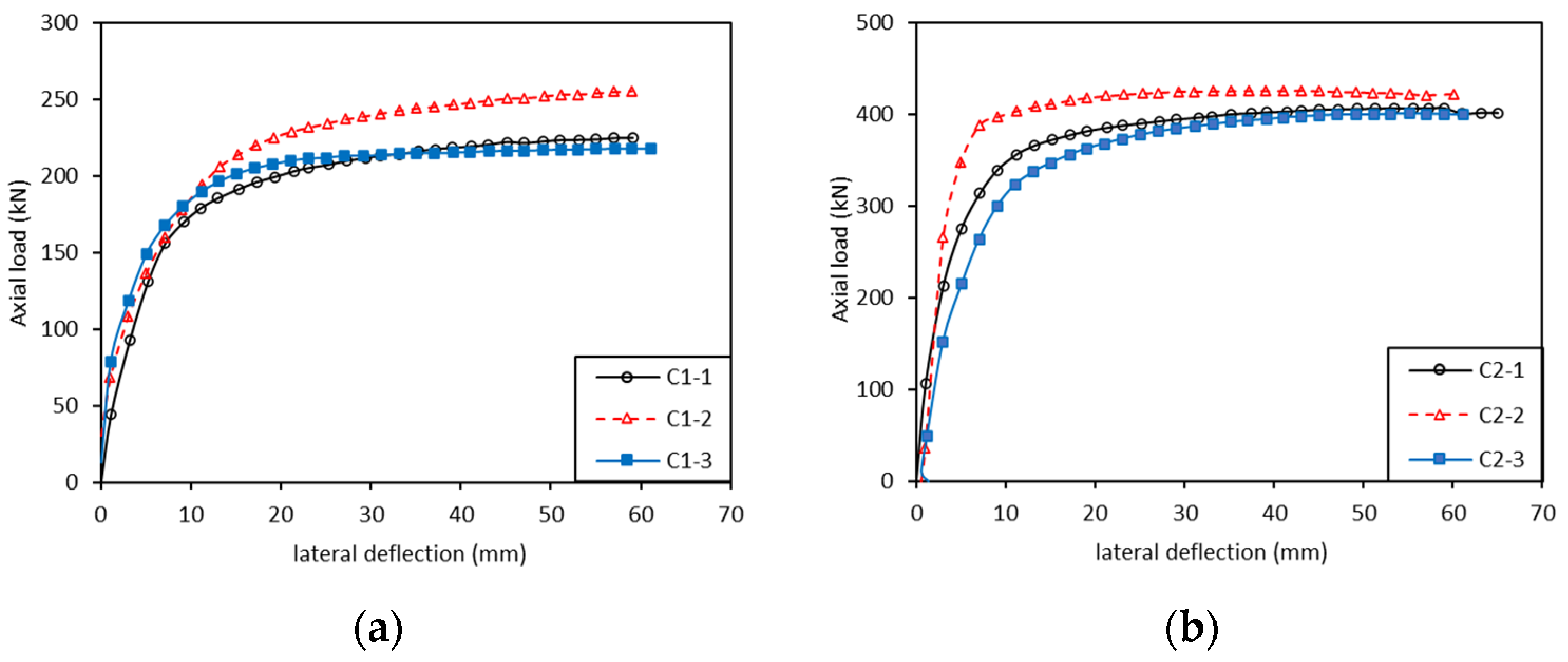
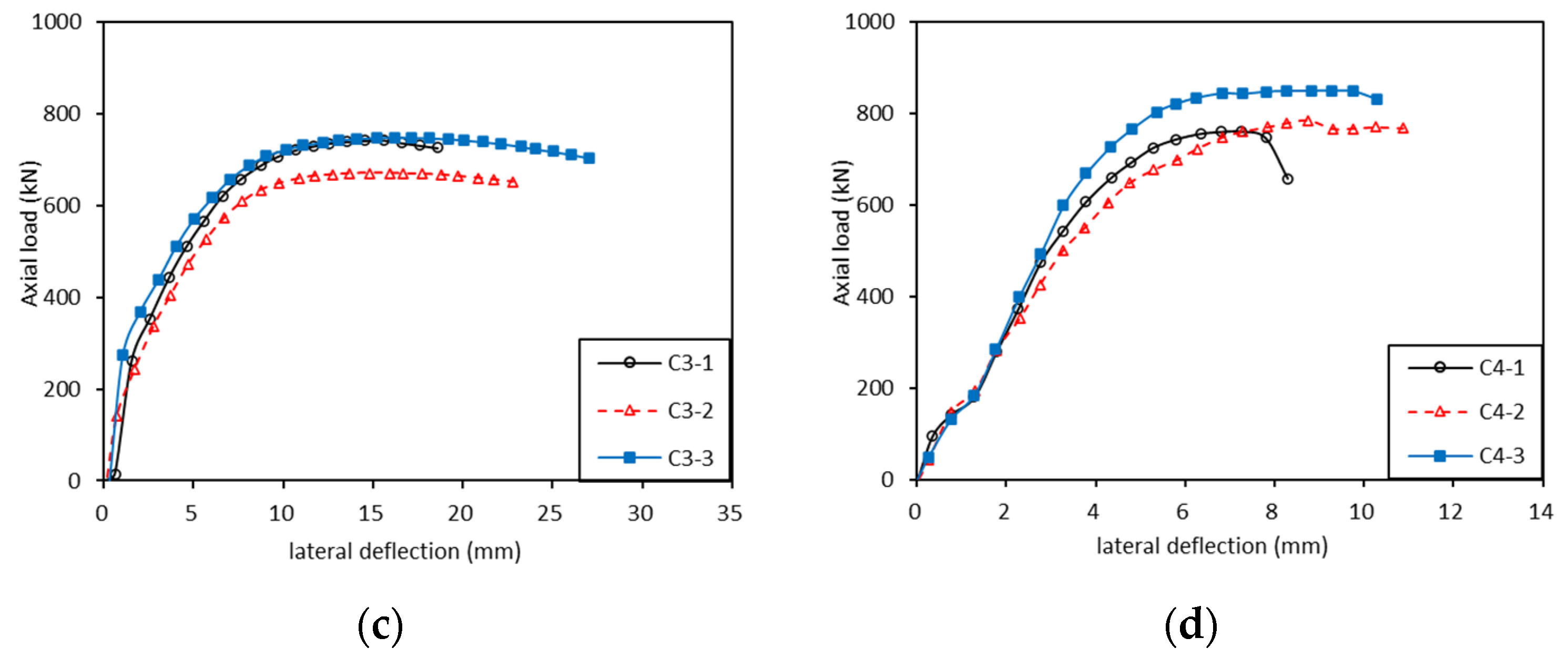
5.1. Results and Analysis of Stability Test
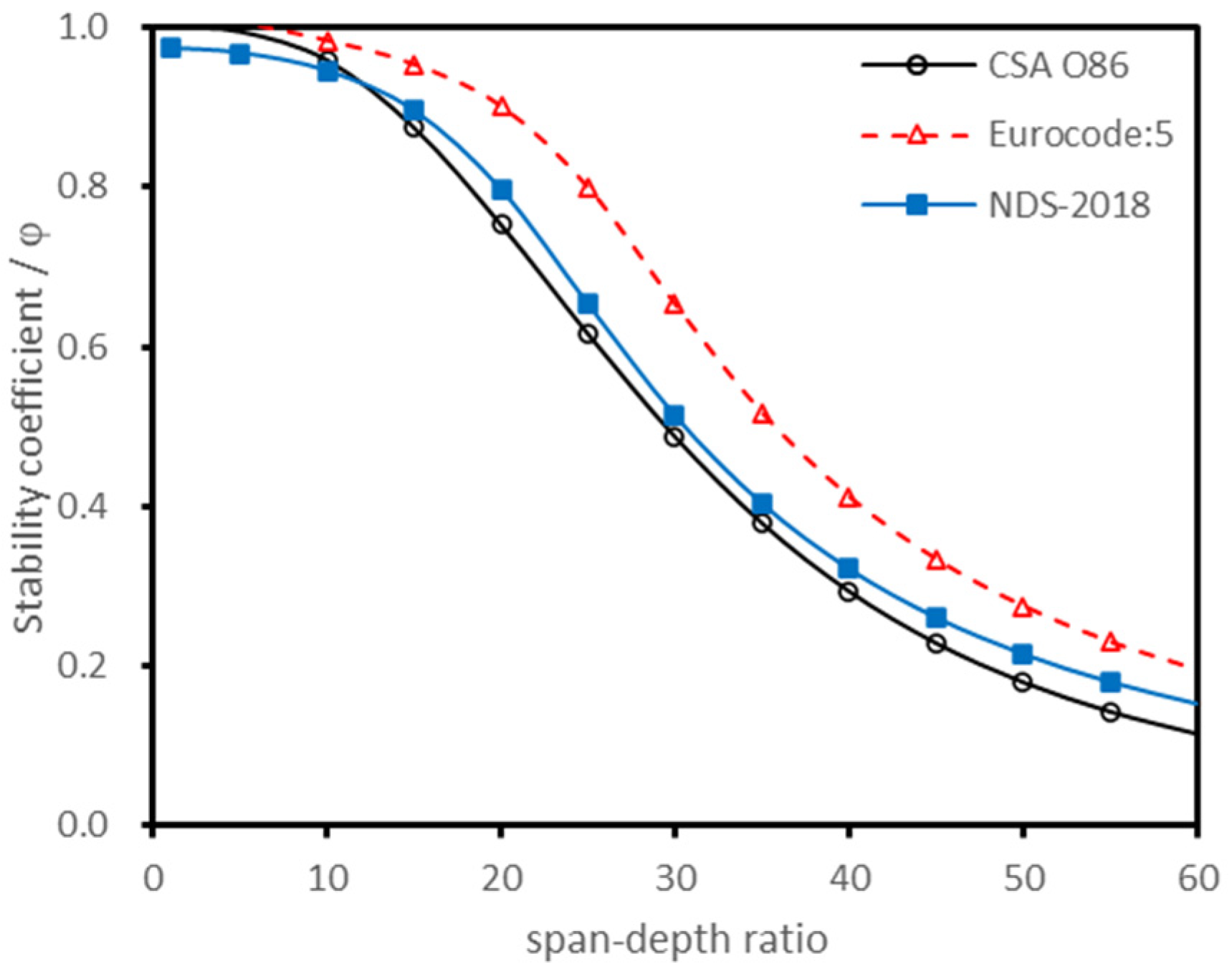
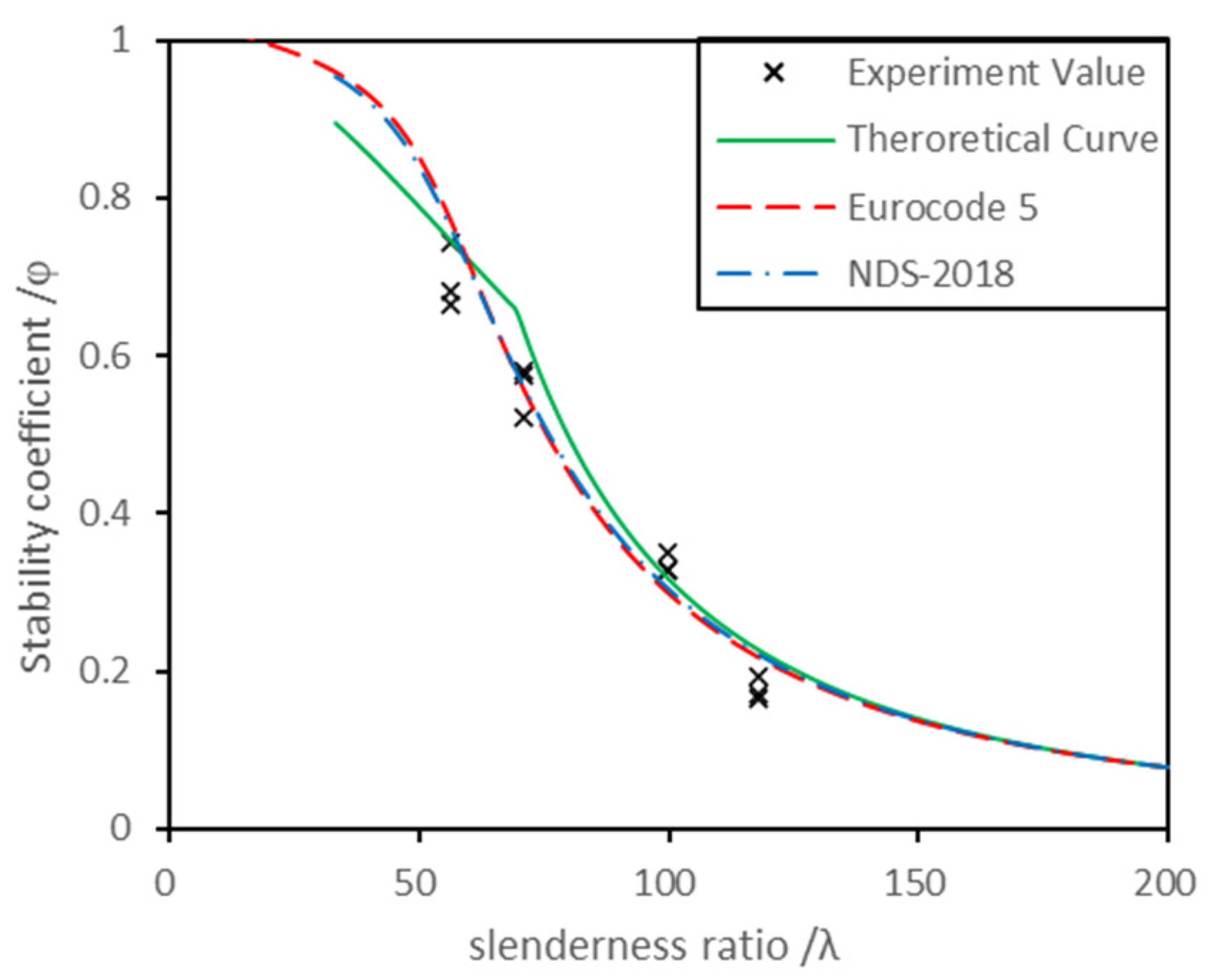
5.2. Stability Coefficient Comparison between Theoretical Curve and Actual Test Results
6. Conclusions
- (1)
- The experiment showed that with the increase in slenderness ratio of the CLT axial compression member, the stability bearing capacity gradually decreased. The C1 (λ = 118.07) and C2 (λ = 99.49) specimens were mainly characterized by elastic instability, and there was almost no damage to the specimens during the test; the C4 (λ = 56.27) specimens mainly showed elastic–plastic instability, and folding and shear failure occurred on the surface of the specimen. Both instability phenomena occurred in group C3 (λ = 70.86).
- (2)
- By considering the CLT as a split limb, the longitudinal lamina as the column limb, and the transverse lamina as the connection between the component limbs, the slenderness ratio conversion theory, was proposed. Combined with the coefficient method, the calculation method of the stability coefficient for CLT elements were proposed.
- (3)
- The material parameters , , of the stability coefficient calculation formulae were 1.00, 2.92, and 3.89, respectively. The curve fit well with the calculated results of the European standard and American standard, and the average deviation was less than 6%. The average deviation between the fitting curve and the actual test results was 8.15%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, M.; Tao, D.; Li, Z. State-of-the-art of research advances on multi-story timber and timber-hybrid structures. J. Build. Struct. 2016, 37, 1–9. [Google Scholar]
- Nehdi, M.L.; Zhang, Y.; Gao, X.; Zhang, L.V.; Suleiman, A.R. Experimental investigation on axial compression of resilient nail-cross-laminated timber panels. Sustainability 2021, 13, 11257. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Mei, F.; Liao, J.; Li, W. Experimental and numerical analysis on fire behaviour of loaded cross-laminated timber panels. Adv. Struct. Eng. 2020, 23, 22–36. [Google Scholar] [CrossRef]
- Xing, Z.; Wang, Y.; Zhang, J.; Ma, H. Comparative study on fire resistance and zero strength layer thickness of CLT floor under natural fire and standard fire. Constr. Build. Mater. 2021, 302, 124368. [Google Scholar] [CrossRef]
- Kosny, J.; Asiz, A.; Smith, I.; Shrestha, S.; Fallahi, A. A review of high R-value wood framed and composite wood wall technologies using advanced insulation techniques. Energy Build. 2014, 72, 441–456. [Google Scholar] [CrossRef]
- Suthon, S.; Zoltán, P.; Hung Anh, L.D.; Hyungsuk, L.; Sataporn, J.; Jaipet, T. Physical, mechanical and thermal properties of cross laminated timber made with coconut wood. Eur. J. Wood Wood Prod. 2021, 79, 1519–1529. [Google Scholar]
- Vanova, R.; Stompf, P.; Stefko, J.; Stefkova, J. Environmental impact of a mass timber building—A case study. Forests 2021, 12, 1571. [Google Scholar] [CrossRef]
- Yao, T.; Zhu, E.; Niu, S. Structure Technique Handbook for Cross-laminated Timber; China Architecture & Building Press: Beijing, China, 2019. [Google Scholar]
- Gagnon, S.; Pirvu, C. CLT Handbook: Cross-Laminated Timber; FPInnovations: Quebec, QC, Canada, 2011. [Google Scholar]
- Sikora, K.S.; McPolin, D.; Harte, A. Effects of the thickness of cross-laminated timber (CLT) panels made from Irish Sitka spruce on mechanical performance in bending and shear. Constr. Build. Mater. 2016, 116, 141–150. [Google Scholar] [CrossRef] [Green Version]
- Pang, S.-J.; Jeong, G.Y. Effects of combinations of lamina grade and thickness, and span-to-depth ratios on bending properties of cross-laminated timber (CLT) floor. Constr. Build. Mater. 2019, 222, 142–151. [Google Scholar] [CrossRef]
- Wang, F.; Wang, X.; Yang, S.; Jiang, G.; Que, Z.; Zhou, H. Effect of different laminate thickness on mechanical properties of cross-laminated timber made from Chinese fir. Sci. Silvae Sin. 2020, 56, 168–175. [Google Scholar]
- Li, Q.; Wang, Z.; Liang, Z.; Li, L.; Gong, M.; Zhou, J. Shear properties of hybrid CLT fabricated with lumber and OSB. Constr. Build. Mater. 2020, 261, 120504. [Google Scholar] [CrossRef]
- Wang, Z.; Fu, H.; Gong, M.; Luo, J.; Dong, W.; Wang, T.; Chui, Y.H. Planar shear and bending properties of hybrid CLT fabricated with lumber and LVL. Constr. Build. Mater. 2017, 151, 172–177. [Google Scholar] [CrossRef]
- Gong, Y.; Ye, Q.; Wu, G.; Ren, H.; Guan, C. Effect of size on compressive strength parallel to the grain of cross-laminated timber made with domestic larch. Chin. J. Wood Sci. Technol. 2020, 35, 42–46. [Google Scholar]
- Gong, Y.; Ye, Q.; Wu, G.; Ren, H.; Guan, C. Prediction of the compressive strength of cross-laminated timber (CLT) made by domestic Larix Kaempferi. J. Northwest For. Univ. 2020, 35, 234–237. [Google Scholar]
- Wei, P.; Wang, B.J.; Li, H.; Wang, L.; Peng, S.; Zhang, L. A comparative study of compression behaviors of cross-laminated timber and glued-laminated timber columns. Constr. Build. Mater. 2019, 222, 86–95. [Google Scholar] [CrossRef]
- Pina, J.C.; Saavedra flores, E.I.; Saavedra, K. Numerical study on the elastic buckling of cross-laminated timber walls subject to compression. Constr. Build. Mater. 2019, 199, 82–91. [Google Scholar] [CrossRef]
- CSA O86-2019. Engineering Design in Wood; Canadian Standards Association: Toronto, ON, Canada, 2019. [Google Scholar]
- NDS-2018. National Design Specification (NDS) for Wood Construction, 2018 ed.; American Forest & Paper Association, American Wood Council: Washington, DC, USA, 2018. [Google Scholar]
- EN 1995-1-1: 2004+A1. Eurocode 5: Design of Timber Structures-Part 1-1: General-Common Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- ANSI/APA PRG 320-2019. Standard for Performance-Rated Cross-Laminated Timber; APA-The Engineered Wood Association: Tacoma, DC, USA, 2019. [Google Scholar]
- GB 50005-2017. Standard for Design of Timber Structure; China Architecture & Building Press: Beijing, China, 2017. [Google Scholar]
- Zhu, E.; Wu, G.; Zhang, D.; Pan, J. Unified method for calculation of stability coefficient of wood members in axial compression. J. Build. Struct. 2016, 37, 10–17. [Google Scholar]
- GB/T 50329-2012. Standard for Test Methods of Timber Structures; China Architecture & Building Press: Beijing, China, 2012. [Google Scholar]
- Fu, Z.-Q.; Ji, B.-H.; Lv, L.; Zhou, W.-J. Behavior of lightweight aggregate concrete filled steel tubular slender columns under axial compression. Adv. Steel Constr. 2011, 7, 144–156. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Wei, Y.; Hu, Y.; Zhai, Z.; Wang, L. Behavior and strength of rectangular bamboo scrimber columns with shape and slenderness effects. Mater. Today Commun. 2020, 25, 101392. [Google Scholar] [CrossRef]
- Wei, P.; Wang, B.J.; Li, H.; Wang, L.; Gong, Y.; Huang, S. Performance evaluation of a novel cross-laminated timber made from flattened bamboo and wood lumber. BioResources 2021, 16, 5187–5202. [Google Scholar] [CrossRef]
- Pan, J.; Xu, T.; Hu, Z. Experimental investigation of load carrying capacity of the slender reinforced concrete columns wrapped with FRP. Constr. Build. Mater. 2007, 21, 1991–1996. [Google Scholar] [CrossRef]


| Countries | Loading Duration | Resistance Partial Coefficient | Form of Formula |
|---|---|---|---|
| China | segmented | ||
| Europe | continuous | ||
| Canada | continuous | ||
| America | continuous |
| Coefficient | PRG 320 | Average | |
|---|---|---|---|
| Eurocode: 5 | NDS-2018 | ||
| 0.99 | 1.02 | 1.00 | |
| 3.06 | 2.77 | 2.92 | |
| 3.81 | 3.98 | 3.89 | |
| Number | Repetition Times | Size/mm | Slenderness Ratio |
|---|---|---|---|
| C1 | 3 | 3950 × 300 × 105 | 118.07 |
| C2 | 3 | 3200 × 300 × 105 | 99.49 |
| C3 | 3 | 1950 × 300 × 105 | 70.86 |
| C4 | 3 | 1200 × 300 × 105 | 56.27 |
| Groups | Slenderness Ratio | ||||||
|---|---|---|---|---|---|---|---|
| C1 | 118.07 | 252.00 | 6.33 | 1311 | 4.42 | 0.192 | 0.227 |
| C2 | 99.49 | 408.67 | 3.00 | 1219 | 7.34 | 0.335 | 0.320 |
| C3 | 70.86 | 719.33 | 4.87 | 1286 | 3.90 | 0.559 | 0.630 |
| C4 | 56.27 | 796.70 | 4.84 | 1143 | 9.00 | 0.697 | 0.745 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Q.; Gong, Y.; Ren, H.; Guan, C.; Wu, G.; Chen, X. Analysis and Calculation of Stability Coefficients of Cross-Laminated Timber Axial Compression Member. Polymers 2021, 13, 4267. https://doi.org/10.3390/polym13234267
Ye Q, Gong Y, Ren H, Guan C, Wu G, Chen X. Analysis and Calculation of Stability Coefficients of Cross-Laminated Timber Axial Compression Member. Polymers. 2021; 13(23):4267. https://doi.org/10.3390/polym13234267
Chicago/Turabian StyleYe, Qi, Yingchun Gong, Haiqing Ren, Cheng Guan, Guofang Wu, and Xu Chen. 2021. "Analysis and Calculation of Stability Coefficients of Cross-Laminated Timber Axial Compression Member" Polymers 13, no. 23: 4267. https://doi.org/10.3390/polym13234267
APA StyleYe, Q., Gong, Y., Ren, H., Guan, C., Wu, G., & Chen, X. (2021). Analysis and Calculation of Stability Coefficients of Cross-Laminated Timber Axial Compression Member. Polymers, 13(23), 4267. https://doi.org/10.3390/polym13234267







