Facile Molecular Weight Determination of Polymer Brushes Grafted from One-Dimensional Diffraction Grating by SI-ATRP Using Reflective Laser System
Abstract
:1. Introduction
2. Experimental Section
2.1. Materials
2.2. Strategy of Molecular Weight Determination with PMAA DGs by Laser Beam System
2.3. Optical Analysis of Reflective STP Grating by a Laser Beam System
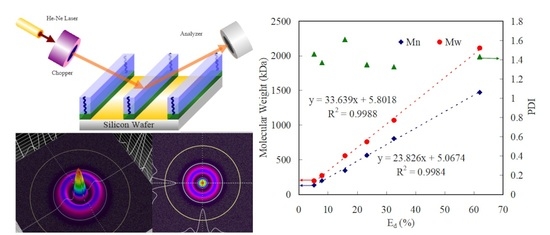
3. Results and Discussion
3.1. Surface Characterization of DGs
3.2. Measurement of Diffraction Efficiency of PMAA DGs
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Milner, S.T. Polymer brushes. Science 1991, 251, 905–914. [Google Scholar] [CrossRef]
- Jiang, H.; Xu, F.-J. Biomolecule-functionalized polymer brushes. Chem. Soc. Rev. 2013, 42, 3394–3426. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.-K.; Zhou, G.-Y.; Huang, C.-F.; Chang, J.-Y. Two-dimensional periodic relief grating as a versatile platform for selective immunosorbent assay and visualizing of antigens. ACS Appl. Mater. Interfaces 2013, 5, 3348–3355. [Google Scholar] [CrossRef]
- Ishihara, K.; Mitera, K.; Inoue, Y.; Fukazawa, K. Effects of molecular interactions at various polymer brush surfaces on fibronectin adsorption induced cell adhesion. Colloids Surf. B Biointerfaces 2020, 194, 111205. [Google Scholar] [CrossRef] [PubMed]
- Krishnamoorthy, M.; Hakobyan, S.; Ramstedt, M.; Gautrot, J.E. Surface-initiated polymer brushes in the biomedical field: Applications in membrane science, biosensing, cell culture, regenerative medicine and antibacterial coatings. Chem. Rev. 2014, 114, 10976–11026. [Google Scholar] [CrossRef] [PubMed]
- Zoppe, J.O.; Ataman, N.C.; Mocny, P.; Wang, J.; Moraes, J.; Klok, H.-A. Surface-initiated controlled radical polymerization: State-of-the-art, opportunities, and challenges in surface and interface engineering with polymer brushes. Chem. Rev. 2017, 117, 1105–1318. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, M.; Fromel, M.; Ranaweera, D.; Rocha, S.; Boyer, C.; Pester, C.W. SI-PET-RAFT: Surface-Initiated Photoinduced Electron Transfer-Reversible Addition–Fragmentation Chain Transfer Polymerization. ACS Macro Lett. 2019, 8, 374–380. [Google Scholar] [CrossRef]
- Chen, J.-K.; Chen, T.-Y. Fabrication of high-aspect-ratio poly (2-hydroxyethyl methacrylate) brushes patterned on silica surfaces by very-large-scale integration process. J. Colloid Interface Sci. 2011, 355, 359–367. [Google Scholar] [CrossRef]
- Leone, G.; Giovanella, U.; Bertini, F.; Hoseinkhani, S.; Porzio, W.; Ricci, G.; Botta, C.; Galeotti, F. Hierarchically structured, blue-emitting polymer hybrids through surface-initiated nitroxide-mediated polymerization and water templated assembly. J. Mater. Chem. C 2013, 1, 6585–6593. [Google Scholar] [CrossRef]
- Lubomirsky, E.; Khodabandeh, A.; Preis, J.; Susewind, M.; Hofe, T.; Hilder, E.F.; Arrua, R.D. Polymeric stationary phases for size exclusion chromatography: A review. Anal. Chim. Acta 2021, 338244. [Google Scholar] [CrossRef] [PubMed]
- Xiang, P.; Petrie, K.; Kontopoulou, M.; Ye, Z.; Subramanian, R. Tuning structural parameters of polyethylene brushes on silica nanoparticles in surface-initiated ethylene “living” polymerization and effects on silica dispersion in a polyolefin matrix. Polym. Chem. 2013, 4, 1381–1395. [Google Scholar] [CrossRef]
- Feng, W.; Brash, J.L.; Zhu, S. Non-biofouling materials prepared by atom transfer radical polymerization grafting of 2-methacryloloxyethyl phosphorylcholine: Separate effects of graft density and chain length on protein repulsion. Biomaterials 2006, 27, 847–855. [Google Scholar] [CrossRef]
- Chen, J.-K.; Hsieh, C.-Y.; Huang, C.-F.; Li, P.-M. Characterization of patterned poly (methyl methacrylate) brushes under various structures upon solvent immersion. J. Colloid Interface Sci. 2009, 338, 428–434. [Google Scholar] [CrossRef]
- Kang, C.; Crockett, R.M.; Spencer, N.D. Molecular-weight determination of polymer brushes generated by SI-ATRP on flat surfaces. Macromolecules 2014, 47, 269–275. [Google Scholar] [CrossRef]
- Chen, J.-K.; Zhou, G.-Y.; Chang, C.-J.; Lee, A.-W.; Chang, F.-C. Label-free DNA detection using two-dimensional periodic relief grating as a visualized platform for diagnosis of breast cancer recurrence after surgery. Biosens. Bioelectron. 2014, 54, 35–41. [Google Scholar] [PubMed]
- Bai, W.; Spivak, D.A. A double-imprinted diffraction-grating sensor based on a virus-responsive super-aptamer hydrogel derived from an impure extract. Angew. Chem. Int. Ed. 2014, 53, 2095–2098. [Google Scholar] [CrossRef]
- Zeng, J.-R.; Cheng, C.-C.; Lee, A.-W.; Wei, P.-L.; Chen, J.-K. Visualization platform of one-dimensional gratings of tethered polyvinyltetrazole brushes on silicon surfaces for sensing of Cr (III). Microchim. Acta 2017, 184, 2723–2730. [Google Scholar] [CrossRef]
- Tian, M.; Huang, Y.; Li, C.; Lv, M. High-performance humidity sensor based on a micro-nano fiber Bragg grating coated with graphene oxide. Opt. Express 2020, 28, 26395–26406. [Google Scholar] [CrossRef]
- Zeng, J.-R.; Cheng, C.-C.; Chang, C.-J.; Huang, C.-H.; Chen, J.-K. Fabrication of two-dimensional photonic crystals of tethered polyvinyltetrazole on silicon surfaces for visualization in Cu2+ ion sensing. Dye. Pigment. 2017, 139, 300–309. [Google Scholar]
- Huang, J.; Jiang, L.; Li, X.; Wei, Q.; Wang, Z.; Li, B.; Huang, L.; Wang, A.; Wang, Z.; Li, M. Cylindrically Focused Nonablative Femtosecond Laser Processing of Long-Range Uniform Periodic Surface Structures with Tunable Diffraction Efficiency. Adv. Opt. Mater. 2019, 7, 1900706. [Google Scholar] [CrossRef]
- Inampudi, S.; Salary, M.M.; Jafar-Zanjani, S.; Mosallaei, H. Rigorous space-time coupled-wave analysis for patterned surfaces with temporal permittivity modulation. Opt. Mater. Express 2019, 9, 162–182. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, Z.-Q.; Chan, C.T. Photonic Floquet media with a complex time-periodic permittivity. Phys. Rev. B 2018, 98, 085142. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.-W.; Huang, B.-R.; Lai, J.-Y.; Lu, C.-H.; Chen, J.-K. Reversibly photoswitchable gratings prepared from azobenzene-modified tethered poly (methacrylic acid) brush as colored actuator. Sens. Actuators B Chem. 2020, 304, 127275. [Google Scholar] [CrossRef]
- Ren, Z.; Wang, Y.; Ma, S.; Duan, S.; Yang, X.; Gao, P.; Zhang, X.; Cai, Q. Effective bone regeneration using thermosensitive poly (N-isopropylacrylamide) grafted gelatin as injectable carrier for bone mesenchymal stem cells. ACS Appl. Mater. Interfaces 2015, 7, 19006–19015. [Google Scholar] [CrossRef]
- Lee, A.-W.; Cheng, C.-C.; Chang, C.-J.; Lu, C.-H.; Chen, J.-K. Optical assay of trypsin using a one-dimensional plasmonic grating of gelatin-modified poly (methacrylic acid). Microchim. Acta 2020, 187, 1–8. [Google Scholar] [CrossRef]
- Chen, W.-T.; Li, S.-S.; Chu, J.P.; Feng, K.C.; Chen, J.-K. Fabrication of ordered metallic glass nanotube arrays for label-free biosensing with diffractive reflectance. Biosens. Bioelectron. 2018, 102, 129–135. [Google Scholar] [CrossRef]
- Taravati, S.; Eleftheriades, G.V. Generalized space-time-periodic diffraction gratings: Theory and applications. Phys. Rev. Appl. 2019, 12, 024026. [Google Scholar] [CrossRef] [Green Version]
- Lin, F.-P.; Hsu, H.-L.; Chang, C.-J.; Lee, S.-C.; Chen, J.-K. Surface lattice resonance of line array of poly (glycidyl methacrylate) with CdS quantum dots for label-free biosensing. Colloids Surf. B Biointerfaces 2019, 179, 199–207. [Google Scholar] [CrossRef]
- Lacik, I.; Stach, M.; Kasak, P.; Semak, V.; Uhelská, L.; Chovancová, A.; Reinhold, G.; Kilz, P.; Delaittre, G.; Charleux, B. SEC analysis of poly (acrylic acid) and poly (methacrylic acid). Macromol. Chem. Phys. 2015, 216, 23–37. [Google Scholar] [CrossRef]
- Weise, W. Image formation of confocal microscopes using Lorentz’s reciprocity theorem. Opt. Commun. 2002, 202, 21–28. [Google Scholar] [CrossRef]
- Mansuripur, M. Trouble with the Lorentz law of force: Incompatibility with special relativity and momentum conservation. Phys. Rev. Lett. 2012, 108, 193901. [Google Scholar] [CrossRef] [Green Version]
- Chaudhary, J.; Thakur, S.; Mamba, G.; Gupta, R.K.; Thakur, V.K. Hydrogel of gelatin in the presence of graphite for the adsorption of dye: Towards the concept for water purification. J. Environ. Chem. Eng. 2021, 9, 104762. [Google Scholar] [CrossRef]
- Shandilya, P.; Mittal, D.; Soni, M.; Raizada, P.; Hosseini-Bandegharaei, A.; Saini, A.K.; Singh, P. Fabrication of fluorine doped graphene and SmVO4 based dispersed and adsorptive photocatalyst for abatement of phenolic compounds from water and bacterial disinfection. J. Clean. Prod. 2018, 203, 386–399. [Google Scholar] [CrossRef]
- Arabi, N.; Zamanian, A.; Rashvand, S.N.; Ghorbani, F. The tunable porous structure of gelatin–bioglass nanocomposite scaffolds for bone tissue engineering applications: Physicochemical, mechanical, and in vitro properties. Macromol. Mater. Eng. 2018, 303, 1700539. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, G.; Chang, C.; Cheng, C. Label-free detection of DNA hybridization using nanopillar arraysbased optical biosensor. Sens. Actuators B 2014, 194, 10–18. [Google Scholar] [CrossRef]












| Sample Type | Diffraction Orders | |||||||
|---|---|---|---|---|---|---|---|---|
| m = +3 | m = +2 | m = +1 | m = +0 | m = −1 | m = −2 | m = −3 | ||
| TE | DG-g-PMAA2 | 28 ± 1 | 18 ± 2 | 11 ± 0 | 0 ± 1 | 11 ± 1 | 18 ± 2 | 28 ± 2 |
| DG-g-PMAA4 | 30 ± 2 | 19 ± 1 | 13 ± 0 | 0 ± 0 | 13 ± 0 | 19 ± 1 | 30 ± 1 | |
| DG-g-PMAA8 | 32 ± 2 | 21 ± 1 | 14 ± 1 | 0 ± 1 | 15 ± 1 | 21 ± 1 | 32 ± 2 | |
| DG-g-PMAA16 | 34 ± 2 | 24 ± 1 | 19 ± 1 | 0 ± 0 | 20± 0 | 24 ± 0 | 30 ± 2 | |
| TM | DG-g-PMAA2 | Ev | Ev | 53 ± 1 | 45 ± 0 | 39 ± 1 | 33 ± 2 | 25 ± 1 |
| DG-g-PMAA4 | Ev | Ev | 54 ± 0 | 45 ± 1 | 37 ± 0 | 30 ± 1 | 24 ± 1 | |
| DG-g-PMAA8 | Ev | Ev | 56 ± 1 | 45 ± 0 | 35 ± 1 | 28 ± 2 | 21 ± 2 | |
| DG-g-PMAA16 | Ev | Ev | 59 ± 1 | 45± 0 | 33 ± 1 | 27 ± 1 | 19 ± 2 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.-K.; Lin, F.-P.; Chang, C.-J.; Lu, C.-H.; Huang, C.-F. Facile Molecular Weight Determination of Polymer Brushes Grafted from One-Dimensional Diffraction Grating by SI-ATRP Using Reflective Laser System. Polymers 2021, 13, 4270. https://doi.org/10.3390/polym13234270
Chen J-K, Lin F-P, Chang C-J, Lu C-H, Huang C-F. Facile Molecular Weight Determination of Polymer Brushes Grafted from One-Dimensional Diffraction Grating by SI-ATRP Using Reflective Laser System. Polymers. 2021; 13(23):4270. https://doi.org/10.3390/polym13234270
Chicago/Turabian StyleChen, Jem-Kun, Feng-Ping Lin, Chi-Jung Chang, Chien-Hsing Lu, and Chih-Feng Huang. 2021. "Facile Molecular Weight Determination of Polymer Brushes Grafted from One-Dimensional Diffraction Grating by SI-ATRP Using Reflective Laser System" Polymers 13, no. 23: 4270. https://doi.org/10.3390/polym13234270
APA StyleChen, J.-K., Lin, F.-P., Chang, C.-J., Lu, C.-H., & Huang, C.-F. (2021). Facile Molecular Weight Determination of Polymer Brushes Grafted from One-Dimensional Diffraction Grating by SI-ATRP Using Reflective Laser System. Polymers, 13(23), 4270. https://doi.org/10.3390/polym13234270