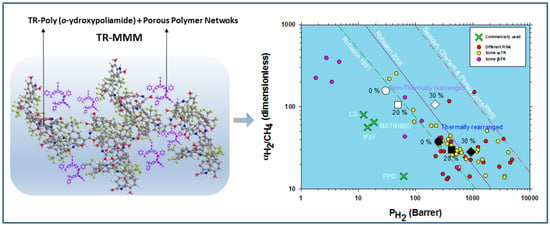
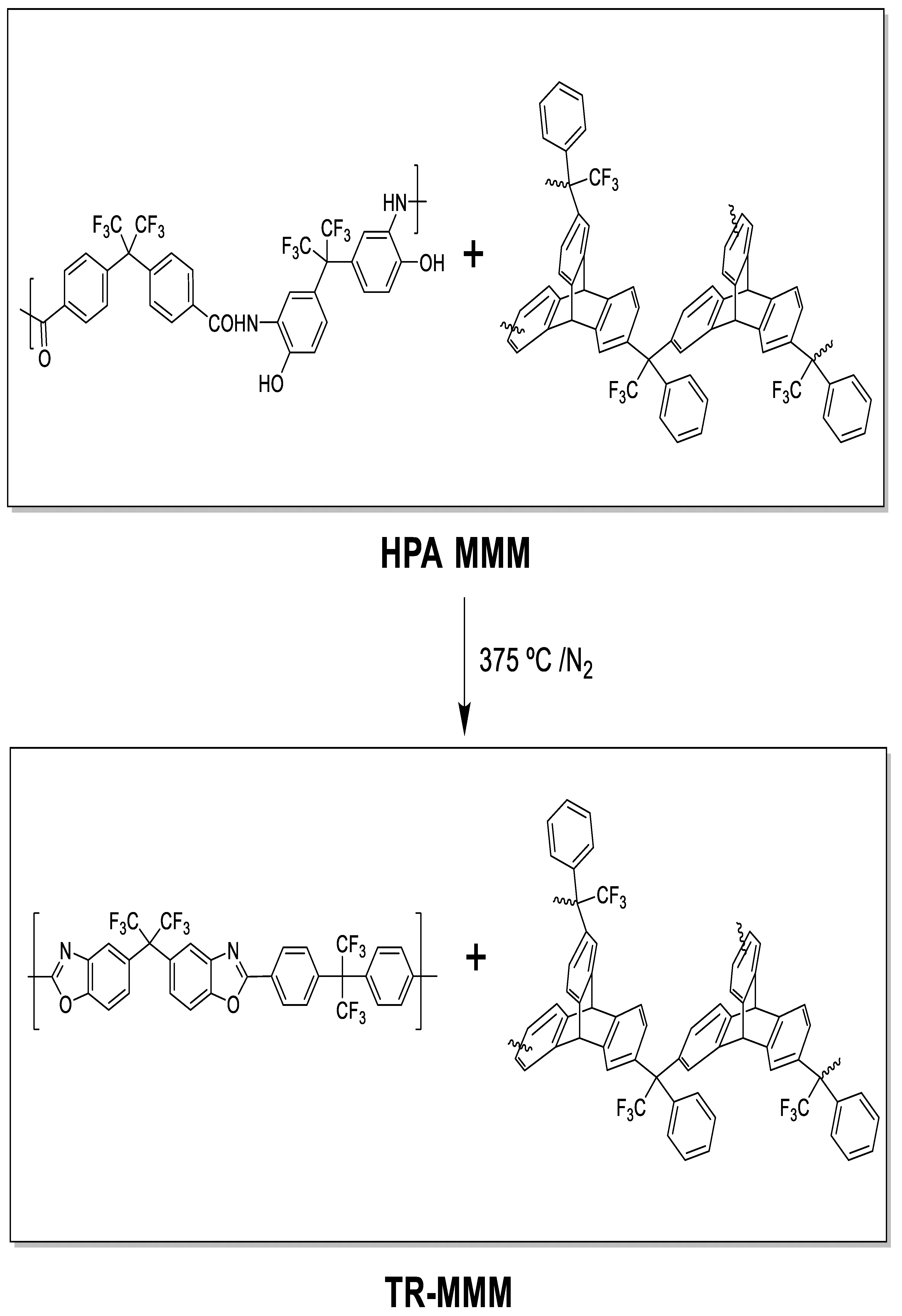
Hydrogen Recovery by Mixed Matrix Membranes Made from 6FCl-APAF HPA with Different Contents of a Porous Polymer Network and Their Thermal Rearrangement
Abstract
:1. Introduction
- Steam–methane reforming (SMR) [9]. This starts by reacting methane with water steam at 750–800 °C to produce syngas, which is a mixture of hydrogen (H2) and carbon monoxide (CO). In the second step, known as a water–gas shift (WGS), CO reacts with water over a catalyst to form H2 and carbon dioxide (CO2). Subsequently, carbon capture and storage or usage (CCS/CCU) can be used to prevent CO2 emissions to the atmosphere.
- Methane cracking separates CH4 at high temperatures under an inert atmosphere to produce elemental carbon (which precipitates) and H2 with no CO2 emissions [10]. This procedure requires unreacted CH4 to be separated from H2 and recirculated into the reactor.
2. Materials and Methods
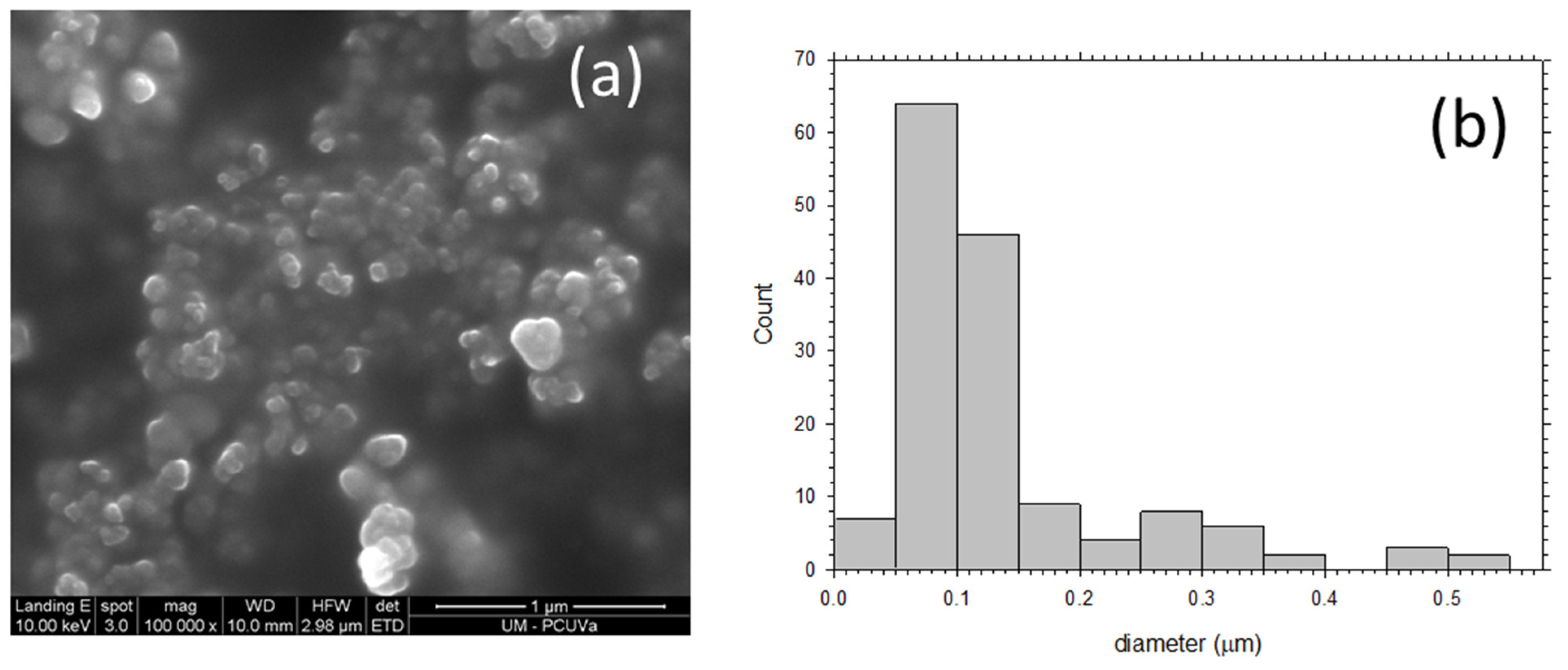
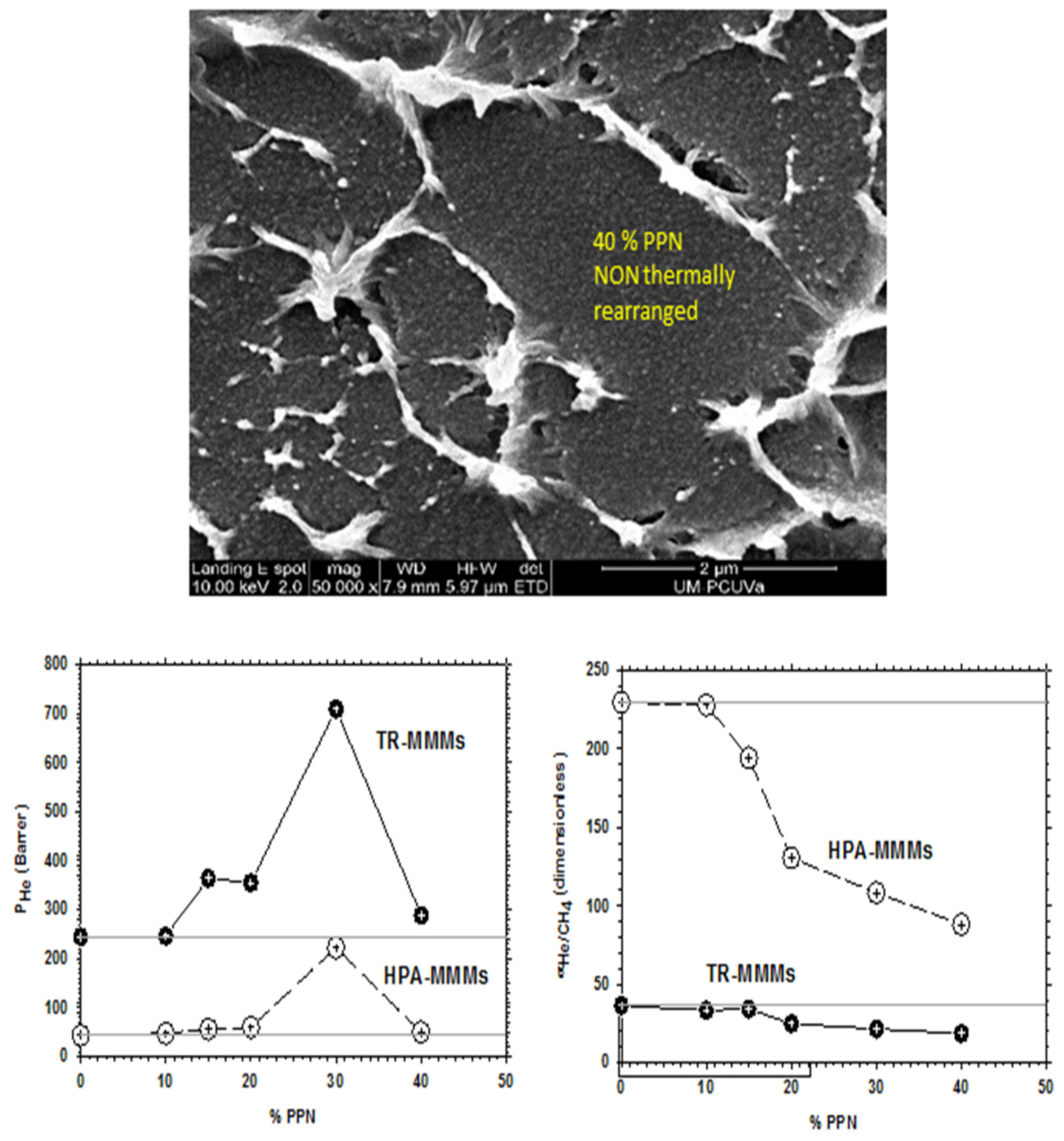
3. Membrane Morphology
3.1. Methodology
3.2. Results
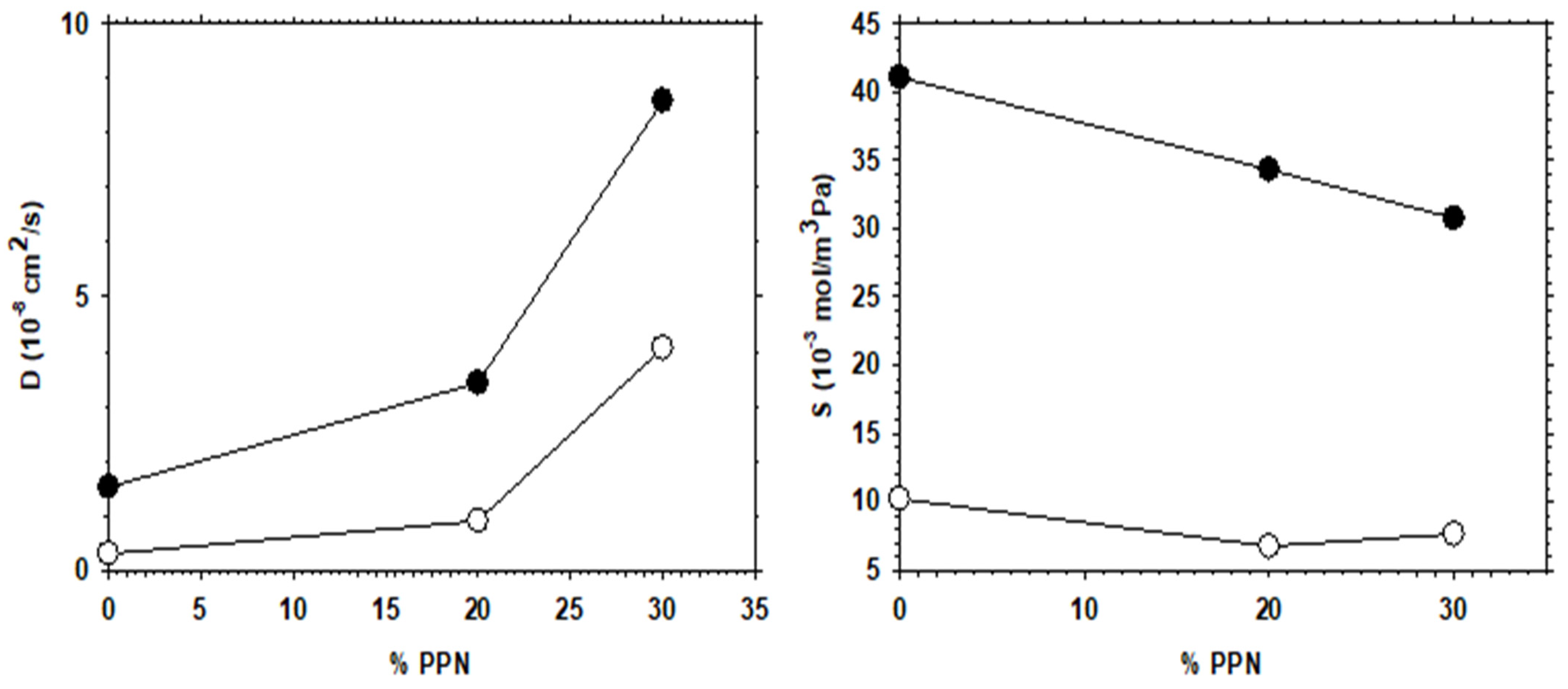
4. Gas Transport Properties
4.1. Methodology
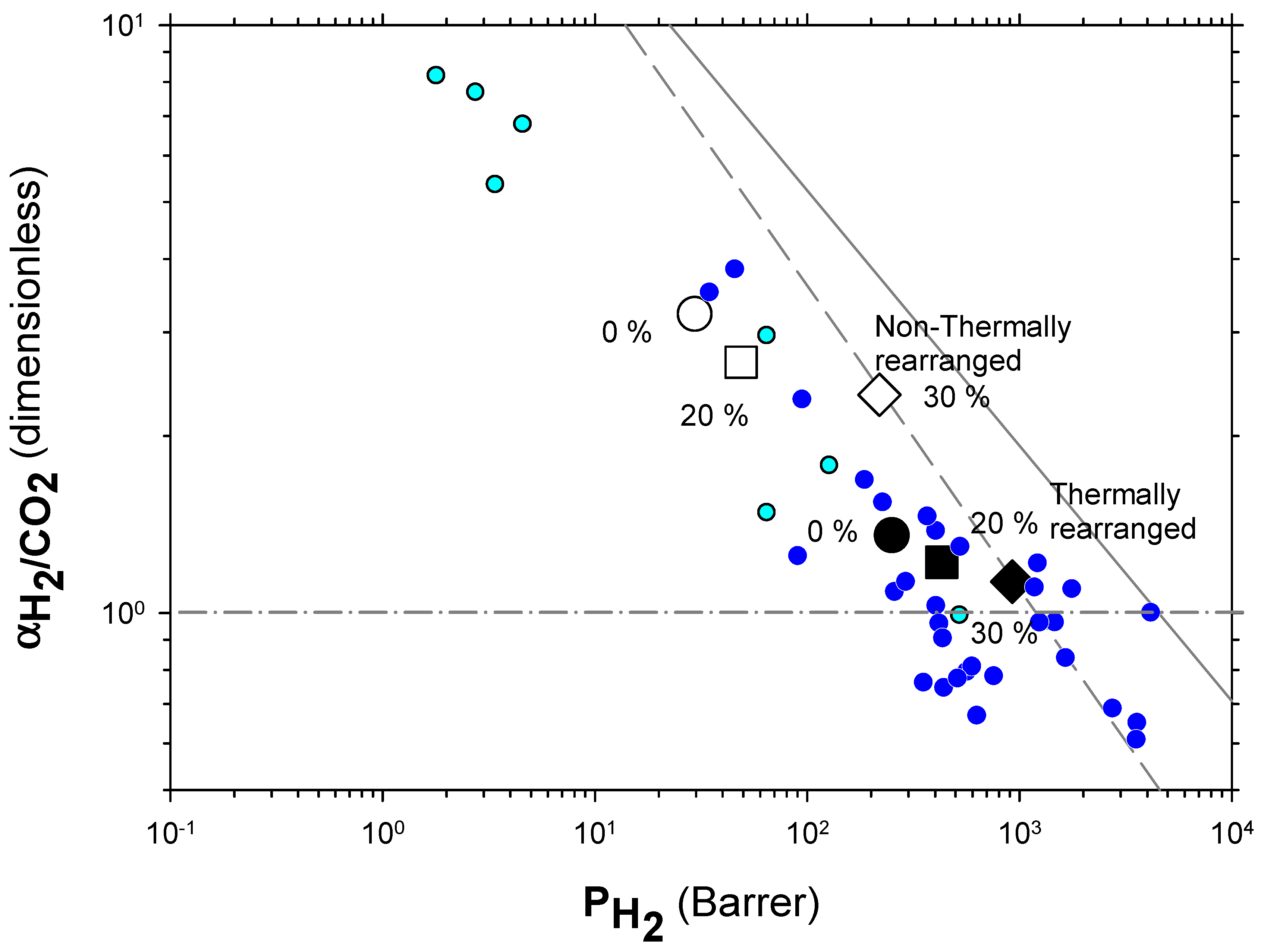
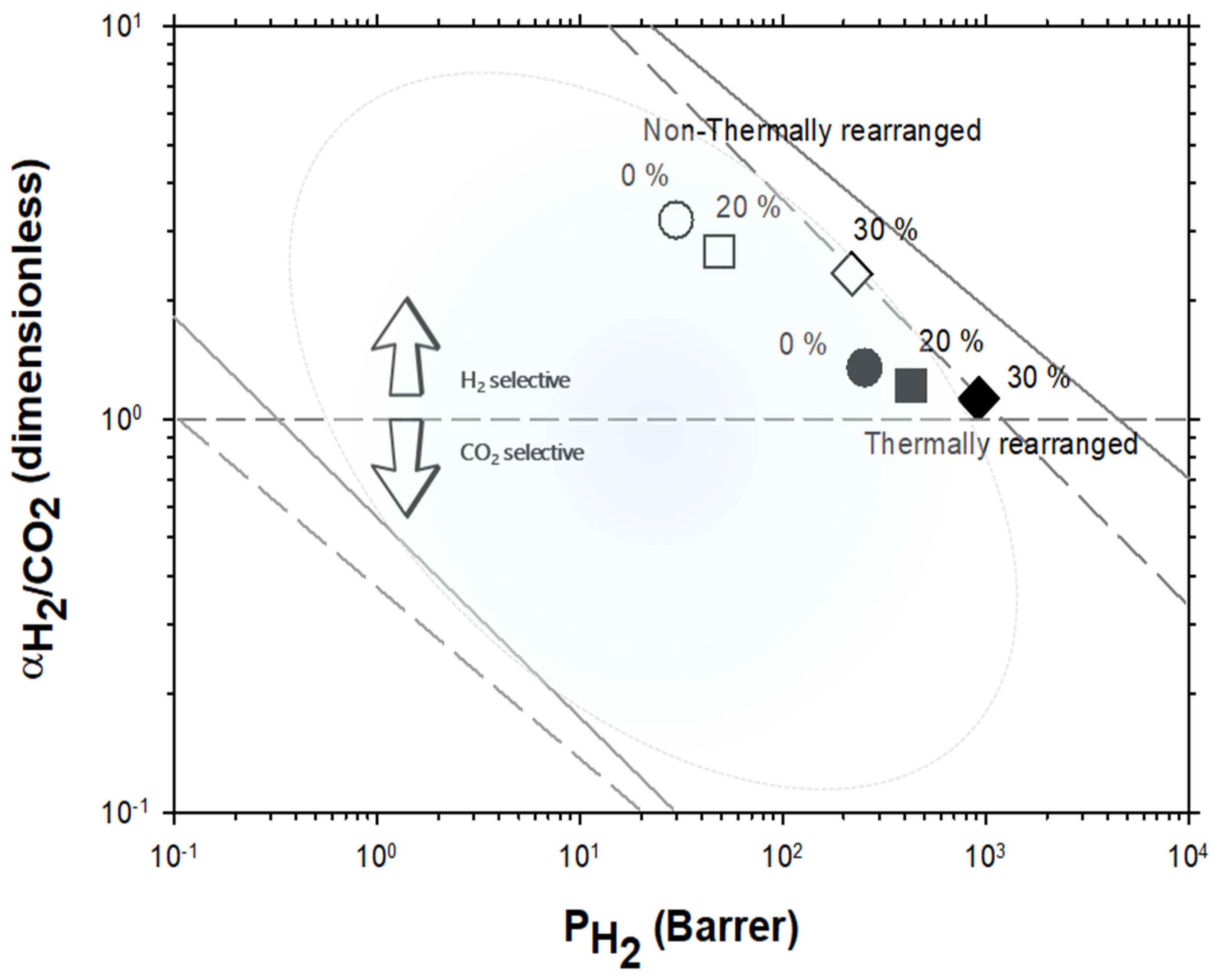
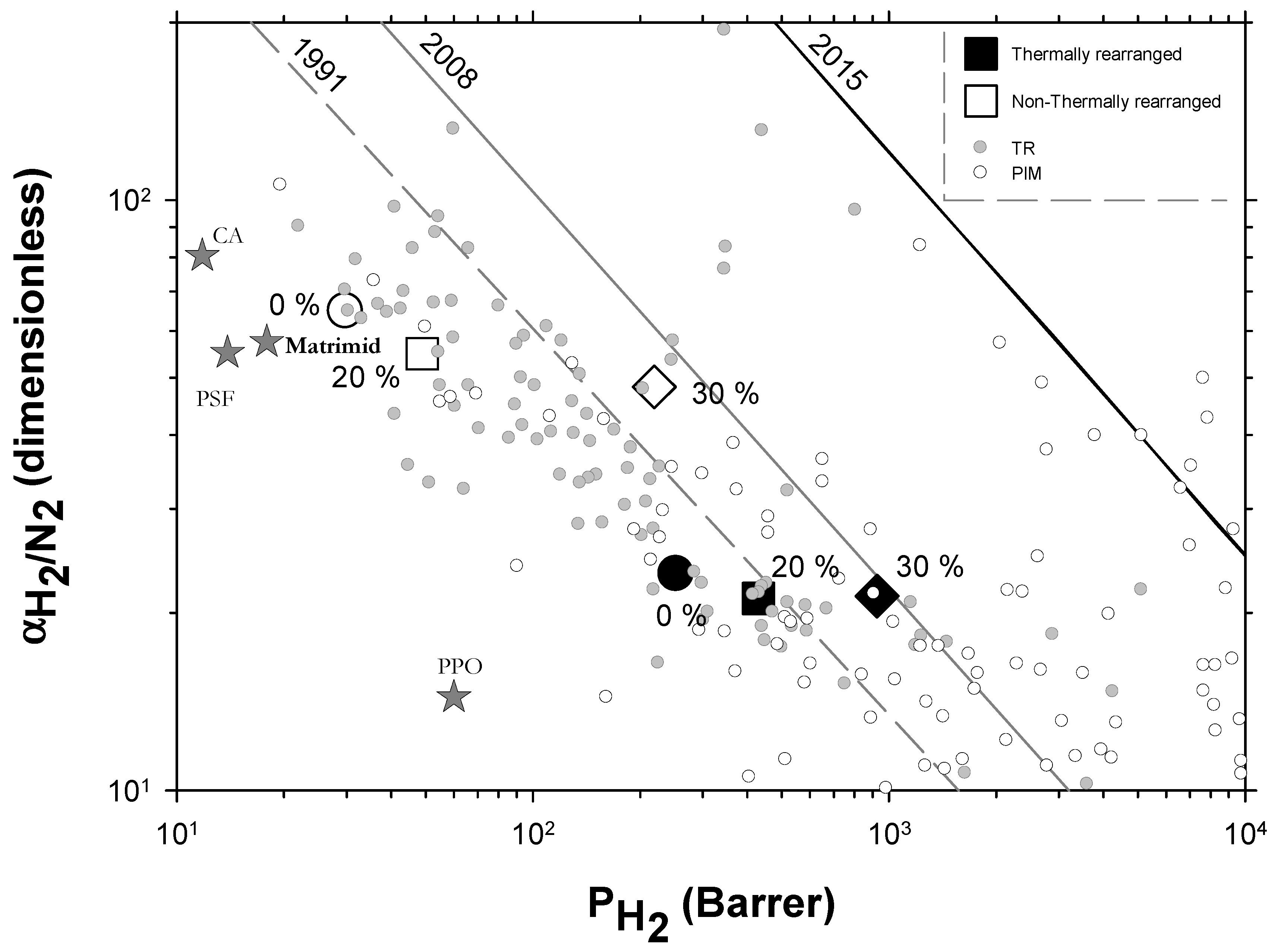
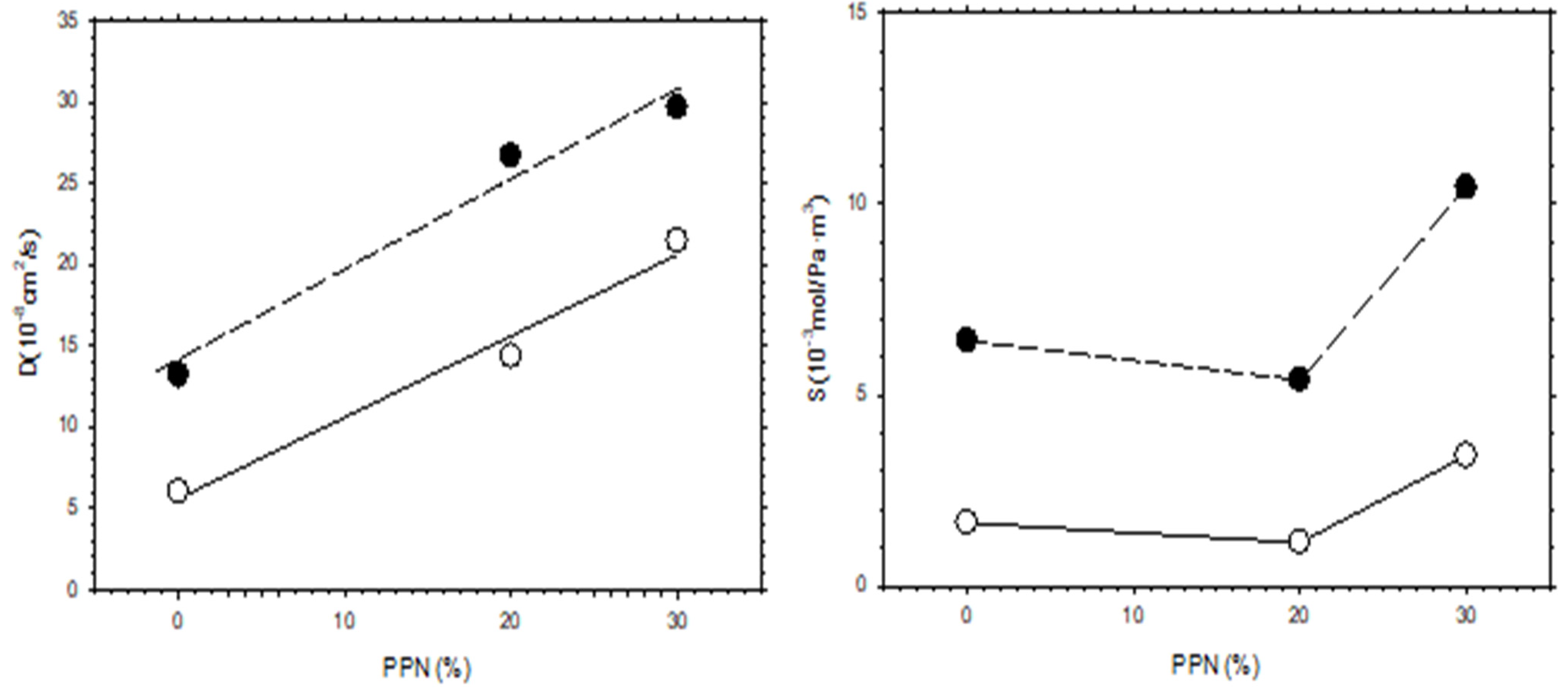
4.2. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boudella, M. Power-to-Gas; De Gruyter: Berlin, Germany, 2018. [Google Scholar] [CrossRef]
- Scipioni, A.; Manzardo, A.; Ren, J. Hydrogen Economy: Supply Chain, Life Cycle Analysis and Energy Transition for Sustainability; Academic Press: London, UK, 2017. [Google Scholar]
- Abdin, Z.; Zafaranloo, A.; Rafiee, A.; Mérida, W.; Lipiński, W.; Khalilpour, K.R. Hydrogen as an energy vector. Renew. Sustain. Energy Rev. 2020, 120, 109620. [Google Scholar] [CrossRef]
- Toro, F.A.; Resch, G.; Held, A.; Ragwitz, M.; Cremer, C.; Weindorf, W.; Bünger, U.; Seydel, P.; Fichtner, M.; Idrissova, F.; et al. The Hydrogen Economy: Opportunities and Challenges; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Hydrogen-Europe, Vision on the Role of Hydrogen and Gas Infrastructure on the Road Toward a Climate Neutral Economy-A Contribution to the Transition of the Gas Market. 2019. Available online: https://ec.europa.eu/info/sites/default/files/hydrogen_europe_-_vision_on_the_role_of_hydrogen_and_gas_infrastructure.pdf (accessed on 19 November 2021).
- Pearson, G.; Leary, M.; Subic, A.; Wellnitz, J. Performance Comparison of Hydrogen Fuel Cell and Hydrogen Internal Combustion Engine Racing Cars. In Sustainable Automotive Technologies; Hung, S., Subic, A., Wellnitz, J., Eds.; Springer: Berlin, Germany, 2011; pp. 85–91. [Google Scholar] [CrossRef]
- Weber, A.Z.; Lipman, T.E. Fuel Cells and Hydrogen Production: Introduction. In Cells and Hydrogen Production: A Volume in the Encyclopedia of Sustainability Science and Technology, 2nd ed.; Lipman, T.E., Weber, A.Z., Eds.; Springer: New York, NY, USA, 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Godula-Jopek, A. Hydrogen Production: By Electrolysis; Wiely VCH: Weinheim, Germany, 2015. [Google Scholar] [CrossRef]
- Kumar, S. Clean Hydrogen Production Methods; Springer: Berling, Germany, 2015. [Google Scholar] [CrossRef]
- Weger, L.; Abánades, A.; Butler, T. Methane cracking as a bridge technology to the hydrogen economy. Int. J. Hydrogen Energy 2017, 42, 720–731. [Google Scholar] [CrossRef] [Green Version]
- Stanislowski, J.; Holmes, M.; Snyder, A.; Tolbert, S.; Curran, T. Advanced CO2 Separation Technologies: Coal Gasification, Warm-gas Cleanup, and Hydrogen Separation Membranes. Energy Procedia 2013, 37, 2316–2326. [Google Scholar] [CrossRef] [Green Version]
- Bharathiraja, B.; Sudharsanaa, T.; Bharghavi, A.; Jayamuthunagai, J.; Praveenkumar, R. Biohydrogen and Biogas–An overview on feedstocks and enhancement process. Fuel 2016, 185, 810–828. [Google Scholar] [CrossRef]
- Rittmann, S.; Herwig, C. A comprehensive and quantitative review of dark fermentative biohydrogen production. Microb. Cell Factories 2012, 11, 115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Yin, Y. Pretreatment of Organic Wastes for Hydrogen Production. In Biohydrogen Production from Organic Wastes; Wang, J., Yin, Y., Eds.; Springer: Singapore, 2017; pp. 123–195. [Google Scholar] [CrossRef]
- Maxwell, G.R. Synthetic Nitrogen Production: A Practical Guide to the Products and Processes; Kluwer Academic/Plenum Press: New York, NY, USA, 2004. [Google Scholar]
- Yang, G.; Guo, H.; Kang, Z.; Zhao, L.; Feng, S.; Jiao, F.; Mintova, S. Green Hydrogen Separation from Nitrogen by Mixed-Matrix Membranes Consisting of Nanosized Sodalite Crystals. ChemSusChem 2018, 12, 4529–4537. [Google Scholar] [CrossRef] [Green Version]
- Miller, G.Q.; Stoecker, J. Selection of a hydrogen separation process. In Proceedings of the National Petroleum Refiners Association Annual Meeting, San Francisco, CA, USA, 19–21 March 1989. Technical Paper AM-89-55. [Google Scholar]
- Al-Mufachi, N.; Rees, N.; Steinberger-Wilkens, R. Hydrogen selective membranes: A review of palladium-based dense metal membranes. Renew. Sustain. Energy Rev. 2015, 47, 540–551. [Google Scholar] [CrossRef]
- Sircar, S.; Golden, T.C. Pressure Swing Adsorption Technology for Hydrogen Production. In Hydrogen and Syngas Production and Purification Technologies; Liu, K., Song, C., Subramani, V., Eds.; John Wiley & Sons: New York, NY, USA, 2009; pp. 414–450. [Google Scholar] [CrossRef]
- Schorer, L.; Schmitz, S.; Weber, A. Membrane based purification of hydrogen system (MEMPHYS). Int. J. Hydrogen Energy 2019, 44, 12708–12714. [Google Scholar] [CrossRef]
- Ockwig, N.W.; Nenoff, T.M. Membranes for Hydrogen Separation. Chem. Rev. 2007, 107, 4078–4110. [Google Scholar] [CrossRef]
- Yang, Q.; Li, L.; Tan, W.; Sun, Y.; Wang, H.; Ma, J.; Zhao, X. Exceptional high selectivity of hydrogen/methane separation on a phosphonate-based MOF membrane with exclusion of methane molecules. Chem. Commun. 2017, 53, 9797–9800. [Google Scholar] [CrossRef]
- Bernardo, P.; Jansen, J. Polymeric membranes for the purification of hydrogen. In Compendium of Hydrogen Energy; Vol. 1.: Hydrogen Production and Purification; Subramani, V., Basile, A., Veziroglu, T.N., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 419–443. [Google Scholar] [CrossRef]
- Naderi, A.; Tashvigh, A.A.; Chung, N.T.-S.; Weber, M.; Maletzko, C. Molecular design of double crosslinked sulfonated polyphenylsulfone /polybenzimidazole blend membranes for an efficient hydrogen purification. J. Membr. Sci. 2018, 563, 726–733. [Google Scholar] [CrossRef]
- Villalobos, L.F.; Hilke, R.; Akhtar, F.H.; Peinemann, K.-V. Fabrication of Polybenzimidazole/Palladium Nanoparticles Hollow Fiber Membranes for Hydrogen Purification. Adv. Energy Mater. 2017, 8, 1701567. [Google Scholar] [CrossRef]
- Noble, R.D. Perspectives on mixed matrix membranes. J. Membr. Sci. 2011, 378, 393–397. [Google Scholar] [CrossRef]
- Chuah, C.Y.; Jiang, X.; Goh, K.; Wang, R. Recent Progress in Mixed-Matrix Membranes for Hydrogen Separation. Membranes 2021, 11, 666. [Google Scholar] [CrossRef]
- Dong, G.; Lee, Y.M. 1.8 Thermally Rearranged Polymeric Membranes: Materials and Applications. In Comprehensive Membrane Science and Engineering, 2nd ed.; Drioli, E., Giorno, L., Fontananova, E., Eds.; Elsevier: Oxford, UK, 2017; pp. 190–215. [Google Scholar] [CrossRef]
- Ma, C.; The Molecular Foundry, Lawrence Berkeley National Laboratory; Urban, J.J. Polymers of Intrinsic Microporosity (PIMs) Gas Separation Membranes: A mini Review. Proc. Nat. Res. Soc. 2018, 2, 02002. [Google Scholar] [CrossRef]
- Bandehali, S.; Amooghin, A.E.; Sanaeepur, H.; Ahmadi, R.; Fuoco, A.; Jansen, J.C.; Shirazian, S. Polymers of intrinsic microporosity and thermally rearranged polymer membranes for highly efficient gas separation. Sep. Purif. Technol. 2021, 278, 119513. [Google Scholar] [CrossRef]
- Díez, B.; Cuadrado, P.; Marcos-Fernández, Á.; de la Campa, J.G.; Tena, A.; Prádanos, P.; Palacio, L.; Lee, Y.M.; Alvarez, C.; Lozano, Á.E.; et al. Thermally rearranged polybenzoxazoles made from poly(ortho-hydroxyamide)s. Characterization and evaluation as gas separation membranes. React. Funct. Polym. 2018, 127, 38–47. [Google Scholar] [CrossRef]
- Dong, G.; Lee, Y.M. Microporous polymeric membranes inspired by adsorbent for gas separation. J. Mater. Chem. A 2017, 5, 13294–13319. [Google Scholar] [CrossRef]
- Galizia, M.; Chi, W.S.; Smith, Z.P.; Merkel, T.C.; Baker, R.W.; Freeman, B.D. 50th Anniversary Perspective: Polymers and Mixed Matrix Membranes for Gas and Vapor Separation: A Review and Prospective Opportunities. Macromolecules 2017, 50, 7809–7843. [Google Scholar] [CrossRef]
- Kim, J.S.; Moon, S.J.; Wang, H.H.; Kim, S.; Lee, Y.M. Mixed matrix membranes with a thermally rearranged polymer and ZIF-8 for hydrogen separation. J. Membr. Sci. 2019, 582, 381–390. [Google Scholar] [CrossRef]
- Soto, C.; Lugo, C.A.; Rodríguez, S.; Palacio, L.; Lozano, Á.E.; Prádanos, P.; Hernandez, A. Enhancement of CO2/CH4 permselectivity via thermal rearrangement of mixed matrix membranes made from an o-hydroxy polyamide with an optimal load of a porous polymer network. Sep. Purif. Technol. 2020, 247, 116895. [Google Scholar] [CrossRef]
- Smith, S.J.; Hou, R.; Lau, C.H.; Konstas, K.; Kitchin, M.; Dong, G.; Lee, J.; Lee, W.H.; Seong, J.G.; Lee, Y.M.; et al. Highly permeable Thermally Rearranged Mixed Matrix Membranes (TR-MMM). J. Membr. Sci. 2019, 585, 260–270. [Google Scholar] [CrossRef]
- Hou, R.; Ghanem, B.S.; Smith, S.J.D.; Doherty, C.M.; Setter, C.; Wang, H.; Pinnau, I.; Hill, M.R. Highly permeable and selective mixed-matrix membranes for hydrogen separation containing PAF-1. J. Mater. Chem. A 2020, 8, 14713–14720. [Google Scholar] [CrossRef]
- Lopez-Iglesias, B.; Suárez-García, F.; Aguilar-Lugo, C.; Ortega, A.G.; Bartolomé, C.; Martinez-Ilarduya, J.M.; De La Campa, J.G.; Lozano, Á.E.; Álvarez, C. Microporous Polymer Networks for Carbon Capture Applications. ACS Appl. Mater. Interfaces 2018, 10, 26195–26205. [Google Scholar] [CrossRef]
- Aguilar-Lugo, C.; Suárez-García, F.; Hernández, A.; Miguel, J.A.; Lozano, Á.E.; De La Campa, J.G.; Álvarez, C. New Materials for Gas Separation Applications: Mixed Matrix Membranes Made from Linear Polyimides and Porous Polymer Networks Having Lactam Groups. Ind. Eng. Chem. Res. 2019, 58, 9585–9595. [Google Scholar] [CrossRef]
- Aroon, M.A.; Ismail, A.; Matsuura, T.; Montazer-Rahmati, M. Performance studies of mixed matrix membranes for gas separation: A review. Sep. Purif. Technol. 2010, 75, 229–242. [Google Scholar] [CrossRef]
- Aguilar-Lugo, C.; Lee, W.H.; Miguel, J.A.; de la Campa, J.G.; Prádanos, P.; Bae, J.Y.; Lee, Y.M.; Álvarez, C.; Lozano, Á.E. Highly Permeable Mixed Matrix Membranes of Thermally Rearranged Polymers and Porous Polymer Networks for Gas Separations. ACS Appl. Polym. Mater. 2021, 3, 5224–5235. [Google Scholar] [CrossRef]
- Carvalho, A.L.; Maugeri, F.; Silva, V.; Hernández, A.; Palacio, L.; Pradanos, P. AFM analysis of the surface of nanoporous membranes: Application to the nanofiltration of potassium clavulanate. J. Mater. Sci. 2011, 46, 3356–3369. [Google Scholar] [CrossRef]
- Semino, R.; Ramsahye, N.; Ghoufi, A.; Maurin, G. Microscopic Model of the Metal–Organic Framework/Polymer Interface: A First Step toward Understanding the Compatibility in Mixed Matrix Membranes. ACS Appl. Mater. Interfaces 2015, 8, 809–819. [Google Scholar] [CrossRef]
- Shimekit, B.; Mukhtar, H.; Murugesan, T. Prediction of the relative permeability of gases in mixed matrix membranes. J. Membr. Sci. 2011, 373, 152–159. [Google Scholar] [CrossRef]
- Mahajan, R.; Koros, W.J. Factors Controlling Successful Formation of Mixed-Matrix Gas Separation Materials. Ind. Eng. Chem. Res. 2000, 39, 2692–2696. [Google Scholar] [CrossRef]
- Mahajan, R.; Burns, R.; Schaeffer, M.; Koros, W.J. Challenges in forming successful mixed matrix membranes with rigid polymeric materials. J. Appl. Polym. Sci. 2002, 86, 881–890. [Google Scholar] [CrossRef]
- Lin, H.; Freeman, B.D. Permeation and difusión. In Springer Handbook of Materials Measurement Methods; Czichos, H., Saito, T., Smith, L., Eds.; Springer: Berlin, Germany, 2006; pp. 371–387. [Google Scholar] [CrossRef]
- Flaconneche, B.; Martin, J.; Klopffer, M.H. Transport Properties of Gases in Polymers: Experimental Methods. Oil Gas. Sci. Technol. Rev. IFP 2001, 56, 245–259. [Google Scholar] [CrossRef] [Green Version]
- Rutherford, S.W.; Do, D.D. Review of time lag permeation technique as a method for characterisation of porous media and membranes. Adsorption 1997, 3, 283–312. [Google Scholar] [CrossRef]
- Monteleone, M.; Esposito, E.; Fuoco, A.; Lanč, M.; Pilnáček, K.; Friess, K.; Bezzu, C.G.; Carta, M.; McKeown, N.B.; Jansen, J.C. A Novel Time Lag Method for the Analysis of Mixed Gas Diffusion in Polymeric Membranes by On-Line Mass Spectrometry: Pressure Dependence of Transport Parameters. Membranes 2018, 8, 73. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Kruczek, B.; Thibault, J. Impact of Measuring Devices and Data Analysis on the Determination of Gas Membrane Properties. J. Membr. Sci. Res. 2018, 4, 4–14. [Google Scholar] [CrossRef]
- Robeson, L.M. Correlation of separation factor versus permeability for polymeric membranes. J. Membr. Sci. 1991, 62, 165–185. [Google Scholar] [CrossRef]
- Robeson, L.M. The upper bound revisited. J. Membr. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
- Kim, S.; Lee, Y.M. Rigid and microporous polymers for gas separation membranes. Prog. Polym. Sci. 2015, 43, 1–32. [Google Scholar] [CrossRef]
- Huang, X.; Yao, H.; Cheng, Z. Hydrogen Separation Membranes of Polymeric Materials. In Nanostructured Materials for Next-Generation Energy Storage and Conversion; Springer-Verlag GmbH: Berlin, Germany, 2017. [Google Scholar] [CrossRef]
- Sanders, D.F.; Smith, Z.P.; Guo, R.; Robeson, L.M.; McGrath, J.E.; Paul, D.R.; Freeman, B.D. Energy-efficient polymeric gas separation membranes for a sustainable future: A review. Polymer 2013, 54, 4729–4761. [Google Scholar] [CrossRef] [Green Version]
- Swaidan, R.; Ghanem, B.; Pinnau, I. Fine-Tuned Intrinsically Ultramicroporous Polymers Redefine the Permeability/Selectivity Upper Bounds of Membrane-Based Air and Hydrogen Separations. ACS Macro Lett. 2015, 4, 947–951. [Google Scholar] [CrossRef] [Green Version]
- Moore, T.T.; Koros, W.J. Non-ideal effects in organic–inorganic materials for gas separation membranes. J. Mol. Struct. 2005, 739, 87–98. [Google Scholar] [CrossRef]




| Membranes | |||
|---|---|---|---|
| PPN Content (%) | Before TR | After TR | |
| dfr | 0 | 1.76 | 1.78 |
| 20 | 1.62 | 1.93 | |
| 30 | 1.92 | 2.03 | |
| Rq (nm) | 0 | 14.90 | 4.32 |
| 20 | 4.77 | 5.06 | |
| 30 | 3.45 | 12.70 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soto, C.; Torres-Cuevas, E.S.; González-Ortega, A.; Palacio, L.; Prádanos, P.; Freeman, B.D.; Lozano, Á.E.; Hernandez, A. Hydrogen Recovery by Mixed Matrix Membranes Made from 6FCl-APAF HPA with Different Contents of a Porous Polymer Network and Their Thermal Rearrangement. Polymers 2021, 13, 4343. https://doi.org/10.3390/polym13244343
Soto C, Torres-Cuevas ES, González-Ortega A, Palacio L, Prádanos P, Freeman BD, Lozano ÁE, Hernandez A. Hydrogen Recovery by Mixed Matrix Membranes Made from 6FCl-APAF HPA with Different Contents of a Porous Polymer Network and Their Thermal Rearrangement. Polymers. 2021; 13(24):4343. https://doi.org/10.3390/polym13244343
Chicago/Turabian StyleSoto, Cenit, Edwin S. Torres-Cuevas, Alfonso González-Ortega, Laura Palacio, Pedro Prádanos, Benny D. Freeman, Ángel E. Lozano, and Antonio Hernandez. 2021. "Hydrogen Recovery by Mixed Matrix Membranes Made from 6FCl-APAF HPA with Different Contents of a Porous Polymer Network and Their Thermal Rearrangement" Polymers 13, no. 24: 4343. https://doi.org/10.3390/polym13244343
APA StyleSoto, C., Torres-Cuevas, E. S., González-Ortega, A., Palacio, L., Prádanos, P., Freeman, B. D., Lozano, Á. E., & Hernandez, A. (2021). Hydrogen Recovery by Mixed Matrix Membranes Made from 6FCl-APAF HPA with Different Contents of a Porous Polymer Network and Their Thermal Rearrangement. Polymers, 13(24), 4343. https://doi.org/10.3390/polym13244343