Using Quantitative Passive Thermography and Modified Paris-Law for Probabilistic Calculation of the Fatigue Damage Development in a CFRP-Aluminum Hybrid Joint
Abstract
:1. Introduction
1.1. Literature Review on Damage in CFRP
1.2. Literature Review on Damage in Hybrid-Joints
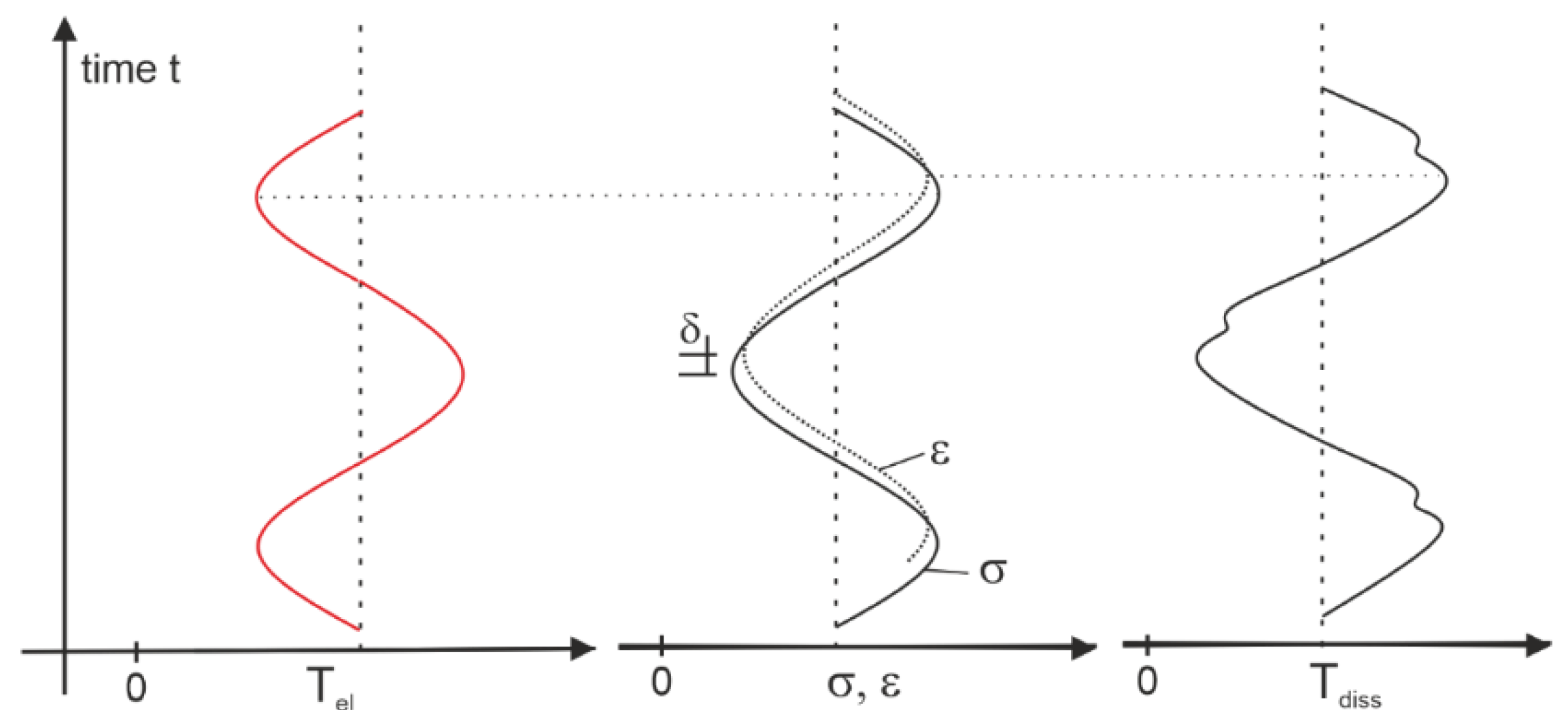
1.3. Literature Review on Thermography for Damage Detection
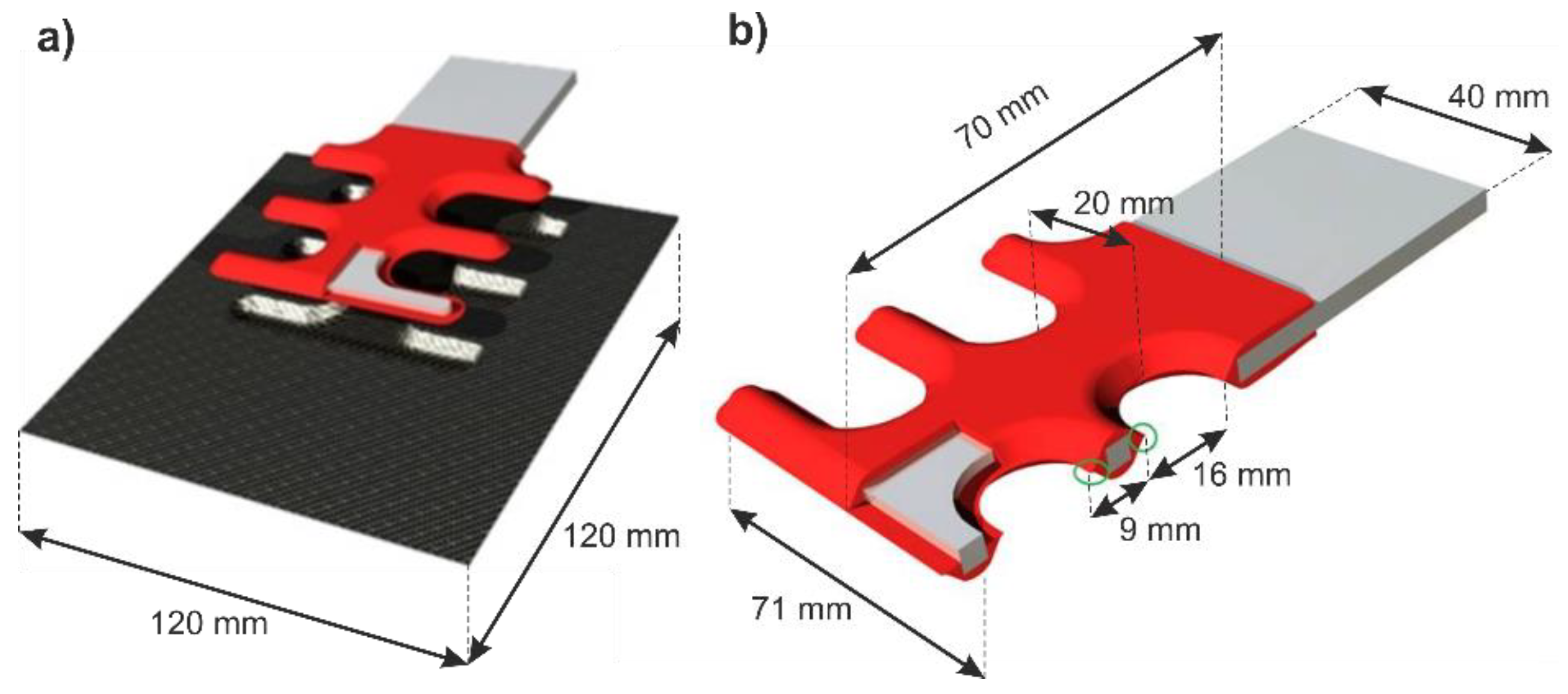
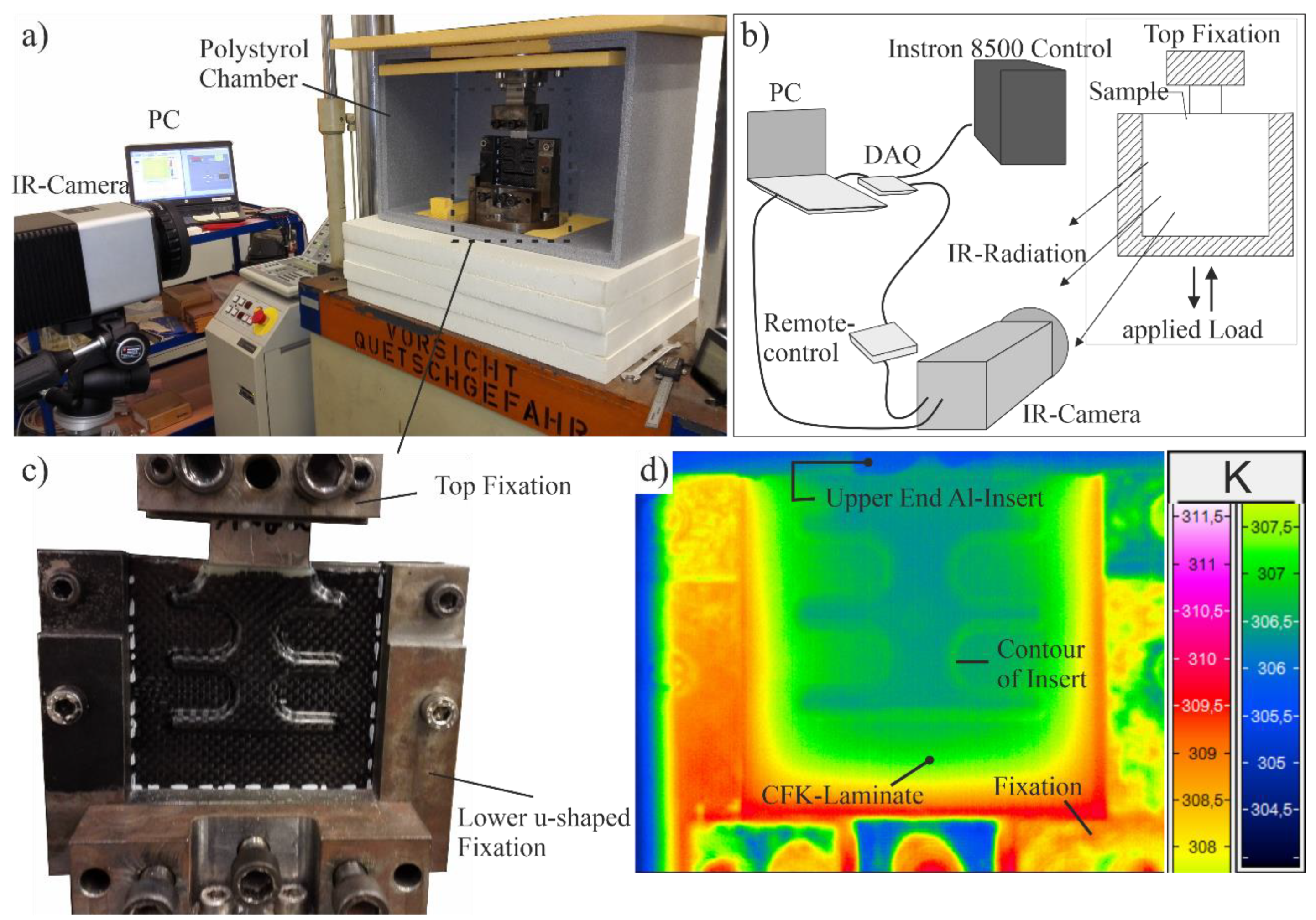
2. Materials and Methods
3. Results
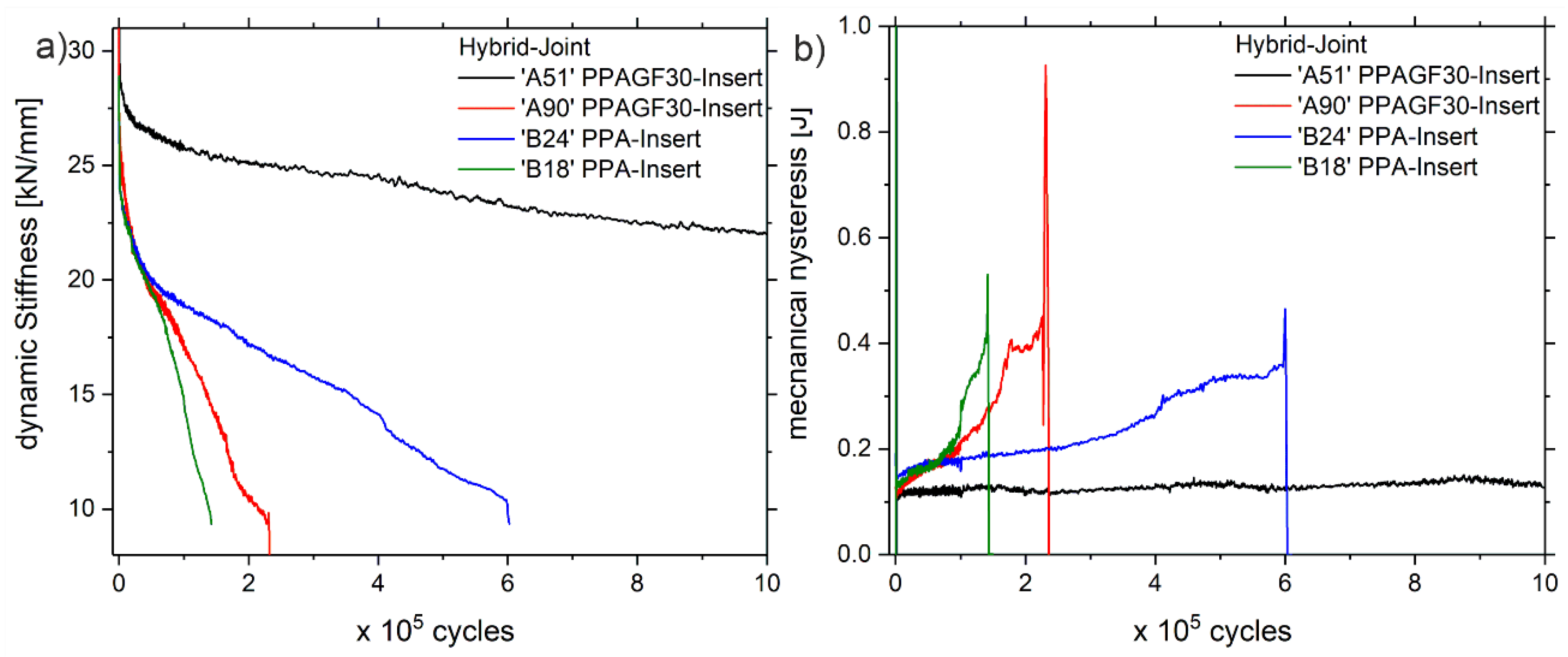
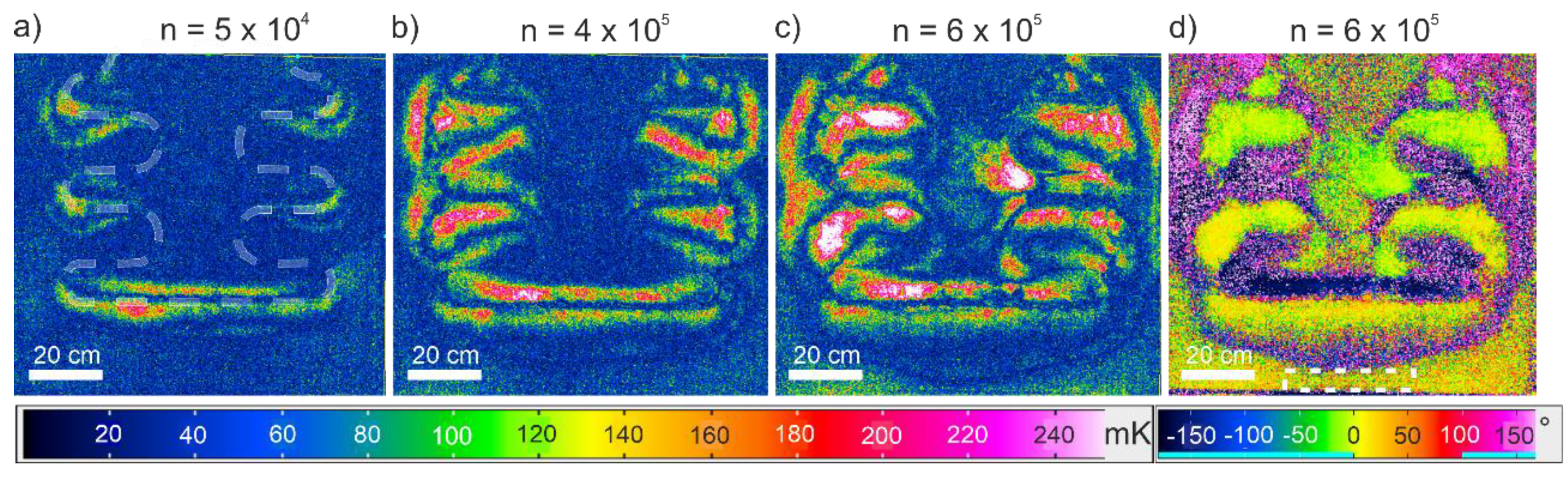
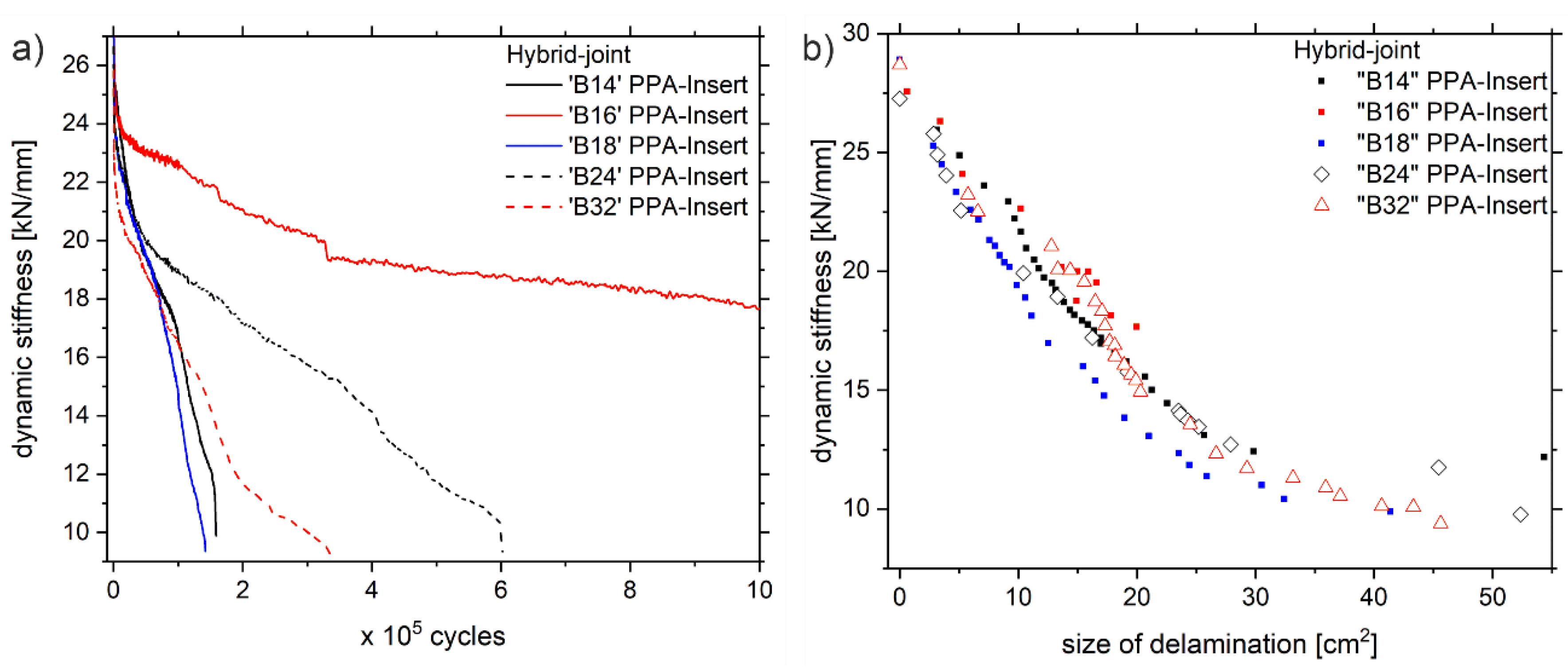
3.1. Fatigue Behavior and Damage Mechanisms
3.2. Mode I Interlaminar Fracture
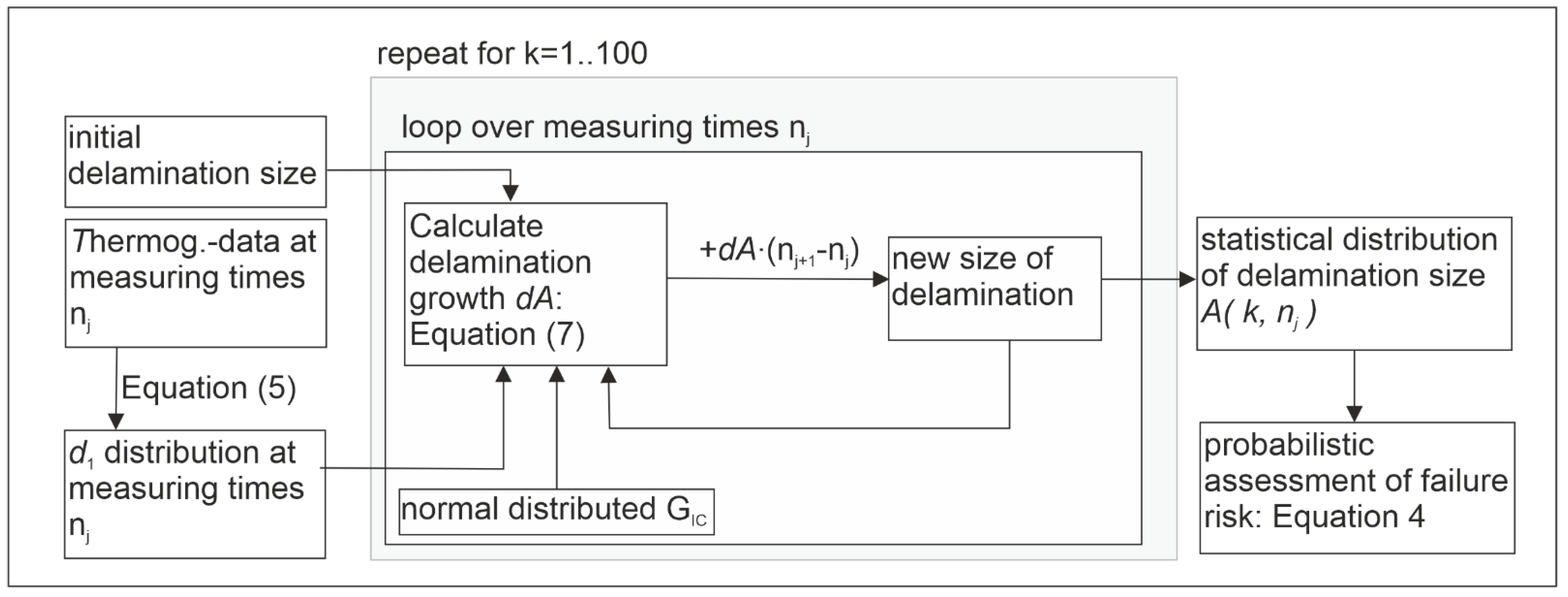
3.3. Calculation Model for Delamination Growth Based on Thermography Data
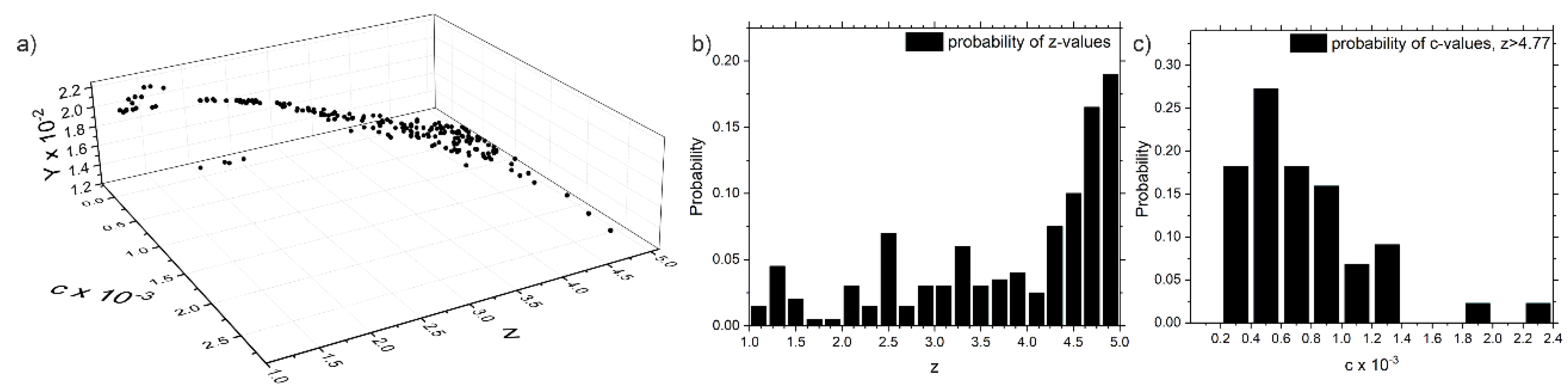
3.4. Determination of the Model Parameters
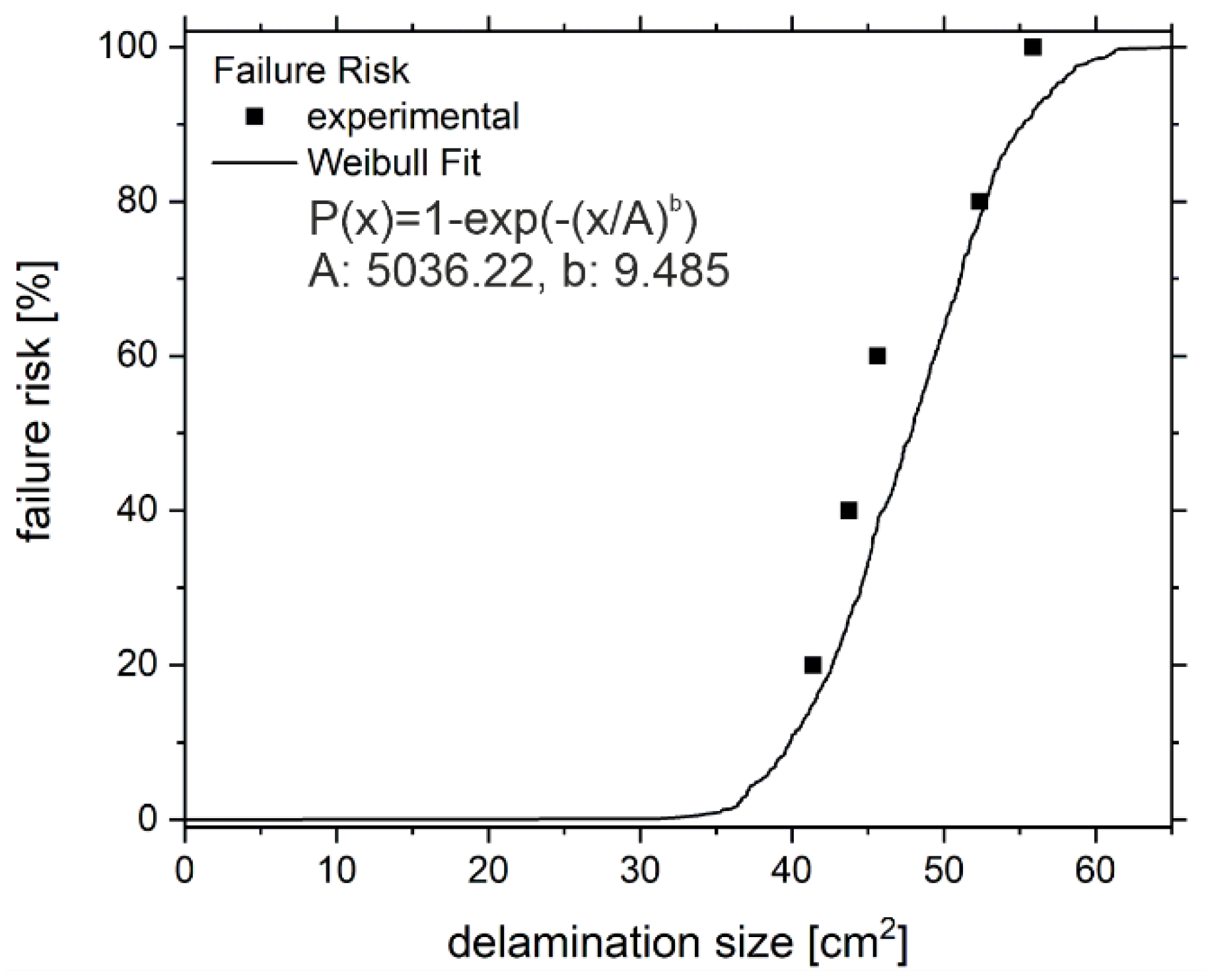
3.5. Model Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Palumbo, D.; de Finis, R.; Demelio, G.P.; Galietti, U. Study of damage evolution in composite materials based on the Thermoelastic Phase Analysis (TPA) method. Compos. Part B Eng. 2017, 117, 49–60. [Google Scholar] [CrossRef]
- Steinberger, R.; Leitão, T.V.; Ladstätter, E.; Pinter, G.; Billinger, W.; Lang, R. Infrared thermographic techniques for non-destructive damage characterization of carbon fibre reinforced polymers during tensile fatigue testing. Int. J. Fatigue 2006, 28, 1340–1347. [Google Scholar] [CrossRef]
- Laiarinandrasana, L.; Morgeneyer, T.F.; Cheng, Y.; Helfen, L.; Le Saux, V.; Marco, Y. Microstructural observations supporting thermography measurements for short glass fibre thermoplastic composites under fatigue loading. Contin. Mech. Thermodyn. 2020, 32, 451–469. [Google Scholar] [CrossRef]
- Goidescu, C.; Welemane, H.; Garnier, C.; Fazzini, M.; Brault, R.; Péronnet, E.; Mistou, S. Damage investigation in CFRP composites using full-field measurement techniques: Combination of digital image stereo-correlation, infrared thermography and X-ray tomography. Compos. Part B Eng. 2013, 48, 95–105. [Google Scholar] [CrossRef] [Green Version]
- Guedes, R.M. Lifetime Prediction of polymer matrix composites under constand or monotonic load. Compos. Part A Appl. Sci. Manuf. 2006, 37, 703–715. [Google Scholar] [CrossRef]
- Thollon, Y.; Hochard, C. A general damage model for woven fabric composite laminates up to first failure. Mech. Mater. 2009, 41, 820–827. [Google Scholar] [CrossRef]
- van Paepegem, W.; Degrieck, J. A new couled approach of residual stiffness and strength for fatigue of fibre-reinforced composites. Int. J. Fatigue 2002, 24, 747–762. [Google Scholar] [CrossRef]
- Cantwell, W.J.; Morton, J. The significance of damage and defects and their detection in composite materials-a review. J. Strain Anal. 1992, 27, 29–42. [Google Scholar] [CrossRef]
- Gamstedt, E.K. Effects of debonding and fiber strength distribution on fatigue-damage propagation in Carbon Fiber-Reinforced Epoxy. J. Appl. Polym. Sci. 2000, 76, 457–474. [Google Scholar] [CrossRef]
- Talreja, R. Damage and fatigue in composites—A personal account. Compos. Sci. Technol. 2008, 68, 2585–2591. [Google Scholar] [CrossRef]
- Liu, Y.; Mahadevan, S. Probabilistic fatigue life prediction using an equivalent initial flaw size distribution. Int. J. Fatigue 2009, 31, 476–487. [Google Scholar] [CrossRef]
- Dragos, D. Cioclov. Failure Risk Assessment by Integration of Probabilistic Fracture Mechanics and Quantitative Non-Destructive Inspection—A structural Health Monitoring View. In New Trends in Smart Technologies; Fraunhofer Verlag: Stuttgart, Germany, 2013; ISBN 978-3-8396-0577-6. [Google Scholar]
- Dragos, D. Cioclov. How simulation of failure risk can improve structural reliability—Application to pressurized components and pipes. In New Trends in Smart Technologies; Fraunhofer Verlag: Stuttgart, Germany, 2013; ISBN 978-3-8396-0577-6. [Google Scholar]
- Ungsuwarungsri, T.; Knauss, W.G. The role of damage-softened material behavior in the fracture of composites and adhesives. Int. J. Fract. 1987, 35, 221–241. [Google Scholar] [CrossRef]
- Ashcroft, I.A.; Hughes, D.J.; Shaw, S.J. Mode I fracture of epoxy bonded composite joints: I. Quasi-static loading. Int. J. Adhes. Adhes. 2001, 21, 87–99. [Google Scholar] [CrossRef]
- Al-Khudairi, O.; Hadavinia, H.; Waggott, A.; Lewis, E.; Little, C. Characterising mode I/mode II fatigue delamination growth in unidirectional fibre reinforced polymer laminates. Mater. Des. 2015, 66, 93–102. [Google Scholar] [CrossRef] [Green Version]
- Skinner, T.; Datta, S.; Chattopadhyay, A.; Hall, A. Fatigue damage behavior in carbon fiber polymer composites under biaxial loading. Compos. Part B Eng. 2019, 174, 106942. [Google Scholar] [CrossRef]
- Deng, J.; Hong, Z.; Yin, Q.; Lu, T.J. A physically-based failure analysis framework for fiber-reinforced composite laminates under multiaxial loading. Compos. Struct. 2020, 241, 112125. [Google Scholar] [CrossRef]
- Amancio-Filho, S.T.; dos Santos, J.F. Joining of polymers and polymer-metal hybrid structures: Recent developments and trends. Polym. Eng. Sci. 2009, 49, 1461–1476. [Google Scholar] [CrossRef]
- Haberstroh, E.; Sickert, M. Thermal Direct Joining of Hybrid Plastic Metal Components. KMUTNB Int. J. Appl. Sci. Technol. 2014, 7, 29–34. [Google Scholar] [CrossRef] [Green Version]
- Barfuss, D.; Grützner, R.; Hirsch, F.; Gude, M.; Müller, R.; Kästner, M. Multi-scale structuring for thermoplastic-metal contour joints of hollow profiles. Prod. Eng. 2018, 12, 229–238. [Google Scholar] [CrossRef]
- Parkes, P.N.; Butler, R.; Meyer, J.; de Oliveira, A. Static strength of metal-composite joints with penetrative reinforcement. Compos. Struct. 2014, 118, 250–256. [Google Scholar] [CrossRef] [Green Version]
- Ucsnik, S.; Scheerer, M.; Zaremba, S.; Pahr, D.H. Experimental investigation of a novel hybrid metal–composite joining technology. Compos. Part A Appl. Sci. Manuf. 2010, 41, 369–374. [Google Scholar] [CrossRef]
- Boyd, S.W.; Blake, J.I.R.; Shenoi, R.A.; Kapadia, A. Integrity of hybrid steel-to-composite joints for marine application. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2004, 218, 235–246. [Google Scholar] [CrossRef] [Green Version]
- Pohl, M.; Stommel, M. Designing a metal-CFRP hybrid by using a structured polymeric somponent on the interface. In Proceedings of the 17th European Conference on Composite Materials, München, Germany, 26–30 June 2016; pp. 4025–4030. [Google Scholar]
- Summa, J.; Becker, M.; Grossmann, F.; Pohl, M.; Stommel, M.; Herrmann, H.-G. Fracture analysis of a metal to CFRP hybrid with thermoplastic interlayers for interfacial stress relaxation using in situ thermography. Compos. Struct. 2018, 193, 19–28. [Google Scholar] [CrossRef]
- Roche, J.-M.; Balageas, D.; Lamboul, B.; Bai, G.; Passilly, F.; Mavel, A.; Grail, G. Passive and active thermography for in situ damage monitoring in woven composites during mechanical testing. In Proceedings of the Review of Progress in Quantitative Nondestructive Evaluation: Volume 32, Denver, CO, USA, 15–20 July 2012; AIP: Melville, NY, USA, 2013; pp. 555–562. [Google Scholar]
- Montesano, J.; Fawaz, Z.; Bougherara, H. Use of infrared thermography to investigate the fatigue behavior of a carbon fiber reinforced polymer composite. Compos. Struct. 2013, 97, 76–83. [Google Scholar] [CrossRef]
- Palumbo, D.; Tamborrino, R.; Galietti, U.; Aversa, P.; Tatì, A.; Luprano, V.A.M. Ultrasonic analysis and lock-in thermography for debonding evaluation of composite adhesive joints. NDT E Int. 2016, 78, 1–9. [Google Scholar] [CrossRef]
- Harizi, W.; Chaki, S.; Bourse, G.; Ourak, M. Mechanical damage assessment of Glass Fiber-Reinforced Polymer composites using passive infrared thermography. Compos. Part B Eng. 2014, 59, 74–79. [Google Scholar] [CrossRef]
- Pitaressi, G.; Paterson, E.A. A review of the general theory of thermoelastic stress analysis. J. Strain Anal. 2003, 5, 405–417. [Google Scholar] [CrossRef]
- Rajic, N.; Rowlands, D. Thermoelastic stress analysis with a compact low-cost microbolometer system. Quant. Infrared Thermogr. J. 2013, 10, 135–158. [Google Scholar] [CrossRef] [Green Version]
- Naderi, M.; Kahirdeh, A.; Khonsari, M.M. Dissipated thermal energy and damage evolution of Glass/Epoxy using infrared thermography and acoustic emission. Compos. Part B Eng. 2012, 43, 1613–1620. [Google Scholar] [CrossRef]
- Jegou, L.; Marco, Y.; Le Saux, V.; Calloch, S. Fast prediction of the Wöhler curve from heat build-up measurements on Short Fiber Reinforced Plastic. Int. J. Fatigue 2013, 47, 259–267. [Google Scholar] [CrossRef]
- Chrysochoos, A.; Louche, H. An infrared image processing to analyse the calorific effects accompanying strain localisation. Int. J. Eng. Sci. 2000, 38, 1759–1788. [Google Scholar] [CrossRef]
- Grujicic, M.; Sellappan, V.; Omar, M.A.; Seyr, N.; Obieglo, A.; Erdmann, M.; Holzleitner, J. An overview of the polymer-to-metal direct-adhesion hybrid technologies for load-bearing automotive components. J. Mater. Process. Technol. 2008, 197, 363–373. [Google Scholar] [CrossRef]
- DIN EN 6033:2015, DIN Deutsches Institut für Normung e.V., Aerospace series—Carbon fibre reinforced plastics—Test method—Determination of interlaminar fracture toughness energy—Mode I—GIC, February 2016, ICS 49.025.40.


| Specimen | 3-1 | 3-2 | 3-3 | 4-1 | 4-2 | 4-3 |
| GIC [J/m2] | 496.5 | 435.7 | 495.9 | 493.0 | 538.2 | 504.6 |
| Mean [J/m2] | 486.7 | |||||
| Standard deviation [J/m2] | 84 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Summa, J.; Herrmann, H.-G. Using Quantitative Passive Thermography and Modified Paris-Law for Probabilistic Calculation of the Fatigue Damage Development in a CFRP-Aluminum Hybrid Joint. Polymers 2021, 13, 349. https://doi.org/10.3390/polym13030349
Summa J, Herrmann H-G. Using Quantitative Passive Thermography and Modified Paris-Law for Probabilistic Calculation of the Fatigue Damage Development in a CFRP-Aluminum Hybrid Joint. Polymers. 2021; 13(3):349. https://doi.org/10.3390/polym13030349
Chicago/Turabian StyleSumma, Jannik, and Hans-Georg Herrmann. 2021. "Using Quantitative Passive Thermography and Modified Paris-Law for Probabilistic Calculation of the Fatigue Damage Development in a CFRP-Aluminum Hybrid Joint" Polymers 13, no. 3: 349. https://doi.org/10.3390/polym13030349
APA StyleSumma, J., & Herrmann, H.-G. (2021). Using Quantitative Passive Thermography and Modified Paris-Law for Probabilistic Calculation of the Fatigue Damage Development in a CFRP-Aluminum Hybrid Joint. Polymers, 13(3), 349. https://doi.org/10.3390/polym13030349






