Temperature Profile in Rubber Injection Molding: Application of a Recently Developed Testing Method to Improve the Process Simulation and Calculation of Curing Kinetics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material and Equipment
2.2. Experimental Setup
2.2.1. Injection Molding Machine
2.2.2. Test Stand
2.2.3. Injection Mold and Rubber Part
2.2.4. Simulation
- 1.
- Simulation of the process cycle assuming that the inlet temperature of the compound equals the set temperature of the dosing unit.
- 2.
- Simulation of the process cycle assuming that the inlet temperature of the compound is higher than the set temperatures in the dosing unit, but still constant, thus corresponding to Fasching’s hypothesis [14].
- 3.
- Simulation of the process cycle considering the actual state of the mass temperature profile at the test stand for the given settings in Table 1.
2.2.5. Characterization
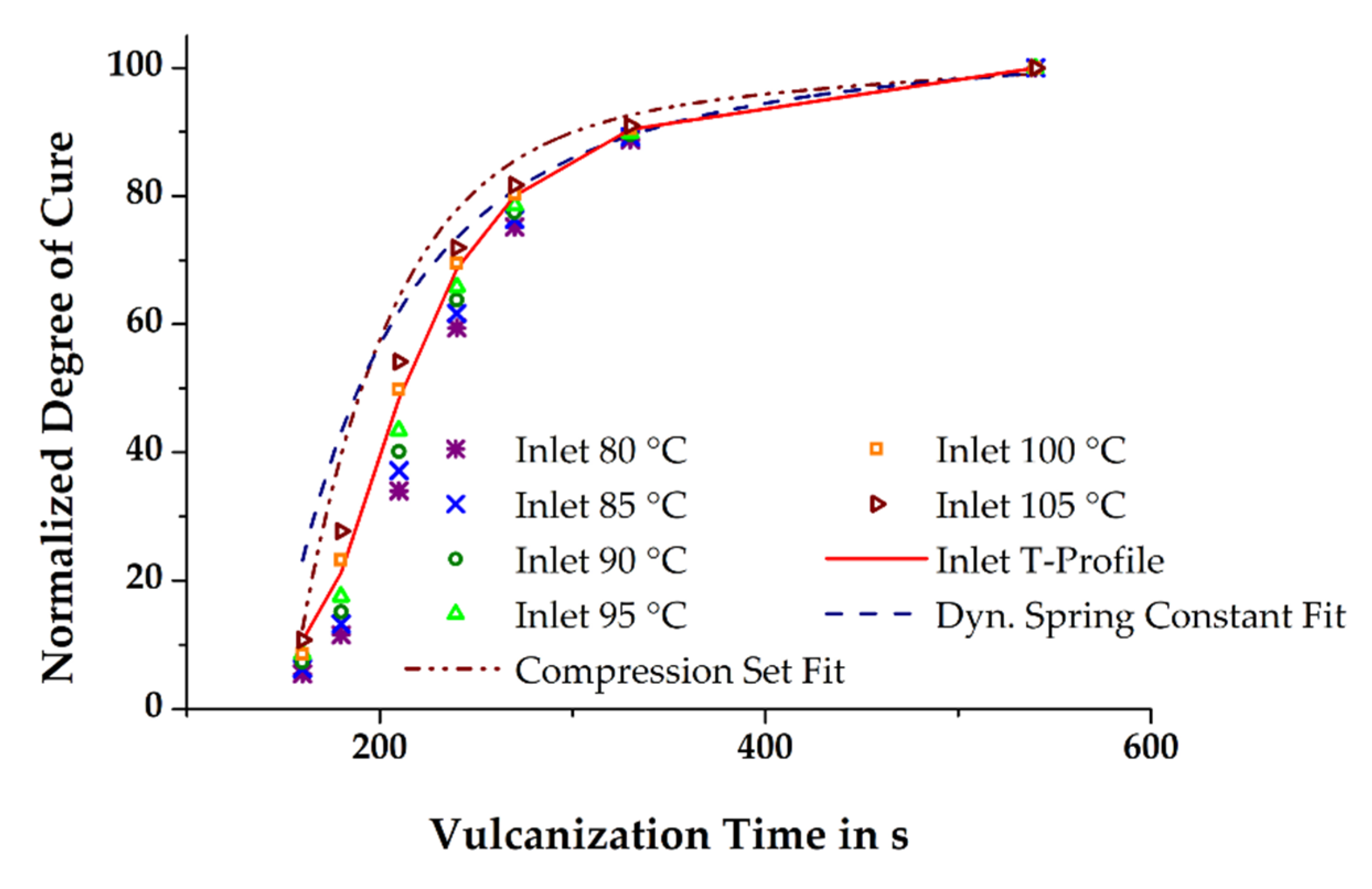
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mitsoulis, E.; Battisti, M.; Neunhäuserer, A.; Perko, L.; Friesenbichler, W.; Ansari, M.; Hatzikiriakos, S.G. Flow behaviour of rubber in capillary and injection moulding dies. Plast. Rubber Compos. 2017, 46, 110–118. [Google Scholar] [CrossRef]
- Friesenbichler, W.; Stieger, S.; Kerschbaumer, R.; Berger-Weber, G.; Neunhaeuserer, A.; Mitsoulis, E. Viscoelastic Modelling of Polymer Melts and Rubber Compounds. In Advances in Polymer Processing 2020; Hopmann, C., Dahlmann, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 270–282. [Google Scholar] [CrossRef]
- Stieger, S.; Kerschbaumer, R.C.; Mitsoulis, E.; Fasching, M.; Berger-Weber, G.R.; Friesenbichler, W.; Sunder, J. Contraction and capillary flow of a carbon black filled rubber compound. Polym. Eng. Sci. 2020, 60, 32–43. [Google Scholar] [CrossRef] [Green Version]
- Rafei, M.; Ghoreishy, M.H.R.; Naderi, G. Development of an advanced computer simulation technique for the modeling of rubber curing process. Comput. Mater. Sci. 2009, 47, 539–547. [Google Scholar] [CrossRef]
- Michaeli, W.; Greif, H.; Kretzschmar, G.; Ehring, F. Training in Injection Molding, 2nd ed.; Carl Hanser Verlag: München, Germany, 2001; ISBN 1569903026. [Google Scholar]
- Johannaber, F.; Michaeli, W. Handbuch Spritzgießen, 2nd ed.; Carl Hanser Verlag: München, Germany, 2004. [Google Scholar]
- Leblanc, J.L. Rubber-filler interactions and rheological properties in filled compounds. Prog. Polym. Sci. 2002, 27, 627–687. [Google Scholar] [CrossRef]
- Pantani, R.; Coccorullo, I.; Speranza, V.; Titomanlio, G. Modeling of morphology evolution in the injection molding process of thermoplastic polymers. Prog. Polym. Sci. 2005, 30, 1185–1222. [Google Scholar] [CrossRef]
- Röthemeyer, F.; Sommer, F. Kautschuk Technologie, 3rd ed.; Carl Hanser Verlag: München, Germany, 2013; ISBN 9783446437760. [Google Scholar]
- Payne, A.R. The Dynamic Properties of Carbon Black-Loaded Natural Rubber Vulcanizates. Part, I.J. Appl. Polym. Sci. 1962, 6, 57–63. [Google Scholar] [CrossRef]
- Fröhlich, J.; Niedermeier, W.; Luginsland, H.D. The effect of filler-filler and filler-elastomer interaction on rubber reinforcement. Compos. Part A: Appl. Sci. Manuf. 2005, 36, 449–460. [Google Scholar] [CrossRef]
- Perko, L.; Fasching, M.; Friesenbichler, W. Model for the prediction of bulk temperature changes and pressure losses in rubber compounds flowing through conical dies: An engineering approach. Polym. Eng. Sci. 2014, 55, 701–709. [Google Scholar] [CrossRef]
- Perko, L. Cure-Time Reduction in Rubber Injection Moulding by Means of Shear- Elongation- and Compression Heating. Ph.D. Thesis, Montanuniversitaet Leoben, Leoben, Austria, 2014. [Google Scholar]
- Fasching, M. Robust Processing in Rubber Injection Molding Using Advanced Simulation Methods and Material Data. Ph.D. Thesis, Montanuniversitaet Leoben, Leoben, Austria, 2015. [Google Scholar]
- Fasching, M.; Berger, G.; Friesenbichler, W.; Filz, P.; Helbich, B. Robust process control for rubber injection moulding with use of systematic simulations and improved material data. Int. Polym. Sci. Technol. 2015, 42, T1–T3. [Google Scholar] [CrossRef]
- Ramorino, G.; Agnelli, S.; Guindani, M. Analysis of Reactive Injection Compression Molding by Numerical Simulations and Experiments. Adv. Polym. Technol. 2020, 2020, 1–8. [Google Scholar] [CrossRef]
- Kerschbaumer, R.C.; Lechner, B.; Graninger, G.; Friesenbichler, W. Characterization of the Temperature Profile during Dosing under Steady State Conditions by Means of a Specially Designed Test Stand. In Proceedings of the 32nd International Conference of the Polymer Processing Society, Lyon, France, 25–29 July 2016. [Google Scholar]
- Kerschbaumer, R.C. Process Model for the Description of the Dosing Process of Rubber Injection Molding Machines. Ph.D. Thesis, Montanuniversitaet Leoben, Leoben, Austria, 2019. [Google Scholar]
- Deutsches Institut für Normung, e.V. DIN ISO 815-1:2010-09 Rubber, vulcanized or thermoplastic – Determination of compression set – Part 1: At ambient or elevated temperatures. Deutsches Institut für Normung e.V.: Berlin, Germany, 2010. [Google Scholar]
- Kerschbaumer, R.C.; Lechner, B.; Friesenbichler, W. Advanced Part Quality Testing – Compression Set vs. Non-Destructive and Fast Measurement Device. In Proceedings of the German Rubber Conference DKT 2018, Nuernberg, Germany, 2–5 July 2018. [Google Scholar]
- Hutterer, T. Data-Driven Fault Detection and Identification in Rubber Injection Molding. Ph.D. Thesis, Montanuniversitaet Leoben, Leoben, Austria, 2020. [Google Scholar]


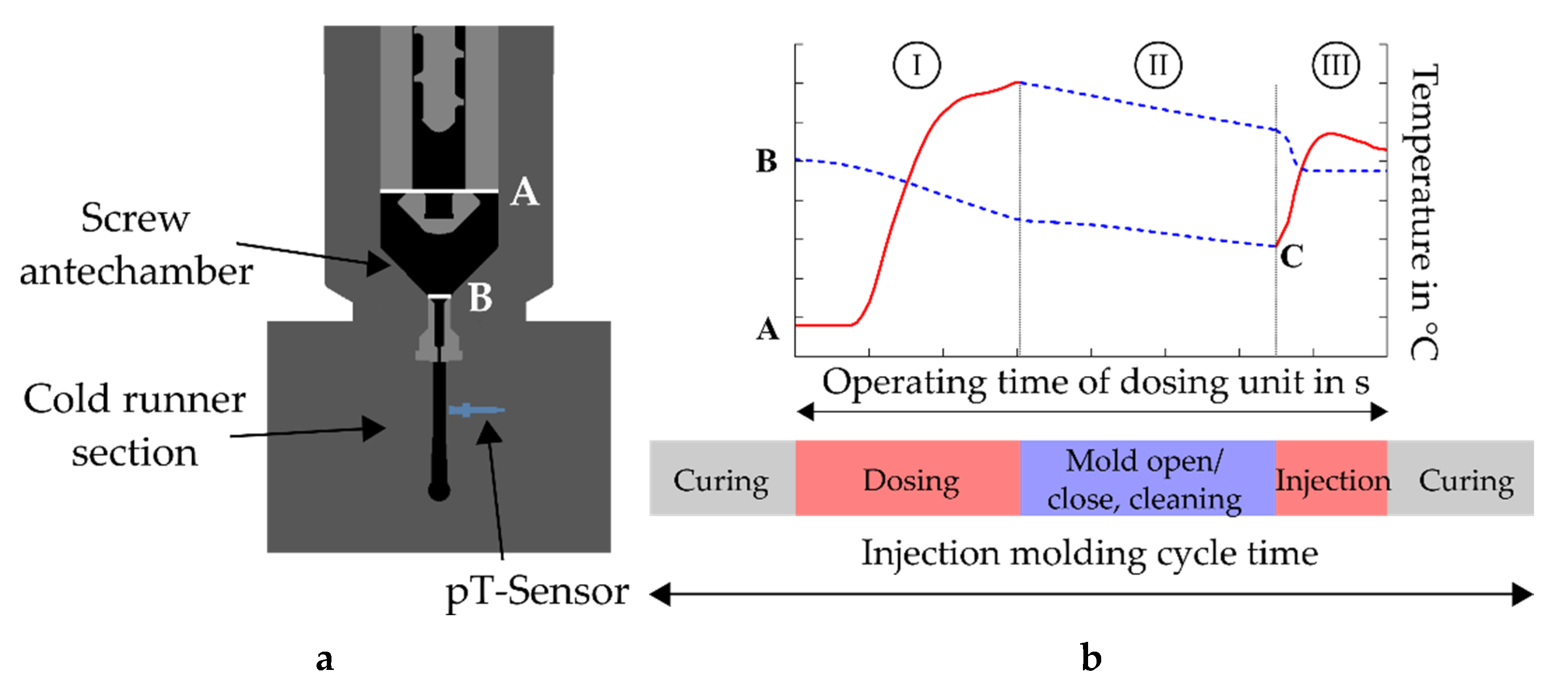
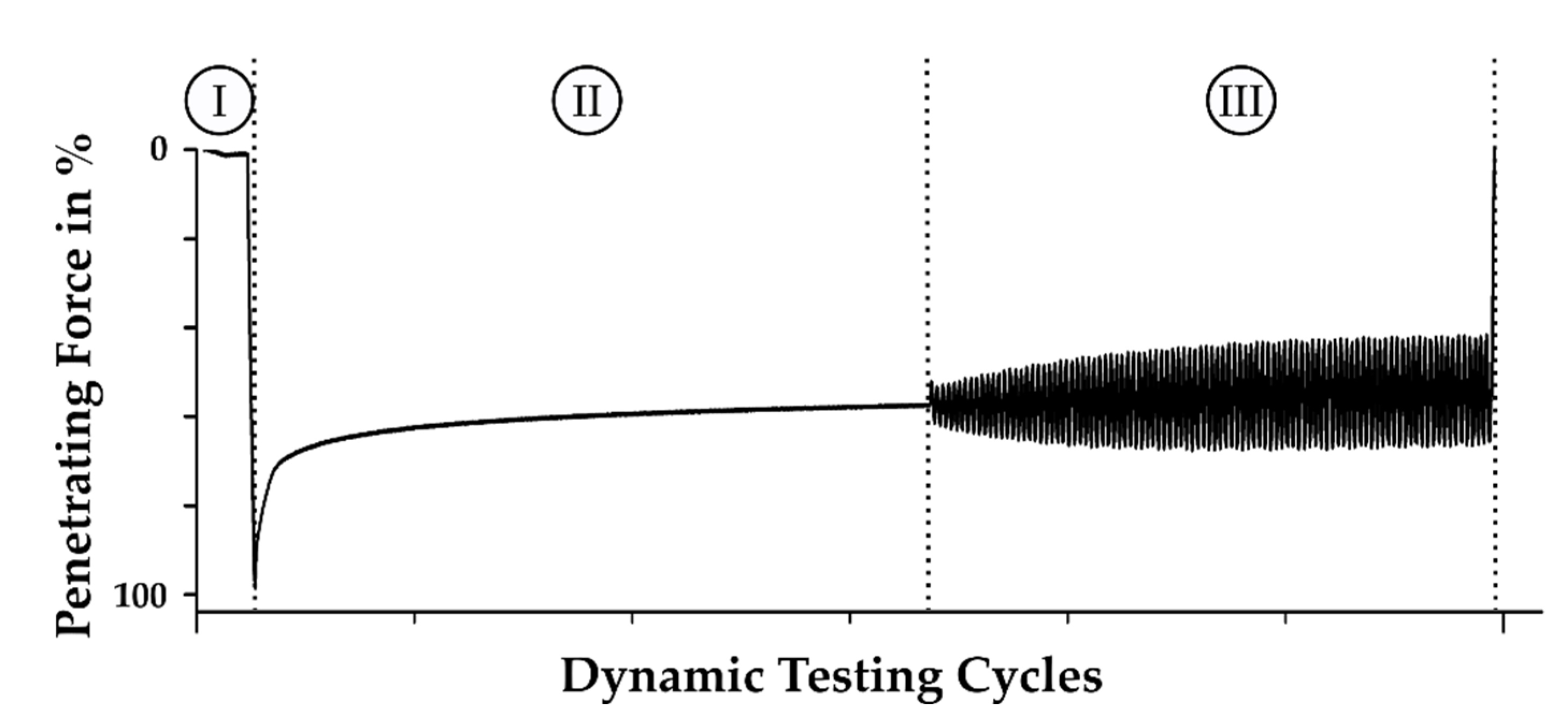

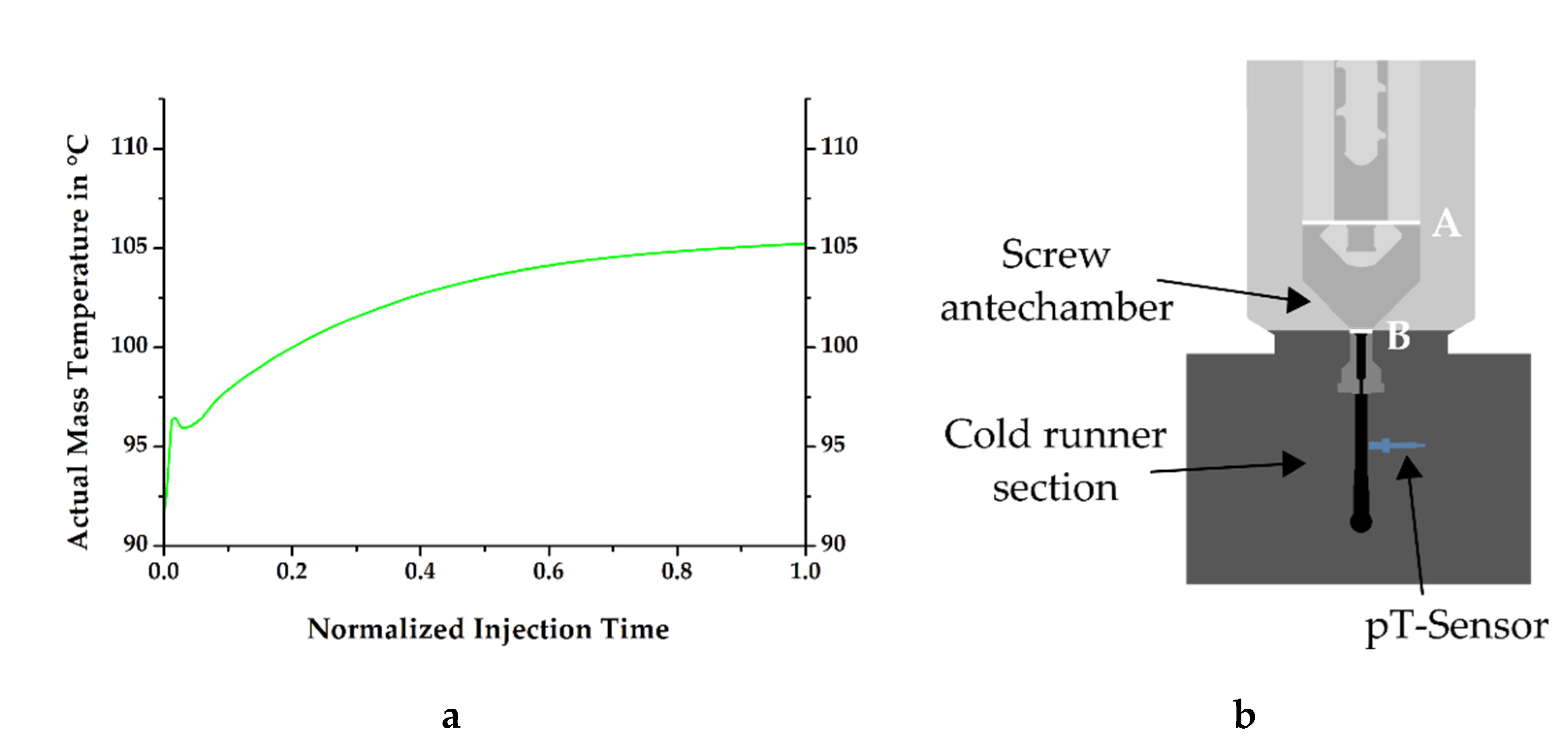

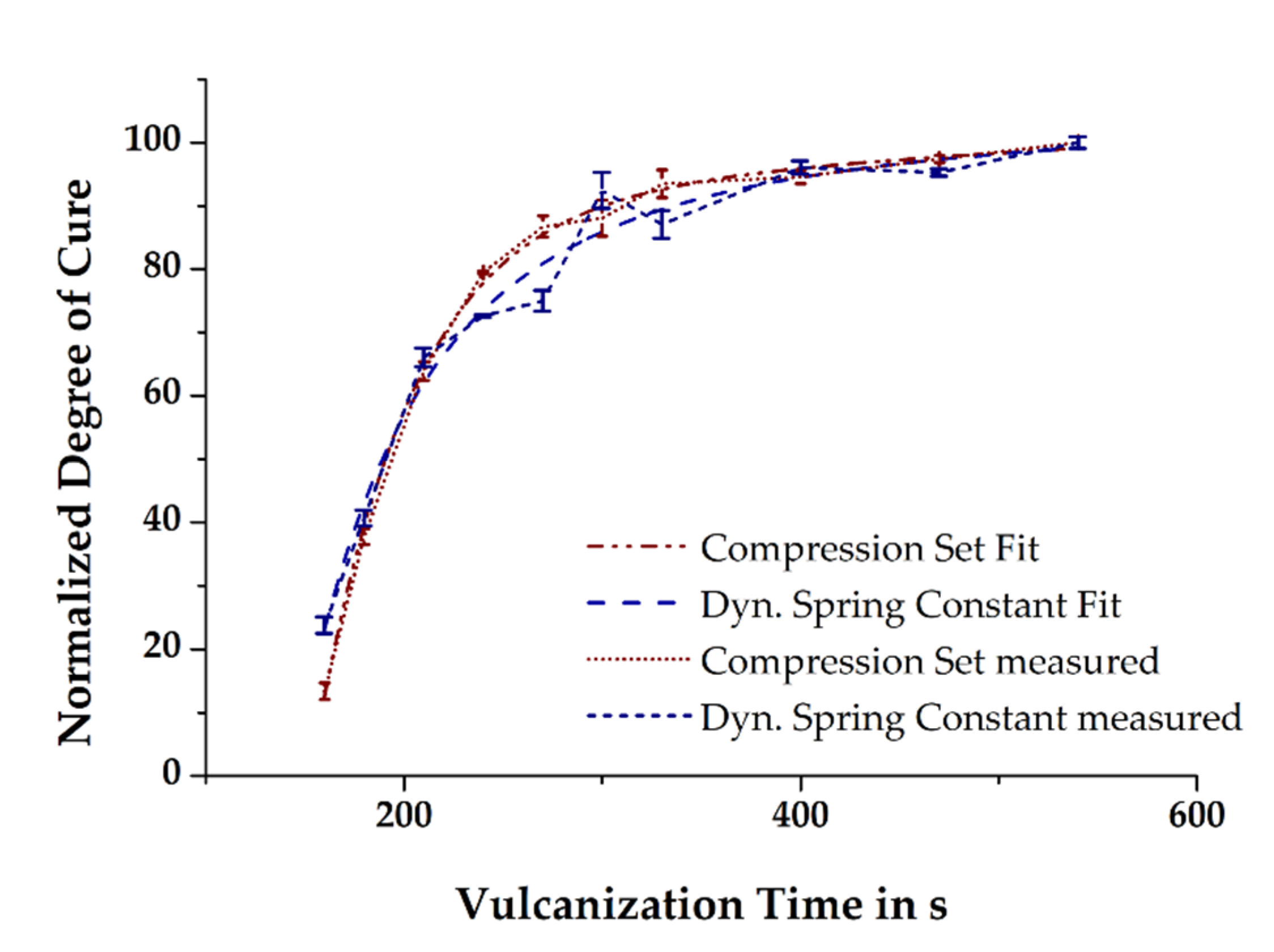
| Temperature Dosing Unit a,b (°C) | Temperature Cold Runner b (°C) | Temperature Cavities b (°C) | Screw Rotational Speed a,b (min−1) | Injection Speed b (cm3 s−1) |
|---|---|---|---|---|
| 80 | 80 | 160 | 90 | 18 |
| Temperature Cold Runner (°C) | Temperature Cavities (°C) | Screw Rotational Speed a (min−1) | Injection Speed (cm3 s−1) | Curing Time Range (s) |
|---|---|---|---|---|
| 80 | 160 | Measured Temperature Profile | 18 | 160–540 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Traintinger, M.; Kerschbaumer, R.C.; Lechner, B.; Friesenbichler, W.; Lucyshyn, T. Temperature Profile in Rubber Injection Molding: Application of a Recently Developed Testing Method to Improve the Process Simulation and Calculation of Curing Kinetics. Polymers 2021, 13, 380. https://doi.org/10.3390/polym13030380
Traintinger M, Kerschbaumer RC, Lechner B, Friesenbichler W, Lucyshyn T. Temperature Profile in Rubber Injection Molding: Application of a Recently Developed Testing Method to Improve the Process Simulation and Calculation of Curing Kinetics. Polymers. 2021; 13(3):380. https://doi.org/10.3390/polym13030380
Chicago/Turabian StyleTraintinger, Martin, Roman Christopher Kerschbaumer, Bernhard Lechner, Walter Friesenbichler, and Thomas Lucyshyn. 2021. "Temperature Profile in Rubber Injection Molding: Application of a Recently Developed Testing Method to Improve the Process Simulation and Calculation of Curing Kinetics" Polymers 13, no. 3: 380. https://doi.org/10.3390/polym13030380
APA StyleTraintinger, M., Kerschbaumer, R. C., Lechner, B., Friesenbichler, W., & Lucyshyn, T. (2021). Temperature Profile in Rubber Injection Molding: Application of a Recently Developed Testing Method to Improve the Process Simulation and Calculation of Curing Kinetics. Polymers, 13(3), 380. https://doi.org/10.3390/polym13030380







