Different Effects of Albumin and Hydroxyethyl Starch on Low Molecular-Weight Solute Permeation through Sodium Hyaluronic Acid Solution
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
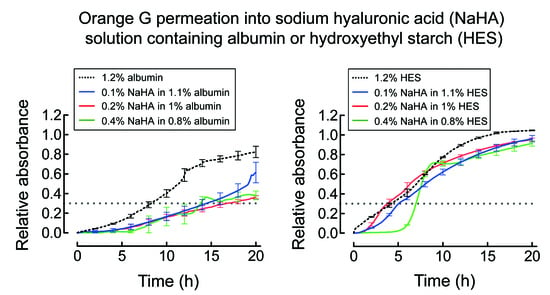
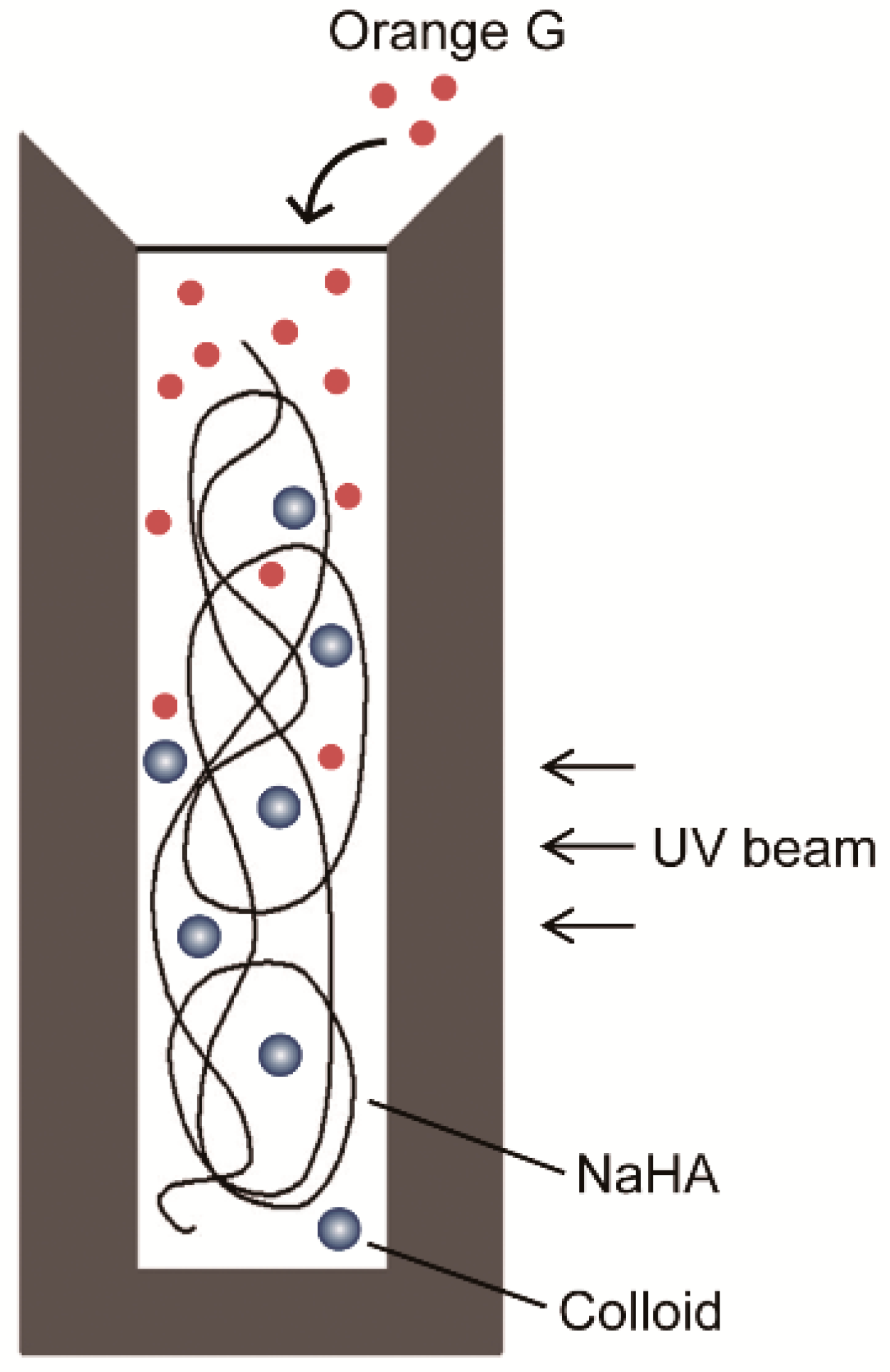
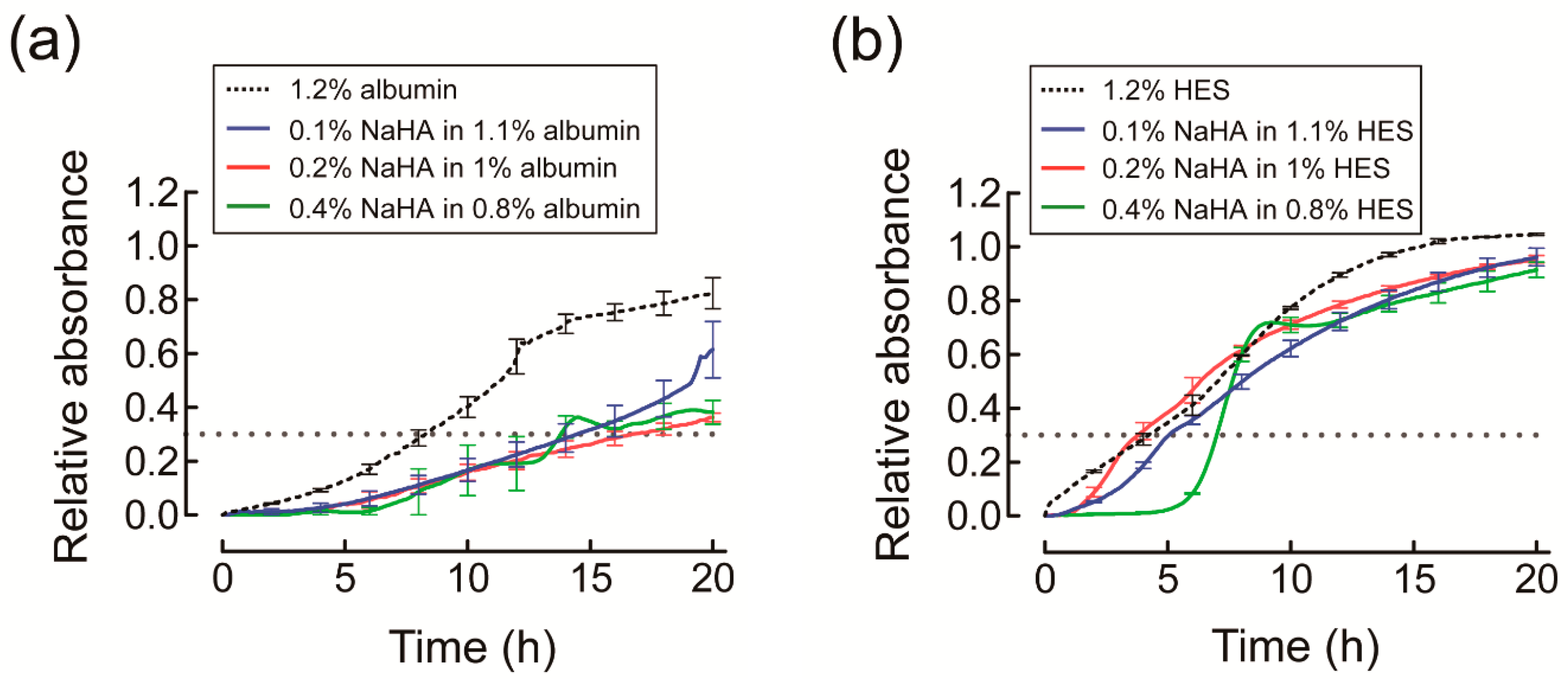
2.2. Permeation of Orange G into NaHA Solutions
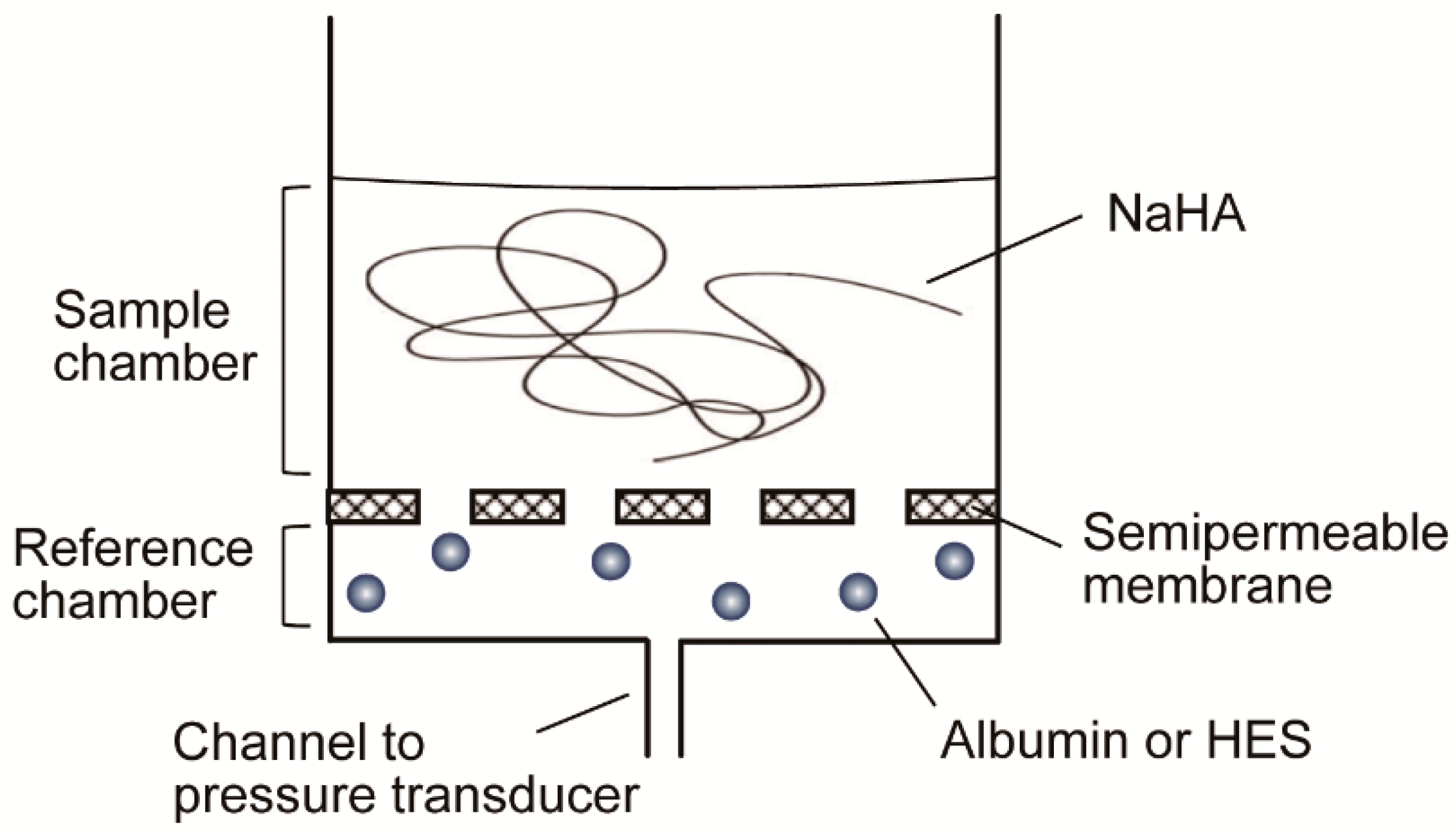
2.3. Effects of Albumin and HES on Osmotic Swelling Pressure of NaHA Solution
2.4. Effects of Albumin and HES on Darcy’s Permeability Coefficient of NaHA Solution
2.5. Effects of Albumin and HES on Dynamic Shear Moduli of NaHA Solution
2.6. Statistical Analysis
3. Results
3.1. Permeation of Orange G into NaHA Solution
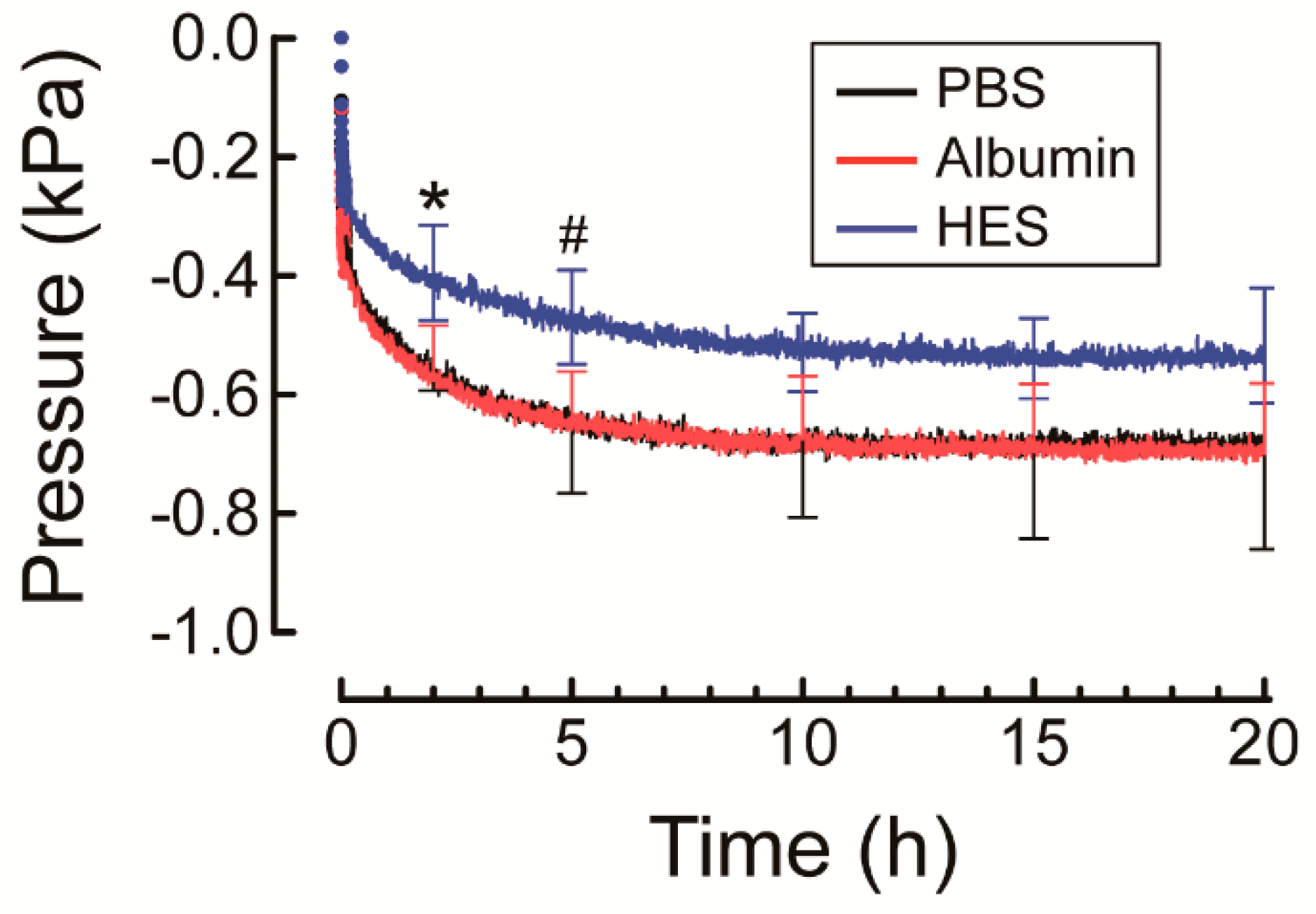
3.2. Effects of Albumin and HES on Osmotic Swelling Pressure of NaHA Solution
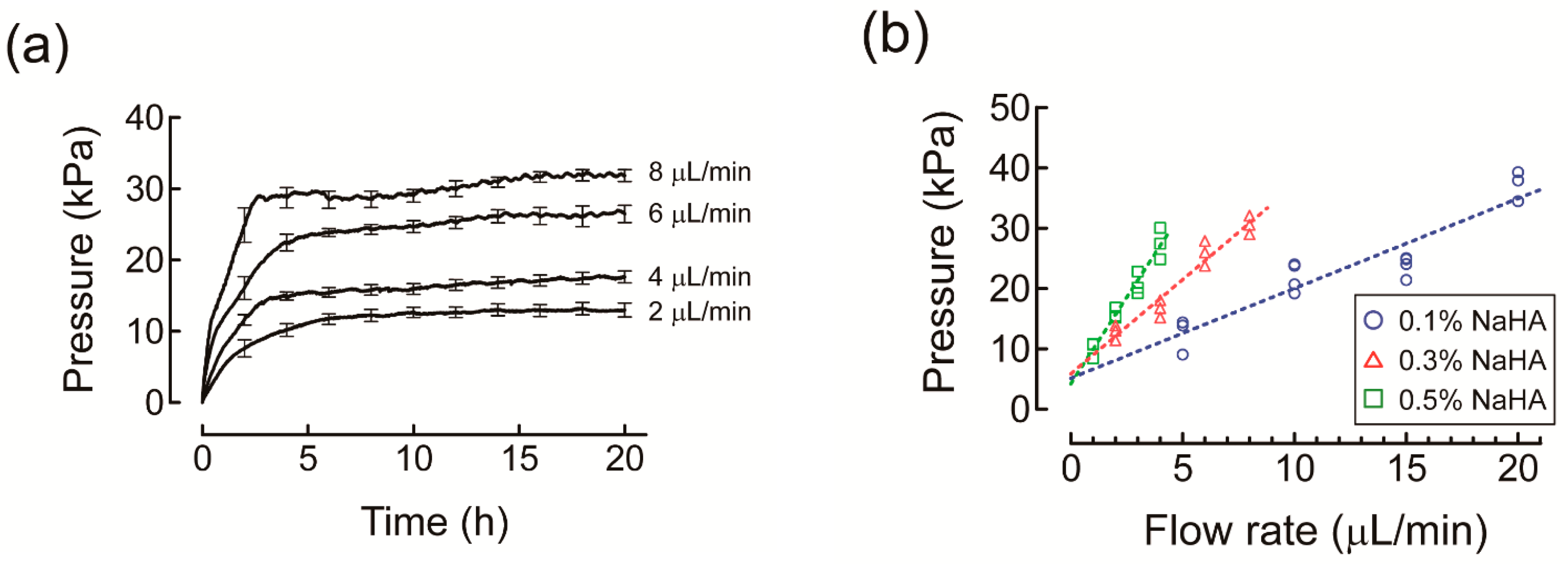
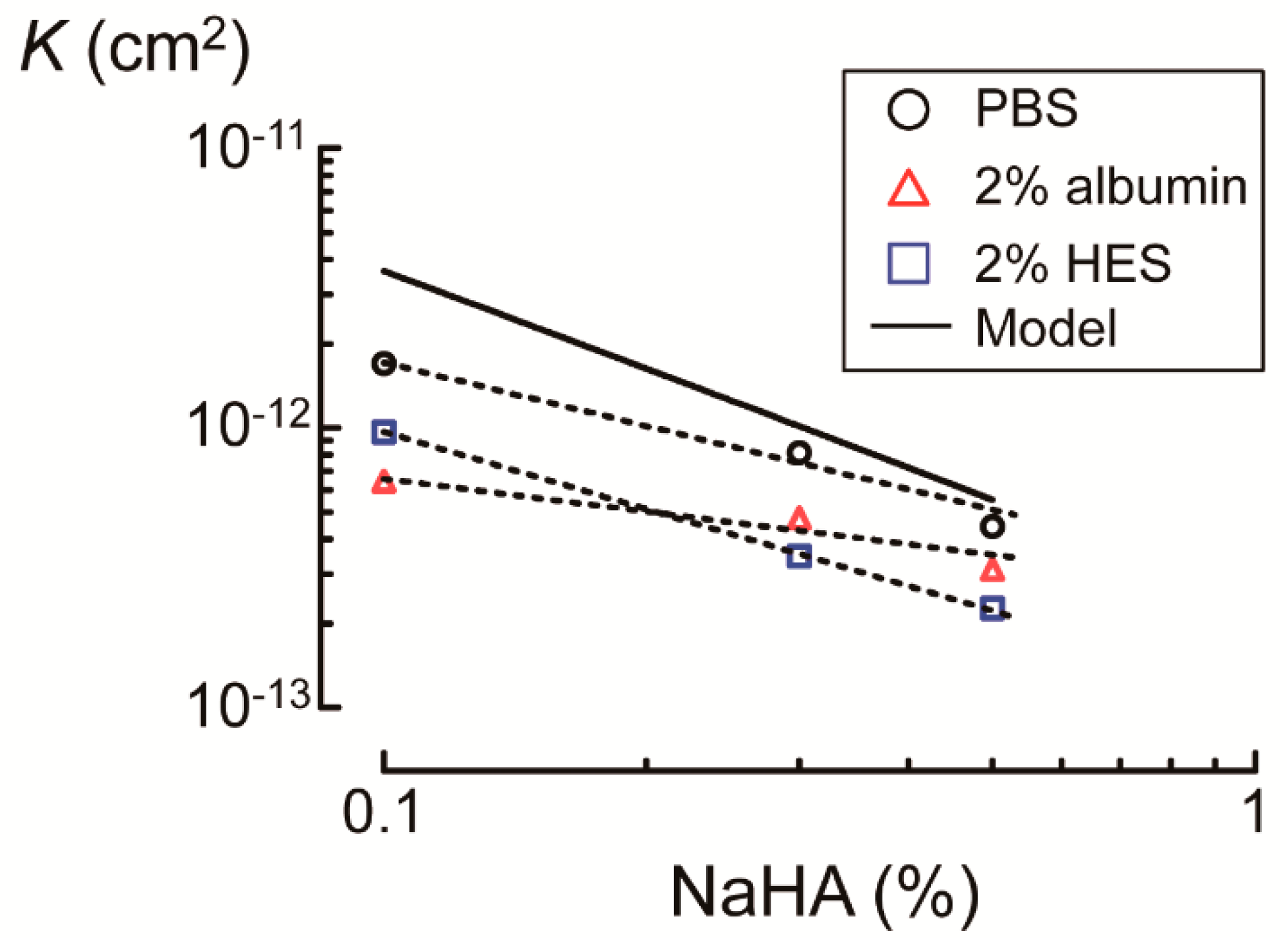
3.3. Effects of Albumin and HES on Darcy’s Permeability Coefficient of NaHA Solution
3.4. Effects of Albumin and HES on Dynamic Shear Moduli of NaHA Solution
4. Discussion
4.1. Permeation of Orange G into NaHA Solution
4.2. Effects of Albumin and HES on Osmotic Swelling Pressure and Darcy’s Permeability Coefficient of NaHA Solution
4.3. Effects of Albumin and HES on Dynamic Shear Moduli of NaHA Solution
4.4. Implications
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Comper, W.D.; Laurent, T.C. Physiological function of connective tissue polysaccharides. Physiol. Rev. 1978, 58, 255–315. [Google Scholar] [CrossRef]
- Levick, J.R. Flow through interstitium and other fibrous matrices. Q. J. Exp. Physiol. 1987, 72, 409–437. [Google Scholar] [CrossRef]
- Cowman, M.K.; Matsuoka, S. Experimental approaches to hyaluronan structure. Carbohydr. Res. 2005, 340, 791–809. [Google Scholar] [CrossRef]
- Fallacara, A.; Baldini, E.; Manfredini, S.; Vertuani, S. Hyaluronic acid in the third millennium. Polymers 2018, 10, 701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fouissac, E.; Milas, M.; Rinaudo, M. Shear-rate, concentration, molecular weight, and temperature viscosity dependences of hyaluronate, a wormlike polyelectrolyte. Macromolecules 1993, 26, 6945–6951. [Google Scholar] [CrossRef]
- Laurent, T.C. In Vitro studies on the transport of macromolecules through the connective tissue. Fed. Proc. 1966, 25, 1128–1134. [Google Scholar] [PubMed]
- Laurent, T.C. Structure of the extracellular matrix and the biology of hyaluronan. In Interstitium, Connective Tissue and Lymphatics; Reed, R.K., McHale, N.G., Bert, J.L., Winlove, C.P., Laine, G.A., Eds.; Portland Press: London, UK, 1995; pp. 1–12. [Google Scholar]
- Chen, W.Y.; Abatangelo, G. Functions of hyaluronan in wound repair. Wound Repair Regen. 1999, 7, 79–89. [Google Scholar] [CrossRef] [PubMed]
- Jain, R.K. Transport of molecules in the tumor interstitium: A review. Cancer Res. 1987, 47, 3039–3051. [Google Scholar]
- Westphal, M.; James, M.F.M.; Kozek-Langenecker, S.; Stocker, R.; Guidet, B.; Van Aken, H. Hydroxyethyl starches: Different products—Different effects. Anesthesiology 2009, 111, 187–202. [Google Scholar] [CrossRef] [Green Version]
- Woodcock, T.E.; Woodcock, T.M. Revised Starling equation and the glycocalyx model of transvascular fluid exchange: An improved paradigm for prescribing intravenous fluid therapy. Br. J. Anaesth. 2012, 108, 384–394. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Yamanaka, J.; Sato, S.; Miyama, I.; Yonese, M. Characteristics of complexes composed of sodium hyaluronate and bovine serum albumin. Chem. Pharm. Bull. 2000, 48, 779–783. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grymonpré, K.R.; Staggemeier, B.A.; Dubin, P.L.; Mattison, K.W. Identification by integrated computer modeling and light scattering studies of an electrostatic serum albumin-hyaluronic acid binding site. Biomacromolecules 2001, 2, 422–429. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tatara, T. Contrasting effects of albumin and hydroxyethyl starch solutions on physical properties of sodium hyaluronate solution. Carbohydr. Polym. 2018, 201, 60–64. [Google Scholar] [CrossRef] [PubMed]
- Doi, M. Soft Matter Physics; Oxford University Press: New York, NY, USA, 2018. [Google Scholar]
- Tatara, T. The contribution of solute-solvent exchange at the membrane surface to the reduction by albumin of the hydraulic permeability coefficient of an artificial semipermeable membrane. Anesth. Analg. 2003, 97, 1137–1142. [Google Scholar] [CrossRef]
- Tatara, T.; Tashiro, C. Analysis using a linear viscoelastic model of the In Vitro osmotic kinetics of polydisperse synthetic colloids. Biomacromolecules 2005, 6, 1732–1738. [Google Scholar] [CrossRef]
- Ogston, A.G. The spaces in a uniform random suspension of fibres. Trans. Faraday Soc. 1958, 54, 1754–1757. [Google Scholar] [CrossRef]
- White, J.A.; Deen, W.M. Agarose-dextran gels as synthetic analogs of glomerular basement membrane: Water permeability. Biophys. J. 2002, 82, 2081–2089. [Google Scholar] [CrossRef] [Green Version]
- Armstrong, J.K.; Wenby, R.B.; Meiselman, H.J.; Fisher, T.C. The hydrodynamic radii of macromolecules and their effect on red blood cell aggregation. Biophys. J. 2004, 87, 4259–4270. [Google Scholar] [CrossRef] [Green Version]
- Sakai, H.; Sato, A.; Takeoka, S.; Tsuchida, E. Mechanism of flocculate formation of highly concentrated phospholipid vesicles suspended in a series of water-soluble biopolymers. Biomacromolecules 2009, 10, 2344–2350. [Google Scholar] [CrossRef]
- Masaro, L.; Zhu, X.X. Physical models of diffusion for polymer solutions, gels, and solids. Prog. Polym. Sci. 1999, 24, 731–775. [Google Scholar] [CrossRef]
- Laurent, T.C.; Ogston, A.G. The interaction between polysaccharides and other macromolecules. 4. The osmotic pressure of mixtures of serum albumin and hyaluronic acid. Biochem. J. 1963, 89, 249–253. [Google Scholar] [CrossRef] [Green Version]
- Jackson, G.W.; James, D.F. The hydrodynamic resistance of hyaluronic acid and its contribution to tissue permeability. Biorheology 1982, 19, 317–330. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Okamoto, A.; Nishinari, K. Viscoelasticity of hyaluronic acid with different molecular weights. Biorheology 1994, 31, 235–244. [Google Scholar] [CrossRef]
- Gribbon, P.; Heng, B.C.; Hardingham, T.E. The molecular basis of the solution properties of hyaluronan investigated by confocal fluorescence recovery after photobleaching. Biophys. J. 1999, 77, 2210–2216. [Google Scholar] [CrossRef] [Green Version]
- Nijenhuis, N.; Mizuno, D.; Spaan, J.A.E.; Schmidt, C.F. Viscoelastic response of a model endothelial glycocalyx. Phys. Biol. 2009, 6, 025014. [Google Scholar] [CrossRef] [PubMed]
- Altman, S. Antibiotics present and future. FEBS Lett. 2014, 588, 1–2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bartzatt, R. Anti-inflammatory drugs and prediction of new structures by comparative analysis. Antiinflamm. Antiallergy Agents Med. Chem. 2012, 11, 151–160. [Google Scholar] [CrossRef] [PubMed]
- Swabb, E.A.; Wei, J.; Gullino, P.M. Diffusion and convection in normal and neoplastic tissues. Cancer Res. 1974, 34, 2814–2822. [Google Scholar]


| Test Solution | Colloid | p Value 2 | |
|---|---|---|---|
| Albumin | HES | ||
| 0.1% NaHA in 1.1% colloid | 3.33 ± 0.69 | 1.16 ± 0.08 | 0.006 |
| 0.2% NaHA in 1% colloid | 1.95 ± 0.32 | 0.92 ± 0.27 | 0.013 |
| 0.4% NaHA in 0.8% colloid | 3.19 ± 1.33 | 1.58 ± 0.03 | 0.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tatara, T. Different Effects of Albumin and Hydroxyethyl Starch on Low Molecular-Weight Solute Permeation through Sodium Hyaluronic Acid Solution. Polymers 2021, 13, 514. https://doi.org/10.3390/polym13040514
Tatara T. Different Effects of Albumin and Hydroxyethyl Starch on Low Molecular-Weight Solute Permeation through Sodium Hyaluronic Acid Solution. Polymers. 2021; 13(4):514. https://doi.org/10.3390/polym13040514
Chicago/Turabian StyleTatara, Tsuneo. 2021. "Different Effects of Albumin and Hydroxyethyl Starch on Low Molecular-Weight Solute Permeation through Sodium Hyaluronic Acid Solution" Polymers 13, no. 4: 514. https://doi.org/10.3390/polym13040514
APA StyleTatara, T. (2021). Different Effects of Albumin and Hydroxyethyl Starch on Low Molecular-Weight Solute Permeation through Sodium Hyaluronic Acid Solution. Polymers, 13(4), 514. https://doi.org/10.3390/polym13040514