Modelling Stretch Blow Moulding of Poly (l-lactic acid) for the Manufacture of Bioresorbable Vascular Scaffold
Abstract
:1. Introduction
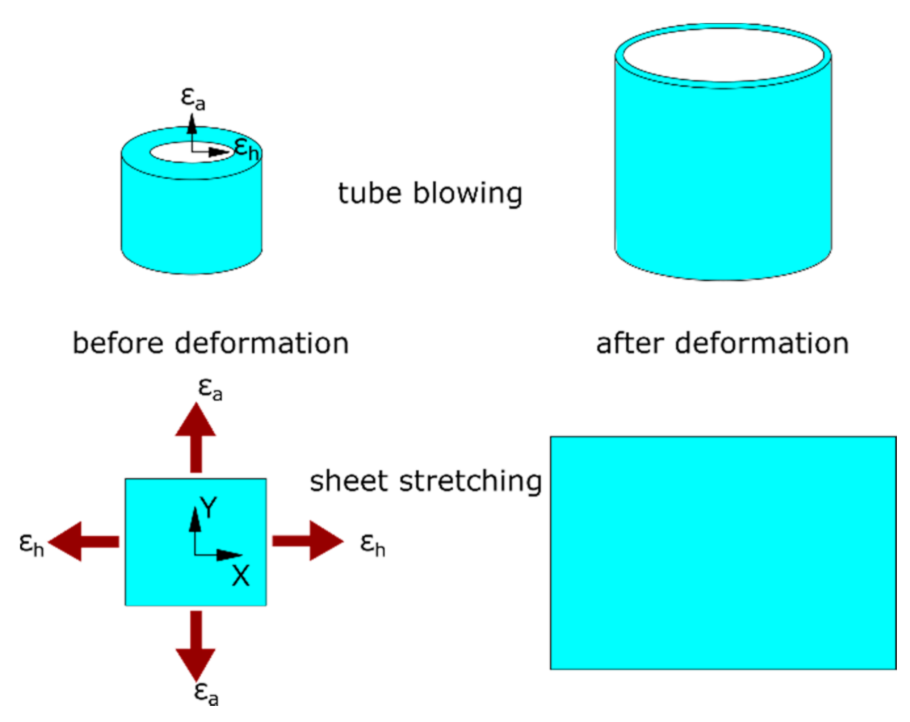
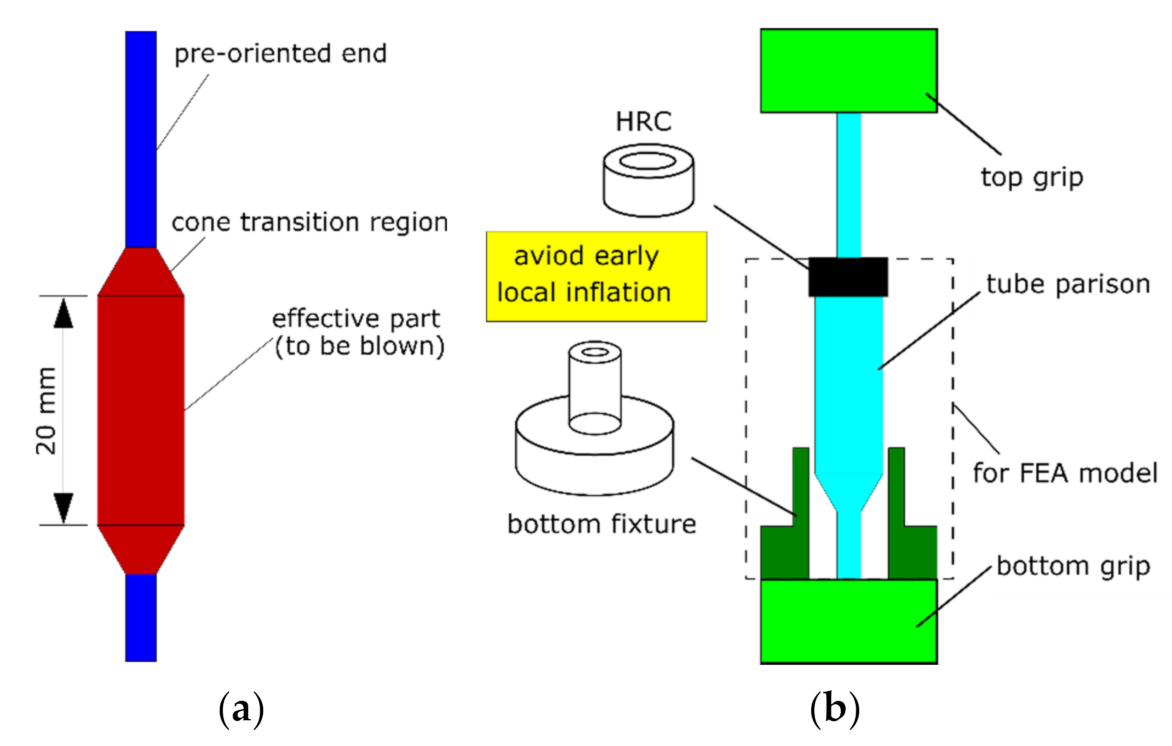
2. Materials and Methods
2.1. Material and Test
2.2. Consitutive Model and Finite Elment Analysis
3. Results
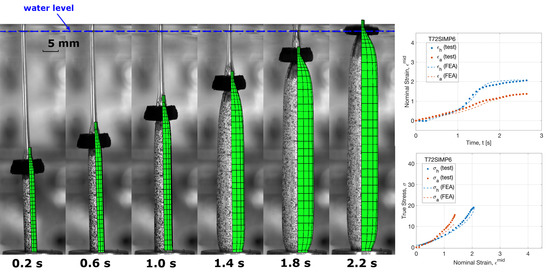
3.1. Strain History of the Replicative Biaxial Test
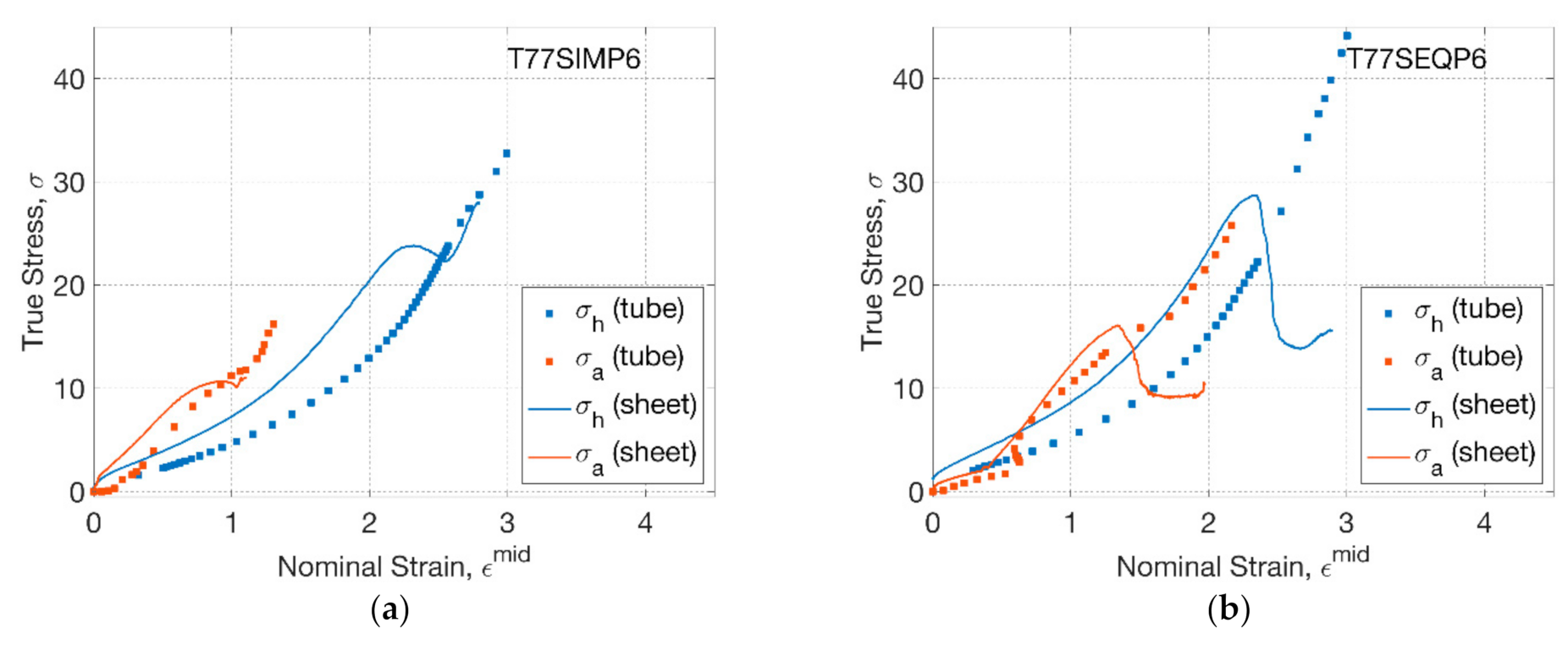
3.2. Stress–Strain Relationship of Tubes and Sheets
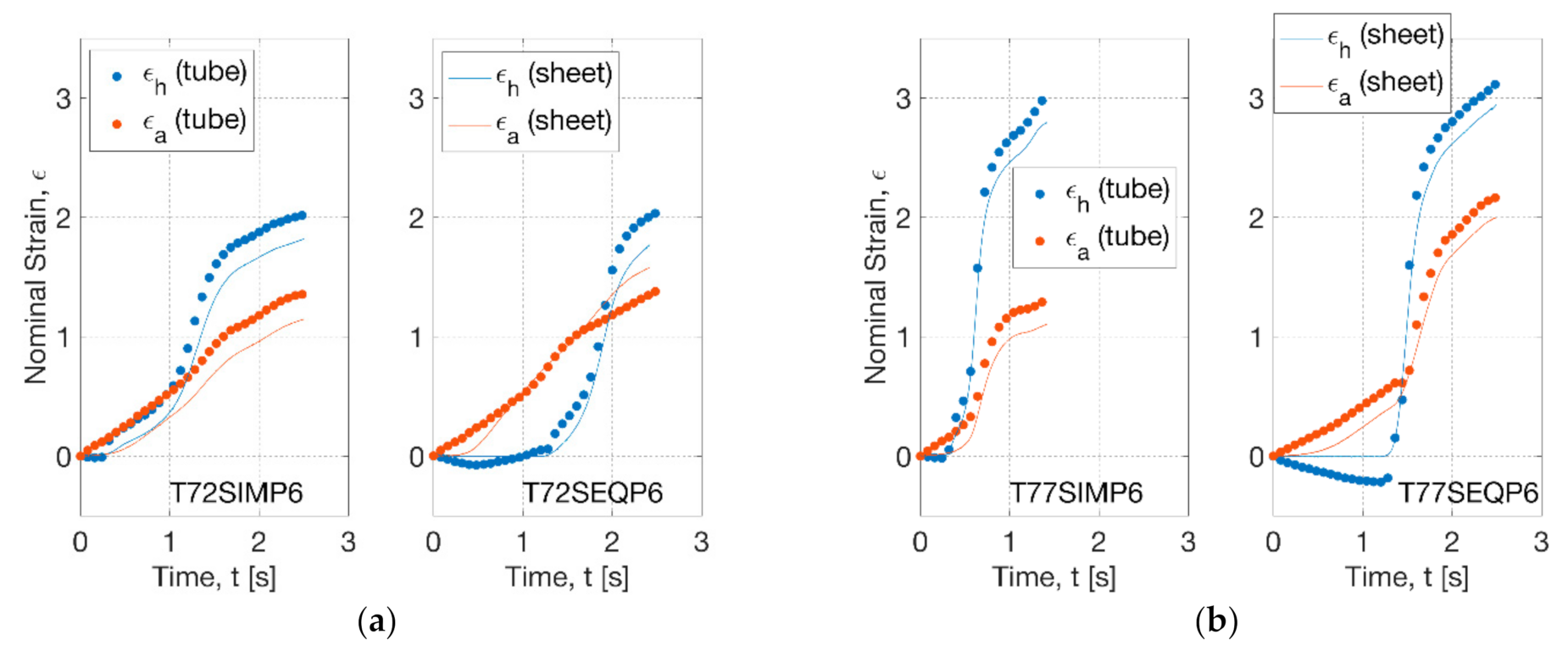
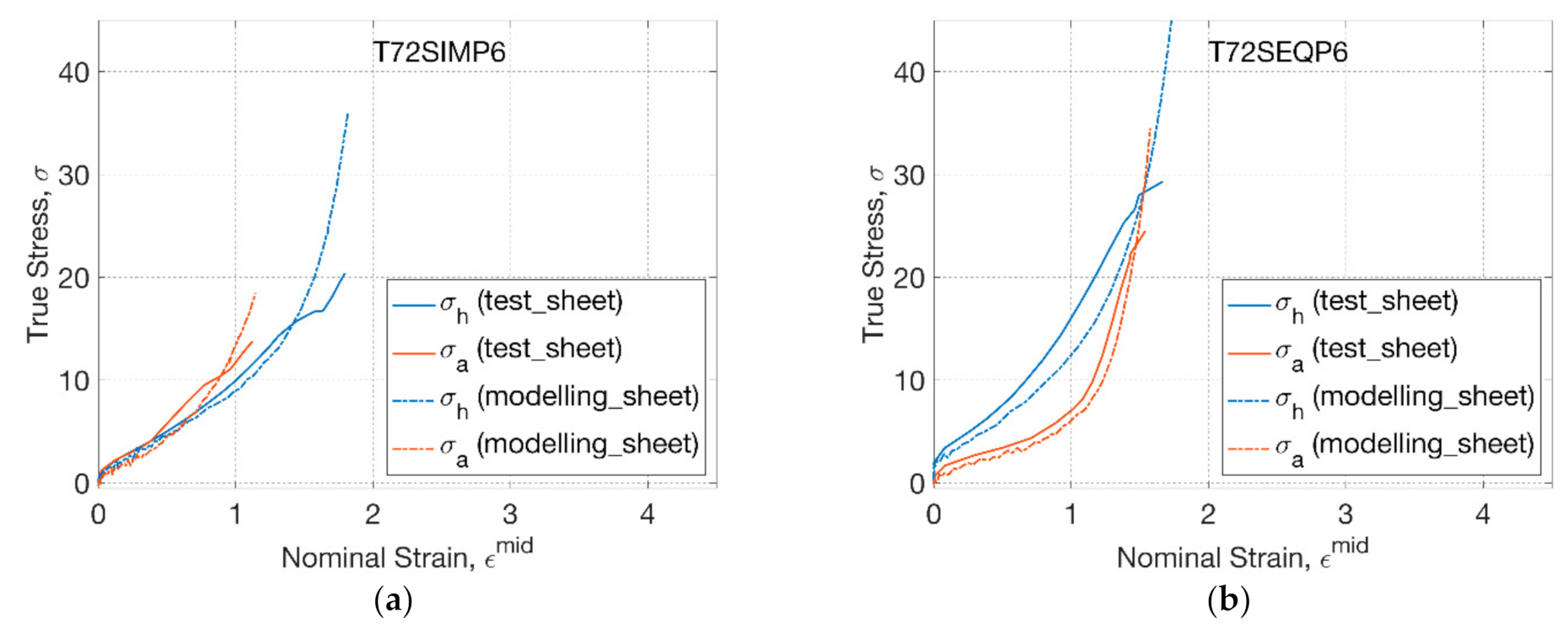
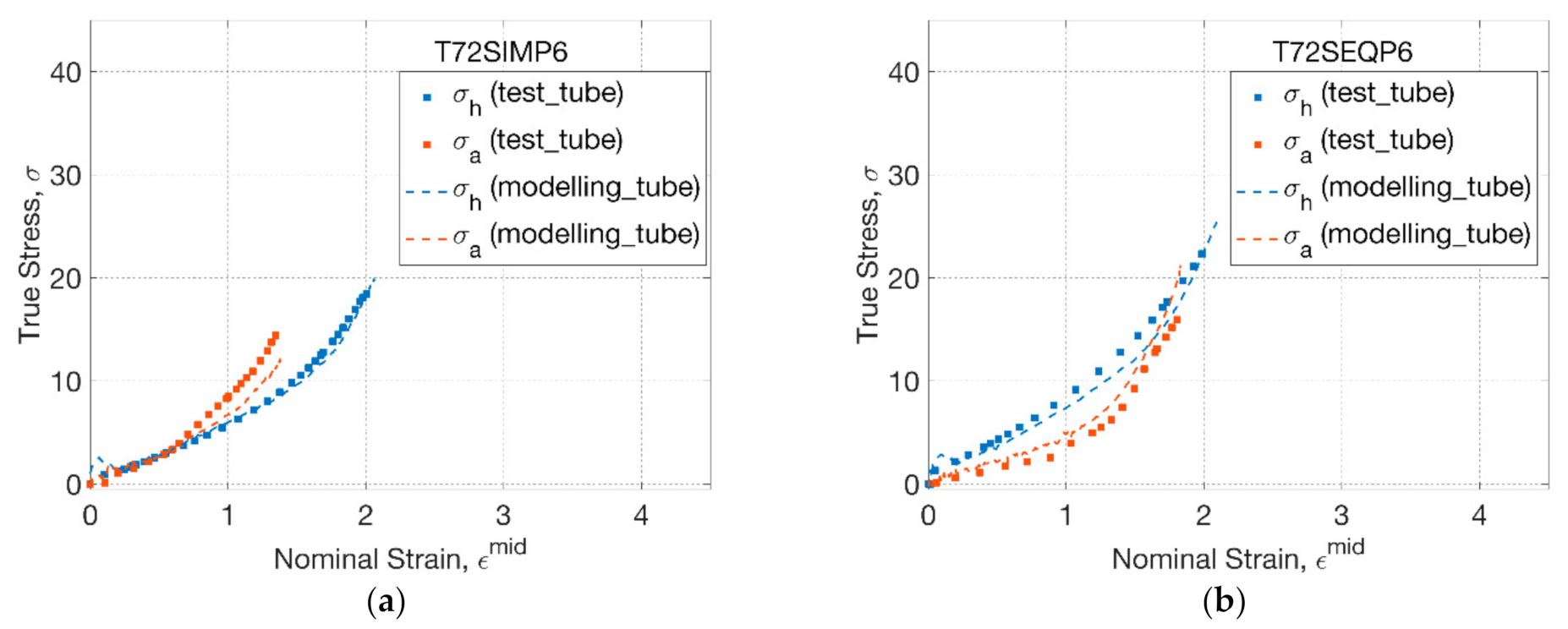
3.3. Modelling Replicative Biaxial Stretch
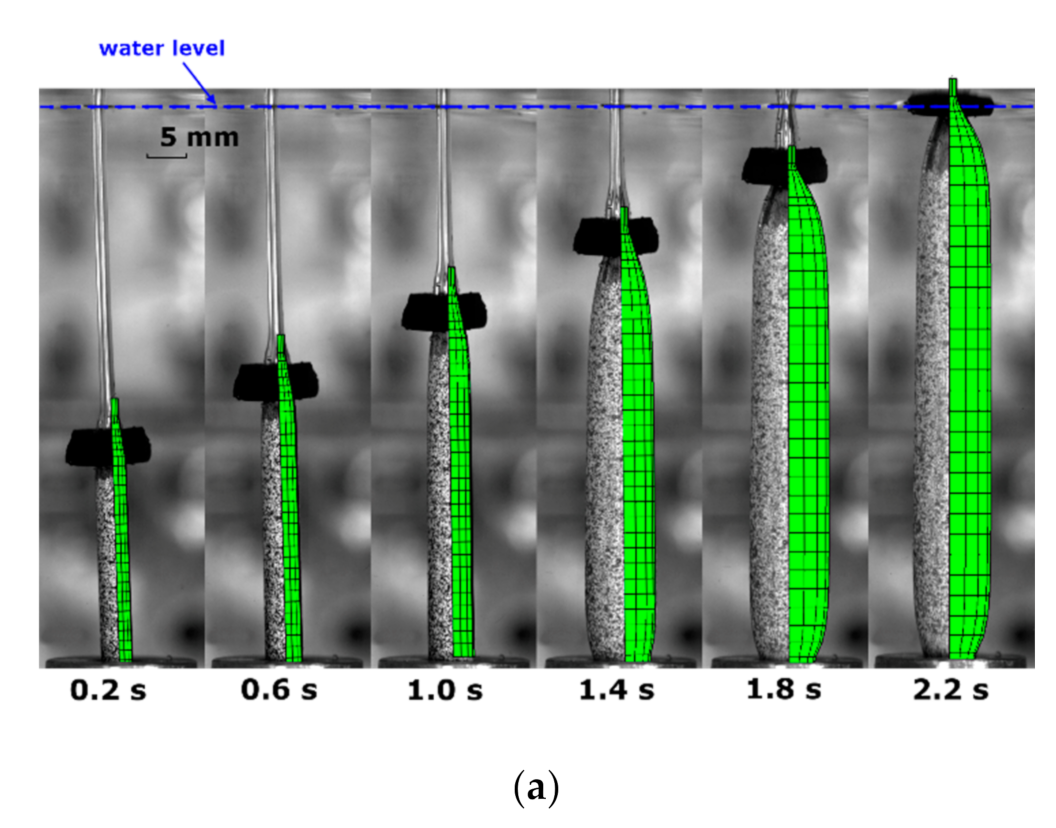
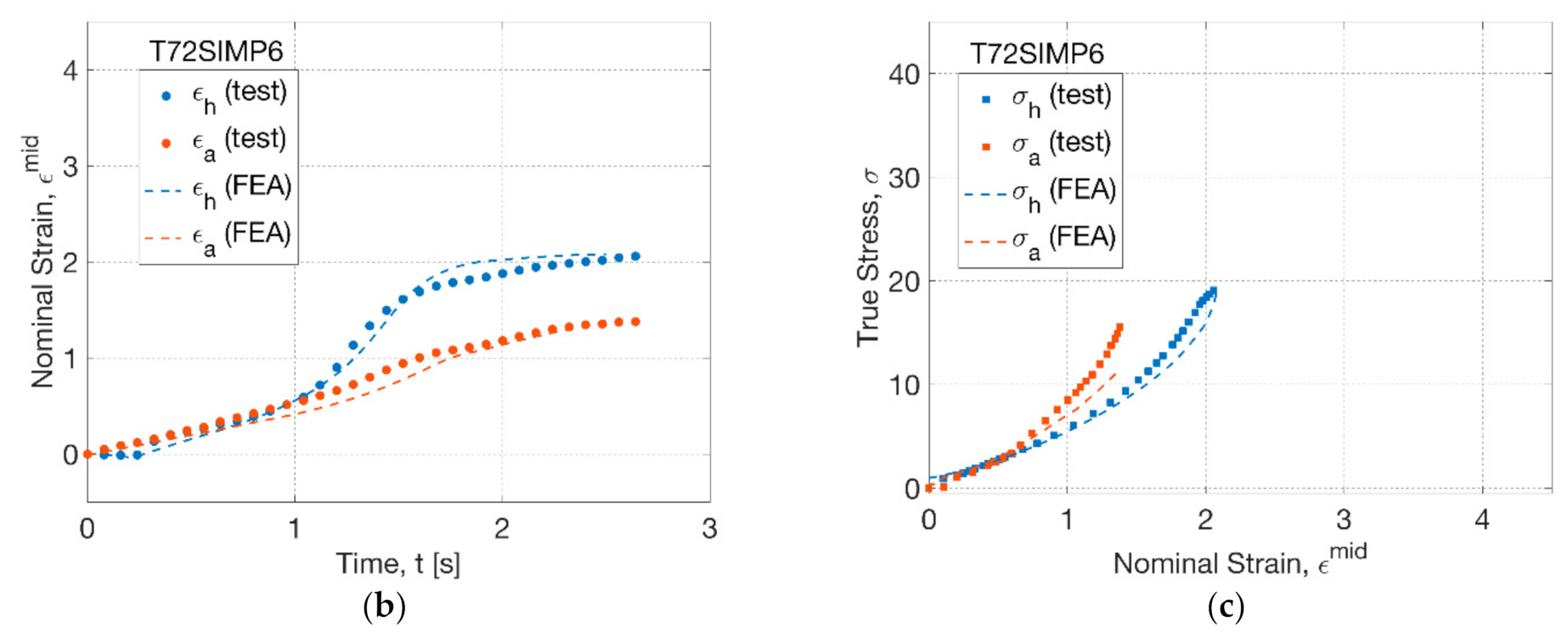
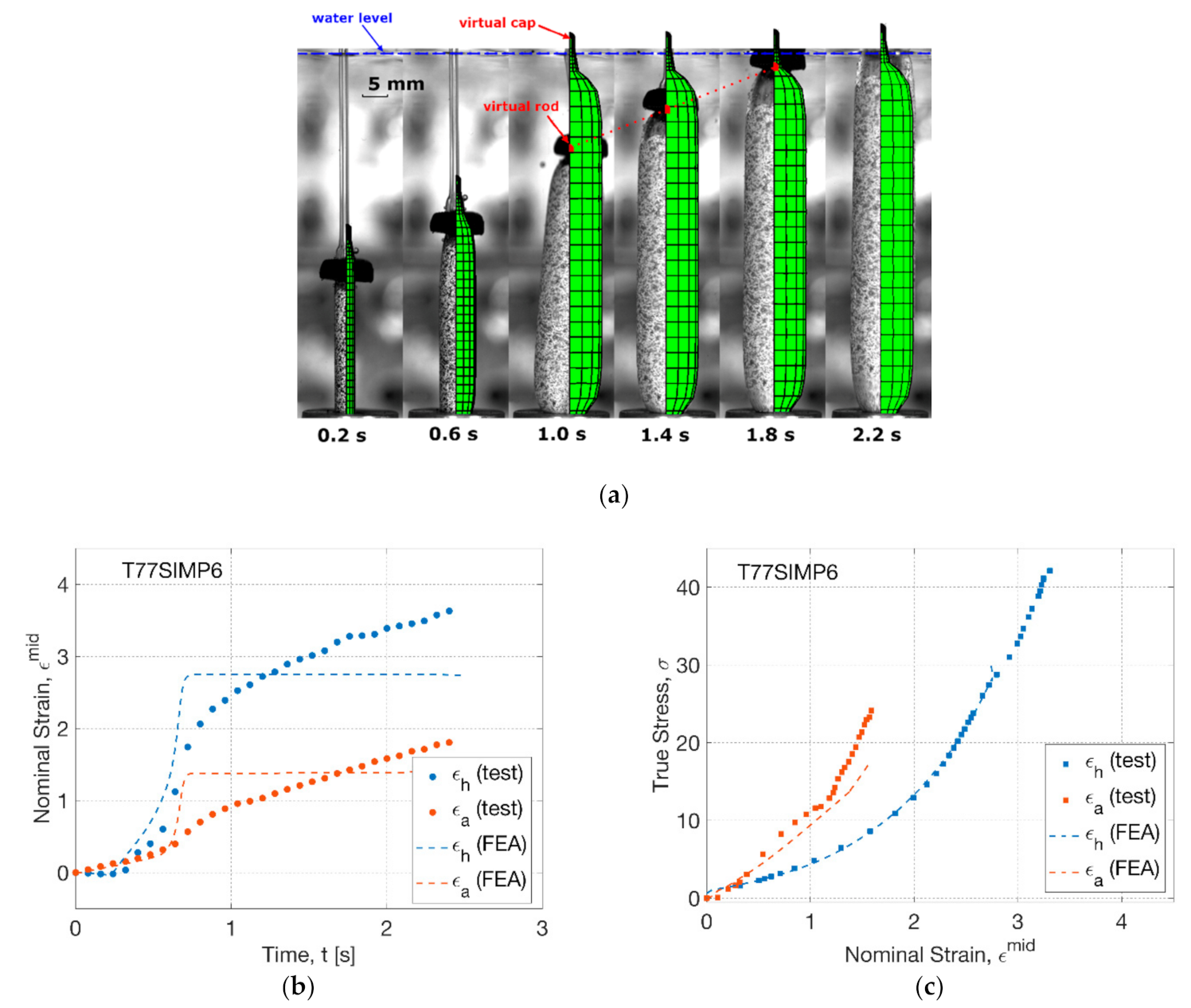
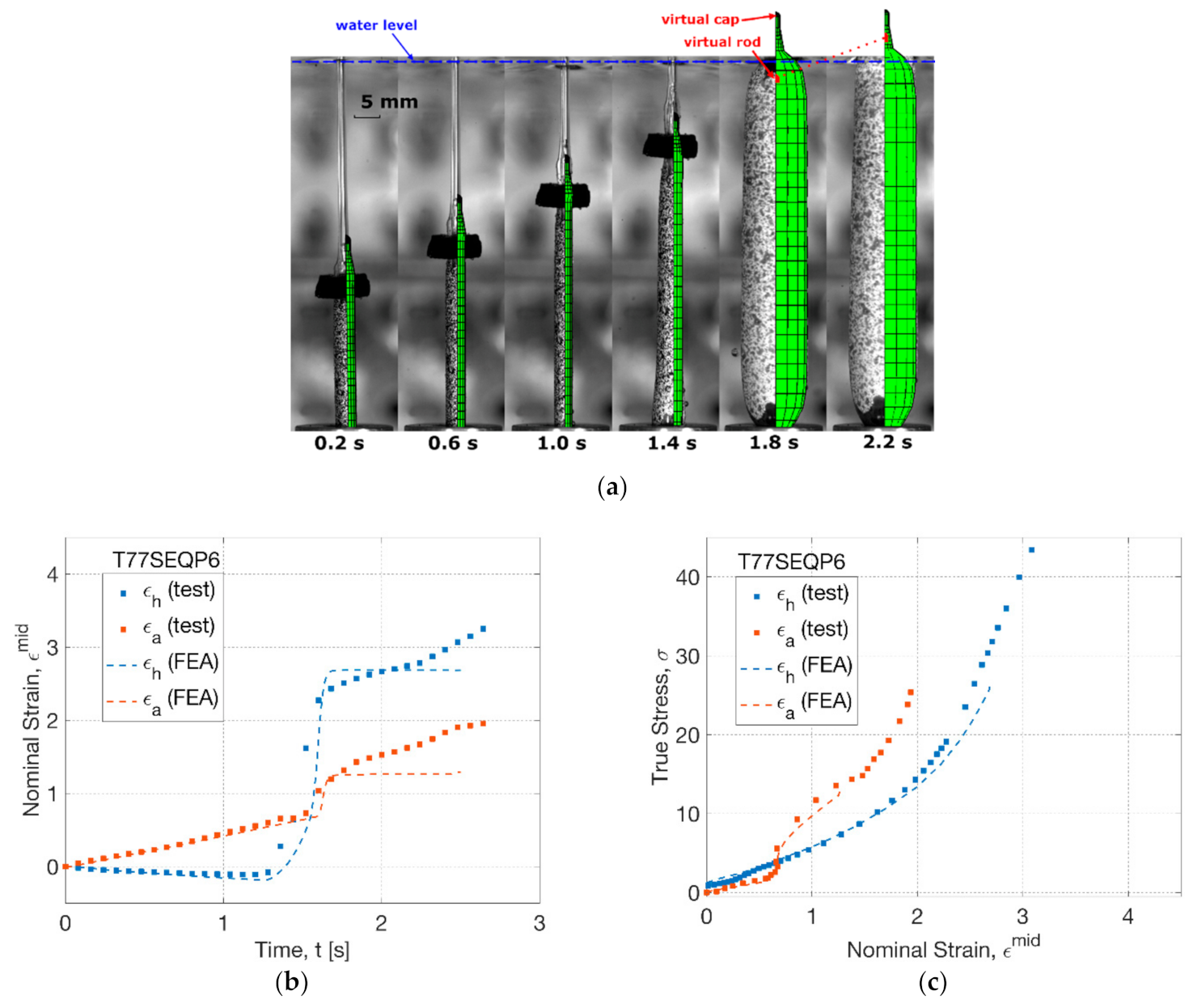
3.4. Process Simulation of Free Stretch Blow
3.4.1. Modelling the Influence of Temperature
3.4.2. Modelling the Influence of Sequence
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chaabane, C.; Otsuka, F.; Virmani, R.; Bochaton-Piallat, M.L. Biological responses in stented arteries. Cardiovasc. Res. 2013, 99, 353–363. [Google Scholar] [CrossRef]
- Tesfamariam, B. Bioresorbable vascular scaffolds: Biodegradation, drug delivery and vascular remodeling. Pharmacol. Res. 2016, 107, 163–171. [Google Scholar] [CrossRef]
- Serruys, P.W.; Katagiri, Y.; Sotomi, Y.; Zeng, Y.; Chevalier, B.; van der Schaaf, R.J.; Baumbach, A.; Smits, P.; van Mieghem, N.M.; Bartorelli, A.; et al. Arterial Remodeling After Bioresorbable Scaffolds and Metallic Stents. J. Am. Coll. Cardiol. 2017, 70, 60–74. [Google Scholar] [CrossRef]
- Onuma, Y.; Serruys, P.W. Bioresorbable scaffold: The advent of a new era in percutaneous coronary and peripheral revascularization? Circulation 2011, 123, 779–797. [Google Scholar] [CrossRef] [Green Version]
- Ang, H.Y.; Bulluck, H.; Wong, P.; Venkatraman, S.S.; Huang, Y.; Foin, N. Backup: Bioresorbable stents: Current and upcoming bioresorbable technologies. Int. J. Cardiol. 2017, 228, 931–939. [Google Scholar] [CrossRef]
- Sakamoto, A.; Jinnouchi, H.; Torii, S.; Virmani, R.; Finn, A. Understanding the Impact of Stent and Scaffold Material and Strut Design on Coronary Artery Thrombosis from the Basic and Clinical Points of View. Bioengineering 2018, 5, 71. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Foin, N.; Lee, R.D.; Torii, R.; Guitierrez-Chico, J.L.; Mattesini, A.; Nijjer, S.; Sen, S.; Petraco, R.; Davies, J.E.; Di Mario, C.; et al. Impact of stent strut design in metallic stents and biodegradable scaffolds. Int. J. Cardiol. 2014, 177, 800–808. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, J.; Onuma, Y.; Ormiston, J.; Abizaid, A.; Waksman, R.; Serruys, P. Bioresorbable scaffolds: Rationale, current status, challenges, and future. Eur. Heart J. 2014, 35, 765–776. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dillon, B.; Doran, P.; Fuenmayor, E.; Healy, A.V.; Gately, N.M.; Major, I.; Lyons, J.G. The influence of low shear microbore extrusion on the properties of high molecular weight poly(l-lactic acid) for medical tubing applications. Polymers 2019, 11, 710. [Google Scholar] [CrossRef] [Green Version]
- Guerra, A.J.; San, J.; Ciurana, J. Fabrication of PCL/PLA Composite Tube for Stent Manufacturing. Procedia CIRP 2017, 65, 231–235. [Google Scholar] [CrossRef]
- Alexy, R.D.; Levi, D.S. Materials and manufacturing technologies available for production of a pediatric bioabsorbable stent. BioMed Res. Int. 2013, 2013. [Google Scholar] [CrossRef] [Green Version]
- Dillon, B.; Doran, P.; Fuenmayor, E.; Healy, A.V.; Gately, N.M.; Major, I.; Lyons, J.G. Influence of Annealing and Biaxial Expansion on the Properties of Poly(l-Lactic Acid) Medical Tubing. Polymers 2019, 11, 1172. [Google Scholar] [CrossRef] [Green Version]
- Løvdal, A.; Andreasen, J.W.; Mikkelsen, L.P.; Agersted, K.; Almdal, K. Characterization of biaxial strain of poly(l-lactide) tubes. Polym. Int. 2016, 65, 133–141. [Google Scholar] [CrossRef] [Green Version]
- Jariyasakoolroj, P.; Tashiro, K.; Wang, H.; Yamamoto, H.; Chinsirikul, W.; Kerddonfag, N.; Chirachanchai, S. Isotropically small crystalline lamellae induced by high biaxial-stretching rate as a key microstructure for super-tough polylactide film. Polymer 2015, 68, 234–245. [Google Scholar] [CrossRef]
- Wu, J.H.; Yen, M.S.; Wu, C.P.; Li, C.H.; Kuo, M.C. Effect of Biaxial Stretching on Thermal Properties, Shrinkage and Mechanical Properties of Poly (Lactic Acid) Films. J. Polym. Environ. 2013, 21, 303–311. [Google Scholar] [CrossRef]
- Løvdal, A.L.V.; Andreasen, J.W.; Mikkelsen, L.P.; Agersted, K.; Almdal, K. Mechanical properties of biaxially strained poly(l-lactide) tubes: Strain rate and temperature dependence. J. Appl. Polym. Sci. 2017, 134, 6–11. [Google Scholar] [CrossRef] [Green Version]
- Ailianou, A.; Ramachandran, K.; Kossuth, M.B.; Oberhauser, J.P.; Kornfield, J.A. Multiplicity of morphologies in poly (l-lactide) bioresorbable vascular scaffolds. Proc. Natl. Acad. Sci. USA 2016, 113, 11670–11675. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stoclet, G.; Seguela, R.; Lefebvre, J.M.; Elkoun, S.; Vanmansart, C. Strain-induced molecular ordering in polylactide upon uniaxial stretching. Macromolecules 2010, 43, 1488–1498. [Google Scholar] [CrossRef]
- Razavi, M.; Wang, S.Q. Why Is Crystalline Poly(lactic acid) Brittle at Room Temperature? Macromolecules 2019, 52, 5429–5441. [Google Scholar] [CrossRef]
- Zhang, X.; Schneider, K.; Liu, G.; Chen, J.; Brüning, K.; Wang, D.; Stamm, M. Structure variation of tensile-deformed amorphous poly(l-lactic acid): Effects of deformation rate and strain. Polymer 2011, 52, 4141–4149. [Google Scholar] [CrossRef]
- Mahendrasingam, A.; Blundell, D.J.; Parton, M.; Wright, A.K.; Rasburn, J.; Narayanan, T.; Fuller, W. Time resolved study of oriented crystallisation of poly(lactic acid) during rapid tensile deformation. Polymer 2005, 46, 6009–6015. [Google Scholar] [CrossRef]
- Iwasaki, H.; Nakamura, M.; Komatsubara, N.; Okano, M.; Nakasako, M.; Sato, H.; Watanabe, S. Controlled Terahertz Birefringence in Stretched Poly(lactic acid) Films Investigated by Terahertz Time-Domain Spectroscopy and Wide-Angle X-ray Scattering. J. Phys. Chem. B 2017, 121, 6951–6957. [Google Scholar] [CrossRef] [PubMed]
- Ou, X.; Cakmak, M. Influence of biaxial stretching mode on the crystalline texture in polylactic acid films. Polymer 2008, 49, 5344–5352. [Google Scholar] [CrossRef]
- Ouchiar, S.; Stoclet, G.; Cabaret, C.; Addad, A.; Gloaguen, V. Effect of biaxial stretching on thermomechanical properties of polylactide based nanocomposites. Polymer 2016, 99, 358–367. [Google Scholar] [CrossRef]
- Delpouve, N.; Delbreilh, L.; Stoclet, G.; Saiter, A.; Dargent, E. Structural dependence of the molecular mobility in the amorphous fractions of polylactide. Macromolecules 2014, 47, 5186–5197. [Google Scholar] [CrossRef] [Green Version]
- Wei, H.; Menary, G.; Buchanan, F.; Yan, S.; Nixon, J. Experimental characterisation on the behaviour of PLLA for stretch blowing moulding of bioresorbable vascular scaffolds. Int. J. Mater. Form. 2020. [Google Scholar] [CrossRef] [Green Version]
- Wei, H.; Yan, S.; Goel, S.; Menary, G. Characterization and modelling the mechanical behaviour of poly (l-lactic acid) for the manufacture of bioresorbable vascular scaffolds by stretch blow moulding. Int. J. Mater. Form. 2020, 13, 43–57. [Google Scholar] [CrossRef] [Green Version]
- Ramachandran, K.; Miscioscia, R.; De Filippo, G.; Pandolfi, G.; Di Luccio, T.; Kornfield, J.A. Tube expansion deformation enables in situ synchrotron X-ray scattering measurements during extensional flow-induced crystallization of Poly L-lactide near the glass transition. Polymers 2018, 10, 288. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cosson, B.; Chevalier, L.; Régnier, G. Simulation of the stretch blow moulding process: From the modelling of the microstructure evolution to the end-use elastic properties of polyethylene terephthalate bottles. Int. J. Mater. Form. 2012, 5, 39–53. [Google Scholar] [CrossRef] [Green Version]
- Nixon, J.; Menary, G.H.; Yan, S. Finite element simulations of stretch-blow moulding with experimental validation over a broad process window. Int. J. Mater. Form. 2017, 10, 793–809. [Google Scholar] [CrossRef] [Green Version]
- Salomeia, Y.; Menary, G.H.; Armstrong, C.G.; Nixon, J.; Yan, S. Measuring and modelling air mass flow rate in the injection stretch blow moulding process. Int. J. Mater. Form. 2016, 9, 531–545. [Google Scholar] [CrossRef] [Green Version]
- Zimmer, J.; Stommel, M. Method for the evaluation of stretch blow molding simulations with free blow trials. IOP Conf. Ser. Mater. Sci. Eng. 2013, 48. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.J.; Harkin-Jones, E.; Menary, G.H.; Armstrong, C.G. A non-isothermal finite element model for injection stretch-blow molding of PET bottles with parametric studies. Polym. Eng. Sci. 2004, 44, 1379–1390. [Google Scholar] [CrossRef]
- Yang, Z.J.; Harkin-Jones, E.M.A.; Armstrong, C.G.; Menary, G.H. Finite element modelling of stretch-blow moulding of PET bottles using Buckley model: Plant tests and effects of process conditions and material parameters. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2004, 218, 237–250. [Google Scholar] [CrossRef]
- Buckley, C.P. Glass-rubber constitutive model for amorphous polymers near the glass transition. Polymer 1995, 36, 3301–3312. [Google Scholar] [CrossRef]
- Buckley, C.P.; Jones, D.C.; Jones, D.P. Hot-drawing of poly(ethylene terephthalate) under biaxial stress: Application of a three-dimensional glass-rubber constitutive model. Polymer 1996, 37, 2403–2414. [Google Scholar] [CrossRef]
- Adams, A.M.; Buckley, C.P.; Jones, D.P. Biaxial hot drawing of poly(ethylene terephthalate): Measurements and modelling of strain-stiffening. Polymer 2000, 41, 771–786. [Google Scholar] [CrossRef]
- Menary, G.H.; Tan, C.W.; Harkin-Jones, E.M.A.; Armstrong, C.G.; Martin, P.J. Biaxial deformation and experimental study of PET at conditions applicable to stretch blow molding. Polym. Eng. Sci. 2012, 52, 671–688. [Google Scholar] [CrossRef]
- Yan, S.; Menary, G.; Nixon, J. A novel methodology to characterize the constitutive behaviour of polyethylene terephthalate for the stretch blow moulding process. Mech. Mater. 2017, 104, 93–106. [Google Scholar] [CrossRef] [Green Version]
- Bergström, J.S.; Hayman, D. An Overview of Mechanical Properties and Material Modeling of Polylactide (PLA) for Medical Applications. Ann. Biomed. Eng. 2016, 44, 330–340. [Google Scholar] [CrossRef]
- Menary, G.H.; Tan, C.W.; Armstrong, C.G.; Salomeia, Y.; Picard, M.; Billon, N.; Harkin-Jones, E.M.A. Validating injection stretch-blow molding simulation through free blow trials. Polym. Eng. Sci. 2010, 50, 1047–1057. [Google Scholar] [CrossRef]
- Wei, H.; Menary, G.; Yan, S.; Buchanan, F. Experiment and Modelling on Biaxial Deformation of PLLA Materials Under Designed Strain History for Stretch Blow Moulding. In Recent Advances in Intelligent Manufacturing; Springer: Singapore, 2018; Volume 923, pp. 228–238. ISBN 978-981-13-2395-9. [Google Scholar]
- Farah, S.; Anderson, D.G. Physical and mechanical properties of PLA, and their functions in widespread applications—A comprehensive review. Adv. Drug Deliv. Rev. 2016, 107, 367–392. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, N.; Yu, X.; Duan, J.; Yang, J.; Huang, T.; Qi, X.; Wang, Y. Comparison study of hydrolytic degradation behaviors between α′- and α-poly(l-lactide). Polym. Degrad. Stab. 2018, 148, 1–9. [Google Scholar] [CrossRef]
- Tsuji, H.; Nakahara, K. Poly(L-lactide). IX. Hydrolysis in acid media. J. Appl. Polym. Sci. 2002, 86, 186–194. [Google Scholar] [CrossRef]
- Chow, W.S.; Leu, Y.Y.; Mohd Ishak, Z.A. Water Absorption of Poly(lactic acid) Nanocomposites: Effects of Nanofillers and Maleated Rubbers. Polym. Plast. Technol. Eng. 2014, 53, 858–863. [Google Scholar] [CrossRef]
- Wei, H. Characterisation and Modelling of Poly (L-Lactic acid) for Stretch Blow Moulding of Bioresorbable Vascular Scaffolds. Ph.D. Thesis, The Queen’s University Belfast, Belfast, UK, 2019. [Google Scholar]
- Yu, L.; Liu, H.; Xie, F.; Chen, L.; Li, X. Effect of annealing and orientation on microstructures and mechanical properties of polylactic acid. Polym. Eng. Sci. 2008, 48, 634–641. [Google Scholar] [CrossRef]
- Zenkiewicz, M.; Richert, J.; Rózański, A. Effects of blow molding ratio on mechanical properties of polylactide nanocomposite films. Polimery/Polymers 2010, 55, 869–876. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Wang, K.; Shao, C.; Li, Q.; Shen, C. Unusual structural evolution of poly(lactic acid) upon annealing in the presence of an initially oriented mesophase. Soft Matter 2014, 10, 1512–1518. [Google Scholar] [CrossRef]
- Zhou, C.; Li, H.; Zhang, W.; Li, J.; Huang, S.; Meng, Y.; DeClaville Christiansen, J.; Yu, D.; Wu, Z.; Jiang, S. Direct investigations on strain-induced cold crystallization behavior and structure evolutions in amorphous poly(lactic acid) with SAXS and WAXS measurements. Polymer 2016, 90, 111–121. [Google Scholar] [CrossRef]
- Yan, S. Modelling the Constitutive Behaviour of Poly (ethylene terephthalate) for the Stretch Blow Moulding Process. Ph.D. Thesis, Queen’s University Belfast, Belfast, UK, 2014. [Google Scholar]
- Dooling, P.J.; Buckley, C.P.; Hinduja, S. The onset of nonlinear viscoelasticity in multiaxial creep of glassy polymers: A constitutive model and its application to PMMA. Polym. Eng. Sci. 1998, 38, 892–904. [Google Scholar] [CrossRef]
- Wu, J.J.; Buckley, C.P. Plastic deformation of glassy polystyrene: A unified model of yield and the role of chain length. J. Polym. Sci. Part B Polym. Phys. 2004, 42, 2027–2040. [Google Scholar] [CrossRef]
- Nixon, J.; Menary, G.H.; Yan, S. Free-stretch-blow investigation of poly(ethylene terephthalate) over a large process window. Int. J. Mater. Form. 2016, 10, 764–777. [Google Scholar] [CrossRef] [Green Version]
- Arbeiter, D.; Schümann, K.; Sahmel, O.; Eickner, T.; Schmitz, K.-P.; Grabow, N. The effect of thermal treatment on the mechanical properties of PLLA tubular specimens. Curr. Dir. Biomed. Eng. 2016, 2, 27–29. [Google Scholar] [CrossRef]




| Product | Zone 1 | Zone 2 | Zone 3 | Zone 4 |
|---|---|---|---|---|
| sheet | 171 | 179 | 189 | 200 |
| tube | 175 | 180 | 185 | 194 |
| Model | Density of Slip-Links for Entanglement (Ns) | Inextensibility of Entanglement Network (α) | Slip-Link Looseness Factor (η) |
|---|---|---|---|
| sheet | 2.5931e26 | 0.2031 | 0.0593 |
| tube | 1.7500e26 | 0.1600 | 0.0000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, H.; Yan, S.; Menary, G. Modelling Stretch Blow Moulding of Poly (l-lactic acid) for the Manufacture of Bioresorbable Vascular Scaffold. Polymers 2021, 13, 967. https://doi.org/10.3390/polym13060967
Wei H, Yan S, Menary G. Modelling Stretch Blow Moulding of Poly (l-lactic acid) for the Manufacture of Bioresorbable Vascular Scaffold. Polymers. 2021; 13(6):967. https://doi.org/10.3390/polym13060967
Chicago/Turabian StyleWei, Huidong, Shiyong Yan, and Gary Menary. 2021. "Modelling Stretch Blow Moulding of Poly (l-lactic acid) for the Manufacture of Bioresorbable Vascular Scaffold" Polymers 13, no. 6: 967. https://doi.org/10.3390/polym13060967
APA StyleWei, H., Yan, S., & Menary, G. (2021). Modelling Stretch Blow Moulding of Poly (l-lactic acid) for the Manufacture of Bioresorbable Vascular Scaffold. Polymers, 13(6), 967. https://doi.org/10.3390/polym13060967