Use of Artificial Neural Networks to Optimize Stacking Sequence in UHMWPE Protections
Abstract
:1. Introduction
2. Methodology
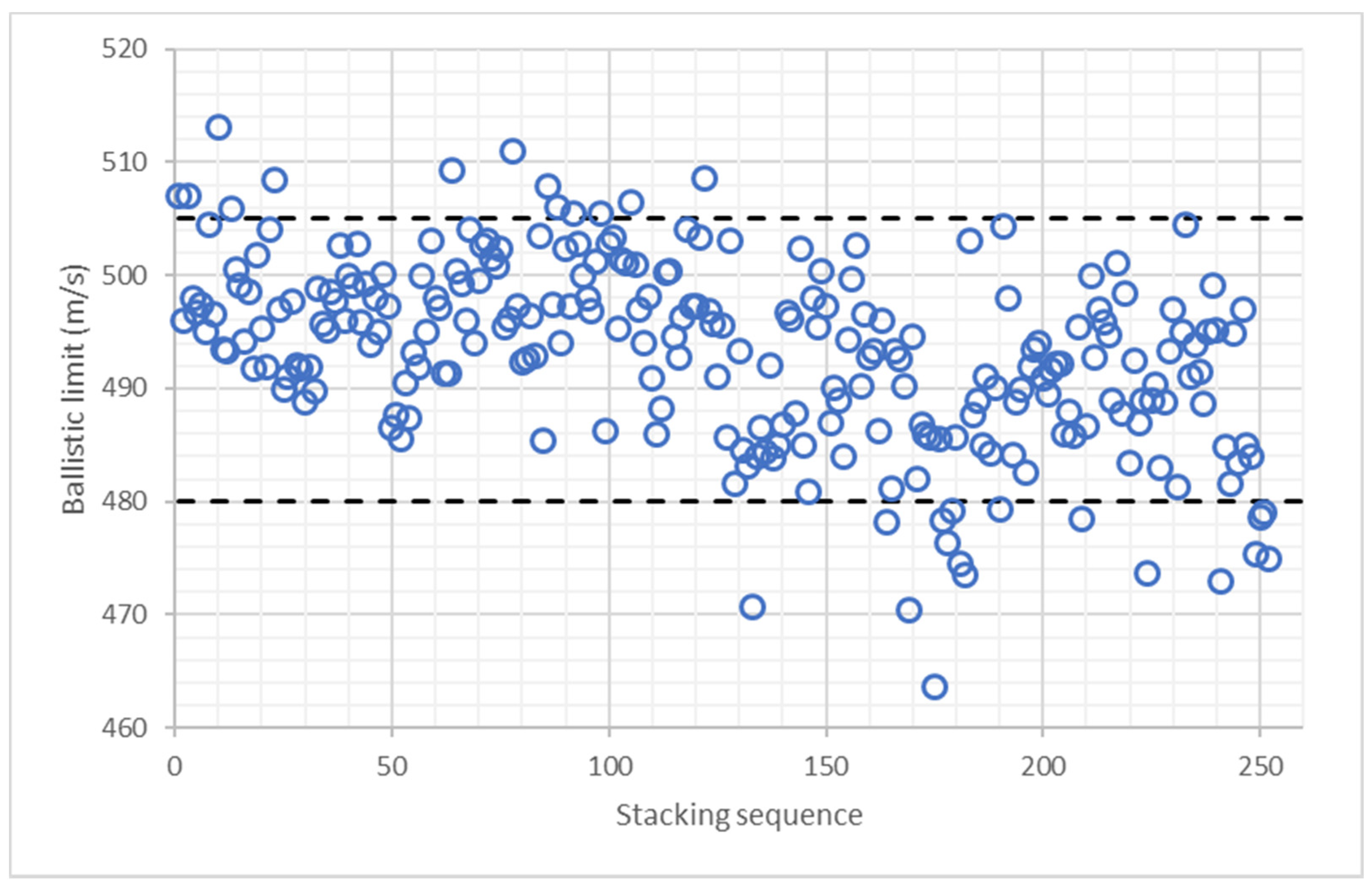
- Influence of layers position. In the first study, the areal density and the number of layers of each material were fixed to analyze the position of each material. A total of 252 configurations were studied by combining two layers of PE1, one layer of PE2 and six layers of PE3.
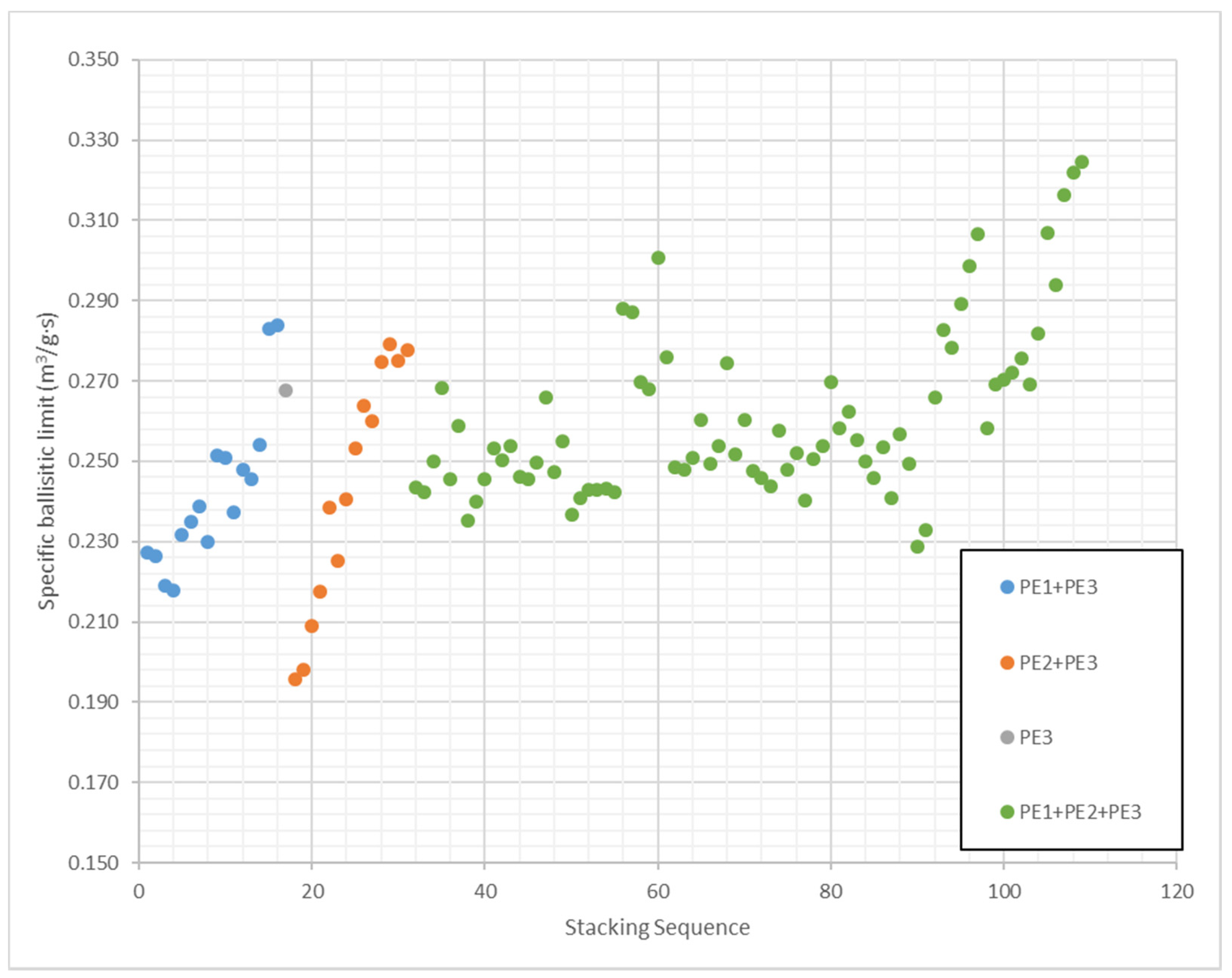
- Influence of weight ratios. In the second study, the areal density and the weight ratio of each material are analyzed. A total of 109 configurations were studied by combining PE1, PE2 and PE3. In this study, all the layers of the same material were packaged in a single block.
2.1. Experimental Procedure
2.2. Numerical Model
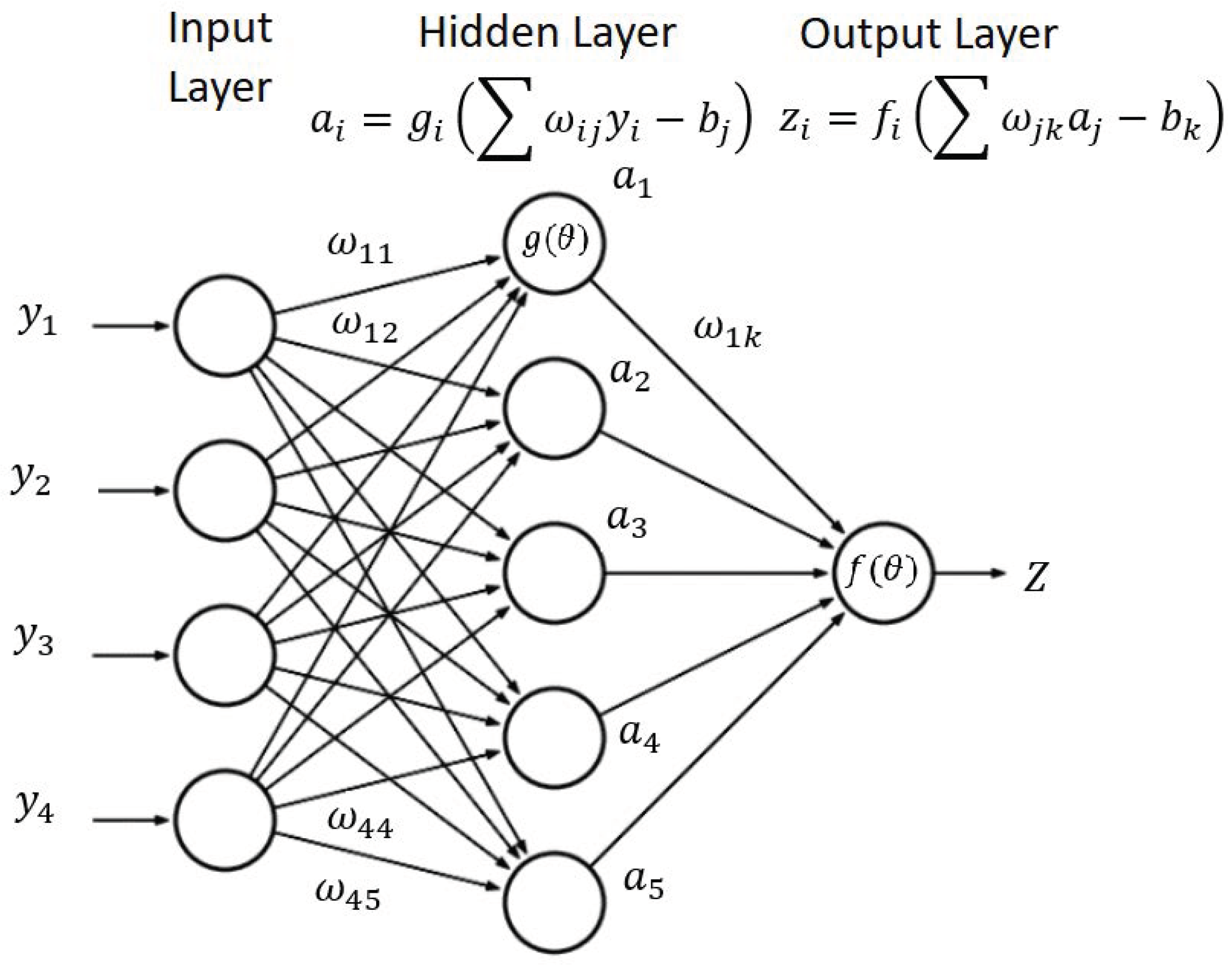
2.3. Artificial Neural Network
3. Validation
3.1. Validation of FEM Model
3.2. Validation of ANN
4. Results and Discussion
4.1. Influence of Layers Position
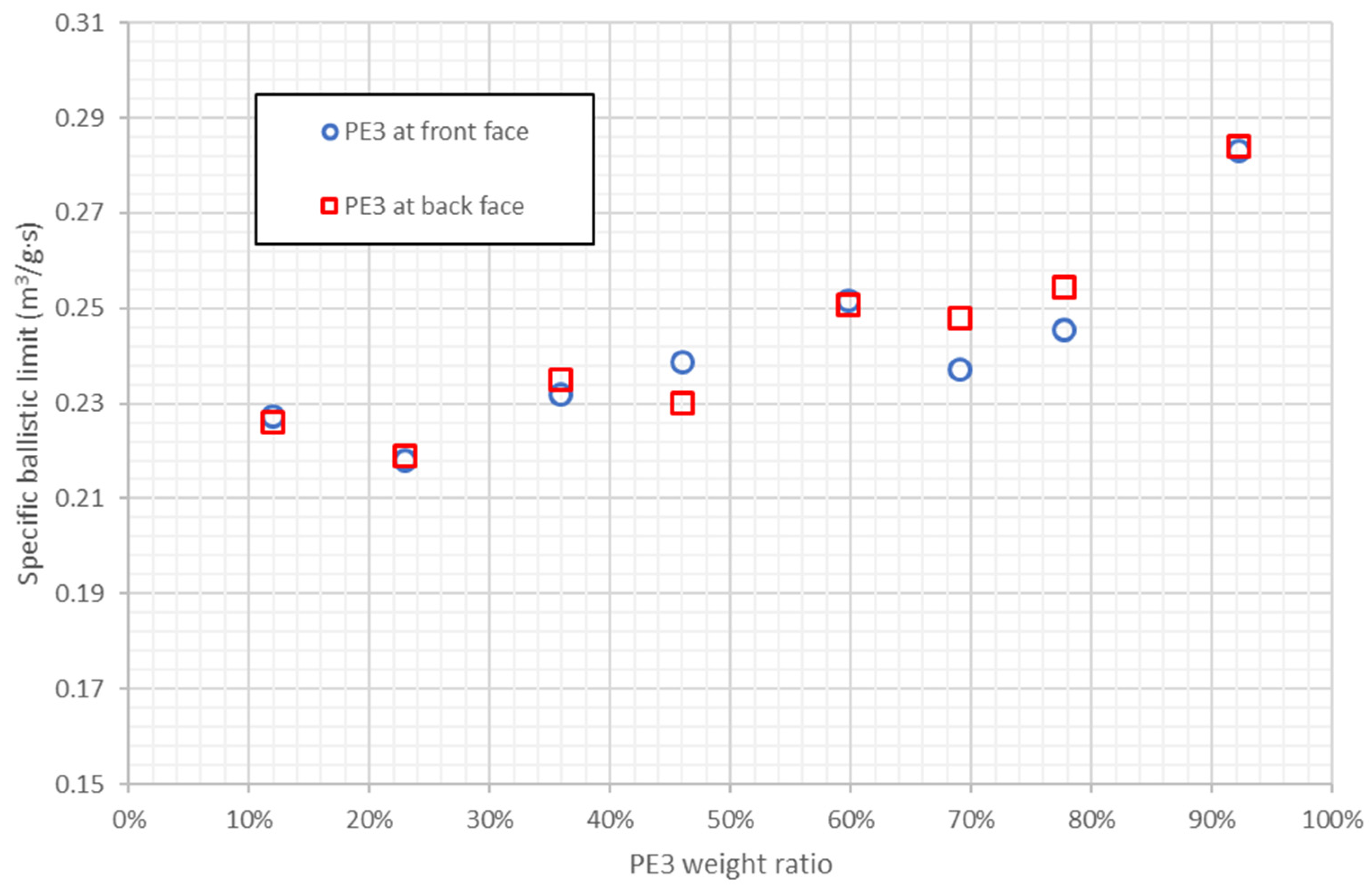
4.2. Influence of Weight Ratios
5. Conclusions
- The FEM model can be considered validated because it is able to reproduce the influence of stacking sequence on ballistic limit.
- The ANN developed using a combined methodology predicts the ballistic limit of different stacking sequences successfully.
- The trained ANN shows a great capability to analysis a huge number of stacking sequences. In the analysis of 252 stacking sequences combining 3 UHMWPE materials with the same weight ratio, it has been observed that ballistic performance can be improved by 10.7% without any weight increase.
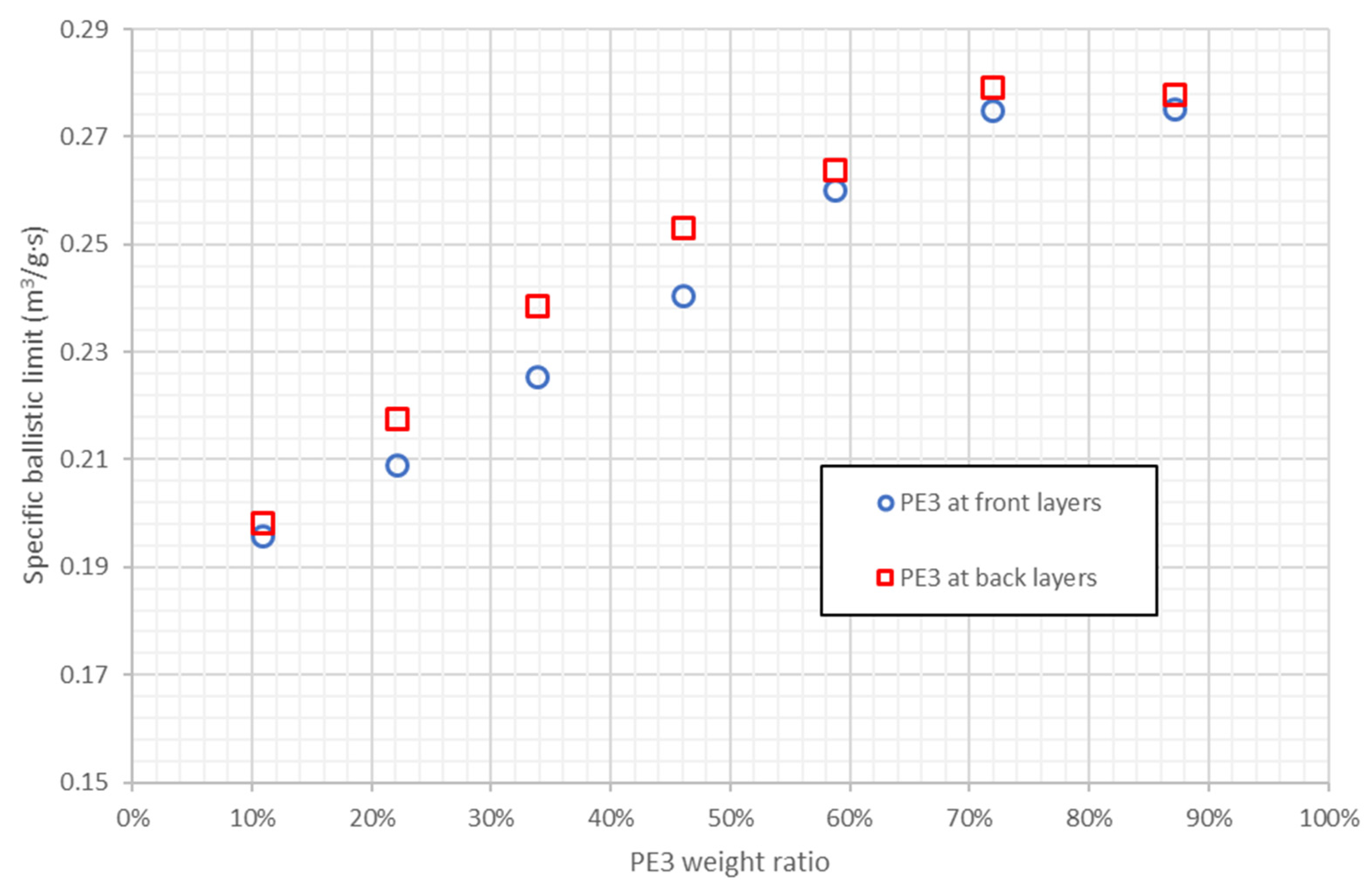
- When the weight ratio of the materials is constant, placing the PE3 layers on the back face is the most effective configuration.
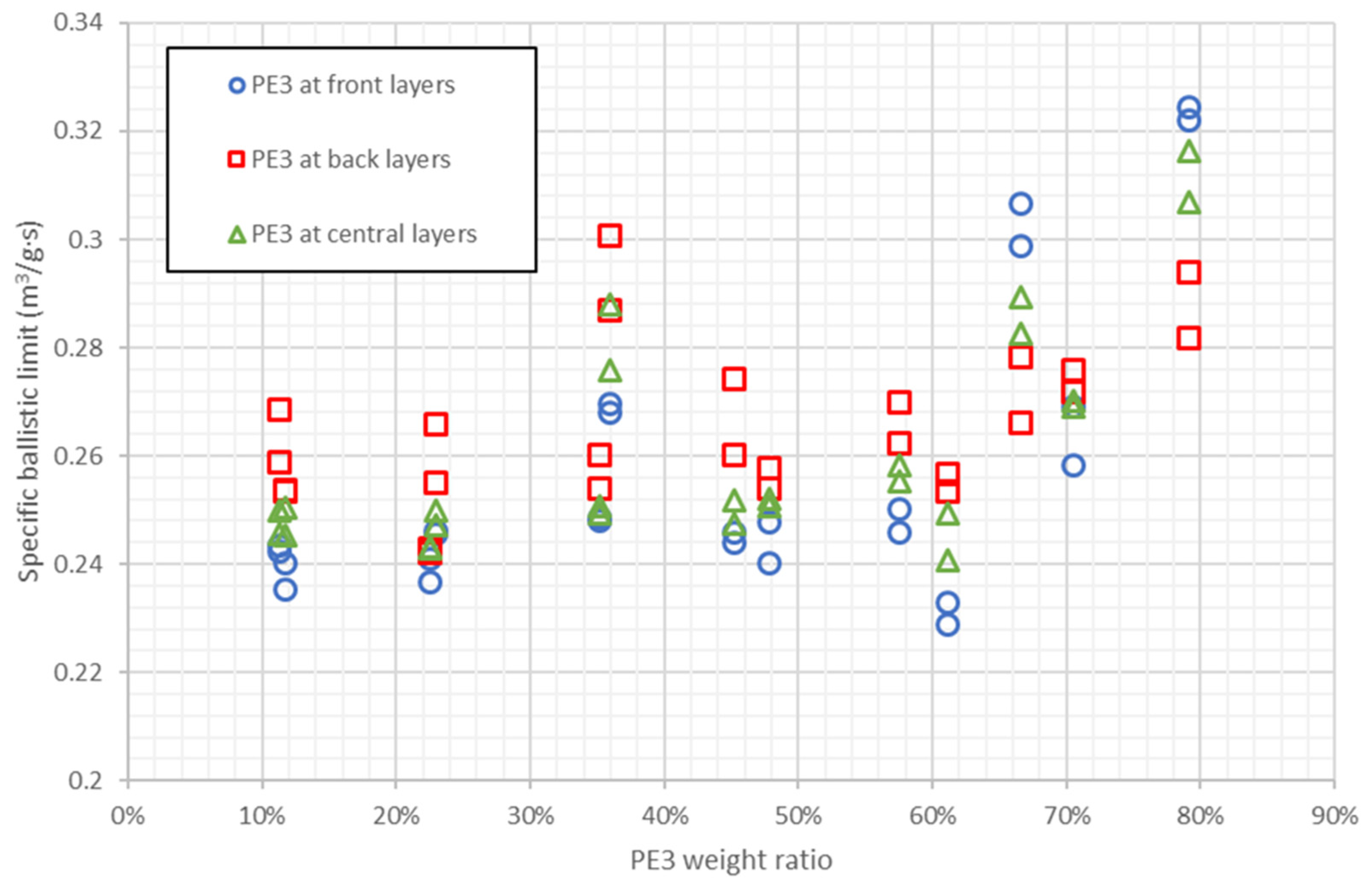
- The analysis of 109 stacking sequences with different weight ratios revealed that when the three materials are properly combined the ballistic performance is better than using only the material with highest quality. Thus, ANN simulations can be used to increase the ballistic limit with lower cost.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cai, S.; Liu, J.; Zhang, P.; Li, C.; Cheng, Y. Dynamic response of sandwich panels with multi-layered aluminum foam/UHMWPE laminate cores under air blast loading. Int. J. Impact Eng. 2020, 138, 103475. [Google Scholar] [CrossRef]
- Duan, Y.; Keefe, M.; Bogetti, T.A.; Powers, B. Finite element modeling of transverse impact on a ballistic fabric. Int. J. Mech. Sci. 2006. [Google Scholar] [CrossRef]
- Chen, L.; Zheng, K.; Fang, Q. Effect of strain rate on the dynamic tensile behaviour of UHMWPE fibre laminates. Polym. Test. 2017, 63, 54–64. [Google Scholar] [CrossRef]
- Zhang, K.; Li, W.; Zheng, Y.; Yao, W.; Zhao, C. Dynamic Constitutive Model of Ultra-High Molecular Weight Polyethylene (UHMWPE): Considering the Temperature and Strain Rate Effects. Polymers 2020, 12, 1561. [Google Scholar] [CrossRef] [PubMed]
- Langston, T. An analytical model for the ballistic performance of ultra-high molecular weight polyethylene composites. Compos. Struct. 2017, 179, 245–257. [Google Scholar] [CrossRef]
- van der Werff, H.; Heisserer, U. High-performance ballistic fibers: Ultra-High Molecular Weight Polyethylene (UHMWPE). In Advanced Fibrous Composite Materials for Ballistic Protection; Elsevier: Amsterdam, The Netherlands, 2016; pp. 71–107. ISBN 9781782424611. [Google Scholar]
- Zhang, B.; Nian, X.; Jin, F.; Xia, Z.; Fan, H. Failure analyses of flexible Ultra-High Molecular Weight Polyethylene (UHMWPE) fiber reinforced anti-blast wall under explosion. Compos. Struct. 2018, 184, 759–774. [Google Scholar] [CrossRef]
- Czechowski, L.; Jankowski, J.; Kubiak, T. Experimental tests of a property of composite material assigned for ballistic products. Fibres Text. East. Eur. 2012, 92, 61–66. [Google Scholar]
- Zhang, T.G.; Satapathy, S.S.; Vargas-Gonzalez, L.R.; Walsh, S.M. Ballistic impact response of Ultra-High-Molecular-Weight Polyethylene (UHMWPE). Compos. Struct. 2015, 133, 191–201. [Google Scholar] [CrossRef]
- Zhou, Y.; Gong, X.; Zhang, S.; Xu, A. A numerical investigation into the influence of layer space on panel ballistic performance. Fibers Polym. 2015, 16, 2663–2669. [Google Scholar] [CrossRef]
- Santiuste, C.; Sánchez-Sáez, S.; Barbero, E. A comparison of progressive-failure criteria in the prediction of the dynamic bending failure of composite laminated beams. Compos. Struct. 2010, 92, 2406–2414. [Google Scholar] [CrossRef] [Green Version]
- Ivañez, I.; Santiuste, C.; Barbero, E.; Sanchez-Saez, S. Numerical modelling of foam-cored sandwich plates under high-velocity impact. Compos. Struct. 2011, 93, 2392–2399. [Google Scholar] [CrossRef] [Green Version]
- Abu Seman, S.A.H.; Ahmad, R.; Md Akil, H. Experimental and numerical investigations of kenaf natural fiber reinforced composite subjected to impact loading. Polym. Compos. 2019, 40, 909–915. [Google Scholar] [CrossRef]
- van der Werff, H.; Heisserer, U.; Phoenix, S.L. Modelling of ballistic impact on fiber composites. Pers. Armour Syst. Symp. 2010, 50, 1–10. [Google Scholar]
- Nguyen, L.H.; Lässig, T.R.; Ryan, S.; Riedel, W.; Mouritz, A.P.; Orifici, A.C. Numerical Modelling of Ultra-High Molecular Weight Polyethylene Composite under Impact Loading. Proc. Eng. 2015, 103, 436–443. [Google Scholar] [CrossRef]
- Min, S.; Chu, Y.; Chen, X. Numerical study on mechanisms of angle-plied panels for ballistic protection. Mater. Des. 2016, 90, 896–905. [Google Scholar] [CrossRef]
- Firouzi, D.; Ching, C.Y.; Rizvi, S.N.; Selvaganapathy, P.R. Development of Oxygen-Plasma-Surface-Treated UHMWPE Fabric Coated with a Mixture of SiC/Polyurethane for Protection against Puncture and Needle Threats. Fibers 2019, 7, 46. [Google Scholar] [CrossRef] [Green Version]
- Aktaş, A.; Aktaş, M.; Turan, F. The effect of stacking sequence on the impact and post-impact behavior of woven/knit fabric glass/epoxy hybrid composites. Compos. Struct. 2013, 103, 119–135. [Google Scholar] [CrossRef]
- Randjbaran, E. The Effects of Stacking Sequence Layers of Hybrid Composite Materials in Energy Absorption under the High Velocity Ballistic Impact Conditions: An Experimental Investigation. J. Mater. Sci. Eng. 2013, 2. [Google Scholar] [CrossRef] [Green Version]
- Bandaru, A.K.; Vetiyatil, L.; Ahmad, S. The effect of hybridization on the ballistic impact behavior of hybrid composite armors. Compos. Part B Eng. 2015, 76, 300–319. [Google Scholar] [CrossRef]
- Zulkifli, F.; Stolk, J.; Heisserer, U.; Yong, A.T.M.; Li, Z.; Hu, X.M. Strategic positioning of carbon fiber layers in an UHMwPE ballistic hybrid composite panel. Int. J. Impact Eng. 2019, 129, 119–127. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, X. Investigation on energy absorption efficiency of each layer in ballistic armour panel for applications in hybrid design. Compos. Struct. 2017, 164, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Zhou, Y.; Wells, G. Numerical and experimental investigations into ballistic performance of hybrid fabric panels. Compos. Part B Eng. 2014, 58, 35–42. [Google Scholar] [CrossRef]
- Birecikli, B.; Karaman, Ö.; Celebi, S.; Turgut, A. The Influence of Composite Laminate Stacking Sequence on Failure Load of Bonding Joints Using Experimental and Artificial Neural Networks Methods. Mech. Eng. 2018. [Google Scholar] [CrossRef]
- Naderpour, H.; Kheyroddin, A.; Amiri, G.G. Prediction of FRP-confined compressive strength of concrete using artificial neural networks. Compos. Struct. 2010, 92, 2817–2829. [Google Scholar] [CrossRef]
- Malik, M.H.; Arif, A.F.M. ANN prediction model for composite plates against low velocity impact loads using finite element analysis. Compos. Struct. 2013, 101, 290–300. [Google Scholar] [CrossRef]
- Bezerra, E.M.; Ancelotti, A.C.; Pardini, L.C.; Rocco, J.A.F.F.; Iha, K.; Ribeiro, C.H.C. Artificial neural networks applied to epoxy composites reinforced with carbon and E-glass fibers: Analysis of the shear mechanical properties. Mater. Sci. Eng. A 2007, 464, 177–185. [Google Scholar] [CrossRef]
- Galatas, A.; Hassanin, H.; Zweiri, Y.; Seneviratne, L. Additive Manufactured Sandwich Composite/ABS Parts for Unmanned Aerial Vehicle Applications. Polymers 2018, 10, 1262. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Fdz, D.; López-Puente, J.; Zaera, R. Prediction of the behaviour of CFRPs against high-velocity impact of solids employing an artificial neural network methodology. Compos. Part A Appl. Sci. Manuf. 2008, 39, 989–996. [Google Scholar] [CrossRef] [Green Version]
- Artero-Guerrero, J.A.; Pernas-Sánchez, J.; Martín-Montal, J.; Varas, D.; López-Puente, J. The influence of laminate stacking sequence on ballistic limit using a combined Experimental/FEM/Artificial Neural Networks (ANN) methodology. Compos. Struct. 2018, 183, 299–308. [Google Scholar] [CrossRef]
- Dhouibi, S.; Boujelbene, M.; Kharrat, M.; Dammak, M.; Maalej, A. Friction Behavior of High Density Polyethylene (HDPE) against 304L Steel: An Experimental Investigation of the Effects of Sliding Direction, Sliding History and Sliding Speed. J. Surfaces Interfaces Mater. 2013, 1, 71–76. [Google Scholar] [CrossRef]
- Hou, J.P.; Petrinic, N.; Ruiz, C.; Hallett, S.R. Prediction of impact damage in composite plates. Compos. Sci. Technol. 2000, 60, 273–281. [Google Scholar] [CrossRef]
- Díaz-Álvarez, J.; Olmedo, A.; Santiuste, C.; Miguélez, M. Theoretical Estimation of Thermal Effects in Drilling of Woven Carbon Fiber Composite. Materials 2014, 7, 4442–4454. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rubio-López, A.; Hoang, T.; Santiuste, C. Constitutive model to predict the viscoplastic behaviour of natural fibres based composites. Compos. Struct. 2016, 155, 8–18. [Google Scholar] [CrossRef]
- Werbos, P.J. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences; Harvard University: Cambridge, MA, USA, 1974. [Google Scholar]
- Ulmer, C.W.; Smith, D.A.; Sumpter, B.G.; Noid, D.I. Computational neural networks and the rational design of polymeric materials: The next generation polycarbonates. Comput. Theor. Polym. Sci. 1998. [Google Scholar] [CrossRef]
- Tarassenko, L.; Forum, N.C.A. Guide to Neural Computing Applications, Hodder Arnold Publication, 3rd ed.; Elsevier Science: Amsterdam, The Netherlands, 1998; ISBN 9780340705896. [Google Scholar]
- Lambert, J.P.; Jonas, G.H. Towards Standardization in Terminal Ballistics Testing: Velocity Representation. 1976, pp. 1–46. Available online: http://www.dtic.mil/docs/citations/ADA021389 (accessed on 23 March 2021).






| PE1 | PE2 | PE3 | |
|---|---|---|---|
| Areal density (g/m2) | 253 | 145.16 | 216.52 |
| Thickness (mm) | 0.3 | 0.18 | 0.252 |
| E11 (GPa) | 78.997 | 52.591 | 55.185 |
| Xt (MPa) | 2807.1 | 1498.8 | 1631.8 |
| Ultimate strain (−) | 0.3 | 0.7 | 0.8 |
| 4th Variable | Front Face | Middle | Back Face |
|---|---|---|---|
| 1 | PE3 | PE2 | PE1 |
| 2 | PE3 | PE1 | PE2 |
| 3 | PE2 | PE3 | PE1 |
| 4 | PE1 | PE3 | PE2 |
| 5 | PE2 | PE1 | PE3 |
| 6 | PE1 | PE2 | PE3 |
| 7 | PE3 | 0 | PE2 |
| 8 | PE3 | 0 | PE1 |
| 9 | PE2 | 0 | PE3 |
| 10 | PE1 | 0 | PE3 |
| 11 | PE3 | 0 | 0 |
| Areal Density | Weight Ratio (%) | Ballistic Limit (m/s) | |||||
|---|---|---|---|---|---|---|---|
| Stacking Sequence | (g/m2) | PE1 | PE2 | PE3 | FEM | Exp. | Error |
| 3·PE1/7·PE3 | 1947 | 22.34 | 0 | 77.66 | 495 | 483.1 | −2.4% |
| 7·PE3/3·PE1 | 1947 | 22.34 | 0 | 77.66 | 478 | 478.8 | 0.2% |
| 3·PE3/8·PE1 | 1808 | 64.16 | 0 | 35.84 | 419 | 434.1 | 3.6% |
| 1·PE2/8·PE3 | 1981 | 0 | 12.77 | 87.23 | 550 | 567.3 | 3.1% |
| 2·PE1/1·PE2/6·PE3 | 1839 | 15.77 | 13.76 | 70.47 | 507 | 518.5 | 2.3% |
| 6·PE3/2·PE1/1·PE2 | 1839 | 15.77 | 13.76 | 70.47 | 495 | 489.6 | −1.1% |
| Weight Ratio | Areal Density | Ballistic Limit | Specific Ballistic Limit | |||
|---|---|---|---|---|---|---|
| Stacking Sequence | PE1 | PE2 | PE3 | (g/m3) | (m/s) | (m3/g·s) |
| [2·PE1/PE2/6·PE3] | 15.8% | 13.8% | 70.5% | 1839 | 513.1 | 0.279 |
| [PE1/PE2/PE1/6·PE3] | 15.8% | 13.8% | 70.5% | 1839 | 511.0 | 0.278 |
| [PE2/2·PE1/6·PE3] | 15.8% | 13.8% | 70.5% | 1839 | 509.4 | 0.277 |
| [2·PE1/PE3/PE2/5·PE3] | 15.8% | 13.8% | 70.5% | 1839 | 508.6 | 0.277 |
| [PE1/PE3/PE1/PE2/5·PE3] | 15.8% | 13.8% | 70.5% | 1839 | 508.5 | 0.276 |
| [PE3/2·PE1/PE2/5·PE3] | 15.8% | 13.8% | 70.5% | 1839 | 507.8 | 0.276 |
| [PE2/PE1/PE3/PE1/5·PE3] | 15.8% | 13.8% | 70.5% | 1839 | 507.0 | 0.276 |
| [PE1/PE2/PE3/PE1/5·PE3] | 15.8% | 13.8% | 70.5% | 1839 | 507.0 | 0.276 |
| [PE1/PE3/PE2/PE1/5·PE3] | 15.8% | 13.8% | 70.5% | 1839 | 506.5 | 0.275 |
| [PE3/PE1/PE2/PE1/5·PE3] | 15.8% | 13.8% | 70.5% | 1839 | 506.1 | 0.275 |
| [7·PE3/1·PE2/1·PE1] | 7.6% | 13.2% | 79.2% | 1910 | 619.9 | 0.325 |
| [7·PE3/1·PE1/1·PE2] | 7.6% | 13.2% | 79.2% | 1910 | 614.9 | 0.322 |
| [1·PE2/7·PE3/1·PE1] | 7.6% | 13.2% | 79.2% | 1910 | 604.2 | 0.316 |
| [6·PE3/2·PE2/1·PE1] | 7.4% | 26.0% | 66.6% | 1947 | 597.1 | 0.307 |
| [1·PE1/7·PE3/1·PE2] | 7.6% | 13.2% | 79.2% | 1910 | 586.1 | 0.307 |
| [4·PE2/1·PE1/3·PE3] | 8.0% | 56.1% | 33.3% | 1805 | 542.9 | 0.301 |
| [6·PE3/1·PE1/2·PE2] | 7.4% | 26.0% | 66.6% | 1947 | 581.7 | 0.299 |
| [1·PE2/1·PE1/7·PE3] | 7.6% | 13.2% | 79.2% | 1910 | 561.6 | 0.294 |
| [2·PE2/6·PE3/1·PE1] | 7.4% | 26.0% | 66.6% | 1947 | 563.2 | 0.289 |
| [1·PE1/3·PE3/4·PE2] | 8.0% | 56.1% | 33.3% | 1805 | 520.0 | 0.288 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peinado, J.; Jiao-Wang, L.; Olmedo, Á.; Santiuste, C. Use of Artificial Neural Networks to Optimize Stacking Sequence in UHMWPE Protections. Polymers 2021, 13, 1012. https://doi.org/10.3390/polym13071012
Peinado J, Jiao-Wang L, Olmedo Á, Santiuste C. Use of Artificial Neural Networks to Optimize Stacking Sequence in UHMWPE Protections. Polymers. 2021; 13(7):1012. https://doi.org/10.3390/polym13071012
Chicago/Turabian StylePeinado, Jairo, Liu Jiao-Wang, Álvaro Olmedo, and Carlos Santiuste. 2021. "Use of Artificial Neural Networks to Optimize Stacking Sequence in UHMWPE Protections" Polymers 13, no. 7: 1012. https://doi.org/10.3390/polym13071012
APA StylePeinado, J., Jiao-Wang, L., Olmedo, Á., & Santiuste, C. (2021). Use of Artificial Neural Networks to Optimize Stacking Sequence in UHMWPE Protections. Polymers, 13(7), 1012. https://doi.org/10.3390/polym13071012







