Non-Isothermal Crystallization Kinetics of Poly(Ethylene Glycol)–Poly(l-Lactide) Diblock Copolymer and Poly(Ethylene Glycol) Homopolymer via Fast-Scan Chip-Calorimeter
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Test Instrument
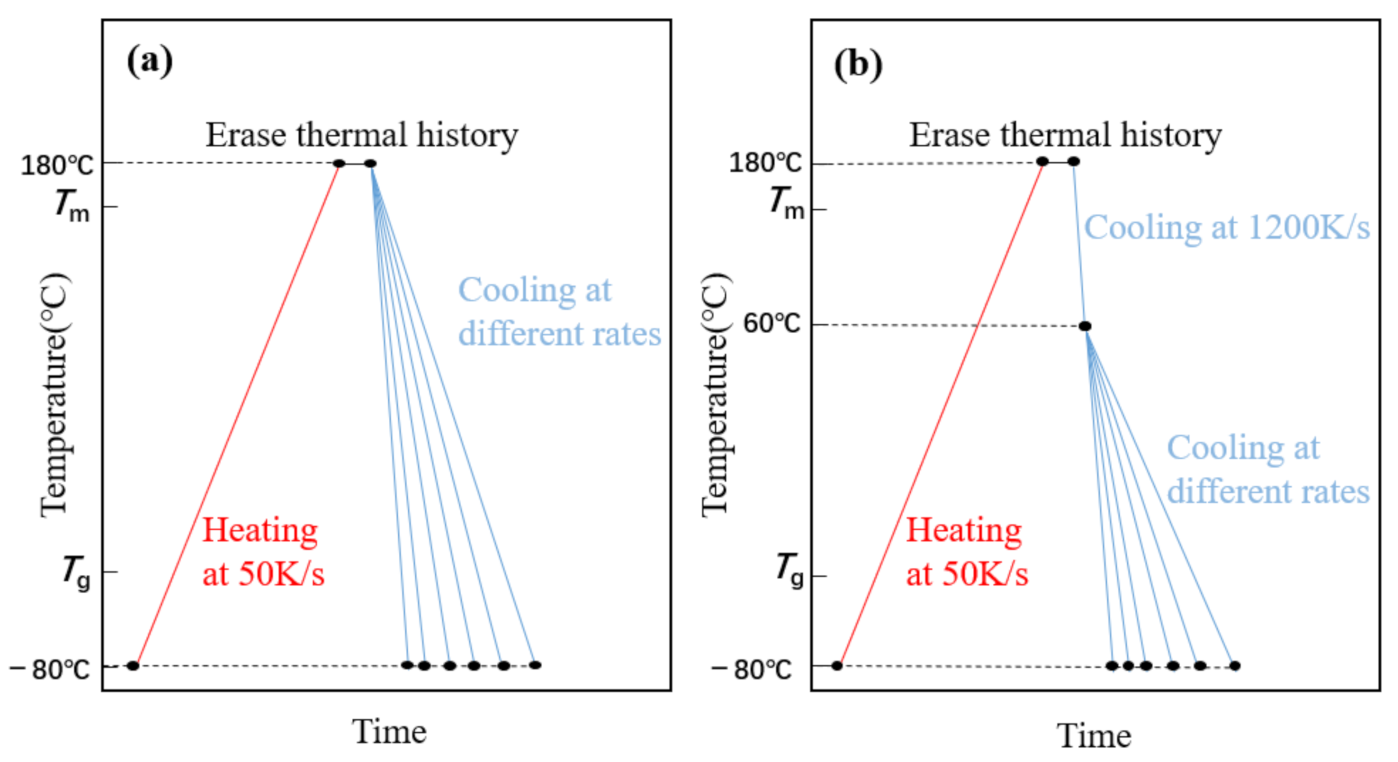
2.3. Methods
3. Results and Discussion
3.1. Analysis of Non-Isothermal Crystallization Curves
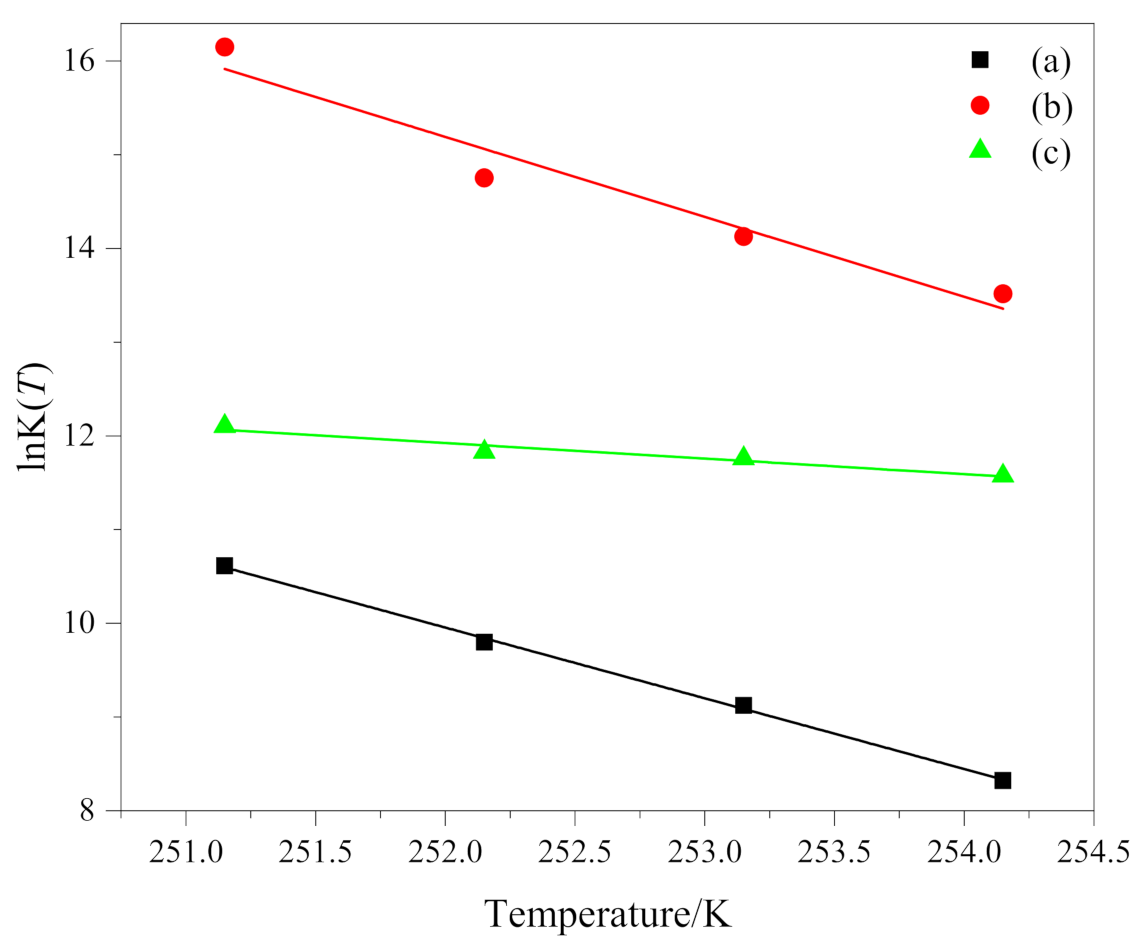
3.2. Analysis by the Ozawa Equation
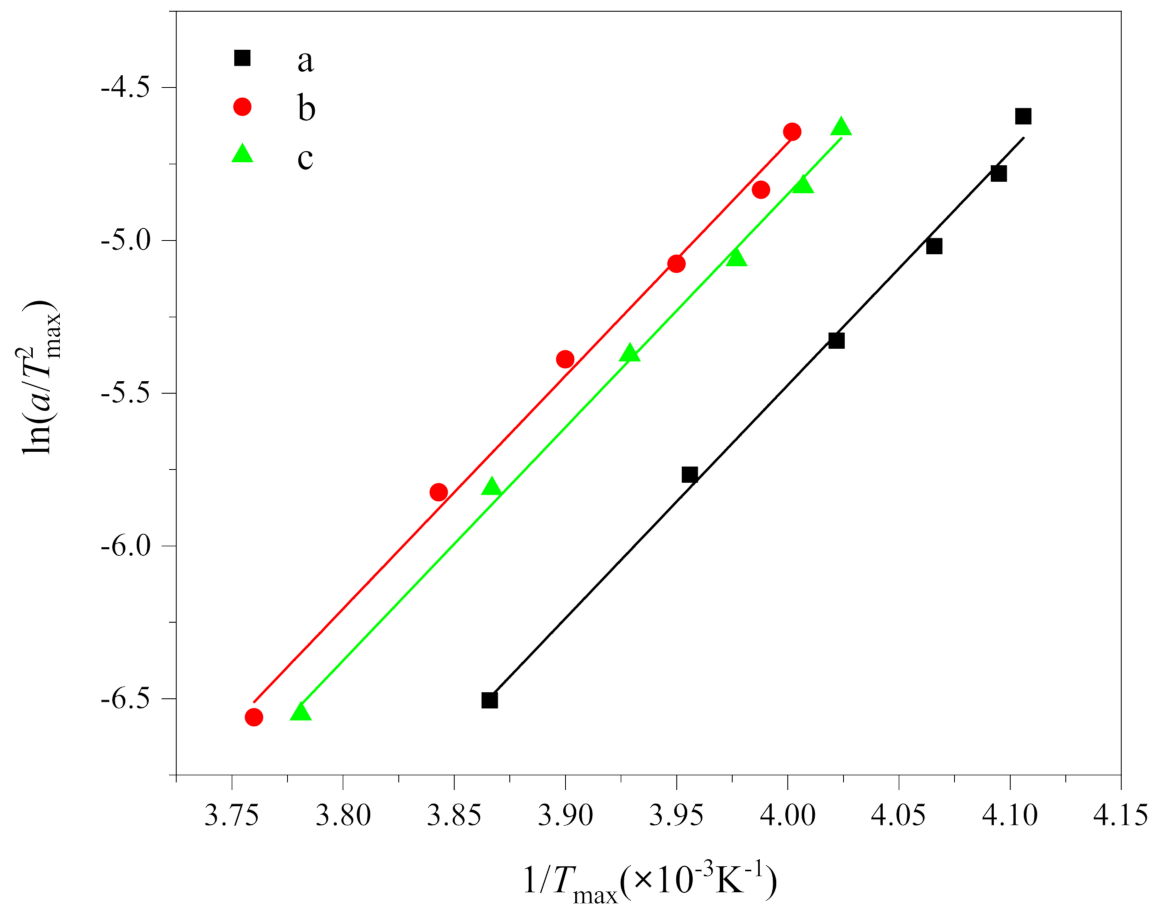
3.3. Crystallization Activation Energy (ΔE)
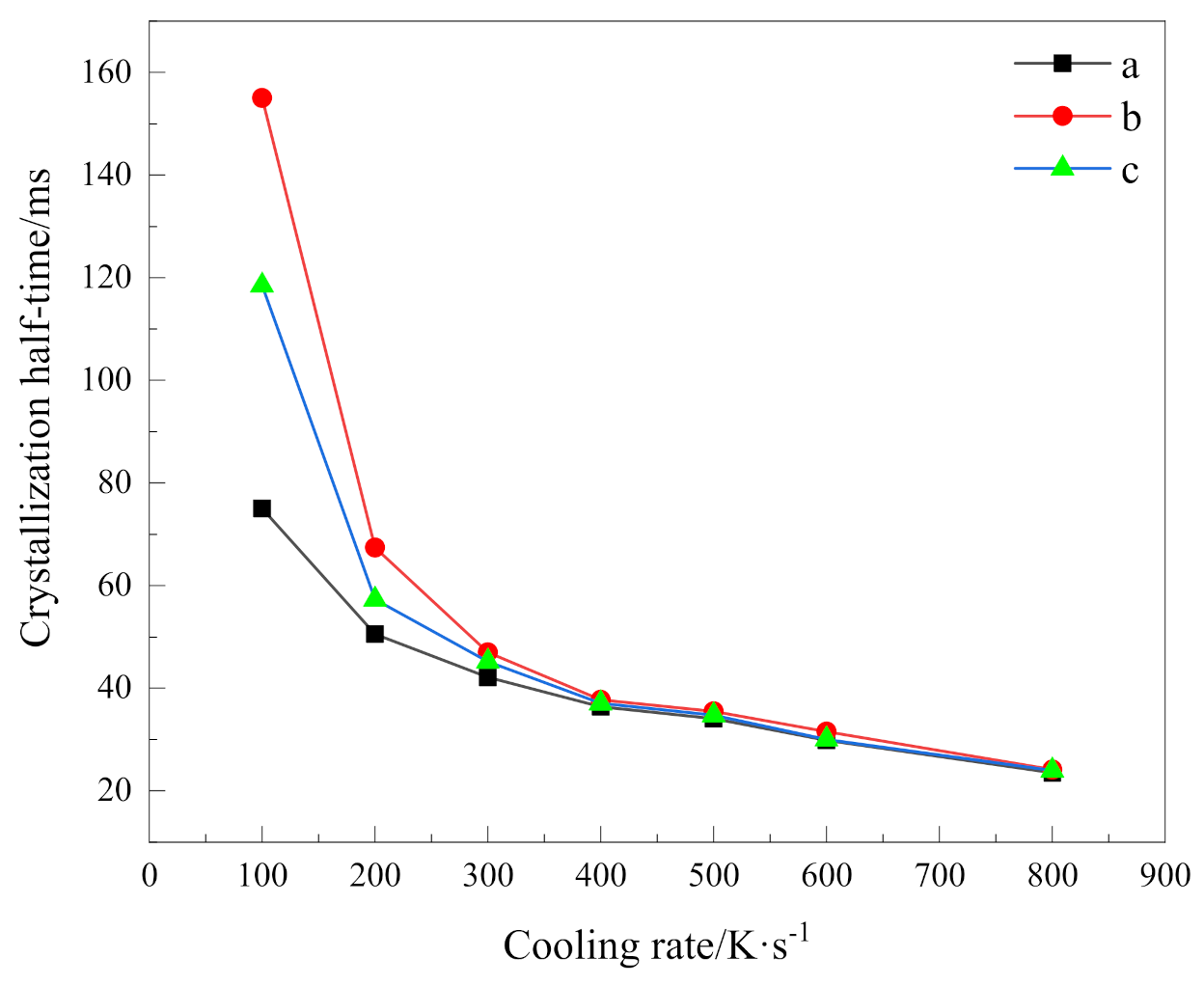
3.4. Analysis of Crystallization Rate
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Basu, A.; Kunduru, K.R.; Doppalapudi, S.; Domb, A.J.; Khan, W. Poly(lactic acid) based hydrogels. Adv. Drug Deliv. Rev. 2016, 107, 192–205. [Google Scholar] [CrossRef] [PubMed]
- Rabanel, J.-M.; Faivre, J.; Tehrani, S.F.; Lalloz, A.; Hildgen, P.; Banquy, X. Effect of the Polymer Architecture on the Structural and Biophysical Properties of PEG-PLA Nanoparticles. ACS Appl. Mater. Interfaces 2015, 7, 10374–10385. [Google Scholar] [CrossRef] [PubMed]
- Tessmar, J.K.; Goepferich, A.M. Customized PEG-derived copolymers for tissue-engineering applications. Macromol. Biosci. 2007, 7, 23–39. [Google Scholar] [CrossRef] [PubMed]
- Shalgunov, V.; Zaytseva-Zotova, D.; Zintchenko, A.; Levada, T.; Shilov, Y.; Andreyev, D.; Dzhumashev, D.; Metelkin, E.; Urusova, A.; Demin, O.; et al. Comprehensive study of the drug delivery properties of poly(l-lactide)-poly (ethylene glycol) nanoparticles in rats and tumor-bearing mice. J. Control. Release 2017, 261, 31–42. [Google Scholar] [CrossRef]
- Xiang, S.; Zhou, D.-D.; Feng, L.-D.; Bian, X.-C.; Li, G.; Chen, X.-S.; Wang, T.-C. Influence of Chain Architectures on Crystallization Behaviors of PLLA Block in PEG/PLLA Block Copolymers. Chin. J. Polym. Sci. 2019, 37, 258–267. [Google Scholar] [CrossRef]
- Zhou, D.; Shao, J.; Li, G.; Sun, J.; Bian, X.; Chen, X. Crystallization behavior of PEG/PLLA block copolymers: Effect of the different architectures and molecular weights. Polymer 2015, 62, 70–76. [Google Scholar] [CrossRef]
- Jabbarzadeh, A.; Halfina, B. Unravelling the effects of size, volume fraction and shape of nanoparticle additives on crystallization of nanocomposite polymers. Nanoscale Adv. 2019, 1, 4704–4721. [Google Scholar] [CrossRef]
- Jabbarzadeh, A. The Origins of Enhanced and Retarded Crystallization in Nanocomposite Polymers. Nanomaterials 2019, 9, 13. [Google Scholar] [CrossRef]
- Kumar, S.K.; Ganesan, V.; Riggleman, R.A. Perspective: Outstanding theoretical questions in polymer-nanoparticle hybrids. J. Chem. Phys. 2017, 147, 18. [Google Scholar] [CrossRef]
- Yang, J.L.; Zhao, T.; Cui, J.J.; Liu, L.J.; Zhou, Y.C.; Li, G.; Zhou, E.L.; Chen, X.S. Nonisothermal crystallization behavior of the poly(ethylene glycol) block in poly(l-lactide)-poly(ethylene glycol) diblock copolymers: Effect of the poly(l-lactide) block length. J. Polym. Sci. Part B-Polym. Phys. 2006, 44, 3215–3226. [Google Scholar] [CrossRef]
- Kong, X.H.; Yang, X.N.; Li, G.; Zhao, X.G.; Zhou, E.L.; Ma, D.Z. Nonisothermal crystallization kinetics: Poly(ethylene terephthalate)-poly(ethylene oxide) segmented copolymer and poly(ethylene oxide) homopolymer. Eur. Polym. J. 2001, 37, 1855–1862. [Google Scholar] [CrossRef]
- Adamovsky, S.A.; Minakov, A.A.; Schick, C. Scanning microcalorimetry at high cooling rate. Thermochim. Acta 2003, 403, 55–63. [Google Scholar] [CrossRef]
- Mathot, V.; Pyda, M.; Pijpers, T.; Vanden Poel, G.; van de Kerkhof, E.; van Herwaardeng, S.; van Herwaardeng, F.; Leenaers, A. The Flash DSC 1, a power compensation twin-type, chip-based fast scanning calorimeter (FSC): First findings on polymers. Thermochim. Acta 2011, 522, 36–45. [Google Scholar] [CrossRef]
- Yu, S.Z.; Li, X.D.; Guo, X.Y.; Li, Z.R.; Zou, M.S. Curing and Characteristics of N,N,N′,N′-Tetraepoxypropyl-4,4′-Diaminodiphenylmethane Epoxy Resin-Based Buoyancy Material. Polymers 2019, 11, 1137. [Google Scholar] [CrossRef]
- Yu, S.Z.; Li, X.D.; Zou, M.S.; Li, Z.R.; Wang, S.; Wang, D.H. Tetrafunctional Epoxy Resin-Based Buoyancy Materials: Curing Kinetics and Properties. Polymers 2020, 12, 1732. [Google Scholar] [CrossRef]
- Cavallo, D.; Gardella, L.; Alfonso, G.C.; Mileva, D.; Androsch, R. Effect of comonomer partitioning on the kinetics of mesophase formation in random copolymers of propene and higher alpha-olefins. Polymer 2012, 53, 4429–4437. [Google Scholar] [CrossRef]
- Tardif, X.; Pignon, B.; Boyard, N.; Schmelzer, J.W.P.; Sobotka, V.; Delaunay, D.; Schick, C. Experimental study of crystallization of PolyEtherEtherKetone (PEEK) over a large temperature range using a nano-calorimeter. Polym. Test. 2014, 36, 10–19. [Google Scholar] [CrossRef]
- Wang, J.; Li, Z.; Perez, R.A.; Mueller, A.J.; Zhang, B.; Grayson, S.M.; Hu, W. Comparing crystallization rates between linear and cyclic poly(epsilon-caprolactones) via fast-scan chip-calorimeter measurements. Polymer 2015, 63, 34–40. [Google Scholar] [CrossRef]
- Sun, J.R.; Hong, Z.K.; Yang, L.X.; Tang, Z.H.; Chen, X.S.; Jing, X.B. Study on crystalline morphology of poly(l-lactide)-poly(ethylene glycol) diblock copolymer. Polymer 2004, 45, 5969–5977. [Google Scholar] [CrossRef]
- Ozawa, T. Kinetics of non-isothermal crystallization. Polymer 1971, 12, 150–158. [Google Scholar] [CrossRef]
- Kissinger, H.E. Variation of peak temperature with heating rate in differential thermal analysis. J. Res. Natl. Bur. Stand. 1956, 57, 217–221. [Google Scholar] [CrossRef]
- Androsch, R.; Schick, C.; Di Lorenzo, M.L. Melting of Conformationally Disordered Crystals (alpha′-Phase) of Poly(l-lactic acid). Macromol. Chem. Phys. 2014, 215, 1134–1139. [Google Scholar] [CrossRef]
- Luo, S.; Kui, X.; Xin, E.; Wang, X.; Xue, G.; Schick, C.; Hu, W.; Zhuravlev, E.; Zhou, D. Interplay between Free Surface and Solid Interface Nucleation on Two-Step Crystallization of Poly(ethylene terephthalate) Thin Films Studied by Fast Scanning Calorimetry. Macromolecules 2018, 51, 5209–5218. [Google Scholar] [CrossRef]
- Minakov, A.A.; Wurm, A.; Schick, C. Superheating in linear polymers studied by ultrafast nanocalorimetry. Eur. Phys. J. E 2007, 23, 43–53. [Google Scholar] [CrossRef]
- Kourtidou, D.; Tarani, E.; Chrysafi, I.; Menyhard, A.; Bikiaris, D.N.; Chrissafis, K. Non-isothermal crystallization kinetics of graphite-reinforced crosslinked high-density polyethylene composites. J. Therm. Anal. Calorim. 2020, 142, 1849–1861. [Google Scholar] [CrossRef]
- Zhao, Y.S.; Yao, C.; Chang, T.; Zhu, Y.L. The Influence of DMDBS on Crystallization Behavior and Crystalline Morphology of Weakly-Phase-Separated Olefin Block Copolymer. Polymers 2019, 11, 12. [Google Scholar] [CrossRef] [PubMed]
- Avrami, M. Kinetics of phase change I—General theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Addonizio, M.L.; Martuscelli, E.; Silvestre, C. Study of the non-isothermal crystallization of poly(ethylene oxide)/poly(methyl methacrylate) blends. Polymer 1987, 28, 183–188. [Google Scholar] [CrossRef]
- Weng, W.G.; Chen, G.H.; Wu, D.J. Crystallization kinetics and melting behaviors of nylon 6/foliated graphite nanocomposites. Polymer 2003, 44, 8119–8132. [Google Scholar] [CrossRef]
- Silva, I.D.S.; Jaques, N.G.; Barros, J.J.P.; Almeida, D.E.O.; Lima, E.P.N.; Araujo, R.N.; Cerqueira, G.R.C.; Pereira, C.A.B.; Silva, A.F.P.; Nepomuceno, N.C.; et al. Clever use of PCL as kinetic controller in PBT/PCL blends. Mater. Res. Express 2019, 6, 115313. [Google Scholar] [CrossRef]
- Eder, M.; Wlochowicz, A. Kinetics of non-isothermal crystallization of polyethylene and polypropylene. Polymer 1983, 24, 1593–1595. [Google Scholar] [CrossRef]
- Caze, C.; Devaux, E.; Crespy, A.; Cavrot, J.P. A new method to determine the Avrami exponent by dsc studies of non-isothermal crystallization from the molten state. Polymer 1997, 38, 497–502. [Google Scholar] [CrossRef]
- Bosq, N.; Guigo, N.; Zhuravlev, E.; Sbirrazzuoli, N. Nonisothermal Crystallization of Polytetrafluoroethylene in a Wide Range of Cooling Rates. J. Phys. Chem. B 2013, 117, 3407–3415. [Google Scholar] [CrossRef]


| Cooling Rate (K/s) | a | b | c | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ts (°C) | Tmax (°C) | Xmax (%) | Ts (°C) | Tmax (°C) | Xmax (%) | Ts (°C) | Tmax (°C) | Xmax (%) | |
| 100 | −6.40 | −14.50 | 0.596 | 9.30 | −7.20 | 0.662 | 3.90 | −8.70 | 0.641 |
| 200 | −9.70 | −20.40 | 0.550 | 1.38 | −12.94 | 0.570 | −2.40 | −14.58 | 0.591 |
| 300 | −11.30 | −24.54 | 0.481 | −3.00 | −16.77 | 0.518 | −6.00 | −18.66 | 0.520 |
| 400 | −13.32 | −27.20 | 0.450 | −6.30 | −19.96 | 0.470 | −7.68 | −21.72 | 0.442 |
| 500 | −14.15 | −28.96 | 0.438 | −8.05 | −22.40 | 0.451 | −8.25 | −23.60 | 0.358 |
| 600 | −16.10 | −29.59 | 0.331 | −10.20 | −23.28 | 0.382 | −11.30 | −24.64 | 0.340 |
| 800 | −19.76 | −30.24 | 0.284 | −12.15 | −24.20 | 0.306 | −13.52 | −24.80 | 0.316 |
| / | = 0.447 | = 0.480 | = 0.458 | ||||||
| Temperature/°C | a | b | c | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | q | lnK(T) | R2 | q | lnK(T) | R2 | q | lnK(T) | |
| −19 | 0.9972 | 1.688 | 8.3218 | 0.9949 | 2.346 | 13.5153 | 0.9949 | 2.053 | 11.5732 |
| −20 | 0.9937 | 1.786 | 9.1223 | 0.9965 | 2.420 | 14.1260 | 0.9922 | 2.061 | 11.7593 |
| −21 | 0.9928 | 1.869 | 9.7976 | 0.9957 | 2.495 | 14.7527 | 0.9935 | 2.047 | 11.8273 |
| −22 | 0.9917 | 1.973 | 10.6133 | 0.9941 | 2.702 | 16.1496 | 0.9904 | 2.068 | 12.1035 |
| / | = 1.829 | = 2.491 | = 2.057 | ||||||
| R2 | Slope (×103) | ΔE (kJ/mol) | |
|---|---|---|---|
| a | 0.9946 | 7.52 | −62.52 |
| b | 0.9937 | 7.10 | −59.03 |
| c | 0.9964 | 7.30 | −60.69 |
| Cooling Rate (K/s) | 100 | 200 | 300 | 400 | 500 | 600 | 800 | |
|---|---|---|---|---|---|---|---|---|
| Crystallization half-time (ms) | a | 75.00 | 50.50 | 42.10 | 36.40 | 34.10 | 29.83 | 23.50 |
| b | 155.00 | 67.40 | 47.00 | 37.70 | 35.50 | 31.53 | 24.14 | |
| c | 118.50 | 57.25 | 45.20 | 37.05 | 34.70 | 30.03 | 23.93 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Lei, L.; Zou, M.; Li, X. Non-Isothermal Crystallization Kinetics of Poly(Ethylene Glycol)–Poly(l-Lactide) Diblock Copolymer and Poly(Ethylene Glycol) Homopolymer via Fast-Scan Chip-Calorimeter. Polymers 2021, 13, 1156. https://doi.org/10.3390/polym13071156
Chen D, Lei L, Zou M, Li X. Non-Isothermal Crystallization Kinetics of Poly(Ethylene Glycol)–Poly(l-Lactide) Diblock Copolymer and Poly(Ethylene Glycol) Homopolymer via Fast-Scan Chip-Calorimeter. Polymers. 2021; 13(7):1156. https://doi.org/10.3390/polym13071156
Chicago/Turabian StyleChen, Dejia, Lisha Lei, Meishuai Zou, and Xiaodong Li. 2021. "Non-Isothermal Crystallization Kinetics of Poly(Ethylene Glycol)–Poly(l-Lactide) Diblock Copolymer and Poly(Ethylene Glycol) Homopolymer via Fast-Scan Chip-Calorimeter" Polymers 13, no. 7: 1156. https://doi.org/10.3390/polym13071156
APA StyleChen, D., Lei, L., Zou, M., & Li, X. (2021). Non-Isothermal Crystallization Kinetics of Poly(Ethylene Glycol)–Poly(l-Lactide) Diblock Copolymer and Poly(Ethylene Glycol) Homopolymer via Fast-Scan Chip-Calorimeter. Polymers, 13(7), 1156. https://doi.org/10.3390/polym13071156








