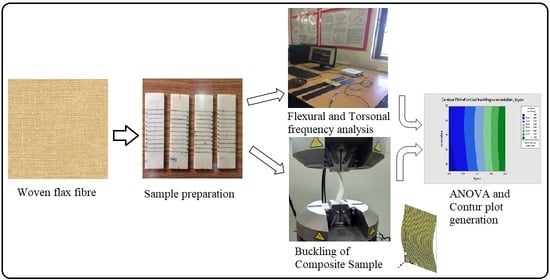
Experimental and Numerical Analyses on the Buckling Characteristics of Woven Flax/Epoxy Laminated Composite Plate under Axial Compression
Abstract
:1. Introduction
2. Response Surface Methodology (RSM)
3. Materials and Fabrication of the Composites
4. Experimental Investigation
4.1. Evaluation of Elastic Constants
4.2. Experimental Buckling Analysis
5. Results and Discussions
5.1. Elastic Constants
5.2. Experimental Buckling
5.3. Numerical Buckling Analysis
5.4. Comparison of Experimental and Numerical Results
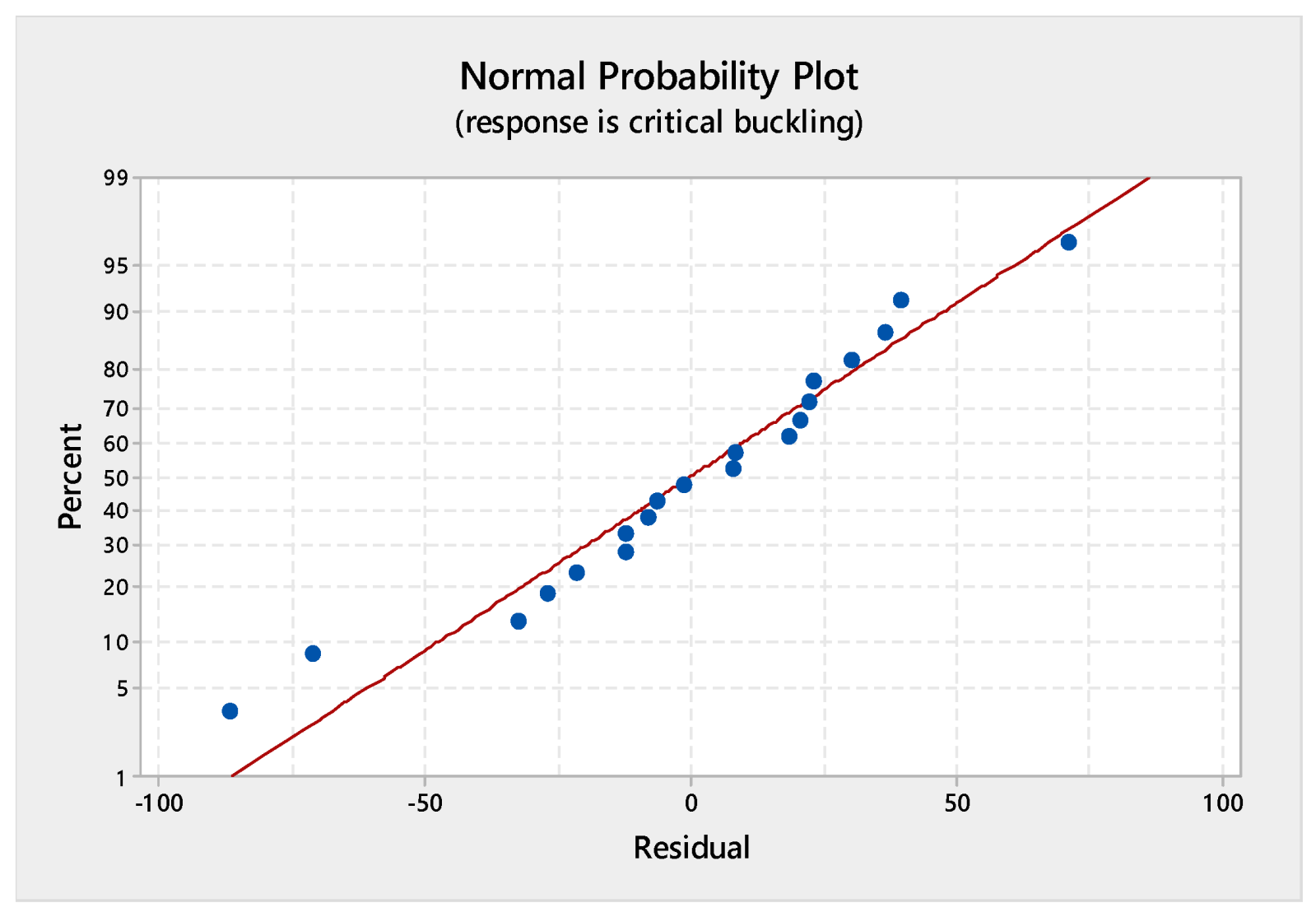
5.5. Analysis of Variance (ANOVA) Assessment for the Regression Model and Regression Equation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Leissa, A.W. A review of laminated composite plate buckling. Appl. Mech. Rev. 1987, 40, 575–591. [Google Scholar] [CrossRef]
- Biggers, S.B.; Srinivasan, S. Compression buckling response of tailored rectangular composite plates. AIAA J. 1993, 31, 590–596. [Google Scholar] [CrossRef]
- Kim, Y.S.; Van Hoa, S. Bi-axial buckling behavior of composite rectangular plates. Compos. Struct. 1995, 31, 247–252. [Google Scholar] [CrossRef]
- Meyer-Piening, H.R.; Farshad, M.; Geier, B.; Zimmermann, R. Buckling loads of CFRP composite cylinders under combined axial and torsion loading—Experiments and computations. Compos. Struct. 2001, 53, 427–435. [Google Scholar] [CrossRef]
- Tafreshi, A. Buckling and post-buckling analysis of composite cylindrical shells with cutouts subjected to internal pressure and axial compression loads. Int. J. Press. Vessel. Pip. 2002, 79, 351–359. [Google Scholar] [CrossRef]
- Zhong, H.; Gu, C. Buckling of symmetrical cross-ply composite rectangular plates under a linearly varying in-plane load. Compos. Struct. 2007, 80, 42–48. [Google Scholar] [CrossRef]
- Priyadarsini, R.S.; Kalyanaraman, V.; Srinivasan, S.M. Numerical and experimental study of buckling of advanced fiber composite cylinders under axial compression. Int. J. Struct. Stab. Dyn. 2012, 12, 12500128-1–12500128-25. [Google Scholar] [CrossRef]
- Prabhakaran, S.; Krishnaraj, V.; Senthil Kumar, M.; Zitoune, R. Sound and vibration damping properties of flax fiber reinforced composites. Procedia Eng. 2014, 97, 573–581. [Google Scholar] [CrossRef] [Green Version]
- Sayer, M. Elastic properties and buckling load evaluation of ceramic particles filled glass/epoxy composites. Compos. Part B Eng. 2014, 59, 12–20. [Google Scholar] [CrossRef]
- Abdellaoui, H.; Bensalah, H.; Echaabi, J.; Bouhfid, R.; Qaiss, A. Fabrication, characterization and modelling of laminated composites based on woven jute fibres reinforced epoxy resin. Mater. Des. 2015, 68, 104–113. [Google Scholar] [CrossRef]
- Triki, A.; Karray, M.; Poilâne, C.; Picart, P.; Gargouri, M. Dielectric analysis of the interfacial polarization of alkali treated woven flax fibers reinforced epoxy composites. J. Electrost. 2015, 76, 67–72. [Google Scholar] [CrossRef]
- Bensadoun, F.; Vallons, K.A.M.; Lessard, L.B.; Verpoest, I.; Van Vuure, A.W. Fatigue behaviour assessment of flax–epoxy composites. Compos. Part A Appl. Sci. Manuf. 2016, 82, 253–266. [Google Scholar] [CrossRef]
- Rajesh, M.; Pitchaimani, J. Mechanical properties of natural fiber braided yarn woven composite: Comparison with conventional yarn woven composite. J. Bionic Eng. 2017, 14, 141–150. [Google Scholar] [CrossRef]
- Rajesh, M.; Pitchaimani, J. Experimental investigation on buckling and free vibration behavior of woven natural fiber fabric composite under axial compression. Compos. Struct. 2017, 163, 302–311. [Google Scholar] [CrossRef]
- Suthenthiraveerappa, V.; Gopalan, V. Elastic constants of tapered laminated woven jute/epoxy and woven aloe/epoxy composites under the influence of porosity. J. Reinf. Plast. Compos. 2017, 36, 1453–1469. [Google Scholar] [CrossRef]
- Rozylo, P.; Teter, A.; Debski, H.; Wysmulski, P.; Falkowicz, K. Experimental and numerical study of the buckling of composite profiles with open cross section under axial compression. Appl. Compos. Mater. 2017, 24, 1251–1264. [Google Scholar] [CrossRef] [Green Version]
- Gopalan, V.; Suthenthiraveerappa, V.; Pragasam, V. Experimental and numerical investigation on the dynamic characteristics of thick laminated plant fiber-reinforced polymer composite plates. Arch. Appl. Mech. 2019, 89, 363–384. [Google Scholar] [CrossRef]
- Suthenthiraveerappa, V.; Gopalan, V.; Arumugam, A.B.; Ramasamy, B. Dynamic characterization of the thickness-tapered laminated plant fiber-reinforced polymer composite plates. Adv. Compos. Mater. 2019, 28, 163–191. [Google Scholar] [CrossRef]
- Xu, C.; Rong, D.; Zhou, Z.; Deng, Z.; Lim, C.W. Vibration and buckling characteristics of cracked natural fiber reinforced composite plates with corner point-supports. Eng. Struct. 2020, 214, 110614. [Google Scholar] [CrossRef]
- Chew, E.; Liu, J.L.; Tay, T.E.; Tran, L.Q.N.; Tan, V.B.C. Improving the mechanical properties of natural fibre reinforced laminates composites through Biomimicry. Compos. Struct. 2021, 258, 113208. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Hafezi, P.; Dabbagh, A. Buckling analysis of embedded graphene oxide powder-reinforced nanocomposite shells. Def. Technol. 2021, 17, 226–233. [Google Scholar] [CrossRef]
- Vallala, S.N.; Srikanth, R.; Sreehari, V.M. Evaluation of structural responses of natural fibre reinforced composite plates and pressure vessels. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2021; Volume 1057, p. 012035. [Google Scholar]
- Tuni, A.; Rentizelas, A.; Duffy, A. Environmental performance measurement for green supply chains. Int. J. Phys. Distrib. Logist. Manag. 2018. [Google Scholar] [CrossRef] [Green Version]
- Goh, S.H. Barriers to low-carbon warehousing and the link to carbon abatement. Int. J. Phys. Distrib. Logist. Manag. 2019, 49, 679–704. [Google Scholar] [CrossRef]
- Carbone, V.; Moatti, V.; Schoenherr, T.; Gavirneni, S. From green to good supply chains. Int. J. Phys. Distrib. Logist. Manag. 2019, 49, 839–860. [Google Scholar] [CrossRef]











| FACTORS | LEVELS | ||
|---|---|---|---|
| −1 | 0 | 1 | |
| LAYERS (X1) | 2 | 3 | 4 |
| WIDTH (X2) | 38 | 40 | 42 |
| ORIENTATION (X3) | 45 | 90 | 60 |
| RUN ORDER | LAYERS (X1) | WIDTH (X2) | ORIENTATION (X3) | |||
|---|---|---|---|---|---|---|
| CODED | UNCODED | CODED | UNCODED | CODED | UNCODED | |
| 1 | −1 | 2 | 0 | 40 | 0 | 90 |
| 2 | −1 | 2 | 0 | 40 | 0 | 90 |
| 3 | 0 | 3 | 1 | 42 | −1 | 45 |
| 4 | −1 | 2 | 0 | 40 | −1 | 45 |
| 5 | 1 | 4 | −1 | 38 | 1 | 60 |
| 6 | 0 | 3 | −1 | 38 | 1 | 60 |
| 7 | 1 | 4 | 0 | 40 | 0 | 90 |
| 8 | 0 | 3 | 1 | 42 | 1 | 60 |
| 9 | 1 | 4 | 0 | 40 | 0 | 90 |
| 10 | 0 | 3 | −1 | 38 | −1 | 45 |
| 11 | −1 | 2 | −1 | 38 | 0 | 90 |
| 12 | 1 | 4 | 1 | 42 | 1 | 60 |
| 13 | −1 | 2 | 0 | 40 | 0 | 90 |
| 14 | −1 | 2 | 1 | 42 | 0 | 90 |
| 15 | 1 | 4 | −1 | 38 | −1 | 45 |
| 16 | 1 | 4 | 1 | 42 | −1 | 45 |
| 17 | −1 | 2 | 0 | 40 | 0 | 90 |
| 18 | −1 | 2 | 0 | 40 | 0 | 90 |
| 19 | 0 | 3 | 0 | 40 | 0 | 90 |
| 20 | −1 | 2 | 0 | 40 | 1 | 60 |
| S.NO | NO OF LAYERS | THICKNESS |
|---|---|---|
| 1 | 2 | 1.5 |
| 2 | 3 | 2.1 |
| 3 | 4 | 2.9 |
| FLEXURAL FREQUENCIES (ff) | TORSIONAL FREQUENCIES (ft) | ||
|---|---|---|---|
| WARP | WEFT | WARP | WEFT |
| 637.750 | 650.000 | 756.250 | 731.250 |
| ELASTIC CONSTANTS | EXPERIMENTAL RESULTS |
|---|---|
| E1 (GPa) | 5.968 |
| E2 (GPa) | 5.392 |
| G12 (GPa) | 1.53 |
| µ12 | 0.396 |
| S.NO | SAMPLE O | SPECIMEN LABEL | MAXIMUM CRITICAL BUCKLING LOAD (N) | COMPRESSIVE STRENGTH (MPa) |
|---|---|---|---|---|
| 1. | 2 | 40/2/90 | 80.32322 | 1.33872 |
| 2. | 20 | 40/2/60 | 88.22679 | 1.47045 |
| 3. | 4 | 40/2/45 | 67.88969 | 1.13149 |
| S.NO | SAMPLE NO | SPECIMEN LABEL | CRITICAL BUCKLING LOAD (N) | % OF DEVIATION | |
|---|---|---|---|---|---|
| EXPERIMENTAL | NUMERICAL (ANSYS16) | ||||
| 1. | 2 | 40/2/90 | 80.32 | 85.88 | 6.92 |
| 2. | 20 | 40/2/60 | 88.23 | 85.98 | 2.55 |
| 3. | 4 | 40/2/45 | 67.89 | 68.71 | 1.21 |
| S.NO | SPECIMEN LABEL | LOAD FACTOR | CRITICAL BUCKLING LOAD, N |
|---|---|---|---|
| 1 | 40/2/90 | 0.6878 | 85.875 |
| 2 | 40/2/90 | 0.6878 | 85.875 |
| 3 | 42/3/45 | 2.47294 | 309.1175 |
| 4 | 40/2/45 | 0.54964 | 68.705 |
| 5 | 38/4/60 | 3.2598 | 407.475 |
| 6 | 38/3/60 | 2.1580 | 269.75 |
| 7 | 40/4/90 | 4.4531 | 556.6375 |
| 8 | 42/3/60 | 2.1187 | 264.83 |
| 9 | 40/4/90 | 4.4531 | 556.6375 |
| 10 | 38/3/45 | 1.2908 | 162.26 |
| 11 | 38/2/90 | 0.8356 | 104.4552 |
| 12 | 42/4/60 | 7.8697 | 983.722 |
| 13 | 40/2/90 | 0.6878 | 85.875 |
| 14 | 42/2/90 | 0.7944 | 99.305 |
| 15 | 38/4/45 | 3.0548 | 381.856 |
| 16 | 42/4/45 | 7.6142 | 951.77 |
| 17 | 40/2/90 | 0.6878 | 85.875 |
| 18 | 40/2/90 | 0.6878 | 85.875 |
| 19 | 40/3/90 | 1.972 | 248.41 |
| 20 | 40/2/60 | 0.6878 | 85.9786 |
| S.NO | SPECIMEN LABEL | CRITICAL BUCKLING, (N) | % OF DEVIATION | |
|---|---|---|---|---|
| FEA | REGRESSION EQUATION | |||
| 1 | 40/2/90 | 85.88 | 89.87 | 4.45 |
| 2 | 40/2/90 | 85.88 | 89.87 | 4.45 |
| 3 | 42/3/45 | 309.12 | 285.29 | 8.35 |
| 4 | 40/2/45 | 68.71 | 89.80 | 4.35 |
| 5 | 38/4/60 | 407.48 | 459.04 | 7.23 |
| 6 | 38/3/60 | 269.75 | 258.76 | 6.58 |
| 7 | 40/4/90 | 556.64 | 540.49 | 2.99 |
| 8 | 42/3/60 | 264.83 | 285.86 | 7.36 |
| 9 | 40/4/90 | 556.64 | 540.49 | 2.97 |
| 10 | 38/3/45 | 162.26 | 197.93 | 8.02 |
| 11 | 38/2/90 | 104.46 | 117.87 | 11.38 |
| 12 | 42/4/60 | 983.72 | 415.70 | 12.45 |
| 13 | 40/2/90 | 85.88 | 89.87 | 4.45 |
| 14 | 42/2/90 | 99.31 | 94.89 | 4.65 |
| 15 | 38/4/45 | 381.86 | 355.34 | 7.46 |
| 16 | 42/4/45 | 951.77 | 372.27 | 14.55 |
| 17 | 40/2/90 | 85.88 | 89.87 | 4.45 |
| 18 | 40/2/90 | 85.88 | 89.87 | 4.45 |
| 19 | 40/3/90 | 248.41 | 289.70 | 12.26 |
| 20 | 40/2/60 | 85.98 | 77.63 | 10.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gopalan, V.; Suthenthiraveerappa, V.; David, J.S.; Subramanian, J.; Annamalai, A.R.; Jen, C.-P. Experimental and Numerical Analyses on the Buckling Characteristics of Woven Flax/Epoxy Laminated Composite Plate under Axial Compression. Polymers 2021, 13, 995. https://doi.org/10.3390/polym13070995
Gopalan V, Suthenthiraveerappa V, David JS, Subramanian J, Annamalai AR, Jen C-P. Experimental and Numerical Analyses on the Buckling Characteristics of Woven Flax/Epoxy Laminated Composite Plate under Axial Compression. Polymers. 2021; 13(7):995. https://doi.org/10.3390/polym13070995
Chicago/Turabian StyleGopalan, Venkatachalam, Vimalanand Suthenthiraveerappa, Jefferson Stanley David, Jeyanthi Subramanian, A. Raja Annamalai, and Chun-Ping Jen. 2021. "Experimental and Numerical Analyses on the Buckling Characteristics of Woven Flax/Epoxy Laminated Composite Plate under Axial Compression" Polymers 13, no. 7: 995. https://doi.org/10.3390/polym13070995
APA StyleGopalan, V., Suthenthiraveerappa, V., David, J. S., Subramanian, J., Annamalai, A. R., & Jen, C.-P. (2021). Experimental and Numerical Analyses on the Buckling Characteristics of Woven Flax/Epoxy Laminated Composite Plate under Axial Compression. Polymers, 13(7), 995. https://doi.org/10.3390/polym13070995