Transient Three-Dimensional Flow Field Measurements by Means of 3D µPTV in Drying Poly(Vinyl Acetate)-Methanol Thin Films Subject to Short-Scale Marangoni Instabilities
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials, Solution Preparation, Coating, and Drying
2.2. Transient 3D Flow-Field Measurements
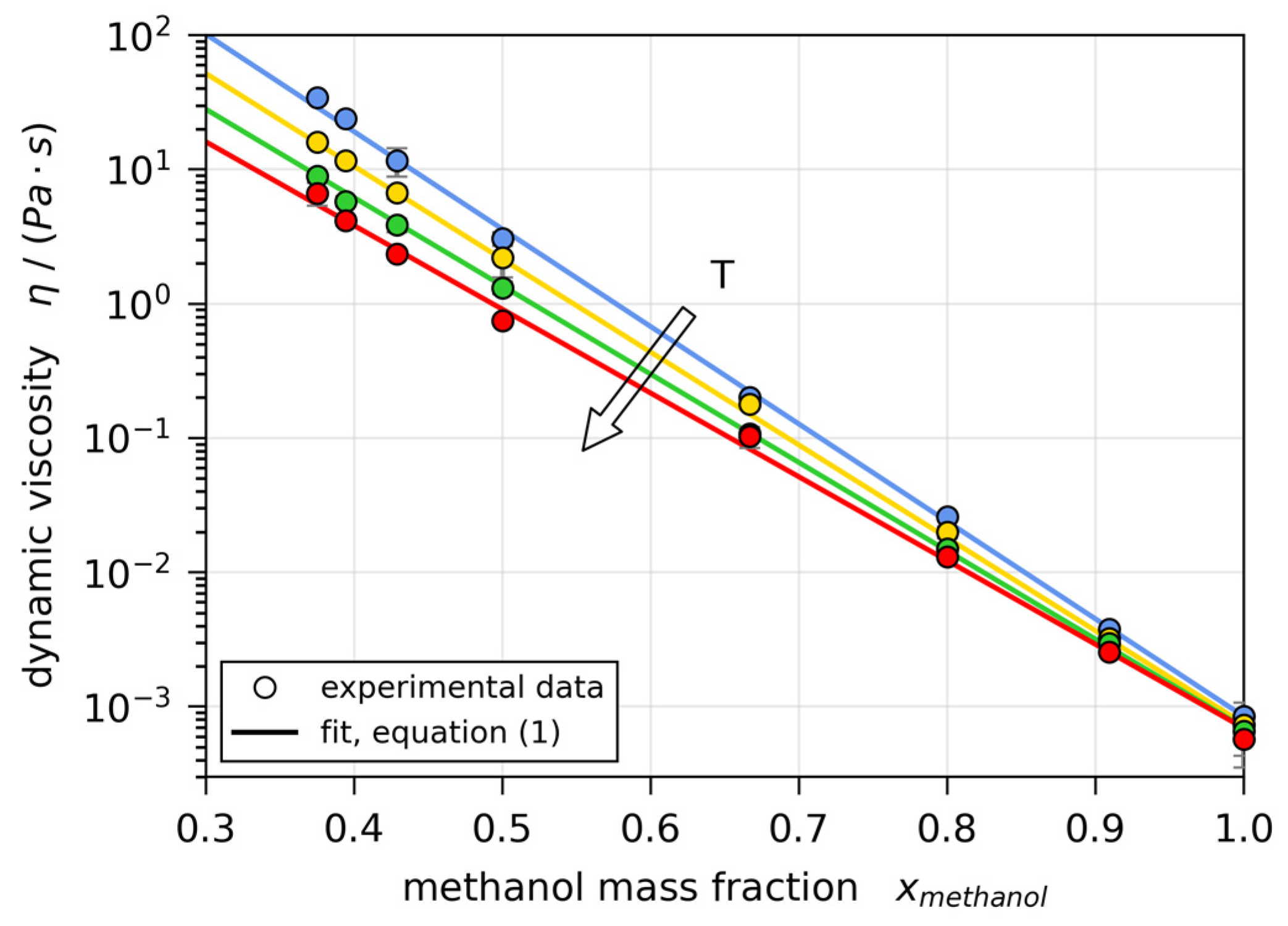
2.3. Material Properties
2.4. Marangoni Number Assessment
3. Results
3.1. Convective (In)Stability
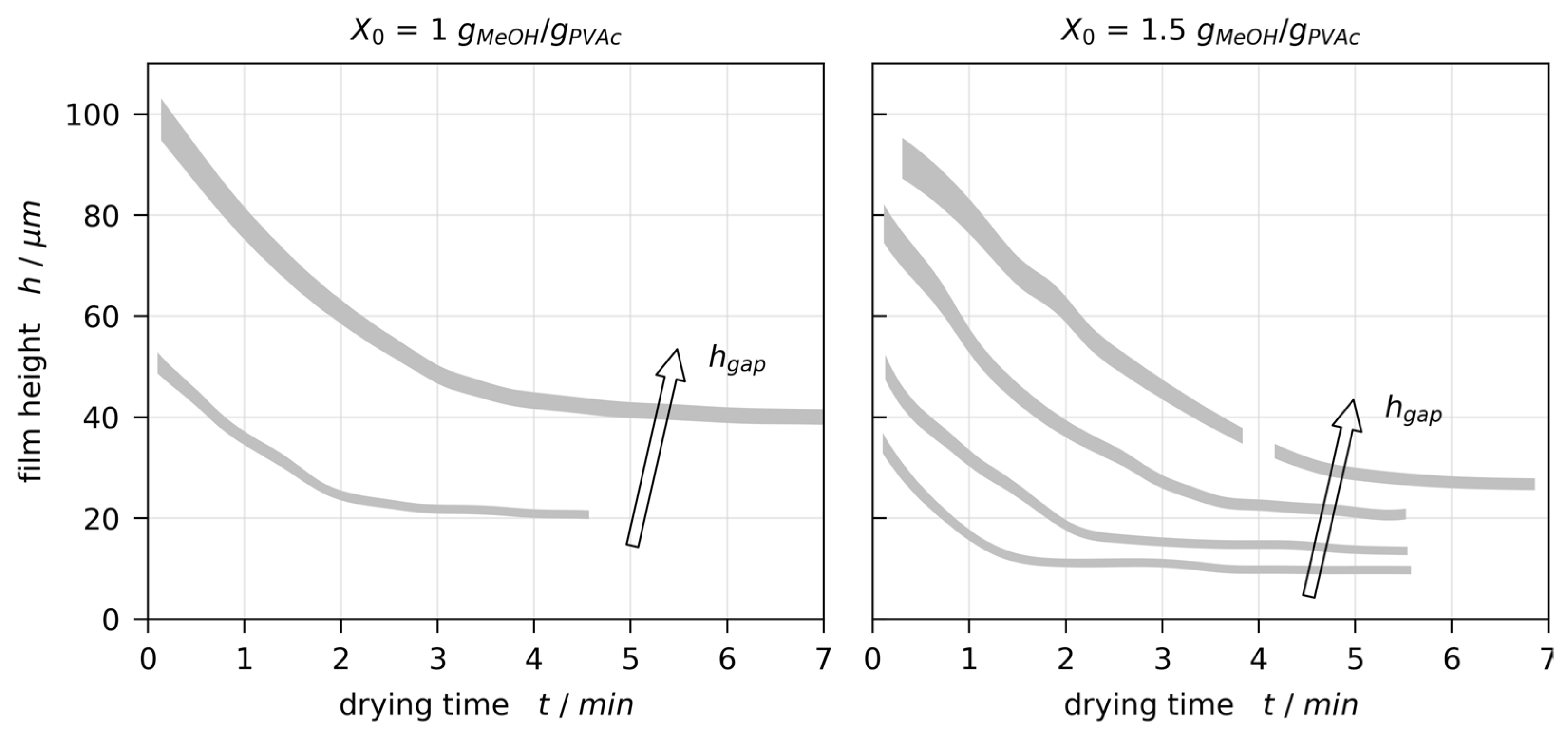
3.2. Film Thickness
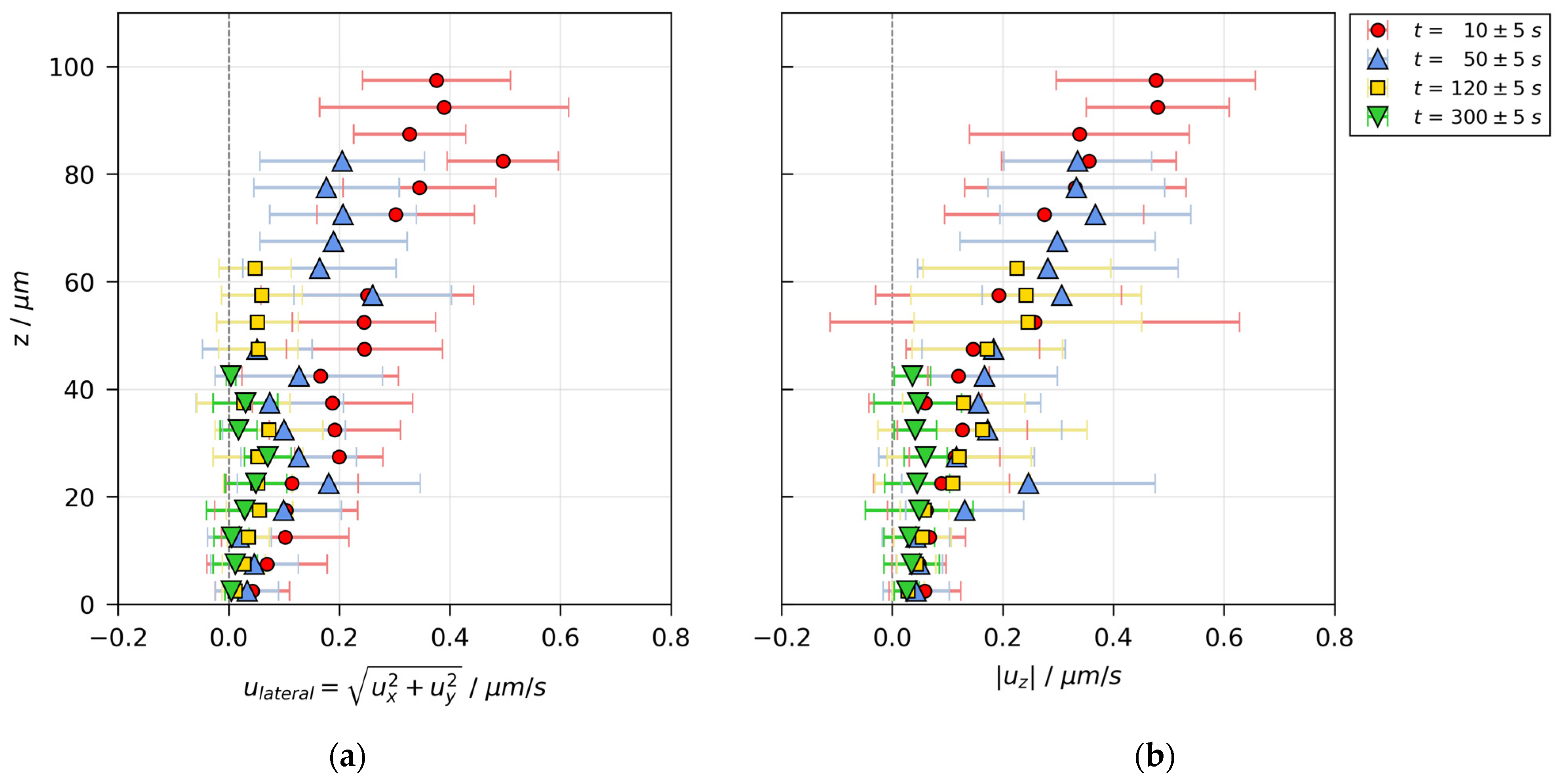
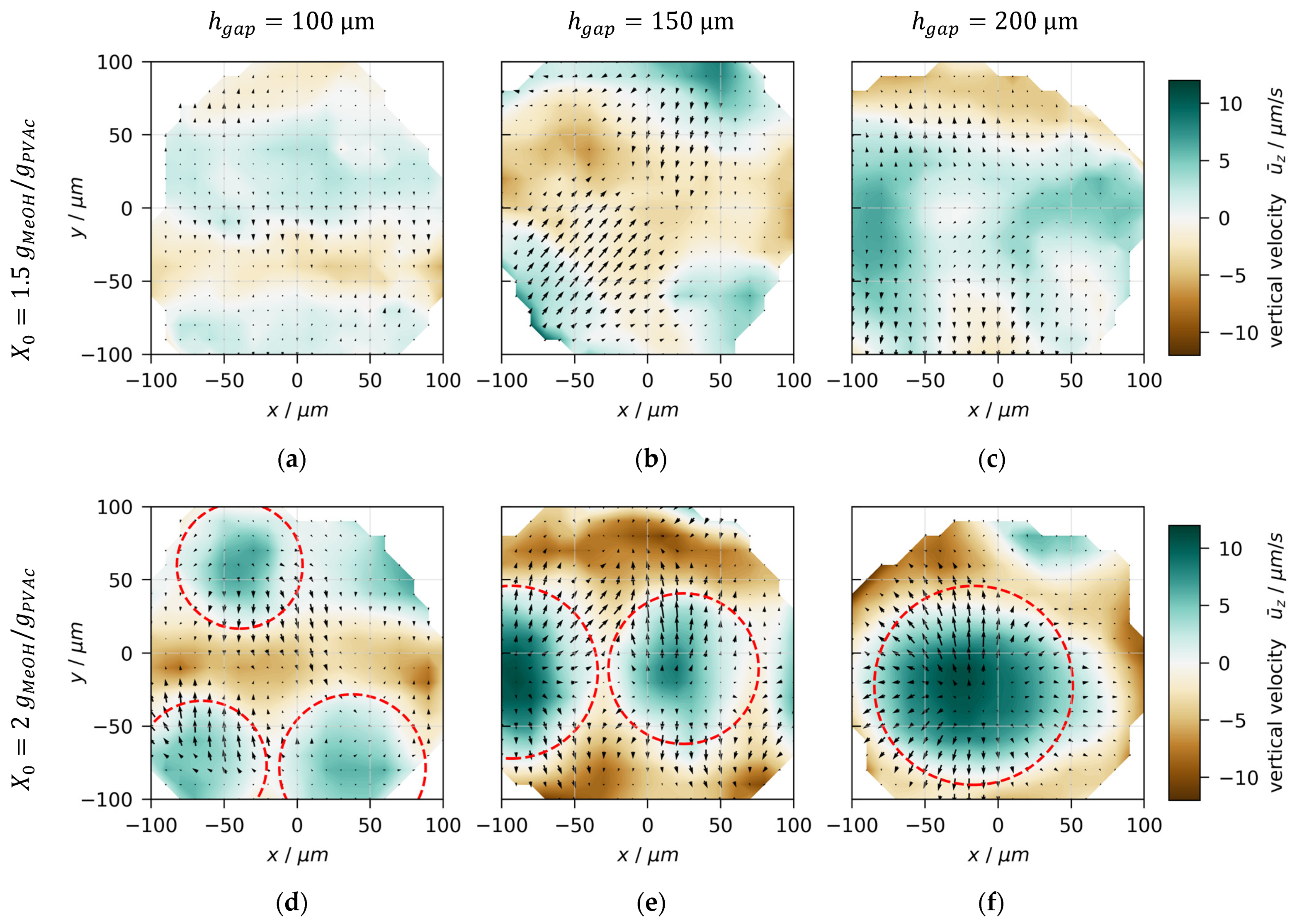
3.3. Velocity Distributions
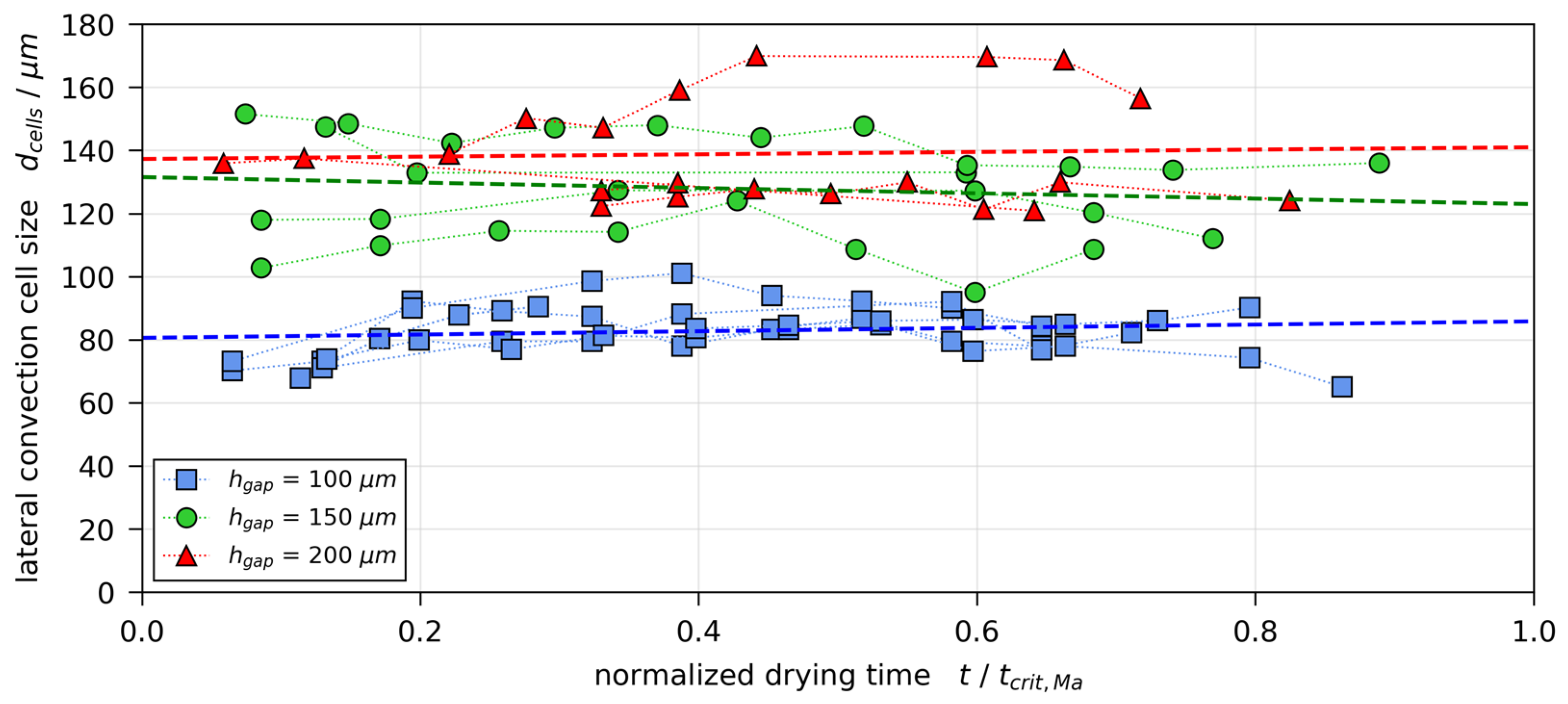
3.4. Convection Cell Pattern and Size
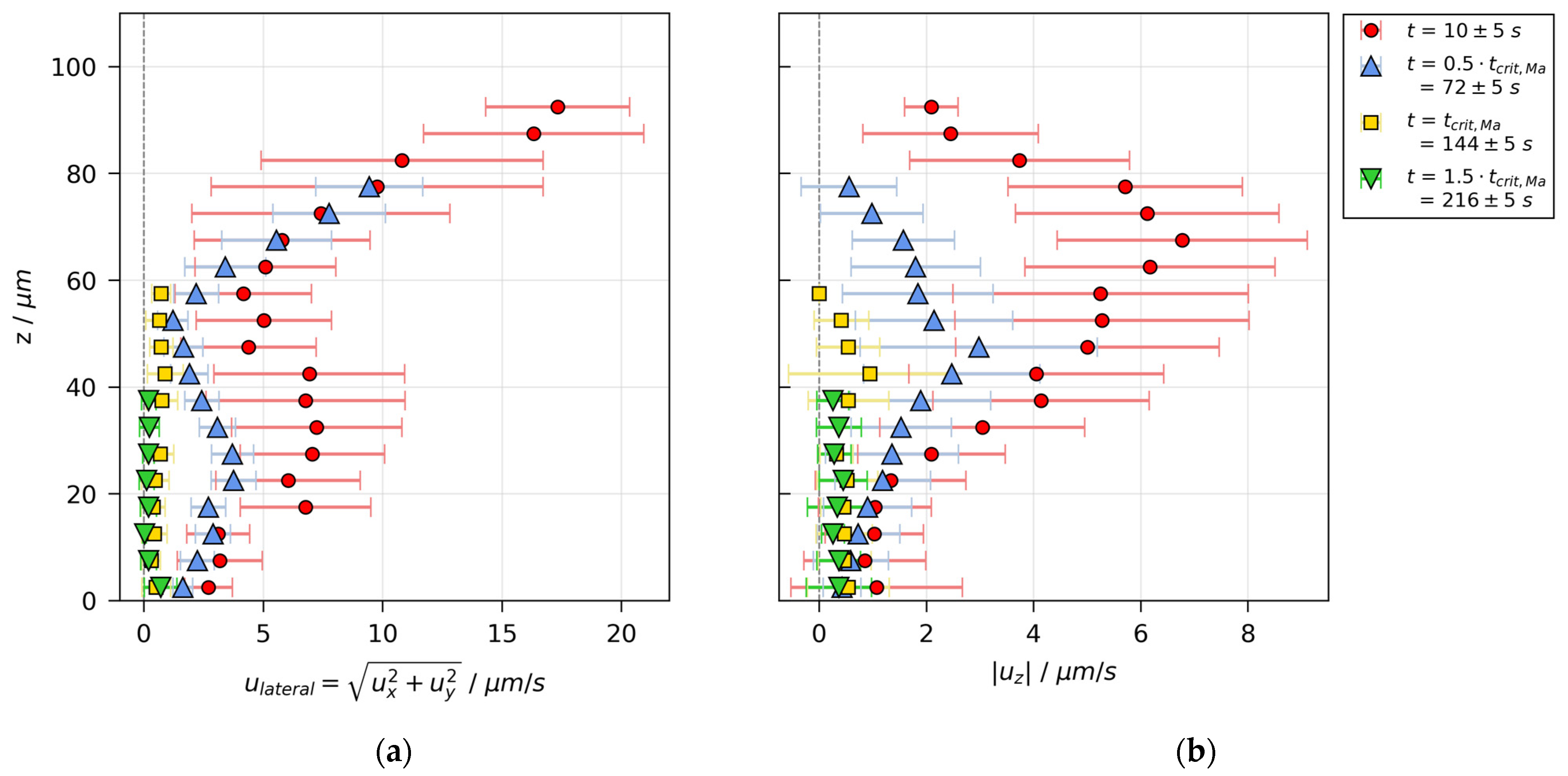
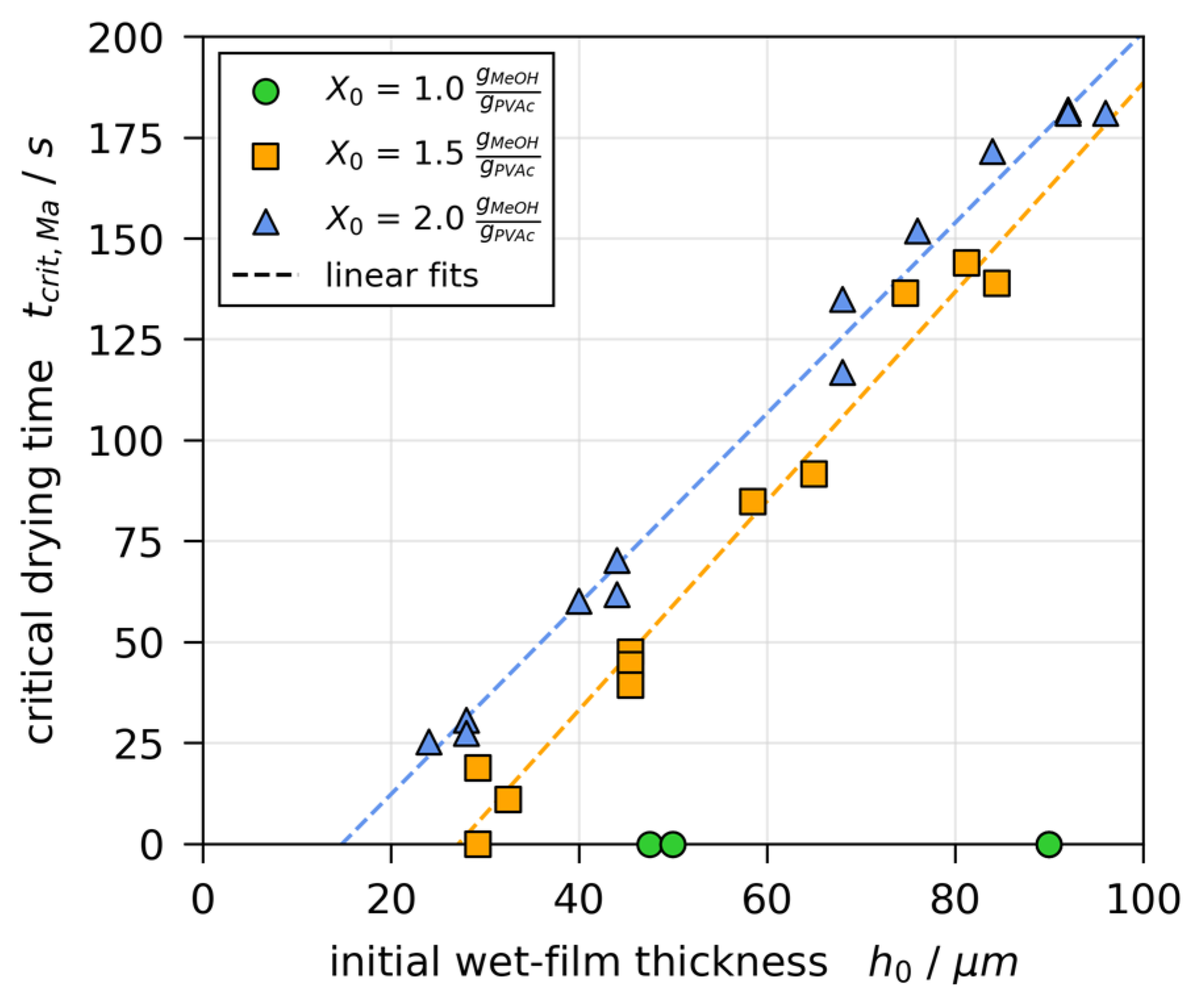
3.5. Stability Threshold and Upper Limit of Marangoni Numbers
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Property | Unit | Value | Source | |
|---|---|---|---|---|
| own data (DMA 4100 M, Anton Paar) | ||||
| own data (Abbemat, Dr. Kernchen) | ||||
| to | [73] | |||
| [73] |
| Property | Unit | Value | Source | |
|---|---|---|---|---|
| [74] | ||||
| own data (Abbemat, Dr. Kernchen) | ||||
| [75] | ||||
| [75] |
| Property | Mixing Rule Equation | Source |
|---|---|---|
| [73] | ||
| [19] | ||
| [73] | ||
| [73] |
Appendix B
Appendix C
References
- Schweizer, P.M. Experimental methods. In Liquid Film Coating; Kistler, S.F., Schweizer, P.M., Eds.; Springer: Berlin/Heidelberg, Germany, 1997; ISBN 978-94-010-6246-6. [Google Scholar]
- Weinstein, S.J.; Palmer, H.J. Capillary hydrodynamics and interfacial phenomena. In Liquid Film Coating; Kistler, S.F., Schweizer, P.M., Eds.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 19–62. ISBN 978-94-010-6246-6. [Google Scholar]
- Bénard, H. Étude expérimentale des courants de convection dans une nappe liquide—Régime permanent: Tourbillons cellulaires. J. Phys. Theor. Appl. 1900, 9, 513–524. [Google Scholar] [CrossRef]
- Bénard, H. Les tourbillons cellulaires dans une nappe liquide—Méthodes optiques d’observation et d’enregistrement. J. Phys. Theor. Appl. 1901, 10, 254–266. [Google Scholar] [CrossRef]
- Pearson, J.R.A. On convection cells induced by surface tension. J. Fluid Mech. 1958, 4, 489. [Google Scholar] [CrossRef]
- Schatz, M.F.; Neitzel, G.P. Experiments on thermocapillary instabilities. Annu. Rev. Fluid Mech. 2001, 33, 93–127. [Google Scholar] [CrossRef]
- Rahal, S.; Cerisier, P.; Azuma, H. Bénard-Marangoni convection in a small circular container: Influence of the Biot and Prandtl numbers on pattern dynamics and free surface deformation. Exp. Fluids 2007, 43, 547–554. [Google Scholar] [CrossRef]
- Craster, R.V.; Matar, O.K. Dynamics and stability of thin liquid films. Rev. Mod. Phys. 2009, 81, 1131–1198. [Google Scholar] [CrossRef]
- Chai, A.-T.; Zhang, N. Experimental study of Marangoni-Benard convection in a liquid layer induced by evaporation. Exp. Heat Transf. 1998, 11, 187–205. [Google Scholar] [CrossRef]
- Zhang, N.; Chao, D.F. Mechanisms of convection instability in thin liquid layers induced by evaporation. Int. Commun. Heat Mass Transf. 1999, 26, 1069–1080. [Google Scholar] [CrossRef]
- Oron, A.; Davis, S.H.; Bankoff, S.G. Long-scale evolution of thin liquid films. Rev. Mod. Phys. 1997, 69, 931–980. [Google Scholar] [CrossRef]
- Gambaryan-Roisman, T. Modulation of Marangoni convection in liquid films: Reinhard Miller, honorary issue. Adv. Colloid Interface Sci. 2015, 222, 319–331. [Google Scholar] [CrossRef] [PubMed]
- Karbalaei, A.; Kumar, R.; Cho, H.J. Thermocapillarity in microfluidics—A review. Micromachines 2016, 7, 13. [Google Scholar] [CrossRef] [PubMed]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids, 5th ed.; McGraw-Hill: New York, NY, USA, 2001; ISBN 0-07-011682-2. [Google Scholar]
- De Gennes, P.G. Instabilities during the evaporation of a film: Non-glassy polymer + volatile solvent. Eur. Phys. J. E 2001, 6, 421–424. [Google Scholar] [CrossRef]
- Yiantsios, S.G.; Serpetsi, S.K.; Doumenc, F.; Guerrier, B. Surface deformation and film corrugation during drying of polymer solutions induced by Marangoni phenomena. Int. J. Heat Mass Transf. 2015, 89, 1083–1094. [Google Scholar] [CrossRef]
- Toussaint, G.; Bodiguel, H.; Doumenc, F.; Guerrier, B.; Allain, C. Experimental characterization of buoyancy- and surface tension-driven convection during the drying of a polymer solution. Int. J. Heat Mass Transf. 2008, 51, 4228–4237. [Google Scholar] [CrossRef]
- Bassou, N.; Rharbi, Y. Role of Bénard-Marangoni instabilities during solvent evaporation in polymer surface corrugations. Langmuir 2009, 25, 624–632. [Google Scholar] [CrossRef] [PubMed]
- Schabel, W. Trocknung von Polymerfilmen. Messung von Konzentrationsprofilen mit der Inversen-Mikro-Raman-Spektroskopie. Ph.D. Thesis, KIT Faculty of Chemical and Process Engineering, Karlsruhe, Germany, June 2004. [Google Scholar]
- Clarke, N. Instabilities in thin-film binary mixtures. Eur. Phys. J. E 2004, 14, 207–210. [Google Scholar] [CrossRef] [PubMed]
- Clarke, N. Toward a model for pattern formation in ultrathin-film binary mixtures. Macromolecules 2005, 38, 6775–6778. [Google Scholar] [CrossRef]
- Bestehorn, M.; Pototsky, A.; Thiele, U. 3D large scale Marangoni convection in liquid films. Eur. Phys. J. E 2003, 33, 457–467. [Google Scholar] [CrossRef]
- Sarkar, J.; Sharma, A. A unified theory of instabilities in viscoelastic thin films: From wetting to confined films, from viscous to elastic films, and from short to long waves. Langmuir 2010, 26, 8464–8473. [Google Scholar] [CrossRef]
- Kaya, H.; Jérôme, B.; Colinet, P. Marangoni effect from density variations in apolar ultrathin films. Europhys. Lett. 2006, 74, 861–867. [Google Scholar] [CrossRef]
- Borcia, R.; Bestehorn, M. Controlled pattern formation in thin liquid layers. Langmuir 2009, 25, 1919–1922. [Google Scholar] [CrossRef] [PubMed]
- McTaggart, C.L. Convection driven by concentration- and temperature-dependent surface tension. J. Fluid Mech. 1983, 134, 301–310. [Google Scholar] [CrossRef]
- Serpetsi, S.K.; Yiantsios, S.G. Stability characteristics of solutocapillary Marangoni motion in evaporating thin films. Phys. Fluids 2012, 24, 122104. [Google Scholar] [CrossRef]
- Hennessy, M.G.; Munch, A. Dynamics of a slowly evaporating solvent-polymer mixture with a deformable upper surface. IMA J. Appl. Math. 2014, 79, 681–720. [Google Scholar] [CrossRef]
- Machrafi, H.; Rednikov, A.; Colinet, P.; Dauby, P. Bénard instabilities in a binary-liquid layer evaporating into an inert gas. J. Colloid Interface Sci. 2010, 349, 331–353. [Google Scholar] [CrossRef]
- Bahloul, A.; Delahaye, R.; Vasseur, P.; Robillard, L. Effect of surface tension on convection in a binary fluid layer under a zero gravity environment. Int. J. Heat Mass Transf. 2003, 46, 1759–1771. [Google Scholar] [CrossRef]
- Wu, K.-H.; Lu, S.-Y.; Chen, H.-L.; Chen, Y.-Y. Two-dimensional Marangoni-instability-induced periodic patterns of polymer blend films cast on tilted substrates. Macromol. Chem. Phys. 2008, 209, 615–624. [Google Scholar] [CrossRef]
- Bormashenko, E.; Pogreb, R.; Musin, A.; Stanevsky, O.; Bormashenko, Y.; Whyman, G.; Gendelman, O.; Barkay, Z. Self-assembly in evaporated polymer solutions: Influence of the solution concentration. J. Colloid Interface Sci. 2006, 297, 534–540. [Google Scholar] [CrossRef]
- Ma, H.; Hao, J. Ordered patterns and structures via interfacial self-assembly: Superlattices, honeycomb structures and coffee rings. Chem. Soc. Rev. 2011, 40, 5457–5471. [Google Scholar] [CrossRef]
- Sakurai, S.; Furukawa, C.; Okutsu, A.; Miyoshi, A.; Nomura, S. Control of mesh pattern of surface corrugation via rate of solvent evaporation in solution casting of polymer film in the presence of convection. Polymer 2002, 43, 3359–3364. [Google Scholar] [CrossRef]
- Weh, L. Surface structures in thin polymer layers caused by coupling of diffusion-controlled Marangoni instability and local horizontal temperature gradient. Macromol. Mater. Eng. 2005, 290, 976–986. [Google Scholar] [CrossRef]
- Bormashenko, E.; Balter, S.; Pogreb, R.; Bormashenko, Y.; Gendelman, O.; Aurbach, D. On the mechanism of patterning in rapidly evaporated polymer solutions: Is temperature-gradient-driven Marangoni instability responsible for the large-scale patterning? J. Colloid Interface Sci. 2010, 343, 602–607. [Google Scholar] [CrossRef] [PubMed]
- Minařík, A.; Smolka, P.; Lapčík, L. Preliminary investigation of factors determining self-organised structures preparation in polymer layers. Int. J. Heat Mass Transf. 2011, 54, 4135–4142. [Google Scholar] [CrossRef]
- Minařík, A.; Rafajová, M.; Rajnohová, E.; Smolka, P.; Mráček, A. Self-organised patterns in polymeric films solidified from diluted solutions—The effect of the substrate surface properties. Int. J. Heat Mass Transf. 2014, 78, 615–623. [Google Scholar] [CrossRef]
- Chmelař, J.; Mrazek, J.; Dusankova, M.; Novotny, J.; Velebny, V. Convective patterns in solution-casted films from acylated hyaluronan. Macromol. Chem. Phys. 2019, 220, 1800515. [Google Scholar] [CrossRef]
- Bormashenko, E.; Pogreb, R.; Stanevsky, O.; Bormashenko, Y.; Gendelman, O. Formation of honeycomb patterns in evaporated polymer solutions: Influence of the molecular weight. Mater. Lett. 2005, 59, 3553–3557. [Google Scholar] [CrossRef]
- Bormashenko, E.; Pogreb, R.; Stanevsky, O.; Bormashenko, Y.; Tamir, S.; Cohen, R.; Nunberg, M.; Gaisin, V.-Z.; Gorelik, M.; Gendelman, O.V. Mesoscopic and submicroscopic patterning in thin polymer films: Impact of the solvent. Mater. Lett. 2005, 59, 2461–2464. [Google Scholar] [CrossRef]
- Cavadini, P.; Krenn, J.; Scharfer, P.; Schabel, W. Investigation of surface deformation during drying of thin polymer films due to Marangoni convection. Chem. Eng. Process. 2013, 64, 24–30. [Google Scholar] [CrossRef]
- Schwarzenberger, K.; Köllner, T.; Linde, H.; Boeck, T.; Odenbach, S.; Eckert, K. Pattern formation and mass transfer under stationary solutal Marangoni instability. Adv. Colloid Interface Sci. 2014, 206, 344–371. [Google Scholar] [CrossRef]
- Wang, J.-M.; Liu, G.-H.; Fang, Y.-L.; Li, W.-K. Marangoni effect in nonequilibrium multiphase system of material processing. Rev. Chem. Eng. 2016, 32, 2. [Google Scholar] [CrossRef]
- Touazi, O.; Chénier, E.; Doumenc, F.; Guerrier, B. Simulation of transient Rayleigh-Bénard-Marangoni convection induced by evaporation. Int. J. Heat Mass Transf. 2010, 53, 656–664. [Google Scholar] [CrossRef]
- Trouette, B.; Chénier, E.; Doumenc, F.; Delcarte, C.; Guerrier, B. Transient Rayleigh-Bénard-Marangoni solutal convection. Phys. Fluids 2012, 24, 74108. [Google Scholar] [CrossRef]
- Siebel, D.K. Zur Mehrkomponentendiffusion in Polymer-Lösemittel-Systemen. Untersuchungen im Kontext der Polymerfilmtrocknung Mittels Inverser Mikro-Raman-Spektroskopie. Ph.D. Thesis, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany, February 2017. [Google Scholar]
- Romdhane, I.H.; Price, P.E.; Miller, C.A.; Benson, P.T.; Wang, S. Drying of glassy polymer films. Ind. Eng. Chem. Res. 2001, 40, 3065–3075. [Google Scholar] [CrossRef]
- Price, P.E.; Romdhane, I.H. Multicomponent diffusion theory and its applications to polymer-solvent systems. AIChE J. 2003, 49, 309–322. [Google Scholar] [CrossRef]
- Arya, R.K. Measurement of concentration profiles in thin film binary polymer-solvent coatings using confocal raman spectroscopy: Free volume model validation. Dry. Technol. 2014, 32, 992–1002. [Google Scholar] [CrossRef]
- Sharma, J.; Arya, R.K.; Verros, G.D. A unified model for the drying of glassy polymer coatings. Prog. Org. Coat. 2019, 134, 219–225. [Google Scholar] [CrossRef]
- Arya, R.K.; Tewari, K.; Shukla, S. Non-Fickian drying of binary polymeric coatings: Depth profiling study using confocal Raman spectroscopy. Prog. Org. Coat. 2016, 95, 8–19. [Google Scholar] [CrossRef]
- Siebel, D.; Scharfer, P.; Schabel, W. Determination of concentration-dependent diffusion coefficients in polymer-solvent systems: Analysis of concentration profiles measured by Raman spectroscopy during single drying experiments excluding boundary conditions and phase equilibrium. Macromolecules 2015, 48, 8608–8614. [Google Scholar] [CrossRef]
- Naseri, A.T.; Cetindag, E.; Bilgili, E.; Davé, R.N. A predictive transport model for convective drying of polymer strip films loaded with a BCS Class II drug. Eur. J. Pharm. Biopharm. 2019, 137, 164–174. [Google Scholar] [CrossRef]
- Guerrier, B.; Bouchard, C.; Allain, C.; Bénard, C. Drying kinetics of polymer films. AIChE J. 1998, 44, 791–798. [Google Scholar] [CrossRef]
- Okazaki, M.; Shioda, K.; Masuda, K.; Toei, R. Drying mechanism of coated film of polymer solution. J. Chem. Eng. Jpn. 1974, 7, 99–105. [Google Scholar] [CrossRef]
- Schabel, W.; Scharfer, P.; Kind, M.; Mamaliga, I. Sorption and diffusion measurements in ternary polymer-solvent-solvent systems by means of a magnetic suspension balance—Experimental methods and correlations with a modified Flory-Huggins and free-volume theory. Chem. Eng. Sci. 2007, 62, 2254–2266. [Google Scholar] [CrossRef]
- Sharma, J.; Tewari, K.; Arya, R.K. Diffusion in polymeric systems—A review on free volume theory. Prog. Org. Coat. 2017, 111, 83–92. [Google Scholar] [CrossRef]
- Mamaliga, I.; Schabel, W.; Kind, M. Measurements of sorption isotherms and diffusion coefficients by means of a magnetic suspension balance. Chem. Eng. Process. 2004, 43, 753–763. [Google Scholar] [CrossRef]
- Scharfer, P. Zum Stofftransport in Brennstoffzellenmembranen. Untersuchungen mit Hilfe der Konfokalen Mikro-Raman-Spektroskopie. Ph.D. Thesis, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany, 2009. [Google Scholar]
- Hiemenz, P.C.; Lodge, T.P. Polymer Chemistry, 2nd ed.; CRC Press: Hoboken, NJ, USA, 2007; ISBN 9781574447798. [Google Scholar]
- Chow, T.S. Molecular interpretation of the glass transition temperature of polymer-diluent systems. Macromolecules 1980, 13, 362–364. [Google Scholar] [CrossRef]
- Sharma, J.; Ahuja, S.; Arya, R.K. Depth profile study of poly(styrene)-poly(methyl methacrylate)-tetrahydrofuran coatings. Prog. Org. Coat. 2019, 134, 297–302. [Google Scholar] [CrossRef]
- Merklein, L.; Eser, J.C.; Börnhorst, T.; Könnecke, N.; Scharfer, P.; Schabel, W. Different dominating mass transport mechanisms for drying and sorption of toluene-PMMA films—Visualized with Raman spectroscopy. Polymer 2021, 222, 123640. [Google Scholar] [CrossRef]
- Kishimoto, A. Diffusion and viscosity of polyvinyl acetate-diluent systems. J. Polym. Sci. 1964, 2, 1421–1439. [Google Scholar] [CrossRef]
- Schnell, M.; Wolf, B.A. Excess viscosity and glass transition. Polymer 2001, 42, 8599–8605. [Google Scholar] [CrossRef]
- Berry, G.C.; Fox, T.G. The viscosity of polymers and their concentrated solutions. In Fortschritte der Hochpolymeren-Forschung; Cantow, H.-J., Dall’Asta, G., Ferry, J.D., Kern, W., Natta, G., Okamura, S., Overberger, C.G., Prins, W., Schulz, G.V., Slichter, W.P., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 1968; pp. 261–357. [Google Scholar]
- Schabel, W.; Ludwig, I.; Kind, M. Measurements of concentration profiles in polymeric solvent coatings by means of an inverse confocal micro raman spectrometer—Initial results. Dry. Technol. 2004, 22, 285–294. [Google Scholar] [CrossRef]
- Cavadini, P.; Weinhold, H.; Tönsmann, M.; Chilingaryan, S.; Kopmann, A.; Lewkowicz, A.; Miao, C.; Scharfer, P.; Schabel, W. Investigation of the flow structure in thin polymer films using 3D µPTV enhanced by GPU. Exp. Fluids 2018, 59, 370. [Google Scholar] [CrossRef]
- Tönsmann, M.; Kröhl, F.; Cavadini, P.; Scharfer, P.; Schabel, W. Calibration routine for quantitative three-dimensional flow field measurements in drying polymer solutions subject to Marangoni convection. Colloids Interfaces 2019, 3, 39. [Google Scholar] [CrossRef]
- Speidel, M.; Jonáš, A.; Florin, E.-L. Three-dimensional tracking of fluorescent nanoparticles with subnanometer precision by use of off-focus imaging. Opt. Lett. 2003, 28, 69. [Google Scholar] [CrossRef] [PubMed]
- Al-Fariss, T.; Al-Zahrani, S. Rheological behaviour of some dilute polymer solutions. Eng. Sci. 1993, 5, 95–109. [Google Scholar] [CrossRef]
- Kind, M.; Martin, H. VDI-Wärmeatlas, 11th ed.; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-19980-6. [Google Scholar]
- Wiley, R.H.; Brauer, G.M. Specific refractivity-temperature data for polyvinyl acetate and polybutyl acrylate. J. Polym. Sci. 1949, 4, 351–357. [Google Scholar] [CrossRef]
- Van Krevelen, D.W.; Nijenhuis, K.T. Their correlation with chemical structure; their numerical estimation and prediction from additive group contributions. In Properties of Polymers, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2009; ISBN 978-0-08-054819-7. [Google Scholar]



| 1 | 200 | |||
| 2 | 200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tönsmann, M.; Scharfer, P.; Schabel, W. Transient Three-Dimensional Flow Field Measurements by Means of 3D µPTV in Drying Poly(Vinyl Acetate)-Methanol Thin Films Subject to Short-Scale Marangoni Instabilities. Polymers 2021, 13, 1223. https://doi.org/10.3390/polym13081223
Tönsmann M, Scharfer P, Schabel W. Transient Three-Dimensional Flow Field Measurements by Means of 3D µPTV in Drying Poly(Vinyl Acetate)-Methanol Thin Films Subject to Short-Scale Marangoni Instabilities. Polymers. 2021; 13(8):1223. https://doi.org/10.3390/polym13081223
Chicago/Turabian StyleTönsmann, Max, Philip Scharfer, and Wilhelm Schabel. 2021. "Transient Three-Dimensional Flow Field Measurements by Means of 3D µPTV in Drying Poly(Vinyl Acetate)-Methanol Thin Films Subject to Short-Scale Marangoni Instabilities" Polymers 13, no. 8: 1223. https://doi.org/10.3390/polym13081223
APA StyleTönsmann, M., Scharfer, P., & Schabel, W. (2021). Transient Three-Dimensional Flow Field Measurements by Means of 3D µPTV in Drying Poly(Vinyl Acetate)-Methanol Thin Films Subject to Short-Scale Marangoni Instabilities. Polymers, 13(8), 1223. https://doi.org/10.3390/polym13081223






