A Novel and Highly Effective Natural Vibration Modal Analysis to Predict Nominal Strength of Open Hole Glass Fiber Reinforced Polymer Composites Structure
Abstract
:1. Introduction
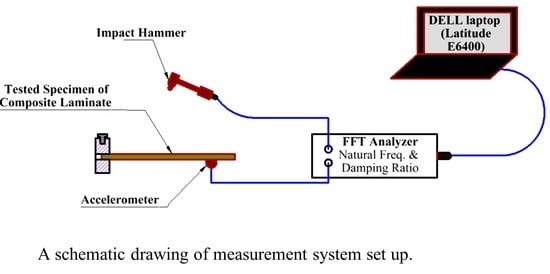
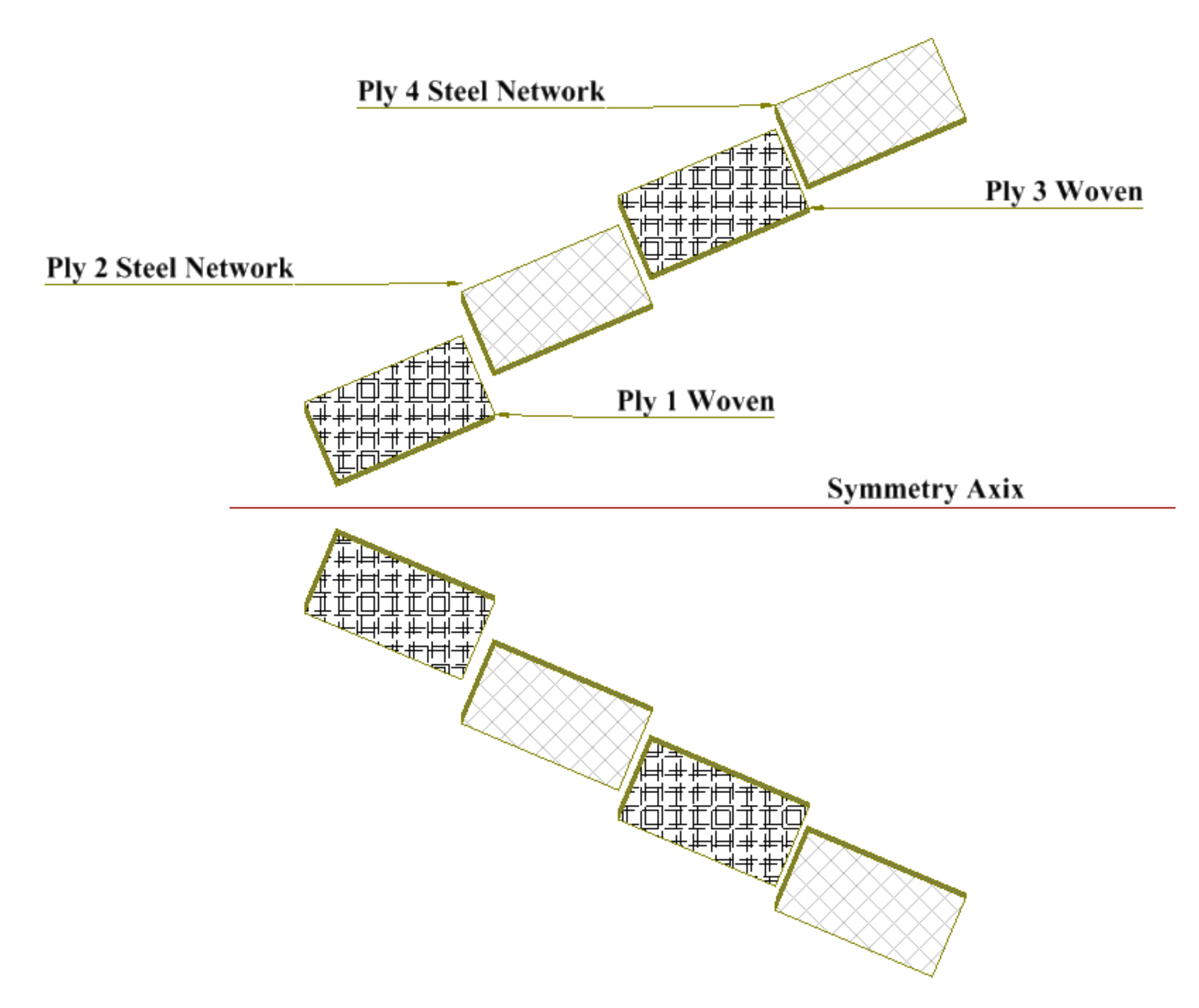
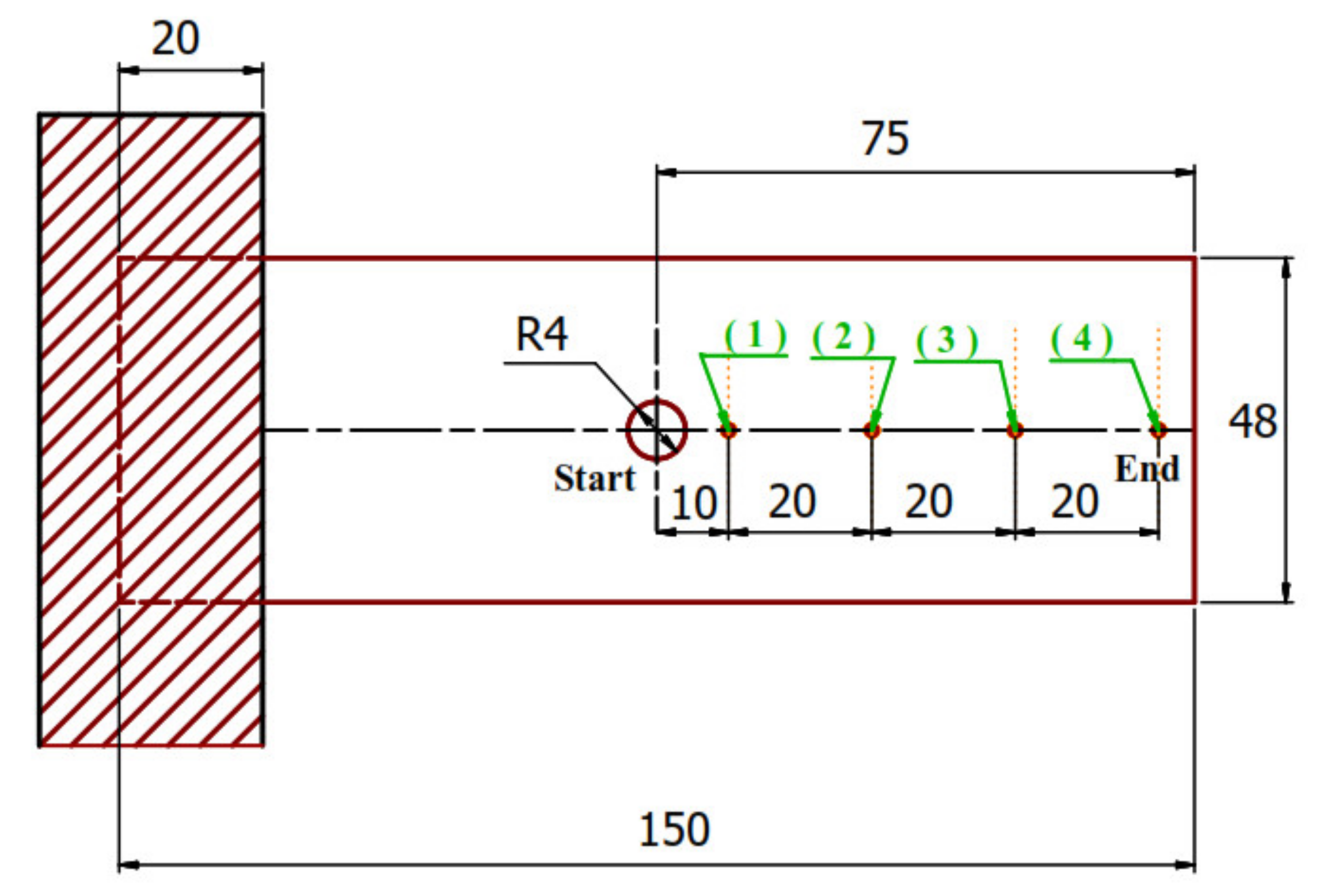
2. Materials and Methods
3. Vibration Modal Analysis
4. Mathematical Modal Analysis
4.1. Elastic Modulus Perdiction Based on Elasticity Theory
4.2. The Nominal Strength of Open Hole Based on LEFM Theory
5. Finite Element Method
6. Results and Discussion
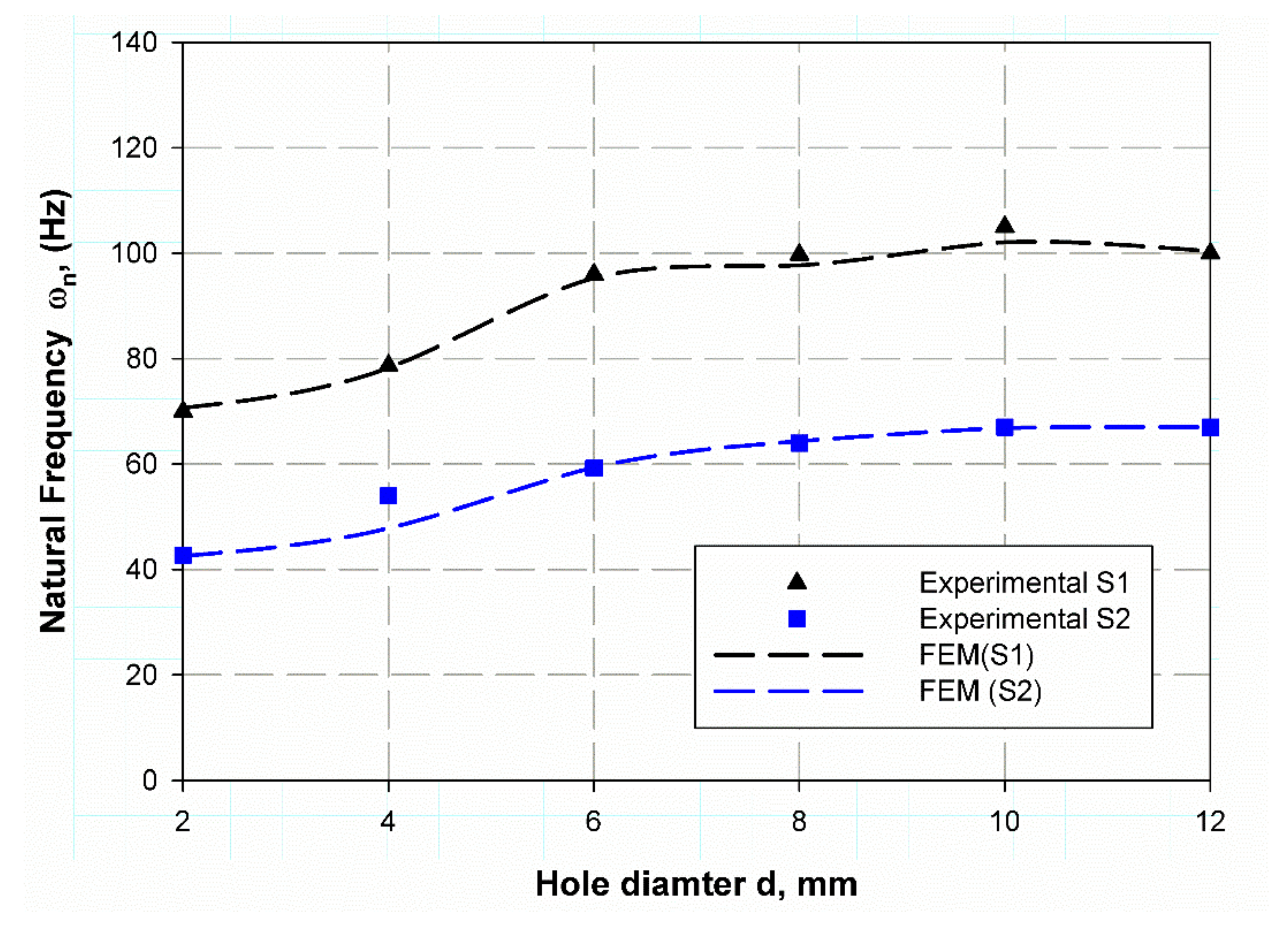
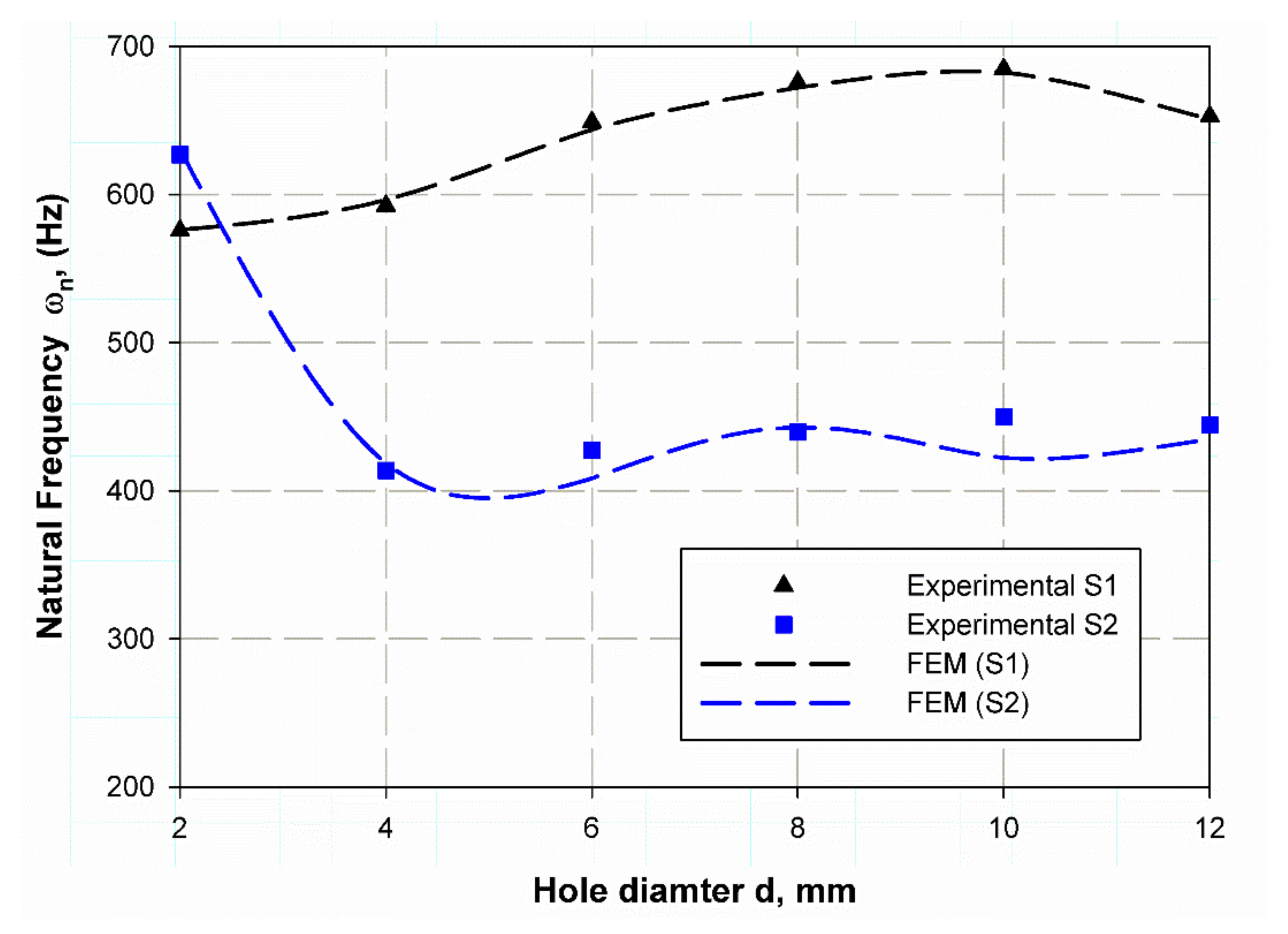
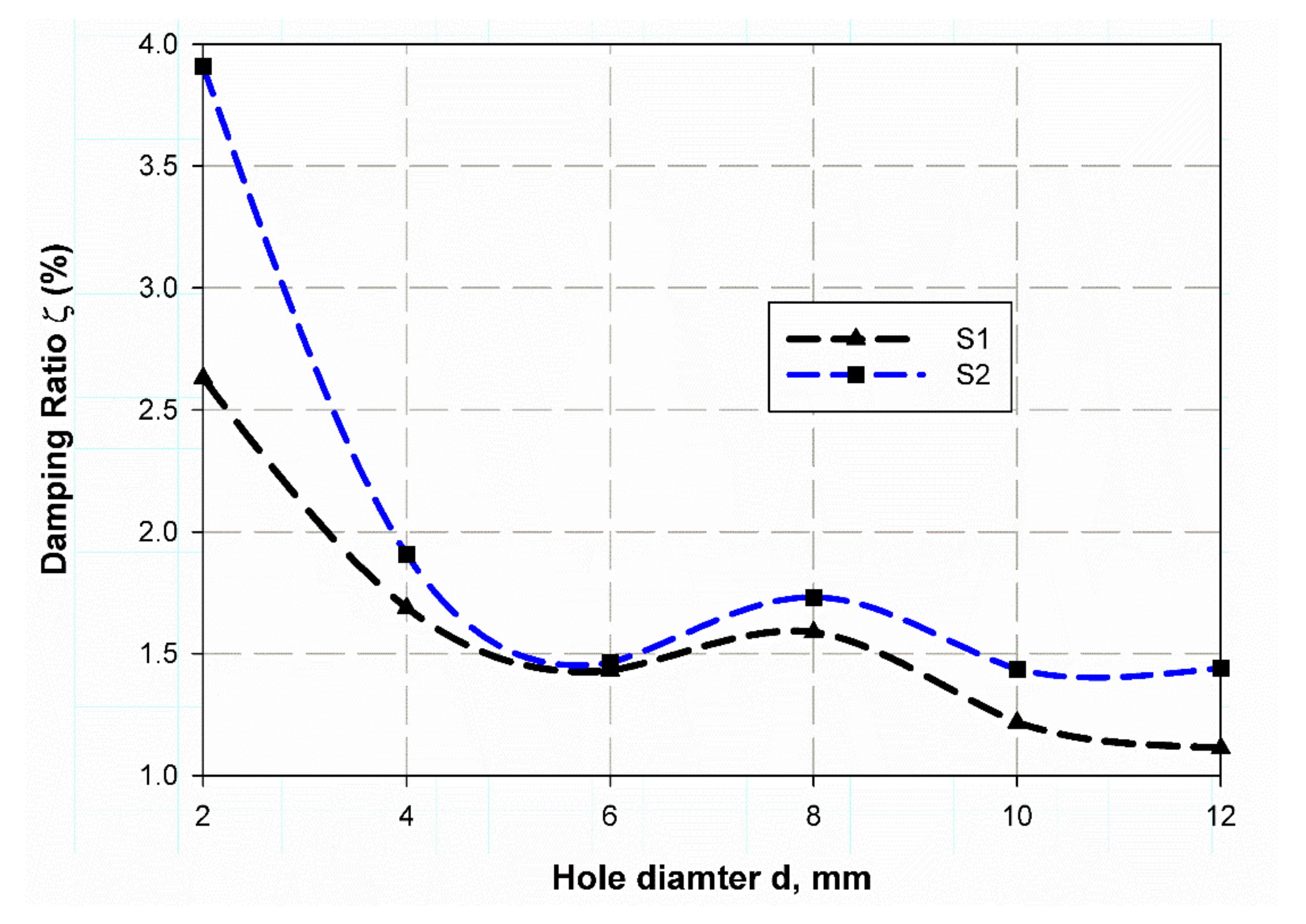
6.1. Modal Analysis
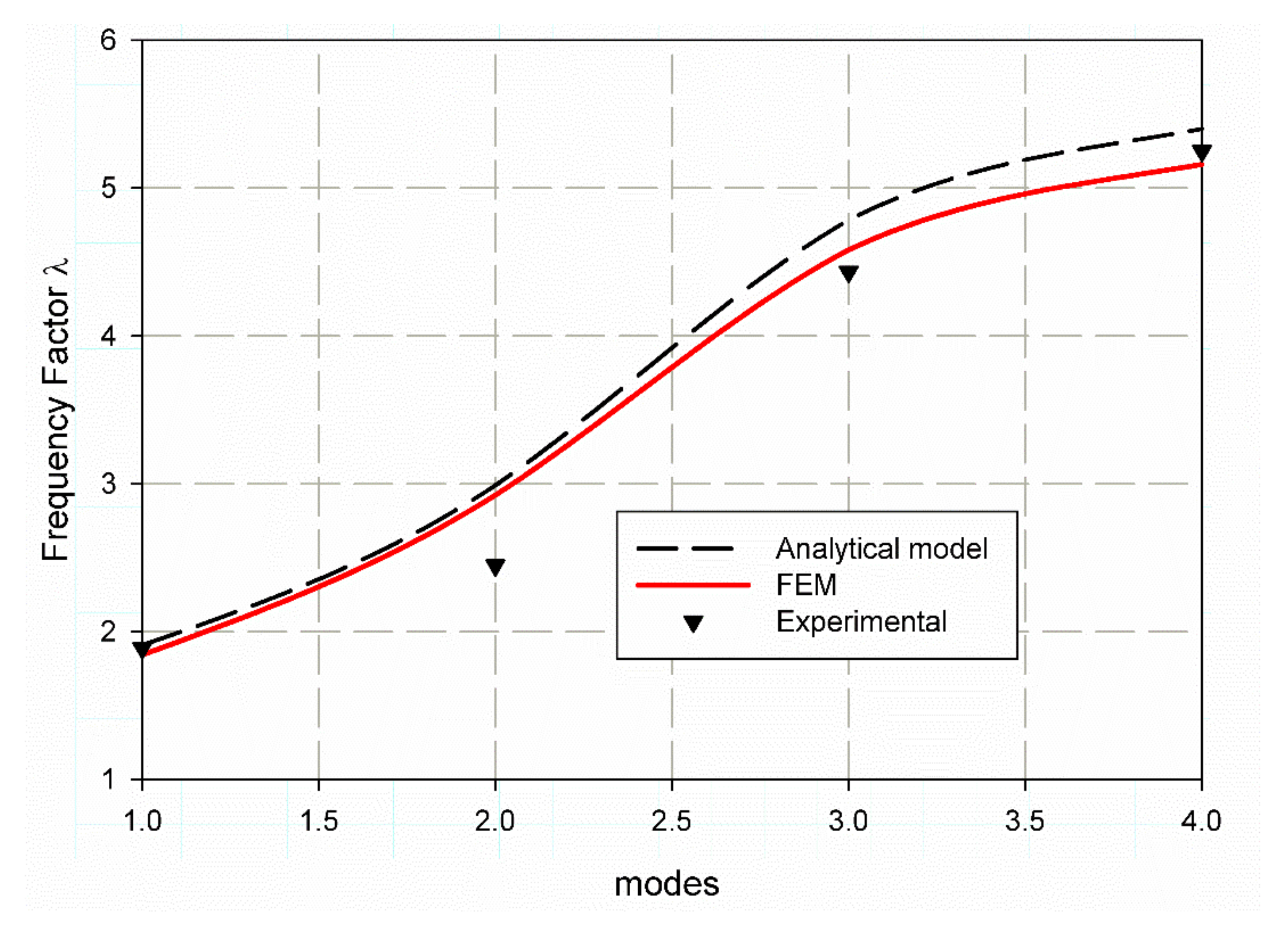
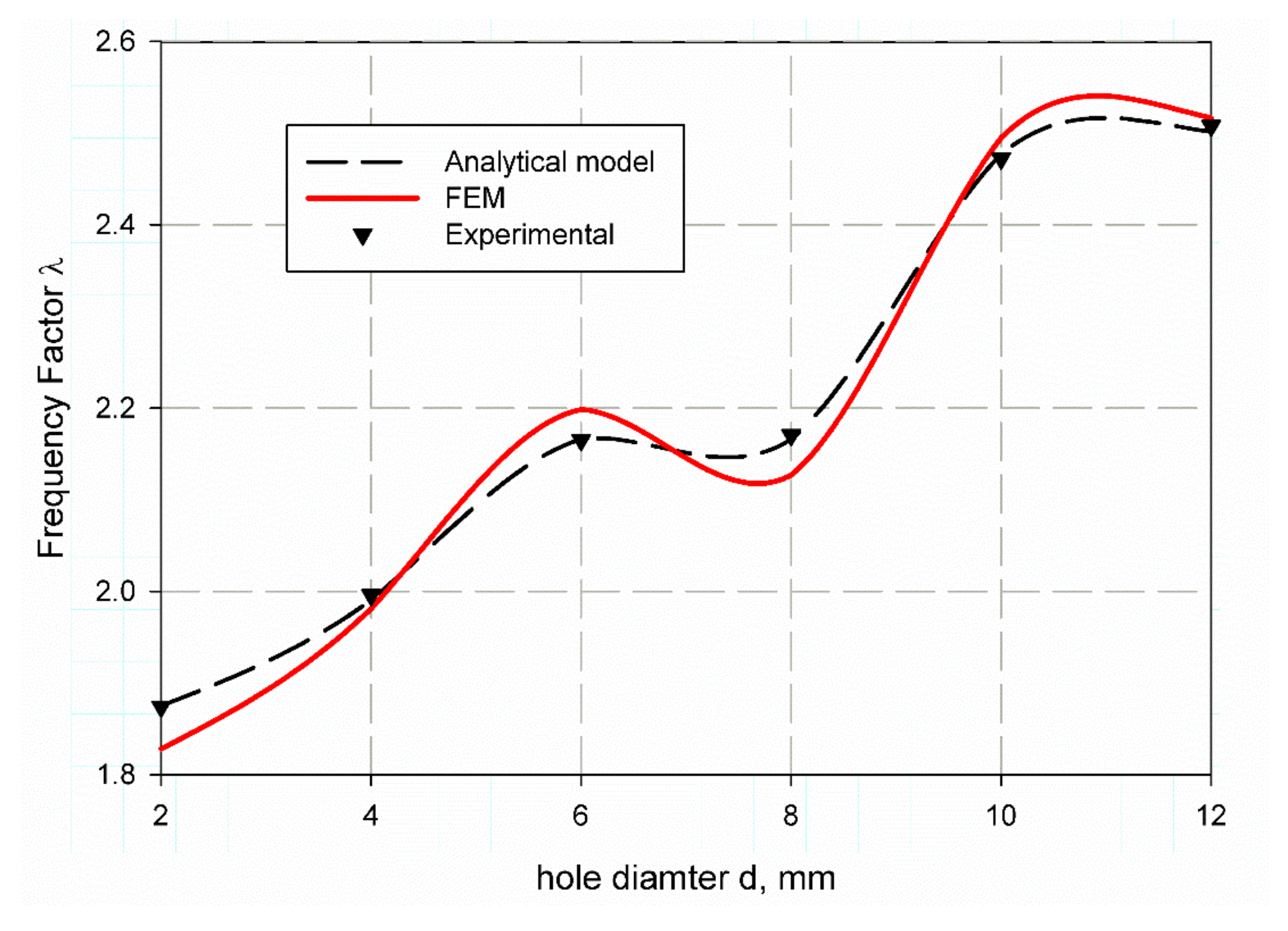
6.2. Frequency Factor Prediction Using FEM
6.3. Strength Prediction
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alharthi, H.; Abdellah, M.Y.; Abdo, H.S.; Hassan, M.K. Size Effect and Fracture Toughness of Glass Fiber Composite Structures. Int. J. Adv. Sci. Technol. 2020, 29, 8567–8577. [Google Scholar]
- Abdellah, M.Y. An approximate analytical model for modification of size effect law for open-hole composite structure under biaxial load. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020. [Google Scholar] [CrossRef]
- Liu, Z.; Ardabilian, M.; Zine, A.; Ichchou, M. Crack damage identification of a thick composite sandwich structure based on Gaussian Processes classification. Compos. Struct. 2021, 255, 112825. [Google Scholar] [CrossRef]
- Abdellah, M.Y.; Mohamed, A.F.; Hasan, M.K. Characteristic Analysis: Vibration Behaviour of Composite Laminated Structures Compared to Monotonic Materials. Int. J. Mech. Mechatron. Eng. IJMME IJENS 2019, 19, 57–69. [Google Scholar]
- Hashemi, S.H.; Atashipour, S.R.; Fadaee, M. An exact analytical approach for in-plane and out-of-plane free vibration analysis of thick laminated transversely isotropic plates. Arch. Appl. Mech. 2011, 82, 677–698. [Google Scholar] [CrossRef]
- Srinivasa, C.V.; Suresh, Y.J.; Kumar, W.P.P. Experimental and finite element studies on free vibration of skew plates. Int. J. Adv. Struct. Eng. 2014, 6, 48. [Google Scholar]
- Song, M.; Gong, Y.; Yang, J.; Zhu, W.; Kitipornchai, S. Nonlinear free vibration of cracked functionally graded graphene platelet-reinforced nanocomposite beams in thermal environments. J. Sound Vib. 2020, 468, 115115. [Google Scholar] [CrossRef]
- Zenkour, A.M.; El-Shahrany, H.D. Hygrothermal vibration of adaptive composite magnetostrictive laminates supported by elastic substrate medium. Eur. J. Mech. A Solids 2021, 85, 104140. [Google Scholar] [CrossRef]
- Sharma, A.K.; Mittal, N.D. Free vibration analysis of laminated composite plates with elastically restrained edges using FEM. Open Eng. 2013, 3, 306–315. [Google Scholar] [CrossRef]
- Noman, M.; Petru, M. Functional properties of sonochemically synthesized zinc oxide nanoparticles and cotton composites. Nanomaterials 2020, 10, 1661. [Google Scholar] [CrossRef]
- Behera, P.; Noman, M.T.; Petru, M. Enhanced Mechanical Properties of Eucalyptus-Basalt-Based Hybrid-Reinforced Cement Composites. Polymers 2020, 12, 2837. [Google Scholar] [CrossRef]
- Abdellah, M.Y.; Alharthi, H.; Hassan, M.K.; Mohamed, A.F. Effect of specimen size on natural vibration of open hole copper/glass-reinforced epoxy laminate composites. AIMS Mater. Sci. 2020, 7, 499–517. [Google Scholar] [CrossRef]
- Liu, G.; Zhao, X.; Dai, K.; Zhong, Z.; Li, G.; Han, X. Static and free vibration analysis of laminated composite plates using the conforming radial point interpolation method. Compos. Sci. Technol. 2008, 68, 354–366. [Google Scholar] [CrossRef]
- Kumar, V.; Singh, S.J.; Saran, V.H.; Harsha, S.P. Vibration characteristics of porous FGM plate with variable thickness resting on Pasternak’s foundation. Eur. J. Mech. A Solids 2021, 85, 104124. [Google Scholar] [CrossRef]
- Foroutan, K.; Carrera, E.; Ahmadi, H. Nonlinear hygrothermal vibration and buckling analysis of imperfect FG-CNTRC cylindrical panels embedded in viscoelastic foundations. Eur. J. Mech. A Solids 2021, 85, 104107. [Google Scholar] [CrossRef]
- Wang, J.; Cao, S.; Zhang, W. Thermal vibration and buckling analysis of functionally graded carbon nanotube reinforced composite quadrilateral plate. Eur. J. Mech. A Solids 2021, 85, 104105. [Google Scholar] [CrossRef]
- Rahimi, A.; Livani, M.; Negahban Boron, A. Free vibration analysis of functionally graded material beams with transverse crack. J. Mech. Eng. 2021, 51, 277–281. [Google Scholar]
- AlHazmi, M.W.; Alsoufi, M.S.; Backar, A.; Zaafrani, A. Finite Element Modeling of a Cantilever for Counteracting Vibration Induced Deflection. Int. J. Mech. Mechatron. Eng. 2019, 19, 131–144. [Google Scholar]
- Yunus, M.; Alsoufi, M.S.; Hussain, H.I. Sound Source Localization and Mapping Using Acoustic Intensity Method for Noise Control in Automobiles and Machines. IJIRSET 2015, 4, 6173–6185. [Google Scholar]
- Rajab, M.I.; El-Benawy, T.A.; Al-Hazmi, M.W. Application of frequency domain processing to X-ray radiographic images of welding defects. J. X Ray Sci. Technol. 2007, 15, 147–156. [Google Scholar]
- Noman, M.T.; Petru, M.; Militký, J.; Azeem, M.; Ashraf, M.A. One-Pot Sonochemical Synthesis of ZnO Nanoparticles for Photocatalytic Applications, Modelling and Optimization. Materials 2019, 13, 14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiao, B.; Huang, Q.; Chen, H.; Chen, X.; Long, G. A Fractal Model for Capillary Flow Through a Single Tortuous Capillary with Roughened Surfaces in Fibrous Porous Media. Fractals 2021, 29, 2150017. [Google Scholar] [CrossRef]
- Xiao, B.; Zhang, Y.; Wang, Y.; Jiang, G.; Liang, M.; Chen, X.; Long, G. A Fractal Model for Kozeny–Carman Constant and Dimensionless Permeability of Fibrous Porous Media with Roughened Surfaces. Fractals 2019, 27, 1950116. [Google Scholar] [CrossRef]
- Khashaba, U. In-plane shear properties of cross-ply composite laminates with different off-axis angles. Compos. Struct. 2004, 65, 167–177. [Google Scholar] [CrossRef]
- Mohammed, Y.; Hassan, M.K.; H, A.E.-A.; Hashem, A. Effect of stacking sequence and geometric scaling on the brittleness number of glass fiber composite laminate with stress raiser. Sci. Eng. Compos. Mater. 2014, 21, 281–288. [Google Scholar] [CrossRef]
- Jones, R.M. Mechanics of Composite Materials; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Mallick, P.K. Composites Engineering Handbook; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- ASTM-D3171. In Standard Test Methods for Constituent Content of Composite Materials Astm International; American Society for Testing and Materials: West Conshohocken, PA, USA, 2011.
- Abdellah, M.Y. Delamination Modeling of Double Cantilever Beam of Unidirectional Composite Laminates. J. Fail. Anal. Prev. 2017, 17, 1011–1018. [Google Scholar] [CrossRef]
- Abdelhaleem, A.M.; Abdellah, M.Y.; Fathi, H.I.; Dewidar, M. Mechanical Properties of ABS Embedded with Basalt Fiber Fillers. J. Manuf. Sci. Prod. 2016, 16, 69–74. [Google Scholar] [CrossRef]
- Mohamed, K.H.; Mohammed, Y.A.; Azabi, K.S.; Marzouk, W.W. Investigation of the Mechanical Behavior of Novel Fiber Metal. Laminates. Int. J. Mech. Mechatron. Eng. IJMME IJENS 2015, 15, 112–118. [Google Scholar]
- Korim, N.S.; Abdellah, M.Y.; Dewidar, M.; Abdelhaleem, A.M.M. Crushable Finite Element Modeling of Mechanical Properties of Titanium Foam. Int. J. Sci. Eng. Res. 2015, 6, 1221–1227. [Google Scholar]
- Hassan, M.K.; Abdellah, M.Y.; Azabi, S.K.; Marzouk, W.W. Fracture Toughness of a Novel GLARE Composite Material. Int. J. Eng. Technol. IJET IJENS 2015, 15, 36–41. [Google Scholar]
- Abdellah, M.Y.; Alsoufi, M.S.; Hassan, M.K.; Ghulman, H.A.; Mohamed, A.F. Extended Finite Element Numerical Analysis of Scale Effect in Notched Glass Fiber Reinforced Epoxy Composite. Arch. Mech. Eng. 2015, 62, 217–236. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, Y.; Hassan, M.K.; Hashem, A. Analytical model to predict multiaxial laminate fracture toughness from 0° ply fracture toughness. Polym. Eng. Sci. 2013, 54, 234–238. [Google Scholar] [CrossRef]
- Mohamed, K.; Hassan, Y.M.; Abu El-Ainin, H. Improvement of Al-6061 alloys mechanical properties by controlling processing parameters. Int. J. Mech. Mechatron. Eng. IJMME IJENS 2012, 12, 14–18. [Google Scholar]
- Golwala, S. Lecture Notes on Classical Mechanics for Physics 106ab; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2014. [Google Scholar]
- Ngo-Cong, D.; Mai-Duy, N.; Karunasena, W.; Tran-Cong, T. Free vibration analysis of laminated composite plates based on FSDT using one-dimensional IRBFN method. Comput. Struct. 2011, 89, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Gowda, C.V.; Rajanna, N.; Udupa, N. Investigating the effects of delamination location and size on the vibration behaviour of laminated composite beams. Mater. Today Proc. 2017, 4, 10944–10951. [Google Scholar] [CrossRef]
- Nikolakopoulos, P.; Katsareas, D.; Papadopoulos, C. Crack identification in frame structures. Comput. Struct. 1997, 64, 389–406. [Google Scholar] [CrossRef]
- Narkis, Y.; Elmalah, E. Crack identification in a cantilever beam under uncertain end conditions. Int. J. Mech. Sci. 1996, 38, 499–507. [Google Scholar] [CrossRef]
- Çolakoğlu, M. Damping and vibration analysis of polyethylene fiber composite under varied temperature. Turk. J. Eng. Environ. Sci. 2007, 30, 351–357. [Google Scholar]
- Sakiyama, T.; Huang, M. Free Vibration Analysis of Rectangular Plates with Variable Thickness. J. Sound Vib. 1998, 216, 379–397. [Google Scholar] [CrossRef] [Green Version]
- Warburton, G.B. The Vibration of Rectangular Plates. Proc. Inst. Mech. Eng. 1954, 168, 371–384. [Google Scholar] [CrossRef]
- Soutis, C.; Curtis, P. A method for predicting the fracture toughness of CFRP laminates failing by fibre microbuckling. Compos. Part A Appl. Sci. Manuf. 2000, 31, 733–740. [Google Scholar] [CrossRef]
- Hahn, G.; Rosenfield, A. Local yielding and extension of a crack under plane stress. Acta Met. 1965, 13, 293–306. [Google Scholar] [CrossRef]
- Perez, N. Crack Tip Plasticity. In Fracture Mechanics; Springer: Cham, Switzerland, 2017; pp. 187–225. [Google Scholar]
- Sonawane, A.R.; Talmale, P.S. Modal Analysis of Single Rectangular Cantilever Plate by Mathematically, FEA and Experimental. Int. Res. J. Eng. Technol. 2017, 4, 264–269. [Google Scholar]
- Azam, S.; Fragoso, A. Experimental and Numerical Simulation Study of the Vibration Properties of Thin Copper Films Bonded to FR4 Composite. Appl. Sci. 2020, 10, 5197. [Google Scholar] [CrossRef]
- Khashaba, U. Tensile and flexural properties of randomly oriented gfrp composites. In 1st International Conference on Mechanical Engineering Advanced Technology for Industrial Production; Assiut University: Assiut, Egypt, 1994; Volume 1, pp. 131–143. [Google Scholar]




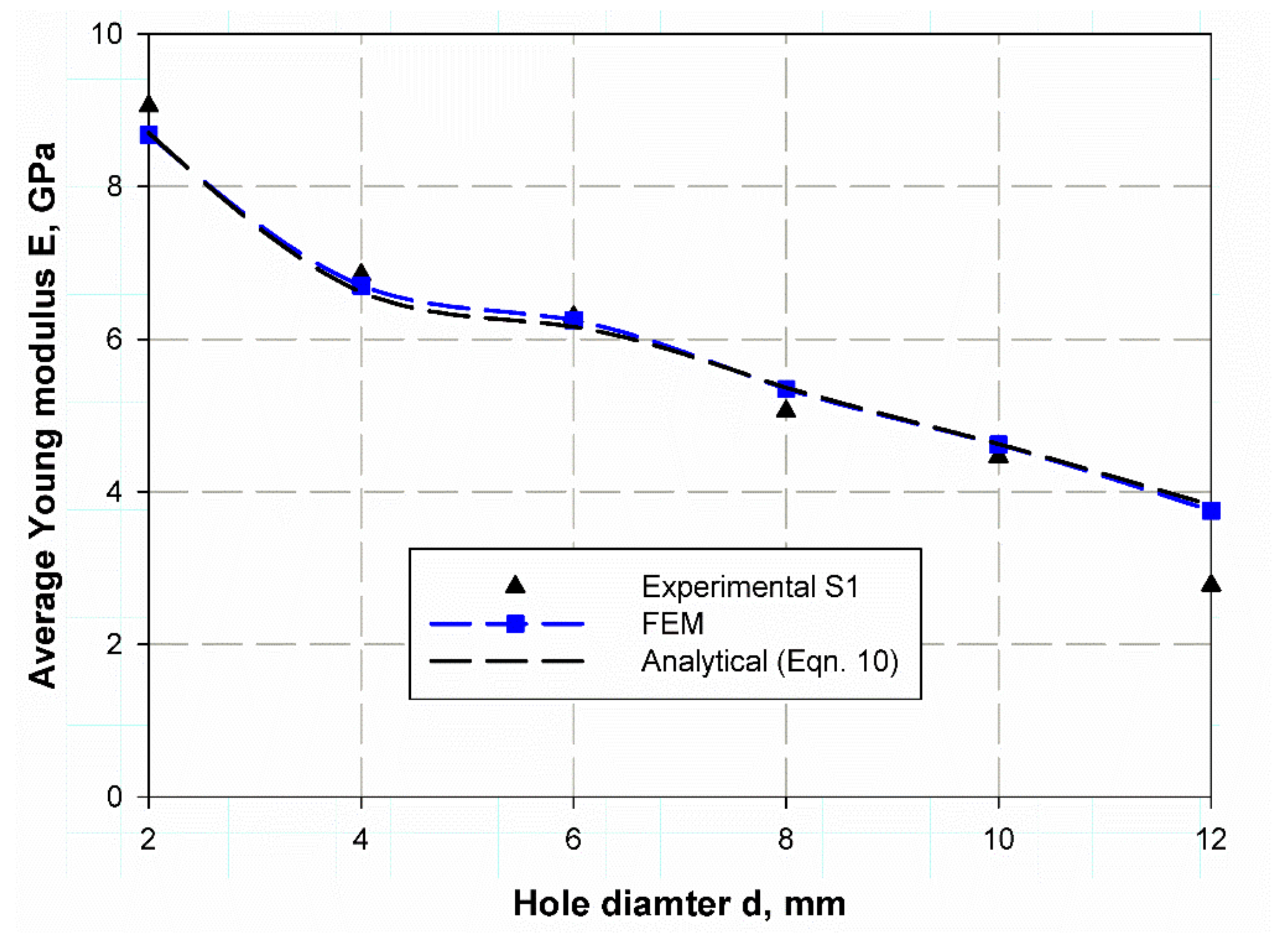
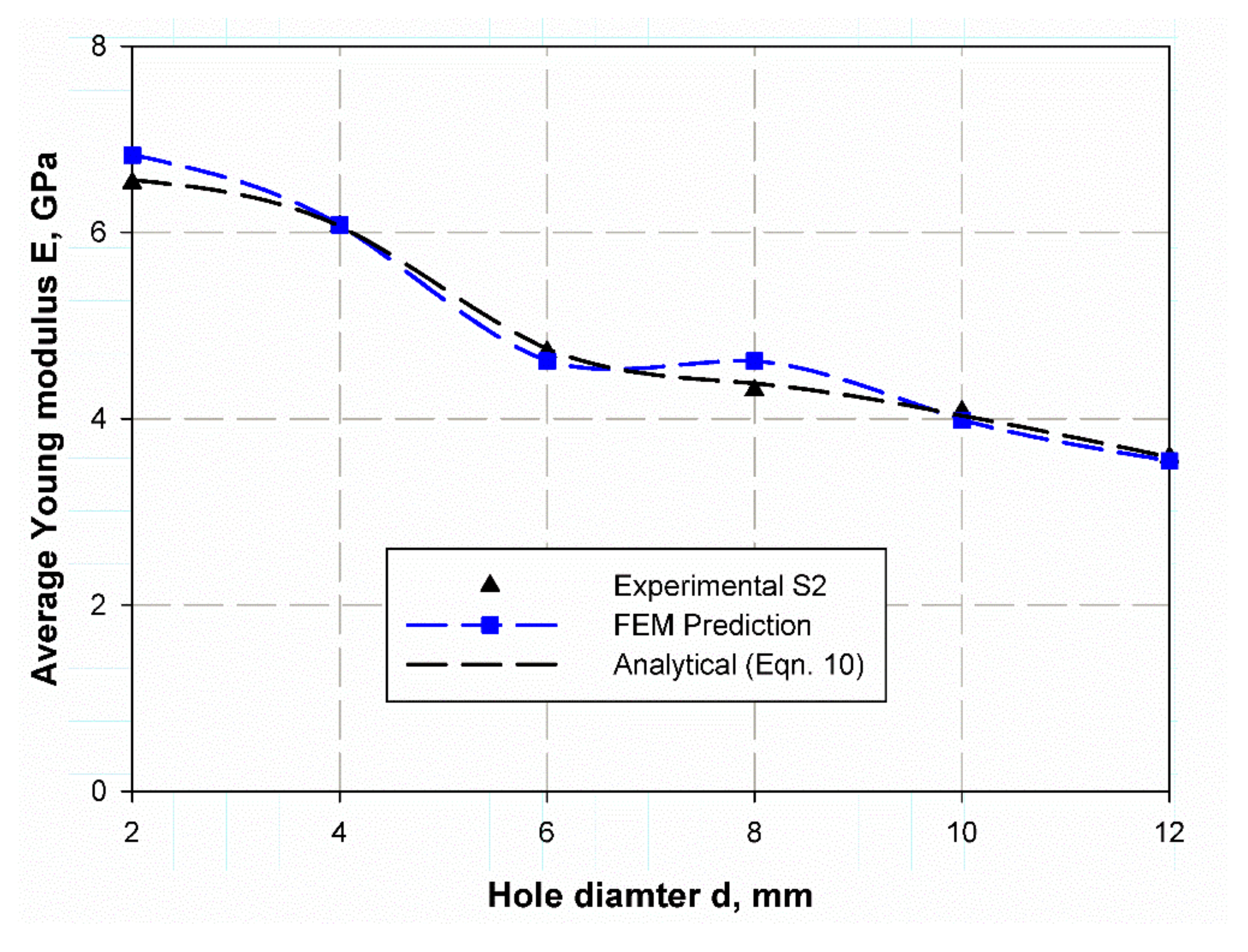
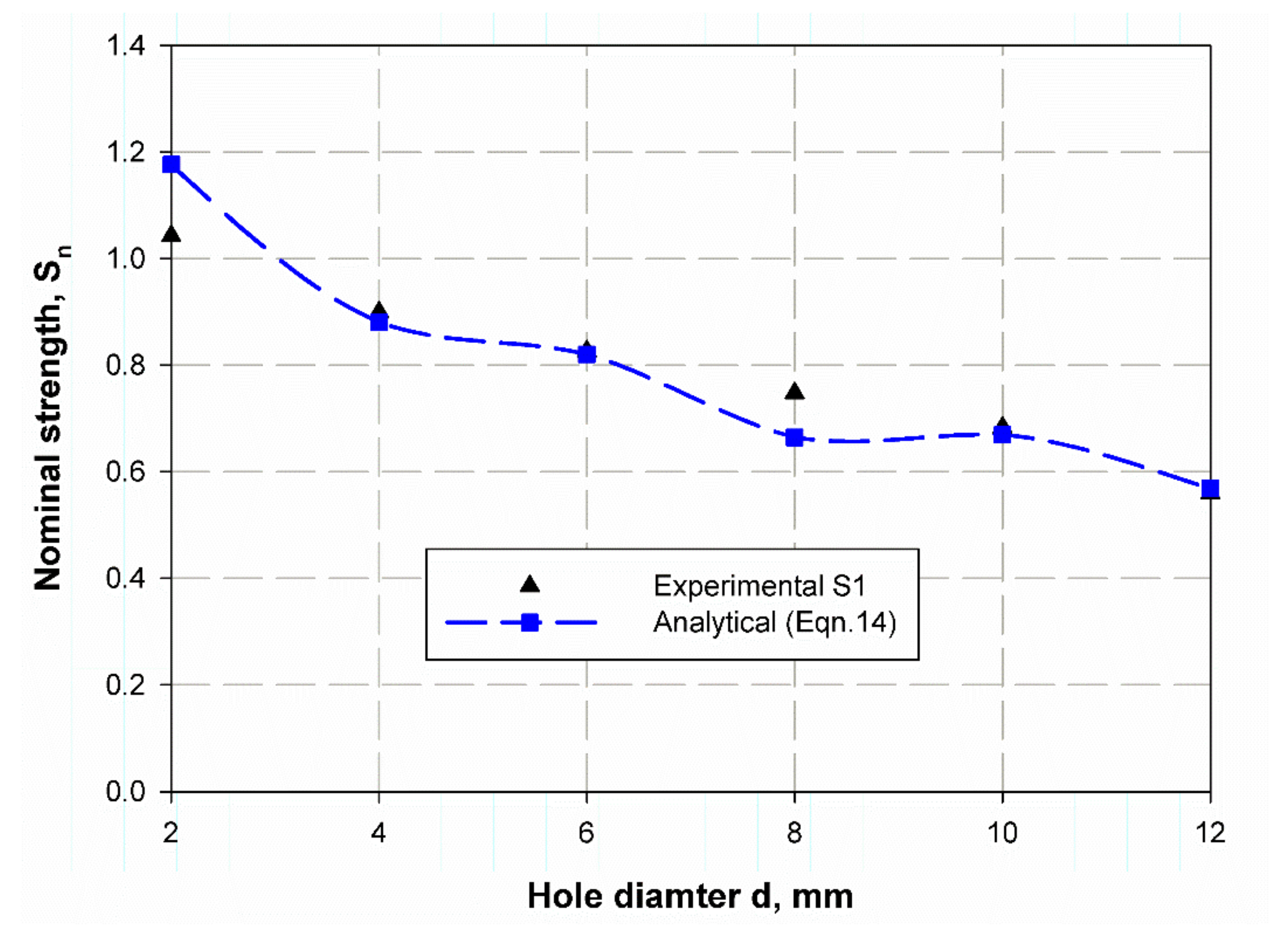
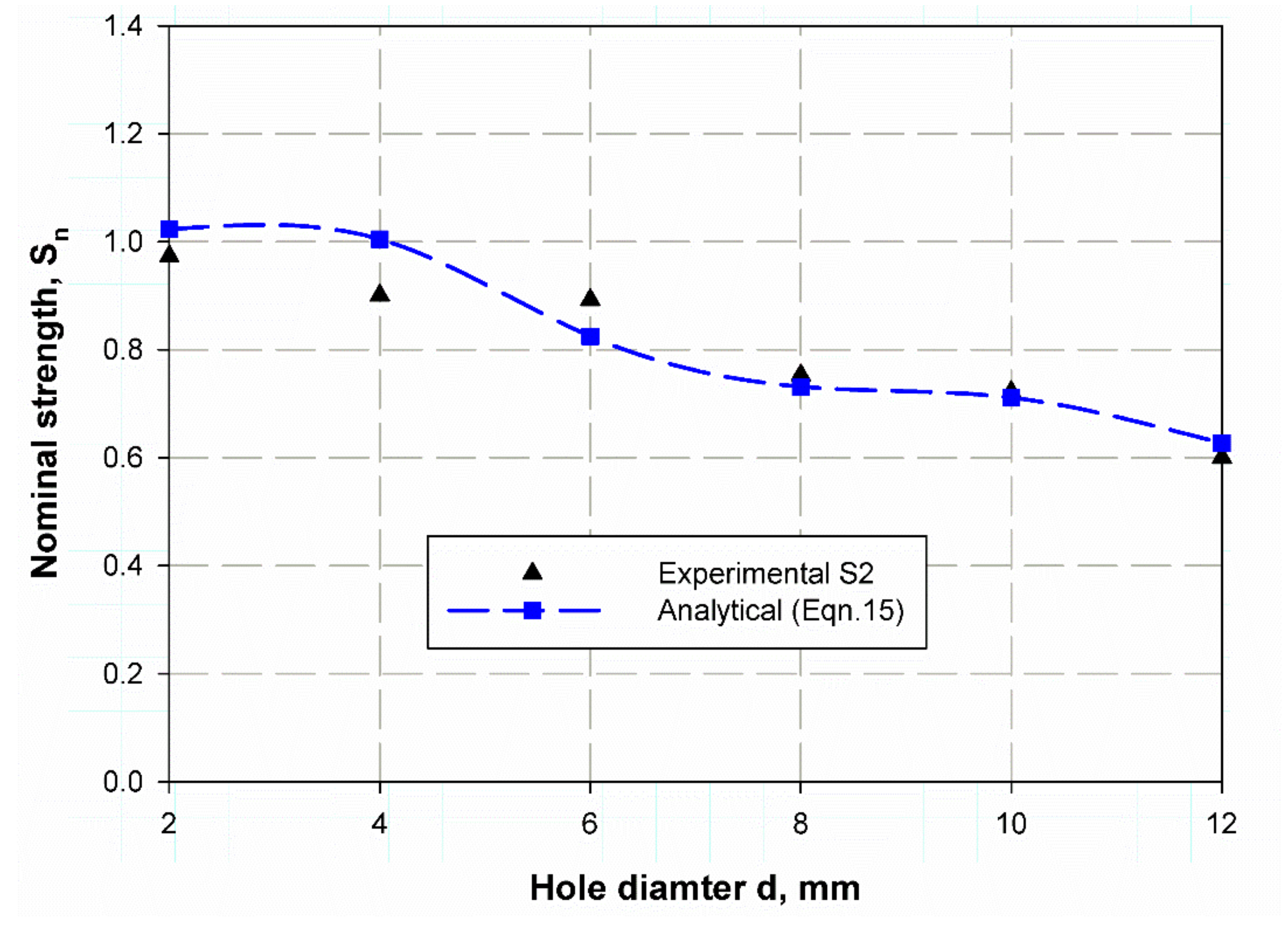
| Properties | E-Glass | Kemapoxy(150RGL) |
|---|---|---|
| Density (kg/m3) | 2540 | 107 ± 2 |
| Tensile strength (MPa) | 2000 | 50–100 |
| Tensile modulus (GPa) | 76 | 1.2–4.5 |
| Passion ratio | 0.25 | 0.35 |
| In plane shear modulus | 30.8 | 1.24 |
| Failure strain | 1.7 |
| Properties | S1 | S2 |
|---|---|---|
| Density (kg/m3) | 1650 | 1850 |
| Equivalent Young’s modulus (GPa) | 13.7793 | 5.6 |
| Volume friction % | ||
| Passion ratio | 0.25 | 0.25 |
| Diameter (mm) | Thickness (mm) | |
|---|---|---|
| S1 | S2 | |
| 2 | 3.30 | 3.50 |
| 4 | 3.35 | 3.30 |
| 6 | 3.35 | 3.00 |
| 8 | 3.60 | 3.00 |
| 10 | 3.08 | 2.90 |
| 12 | 3.00 | 2.80 |
| Average | 3.28 | 3.08 |
| Specimen | GIC (Experimental) KJ/m2 | Crack Opening, µmm |
|---|---|---|
| S1 | 31.54 | 7.50 |
| S2 | 30.39 | 9.12 |
| Properties | Value | |
|---|---|---|
| S1 | S2 | |
| E1 (GPa) | 24.6 | 8.18 |
| E2 (GPa) | 24.6 | 8.18 |
| E3 (GPa) | 5.30 | 5.30 |
| G1, G2, G3 (GPa) | 2.18 | 1.20 |
| µ1, µ2, µ3 | 0.17 | 0.17 |
| Diameter (mm) | Mass (mm) | |
|---|---|---|
| S1 | S2 | |
| 2 | 8.09 | 17.38 |
| 4 | 16.92 | 30.13 |
| 6 | 25.71 | 39.46 |
| 8 | 36.76 | 51.28 |
| 10 | 42.12 | 69.27 |
| 12 | 53.32 | 96.20 |
| Average | 30.49 | 50.62 |
| Node Number | Mode 1 | Mode 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Natural Frequency (Hz) | Damping Ratio (%) | Natural Frequency (Hz) | Damping Ratio (%) | |||||
| S1 | S2 | S1 | S2 | S1 | S2 | S1 | S2 | |
| average | 78.37 | 83.1 | 2.39 | 1.90 | 178.32 | 139.8 | 2.40 | 3.23 |
| Modes | S1 | %Error | S2 | %Error | Reference [43] |
|---|---|---|---|---|---|
| 1 | 1.9721 | 3.3 | 1.8432 | 3.44 | 1.909 |
| 2 | 3.0787 | 2.97 | 2.9238 | 2.21 | 2.990 |
| 3 | 4.8744 | 1.91 | 4.5822 | 4.19 | 4.783 |
| 4 | 5.5029 | 1.92 | 5.1602 | 4.42 | 5.399 |
| Specimen | Mode 1 | Mode 2 | ||
|---|---|---|---|---|
| S1 | S2 | S1 | S2 | |
| 2 | 1.8749 | 1.8279 | 5.374773 | 7.207791 |
| 4 | 1.9882 | 1.9812 | 5.412220 | 5.530115 |
| 6 | 2.1524 | 2.1985 | 5.618912 | 5.793477 |
| 8 | 2.1663 | 2.1270 | 5.645730 | 5.598823 |
| 10 | 2.4563 | 2.4950 | 6.279644 | 6.444072 |
| 12 | 2.5217 | 2.5170 | 6.401345 | 6.443426 |
| Specimen | S1 | % Error | S2 | % Error | ||
|---|---|---|---|---|---|---|
| Strength (Experimental) MPa | Strength (Predicted) MPa | Strength (Experimental) MPa | Strength (Predicted) MPa | |||
| Un-notch | 208.76 | 209 | 0.11 | 166.5 | 163.47 | 1.82 |
| 2 | 218 | 245.88 | −12.79 | 162 | 170.35 | −5.79 |
| 4 | 188 | 184.12 | 2.06 | 150 | 167.24 | −11.49 |
| 6 | 172.7 | 171.46 | 0.72 | 148.6 | 137.30 | 6.79 |
| 8 | 156.3 | 138.88 | 11.14 | 125.35 | 121.81 | 0.63 |
| 10 | 142.8 | 139.96 | 1.99 | 120.26 | 118.45 | 2.96 |
| 12 | 117 | 118.79 | 0.11 | 100 | 163.47 | −4.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdellah, M.Y.; Hassan, M.K.; Mohamed, A.F.; Khalil, K.A. A Novel and Highly Effective Natural Vibration Modal Analysis to Predict Nominal Strength of Open Hole Glass Fiber Reinforced Polymer Composites Structure. Polymers 2021, 13, 1251. https://doi.org/10.3390/polym13081251
Abdellah MY, Hassan MK, Mohamed AF, Khalil KA. A Novel and Highly Effective Natural Vibration Modal Analysis to Predict Nominal Strength of Open Hole Glass Fiber Reinforced Polymer Composites Structure. Polymers. 2021; 13(8):1251. https://doi.org/10.3390/polym13081251
Chicago/Turabian StyleAbdellah, Mohammed Y., Mohamed K. Hassan, Ahmed F. Mohamed, and Khalil Abdelrazek Khalil. 2021. "A Novel and Highly Effective Natural Vibration Modal Analysis to Predict Nominal Strength of Open Hole Glass Fiber Reinforced Polymer Composites Structure" Polymers 13, no. 8: 1251. https://doi.org/10.3390/polym13081251
APA StyleAbdellah, M. Y., Hassan, M. K., Mohamed, A. F., & Khalil, K. A. (2021). A Novel and Highly Effective Natural Vibration Modal Analysis to Predict Nominal Strength of Open Hole Glass Fiber Reinforced Polymer Composites Structure. Polymers, 13(8), 1251. https://doi.org/10.3390/polym13081251