On the Structural Performance of Recycled Aggregate Concrete Columns with Glass Fiber-Reinforced Composite Bars and Hoops
Abstract
:1. Introduction
2. Materials and Methodology
2.1. Materials
2.1.1. Geopolymer Recycled Aggregate Concrete
2.1.2. GFRP Bars
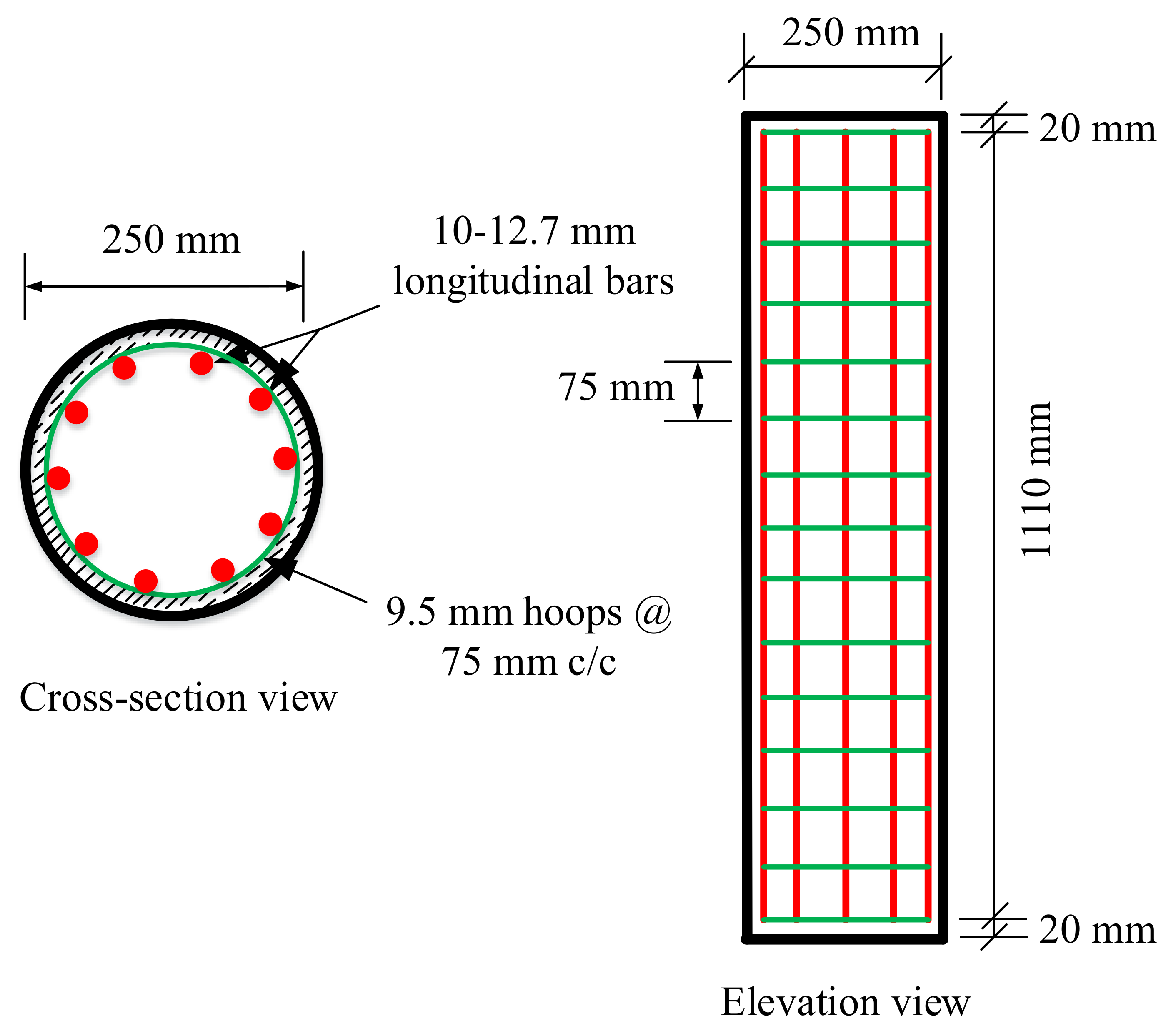
2.2. Specimen Details and Fabrication
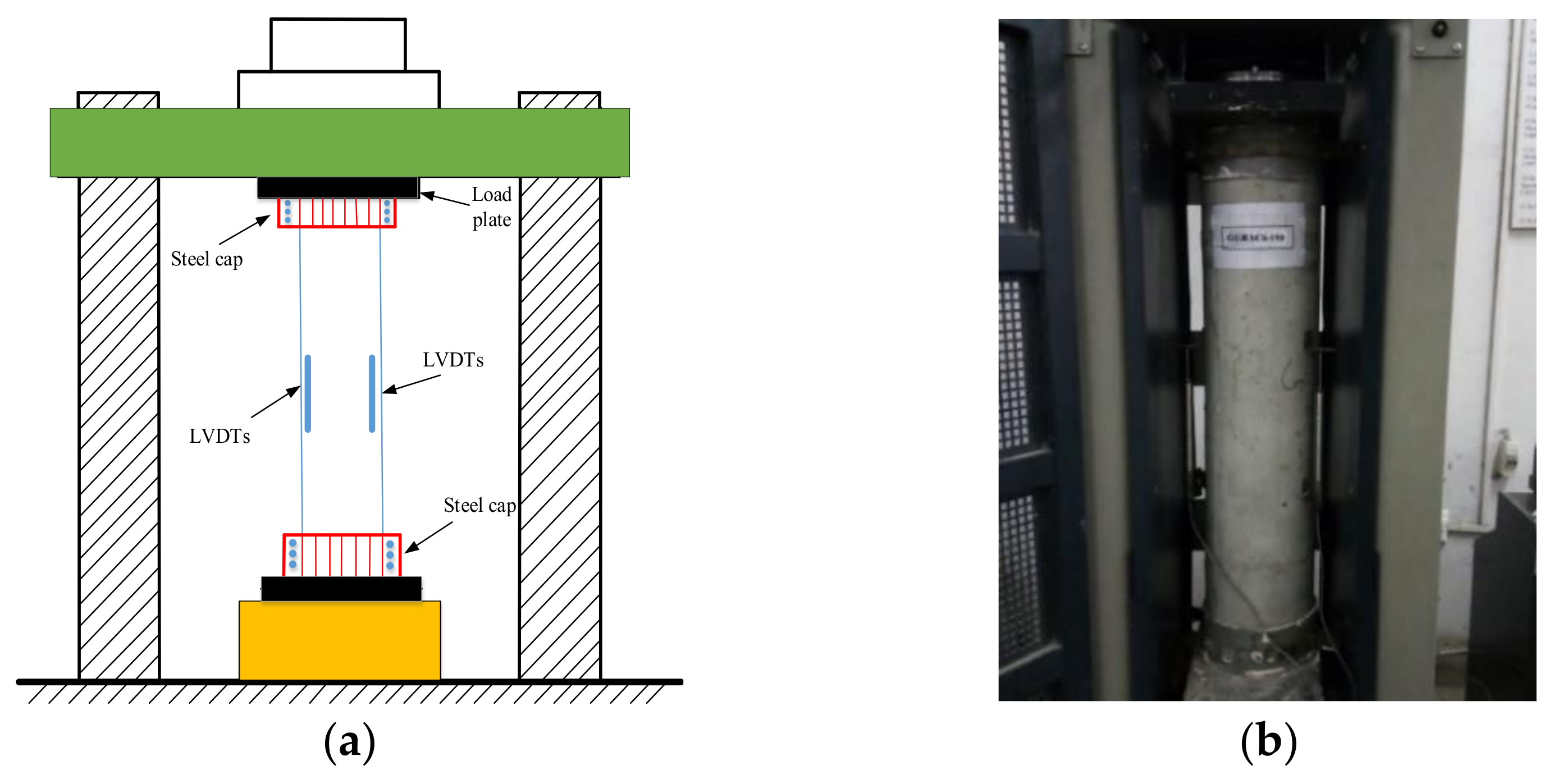
2.3. Testing and Instrumentation
3. Results and Discussion
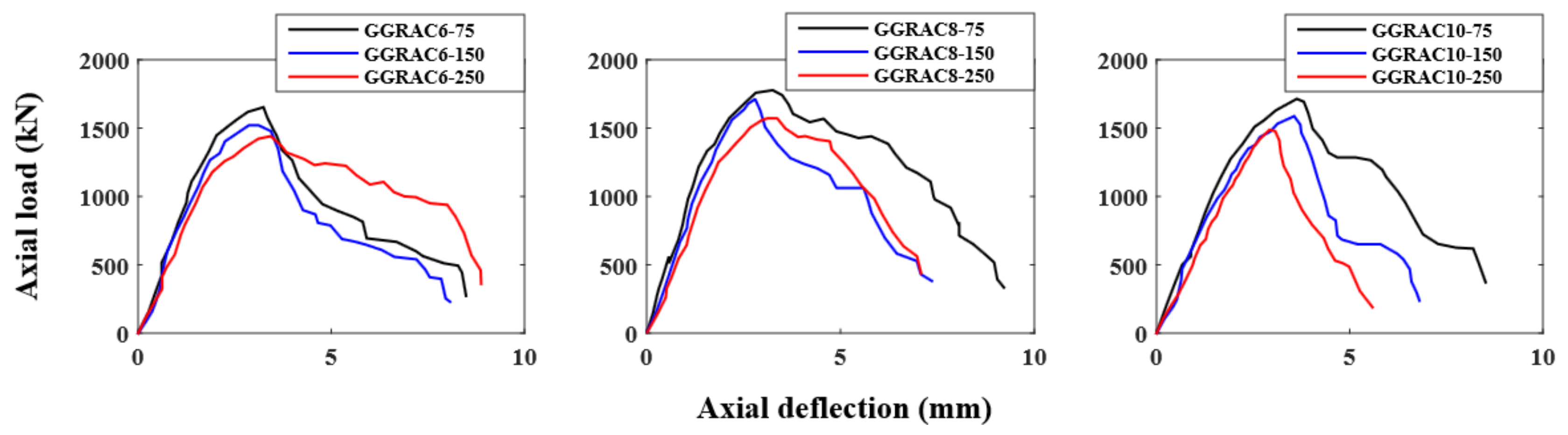
3.1. Load–Deflection Behavior
3.2. Failure Process
3.3. Ductility
3.4. Effect of Longitudinal Reinforcement Ratio
3.5. Effect of Stirrup Spacing
4. Theoretical Calculations
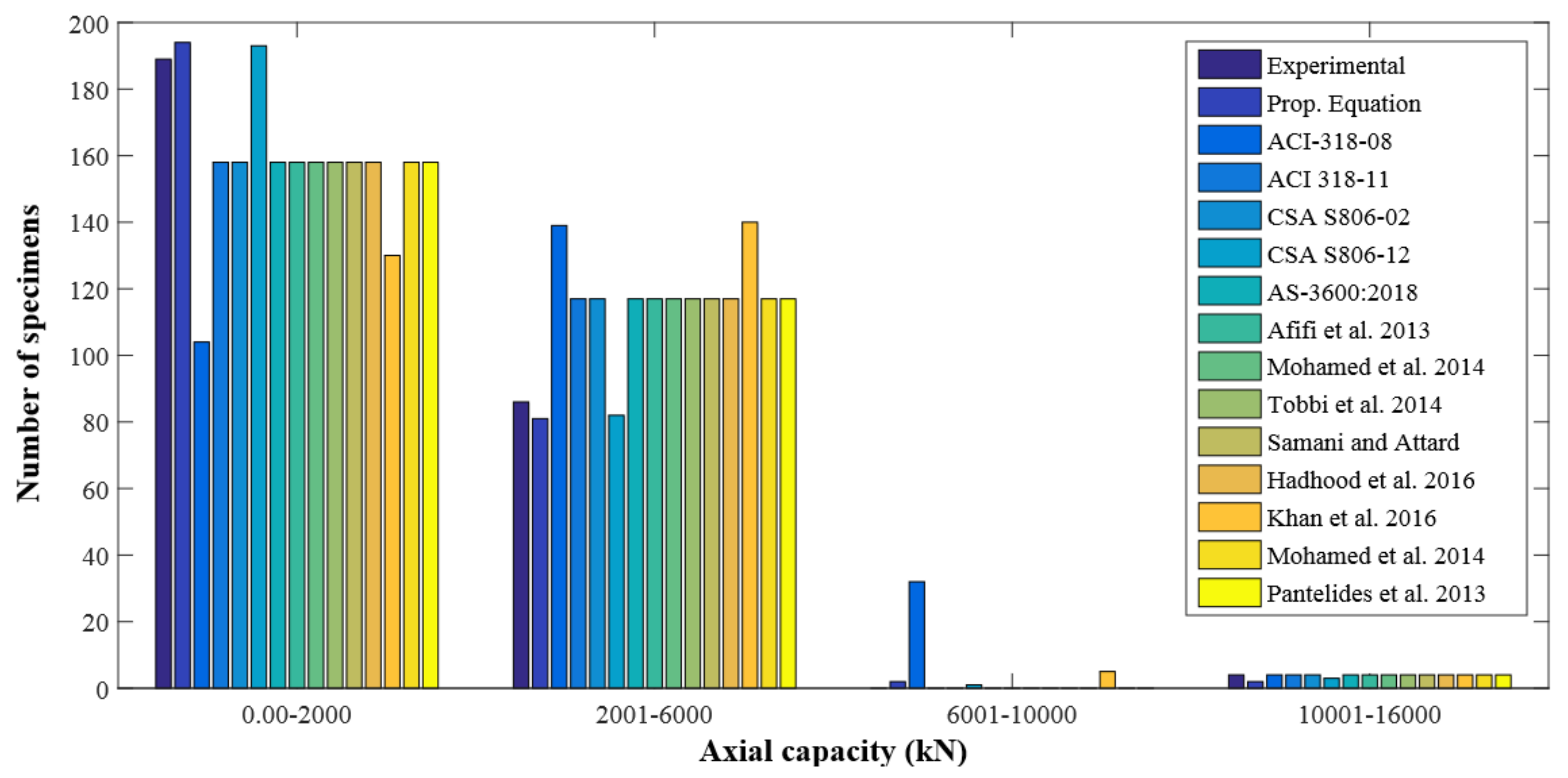
4.1. Experimental Database
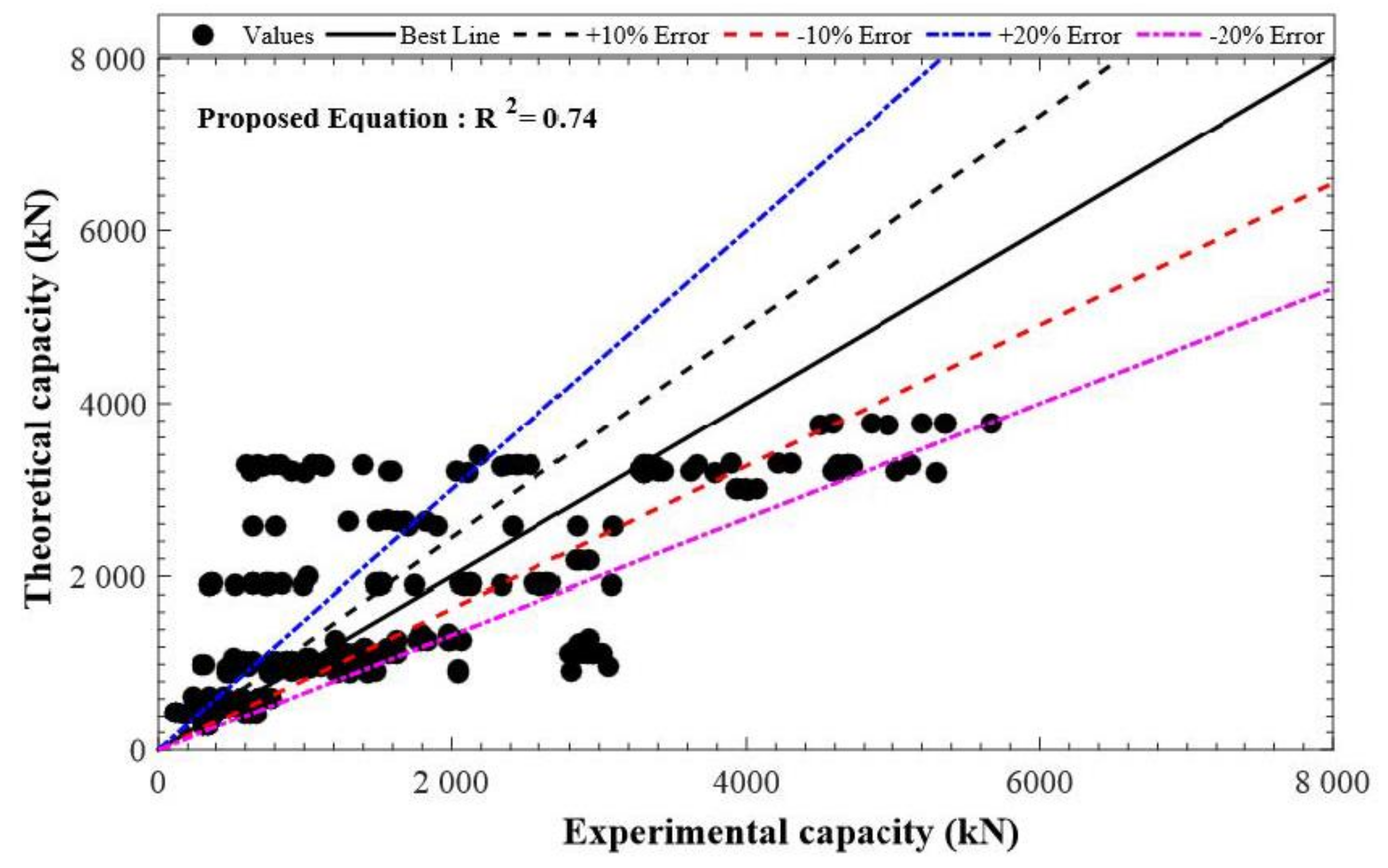
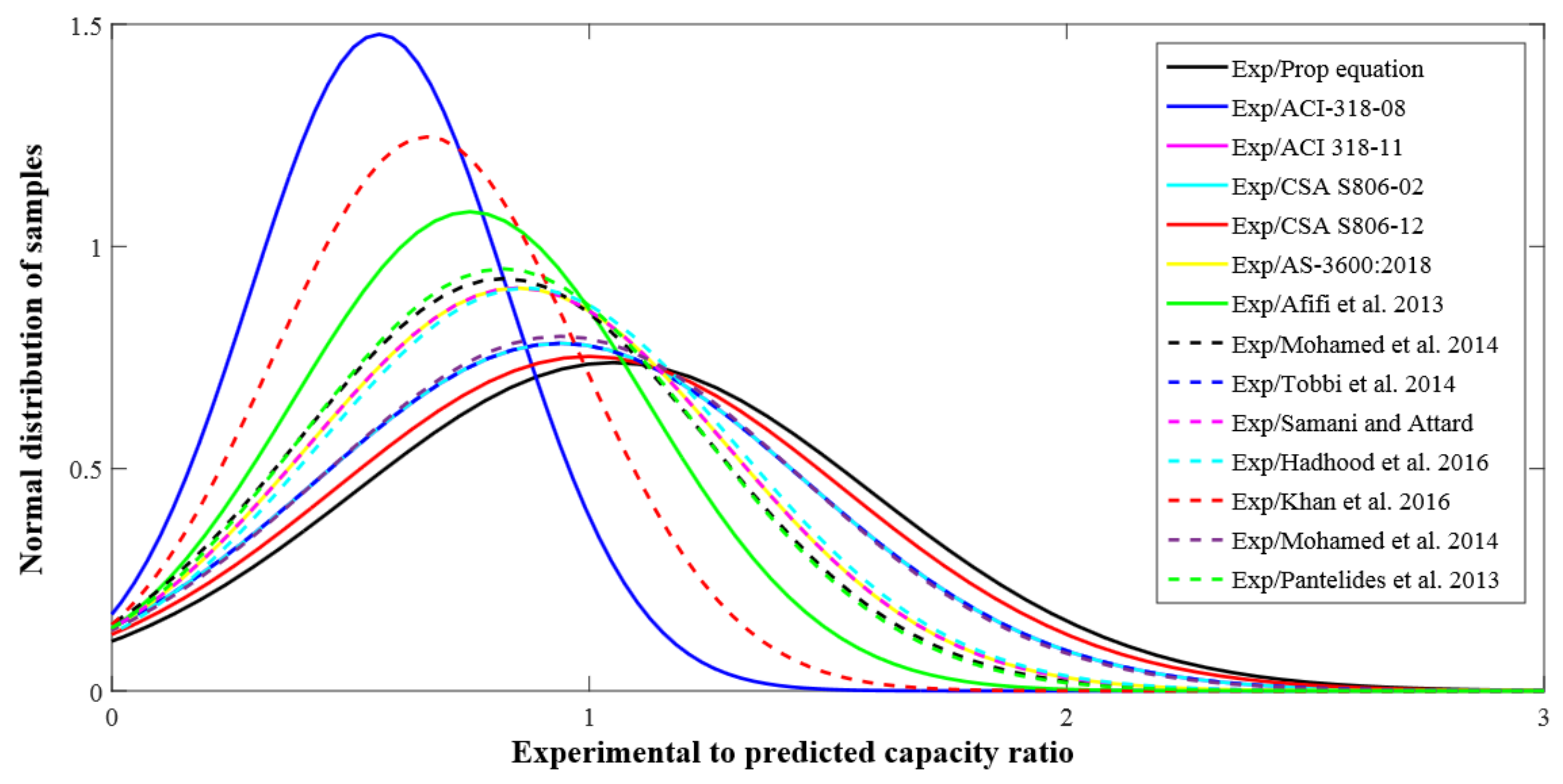
4.2. Assessment of Previous Equations
4.3. Confinement Effect
4.4. Proposed Equation for Axial Load-Carrying Capacity
5. Conclusions
- All the GGRAC compressive members showed similar failure modes and processes. Commonly, the failure was detected in the middle portion of compressive members. The compressive members failed due to a fracture arising in the longitudinal bars and rupture in the GFRP ties.
- The compressive members with a lesser spacing of GFRP hoops showed higher ductility indices because of the ability of the well-restrained longitudinal bars and efficient transverse confinement of the concrete to absorb greater energy.
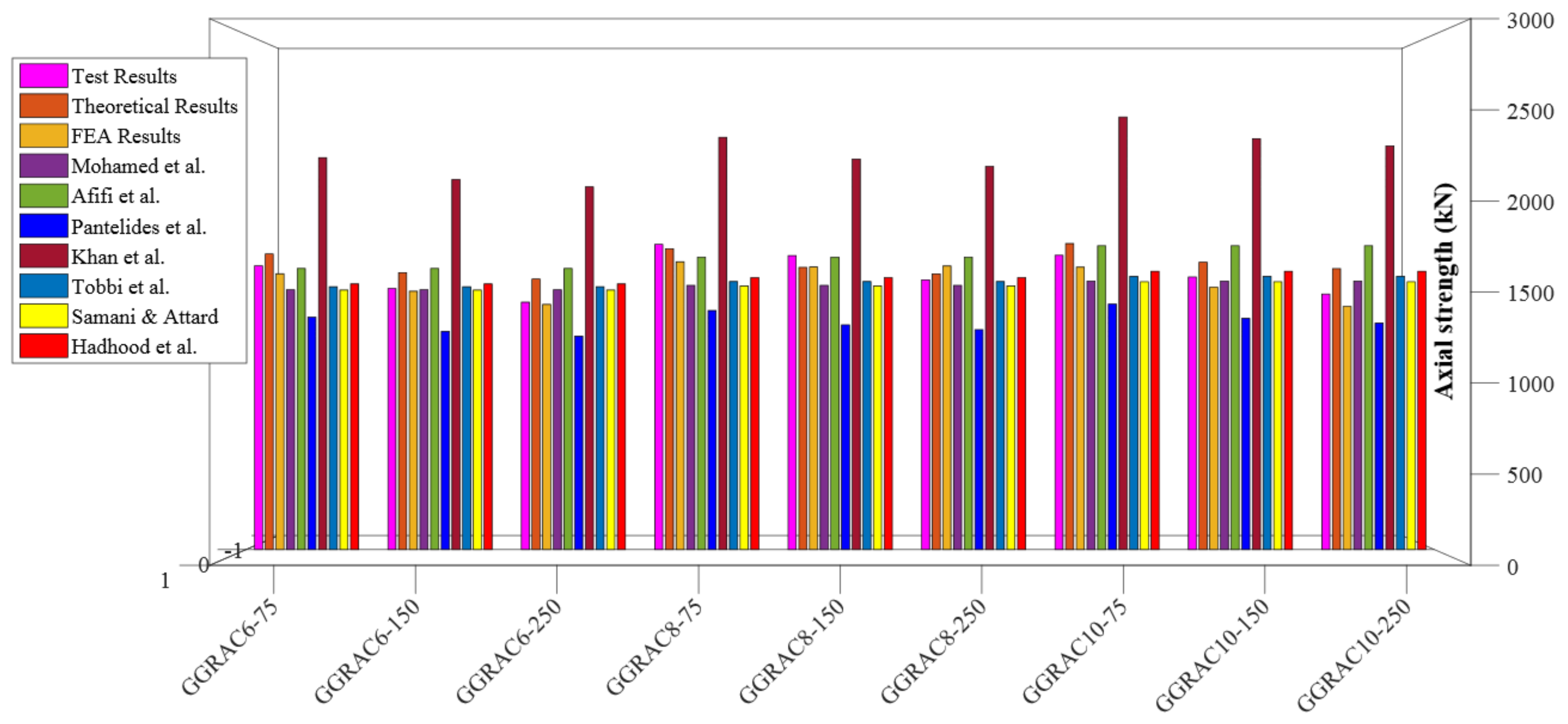
- The reduction in the pitch of GFRP hoops led to an increase in the LCC of GGRAC members. Reduction in the vertical pitch of GFRP hoops from 150 mm to 75 mm resulted in an improvement of 3.65% in the LCC of specimens. When the vertical spacing of GFRP hoops was reduced from 250 mm to 150 mm, a percentage reduction of 11.6% was noticed in the LCC of GGRAC specimens.
- The increase in the quantity of longitudinal GFRP bars up to eight improved the axial LCC of GGRAC specimens while using ten longitudinal bars decreased the axial LCC of specimens.
- The recommended mathematical model considered the axial involvement of the main GFRP bars and the confining phenomenon of lateral GFRP hoops and presented a discrepancy of only 5.18% from the experimental tests. These comparative assessments solidly authenticate the applicability of the suggested model for capturing the axial LCC of GGRAC compressive members. Consequently, the GFRP-reinforced geopolymer recycled aggregate concrete compressive members perform well in terms of axial LCC, failure modes, and ductility. The present study proposes a novel compressive member for sustainable and green concrete construction. Future work is recommended to examine the performance of GFRP reinforcement in various GPC members including beams and slabs.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- McGinnis, M.J.; Davis, M.; De La Rosa, A.; Weldon, B.D.; Kurama, Y.C. Quantified sustainability of recycled concrete aggregates. Mag. Concr. Res. 2017, 69, 1203–1211. [Google Scholar] [CrossRef]
- Coelho, A.; de Brito, J. Influence of construction and demolition waste management on the environmental impact of buildings. Waste Manag. 2012, 32, 532–541. [Google Scholar] [CrossRef] [PubMed]
- Azúa, G.; González, M.; Arroyo, P.; Kurama, Y. Recycled coarse aggregates from precast plant and building demolitions: Environmental and economic modeling through stochastic simulations. J. Clean. Prod. 2019, 210, 1425–1434. [Google Scholar] [CrossRef]
- Xiao, J.; Wang, C.; Ding, T.; Akbarnezhad, A. A recycled aggregate concrete high-rise building: Structural performance and embodied carbon footprint. J. Clean. Prod. 2018, 199, 868–881. [Google Scholar] [CrossRef]
- Silva, R.; de Brito, J.; Dhir, R. Fresh-state performance of recycled aggregate concrete: A review. Constr. Build. Mater. 2018, 178, 19–31. [Google Scholar] [CrossRef]
- Fanaradelli, T.D.; Rousakis, T.C. Prediction of Ultimate Strain for Rectangular Reinforced Concrete Columns Confined with Fiber Reinforced Polymers under Cyclic Axial Compression. Polymers 2020, 12, 2691. [Google Scholar] [CrossRef]
- Ma, H.; Xue, J.; Zhang, X.; Luo, D. Seismic performance of steel-reinforced recycled concrete columns under low cyclic loads. Constr. Build. Mater. 2013, 48, 229–237. [Google Scholar] [CrossRef]
- Yang, J.-M.; Min, K.-H.; Shin, H.-O.; Yoon, Y.-S. Effect of steel and synthetic fibers on flexural behavior of high-strength concrete beams reinforced with FRP bars. Compos. Part B Eng. 2012, 43, 1077–1086. [Google Scholar] [CrossRef]
- Raza, A.; Rehman, A.U.; Masood, B.; Hussain, I. Finite element modelling and theoretical predictions of FRP-reinforced concrete columns confined with various FRP-tubes. Structures 2020, 26, 626–638. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Fanggi, B.A.L.; Zheng, J. Confinement model for concrete in circular and square FRP–concrete–steel double-skin composite columns. Mater. Des. 2016, 96, 458–469. [Google Scholar] [CrossRef]
- Rashedi, A.; Sridhar, I.; Tseng, K.; Srikanth, N.; Idapalapati, S. Minimum mass design of thin tubular structures under eccentric compressive loading. Thin-Walled Struct. 2015, 90, 191–201. [Google Scholar] [CrossRef]
- Rashedi, A.; Sridhar, I.; Tseng, K. Fracture characterization of glass fiber composite laminate under experimental biaxial loading. Compos. Struct. 2016, 138, 17–29. [Google Scholar] [CrossRef]
- Jiang, C.; Wu, Y.-F. Axial Strength of Eccentrically Loaded FRP-Confined Short Concrete Columns. Polymers 2020, 12, 1261. [Google Scholar] [CrossRef] [PubMed]
- Aslam, H.M.U.; Khan, Q.U.Z.; Sami, A.; Raza, A. Axial compressive behavior of damaged steel and GFRP bars reinforced concrete columns retrofitted with CFRP laminates. Compos. Struct. 2021, 258, 113206. [Google Scholar] [CrossRef]
- Raza, A.; Manalo, A.C.; Rafique, U.; AlAjarmeh, O.S.; Khan, Q.U.Z. Concentrically Loaded Recycled Aggregate Geopolymer Concrete Columns Reinforced with GFRP Bars and Spirals. Compos. Struct. 2021, 268, 113968. [Google Scholar] [CrossRef]
- Zeng, J.; Guo, Y.; Li, L.; Chen, W. Behavior and Three-Dimensional Finite Element Modeling of Circular Concrete Columns Partially Wrapped with FRP Strips. Polymers 2018, 10, 253. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, O.A.; KewalRamani, M.; Khattab, R. Fiber Reinforced Polymer Laminates for Strengthening of RC Slabs against Punching Shear: A Review. Polymers 2020, 12, 685. [Google Scholar] [CrossRef] [Green Version]
- Raza, A.; Ali, B.; Masood, B.; Rehman, A.U. Axial performance of GFRP composite bars and spirals in circular hollow concrete columns. Structures 2021, 29, 600–613. [Google Scholar] [CrossRef]
- Abdelkarim, O.I.; ElGawady, M.A. Dynamic and Static Behavior of Hollow-Core FRP-Concrete-Steel and Reinforced Concrete Bridge Columns under Vehicle Collision. Polymers 2016, 8, 432. [Google Scholar] [CrossRef] [Green Version]
- Ghatte, H.F.; Comert, M.; Demir, C.; Ilki, A. Evaluation of FRP Confinement Models for Substandard Rectangular RC Columns Based on Full-Scale Reversed Cyclic Lateral Loading Tests in Strong and Weak Directions. Polymers 2016, 8, 323. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raza, A.; Khan, Q.U.Z.; Ahmad, A. Numerical Investigation of Load-Carrying Capacity of GFRP-Reinforced Rectangular Concrete Members Using CDP Model in ABAQUS. Adv. Civ. Eng. 2019, 2019, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Raza, A.; Khan, Q.U.Z.; Ahmad, A. Investigation of HFRC columns reinforced with GFRP bars and spirals under concentric and eccentric loadings. Eng. Struct. 2021, 227, 111461. [Google Scholar] [CrossRef]
- Raza, A.; Rafique, U. Efficiency of GFRP bars and hoops in recycled aggregate concrete columns: Experimental and numerical study. Compos. Struct. 2021, 255, 112986. [Google Scholar] [CrossRef]
- Lee, K.S.; Lee, B.Y.; Seo, S.Y. A Seismic Strengthening Technique for Reinforced Concrete Columns Using Sprayed FRP. Polymers 2016, 8, 107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Afifi, M.Z.; Mohamed, H.M.; Benmokrane, B. Axial Capacity of Circular Concrete Columns Reinforced with GFRP Bars and Spirals. J. Compos. Constr. 2014, 18, 04013017. [Google Scholar] [CrossRef]
- Tobbi, H.; Farghaly, A.S.; Benmokrane, B. Concrete Columns Reinforced Longitudinally and Transversally with Glass Fiber-Reinforced Polymer Bars. ACI Struct. J. 2012, 109. [Google Scholar] [CrossRef]
- Iqbal, S.; Ali, A.; Holschemacher, K.; Bier, T.A.; Shah, A.A. Strengthening of RC beams using steel fiber reinforced high strength lightweight self-compacting concrete (SHLSCC) and their strength predictions. Mater. Des. 2016, 100, 37–46. [Google Scholar] [CrossRef]
- Mohamed, H.M.; Afifi, M.Z.; Benmokrane, B. Performance Evaluation of Concrete Columns Reinforced Longitudinally with FRP Bars and Confined with FRP Hoops and Spirals under Axial Load. J. Bridg. Eng. 2014, 19, 04014020. [Google Scholar] [CrossRef]
- Hadi, M.N.S.; Karim, H.; Sheikh, M.N. Experimental Investigations on Circular Concrete Columns Reinforced with GFRP Bars and Helices under Different Loading Conditions. J. Compos. Constr. 2016, 20, 04016009. [Google Scholar] [CrossRef] [Green Version]
- Xiong, M.; Xu, Z.; Chen, G.; Lan, Z. FRP-confined steel-reinforced recycled aggregate concrete columns: Concept and behaviour under axial compression. Compos. Struct. 2020, 246, 112408. [Google Scholar] [CrossRef]
- Hadi, M.N.; Ahmad, J.; Yu, T. Tests of geopolymer concrete columns with basalt-fibre-reinforced-polymer bars and tubes. Proc. Inst. Civ. Eng. Struct. Build. 2020, 1–41. [Google Scholar] [CrossRef]
- Danda, U.K.; Y, H.K.; B, S.C.K. Experimental study on reinforced geopolymer concrete columns using GGBS. Mater. Today Proc. 2020, 33, 632–636. [Google Scholar] [CrossRef]
- Górski, M.; Wielgus, N.; Loska, K.; Kozioł, M.; Landrat, M.; Ścierski, W.; Pikoń, K. Characteristics of Metakaolin-Based Geopolymer with Cathode Ray Tube Glass. Polymers 2021, 13, 1149. [Google Scholar] [CrossRef] [PubMed]
- Gunasekara, C.; Atzarakis, P.; Lokuge, W.; Law, D.; Setunge, S. Novel Analytical Method for Mix Design and Performance Prediction of High Calcium Fly Ash Geopolymer Concrete. Polymers 2021, 13, 900. [Google Scholar] [CrossRef] [PubMed]
- Saranya, P.; Nagarajan, P.; Shashikala, A. Behaviour of GGBS-dolomite geopolymer concrete short column under axial loading. J. Build. Eng. 2020, 30, 101232. [Google Scholar] [CrossRef]
- Maranan, G.; Manalo, A.; Benmokrane, B.; Karunasena, W.; Mendis, P. Behavior of concentrically loaded geopolymer-concrete circular columns reinforced longitudinally and transversely with GFRP bars. Eng. Struct. 2016, 117, 422–436. [Google Scholar] [CrossRef]
- Standard Test Method for Slump of Hydraulic-Cement Concrete; ASTM C143/C143M-15; ASTM International: West Conshohocken, PA, USA, 2015.
- Standard Test Method for Time of Setting of Hydraulic Cement Mortar by Modified Vicat Needle; ASTM C807-13; ASTM International: West Conshohocken, PA, USA, 2013.
- American Concrete Institute (ACI 440-3R). Guide Test Methods for Fiber-Reinforced Polymers (FRP) Composites for Reinforcing or Strengthening Concrete and Masonry Structures; American Concrete Institute: Indianapolis, IN, USA, 2012. [Google Scholar]
- Canadian Standards Association (CAN/CSA S807-10). Specification for Fibre-Reinforced Polymers; Canadian Standards Association: Rexdale, ON, Canada, 2010. [Google Scholar]
- Raza, A.; Shah, S.; Alhazmi, H.; Abrar, M.; Razzaq, S. Strength Profile Pattern of FRP-Reinforced Concrete Structures: A Performance Analysis through Finite Element Analysis and Empirical Modeling Technique. Polymers 2021, 13, 1265. [Google Scholar] [CrossRef]
- Hadi, M.N.S.; Youssef, J. Experimental Investigation of GFRP-Reinforced and GFRP-Encased Square Concrete Specimens under Axial and Eccentric Load, and Four-Point Bending Test. J. Compos. Constr. 2016, 20, 04016020. [Google Scholar] [CrossRef] [Green Version]
- Elchalakani, M.; Dong, M.; Karrech, A.; Li, G.; Ali, M.S.M.; Yang, B. Experimental Investigation of Rectangular Air-Cured Geopolymer Concrete Columns Reinforced with GFRP Bars and Stirrups. J. Compos. Constr. 2019, 23, 04019011. [Google Scholar] [CrossRef]
- Canadian Standard Association (CAN/CSA S806-12). Design and Construction of Building Structures with Fibre-Reinforced Polymer; Canadian Standard Association: Toronto, ON, Canada, 2012. [Google Scholar]
- American Concrete Institute (ACI-318-08). Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures; American Concrete Institute: Farmington Hills, MI, USA, 2008. [Google Scholar]
- American Concrete Institute (ACI-318-11). Building Code Requirements for Structural Concrete and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 2011; pp. 318–411. [Google Scholar]
- Australian Standard AS-3600:2018; Standards Australia: Sydney, Australia, 2018.
- Elchalakani, M.; Dong, M.; Karrech, A.; Mohamed Ali, M.S.; Huo, J.S. Circular concrete columns and beams reinforced with GFRP bars and spirals under axial, eccentric, and flexural loading. J. Compos. Constr. 2020, 24, 04020008. [Google Scholar] [CrossRef]
- Tobbi, H.; Farghaly, A.S.; Benmokrane, B. Behavior of Concentrically Loaded Fiber-Reinforced Polymer Reinforced Concrete Columns with Varying Reinforcement Types and Ratios. ACI Struct. J. 2014, 111, 375–386. [Google Scholar] [CrossRef]
- Samani, A.K.; Attard, M.M. A stress–strain model for uniaxial and confined concrete under compression. Eng. Struct. 2012, 41, 335–349. [Google Scholar] [CrossRef]
- Hadhood, A.; Mohamed, H.M.; Benmokrane, B. Axial Load–Moment Interaction Diagram of Circular Concrete Columns Reinforced with CFRP Bars and Spirals: Experimental and Theoretical Investigations. J. Compos. Constr. 2017, 21, 04016092. [Google Scholar] [CrossRef]
- Khan, Q.S.; Sheikh, M.N.; Hadi, M.N.S. Axial-Flexural Interactions of GFRP-CFFT Columns with and without Reinforcing GFRP Bars. J. Compos. Constr. 2017, 21, 04016109. [Google Scholar] [CrossRef] [Green Version]
- Hadhood, A.; Mohamed, H.M.; Benmokrane, B. Failure Envelope of Circular Concrete Columns Reinforced with GFRP Bars and Spirals. ACI Struct. J. 2017, 114, 1417–1428. [Google Scholar] [CrossRef]
- Afifi, M.Z.; Mohamed, H.M.; Benmokrane, B. Theoretical stress–strain model for circular concrete columns confined by GFRP spirals and hoops. Eng. Struct. 2015, 102, 202–213. [Google Scholar] [CrossRef]
- Parvin, A.; Raad, J. Internal and External Reinforcement of Concrete Members by Use of Shape Memory Alloy and Fiber Reinforced Polymers under Cyclic Loading-A Review. Polymers 2018, 10, 376. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef] [Green Version]
- Xiao, B.; Huang, Q.; Chen, H.; Chen, X.; Long, G. A Fractal model for capillary flow through a single tortuous capillary with roughened surfaces in fibrous porous media. Fractals 2021, 29, 2150017. [Google Scholar] [CrossRef]
- Rashedi, A.; Khanam, T. Life cycle assessment of most widely adopted solar photovoltaic energy technologies by mid-point and end-point indicators of ReCiPe method. Environ. Sci. Pollut. Res. 2020, 27, 29075–29090. [Google Scholar] [CrossRef]
- Rashedi, A.; Khanam, T.; Jonkman, M. On Reduced Consumption of Fossil Fuels in 2020 and Its Consequences in the Global Environment and Exergy Demand. Energies 2020, 13, 6048. [Google Scholar] [CrossRef]
- Lee, W.-H.; Lin, K.-L.; Chang, T.-H.; Ding, Y.-C.; Cheng, T.-W. Sustainable Development and Performance Evaluation of Marble-Waste-Based Geopolymer Concrete. Polymers 2020, 12, 1924. [Google Scholar] [CrossRef] [PubMed]







| Feature | Value | Feature | Value |
|---|---|---|---|
| Water absorption | 7.39% | Maximum size | 10 mm |
| Apparent density | 2632 kg/m3 | Specific gravity | 2.23 |
| Bulk density | 1295 kg/m3 | Los Angeles abrasion | 40.32% |
| 10% fine value | 135 | Minimum size | 4.75 mm |
| Ingredient | Quantity | Ingredient | Quantity |
|---|---|---|---|
| RCA | 1186 kg/m3 | Fly ash | 245 kg/m3 |
| Sand | 501 kg/m3 | GGBS | 163 kg/m3 |
| Water | 123 kg/m3 | Superplasticizer | 3.8 kg/m3 |
| NaOH solution (14M) | 39 kg/m3 | Na2SiO3 | 105 kg/m3 |
| Bar Number | Diameter (mm) | Area (mm2) | Tensile Strength (MPa) | Elastic Moduli (MPa) | Ultimate Tensile Strain (%) |
|---|---|---|---|---|---|
| No. 3 | 9.5 | 70.8 | 765 ± 4 | 48,000 ± 500 | 2.12 ± 0.02 |
| No. 4 | 12.7 | 126.6 | 830 ± 5 | 50,000 ± 500 | 2.03 ± 0.02 |
| Column Identifier | Longitudinal Reinforcement | Transverse Reinforcement | ||||
|---|---|---|---|---|---|---|
| Nominal Diameter (mm) | No. of Bars | Reinforcement Ratio (%) | Nominal Diameter (mm) | Pitch (mm) | Volumetric Ratio (%) | |
| GGRAC6-75 | 12.7 ± 0.3 | 6 | 1.57 ± 0.5 | 9.5 ± 0.2 | 75 | 1.42 ± 0.2 |
| GGRAC6-150 | 150 | 0.71 ± 0.2 | ||||
| GGRAC6-250 | 250 | 0.50 ± 0.2 | ||||
| GGRAC8-75 | 12.7 ± 0.3 | 8 | 2.11 ± 0.5 | 9.5 ± 0.2 | 75 | 1.42 ± 0.2 |
| GGRAC8-150 | 150 | 0.71 ± 0.2 | ||||
| GGRAC8-250 | 250 | 0.50 ± 0.2 | ||||
| GGRAC10-75 | 12.7 ± 0.3 | 10 | 2.65 ± 0.5 | 9.5 ± 0.2 | 75 | 1.42 ± 0.2 |
| GGRAC10-150 | 150 | 0.71 ± 0.2 | ||||
| GGRAC10-250 | 250 | 0.50 ± 0.2 | ||||
| Sample Label | Peak Load (KN) | Axial Deflection at Peak Load (mm) | Ultimate Axial Deflections (mm) | Ductility Index |
|---|---|---|---|---|
| GGRAC6-75 | 1652.8 | 3.24 | 8.49 | 1.78 ± 0.15 |
| GGRAC6-150 | 1520.7 | 3.11 | 8.11 | 1.65 ± 0.15 |
| GGRAC6-250 | 1440.9 | 3.43 | 9.28 | 1.72 ± 0.15 |
| GGRAC8-75 | 1777.3 | 3.25 | 8.79 | 1.93 ± 0.15 |
| GGRAC8-150 | 1712.3 | 2.79 | 7.45 | 1.55 ± 0.15 |
| GGRAC8-250 | 1571.1 | 3.36 | 7.23 | 1.43 ± 0.15 |
| GGRAC10-75 | 1713.8 | 3.63 | 8.87 | 1.83 ± 0.15 |
| GGRAC10-150 | 1587.4 | 3.56 | 7.13 | 1.51 ± 0.15 |
| GGRAC10-250 | 1488.1 | 2.92 | 5.74 | 1.27 ± 0.15 |
| Parameter | B (mm) | D (mm) | H (mm) | Ag (mm2) | fc’ (MPa) | (MPa) | (GPa) | (%) | (%) | (%) | Af (mm2) | (kN) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Minimum | 150 | 150 | 150 | 17,662 | 20.0 | 406 | 23.4 | 0.97 | 0.55 | 0.01 | 212.53 | 114 |
| Maximum | 610 | 305 | 610 | 372,100 | 70.2 | 1680 | 141 | 2.42 | 5.3 | 5.3 | 4051.60 | 15,235 |
| Mean | 249 | 258 | 272 | 66,289 | 36.2 | 1010 | 56.7 | 1.78 | 2.09 | 1.38 | 1214.58 | 1814 |
| St. Dev | 114 | 54 | 114 | 53,039 | 12.6 | 339 | 25.1 | 0.39 | 1.06 | 1.06 | 764.62 | 1877 |
| COV | 0.46 | 0.21 | 0.43 | 0.81 | 0.35 | 0.34 | 0.45 | 0.22 | 0.51 | 0.77 | 0.63 | 1.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raza, A.; Rashedi, A.; Rafique, U.; Hossain, N.; Akinyemi, B.; Naveen, J. On the Structural Performance of Recycled Aggregate Concrete Columns with Glass Fiber-Reinforced Composite Bars and Hoops. Polymers 2021, 13, 1508. https://doi.org/10.3390/polym13091508
Raza A, Rashedi A, Rafique U, Hossain N, Akinyemi B, Naveen J. On the Structural Performance of Recycled Aggregate Concrete Columns with Glass Fiber-Reinforced Composite Bars and Hoops. Polymers. 2021; 13(9):1508. https://doi.org/10.3390/polym13091508
Chicago/Turabian StyleRaza, Ali, Ahmad Rashedi, Umer Rafique, Nazia Hossain, Banjo Akinyemi, and Jesuarockiam Naveen. 2021. "On the Structural Performance of Recycled Aggregate Concrete Columns with Glass Fiber-Reinforced Composite Bars and Hoops" Polymers 13, no. 9: 1508. https://doi.org/10.3390/polym13091508
APA StyleRaza, A., Rashedi, A., Rafique, U., Hossain, N., Akinyemi, B., & Naveen, J. (2021). On the Structural Performance of Recycled Aggregate Concrete Columns with Glass Fiber-Reinforced Composite Bars and Hoops. Polymers, 13(9), 1508. https://doi.org/10.3390/polym13091508







