Multiferroic Coupling of Ferromagnetic and Ferroelectric Particles through Elastic Polymers
Abstract
:1. Introduction
2. Materials and Methods
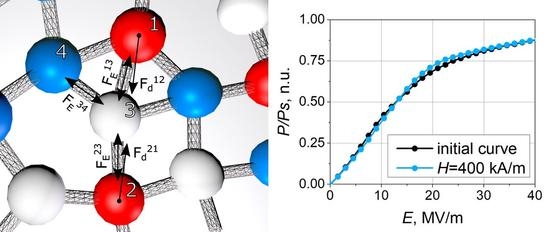
2.1. Numerical Model
2.2. Experiment
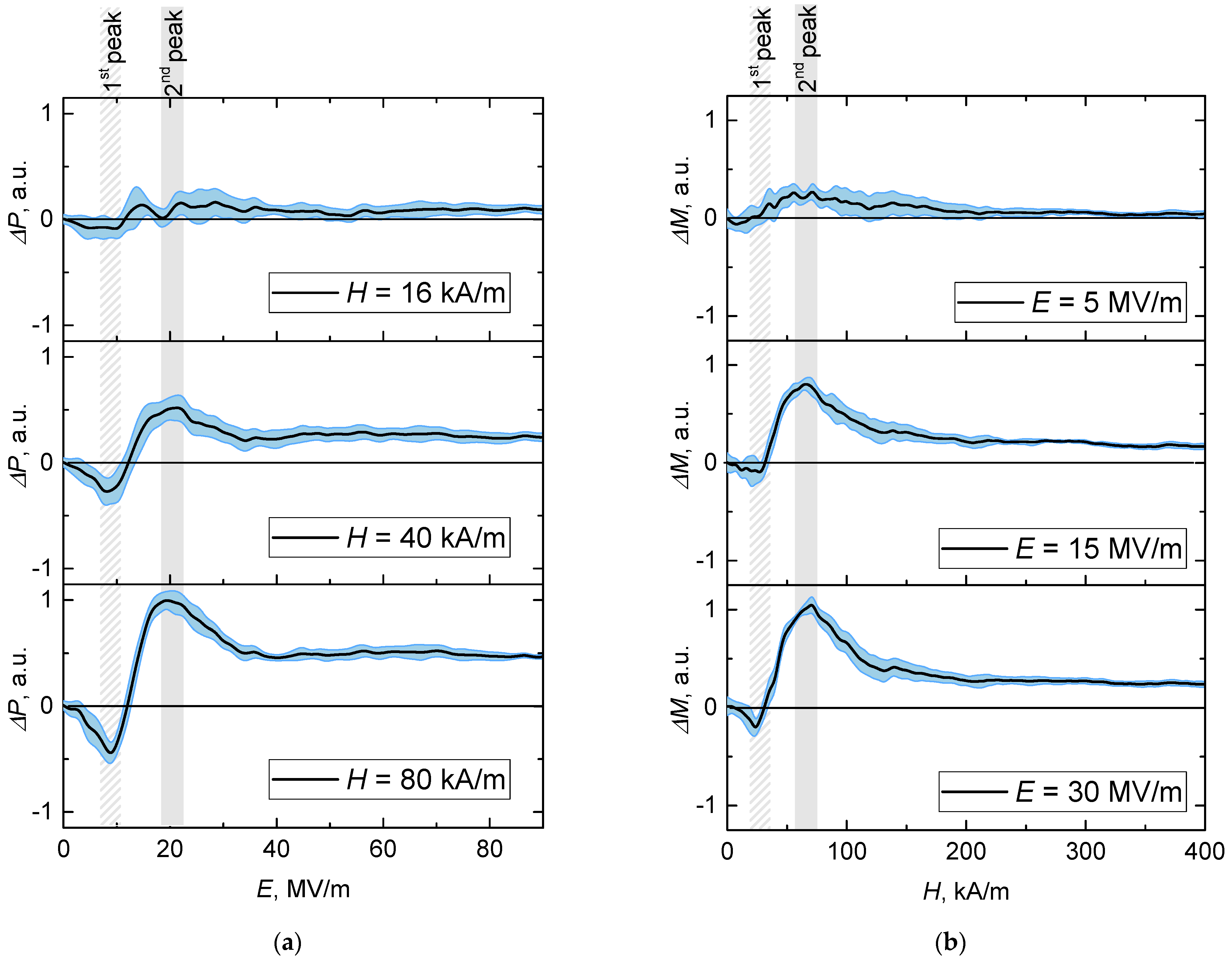
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Spaldin, N.A.; Ramesh, R. Advances in magnetoelectric multiferroics. Nat. Mater. 2019, 18, 203–212. [Google Scholar] [CrossRef]
- Spaldin, N.A. Materials Science: The Renaissance of Magnetoelectric Multiferroics. Science 2005, 309, 391–392. [Google Scholar] [CrossRef]
- Pereira, N.; Lima, A.C.; Lanceros-Mendez, S.; Martins, P. Magnetoelectrics: Three Centuries of Research Heading Towards the 4.0 Industrial Revolution. Materials 2020, 13, 4033. [Google Scholar] [CrossRef]
- Jiang, Q.; Liu, F.; Yan, H.; Ning, H.; Libor, Z.; Zhang, Q.; Cain, M.; Reece, M.J. Magneto-electric properties of multiferroic Pb(Zr0.52Ti0.48)O3-NiFe2O4 nanoceramic composites. J. Am. Ceram. Soc. 2011, 94, 2311–2314. [Google Scholar] [CrossRef]
- Stognij, A.I.; Novitskii, N.N.; Trukhanov, S.V.; Trukhanov, A.V.; Panina, L.V.; Sharko, S.A.; Serokurova, A.I.; Poddubnaya, N.N.; Ketsko, V.A.; Dyakonov, V.P.; et al. Interface magnetoelectric effect in elastically linked Co/PZT/Co layered structures. J. Magn. Magn. Mater. 2019, 485, 291–296. [Google Scholar] [CrossRef]
- Zhang, J.; Li, P.; Wen, Y.; He, W.; Yang, A.; Lu, C. Shear-mode self-biased magnetostrictive/piezoelectric laminate multiferroic heterostructures for magnetic field detecting and energy harvesting. Sens. Actuators A Phys. 2014, 214, 149–155. [Google Scholar] [CrossRef]
- Omelyanchik, A.; Antipova, V.; Gritsenko, C.; Kolesnikova, V.; Murzin, D.; Han, Y.; Turutin, A.V.; Kubasov, I.V.; Kislyuk, A.M.; Ilina, T.S.; et al. Boosting Magnetoelectric Effect in Polymer-Based Nanocomposites. Nanomaterials 2021, 11, 1154. [Google Scholar] [CrossRef] [PubMed]
- Miehe, C.; Vallicotti, D.; Teichtmeister, S. Homogenization and multiscale stability analysis in finite magneto-electro-elasticity. Application to soft matter EE, ME and MEE composites. Comput. Methods Appl. Mech. Eng. 2016, 300, 294–346. [Google Scholar] [CrossRef]
- Shi, Z.; Nan, C.W.; Liu, J.M.; Filippov, D.A.; Bichurin, M.I. Influence of mechanical boundary conditions and microstructural features on magnetoelectric behavior in a three-phase multiferroic particulate composite. Phys. Rev. B-Condens. Matter Mater. Phys. 2004, 70, 1–6. [Google Scholar] [CrossRef]
- Bastola, A.K.; Hossain, M. A review on magneto-mechanical characterizations of magnetorheological elastomers. Compos. Part B Eng. 2020, 200, 108348. [Google Scholar] [CrossRef]
- Chertovich, A.V.; Stepanov, G.V.; Kramarenko, E.Y.; Khokhlov, A.R. New composite elastomers with giant magnetic response. Macromol. Mater. Eng. 2010, 295, 336–341. [Google Scholar] [CrossRef]
- Kramarenko, E.Y.; Stepanov, G.V.; Khokhlov, A.R. Magnetically Active Silicone Elastomers: Twenty Years of Development. INEOS OPEN 2020, 2, 178–184. [Google Scholar] [CrossRef]
- Ginder, J.M.; Nichols, M.E.; Elie, L.D.; Tardiff, J.L. Magnetorheological elastomers: Properties and applications. In Proceedings of the Smart Structures and Materials 1999: Smart Materials Technologies, Newport Beach, CA, USA, 3–4 March 1999; Wuttig, M.R., Ed.; International Society for Optics and Photonics: Bellingham, WA, USA, 1999; pp. 131–138. [Google Scholar]
- Ubaidillah; Sutrisno, J.; Purwanto, A.; Mazlan, S.A. Recent progress on magnetorheological solids: Materials, fabrication, testing, and applications. Adv. Eng. Mater. 2015, 17, 563–597. [Google Scholar] [CrossRef]
- Makarova, L.A.; Alekhina, J.; Isaev, D.A.; Khairullin, M.F.; Perov, N.S. Tunable layered composites based on magnetoactive elastomers and piezopolymer for sensors and energy harvesting devices. J. Phys. D Appl. Phys. 2020, 54, 015003. [Google Scholar] [CrossRef]
- Hu, W.; Lum, G.Z.; Mastrangeli, M.; Sitti, M. Small-scale soft-bodied robot with multimodal locomotion. Nature 2018, 554, 81–85. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, M.; Yang, Y.; Huang, Q.; Fukuda, T.; Wang, Z.; Shen, Y. A bioinspired multilegged soft millirobot that functions in both dry and wet conditions. Nat. Commun. 2018, 9, 3944. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.; Parada, G.A.; Liu, S.; Zhao, X. Ferromagnetic soft continuum robots. Sci. Robot. 2019, 4. [Google Scholar] [CrossRef] [PubMed]
- Seo, K.S.; Wi, R.; Im, S.G.; Kim, D.H. A superhydrophobic magnetic elastomer actuator for droplet motion control. Polym. Adv. Technol. 2013, 24, 1075–1080. [Google Scholar] [CrossRef]
- Shamonin, M.; Kramarenko, E.Y. Highly Responsive Magnetoactive Elastomers. In Novel Magnetic Nanostructures; Elsevier: Amsterdam, The Netherlands, 2018; Volume i, pp. 221–245. [Google Scholar]
- Schümann, M.; Odenbach, S. In-situ observation of the particle microstructure of magnetorheological elastomers in presence of mechanical strain and magnetic fields. J. Magn. Magn. Mater. 2017, 441, 88–92. [Google Scholar] [CrossRef]
- Makarova, L.A.; Rodionova, V.V.; Alekhina, Y.A.; Rusakova, T.S.; Omelyanchik, A.S.; Perov, N.S. New Multiferroic Composite Materials Consisting of Ferromagnetic, Ferroelectric, and Polymer Components. IEEE Trans. Magn. 2017, 53, 1–7. [Google Scholar] [CrossRef]
- Makarova, L.A.; Alekhina, Y.A.; Omelyanchik, A.S.; Rodionova, V.V.; Malyshkina, O.V.; Perov, N.S. Elastically coupled ferromagnetic and ferroelectric microparticles: New multiferroic materials based on polymer, NdFeB and PZT particles. J. Magn. Magn. Mater. 2019, 470, 89–92. [Google Scholar] [CrossRef]
- Semisalova, A.S.; Perov, N.S.; Stepanov, G.V.; Kramarenko, E.Y.; Khokhlov, A.R. Strong magnetodielectric effects in magnetorheological elastomers. Soft Matter 2013, 9, 11318–11324. [Google Scholar] [CrossRef]
- Kostrov, S.A.; Shamonin, M.; Stepanov, G.V.; Kramarenko, E.Y. Magnetodielectric response of soft magnetoactive elastomers: Effects of filler concentration and measurement frequency. Int. J. Mol. Sci. 2019, 20, 2230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Minina, E.S.; Sánchez, P.A.; Likos, C.N.; Kantorovich, S.S. The influence of the magnetic filler concentration on the properties of a microgel particle: Zero-field case. J. Magn. Magn. Mater. 2018, 459, 226–230. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Raikher, Y.L. Structural changes in microferrogels cross-linked by magnetically anisotropic particles. J. Magn. Magn. Mater. 2017, 431, 192–195. [Google Scholar] [CrossRef]
- Han, Y.; Zhang, Z.; Faidley, L.E.; Hong, W. Microstructure-based modeling of magneto-rheological elastomers. In Proceedings of the Behavior and Mechanics of Multifunctional Materials and Composites 2012, San Diego, CA, USA, 12–15 March 2012. [Google Scholar]
- Stolbov, O.V.; Raikher, Y.L.; Balasoiu, M. Modelling of magnetodipolar striction in soft magnetic elastomers. Soft Matter 2011, 7, 8484–8487. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Melenev, P.V.; Holm, C.; Raikher, Y.L. Coarse-grained molecular dynamics simulation of small ferrogel objects. J. Magn. Magn. Mater. 2015, 383, 277–280. [Google Scholar] [CrossRef]
- Sánchez, P.A.; Minina, E.S.; Kantorovich, S.S.; Kramarenko, E.Y. Surface relief of magnetoactive elastomeric films in a homogeneous magnetic field: Molecular dynamics simulations. Soft Matter 2019, 15, 175–189. [Google Scholar] [CrossRef] [Green Version]
- Verlet, L. Computer “experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]

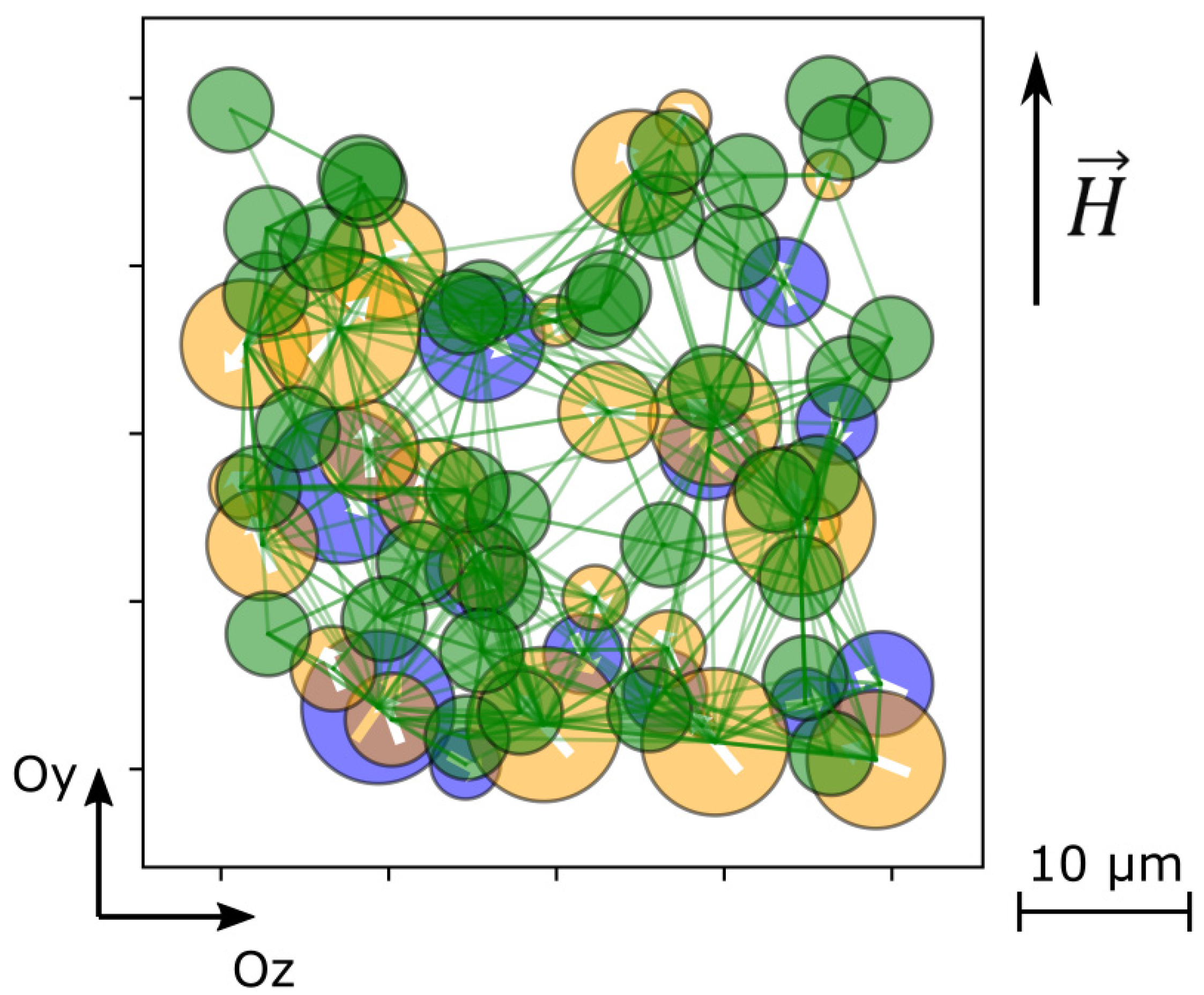



| Type of Particles | Density, kg/m3 | Volume Concentration, % | Number of Particles in the System | |
|---|---|---|---|---|
| Polymeric | 1003 | 7 | 17113 | – |
| Ferromagnetic | 7874 | 10 | 9658 | 1700 kA/m |
| Ferroelectric | 4700 | 10 | 9717 | 4000 mC/m2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makarova, L.A.; Isaev, D.A.; Omelyanchik, A.S.; Alekhina, I.A.; Isaenko, M.B.; Rodionova, V.V.; Raikher, Y.L.; Perov, N.S. Multiferroic Coupling of Ferromagnetic and Ferroelectric Particles through Elastic Polymers. Polymers 2022, 14, 153. https://doi.org/10.3390/polym14010153
Makarova LA, Isaev DA, Omelyanchik AS, Alekhina IA, Isaenko MB, Rodionova VV, Raikher YL, Perov NS. Multiferroic Coupling of Ferromagnetic and Ferroelectric Particles through Elastic Polymers. Polymers. 2022; 14(1):153. https://doi.org/10.3390/polym14010153
Chicago/Turabian StyleMakarova, Liudmila A., Danil A. Isaev, Alexander S. Omelyanchik, Iuliia A. Alekhina, Matvey B. Isaenko, Valeria V. Rodionova, Yuriy L. Raikher, and Nikolai S. Perov. 2022. "Multiferroic Coupling of Ferromagnetic and Ferroelectric Particles through Elastic Polymers" Polymers 14, no. 1: 153. https://doi.org/10.3390/polym14010153
APA StyleMakarova, L. A., Isaev, D. A., Omelyanchik, A. S., Alekhina, I. A., Isaenko, M. B., Rodionova, V. V., Raikher, Y. L., & Perov, N. S. (2022). Multiferroic Coupling of Ferromagnetic and Ferroelectric Particles through Elastic Polymers. Polymers, 14(1), 153. https://doi.org/10.3390/polym14010153