Sliding Dynamics of Ring Chains on Two Asymmetric/Symmetric Chains in a Simple Slide-Ring Gel
Abstract
:1. Introduction
2. Model
2.1. Coarse-Grained Model of Rotaxane
2.2. Molecular Dynamics Simulation
3. Results and Discussion
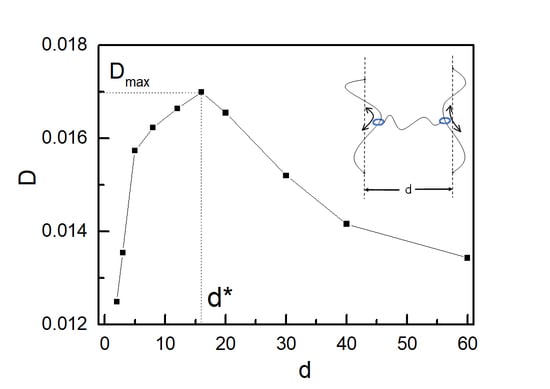
3.1. Sliding Dynamics of Ring Chains on Two Symmetric Chains (K1 = K2)
3.2. Sliding Dynamics of Ring Chains on Two Asymmetric Chains (K1 ≠ K2)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Harrison, I.T.; Harrison, S. The synthesis of a stable complex of a macrocycle and a threaded chain. J. Am. Chem. Soc. 1967, 89, 5723–5724. [Google Scholar] [CrossRef]
- Sofia, M.H.; Emilio, M.P. Mechanically interlocked materials: Rotaxanes and catenanes beyond the small molecules. Chem. Soc. Rev. 2019, 48, 5016–5032. [Google Scholar]
- Clavel, C.; Romuald, C.; Brabet, E.; Coutrot, F. A pH-Sensitive lasso-based rotaxane molecular switch. Chem. Eur. J. 2013, 19, 2982–2989. [Google Scholar] [CrossRef]
- Anelli, P.L.; Spencer, N.; Stoddart, J.F. A molecular shuttle. J. Am. Chem. Soc. 1991, 113, 5131–5133. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Murakami, H.; Kawabuchi, A.; Kotoo, K.; Kunitake, M.; Nakashima, N. A light-driven molecular shuttle based on a rotaxane. J. Am. Chem. Soc. 1997, 119, 7605–7606. [Google Scholar] [CrossRef]
- Leigh, D.A.; Wong, J.K.Y.; Dehez, F.; Zerbetto, F. Unidirectional rotation in a mechanically interlocked molecular rotor. Nature 2003, 424, 174–179. [Google Scholar] [CrossRef] [PubMed]
- Schliwa, M. Molecular Motors; Wiley-VCH: Weinheim, Germany, 2003. [Google Scholar]
- Bruns, C.J.; Storddart, J.F. Rotaxane-based molecular muscles. Acc. Chem. Res. 2014, 47, 2186–2199. [Google Scholar] [CrossRef]
- Mayumi, K.; Ito, K. Structure and dynamics of polyrotaxane and slide-ring materials. Polymer 2010, 51, 959–967. [Google Scholar] [CrossRef] [Green Version]
- Yui, N.; Ooya, T. Molecular mobility of interlocked structures exploiting new functions of advanced biomaterials. Chem. Eur. J. 2006, 12, 6730–6737. [Google Scholar] [CrossRef] [PubMed]
- Lohmann, F.; Ackermann, D.; Famulok, M. Reversible light switch for macrocycle mobility in a DNA rotaxane. J. Am. Chem. Soc. 2012, 134, 11884–11887. [Google Scholar] [CrossRef]
- Zhang, Z.; Hou, G.; Shen, J.; Liu, J.; Gao, Y.; Zhao, X.; Zhang, L. Designing the slide-ring polymer network with both good mechanical and damping properties via molecular dynamics simulation. Polymers 2018, 10, 964. [Google Scholar] [CrossRef] [Green Version]
- Yasuke, Y.; Toda, M.; Mayumi, K.; Yokoyama, H.; Morita, H.; Ito, K. Sliding dynamics of ring on polymer in rotaxane: A coarse-grained molecular dynamics study. Macromolecules 2019, 52, 3787–3793. [Google Scholar]
- Kato, K.; Ohara, A.; Michishio, K.; Ito, K. Effects of ring size on the dynamics of polyrotaxane glass. Macromolecules 2020, 53, 8910–8917. [Google Scholar] [CrossRef]
- Rauscher, P.M.; Schweizer, K.S.; Rowan, S.J.; de Pablo, J.J. Dynamics of poly[n]catenane melts. J. Chem. Phys. 2020, 152, 214901. [Google Scholar] [CrossRef]
- Wang, Z.H.; Lu, Y.Y.; Jin, H.; Luo, C.F.; An, L.J. Diffusion of a ring threaded on a linear chain. Chin. J. Polym. Sci. 2020, 38, 1409–1417. [Google Scholar] [CrossRef]
- Li, K.; Wang, Y.X.; Guo, F.C.; He, L.L.; Zhang, L.X. Sliding dynamics of multi-rings on a semiflexible polymer in poly[n]catenanes. Soft Matter 2021, 17, 2557–2567. [Google Scholar] [CrossRef]
- Guo, F.C.; Li, K.; Wu, J.X.; Wang, Y.X.; Zhang, L.X. Sliding dynamics of ring chain on a knotted polymer in rotaxane. Polymer 2021, 235, 124226. [Google Scholar] [CrossRef]
- Okumura, Y.; Ito, K. The polyrotaxane gel: A topological gel by figure-of-eight cross-links. Adv. Mater. 2001, 13, 485–487. [Google Scholar] [CrossRef]
- Ito, K. Novel entropic elasticity of polymeric materials: Why is slide-ring gel so soft? Polym. J. 2012, 44, 38–41. [Google Scholar] [CrossRef] [Green Version]
- Mayumi, K.; Tezuka, M.; Bando, A.; Ito, K. Mechanics of slide-ring gels: Novel entropic elasticsity of a topological network formed by ring and string. Soft Matter 2012, 8, 8179–8183. [Google Scholar] [CrossRef]
- Liu, C.; Kadono, H.; Mayumi, K.; Kato, K.; Yokoyama, H.; Ito, K. Unusual fracture behavior of slide-ring gels with movable cross-links. ACS Macro Lett. 2017, 6, 1409–1413. [Google Scholar] [CrossRef]
- Kato, K.; Ito, K. Dynamic transition between rubber and sliding states attributed to slidable cross-links. Soft Matter 2011, 7, 8737–8740. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Gilles, F.M.; Llubaroff, R.; Pastorino, C. Fluctuation-induced forces between rings threaded around a polymer chain under tension. Phys. Rev. E 2016, 94, 032503. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Lu, W. Effect of mechanical load on the shuttling operation of molecular muscles. Appl. Phys. Lett. 2009, 94, 233114. [Google Scholar] [CrossRef] [Green Version]
- Guo, F.C.; Li, K.; Wu, J.X.; He, L.L.; Zhang, L.X. Effects of topological constraints on penetration structures of semi-Flexible ring polymers. Polymers 2020, 12, 2659. [Google Scholar] [CrossRef]
- Zhou, X.L.; Jiang, Y.W.; Chen, J.M.; He, L.L.; Zhang, L.X. Size-dependent nanoparticle dynamics in semiflexible ring polymer nanocomposites. Polymer 2017, 131, 243–251. [Google Scholar] [CrossRef]
- Zhou, X.L.; Guo, F.C.; Li, K.; He, L.L.; Zhang, L.X. Entropy-induced separation of binary semiflexible ring polymer mixtures in spherical confinement. Polymers 2019, 11, 1992. [Google Scholar] [CrossRef] [Green Version]
- Deng, Z.Y.; Jiang, Y.W.; He, L.L.; Zhang, L.X. Aggregation–dispersion transition for nanoparticles in semiflexible ring polymer nanocomposite melts. J. Phys. Chem. B 2016, 120, 11574–11581. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Gavrilov, A.A.; Potemkin, I.I. Adaptive structure of gels and microgels with sliding cross-links: Enhanced softness, stretchability and permeability. Soft Matter 2018, 14, 5098–5105. [Google Scholar] [CrossRef] [PubMed]
- Poier, P.; Likos, C.N.; Matthews, R. Influence of rigidity and knot complexity on the knotting of confined polymers. Macromolecules 2014, 47, 3394–3400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Curro, J.G.; Mark, J.E. A non-Gaussian theory of rubberlike elasticity based on rotational isomeric state simulations of network chain configurations. II. Bimodal poly(dimethylsiloxane) networks. J. Chem. Phys. 1984, 80, 4521. [Google Scholar] [CrossRef]
- Yuan, Q.W.; Kloczkowski, A.; Mark, J.E.; Sharf, M.A. Simulations on the reinforcement of poly (dimethylsiloxane) elastomers by randomly distributed filler particles. J. Polym. Sci. Part B Polym. Phys. 1996, 34, 1647–1657. [Google Scholar] [CrossRef]
- Mark, J.E. Some recent theory, experiments, and simulations on rubberlike elasticity. J. Phys. Chem. 2003, 107, 903–913. [Google Scholar] [CrossRef]
- Zhang, L.X.; Jiang, Z.T.; Zhao, D.L. Elastic behavior of bimodal poly (dimethylsiloxane) networks. J. Polym. Sci. Part B Polym. Phys. 2002, 40, 105–116. [Google Scholar] [CrossRef]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Guo, F.; Li, K.; Zhang, L. Sliding Dynamics of Ring Chains on Two Asymmetric/Symmetric Chains in a Simple Slide-Ring Gel. Polymers 2022, 14, 79. https://doi.org/10.3390/polym14010079
Wu J, Guo F, Li K, Zhang L. Sliding Dynamics of Ring Chains on Two Asymmetric/Symmetric Chains in a Simple Slide-Ring Gel. Polymers. 2022; 14(1):79. https://doi.org/10.3390/polym14010079
Chicago/Turabian StyleWu, Jiaxin, Fuchen Guo, Ke Li, and Linxi Zhang. 2022. "Sliding Dynamics of Ring Chains on Two Asymmetric/Symmetric Chains in a Simple Slide-Ring Gel" Polymers 14, no. 1: 79. https://doi.org/10.3390/polym14010079
APA StyleWu, J., Guo, F., Li, K., & Zhang, L. (2022). Sliding Dynamics of Ring Chains on Two Asymmetric/Symmetric Chains in a Simple Slide-Ring Gel. Polymers, 14(1), 79. https://doi.org/10.3390/polym14010079