Magneto-Dielectric Effects in Polyurethane Sponge Modified with Carbonyl Iron for Applications in Low-Cost Magnetic Sensors
Abstract
:1. Introduction
2. Materials and Methods
2.1. Manufacturing Magnetizable Polyurethane Sponges (MSs)
- (a)
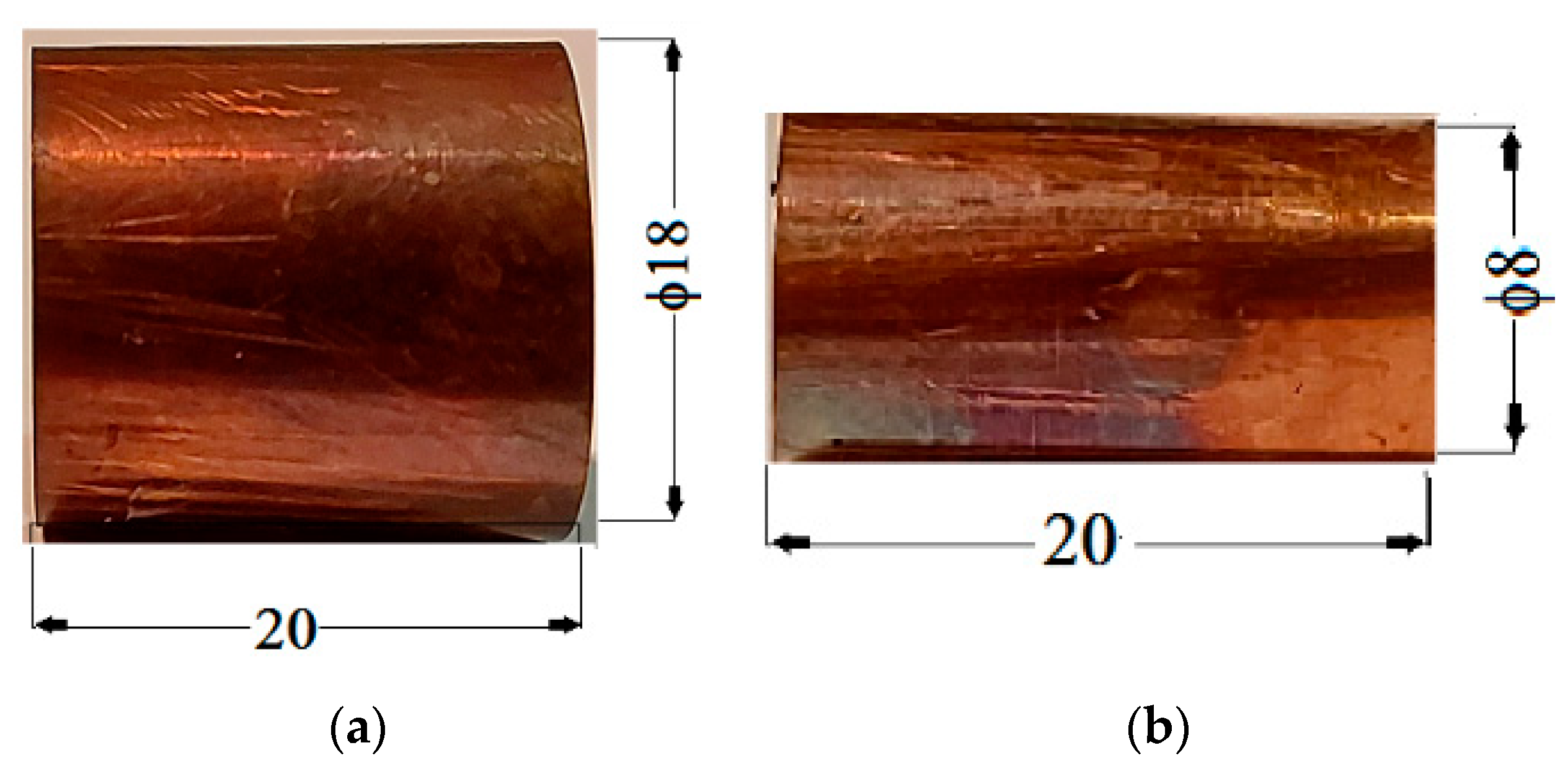
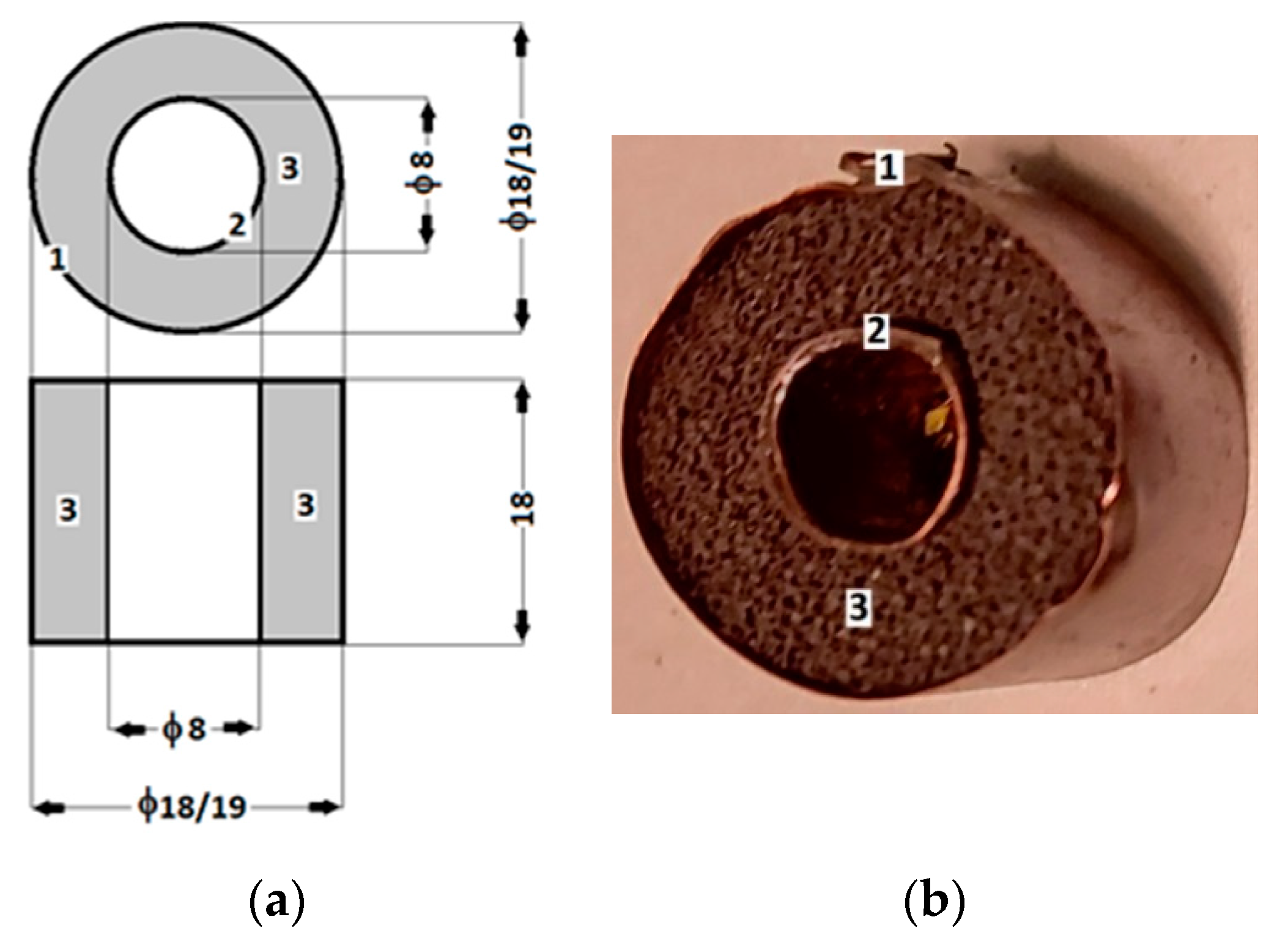
- The polymeric porous matrix (PPM) from polyurethane sponges (PSs): PSs were produced in China and distributed by SC Just Master Activities SRL, Bucharest, Romania. Each PS had the shape of a porous cylinder (Figure 1a). The shapes of the pores and fibers were visualized using a digital microscope (Figure 1b). The length of the PS was , the exterior diameter was , and the interior diameter was . Thus, the volume of the PPM matrix was . The mass of the PPM matrix was measured using an analytical balance type ALN60 produced by Axis, Gdańsk Poland, and found to be Calculating the mass density of the PPM matrix at a room temperature of , we obtained .
- (b)
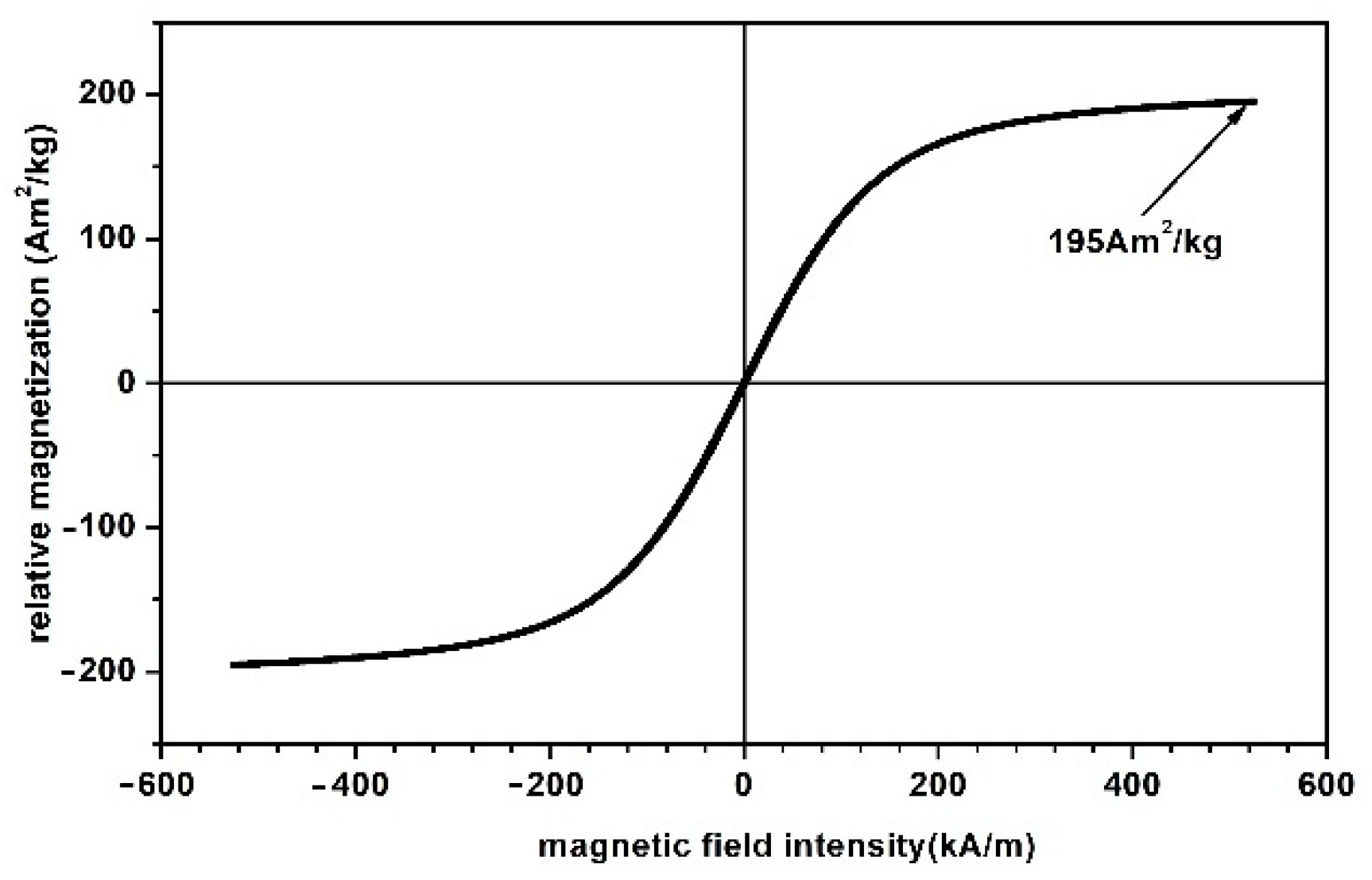
- The carbonyl iron microparticles (CIPs) were produced by Sigma-Aldrich (St. Louis, MO, USA) and sold in powdered form with a medium diameter of . At a temperature of , the CIP microparticle density was . Figure 2 shows the magnetization slope for CIPs obtained using the experimental setup in [24]. The maximum specific magnetization of CIPs was for a magnetic field intensity of .
2.2. Manufacturing Cylindrical Capacitors (CCs)
- (a)
- A copper sheet (FCu) with a size of 500 × 500 × 0.50 mm (composition code CW004A (CuETP), product code HOBC005, and delivered by emag.ro);
- (b)
- samples, described in Table 1.
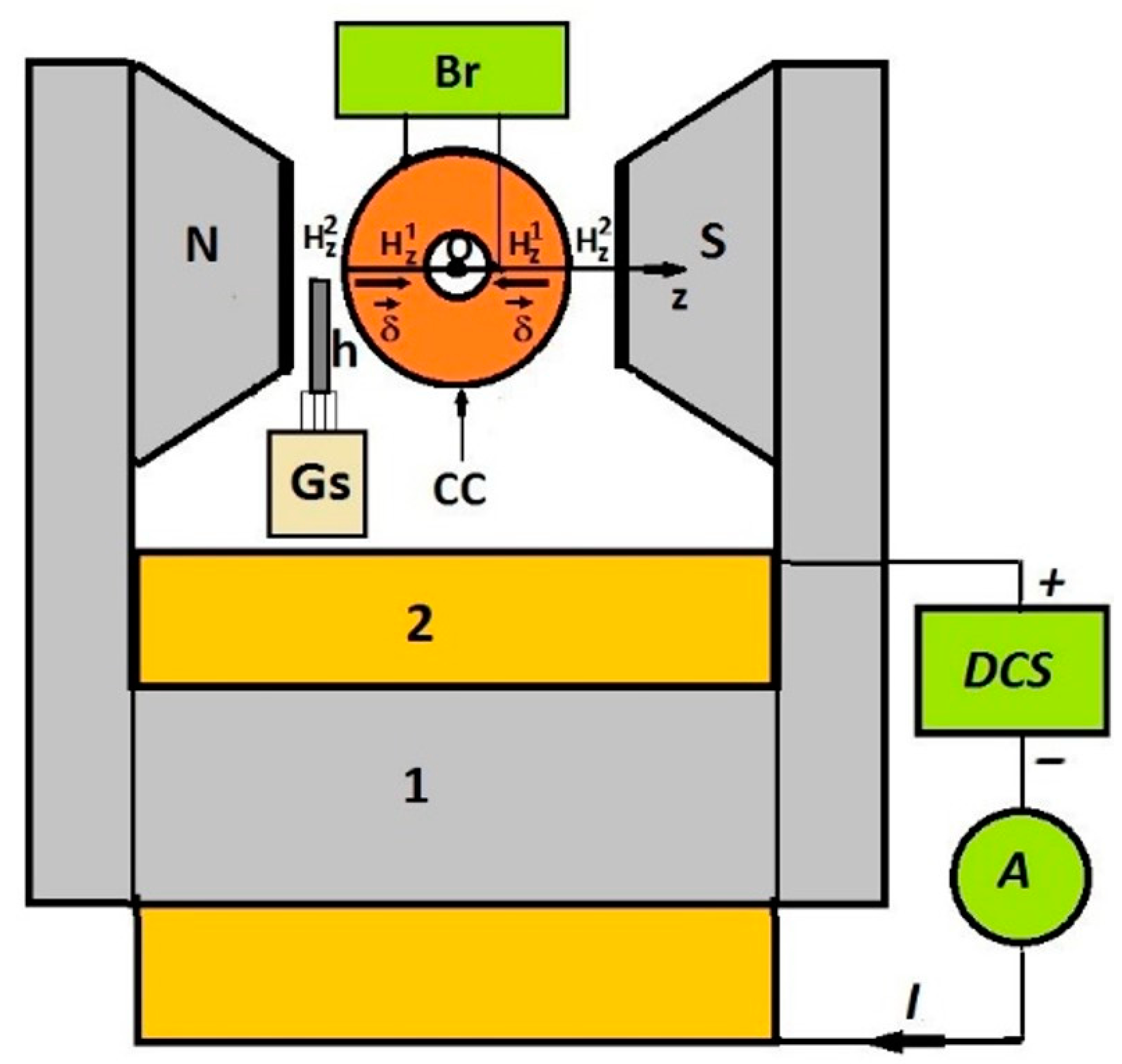
2.3. Experimental Setup
3. Results and Discussion
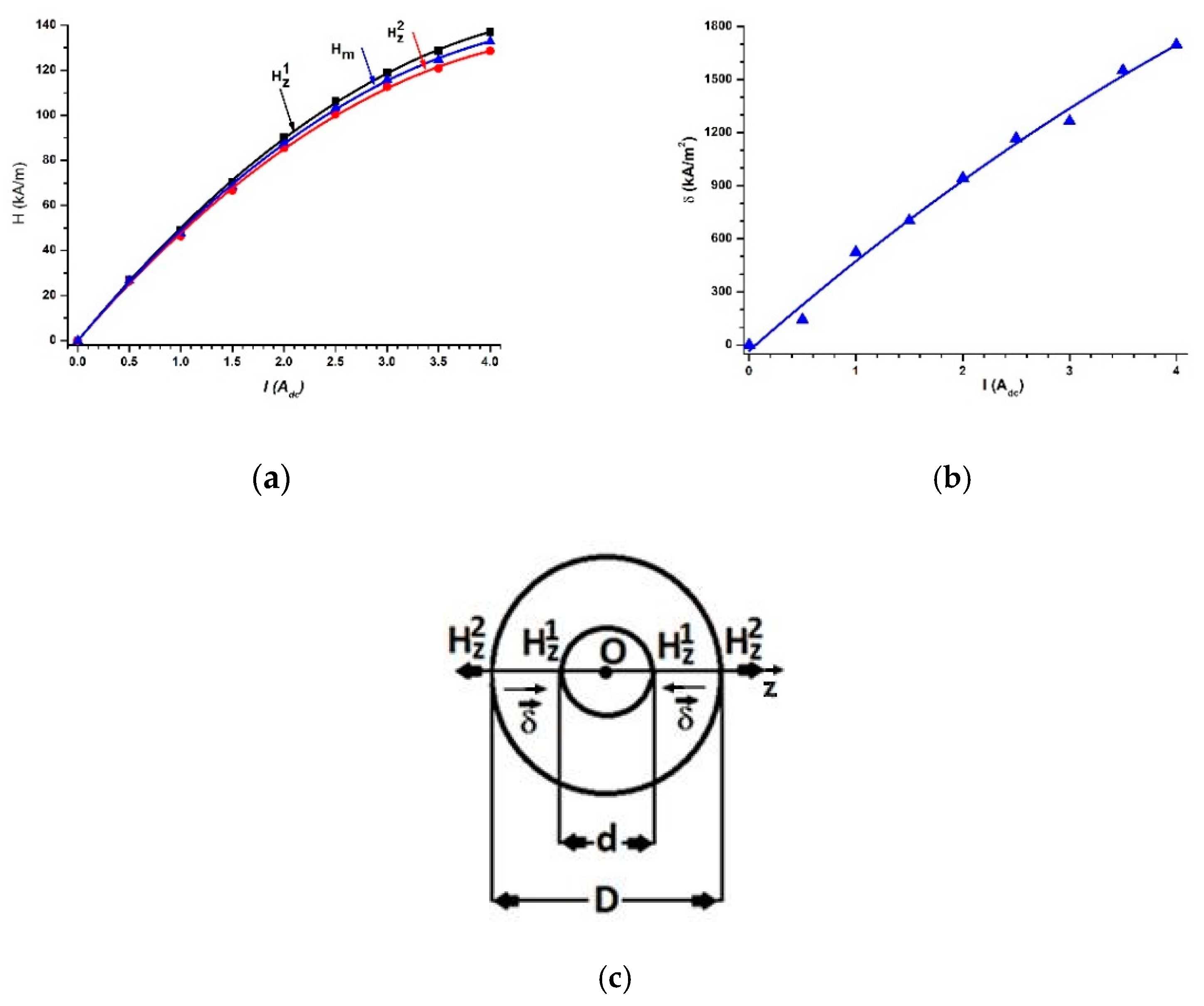
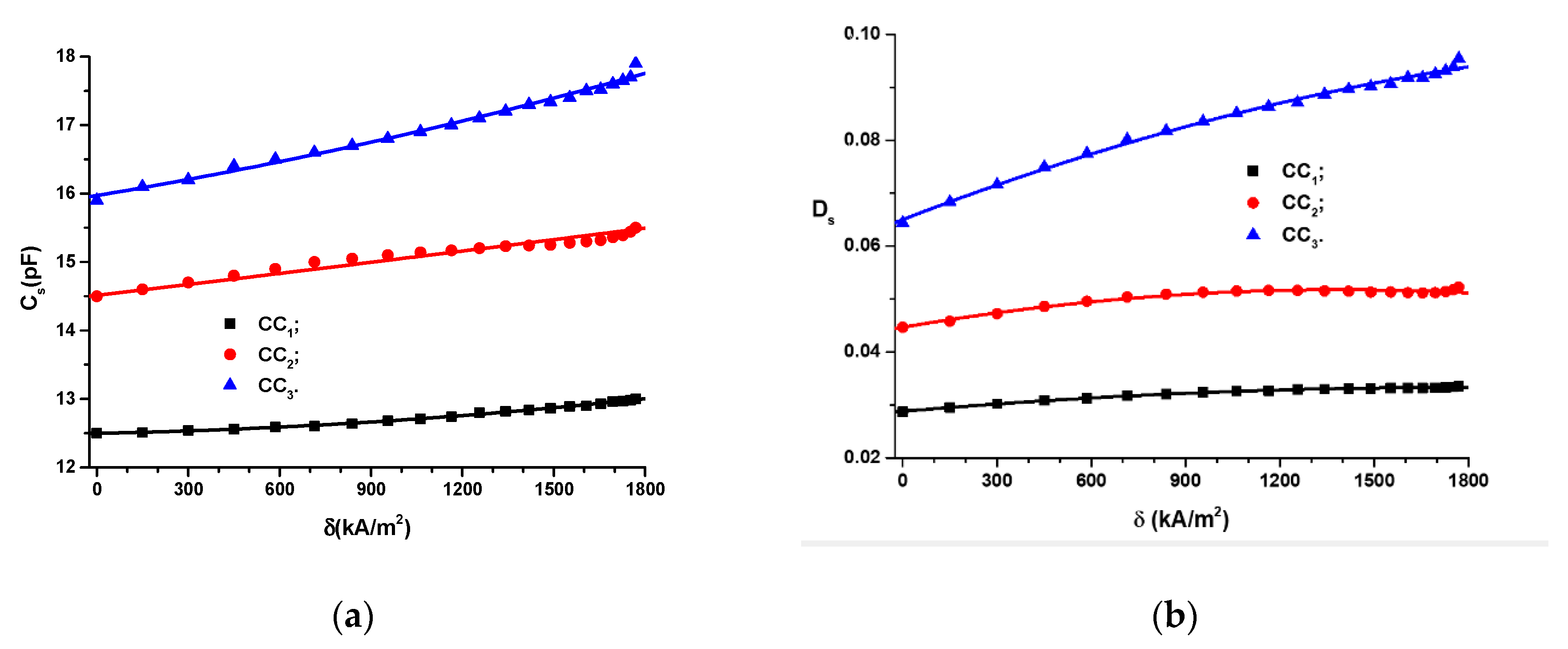
3.1. Measurements and Experimental Data
3.2. Comparison with Data Reported in the Literature
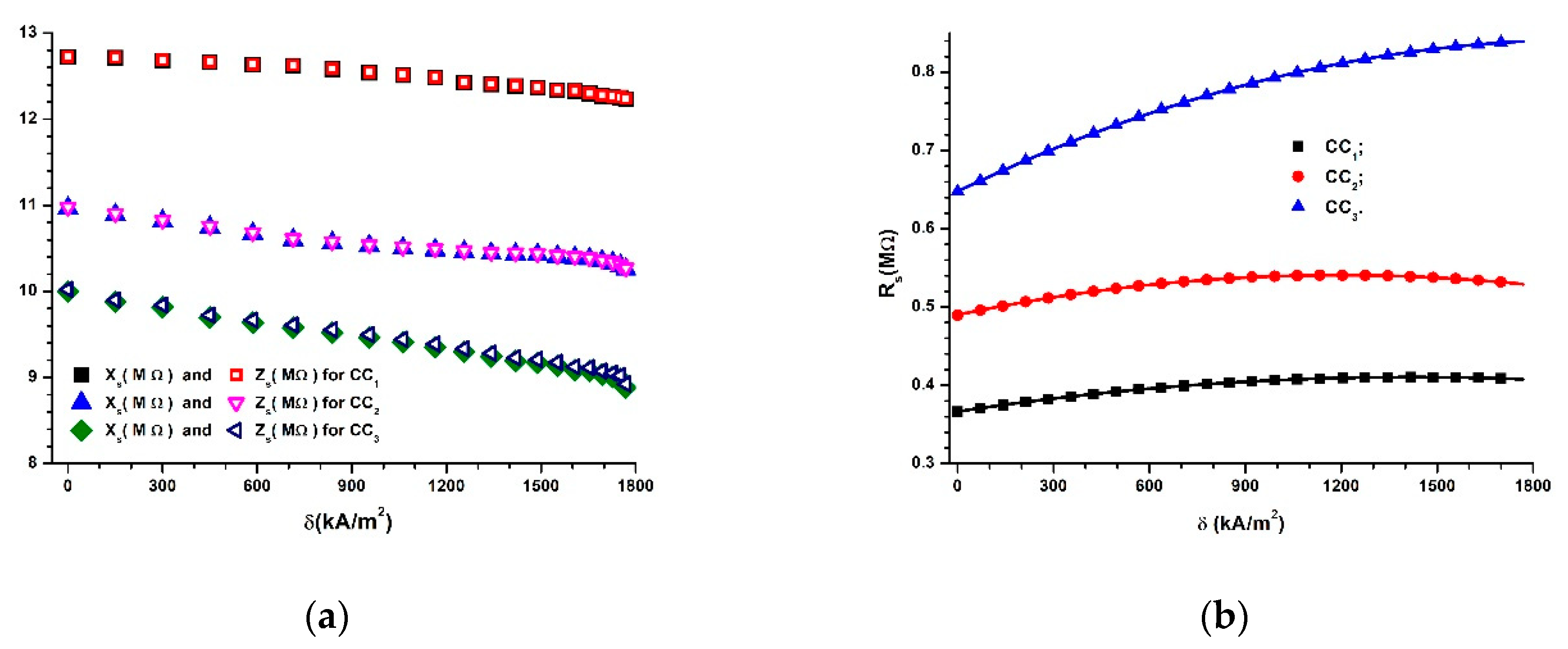
3.3. Equivalent Electrical Scheme of CCs
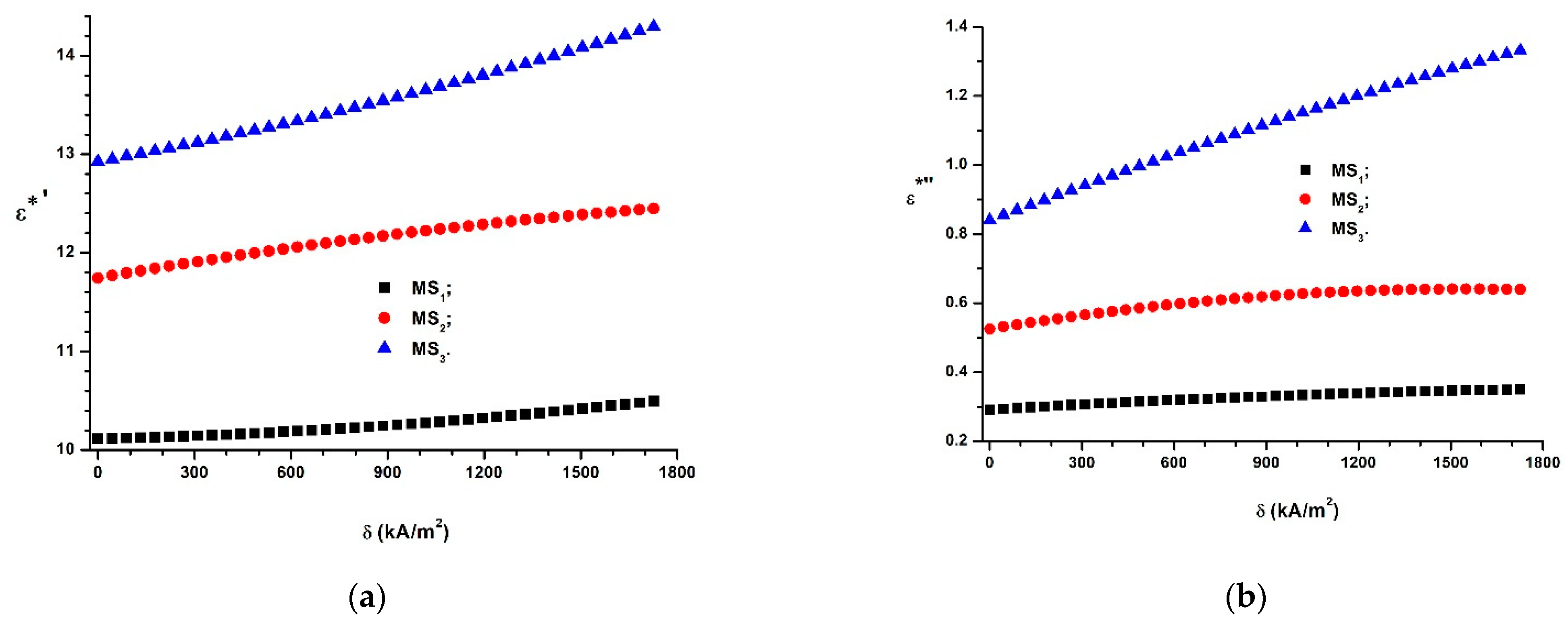
3.4. The Components of the Complex Dielectric Permittivity of MSs in the Absence of the Magnetic Field
3.5. The Components of the Complex Dielectric Permittivity of MSs in the Presence of the Magnetic Field (Theoretical Model)
3.6. Time Constant of CCs
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Norhaniza, R.; Mazlan, S.A.; Ubaidillah, U.; Sedlacik, M.; Aziz, S.A.A.; Nazmi, N.; Homma, K.; Rambat, S. Sensitivities of Rheological Properties of Magnetoactive Foam for Soft Sensor Technology. Sensors 2021, 21, 1660. [Google Scholar] [CrossRef] [PubMed]
- Cramer, J.; Cramer, M.; Demeester, E.; Kellens, K. Exploring the potential of magnetorheology in robotic grippers. Procedia CIRP 2018, 76, 127–132. [Google Scholar] [CrossRef]
- Wang, H.; Totaro, M.; Beccai, L. Toward Perceptive Soft Robots: Progress and Challenges. Adv. Sci. 2018, 5, 1800541. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Zhang, X.; Zang, X.; Liu, Y.; Ding, G.; Yin, W.; Zhao, J. Feature sensing and robotic grasping of objects with uncertain information: A review. Sensors 2020, 20, 3707. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Wang, B.; Li, Y.; Huang, W.; Li, Y. Magnetostrictive Tactile Sensor Array for Object Recognition. IEEE Trans. Magn. 2019, 55, 1–7. [Google Scholar] [CrossRef]
- Plachy, T.; Kratina, O.; Sedlacik, M. Porous magnetic materials based on EPDM rubber filled with carbonyl iron particles. Compos. Struct. 2018, 192, 126–130. [Google Scholar] [CrossRef]
- Davino, D.; Mei, P.; Sorrentino, L.; Visone, C. Polymeric composite foams with properties controlled by the magnetic field. IEEE Trans. Magn. 2012, 48, 3043–3046. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J.; Wang, G.; Fu, F.; Gao, X.; Niu, F.; Wei, O.; Yang, X. Preparation of Superhydrophobic Magnetic Polyurethane Sponge for Removing Oil Pollutants from Water. IOP Conf. Ser. Mater. Sci. Eng. 2018, 392, 042003. [Google Scholar] [CrossRef]
- Jiang, P.; Li, K.; Chen, X.; Dan, R.; Yu, Y. Magnetic and Hydrophobic Composite Polyurethane Sponge for Oil–Water Separation. Appl. Sci. 2020, 10, 1453. [Google Scholar] [CrossRef] [Green Version]
- Elhajjar, R.; Law, C.T.; Pegoretti, A. Magnetostrictive polymer composites: Recent advances in materials, structures and properties. Prog. Mater. Sci. 2018, 97, 204–229. [Google Scholar] [CrossRef]
- Park, Y.-J.; Yoon, J.-Y.; Kang, B.-H.; Kim, G.-W.; Choi, S.-B. A tactile device generating repulsive forces of various human tissues fabricated from magnetic-responsive fluid in porous polyurethane. Materials 2020, 13, 1062. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Makarova, L.A.; Alekhina, Y.A.; Omelyanchik, A.S.; Peddis, D.; Spiridonov, V.V.; Rodionova, V.V.; Perov, N.S. Magnetorheological foams for multiferroic applications. J. Magn. Magn. Mater. 2019, 485, 413–418. [Google Scholar] [CrossRef]
- Bastola, A.K.; Hossain, M. A review on magneto-mechanical characterizations of magnetorheological elastomers. Compos. Part B Eng. 2020, 200, 108348. [Google Scholar] [CrossRef]
- Muhazeli, N.S.; Nordin, N.A.; Mazlan, S.A.; Rizuan, N.; Abdul Aziz, S.A.; Abd Fatah, A.Y.; Ibrahim, Z.; Ubaidillah, U.; Choi, S.B. Characterization of morphological and rheological properties of rigid magnetorheological foams via in situ fabrication method. J. Mater. Sci. 2019, 54, 13821–13833. [Google Scholar] [CrossRef]
- Gong, Q.; Wu, J.; Gong, X.; Fan, Y.; Xia, H. Smart polyurethane foam with magnetic field controlled modulus and anisotropic compression property. RSC Adv. 2013, 3, 3241–3248. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E.M.; Chirigiu, L. Hybrid magnetorheological composites for electric and magnetic field sensors and transducers. Nanomaterials 2020, 10, 2060. [Google Scholar] [CrossRef]
- Bunoiu, M.; Anitas, E.M.; Pascu, G.; Chirigiu, L.M.E.; Bica, I. Electrical and magnetodielectric properties of magneto-active fabrics for electromagnetic shielding and health monitoring. Int. J. Mol. Sci. 2020, 21, 4785. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E.M.; Averis, L.M.E. Magnetic Control of Light Transmission and of Electrical Conductivity in (Hybrid) Magnetorheological Suspensions Based on Bioactive Components. Rom. J. Phys. 2020, 65, 605. [Google Scholar]
- Balasoiu, M.; Bunoiu, M.; Chirigiu, L.M.E.; Bica, I. Electrical devices based on hybrid magnetorheological suspensions: Realization, phenomenological modeling and technical characteristics. Rom. J. Phys. 2021, 66, 604. [Google Scholar]
- Bica, I.; Anitas, E.M. Electrical devices based on hybrid membranes with mechanically and magnetically controllable, resistive, capacitive and piezoelectric properties. Smart Mater. Struct. 2022, 31, 045001. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E.M. Light transmission, magnetodielectric and magnetoresistive effects in membranes based on hybrid magnetorheological suspensions in a static magnetic field superimposed on a low/medium frequency electric field. J. Magn. Magn. Mat. 2020, 511, 166975. [Google Scholar] [CrossRef]
- Uche, U.I.; Naidenko, O.V. Development of health-based exposure limits for radiofrequency radiation from wireless devices using a benchmark dose approach. Environ. Health 2021, 20, 84. [Google Scholar] [CrossRef] [PubMed]
- Tzima, E.; Martin, C.J. An evaluation of safe practices to restrict exposure to electric and magnetic fields from therapeutic and surgical diathermy equipment. Physiol. Meas. 1994, 15, 201–216. [Google Scholar] [CrossRef] [PubMed]
- Ercuta, A. Sensitive AC Hysteresigraph of Extended Driving Field Capability. IEEE Trans. Instrum. Meas. 2020, 69, 1643–1651. [Google Scholar] [CrossRef]
- Japka, J.E. Microstructure and Properties of Carbonyl Iron Powder. JOM 1988, 40, 18–21. [Google Scholar] [CrossRef]
- Atkins, A.J.; Bauer, M.; Jacob, C.R. High-resolution X-ray absorption spectroscopy of iron carbonyl complexes. Phys. Chem. Chem. Phys. 2015, 17, 13937–13948. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- König, R.; Müller, S.; Dinnebier, R.E.; Hinrichsen, B.; Müller, P.; Ribbens, A.; Hwang, J.; Liebscher, R.; Etter, M.; Pistidda, C. The crystal structures of carbonyl iron powder—revised using in situ synchrotron XRPD. Z. Kristallogr. Cryst. Mater. 2017, 232, 835–842. [Google Scholar] [CrossRef]
- Huang, C.; Niu, H.; Wu, J.; Ke, Q.; Mo, X.; Lin, T. Needleless eletrospinning of polystyrene fibers with an oriented surface line texture. J. Nanomater. 2012, 2012, 473872. [Google Scholar] [CrossRef] [Green Version]
- Bica, I.; Anitas, E.M.; Chirigiu, L.; Bunoiu, M.; Juganaru, I.; Tatu, R.F. Magnetodielectric effects in hybrid magnetorheological suspensions. J. Ind. Eng. Chem. 2015, 22, 53–62. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E.M.; Chirigiu, L. Magnetic field intensity effect on plane capacitors based on hybrid magnetorheological elastomers with graphene nanoparticles. J. Ind. Eng. Chem. 2017, 56, 407–412. [Google Scholar] [CrossRef]
- Bica, I.; Anitas, E.M.; Averis, L.M.E. Influence of magnetic field on dispersion and dissipation of electric field of low and medium frequencies in hybrid magnetorheological suspensions. J. Ind. Eng. Chem 2015, 27, 334–340. [Google Scholar] [CrossRef]
- Moliton, A. Applied Electromagnetism and Materials; Springer: Cham, Switzerland, 2007. [Google Scholar] [CrossRef] [Green Version]







| 0.169 | 0.2525 | 0.0322 | 4.9678 | 41.92 | 0.37 | 57.71 | ||
| 0.169 | 0.3380 | 0.0430 | 4.9570 | 41.92 | 0.49 | 57.59 | ||
| 0.169 | 0.5070 | 0.0645 | 4.9355 | 41.92 | 0.75 | 57.33 |
| 12.49874/0.00644 | 8.40272/ | 1.09443/ | |
| 14.51244/0.02785 | 5.27391/ | 1.012271/ | |
| 15971/0.03966 | 7.39757/ | 1.39335/ |
| 0.02881/5.69773 | 5.06593/6.07483 | 1.421986.81121 | |
| 0.04469/2.56596 | 1.018025/4.227 | 3.65438/3.06785 | |
| 0.06503/4.27432 | 2.29278/1.01193 | 3.83616 |
| EDs | Equivalent Electrical Capacities | Reference |
|---|---|---|
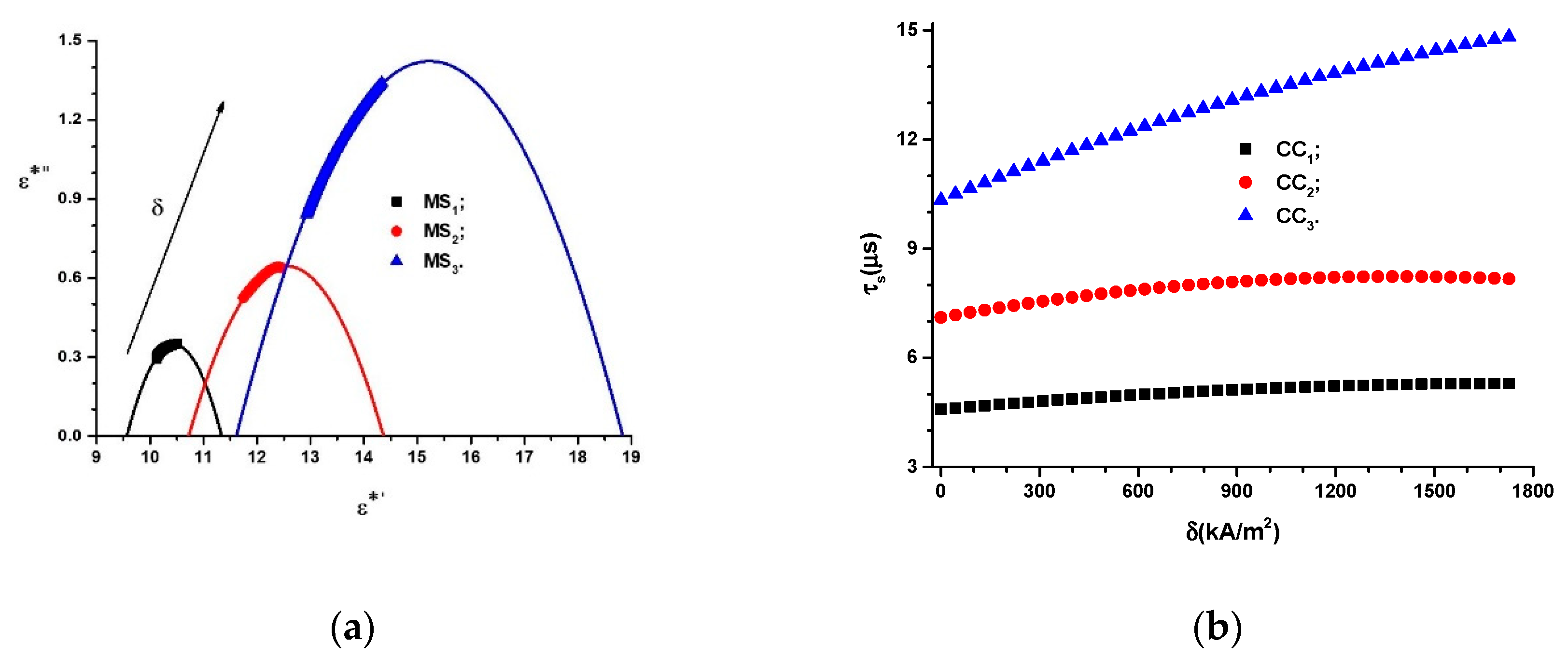
| for (Table 1) at si f = 1 kHz for (Table 1) 1 at si f = 1 kHz for (Table 1) 1 at si f = 1 kHz. | Present work Figure 8a | |
| for with at and for with at and for with at and | [29] | |
| for with at si f = 1 kH and for with at and for with at and for with at and | [30] |
| 10.1239794 | 0.291671846514 | |
| 11.7550764 | 0.525334364316 | |
| 12.93651 | 0.8412612453 |
| 18.01068434/2.74233 | 1.21084/7.16058 | 1.57708/3.91903 | |
| 20.91242604/1.4432 | 0.001/3.76839 | 1.61782/2.06246 | |
| 23.014211/8.56713 | 0.00107/2.23699 | 2.00781/1.22432 |
| 0.5188/1.93415 | 9.46878/5.05033 | 1.9994/2.76408 | |
| 0.93367/3.22217 | 2.64798/8.41352 | 8.43646/4.60478 | |
| 1.49618/2.22621 | 5.99923/5.81293 | 5.35567/3.18145 |
| −47.86851/0.98815 | 9.22566/0.10782 | 0.44131/0.00524 | |
| −29.96986/0.21044 | 4.88146/0.03473 | 0.19458/0.00143 | |
| −23.85768/0.07655 | 3.32095/0.01126 | 0.10906/4.13649 |
| 12.49874/0.00644 | 8.40272/ | 1.09443/ | |
| 14.51244/0.02785 | 5.27391/ | 1.012271/ | |
| 15.971/0.03966 | 7.39757/ | 1.39335/ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bica, I.; Iacobescu, G.-E. Magneto-Dielectric Effects in Polyurethane Sponge Modified with Carbonyl Iron for Applications in Low-Cost Magnetic Sensors. Polymers 2022, 14, 2062. https://doi.org/10.3390/polym14102062
Bica I, Iacobescu G-E. Magneto-Dielectric Effects in Polyurethane Sponge Modified with Carbonyl Iron for Applications in Low-Cost Magnetic Sensors. Polymers. 2022; 14(10):2062. https://doi.org/10.3390/polym14102062
Chicago/Turabian StyleBica, Ioan, and Gabriela-Eugenia Iacobescu. 2022. "Magneto-Dielectric Effects in Polyurethane Sponge Modified with Carbonyl Iron for Applications in Low-Cost Magnetic Sensors" Polymers 14, no. 10: 2062. https://doi.org/10.3390/polym14102062
APA StyleBica, I., & Iacobescu, G.-E. (2022). Magneto-Dielectric Effects in Polyurethane Sponge Modified with Carbonyl Iron for Applications in Low-Cost Magnetic Sensors. Polymers, 14(10), 2062. https://doi.org/10.3390/polym14102062







