Evaluating the Effect of Polymer Modification on the Low-Temperature Rheological Properties of Asphalt Binder
Abstract
:1. Introduction
2. Theoretical Background
2.1. Linear Viscoelastic Rheological Characterization
2.2. Spectrum of Relaxation Times
3. Materials and Methods
3.1. Binders
3.2. Preparation of Compounded and Modified Binders
3.3. Conventional Properties of Binders
3.4. Rheological Testing
4. Results and Discussion
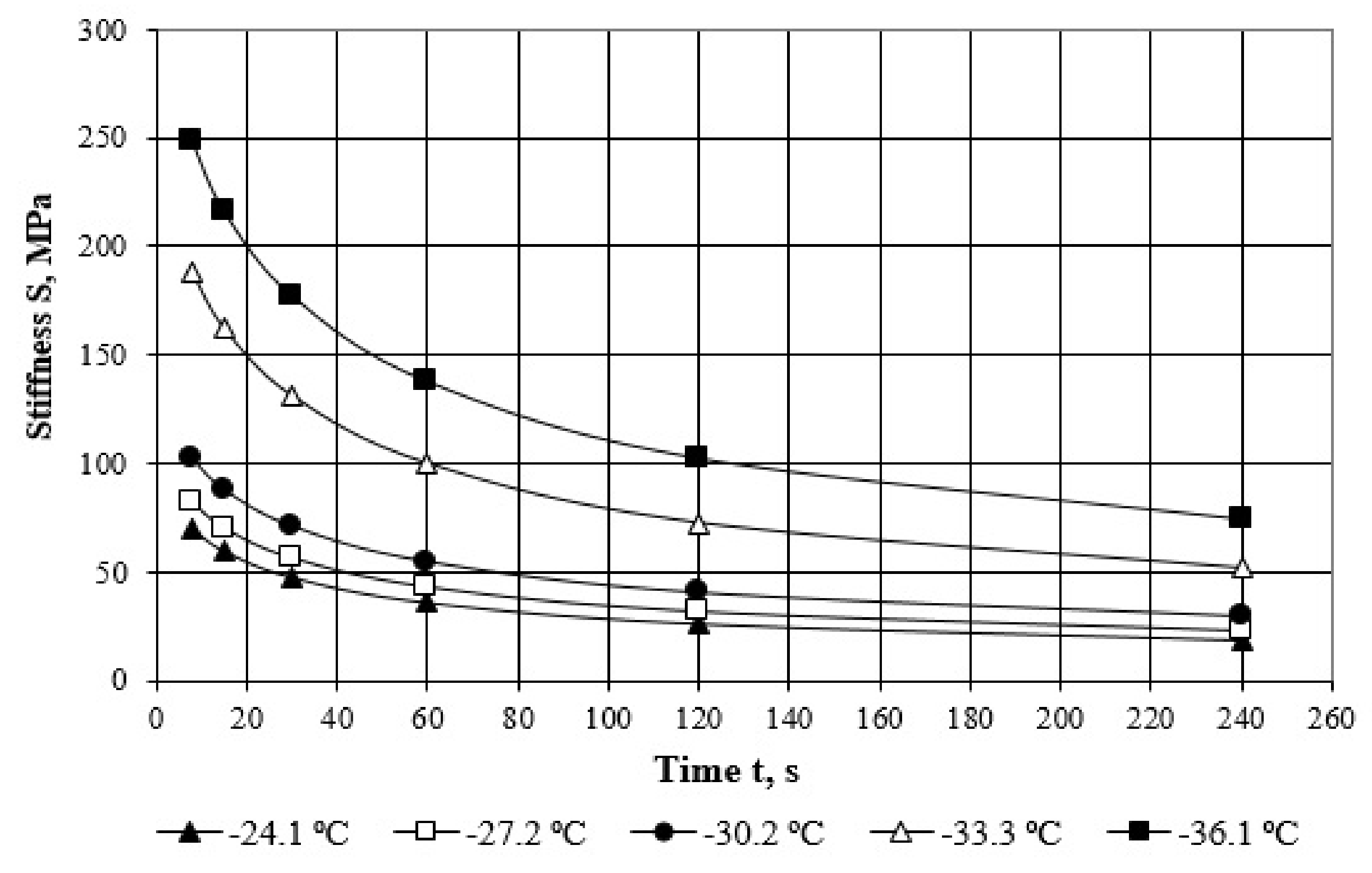
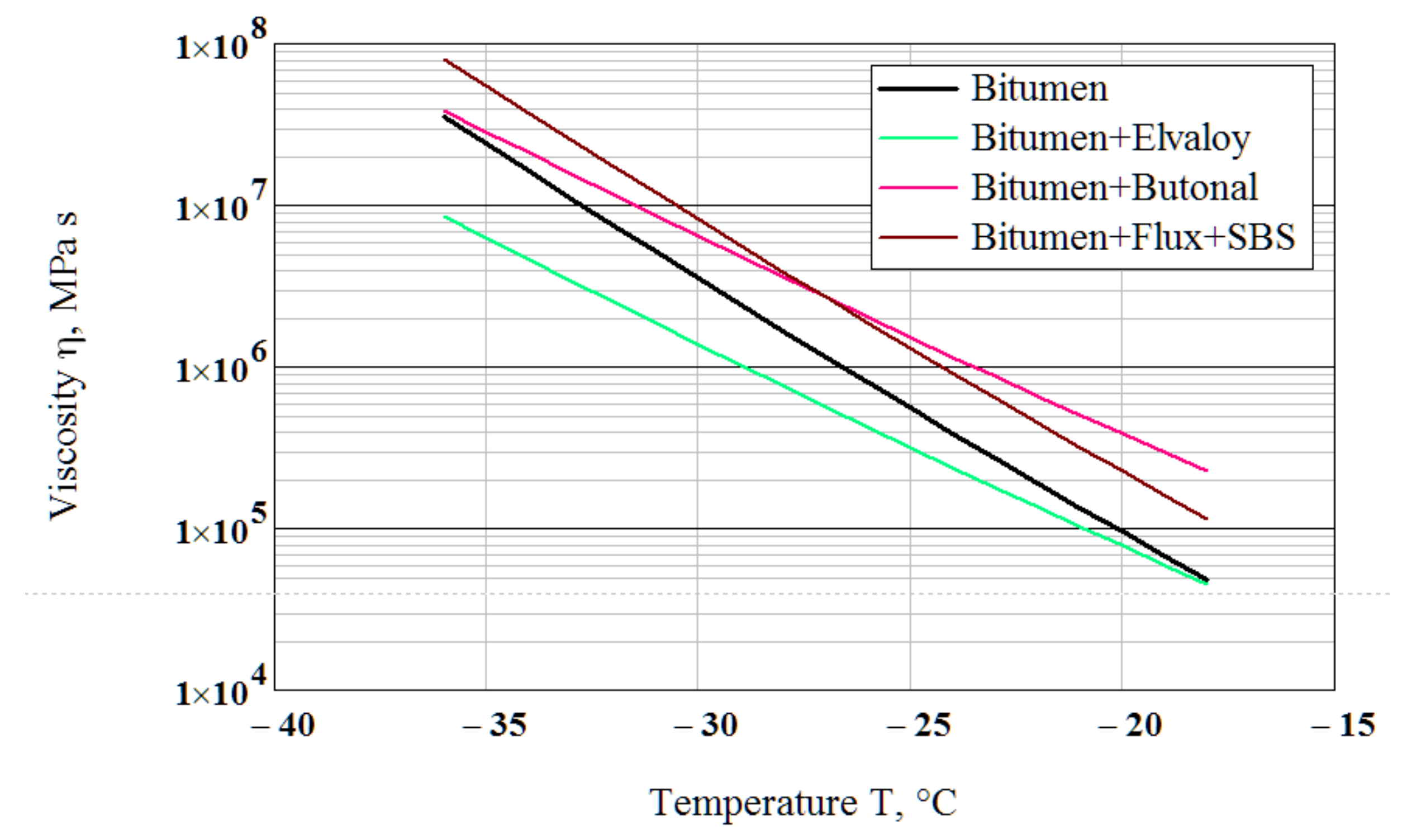
4.1. Stiffness and Viscosity
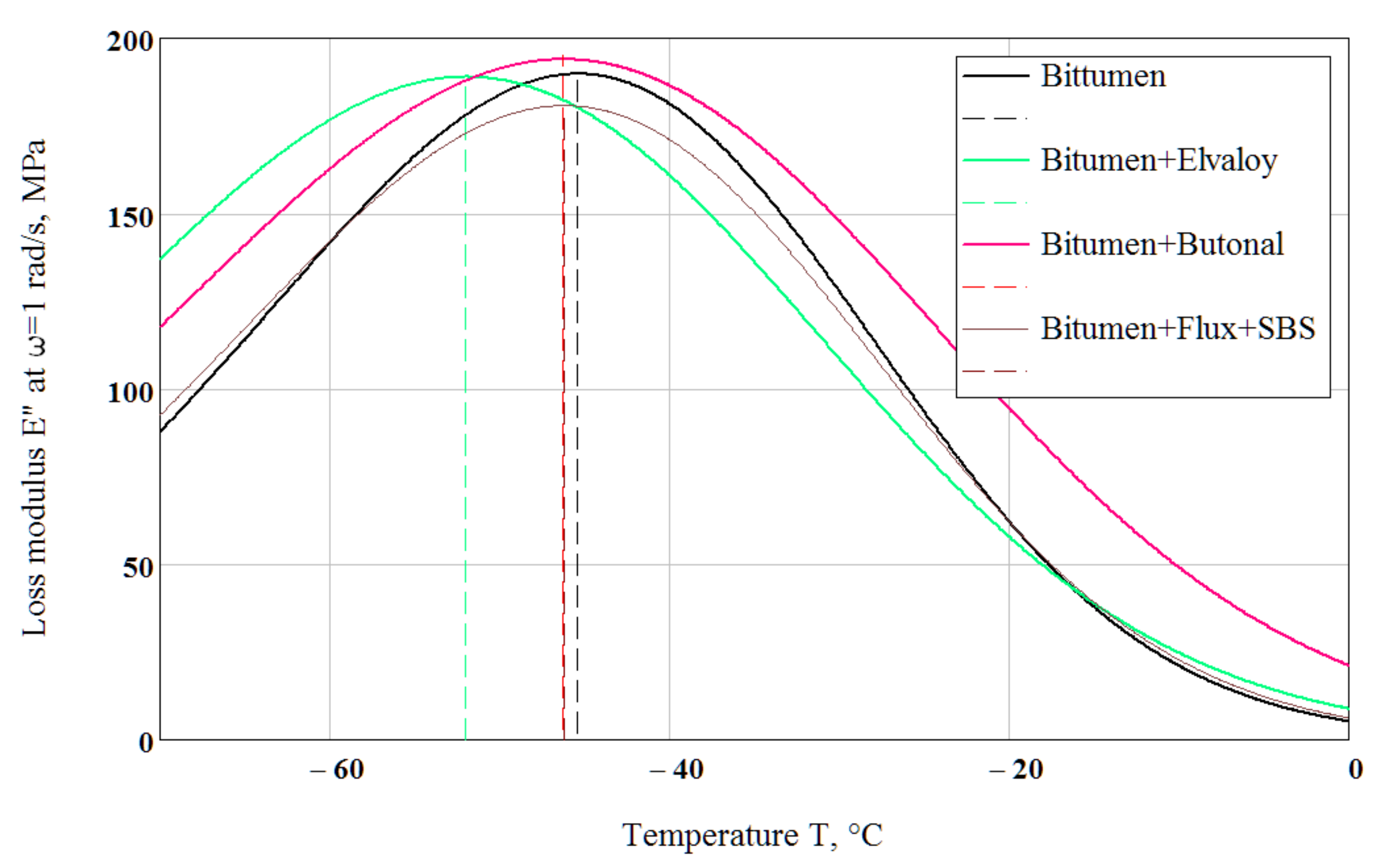
4.2. Glass Transition Temperature in Terms of Loss Modulus
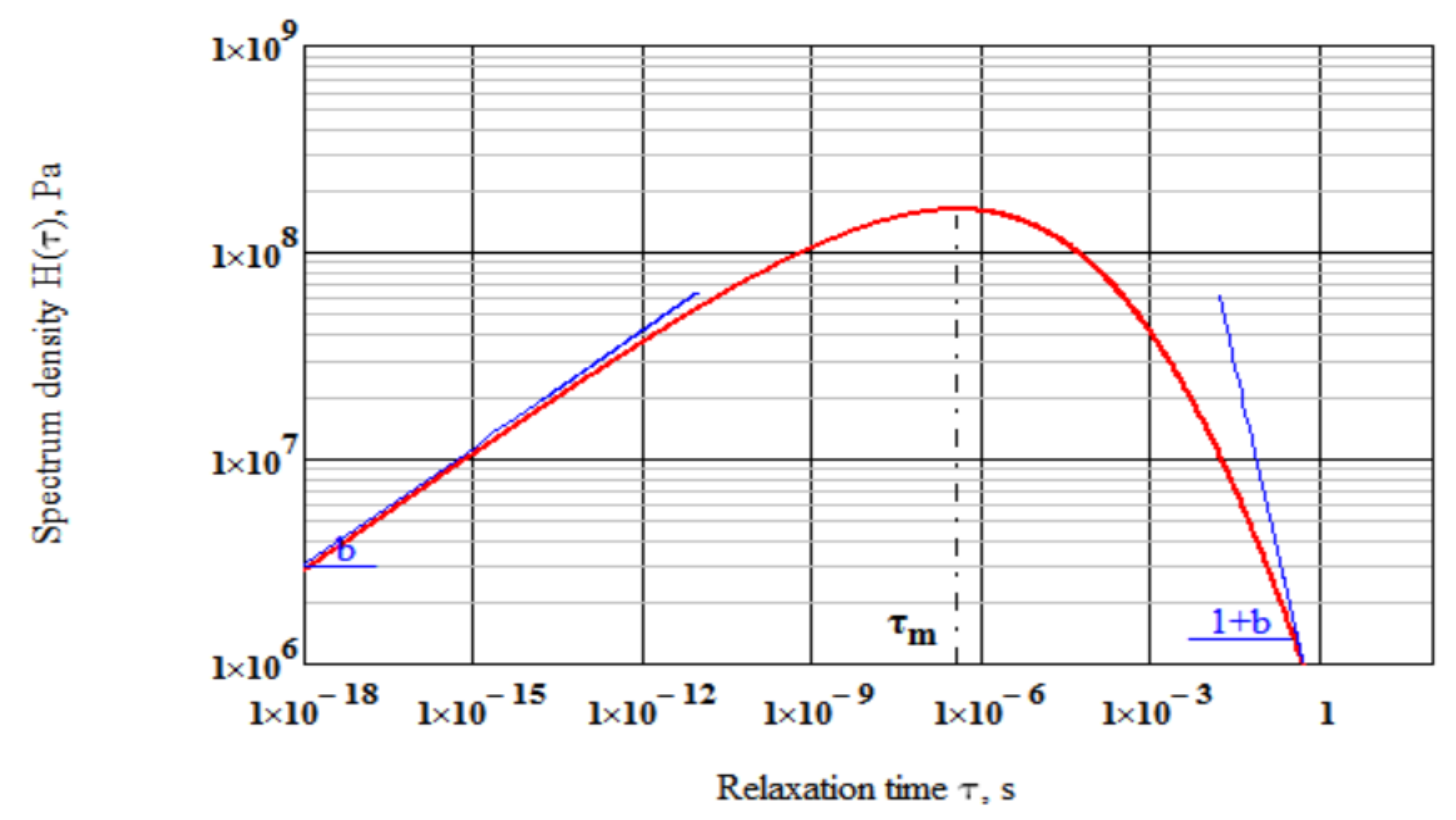
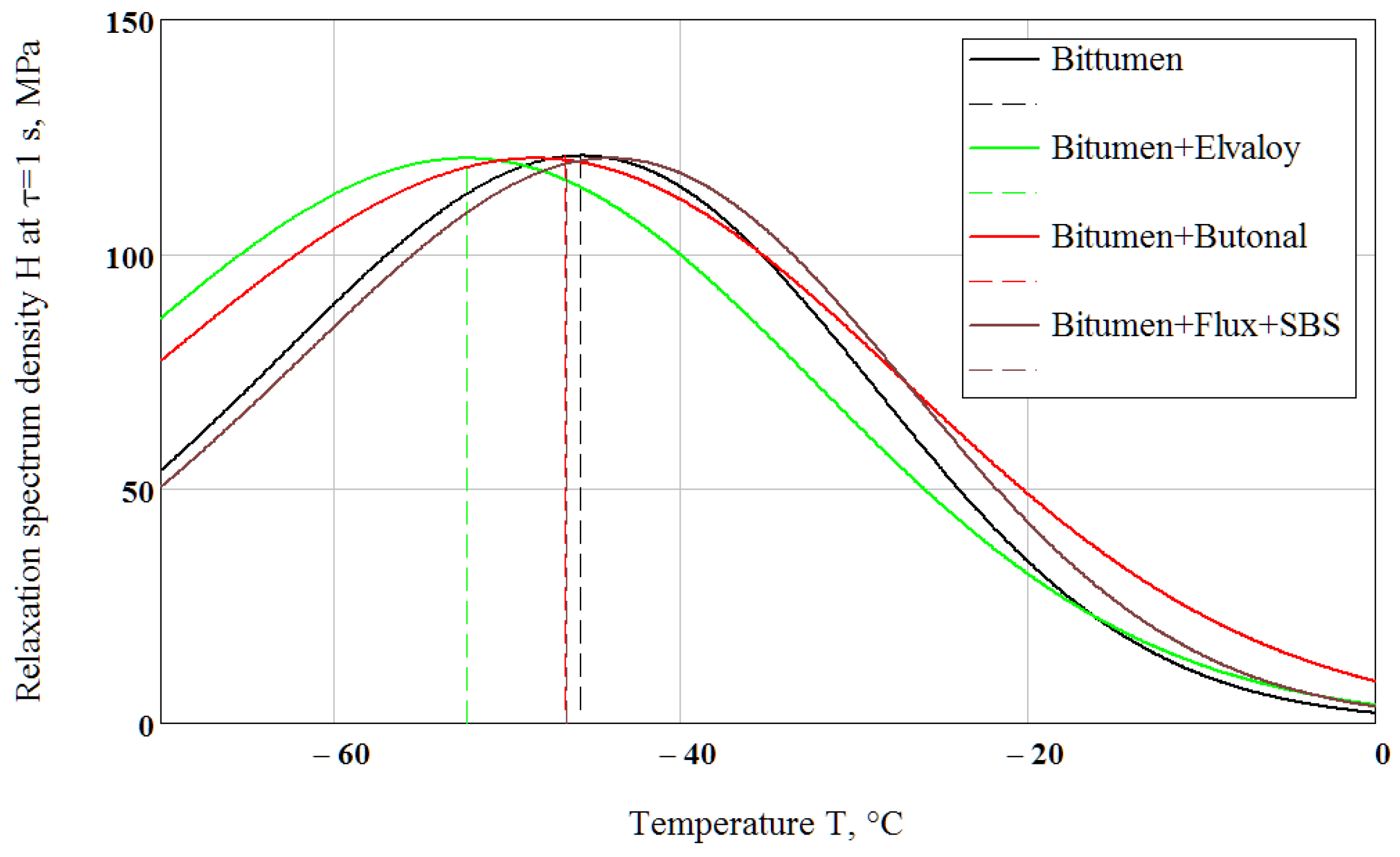
4.3. Glass Transition Temperature in Terms of Relaxation Time Spectrum
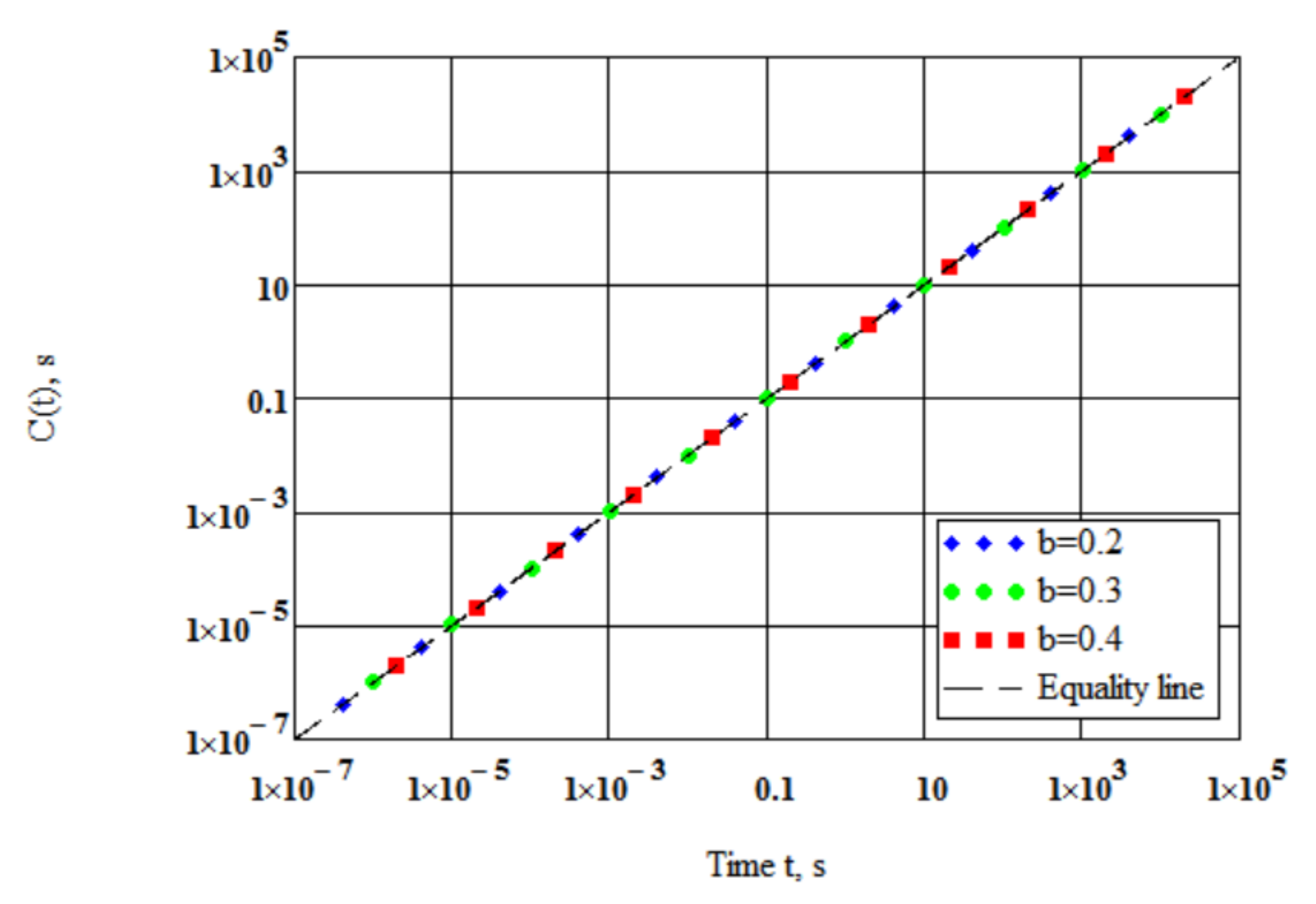
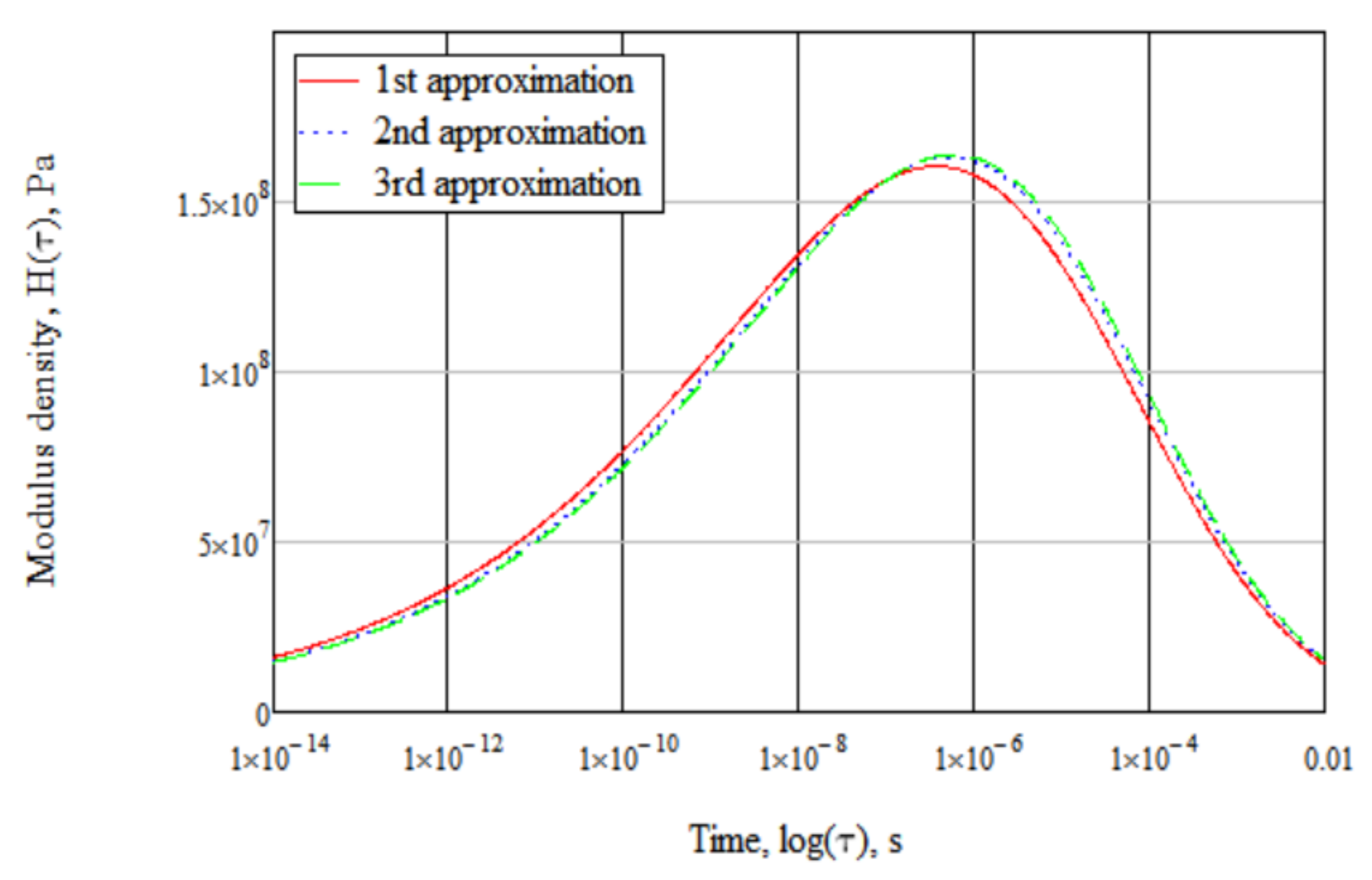
4.3.1. Interrelations between Loss Modulus and Relaxation Spectrum
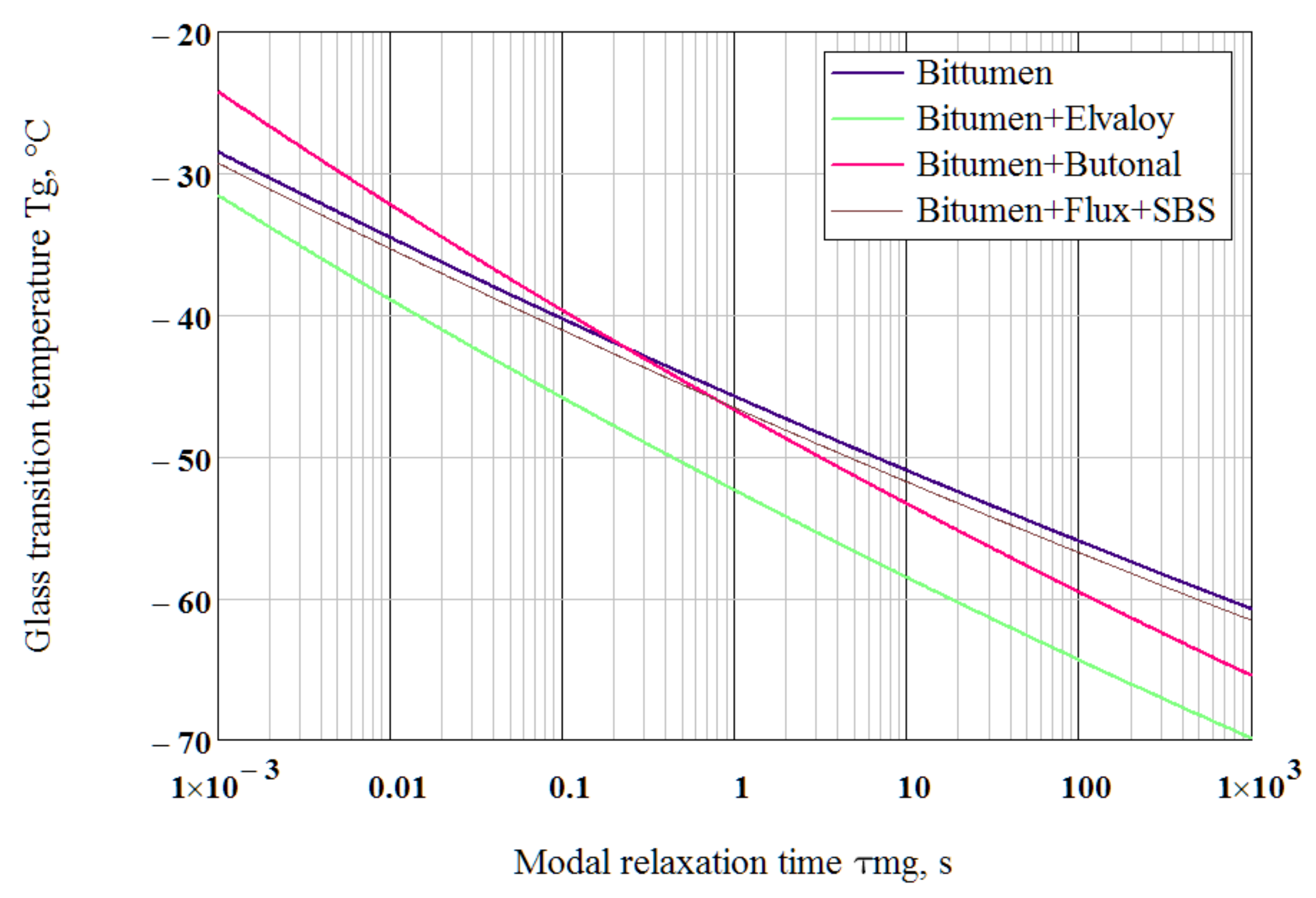
4.3.2. Glass Transition Temperature
5. Conclusions
- An approximate interrelation between a loss modulus and a relaxation–time spectrum was presented.
- The glass transition temperature of binders was calculated by the presented rheological method in terms of the relaxation–time spectrum. Calculations by this method showed that: (1) modification of bitumen with 3% Butanol NS 198 that primarily aims to improve the high-temperature properties does not show a positive effect at subzero temperatures compared with the base pure bitumen; modification of bitumen with 1.4% Elvaloy 4170, which is primarily intended to enhance the high-temperature properties, also improved the low-temperature properties; modification with Elvaloy lowered the temperature susceptibility of binder, lowered the low-temperature viscosity and lowered the glass transition temperature by about six degrees (from −45.4 °C to −52.0 °C).
- The proposed model for stiffness modulus (Equation (1)) enables the estimation of the viscosity of the binder at low temperature indirectly from conventional BBR testing. Viscosity values at temperature −30 °C were 3.520 × 106 MPa∙s for the oxidized bitumen of penetration grade 100/130, 1.374 × 106 MPa∙s for the bitumen modified by the polymer Elvaloy, 6.411 × 106 MPa∙s for the bitumen modified by the polymer Butanol and 8.143 × 106 MPa∙s for the bitumen compounded by flux and modified by the polymer SBS. The temperature susceptibility of the Elvaloy- and Butanol-modified binders was lower than for the neat bitumen and the flux compounded and SBS modified bitumen.
- In order to determine the optimal content of polymers in bitumens, it is recommended to continue the study of their rheological and other characteristics in the future by varying the technological conditions of modification.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Walkering, C.P.; Vonk, W.C.; Whiteoak, C.D. Improved Asphalt Properties Using SBS modified Bitumens. Shell Bitum. Rev. 1992, 66, 9–11. [Google Scholar]
- Lu, X.; Isacsson, U.; Ecblad, J. Influence of polymer modification on low temperature behavior of bituminous binders and mixtures. In Proceedings of the 6th RILEM Symposium PTEBM’03, Zurich, Switzerland, 14–16 April 2003; pp. 435–441. [Google Scholar]
- Abdelaziz, A.; Ho, C.-H.; Snyder, M. Evaluating the influence of polymer-modified asphalt binders on low temperature properties. MATEC Web Conf. 2018, 163, 05012. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Wang, H.; You, Z.; Gao, J.; Irfan, M. Performance test on Styrene-Butadiene-Styrene (SBS) modified asphalt based on the different evaluation methods. Appl. Sci. 2019, 9, 467. [Google Scholar] [CrossRef] [Green Version]
- Peng, G. Study on high and low temperature properties of SBS modified asphalt with fasir. In Proceedings of the 2016 4th International Conference on Mechanical Materials and Manufacturing Engineering; Atlantis Press: Paris, France, 2016; pp. 490–492. [Google Scholar]
- Lu, X.; Isacsson, U.; Ekblad, J. Influence of polymer modification on low temperature behavior of bituminous binder sand mixtures. Mater. Struc. 2003, 36, 652–656. [Google Scholar] [CrossRef]
- Hesp, S.A.M.; Terlouw, T.; Vonk, W.C. Low temperature performance of SBS-modified asphalt mixes. J. Assoc. Asph. Paving Technol. 2000, 69, 540–574. [Google Scholar]
- Fromm, H.J.; Phang, W.A. A study of transverse cracking of bituminous pavements. J. Assoc. Asph. Paving Technol. 1972, 41, 383–423. [Google Scholar]
- McLeod, N.W. A 4-year survey of low temperature transverse pavement cracking on three Ontario test roads. J. Assoc. Asph. Paving Technol. 1972, 41, 424–493. [Google Scholar]
- Kandhal, P.S. Low-Temperature Ductility in Relation to Pavement Performance; ASTM International: West Conshohocken, PA, USA, 1977; Volume 628, pp. 95–106. [Google Scholar]
- Deme, I.J.; Young, F.D. Ste. Anne Test Road revisited twenty years later. Proceed. Canad. Techn. Asph. Assoc. 1987, 32, 254–283. [Google Scholar]
- Bouldin, M.G.; Dongre, R.N.; Rowe, G.M.; Sharrock, M.J.; Anderson, D.A. Predicting thermal cracking of pavements from binder properties: Theoretical basis and field validation. J. Assoc. Asph. Paving Technol. 2000, 69, 455–496. [Google Scholar]
- Vander Poel, C. A general system describing the viscoelastic properties of bitumen and its relation to routine test data. J. Appl. Chem. 1954, 4, 221–236. [Google Scholar] [CrossRef]
- Di Benedetto, H.; Olard, F.; Sauzeat, C.; Delaporte, B. Linear viscoelastic behavior of bituminous materials: From binders to mixes. Road Mat. Pavemement Des. 2004, 5, 163–202. [Google Scholar] [CrossRef]
- Secor, K.E.; Monismith, C.L. Analysis and interrelation of stress-strain-time data for asphalt concrete. Transact. Soc. Rheol. 1964, 8, 19–32. [Google Scholar] [CrossRef]
- Heukelom, W. Observations on the rheology and fracture of bitumens and asphalt mixes. J. Assoc. Asph. Paving Technol. 1966, 35, 358–399. [Google Scholar]
- Vinogradov, G.V.; Isayev, A.I.; Zolotarev, V.A.; Verebskaya, E.A. Rheological properties of road bitumens. Rheol. Acta 1977, 16, 266–281. [Google Scholar] [CrossRef]
- Jongepier, R.; Kuilman, B. Characteristics of the rheology of bitumens. J. Assoc. Asph. Paving Technol. 1969, 38, 98–122. [Google Scholar]
- Christensen, D.W.; Anderson, D.A. Interpretation of dynamic mechanical test data for paving grade asphalt cements. J. Assoc. Asph. Paving Technol. 1992, 61, 67–116. [Google Scholar]
- Airey, G.D. Rheological Characteristics of Polymer Modified and Aged Bitumens. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 1997. [Google Scholar]
- Monismith, C.L.; Secor, G.A.; Secor, K.E. Temperature induced stresses and deformations in asphalt concrete. J. Assoc. Asph. Paving Technol. 1965, 34, 248–285. [Google Scholar]
- Christison, J.T.; Murray, D.W.; Anderson, K.O. Stress prediction and low temperature fracture susceptibility of asphaltic concrete pavements. J. Assoc. Asph. Paving Technol. 1972, 41, 494–523. [Google Scholar]
- Teltayev, B. Evaluation of low temperature cracking indicators of hot mix asphalt pavement. Int. J. Pavem. Resear. Technol. 2014, 5, 343–351. [Google Scholar]
- Teltayev, B.; Radovskiy, B. Predicting thermal cracking of asphalt pavements from bitumen and mix properties. Road Mater. Pav. Des. 2018, 19, 1832–1847. [Google Scholar] [CrossRef]
- Marasteanu, M.; Buttlar, W.; Bahia, H.; Williams, C.; Moon, K.H.; Teshale, E.Z.; Falchetto, A.C.; Turos, M.; Dave, E.; Paulino, G.; et al. Investigation of Low Temperature Cracking in Asphalt Pavements, National Pooled Fund Study–Phase II 2012; University of Wisconsin-Madison: Madison, WI, USA, 2012; 323p. [Google Scholar]
- Farar, M.J.; Hajj, E.Y.; Planche, J.P.; Alavi, M.Z. A method to estimate the thermal stress build-up in an asphalt mixture from a single-cooling event, Road Mater. Pav. Des. 2013, 14, 201–211. [Google Scholar]
- Wang, T.; Xiao, F.; Amirkhanian, S.; Zheng, M. A review on low temperature performances of rubberized asphalt materials. Constr. Build. Mater. 2017, 145, 483–505. [Google Scholar] [CrossRef]
- Shields, D.H.; Zeng, M.; Kwok, R. Nonlinear Viscoelastic Behavior of Asphalt Concrete in Stress Relaxation. J. Assoc. Asph. Paving Technol. 1998, 67, 358–385. [Google Scholar]
- Cheung, C.Y.; Cebon, D. Experimental study of pure bitumens in tension, compression, and shear. J. Rheol. 1997, 41, 45–73. [Google Scholar] [CrossRef]
- Stock, A.F.; Arand, W. Low Temperature Cracking in Polymer Modified Binder. J. Assoc. Asph. Paving Technol. 1993, 62, 23–53. [Google Scholar]
- Olard, F.; Di Benedetto, H.; Eckmann, B.; Vaniscote, J.-C. Low-temperature failure behavior of bituminous binder sand mixes. In Proceedings of the Soft, The 3rd Euro Mitumen and Euro Asphalt Congress, Vienne, Austria, 12–14 May 2004; pp. 1476–1490. [Google Scholar]
- Molenaar, A.A.A.; Li, N. Prediction of compressive and tensile strength of asphalt concrete. Inter. J. Pav. Res. Technol. 2014, 7, 324–331. [Google Scholar]
- Anderson, M.; King, G.; Hanson, D.; Blankenship, P. Evaluation of the relationship between asphalt binder properties and non-load related cracking. J. Assoc. Asph. Paving Technol. 2011, 80, 615–649. [Google Scholar]
- Glover, C.J.; Davison, R.R.; Domke, C.H.; Ruan, Y.; Juristyarini, P.; Knorr, D.B.; Jung, S.H. Development of a New Method for Assessing Asphalt Binder Durability with Field Validation; Report No. FHWA/TX-05/1872-2; Texas Transportation Institute: College Station, TX, USA, 2005. [Google Scholar]
- Rowe, G.M. Prepared Discussion presented in response to M. Anderson et al. J. Assoc. Asph. Paving Technol. 2011, 80, 649–663. [Google Scholar]
- Speight, J.G. The Chemistry and Technology of Petroleum, 4th ed.; Taylor & Francis Group: New York, NY, USA, 2007. [Google Scholar]
- Pink, H.S.; Merz, R.E.; Bosniack, D.S. Asphalt rheology: Experimental determination of dynamic moduli at low temperature. J. Assoc. Asph. Paving Technol. 1980, 49, 64–94. [Google Scholar]
- Goodrich, J.L. Asphalt and polymer modified asphalt properties related to the performance of asphalt concrete mixes. J. Assoc. Asph. Paving Technol. 1988, 57, 116–176. [Google Scholar]
- Schmidt, R.J.; Santucci, L.E. A practical method for determining the glass transition temperature of asphalt sand calculation of their low temperature viscosities. J. Assoc. Asph. Paving Technol. 1966, 35, 61–90. [Google Scholar]
- Bahia, H.U.; Anderson, D.A. Glass transition behavior and physical hardening of asphalt binders. J. Assoc. Asph. Paving Technol. 1993, 62, 93–129. [Google Scholar]
- Anderson, D.A.; Marasteanu, M.O.; Liu, Y. Dilatometric measurements of glass transition temperatures. In Proceedings of the Eurobitumen Workshop on Performance Related Properties for Bitumen Binder, Luxemburg, 3–6 May 1999. [Google Scholar]
- Kriz, P.; Stastna, J.; Zanzotto, L. Glass transition and phase stability in asphalt binders. Road Mater. Pav. Des. 2008, 9, 37–65. [Google Scholar] [CrossRef]
- Planche, J.-P.; Martin, D.; Claudy, P.; Letoffe, J.M.; Lesueur, D.; King, G.N. Evaluation of the low temperature properties of bituminous binders using calorimetry and rheology. In Proceedings of the Rheology of Bituminous Binders, European Workshop, Brussels, Belgium, 5–7 April 1995. [Google Scholar]
- Reinke, G.H.; Engber, S.L. Impact of factors affecting determination of glass transition temperature using a dynamic shear rheometer. J. Assoc. Asph. Paving Technol. 2001, 70, 483–493. [Google Scholar]
- Sun, Y.; Huang, B.; Edwin, G.; Chen, J.; Jia, X.; Ding, Y. Characterizing rheological behavior of asphalt binder over a complete range of pavement service loading frequency and temperature. Constr. Build. Mater. 2016, 123, 661–672. [Google Scholar] [CrossRef]
- Radovskiy, B.; Teltayev, B. Viscoelastic Properties of Asphalt Based on Penetration and Softening Point; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Teltayev, B.B.; Amirbayev, E.D.; Radovskiy, B.S. Viscoelastic characteristics of blown bitumen at low temperatures. Constr. Build. Mater. 2018, 189, 54–61. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley & Sons Inc.: New York, NY, USA, 1980. [Google Scholar]
- Schwarzl, F.R.L.; Struik, C.E. Analysis of relaxation measurements. Adv. Molec. Relax. Proc. 1968, 1, 201–255. [Google Scholar] [CrossRef]
- Koppelmann, J. Über die Bestimmung des dynamischen Elastizitätsmoduls und des dynamischen Schubmoduls im Frequenzbereich von 10−5 bis 10−1 Hz. Rheol. Acta. 1958, 1, 20–28. [Google Scholar] [CrossRef]
- Bernstein, S. Sur les fonctions absolument monotones. Acta Math. 1929, 52, 1–66. [Google Scholar] [CrossRef]
- Gross, B. Mathematical Structure of the Theories of Viscoelasticity; Herman net Cie: Paris, France, 1953. [Google Scholar]
- Widder, D.V. The Inversion of the Laplace Integral and the Related Moment Problem. Transact. Amer. Math. Soc. 1934, 36, 107–200. [Google Scholar] [CrossRef]
- Riande, E.; Diaz-Calleja, R.; Prolongo, M.; Masegosa, R.; Salom, C. Polymer Viscoelasticity: Stress and Strain in Practice; Marcel Dekker: New York, NY, USA, 2000. [Google Scholar]
- RRK218-80-2010; Recommendations for the Use of Elvaloy Polymer for the Modification of Bitumen and Asphalt Concrete. JSC Kazdor NII: Almaty, Kazakhstan, 2010.
- RRK218-93-2011; Recommendations for the Use of Butonal NS Modifier in Road Construction. JSC Kazdor NII: Almaty, Kazakhstan, 2011.
- Teltayev, B.; Seilkhanov, T.; Rossi, C.O.; Amirbayev, Y.; Begaliyeva, S. Low temperature resistance increase for bitumen by compounding with tar. Appl Sci. 2021, 11, 8579. [Google Scholar] [CrossRef]
- ASTM E1640-09; Standard Test Method for Assignment of the Glass Transition Temperature by Dynamic Mechanical Analysis. West Conshohocken: Montgomery, PA, USA, 2019.
- Anderson, D.A.; Marasteanu, M.O. Physical hardening of asphalt binders relative to their glass transition temperatures. Transp. Res. Rec. 1999, 1661, 27–34. [Google Scholar] [CrossRef]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press Ithaca: New York, NY, USA, 1979. [Google Scholar]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Speedy, R.J. The hard sphere glass transition. Mol. Phys. 1998, 95, 169–178. [Google Scholar] [CrossRef]


| Property | Standard | Bitumen | Bitumen Modified by | ||
|---|---|---|---|---|---|
| Elvaloy | Butanol | Flux + SBS | |||
| Penetration, 25 °C (0.1 mm) | ASTM D5 | 103 | 86 | 88 | 73 |
| Penetration index PI | EN 12591 | −0.70 | - | - | - |
| Ductility (cm), 25 °C (cm) | ASTM D113 | >150 | 32 | 63 | 70 |
| Softening point (°C) | ASTM D36 | 45.0 | 62.5 | 62.0 | 76.5 |
| Fraass breaking point (°C) | EN 12593 | −26.4 | −25.8 | −25.4 | −23.0 |
| Flash point (°C) | ASTM D92 | 265 | 250 | 265 | - |
| Dynamic viscosity, 60 °C (Pa·s) | ASTM D2171 | 167 | - | - | - |
| Kinematic viscosity, 135 °C (mm2/s) | ASTM D445 | 394 | - | - | - |
| Elastic recovery, 25 °C (%) | ASTM D6084 | - | 87 | 81 | 98 |
| Binder | at = −30 °C, MPa∙s | , J/mol | b |
|---|---|---|---|
| Bitumen | 3.520 × 106 | 1.847 × 105 | 0.1418 |
| Bitumen + Elvaloy | 1.374 × 106 | 1.468 × 105 | 0.1412 |
| Bitumen + Butanol | 6.411 × 106 | 1.437 × 105 | 0.1452 |
| Bitumen + Flux + SBS | 8.143 × 106 | 1.833 × 105 | 0.1346 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teltayev, B.; Amirbayev, E.; Radovskiy, B. Evaluating the Effect of Polymer Modification on the Low-Temperature Rheological Properties of Asphalt Binder. Polymers 2022, 14, 2548. https://doi.org/10.3390/polym14132548
Teltayev B, Amirbayev E, Radovskiy B. Evaluating the Effect of Polymer Modification on the Low-Temperature Rheological Properties of Asphalt Binder. Polymers. 2022; 14(13):2548. https://doi.org/10.3390/polym14132548
Chicago/Turabian StyleTeltayev, Bagdat, Erik Amirbayev, and Boris Radovskiy. 2022. "Evaluating the Effect of Polymer Modification on the Low-Temperature Rheological Properties of Asphalt Binder" Polymers 14, no. 13: 2548. https://doi.org/10.3390/polym14132548
APA StyleTeltayev, B., Amirbayev, E., & Radovskiy, B. (2022). Evaluating the Effect of Polymer Modification on the Low-Temperature Rheological Properties of Asphalt Binder. Polymers, 14(13), 2548. https://doi.org/10.3390/polym14132548







